Research on Nonlinear Coupling Anti-Swing Control Method of Double Pendulum Gantry Crane Based on Improved Energy
Abstract
1. Introduction
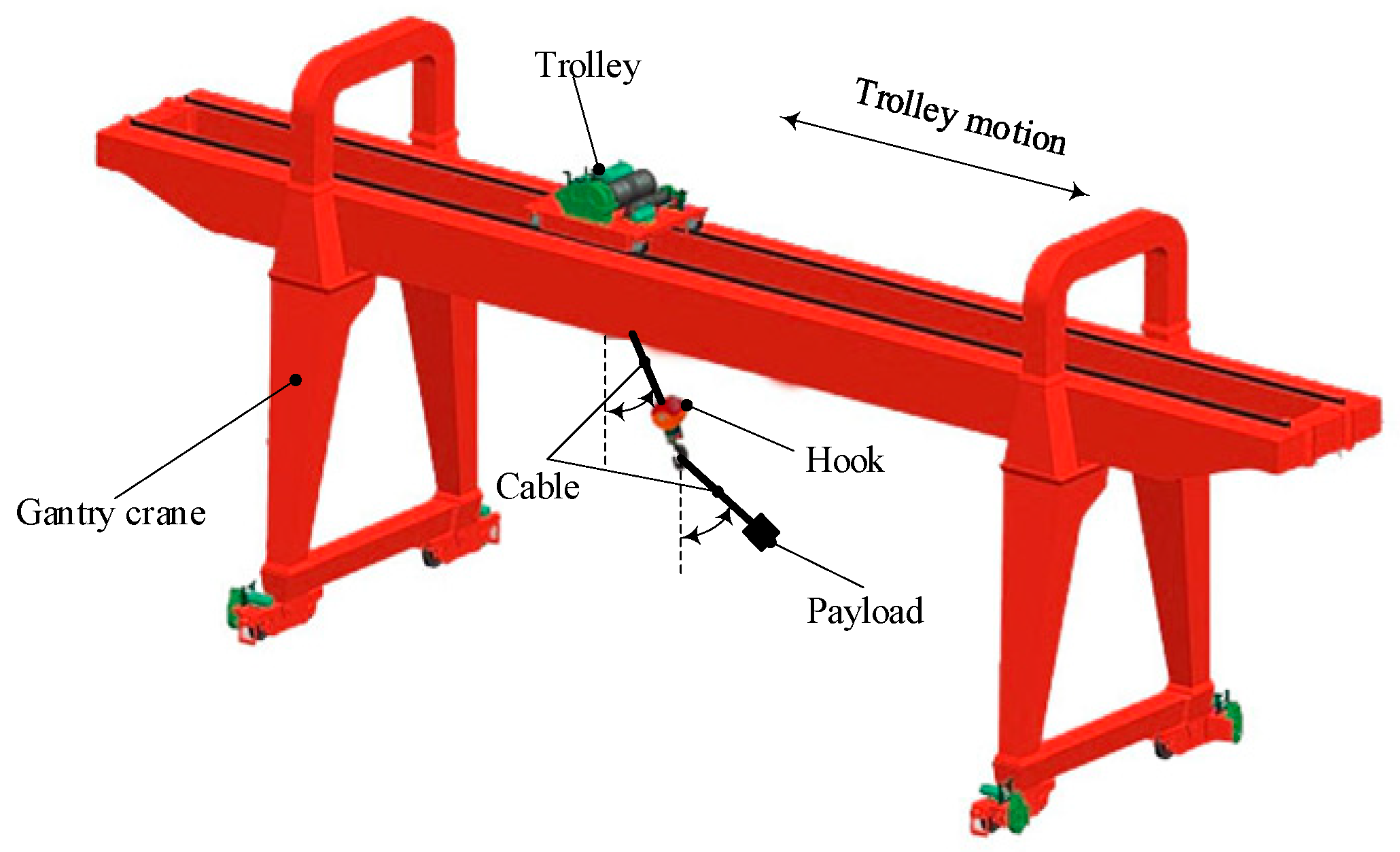
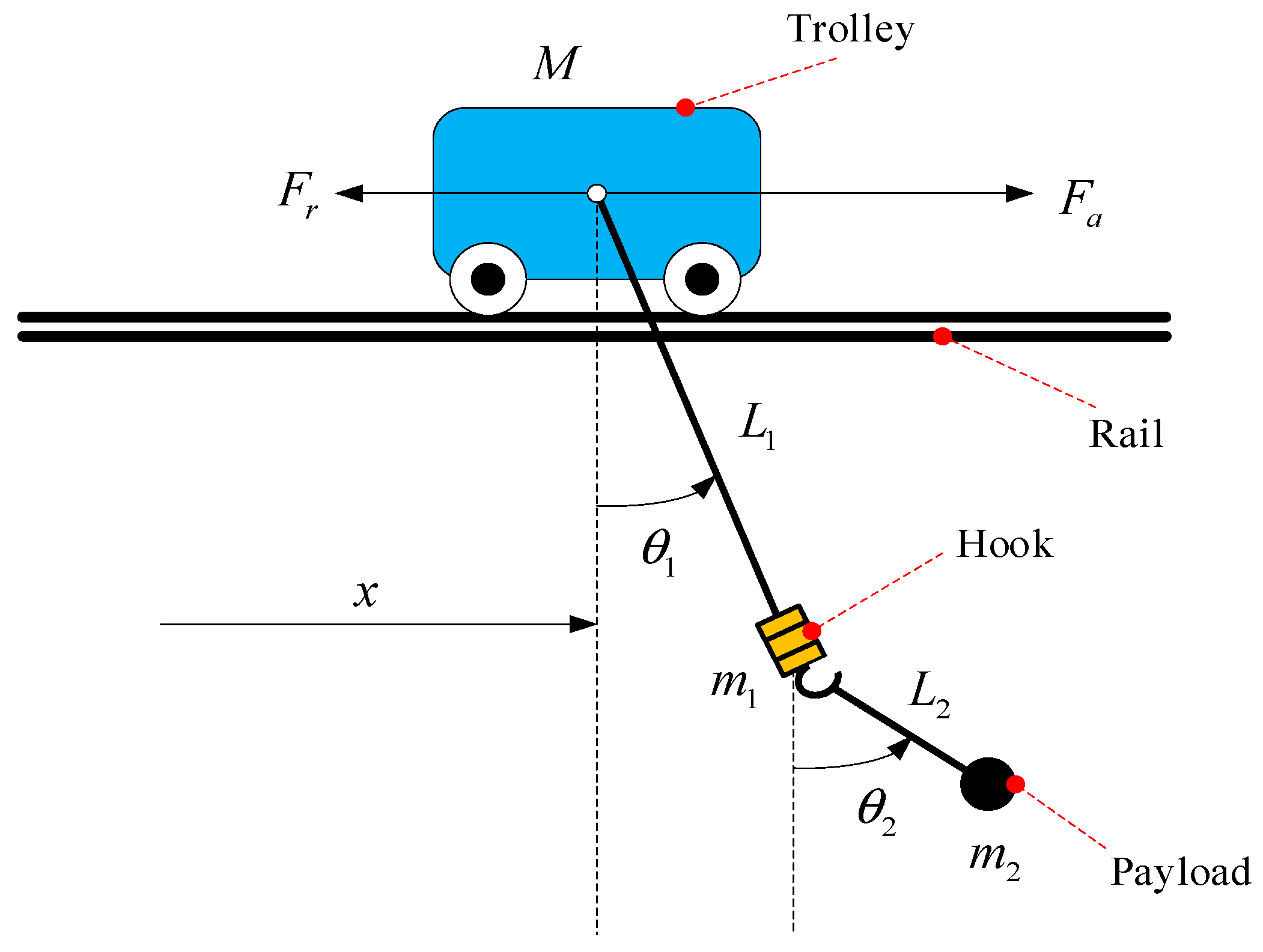
2. Dynamics of Gantry Crane with Double-Pendulum
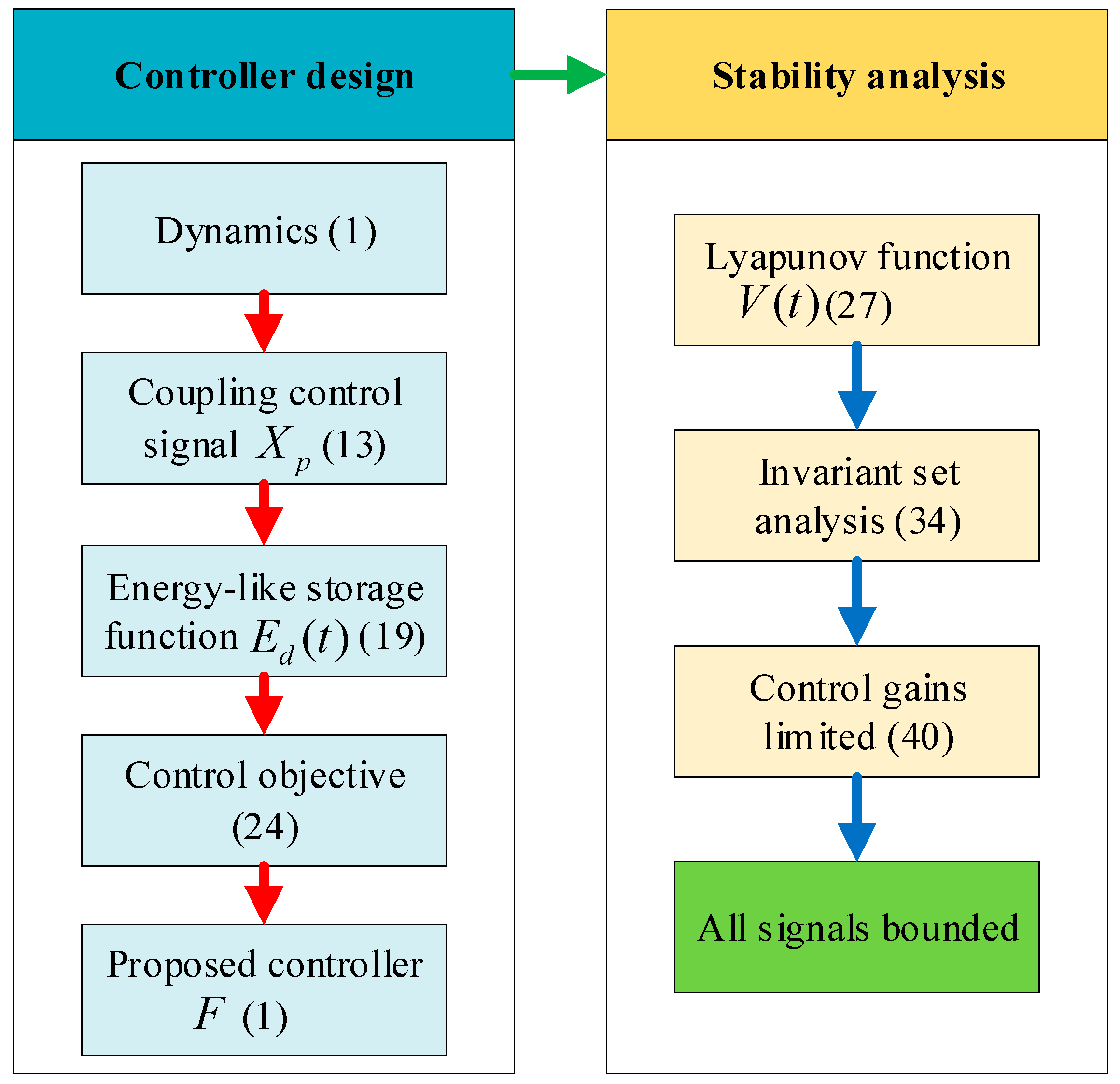
3. Main Results
3.1. Controller Design
3.2. Stability Analysis
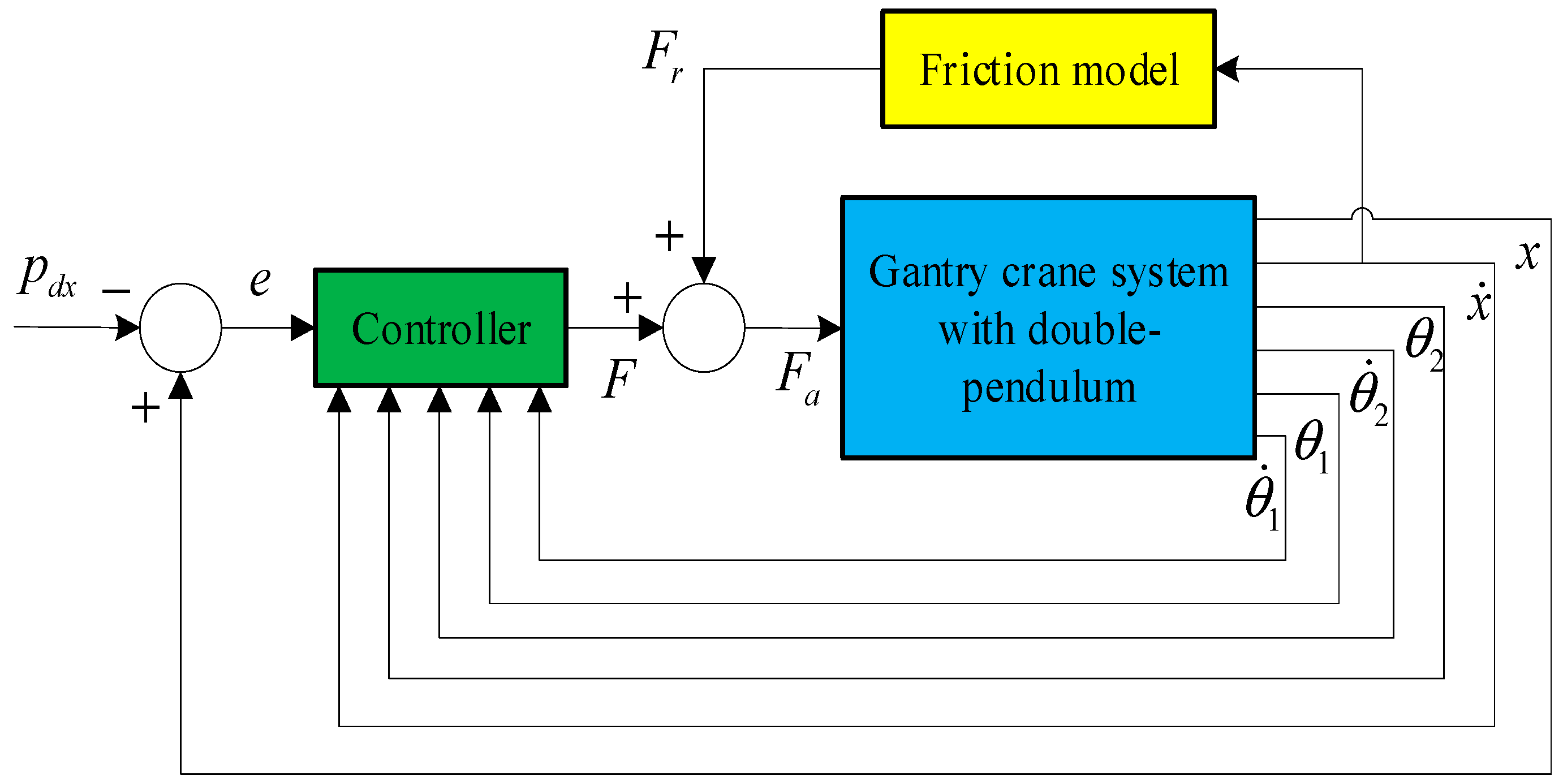
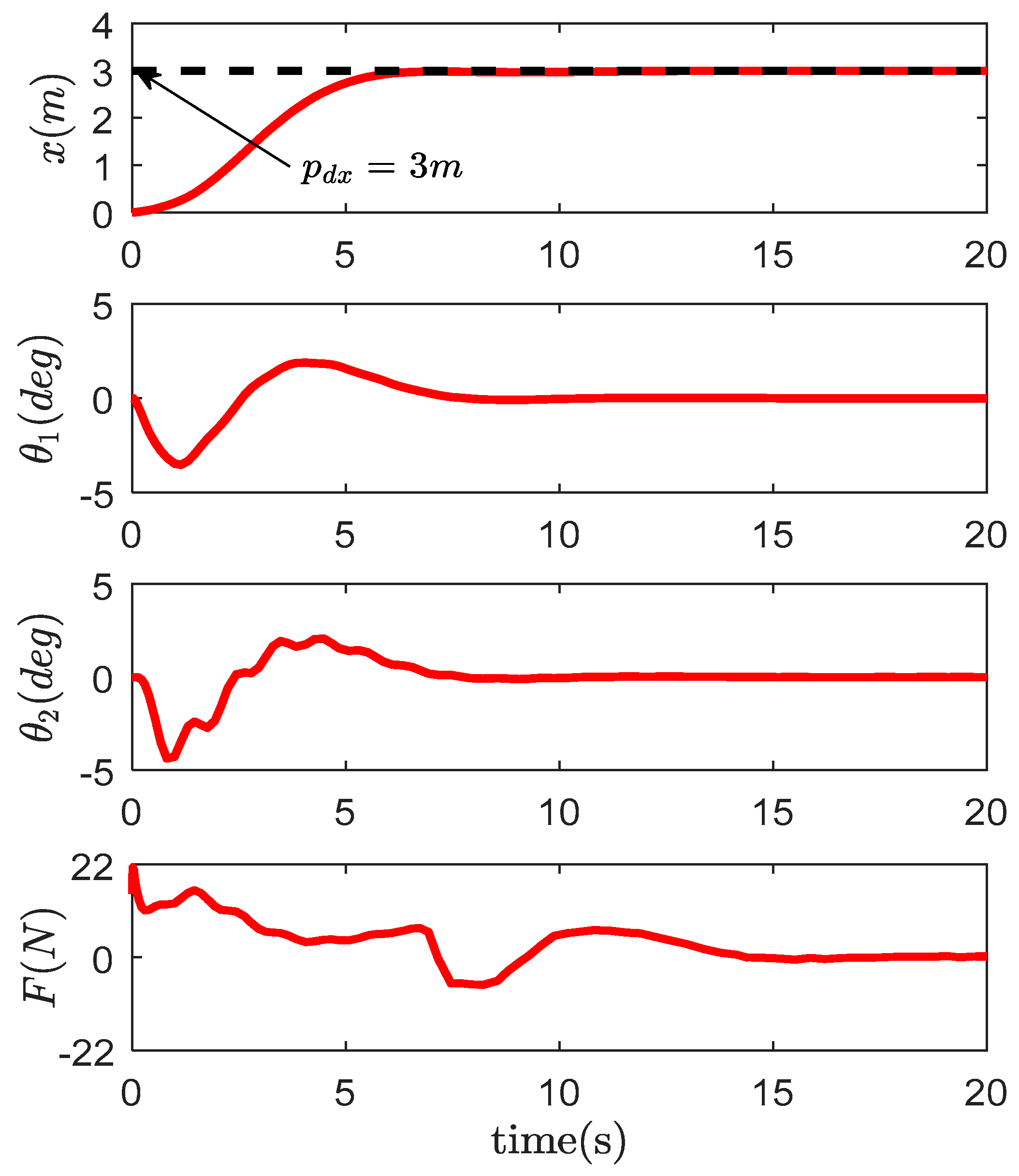
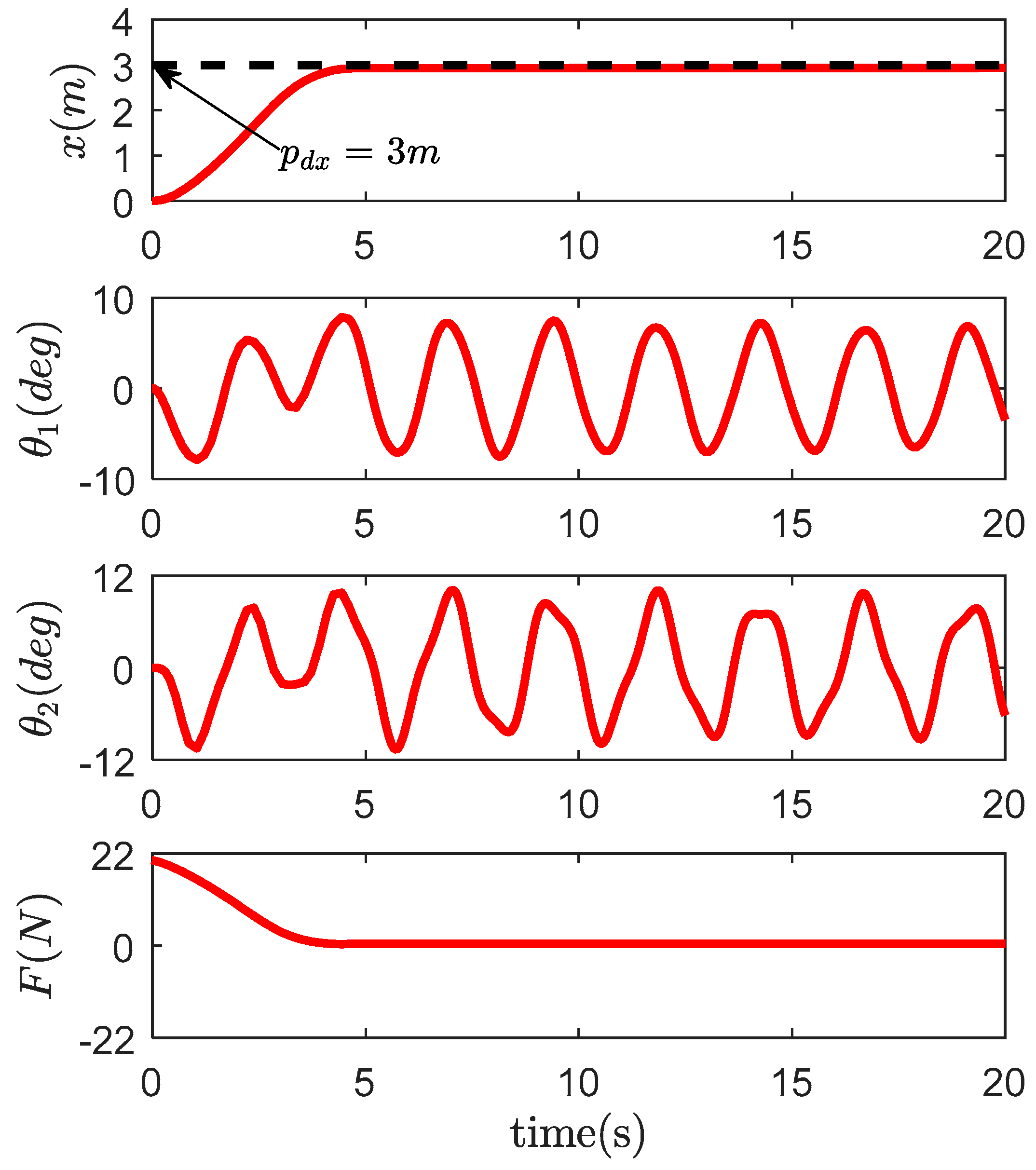
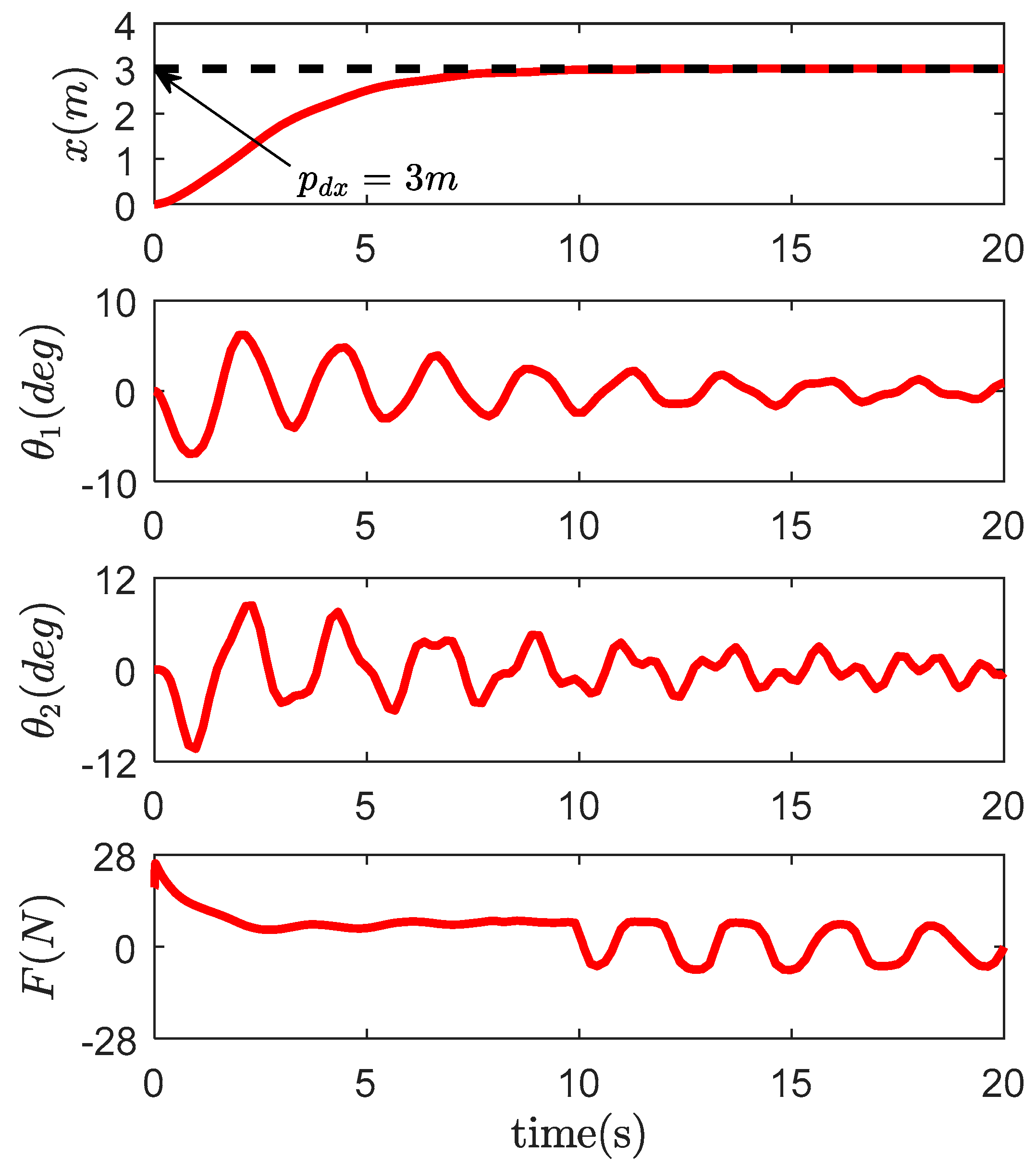
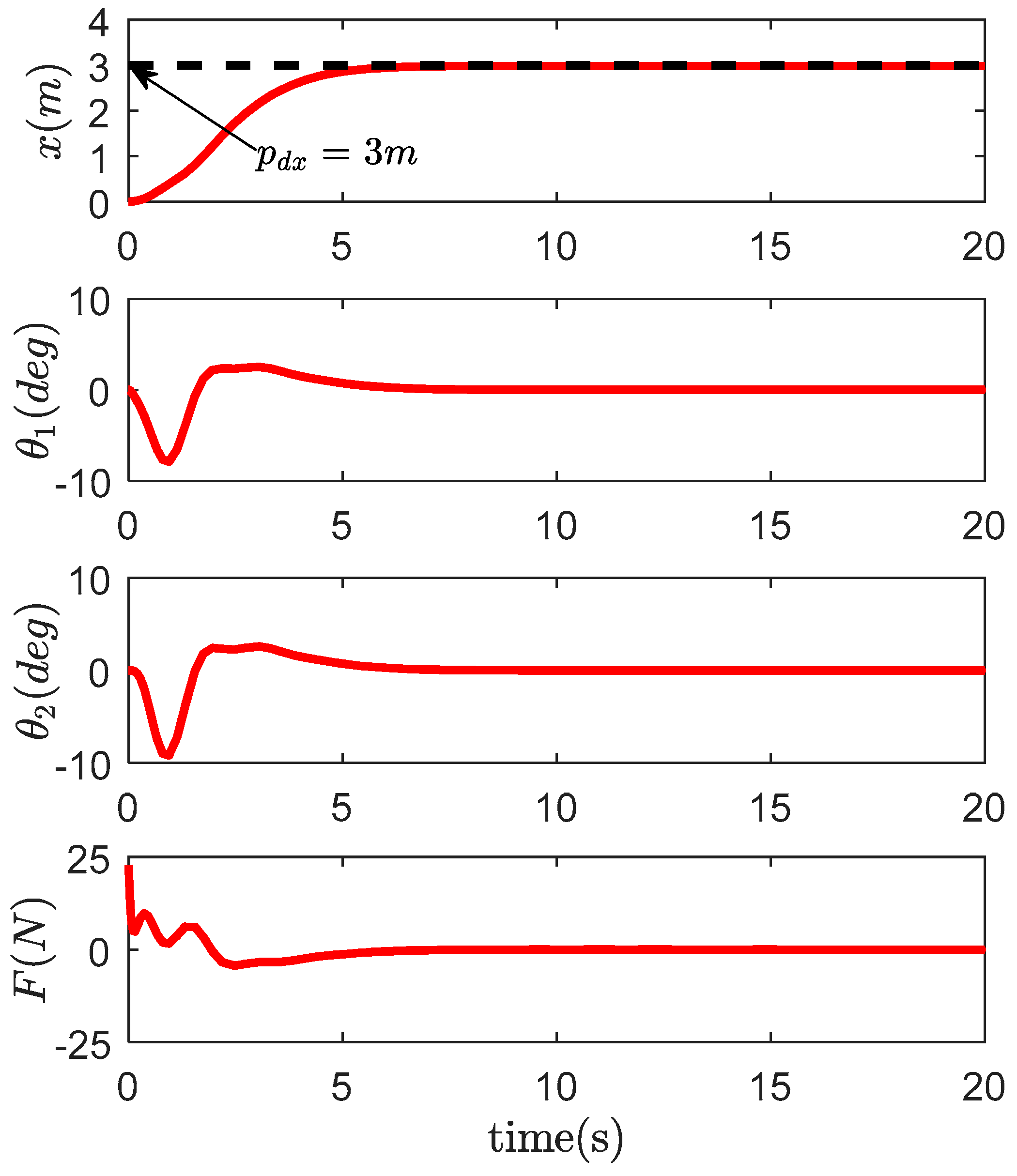
4. Simulation Results and Analysis
4.1. Comparative Study
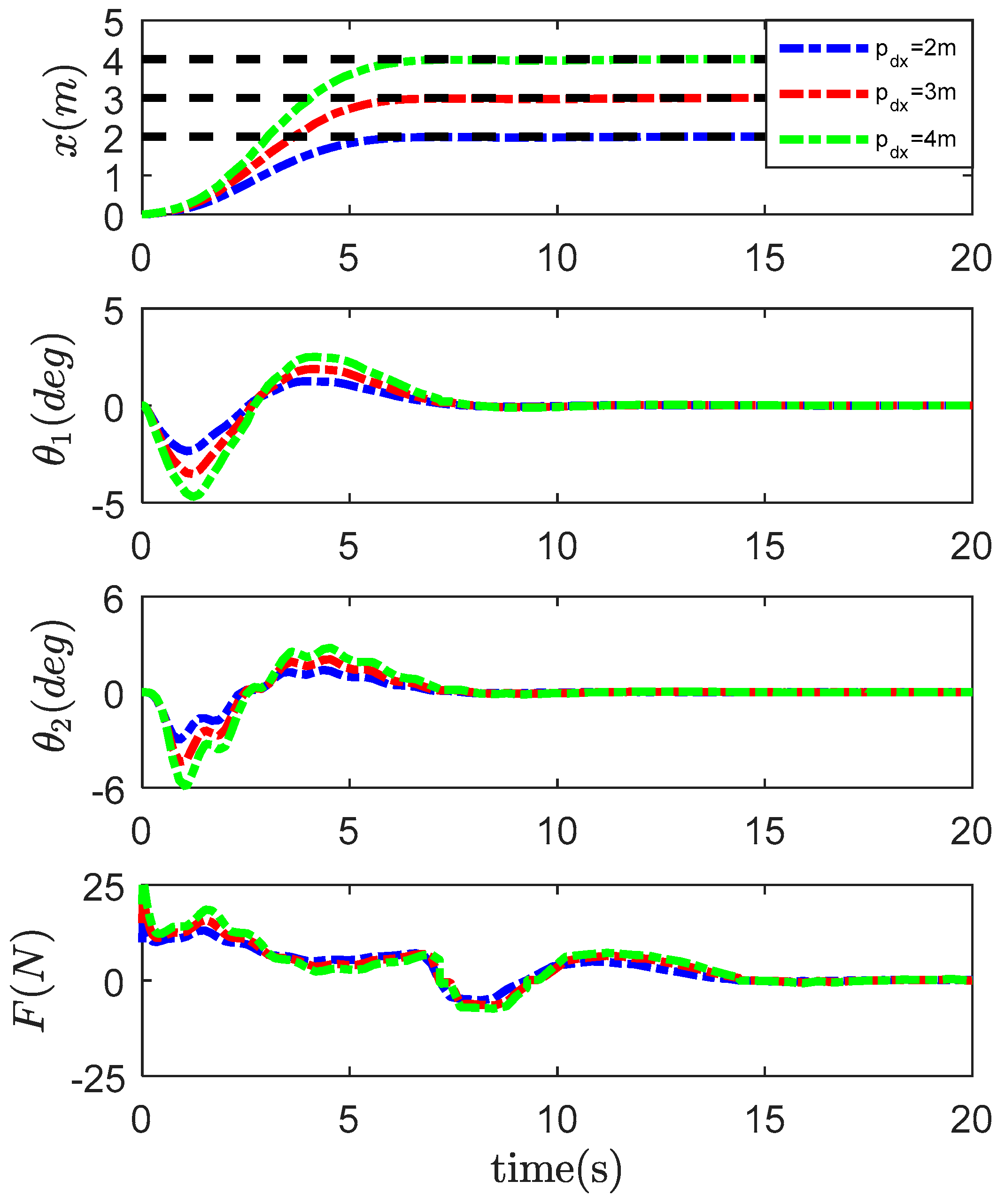
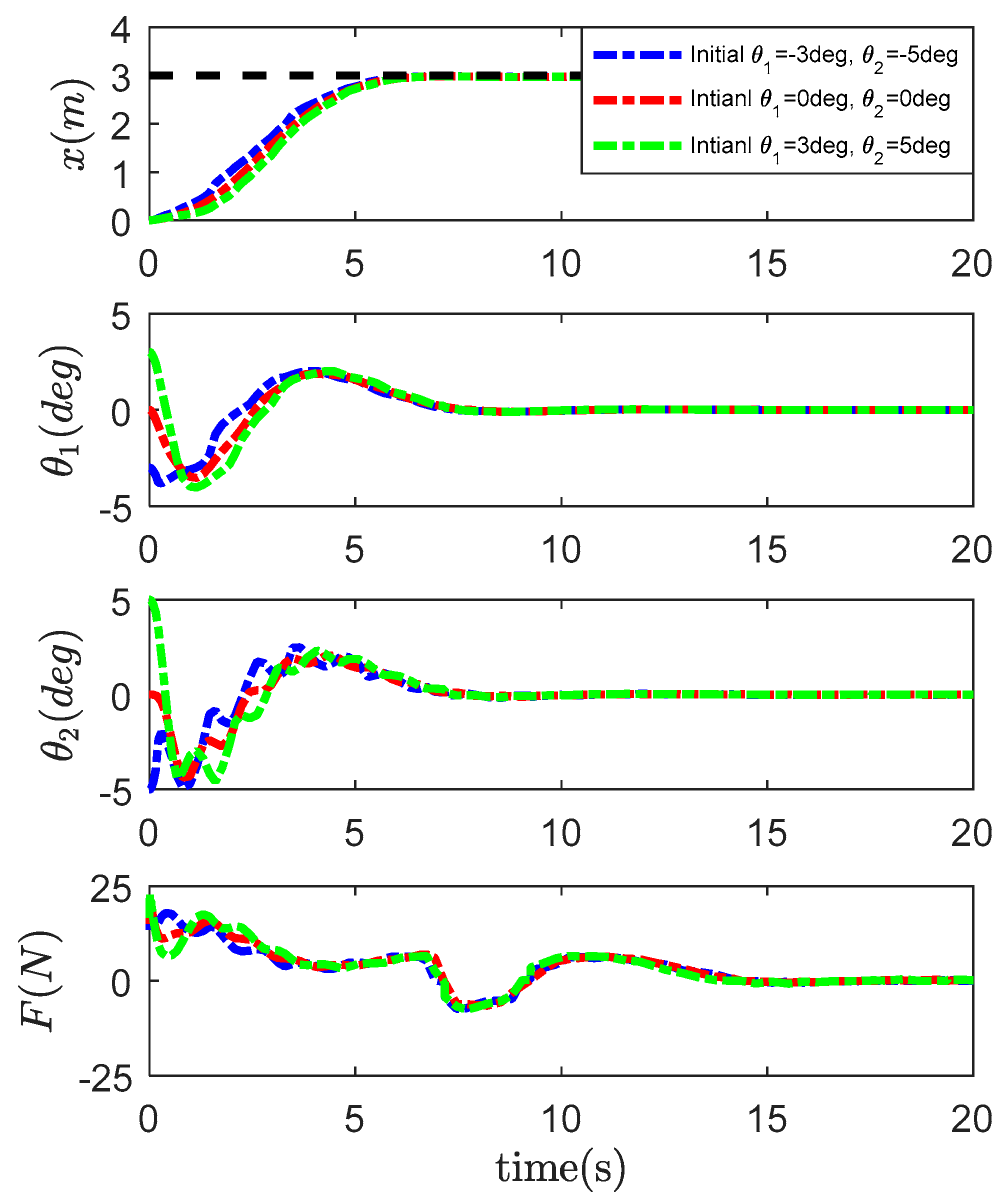
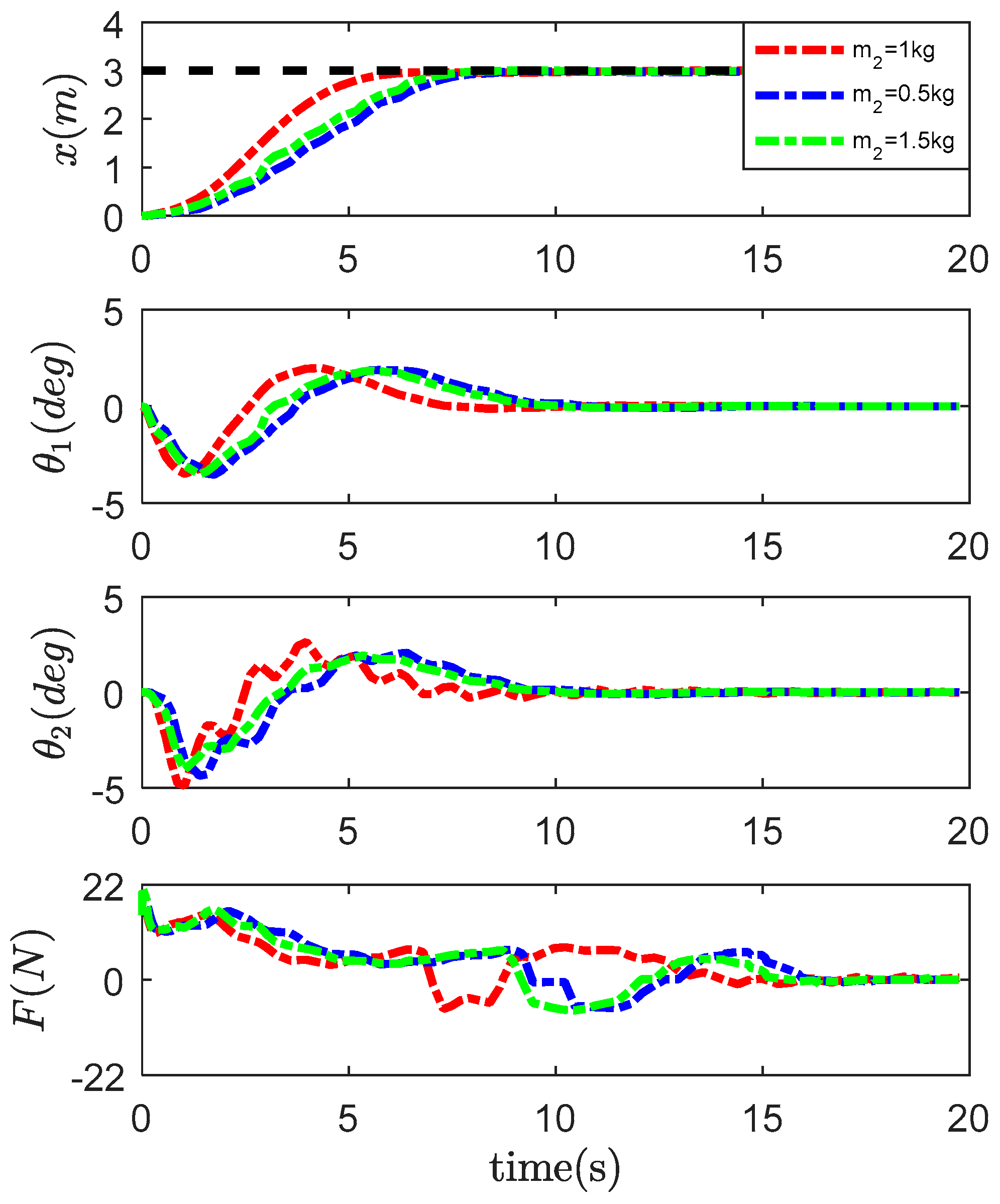
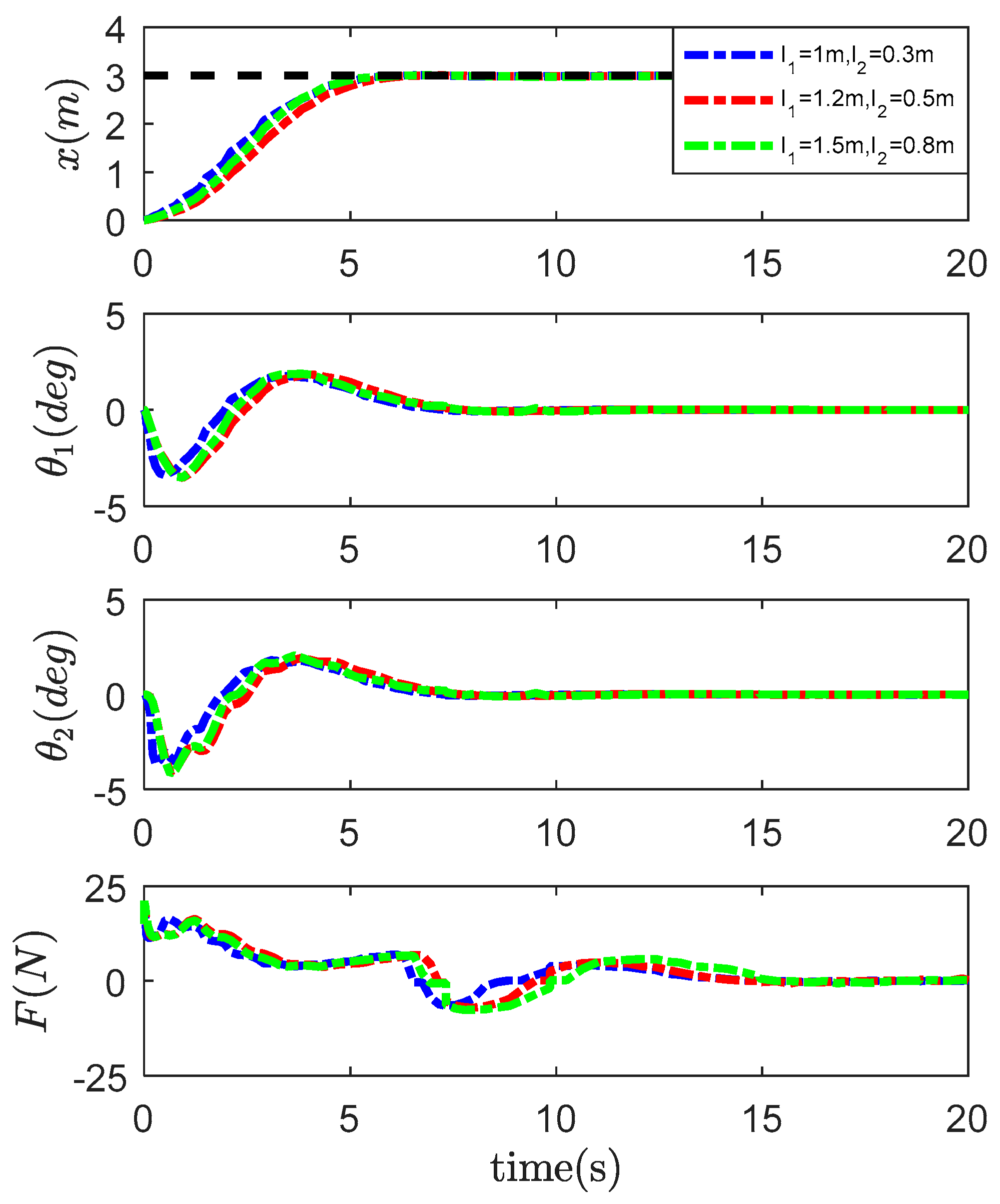
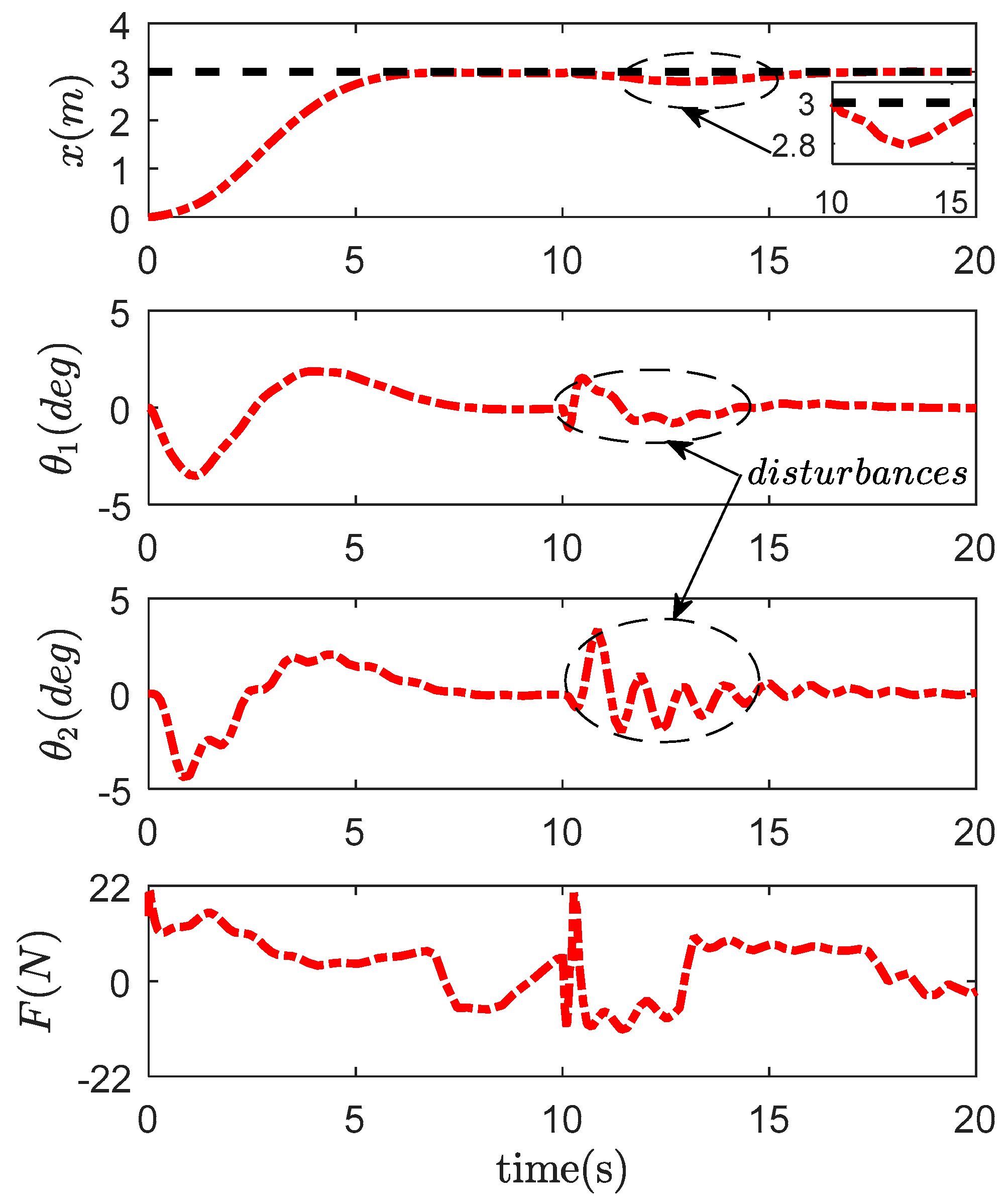
4.2. Robustness Verification
- m;
- m;
- m.
- Initial ;
- Initial ;
- Initial .
- kg;
- kg;
- kg.
- ;
- ;
- .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ramli, L.; Mohamed, Z.; Abdullahi, A.M.; Jaafar, H.I.; Lazim, I.M. Control Strategies for Crane Systems: A Comprehensive Review. Mech. Syst. Signal Process. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Sun, N.; Zhang, J.; Xin, X.; Yang, T.; Fang, Y. Nonlinear output feedback control of flexible rope crane systems with state constraints. IEEE Access 2019, 7, 136193–136202. [Google Scholar] [CrossRef]
- Shi, H.; Li, G.; Bai, X.; Huang, J. Research on Nonlinear Control Method of Underactuated Gantry Crane Based on Machine Vision Positioning. Symmetry 2019, 11, 987. [Google Scholar] [CrossRef]
- Thakar, P.S.; Bandyopadhyay, B.; Gandhi, P. Improved output-feedback second order sliding mode control design with implementation for underactuated slosh-container system having confined track length. IET Control Theory Appl. 2017, 11, 1316–1323. [Google Scholar]
- Paliotta, C.; Lefeber, E.; Pettersen, K.Y.; Pinto, J.; Coast, M.; de Sousa, J.T.d.B. Trajectory Tracking and Path Following for Underactuated Marine Vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 1423–1437. [Google Scholar] [CrossRef]
- Yang, C.; Luo, J.; Pan, Y.; Liu, Z.; Su, C.-Y. Personalized Variable Gain Control With Tremor Attenuation for Robot Teleoperation. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1759–1770. [Google Scholar] [CrossRef]
- Xu, B. Composite Learning Finite-Time Control with Application to Quadrotors. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1–10. [Google Scholar] [CrossRef]
- Li, F.; Zhang, C.; Sun, B. A Minimum-Time Motion Online Planning Method for Underactuated Overhead Crane Systems. IEEE Access. 2019, 7, 54586–54594. [Google Scholar] [CrossRef]
- Peng, H.; Shi, B.; Wang, X.; Li, C. Interval estimation and optimization for motion trajectory of overhead crane under uncertainty. Nonlinear Dyn. 2019, 96, 1693–1715. [Google Scholar] [CrossRef]
- Elharfi, A. Exponential stabilization and motion planning of an overhead crane system. IMA J. Math. Control Inf. 2017, 34, 1299–1321. [Google Scholar] [CrossRef]
- Blajer, W.; Kołodziejczyk, K. Control of underactuated mechanical systems with servo-constraints. Nonlinear Dyn. 2007, 50, 781–791. [Google Scholar] [CrossRef]
- Le, A.T.; Lee, S.G. 3D cooperative control of tower cranes using robust adaptive techniques. J. Frankl. Inst. 2017, 354, 8333–8357. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Mohamed, Z.H.; Selamat, H.R. Adaptive output-based command shaping for sway control of a 3D overhead crane with payload hoisting and wind disturbance. Mech. Syst. Signal. Process. 2018, 98, 157–172. [Google Scholar] [CrossRef]
- Sun, N.; Yang, T.; Chen, H. Adaptive Anti-Swing and Positioning Control for 4-DOF Rotary Cranes Subject to Uncertain/Unknown Parameters with Hardware Experiments. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1309–1321. [Google Scholar] [CrossRef]
- Liu, R.; Li, S.; Ding, S. Nested saturation control for overhead crane systems. Trans. Inst. Meas. Control 2012, 34, 862–875. [Google Scholar] [CrossRef]
- Wu, X.; He, X. Nonlinear Energy-Based Regulation Control of Three-Dimensional Overhead Cranes. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1297–1308. [Google Scholar] [CrossRef]
- Wei, H.; Shuzhi, S. Cooperative control of a nonuniform gantry crane with constrained tension. Automatica 2016, 66, 146–154. [Google Scholar]
- Sun, N.; Fang, Y.; Chen, H. Nonlinear Stabilizing Control for Ship-Mounted Cranes with Ship Roll and Heave Movements: Design, Analysis, and Experiments. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1781–1793. [Google Scholar] [CrossRef]
- Kolar, B.; Rams, H.; Schlacher, K. Time-Optimal flatness based control of a gantry crane. Control. Eng. Pract. 2017, 60, 18–27. [Google Scholar] [CrossRef]
- Golovin, I.; Palis, S. Robust control for active damping of elastic gantry crane vibrations. Mech. Syst. Signal. Process. 2019, 121, 264–278. [Google Scholar] [CrossRef]
- Cui, L.; Zheng, D. Visual Servoing of a Flexible Gantry Crane With a Sway Range Constraint. IEEE Control Syst. Lett. 2019, 3, 138–143. [Google Scholar] [CrossRef]
- Smoczek, J.; Szpytko, J. Particle Swarm Optimization-Based Multivariable Generalized Predictive Control for an Overhead Crane. IEEE/ASME Trans. Mechatron. 2016, 22, 258–268. [Google Scholar] [CrossRef]
- Mohamed, H.; Raafat, S.; Mostafa, S. A Hybrid Partial Feedback Linearization and Deadbeat Control Scheme for a Nonlinear Gantry Crane. J. Frankl. Inst. 2018, 355, 6286–6299. [Google Scholar]
- Zhou, Y.S.; Wang, Z.H. Robust motion control of a two-wheeled inverted pendulum with an input delay based on optimal integral sliding mode manifold. Nonlinear Dyn. 2016, 85, 2065–2074. [Google Scholar] [CrossRef]
- Vyhlidal, T.; Anderle, M.; Busek, J. Time delay algorithms for damping oscillations of suspended payload by adjusting the cable length. IEEE/ASME Trans. Mechatron. 2017, 22, 2319–2329. [Google Scholar] [CrossRef]
- Zavari, K.; Pipeleers, G.; Swevers, J. Gain-Scheduled Controller Design: Illustration on an Overhead Crane. IEEE Trans. Ind. Electron. 2014, 61, 3713–3718. [Google Scholar] [CrossRef]
- Chwa, D. Sliding Mode Control-based Robust Finite-Time Anti-Sway Tracking Control of 3-D Overhead Cranes. IEEE Trans. Ind. Electron. 2017, 64, 6775–6784. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Continuous Sliding Mode Control Strategy for a Class of Nonlinear Underactuated Systems. IEEE Trans. Autom. Control 2018, 63, 3471–3478. [Google Scholar] [CrossRef]
- Frikha, S.; Djemel, M.; Derbel, N. A New Adaptive Neuro-Sliding Mode Control for Gantry Crane. Int. J. Control Autom. Syst. 2018, 16, 559–565. [Google Scholar] [CrossRef]
- Bock, M.; Kugi, A. Real-Time Nonlinear Model Predictive Path-Following Control of a Laboratory Tower Crane. IEEE Trans. Control Syst. Technol. 2014, 22, 1461–1473. [Google Scholar] [CrossRef]
- Küchler, S.; Mahl, T.; Jörg, N. Active Control for an Offshore Crane Using Prediction of the Vessel’s Motion. IEEE/ASME Trans. Mechatron. 2011, 16, 297–309. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, X.; Zhu, B. Model predictive control for improving operational efficiency of overhead cranes. Nonlinear Dyn. 2015, 79, 2639–2657. [Google Scholar] [CrossRef]
- Nakagawa, K.; Watanabe, T.; Seto, K. H infinity robust motion and vibration control of three dimensional two link flexible robot arm taking account of variation of orientation. Trans. Jpn. Soc. Mech. Eng. Ser. C 2012, 78, 1085–1096. [Google Scholar] [CrossRef]
- Mystkowski, A.; Pawluszewicz, E. Remarks on some robust nonlinear observer and state-feedback zero-bias control of AMB. In Proceedings of the IEEE 2015 16th International Carpathian Control. Conference (ICCC), Szilvasvarad, Hungary, 2015; pp. 328–333. [Google Scholar]
- Fang, Y. Nonlinear Coupling Control Laws for an Underactuated Overhead Crane System. IEEE/ASME Trans. Mechatoronics 2003, 8, 418–423. [Google Scholar] [CrossRef]
- Guo, W.; Liu, D.; Yi, J.; Zhao, D. Passivity-based control for double-pendulum-type overhead cranes. In Proceedings of the IEEE Region 10th Conference Analog and Digital Techniques in Electrical Engineering TENCON, Chiang Mai, Thailand, 24 November 2004; pp. 546–549. [Google Scholar]
- Tuan, L.A.; Lee, S.G. Sliding mode controls of double-pendulum crane systems. J. Mech. Sci. Technol. 2013, 27, 1863–1873. [Google Scholar] [CrossRef]
- Qian, D.; Tong, S.; Yang, B. Design of simultaneous input-shaping-based SIRMs fuzzy control for double-pendulum-type overhead cranes. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 887–896. [Google Scholar] [CrossRef]
- Sun, N.; Yang, T.; Fang, Y. Transportation Control of Double-Pendulum Cranes with a Nonlinear Quasi-PID Scheme: Design and Experiments. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1408–1418. [Google Scholar] [CrossRef]
- Sun, N.; Wu, Y.; Fang, Y. Nonlinear Antiswing Control for Crane Systems with Double-Pendulum Swing Effects and Uncertain Parameters: Design and Experiments. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1413–1422. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, X.; Rong, X. A novel energy-coupling-based control method for double-pendulum overhead cranes with initial control force constraint. Adv. Mech. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Cheng, X. An Enhanced Coupling PD with Sliding Mode Control Method for Underactuated Double-pendulum Overhead Crane Systems. Int. J. Control Autom. Syst. 2019, 17, 1579–1588. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, X.; Chai, H. A novel online motion planning method for double-pendulum overhead cranes. Nonlinear Dyn. 2016, 85, 1079–1090. [Google Scholar] [CrossRef]
- Boscariol, P.; Richiedei, D. Robust point-to-point trajectory planning for nonlinear underactuated systems: Theory and experimental assessment. Robot. Comput. Integr. Manuf. 2018, 50, 256–265. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems, 3rd ed.; Englewood Cliffs NJ: Bergen, NJ, USA, 2002. [Google Scholar]
- Maghsoudi, M.J.; Mohamed, Z.; Sudin, S. An improved input shaping design for an efficient sway control of a nonlinear 3D overhead crane with friction. Mech. Syst. Signal. Process. 2017, 92, 364–378. [Google Scholar] [CrossRef]
- Soon, C.; Ghazali, R.; Hazriq, I. Robustness Analysis of an Optimized Controller via Particle Swarm Algorithm. Adv. Sci. Lett. 2017, 23, 11187–11191. [Google Scholar] [CrossRef]
| Name | Symbol | Numerical Value | Unit |
|---|---|---|---|
| Trolley mass | 12 | kg | |
| Hook mass | 1.5 | kg | |
| Payload mass | 1 | kg | |
| Gravity acceleration | 9.8 | m/s2 | |
| Cable length 1 | 1.2 | m | |
| Cable length 2 | 0.5 | m | |
| Desired trolley location | 3 | m | |
| Static friction-related coefficient 1 | 8 | NA | |
| Static friction-related coefficient 2 | 0.01 | NA | |
| Viscous friction-related parameter | −1.2 | NA |
| Controllers | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Proposed method | 5 | 15 | 6 | 1 | NANA | NA | NA | NA | NA | NA |
| PD | 6.8 | 2 | NA | NA | NA | NA | NA | NA | NA | NA |
| Passivity-based | 6.5 | 20 | NA | NA | 1 | 1 | NA | NA | NA | NA |
| CSMC | NA | NA | NA | NA | NA | NA | 0.5 | 17 | −11 | 30 |
| Controllers | (deg) | (deg) | (deg) | (deg) | (m) | (s) | (N) |
|---|---|---|---|---|---|---|---|
| Proposed method | 3.47 | 4.29 | 0.03 | 0.02 | 3.005 | 7.46 | 21.27 |
| PD | 7.85 | 10.62 | 7.20 | 9.69 | 2.936 | > 20 | 21.40 |
| Passivity-based | 6.94 | 9.95 | 1.69 | 2.37 | 2.989 | > 20 | 25.40 |
| CSMC | 7.89 | 9.18 | 0.04 | 0.04 | 2.986 | 7.75 | 22.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Li, G.; Ma, X.; Sun, J. Research on Nonlinear Coupling Anti-Swing Control Method of Double Pendulum Gantry Crane Based on Improved Energy. Symmetry 2019, 11, 1511. https://doi.org/10.3390/sym11121511
Shi H, Li G, Ma X, Sun J. Research on Nonlinear Coupling Anti-Swing Control Method of Double Pendulum Gantry Crane Based on Improved Energy. Symmetry. 2019; 11(12):1511. https://doi.org/10.3390/sym11121511
Chicago/Turabian StyleShi, Huaitao, Gang Li, Xin Ma, and Jie Sun. 2019. "Research on Nonlinear Coupling Anti-Swing Control Method of Double Pendulum Gantry Crane Based on Improved Energy" Symmetry 11, no. 12: 1511. https://doi.org/10.3390/sym11121511
APA StyleShi, H., Li, G., Ma, X., & Sun, J. (2019). Research on Nonlinear Coupling Anti-Swing Control Method of Double Pendulum Gantry Crane Based on Improved Energy. Symmetry, 11(12), 1511. https://doi.org/10.3390/sym11121511





