Multivariate Skew-Power-Normal Distributions: Properties and Associated Inference
Abstract
1. Introduction
2. Multivariate Skew Models
3. The Symmetric Multivariate PN Distribution
3.1. The New Model
- 1.
- for .
- 2.
- The joint PDF of is symmetric.
- 3.
- The product moment of iswhere is the moment of the positive part of .
- 4.
- The joint PDF of is multimodal if for .
3.2. Inference
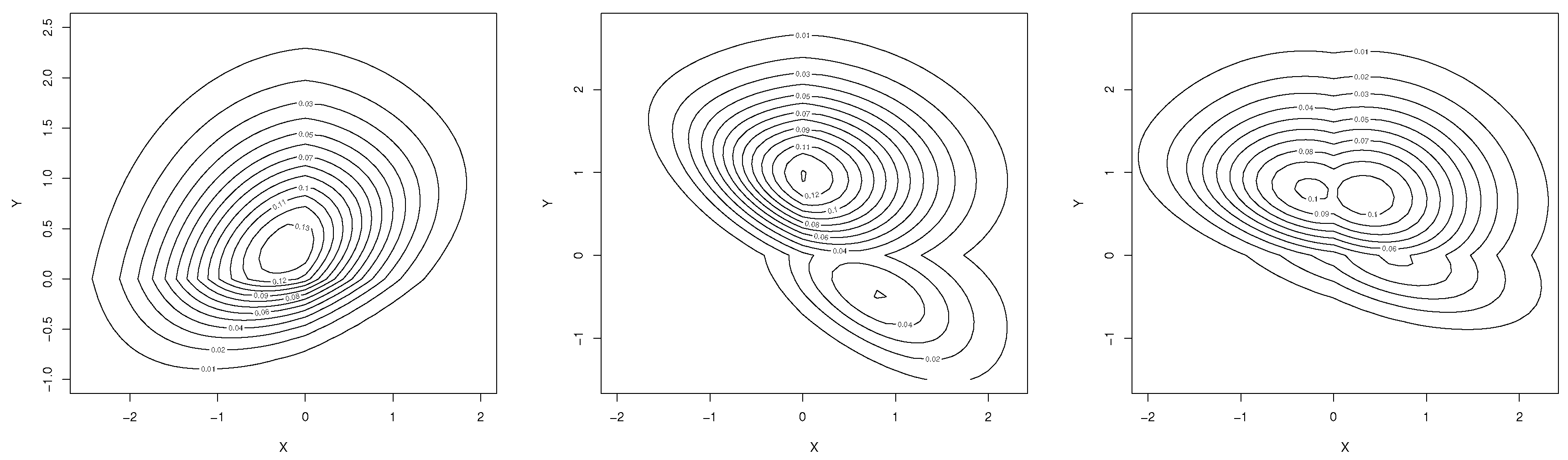
3.3. A Short Simulation Study
3.4. Location-Scale Extension
4. The Asymmetric Multivariate PN Model
4.1. The New Model
- 1.
- If , then the MABPN model reduces to the MBPN model.
- 2.
- .
- 3.
- If , then the MABPN model reduces to the SN model, where is a d-vector of ones.
- 4.
- The product moment of is given bywhere for .
4.2. Location-Scale Extension
4.3. Inference
4.4. Observed Information Matrix
4.5. Expected Information Matrix
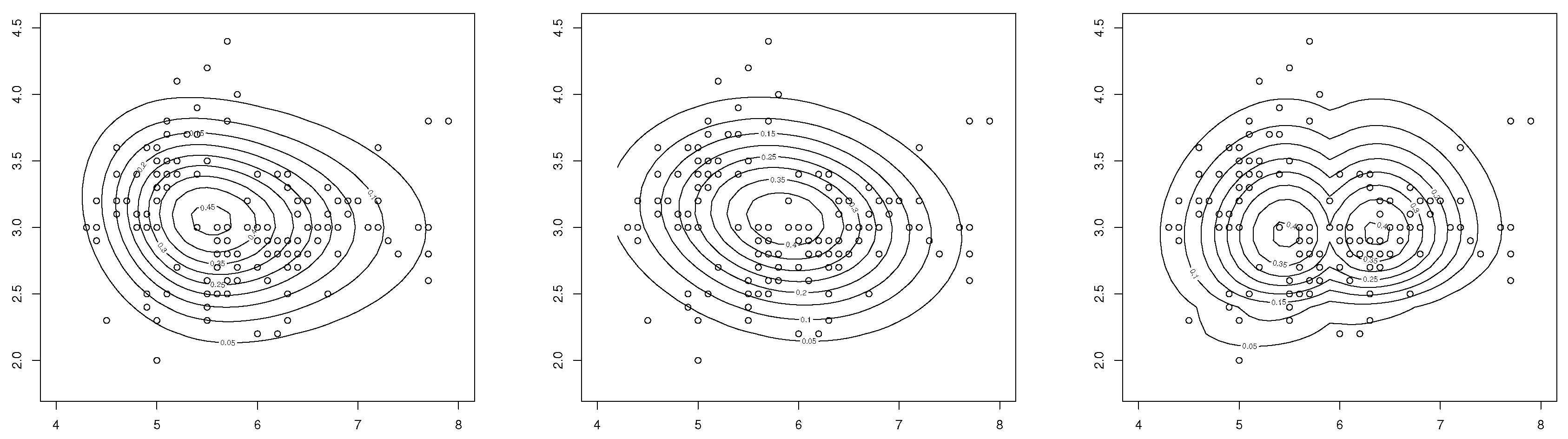
5. Numerical Illustration
6. Elliptical Family Extension
- 1.
- If , then MES.
- 2.
- MESS.
- 3.
- For regression functions are of linear typewhere
6.1. ML Estimation
6.2. Expected Information Matrix
7. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Fernandez, C.; Steel, M.F.J. On Bayesian modeling of fat tails and skewness. J. Am. Stat. Assoc. 1998, 93, 359–371. [Google Scholar]
- Mudholkar, G.S.; Hutson, A.D. The epsilon-skew-normal distribution for analyzing near-normal data. J. Stat. Plan. Inference 2000, 83, 291–309. [Google Scholar] [CrossRef]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Pewsey, A.; Gómez, H.W.; Bolfarine, H. Likelihood-based inference for power distributions. Test 2012, 21, 775–789. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Arnold, B.C.; Bolfarine, H.; Gómez, H.W. The multivariate alpha-power model. J. Stat. Plan. Inference 2013, 143, 1244–1255. [Google Scholar] [CrossRef]
- Henze, N. A probabilistic representation of the skew-normal distribution. Scand. J. Stat. 1986, 13, 271–275. [Google Scholar]
- Chiogna, M. A note on the asymptotic distribution of the maximum likelihood estimator for the scalar skew-normal distribution. Stat. Methods Appl. 2005, 14, 331–341. [Google Scholar] [CrossRef]
- Pewsey, A. Problems of inference for Azzalini’s skew-normal distribution. J. Appl. Stat. 2000, 27, 859–870. [Google Scholar] [CrossRef]
- Gómez, H.W.; Salinas, H.S.; Bolfarine, H. Generalized skew-normal models: Properties and inference. Statistics 2006, 40, 495–505. [Google Scholar] [CrossRef]
- Gómez, H.W.; Venegas, O.; Bolfarine, H. Skew-symmetric distributions generated by the distribution function of the normal distribution. Environmetrics 2007, 18, 395–407. [Google Scholar]
- Gupta, R.D.; Gupta, R.C. Analyzing skewed data by power normal model. Test 2008, 17, 197–210. [Google Scholar] [CrossRef]
- Bolfarine, H.; Martínez-Flórez, G.; Salinas, H.S. Bimodal symmetric-asymmetric power-normal families. Commun. -Stat. –Theory Methods 2018, 47, 259–276. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally specified multivariate skewed distributions. Sankhya A 2002, 64, 206–226. [Google Scholar]
- Azzalini, A.; Dalla Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Gupta, A.K.; Huang, W.J. Quadratic forms in skew normal variates. J. Math. Anal. Appl. 2002, 273, 558–564. [Google Scholar] [CrossRef][Green Version]
- Gupta, A.K.; Chang, F.C.; Huang, W.J. Some skew-symmetric models. Random Oper. Stoch. Equ. 2002, 10, 133–140. [Google Scholar] [CrossRef]
- Genton, M.G. Skew-Elliptical Distributions and Their Applications: A Journey beyond Normality; Chapman and Hall/CRC: New York, NY, USA, 2004. [Google Scholar]
- Arellano-Valle, R.B.; Azzalini, A. On the unification of families of skew-normal distributions. Scand. J. Stat. 2006, 33, 561–574. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A. The centred parametrization for the multivariate skew-normal distribution. J. Multivar. Anal. 2008, 99, 1362–1382. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G. On fundamental skew distributions. J. Multivar. Anal. 2005, 96, 93–116. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chen, J.T. A class of multivariate skew-normal models. Ann. Inst. Stat. Math. 2004, 56, 305–315. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chang, F.C. Multivariate skew-symmetric distributions. Appl. Math. Lett. 2003, 16, 643–646. [Google Scholar] [CrossRef][Green Version]
- Azzalini, A.; Capitanio, A. The Skew-Normal and Related Families; IMS Monographs Series; Cambridge University Press: UK, London, 2014. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Cox, D.R.; Hinkley, D.V. Theoretical Statistics; Chapman and Hall: London, UK, 1974. [Google Scholar]
- Cox, D.R.; Reid, N. Parameter orthogonality and approximate conditional inference. J. R. Stat. Soc. B 1987, 40, 1–39. [Google Scholar] [CrossRef]
- Pesta, M. Total least squares and bootstrapping with application in calibration. Statistics 2013, 47, 966–991. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Villasenor, J.A.; González, E. A generalization of Shapiro-Wilk’s test for multivariate normality. Commun. -Stat. –Theory Methods 2009, 38, 1870–1883. [Google Scholar] [CrossRef]
- Mardia, K.V. Measures of multivariate skewness and kurtosis with applications. Biometrika 1970, 57, 519–530. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
| 0.25 | 0.5914 | 0.5416 | 0.5201 | 0.5158 | 0.5286 | 0.3117 | 0.2644 | 0.2462 | |
| 0.5 | 2.5 | 0.5776 | 0.5501 | 0.5328 | 0.5180 | 2.5586 | 2.5168 | 2.4898 | 2.4932 |
| 4.75 | 0.5932 | 0.5571 | 0.5386 | 0.5226 | 4.8880 | 4.7870 | 4.7658 | 4.7476 | |
| 0.25 | 1.5205 | 1.5172 | 1.5123 | 1.5048 | 0.5386 | 0.3188 | 0.2675 | 0.2465 | |
| 1.5 | 2.5 | 1.5551 | 1.5156 | 1.5083 | 1.5058 | 2.5399 | 2.5151 | 2.5067 | 2.5046 |
| 4.75 | 1.5492 | 1.5200 | 1.5131 | 1.5119 | 4.8714 | 4.7635 | 4.7601 | 4.7526 | |
| 0.25 | 2.5295 | 2.5212 | 2.5108 | 2.5093 | 0.5439 | 0.2921 | 0.2740 | 0.2497 | |
| 2.5 | 2.5 | 2.5234 | 2.5207 | 2.5174 | 2.5078 | 2.5258 | 2.5071 | 2.5063 | 2.5054 |
| 4.75 | 2.5300 | 2.4895 | 2.5027 | 2.5008 | 4.7690 | 4.7672 | 4.7608 | 4.7467 | |
| 0.25 | 0.5875 | 0.2920 | 0.1951 | 0.1212 | 0.5204 | 0.2621 | 0.1967 | 0.1274 | |
| 0.5 | 2.5 | 0.5788 | 0.2910 | 0.2010 | 0.1196 | 0.8049 | 0.3493 | 0.2366 | 0.1381 |
| 4.75 | 0.5689 | 0.2846 | 0.1874 | 0.1091 | 0.8985 | 0.4181 | 0.2827 | 0.1633 | |
| 0.25 | 0.7280 | 0.3054 | 0.2272 | 0.1282 | 0.5066 | 0.2632 | 0.1933 | 0.1254 | |
| 1.5 | 2.5 | 0.6811 | 0.3112 | 0.2146 | 0.1244 | 0.7990 | 0.3535 | 0.2453 | 0.1363 |
| 4.75 | 0.7376 | 0.3048 | 0.2087 | 0.1220 | 0.9571 | 0.4146 | 0.2867 | 0.1655 | |
| 0.25 | 0.7814 | 0.3280 | 0.2308 | 0.1291 | 0.4912 | 0.2560 | 0.1994 | 0.1269 | |
| 2.5 | 2.5 | 0.7382 | 0.3387 | 0.2322 | 0.1339 | 0.7812 | 0.3373 | 0.2445 | 0.1437 |
| 4.75 | 0.7911 | 0.3263 | 0.2348 | 0.1340 | 0.9670 | 0.4077 | 0.2900 | 0.1685 | |
| 0.25 | 0.350 | 0.347 | ||||||||
| 1.75 | 0.349 | 0.345 | ||||||||
| 3.5 | 0.75 | 0.333 | 0.331 | |||||||
| 7.0 | 0.285 | 0.280 | ||||||||
| 15 | 0.186 | 0.183 | ||||||||
| 0.25 | 0.385 | 0.382 | ||||||||
| 1.75 | − | 0.383 | 0.385 | |||||||
| 3.5 | 2.5 | − | 0.367 | 0.367 | ||||||
| 7.0 | − | 0.321 | 0.316 | |||||||
| 15 | 0.220 | 0.221 | ||||||||
| 0.25 | 0.419 | 0.414 | ||||||||
| 1.75 | 0.419 | 0.418 | ||||||||
| 3.5 | 5.0 | 0.403 | 0.402 | |||||||
| 7.0 | 0.354 | 0.352 | ||||||||
| 15 | 0.258 | 0.257 | ||||||||
| Link Model | ER | ||
|---|---|---|---|
| SN | 3.76 | 6.55 | 0.131 |
| Conditional SN | 8.30 | 63.43 | 0.013 |
| ABPN | 0.00 | 1.00 | 0.856 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Flórez, G.; Lemonte, A.J.; Salinas, H.S. Multivariate Skew-Power-Normal Distributions: Properties and Associated Inference. Symmetry 2019, 11, 1509. https://doi.org/10.3390/sym11121509
Martínez-Flórez G, Lemonte AJ, Salinas HS. Multivariate Skew-Power-Normal Distributions: Properties and Associated Inference. Symmetry. 2019; 11(12):1509. https://doi.org/10.3390/sym11121509
Chicago/Turabian StyleMartínez-Flórez, Guillermo, Artur J. Lemonte, and Hugo S. Salinas. 2019. "Multivariate Skew-Power-Normal Distributions: Properties and Associated Inference" Symmetry 11, no. 12: 1509. https://doi.org/10.3390/sym11121509
APA StyleMartínez-Flórez, G., Lemonte, A. J., & Salinas, H. S. (2019). Multivariate Skew-Power-Normal Distributions: Properties and Associated Inference. Symmetry, 11(12), 1509. https://doi.org/10.3390/sym11121509






