Abstract
The univariate power-normal distribution is quite useful for modeling many types of real data. On the other hand, multivariate extensions of this univariate distribution are not common in the statistic literature, mainly skewed multivariate extensions that can be bimodal, for example. In this paper, based on the univariate power-normal distribution, we extend the univariate power-normal distribution to the multivariate setup. Structural properties of the new multivariate distributions are established. We consider the maximum likelihood method to estimate the unknown parameters, and the observed and expected Fisher information matrices are also derived. Monte Carlo simulation results indicate that the maximum likelihood approach is quite effective to estimate the model parameters. An empirical application of the proposed multivariate distribution to real data is provided for illustrative purposes.
1. Introduction
Asymmetric univariate distributions that can be used for explaining real data which are not adequately fitted by the usual normal distribution were studied in Azzalini [1], Fernández and Steel [2], Mudholkar and Hutson [3], Durrans [4], Pewsey et al. [5], and Martínez-Flórez et al. [6], among others. In particular, Azzalini [1] has considered a general structure for asymmetric distributions in the univariate setting, which is given by
where controls the amount of asymmetry in the distribution, f is a symmetric (around zero) probability density function (PDF), and G is an absolutely continuous cumulative distribution function (CDF). The special case and corresponds to the well-known skew-normal (SN) distribution, where and are the PDF and CDF of the standard normal distribution, respectively. We have that . The skew-normal distribution have been extensively studied in the statistic literature. To mention a few, but not limited to, the reader is referred to Henze [7], Chiogna [8], Pewsey [9], Gómez et al. [10], and Gómez et al. [11], among many others. Another important reference regarding univariate asymmetric distributions is the work of Durrans [4], who introduced the fractional order statistics distribution with PDF given by
where is a shape parameter that controls the amount of asymmetry in the distribution, F is an absolutely continuous CDF, and is the corresponding PDF. The special case corresponds to the well-known power-normal (PN) distribution (Gupta and Gupta [12]). Note also that . It is worth emphasizing that the fractional order statistics distribution studied by Durrans [4] is very flexible and, in addition, the corresponding expected Fisher information is not singular at . On the other hand, the expected Fisher information matrix for the SN distribution introduced by Azzalini [1] is singular at . Therefore, the fractional order statistics distribution has this interesting advantage in relation to the SN distribution.
The univariate models previously mentioned are only adequate for fitting unimodal data. A univariate bimodal distribution was introduced in Bolfarine et al. [13], whose PDF is given by
where , , F is an absolutely continuous CDF with PDF symmetric around zero, G is an absolutely continuous CDF which is symmetric around zero, and is the normalizing constant. In particular, if , then we have the univariate asymmetric bimodal power-normal (ABPN) distribution. We use the notation ABPN to refer to this univariate asymmetric bimodal distribution. It follows that the ABPN distribution is bimodal for , and unimodal otherwise. Additionally, leads to a symmetric (around zero) bimodal distribution, and we use the notation BPN to refer to this univariate symmetric bimodal distribution. Note also that and hence the ABPN distribution reduces to the PDF in (1) when . Also, .
In this paper, we generalize the univariate ABPN distribution to the multivariate setting by using the approach in Arnold et al. [14]. The new multivariate distributions we propose are quite flexible and therefore can be very useful in analyzing many types of multivariate real data which occurs frequently in practice. Additionally, maximum likelihood (ML) estimation is implemented, and (observed and expected) Fisher information matrices are derived. Finally, extensions to multivariate elliptical scenarios are also discussed. It is worth emphasizing that an important claim to introduce new multivariate distributions relies on the fact that the practitioners will have new multivariate models to use in multivariate settings. Additionally, the formulae related with the new multivariate models are manageable and with the use of modern computer resources and its numerical capabilities, the proposed multivariate models may prove to be an useful addition to the arsenal of applied statisticians. We hope that the new multivariate distributions introduced in this paper may serve as alternative multivariate models to some well-known multivariate models available in the statistical literature as, for example, the multivariate SN distribution [15], and the conditional multivariate SN distribution [14], among others. We also hope that the new multivariate models may work better (at least in terms of model fitting) than some multivariate distributions available in the literature in certain practical situations, although it cannot always be guaranteed.
The paper is organized as follows. Section 2 presents a short revision of existing asymmetric multivariate models, which are used to fit unimodal data. In Section 3, we consider the symmetric multivariate PN extension with possible bimodality. ML estimation is also implemented in this section. Section 4 is devoted to the study of the asymmetric multivariate PN model with extension implemented to the location-scale situation. ML estimation is also considered in this section. Real data application is presented in Section 5. The real data illustration shows that the new multivariate distribution can be better in terms of model fitting than unimodal alternative multivariate models for analyzing multivariate data. Multivariate extension of the univariate PN model in the elliptical context is considered in Section 6. In Section 7 some concluding remarks are provided.
2. Multivariate Skew Models
In the last two decades, statistical literature has given great emphasis on multivariate extensions of the SN model. Important extensions are the multivariate SN distributions (Azzalini and Dalla Valle, [15]), the conditionally specified multivariate SN distribution (Arnold et al. [14]), and the multivariate alpha-power model (Martínez-Flórez et al. [6]), among others. The multivariate SN distribution has been studied by several authors, including Azzalini and Capitanio [16], Gupta and Huang [17], Gupta et al. [18], and Genton [19]. Extensions of this model have been the subject of study in Arrellano-Valle and Azzalini [20,21], Arellano-Valle and Genton [22], Gupta and Chen [23], and Gupta and Chang [24]. The d-dimensional SN PDF can be expressed as
where is the joint PDF of a multivariate normal distribution, is a positive definite variance-covariance matrix, is the location parameter, is a parameter vector which controls skewness, and is a diagonal matrix composed by the standard deviations from the variance-covariance matrix . We use the notation SN to refer to this distribution; see Azzalini and Capitanio [25] for more details about multivariate SN models. Another useful multivariate model based on conditional SN distributions was studied in Arnold et al. [14], whose joint PDF takes the form
where and (for ) are location and scale parameters, respectively, and is a shape parameter. We use the notation SNC to refer to this distribution. Similarly to the univariate setting, the expected Fisher information matrix for the multivariate SN distribution is singular at , where denotes a k-vector of zeros. On the other hand, expected Fisher information matrix for the conditional multivariate SN distribution is not singular at .
3. The Symmetric Multivariate PN Distribution
The multivariate SN and SNC models presented in Section 2 are alternative models to the multivariate normal distribution for fitting multivariate asymmetric data. However, these multivariate distributions are only adequate for fitting unimodal data. Therefore, it is interesting to develop new multivariate models (and simple as well) that are able to adequately fit data with possible bimodality.
3.1. The New Model
Initially, we define the symmetric multivariate PN (MBPN) distribution, whose joint PDF is given by
where is the joint PDF of a d-dimensional multivariate normal distribution with standardized marginals, is the identity matrix of order d, is the d-vector of shape parameters, and is a normalizing constant. We use the notation MBPN to refer to this new multivariate distribution. We have the following proposition.
Proposition 1.
Let . We have that
- 1.
- for .
- 2.
- The joint PDF of is symmetric.
- 3.
- The product moment of iswhere is the moment of the positive part of .
- 4.
- The joint PDF of is multimodal if for .
Let and hence we have the bivariate BPN model. Thus, differentiating with respect to for and equating to zero, we obtain
If in (2), then there is no solution. Moreover, for the bivariate normal distribution has solution , and for we obtain two solutions: for , and for . For these solutions we have the determinant
where . Evaluating D at the critical points it follows that
and so we conclude that the joint bivariate PDF is bimodal if or .
3.2. Inference
We consider the ML procedure to estimate the parameter vector of the MBPN distribution. Let , …, be an observed sample of size n from . The log-likelihood function takes the form
The ML estimate of is obtained by maximizing the log-likelihood function with respect to . The maximization can be performed, for example, in the R software (R Core Team [26]) by using the optim(...) function. The partial derivatives of the log-likelihood function with respect to the model parameters become
The ML estimate can also be obtained by solving simultaneously the nonlinear system of equations for , which has no closed-form and, hence, the ML estimates need to be obtained through a numerical maximization of the log-likelihood function using nonlinear optimization algorithms.
Since the new MBPN distribution corresponds to a regular ML problem, we have that the standard asymptotics apply; that is, the ML estimators of the model parameters are asymptotically normal, asymptotically unbiased and have asymptotic variance-covariance matrix given by the inverse of the expected Fisher information matrix. Let be the expected Fisher information matrix. So, when n is large and under some mild regularity conditions (Cox and Hinkley [27]), we have that , where means approximately distributed. It can be shown that
Therefore, we immediately observe that the parameters ’s are globally orthogonal (Cox and Reid [28]). The above asymptotic normal distribution can be used to construct approximate confidence intervals (CI) for the model parameters. Let be the significance level. The asymptotic CI of given by for , with asymptotic coverage of . Here, is the square root of the diagonal element of corresponding to each parameter (i.e., the asymptotic standard error), and denotes the standard normal quantile function.
3.3. A Short Simulation Study
We conduct Monte Carlo simulation experiments in order to explore the performance of the ML method in estimating the MBPN model parameters in finite-samples in the bivariate case (i.e., ). Parameter values to generate the data are , 1.5 and 2.5, and , 2.5 and 4.75. Sample sizes considered were , 250, 500 and 1500. In this study, 10,000 random samples were generated for each sample size. To generate random variates from MBPN distribution, we generate two independent uniform random variables, say and , such that
for , leading to the following relation
The ML estimates are evaluated by considering the following quantities: the empirical mean, and squared root of the mean squared error (), which are computed from Monte Carlo replications. All simulations were performed using the R language with the optimization of the log-likelihood function obtained by using the optim(...) function. From Table 1 and Table 2, it is evident that the performance of the ML estimators of the MBPN model parameters is good; that is, they are very close to the true parameter values in all cases, and the decreases as the sample size increases, as expected, since the ML estimators are consistent. In short, the numerical results provide a clear indication that the ML method can be used quite effectively to estimate the MBPN model parameters.

Table 1.
Empirical mean.

Table 2.
Squared root of the mean squared error ().
3.4. Location-Scale Extension
The joint PDF of the MBPN model in the location-scale context is simply given by
where with (for ) being scale parameters, and is a d-vector of location parameters. We shall use the notation MBPN, where .
4. The Asymmetric Multivariate PN Model
4.1. The New Model
Although the MBPN model defined in Section 3 can present multimodality, it corresponds to a symmetric multivariate distribution. An immediate extension for fitting asymmetric (possibly multimodal) multivariate data is given by the joint PDF
where is a parameter vector which controls skewness. The above joint PDF corresponds to the multivariate extension of the univariate ABPN model, and we shall use the notation MABPN to refer to this multivariate distribution. Let and hence we have the bivariate ABPN model with parameter vector . Some contour plots of the joint bivariate PDF are presented in Figure 1. Note that the joint PDF can take different forms and will therefore be useful in analyzing bivariate data. Additionally, note that it can be unimodal or bimodal. According to an anonymous referee, the MABPN distribution has a straightforward utilization within the errors-in-variables models, especially for an application in calibration; see, for example, [29].
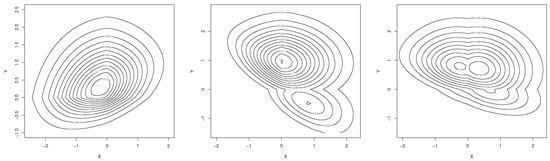
Figure 1.
Contour plots for some parameter values : (left), (middle), and (right).
We have the following proposition.
Proposition 2.
Let . We have that
- 1.
- If , then the MABPN model reduces to the MBPN model.
- 2.
- .
- 3.
- If , then the MABPN model reduces to the SN model, where is a d-vector of ones.
- 4.
- The product moment of is given bywhere for .
From Proposition 2, note that even moments of do not depend on the parameter vector . It implies that the correlation coefficient between the random variables and , where for , depends basically on the parameter vector . Note that the covariance between and , say , reduces to
where and are computed under the marginal PDF of and , respectively. Therefore, the parameter vector also governs the correlation. To illustrate it, we compute the correlation in the bivariate case (i.e., ), where and . The parameter values we consider are , 1.75, 3.5, 7.0 and 15, , 2.5 and 5.0, and 1.5, and and 2.5. Table 3 lists the results for the correlation. Note that if or goes to zero, independently of the values for and , the correlation tends to zero, illustrating the fact that the parameter vector dominates the dependence between the random variables. It is interesting to note that values of and with the same sign lead to a negative correlation and in situations where their signs are opposite, the correlation is positive.

Table 3.
Correlation for the bivariate ABPN distribution.
4.2. Location-Scale Extension
The location-scale version of the MABPN model has joint PDF in the form
where the matrix and the d-vector were previously defined. We shall use the notation MABPN to refer to this location-scale MABPN distribution.
4.3. Inference
Let be the parameter vector of interest. The log-likelihood function for , given the observed sample , …, of size n from , is given by
where for and . The ML estimate of , where , , and , is obtained by maximizing the log-likelihood function with respect to by using, for example, the R function optim(...). The first-order partial derivatives of (3) become ()
where , , and for and . We are using the notation , , , and so on. The ML estimates can also be obtained by solving simultaneously the nonlinear system of equations , , and for , which has no closed-form and, hence, the ML estimates need to be obtained through a numerical maximization of the log-likelihood function using nonlinear optimization algorithms.
4.4. Observed Information Matrix
Let be the observed information matrix, whose elements are denoted by for . After some algebraic manipulations, we have that
4.5. Expected Information Matrix
Let be the expected information matrix, and be the corresponding elements for . These elements can be computed by using numerical procedures. When n is large and under some mild regularity conditions, we have that . From this asymptotic normal distribution, approximate CIs for the model parameters are computed in the usual manner. In particular, for and (), the expected Fisher information matrix can be expressed as
where , with and , and denotes the signum function. After some algebraic manipulations, it can be shown that
Therefore, the expected Fisher information matrix of the MABPN distribution is nonsingular at the vicinity of symmetry. This is not the case, however, with the multivariate SN distribution (Azzalini and Dalla-Valle [15]), whose expected Fisher information matrix is singular at the vicinity of symmetry, i.e., .
5. Numerical Illustration
In this section, we present an application of the proposed bivariate ABPN distribution to real data for illustrative purposes. For the sake of comparison, we also consider the bivariate SN distribution (Azzalini and Dalla Valle [15]), and the conditional bivariate SN distribution (Arnold et al. [14]). All bivariate distributions were fitted using the location-scale extension. We shall consider the real data (see, for example, Fisher [30]) corresponding to measurements of the flowers of fifty plants each of the three species found growing together in the same colony, namely: Iris-setosa, Iris-versicolor, and Iris-virginica. Two flower measurements are considered: sepal length, and sepal width. We pooled together, the 50 Iris-setosa data points, the 50 Iris-versicolor data points and the 50 Iris-virginica data points, to get a total sample size of ; that is, 150 sepal lengths, and 150 sepal widths. The observed value of the Shapiro-Wilk test for multivariate normality (see Villasenor and González [31]) is 0.9845 (p-value ). We also compute the multivariate skewness based on Mardia [32]. The observed value of the multivariate skewness is 0.37 (p-value ), which clearly suggests the presence of skewness and hence of nonnormality. Hence, the bivariate normal distribution is not a tenable model for the data under study and an alternative model that is able to incorporate some degree of asymmetry would probably fit the data better. We now consider the bivariate SN distribution, the conditional bivariate SN distribution, and the bivariate ABPN distribution to fit these real data. In order to compare the model fitting of these competing bivariate distributions, we make use of the Akaike information criterion (AIC). For fitting the bivariate SN model, we use the R function msn.mle, leading to the following ML estimates (standard errors in parentheses): , , and . The estimated variance-covariance matrix is
For the the bivariate SN model, we obtain AIC . The ML estimates of the conditional bivariate SN model parameters (standard errors in parentheses) are: , , , and . For the the bivariate conditional SN model, we obtain AIC . Also, the ML estimates of the proposed bivariate ABPN model parameters (standard errors in parentheses) are: , , , , , , and . For the the proposed bivariate ABPN model, we have that AIC, which indicates that the proposed bivariate ABPN model outperforms the bivariate SN distribution and the conditional bivariate SN distribution to model the bivariate data. Finally, Figure 2 displays the scatter plot of real data and contour levels of the fitted bivariate PDFs. Visual inspection reveals a satisfactory fit of the bivariate ABPN PDF to the real bivariate data.
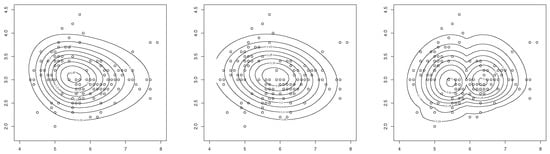
Figure 2.
Scatter plot of real data and contour level of the fitted PDFs: (left) bivariate SN distribution, (middle) conditional SN distribution, and (right) bivariate ABPN distribution.
We would like to point out that there is some uncertainty as to what constitutes a “substantial” difference in AIC values in practical situations. The empirical evidence scale of [33] uses the AIC difference over all candidate models, where , and T denotes the total number of models considered. The models with values of have substantial support to be considered as good as the best approximating model. Two additional measures are then introduced to provide the “strengths” of each model: the evidence ratio (ER) and the weight () of model m. These measures are defined as
and . The values of ER can be interpreted as the greater likelihood of the best approximating model with respect to model m, whereas the values of can be interpreted as the probability of a given model being the best approximating model. The values of these measures are given in Table 4. For example, we conclude from this table that the bivariate ABPN distribution is about 7 and 63 times more likely to be the best approximating model than the bivariate SN distribution and conditional SN distribution, respectively. Additionally, the chance of these models with respect to the bivariate ABPN distribution is also non-existent. The best bivariate ABPN distribution has a weight approximately 0.856; that is, there is (approximately) a 86% chance that it really is the best approximating model among the current models to describe these data. Notice that, by definition, the strength of evidence in favor of model i over the model j can be obtained simply by considering .

Table 4.
Some measures for the fitted models.
6. Elliptical Family Extension
In the previous sections, the d-dimensional normal distribution played an important role in deriving the multivariate ABPN distribution. In this section, we extend those results by considering the elliptical family of distributions. For the case of a random variable (one-dimensional case), elliptical distributions correspond to all symmetric distributions in . Specifically, a random variable X follows an symmetric distribution if its PDF is given by
where (for ) is a nonnegative real function and corresponds to the kernel of the PDF, and c is a normalizing constant such that is a PDF. We use the notation EC according to (4). In general, is the location parameter and coincides with the mean if the first moment of the distribution exists, and is the scale parameter.
First, we shall introduce a multivariate elliptical PN family of distributions. A random vector follows a multivariate elliptical PN distribution if its joint PDF is given by
where is defined in (4), and corresponds to its CDF for . Clearly, since belongs to the elliptical family, then it can be easily shown that so that is a symmetric (around zero) PDF. We use the notation MES to refer to this distribution. From Lemma 1 of Gupta and Chang [24], we have the following generalization.
Proposition 3.
Let be a random vector with joint PDF , and be a random vector with absolutely continuous CDF G. Then
is a joint PDF of a random vector for any .
Proof.
We will use the methodology given in Gupta and Chang [24]. Given that and for any , it then follows that . Let
Lebesgue’s dominated convergence theorem implies that
Moreover, given that is an odd function, we have
Therefore, it allows us to conclude that is a constant and, hence, given that , we have that is a joint PDF. □
The new multivariate distribution defined in Proposition 3 will be denoted by MESS. We have the following proposition.
Proposition 4.
Let MESS. We have that
- 1.
- If , then MES.
- 2.
- MESS.
- 3.
- For regression functions are of linear typewhere
The product moment of MESS are provided in the next proposition.
Proposition 5.
If MESS, then
where .
Proof.
Let MESS and . Also, let be the characteristic function of . We have that
where is independent of . Thus,
for even, so that
The previous result implies that even moments of do not depend on , so that
where is the moment of the positive part of the variable as defined before. □
6.1. ML Estimation
Let , …, be an observed sample of size n from . The log-likelihood function takes the form
where for and , and . The first-order partial derivatives are given by
where .
6.2. Expected Information Matrix
Let , , …, be the elements of the expected information matrix. Also, define , , , , and , where , and . We have
where , , , , , and for and .
7. Concluding Remarks
The univariate power-normal distribution has been quite useful in the modeling of many types of real data. On the other hand, extensions of the univariate power-normal distribution to the multivariate setup have been little explored in the statistic literature. We have proposed new multivariate power-normal distributions, which are quite simple and can be useful in the modeling of multivariate data. The new multivariate power-normal distributions are absolutely continuous distributions. The joint probability density functions of the new multivariate power-normal distributions do not involve any complicated function and, hence, they can be computed easily. By employing the frequentist approach, the estimation of the multivariate power-normal distribution parameters is conducted by the maximum likelihood method. We also provide closed-form expressions for the observed and expected Fisher information matrices. We illustrate the methodology developed in this paper by means of an application to real data. We verify through the real data application that the proposed bivariate power-normal distribution was superior to the well-known bivariate skew-normal distribution (Azzalini and Dalla Valle [15]), as well as conditional bivariate skew-normal distribution (Arnold et al. [14]). Finally, it is worth stressing that the formulas related with the multivariate power-normal distributions are manageable (such as log-likelihood function, score function, and observed and expected Fisher information matrices, etc), and with the use of modern computer resources and its numerical capabilities, the proposed multivariate distributions may prove to be an useful addition to the arsenal of applied statisticians. Finally, we have also introduced in this paper multivariate PN distributions by considering the elliptical family of distributions, and discussed some of its properties.
Author Contributions
Individual contributions to this article: conceptualization, G.M.-F., A.J.L., and H.S.S.; methodology, G.M.-F., A.J.L., and H.S.S.; validation, G.M.-F., A.J.L., and H.S.S.; software, G.M.-F., A.J.L., and H.S.S.; investigation, G.M.-F., A.J.L., and H.S.S.; resources, G.M.-F., A.J.L., and H.S.S.; writing–original draft preparation, G.M.-F., A.J.L., and H.S.S.; writing–review and editing, G.M.-F., A.J.L., and H.S.S.; funding acquisition, A.J.L.
Funding
This research was funded in part by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq/Brazil) under grant 301808/2016–3.
Acknowledgments
We thank the anonymous referees for helpful suggestions which improved the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Fernandez, C.; Steel, M.F.J. On Bayesian modeling of fat tails and skewness. J. Am. Stat. Assoc. 1998, 93, 359–371. [Google Scholar]
- Mudholkar, G.S.; Hutson, A.D. The epsilon-skew-normal distribution for analyzing near-normal data. J. Stat. Plan. Inference 2000, 83, 291–309. [Google Scholar] [CrossRef]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Pewsey, A.; Gómez, H.W.; Bolfarine, H. Likelihood-based inference for power distributions. Test 2012, 21, 775–789. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Arnold, B.C.; Bolfarine, H.; Gómez, H.W. The multivariate alpha-power model. J. Stat. Plan. Inference 2013, 143, 1244–1255. [Google Scholar] [CrossRef]
- Henze, N. A probabilistic representation of the skew-normal distribution. Scand. J. Stat. 1986, 13, 271–275. [Google Scholar]
- Chiogna, M. A note on the asymptotic distribution of the maximum likelihood estimator for the scalar skew-normal distribution. Stat. Methods Appl. 2005, 14, 331–341. [Google Scholar] [CrossRef]
- Pewsey, A. Problems of inference for Azzalini’s skew-normal distribution. J. Appl. Stat. 2000, 27, 859–870. [Google Scholar] [CrossRef]
- Gómez, H.W.; Salinas, H.S.; Bolfarine, H. Generalized skew-normal models: Properties and inference. Statistics 2006, 40, 495–505. [Google Scholar] [CrossRef]
- Gómez, H.W.; Venegas, O.; Bolfarine, H. Skew-symmetric distributions generated by the distribution function of the normal distribution. Environmetrics 2007, 18, 395–407. [Google Scholar]
- Gupta, R.D.; Gupta, R.C. Analyzing skewed data by power normal model. Test 2008, 17, 197–210. [Google Scholar] [CrossRef]
- Bolfarine, H.; Martínez-Flórez, G.; Salinas, H.S. Bimodal symmetric-asymmetric power-normal families. Commun. -Stat. –Theory Methods 2018, 47, 259–276. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally specified multivariate skewed distributions. Sankhya A 2002, 64, 206–226. [Google Scholar]
- Azzalini, A.; Dalla Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Gupta, A.K.; Huang, W.J. Quadratic forms in skew normal variates. J. Math. Anal. Appl. 2002, 273, 558–564. [Google Scholar] [CrossRef][Green Version]
- Gupta, A.K.; Chang, F.C.; Huang, W.J. Some skew-symmetric models. Random Oper. Stoch. Equ. 2002, 10, 133–140. [Google Scholar] [CrossRef]
- Genton, M.G. Skew-Elliptical Distributions and Their Applications: A Journey beyond Normality; Chapman and Hall/CRC: New York, NY, USA, 2004. [Google Scholar]
- Arellano-Valle, R.B.; Azzalini, A. On the unification of families of skew-normal distributions. Scand. J. Stat. 2006, 33, 561–574. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A. The centred parametrization for the multivariate skew-normal distribution. J. Multivar. Anal. 2008, 99, 1362–1382. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G. On fundamental skew distributions. J. Multivar. Anal. 2005, 96, 93–116. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chen, J.T. A class of multivariate skew-normal models. Ann. Inst. Stat. Math. 2004, 56, 305–315. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chang, F.C. Multivariate skew-symmetric distributions. Appl. Math. Lett. 2003, 16, 643–646. [Google Scholar] [CrossRef][Green Version]
- Azzalini, A.; Capitanio, A. The Skew-Normal and Related Families; IMS Monographs Series; Cambridge University Press: UK, London, 2014. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Cox, D.R.; Hinkley, D.V. Theoretical Statistics; Chapman and Hall: London, UK, 1974. [Google Scholar]
- Cox, D.R.; Reid, N. Parameter orthogonality and approximate conditional inference. J. R. Stat. Soc. B 1987, 40, 1–39. [Google Scholar] [CrossRef]
- Pesta, M. Total least squares and bootstrapping with application in calibration. Statistics 2013, 47, 966–991. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Villasenor, J.A.; González, E. A generalization of Shapiro-Wilk’s test for multivariate normality. Commun. -Stat. –Theory Methods 2009, 38, 1870–1883. [Google Scholar] [CrossRef]
- Mardia, K.V. Measures of multivariate skewness and kurtosis with applications. Biometrika 1970, 57, 519–530. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).