Abstract
The predictive performance of different granular models (GMs) was compared and analyzed for methods that evenly divide linguistic context in information granulation-based GMs and perform flexible partitioning. GMs are defined by input and output space information transformations using context-based fuzzy C-means clustering. The input space information transformation is directly induced by the output space context. Usually, the output space context is evenly divided. In this paper, the linguistic context was flexibly divided by stochastically distributing data in the output space. Unlike most fuzzy models, this GM yielded information segmentation. Their performance is usually evaluated using the root mean square error, which utilizes the difference between the model’s output and ground truth. However, this is inadequate for the performance evaluation of information innovation-based GMs. Thus, the GM performance was compared and analyzed using the linguistic context partitioning by selecting the appropriate performance evaluation method for the GM. The method was augmented by the coverage and specificity of the GMs output as the performance index. For the GM validation, its performance was compared and analyzed using the auto MPG dataset. The GM with flexible partitioning of linguistic context performed better. Performance evaluation using the coverage and specificity of the membership function was validated.
1. Introduction
Fuzzy modeling seeks to develop relationships between fuzzy sets or information granulations considered as fuzzy relations. Various methods, structures, and algorithms have been explored in the field of fuzzy modeling. Das [1] proposed an evolutionary interval type-2 neural fuzzy inference system (IT2FIS), based on the Takagi–Sugeno–Kang fuzzy inference system and a completely sequential learning algorithm. Jang [2] proposed an adaptive neuro-fuzzy inference system by fusing a fuzzy inference system and an artificial neural network. Zhang [3] proposed a new fuzzy logic system (FLS) modeling framework, termed the “data-driven elastic FLS” (DD-EFLS). Alizadeh [4] proposed an eigen fuzzy inference system (eHFIS) that can simultaneously perform local input selection and system identification of a fuzzy inference system. Cevantes [5] proposed a neuro-fuzzy system that implements differential neural networks (DNNs) using the Takagi–Sugeno (T-S) fuzzy inference rules. Despite the variety of design approaches that exploit the fuzzy modeling paradigm, one feature is common to all of them, i.e., that all of them yield constant values, regardless of the use of the fuzzy set technique [6,7].
Pedrycz [8] proposed a granular model (GM) that yields a fuzzy number that is not a constant. The GM directly uses the fundamental idea of fuzzy C-means (FCM) clustering. Information granulation is generated using the context-based FCM (CFCM) clustering method [9]. This method implements clustering using the homogeneity of data between the classifier’s input and output spaces. The GM can capture the relationship between the information granulation expressed by the CFCM clustering method.
The accuracy and clarity of a model are essential and important criteria for the model’s evaluation [10]. Some of the most widely used accuracy criteria are the mean absolute error (MAE), the mean absolute percentage error (MAPE), and the root mean square error (RMSE). The MAE quantifies the performance of the model by averaging the absolute difference between the actual value (ground truth) and the value predicted by the model. Juneja [11] proposed a fuzzy-filtered neural-fuzzy framework to predict the flaws of internal and external software projects and confirmed the model’s performance using the MAE. Chen [12] proposed a hybrid set and entropy consensus fuzzy collaborative intelligence (FCI) method and confirmed the method’s performance using the MAE. Sarabakha [13] used the MAE to verify the performance of pre-tuned type-1 fuzzy logic controllers and pre-tuned type-2 fuzzy logic controllers. Yeom [14] proposed a TSK-based extreme learning machine capable of knowledge representation and confirmed the performance of the model using the MAE. Maroufpoor [15] proposed a hybrid intelligent model, ANFIS-GWO, and confirmed the performance of the model using the MAE.
On the other hand, the MAPE metric evaluates the performance of the model by subtracting the ground truth from the value predicted by the model and then dividing by the value predicted by the model. In this regard, Ali [16] proposed a fuzzy-neuro model for predicting the temperature and humidity of Mubi in Adamawa and validated the model’s performance using the MAPE metric. Bacani [17] developed a fuzzy inference framework, based on the fuzzy relationship, for predicting the temperature and humidity of a greenhouse for Brazilian coffee crops and validated the model’s performance in terms of the MAPE metric. Tak [18] proposed a meta-fuzzy function based on the FCM clustering method and confirmed the model’s performance using the MAPE metric. Carvalho [19] proposed a hybrid method that combines classical time series modeling and fuzzy set theory to improve the performance of the predictive algorithm and confirmed the performance of the model using the MAPE metric. Roy [20] proposed a method for predicting the maximal yield of the almond oil using an interval type-2 fuzzy logic approach and confirmed the model’s performance using the MAPE metric.
Different from the previous two methods, the RMSE method evaluates the performance of the model by averaging the square of the difference between the ground truth and the predicted value and taking the square root of the resulting average. Khalifa [21] proposed a type-2 fuzzy winner structure with a cascade structure and validated the model using the RMSE measure. Naderi [22] used two rule-based fuzzy reasoning systems based on the Mamdani-type and TSK model to predict oil economic variables and confirmed the performance of the model using the RMSE metric. Xie [23] proposed a hybrid fuzzy control method by combining a type-1 fuzzy logic controller and a type-2 fuzzy logic controller and confirmed the performance of the model in terms of the RMSE metric. Altunkaynak [24] predicted river levels using combined DWT-fuzzy and CWT-fuzzy models and confirmed the resultant model’s performance using the RMSE metric. Yeom [25] proposed an improved incremental model (IIM) that combines linear regression and the linguistic model and confirmed the performance of the model using the RMSE metric.
While many methods for model accuracy quantification have been developed, methods for evaluating model clarity and interpretability are still explored. Pedrycz proposed a method to evaluate the performance of a model by calculating the performance index (PI), which uses the coverage and specificity of the membership function. In this study, the performance of the proposed model was evaluated in terms of coverage and specificity. Tsehayae [26] proposed a refined fuzzy modeling method to extract the labor productivity knowledge and confirmed the performance of the proposed method in terms of the coverage and specificity. Pedrycz [27] introduced the concept of hierarchical refined FCM clustering, proposed an algorithm, and confirmed the performance of the model in terms of the coverage and specificity. Pedrycz [28] designed a fuzzy set using the principle of granular parameters and confirmed the model’s performance by justification. Zhu [29] considered the reconstruction ability of the designed information granulation system, designed a set of meaningful elliptical information granulations using the principle of granularity, and confirmed the performance of the model in terms of the coverage and specificity. Hu [30] proposed a granular evaluation method of a fuzzy model from a generally accepted position and confirmed the performance of the fuzzy model by forming an information granulation around the parameters and the numerical values of the model. Zhu [31] proposed a novel design methodology for a refined fuzzy model and introduced additional generalizations in the form of a higher-type refined fuzzy model. The detection and characterization of outliers expressed for the constructed information granulation was described. Galaviz [32] studied the design of a detailed fuzzy model. We proposed a model that intuitively constructed a set of interval information granulations described in the output space and a set of derived information granulations in the input space, and confirmed the performance of the proposed model in terms of the coverage and specificity. In general, the performance evaluation is commonly performed by root mean square error (RMSE), representing the error between the model output and the actual output in the existing studies. However, because the output of the GM is in the form of fuzzy number, the traditional performance evaluation methods are not suitable. In addition, the contexts generated in the previous works are divided evenly in the design of the GM. In this paper, we focus on the theory that the contexts are flexibly divided, according to the data distribution, to improve the prediction performance.
In this paper, we analyzed the different performance evaluation methods for the GM evaluation. We evaluated the relation of a fuzzy set (i.e., information granulation) generated in the GM’s input and output spaces using performance evaluation methods, which utilize coverage and specificity, rather than using general performance evaluation methods, such as MAE, MAPE, and RMSE. To validate the performance evaluation method, we conducted experiments on the estimation of fuel consumption of automobiles and the prediction using the auto MPG dataset. This paper is organized as follows. Chapter 1 provides the background for this research. Chapter 2 explains the GM, while Chapter 3 explains the general performance evaluation method and the GM performance evaluation method. Chapter 4 uses the auto MPG dataset to predict and compare the performance of the car fuel consumption. Chapter 5 compares and analyzes car fuel consumption forecasts. Finally, conclusions and future research plans are stated in Chapter 6.
2. GM
2.1. CFCM Clustering
The GM was constructed using the information granulation generated by the CFCM clustering method proposed by Pedrycz [8]. Unlike the conventional FCM clustering method, the CFCM clustering method can group the information granulation more precisely, because data homogeneity is assumed between the input and output spaces. This explains why the GM uses a set of information granulations in the input and output spaces. A brief description of the CFCM clustering method is as follows. The fuzzy set of the output space is defined as:
where is the entire set of output variables and the value of the context is available for a given datum. represents the degree of inclusion of th datum in an arbitrary fuzzy set, generated in the output space. Here, the value of represents the belonging value between 0 and 1. If the requirement of the belonging matrix is modified by these characteristics, Equation (2) is obtained. The modified membership matrix is shown in Equation (3).
where represents the fuzzification coefficient and, generally, is used. The linguistic context consists of an overlap between the consecutive fuzzy sets and is generated as a triangular membership function that is evenly distributed in the output space. Figure 1 shows the concept of the CFCM clustering method. There were six equal contexts in the output space, indicating that three clusters were created in each context. The CFCM clustering method proceeded in the following order. The linguistic contexts were produced by several fuzzy sets in the output space. These contexts were used when context-based fuzzy c-means clustering was performed. In general, the linguistic contexts were generated through a series of triangle membership functions, equally spaced in output space. However, the contexts produced in this paper were divided by a stochastic data distribution in the output space.
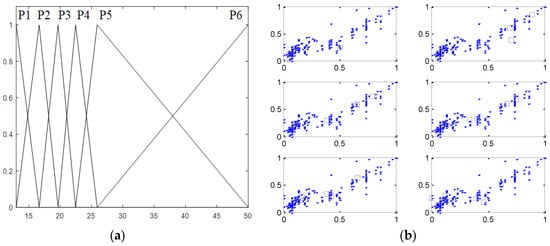
Figure 1.
Conceptual description of the context-based fuzzy C-means (CFCM) clustering method: (a) Linguistic context generated in the output space; (b) clusters estimated for each context.
- [Step 1]
- The number of linguistic contexts (2 to 20) and the number of clusters to be created in each context (2 to 20) was selected. The belonging matrix was initialized to an arbitrary value between 0 and 1.
- [Step 2]
- A linguistic context was created using a triangular membership function that was evenly distributed in the output space.
- [Step 3]
- For each context, the cluster center and the belonging value were calculated.
- [Step 4]
- The objective function was calculated, as given by Equation (6), and if the degree of improvement obtained through the previous iteration wasless than the threshold value, the process was stopped.Here, represents the Euclidean distance between the center of the i-th cluster and th datum. The parameter is the number of repetitions.
- [Step 5]
- The new membership matrix U was calculated from Equation (3), and control was returned to [Step 3].
2.2. Structure of the GM
Figure 2 shows the structure of the GM, with the input layer, the output layer, and three intermediate layers. The input space represents the input data, and layer 1 represents the set of activation levels of the CFCM clustering method. In layer 2, conditional clustering was performed on the linguistic context, and layers 1 and 2 were connected to each other. Given a linguistic context, clusters were inferred considering each context. Layer 3 was composed of single-particle neurons in the output layer and it calculated the final output. The main goal of making this granulation available was to create a model on the information granulation level. The characteristics of the GM were as follows. First, it was designed in terms of a set of information granulations in the input and output spaces. The information granulation of the input space was determined by the information granulation of the output space. Second, the final output value of the GM was represented by the information granulation, not by the numerical value. The final output value of the GM was calculated by the number of fuzzy numbers, as shown by Equation (7), in which generalized addition and multiplication (⊕, ⊗) operation signs are used to emphasize the information granulation.
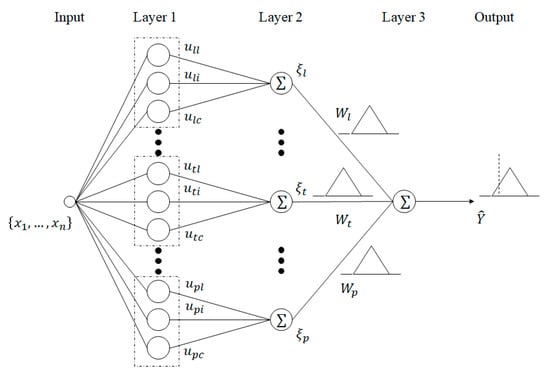
Figure 2.
Schematic of the granular model (GM).
Figure 3 shows the output of the GM with the actual output and fuzzy numbers. The output value of the GM is a triangle that consists of a lower limit value, a model-generated value, and an upper limit value. The respective formulae are as follows:
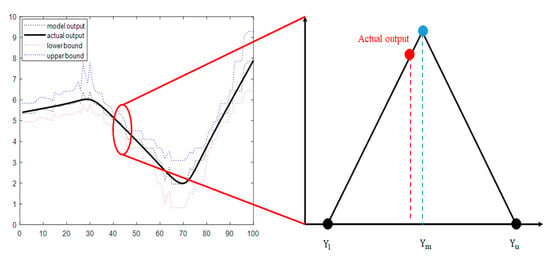
Figure 3.
Structure of a triangular fuzzy number.
2.3. Structure of the GM
In the structure of the GM, the parameters of the premises were obtained in terms of the clusters’ centroids obtained, using the CFCM clustering method. The linguistic context generated in the output space was the conclusion parameter. A typical GM uniformly divides linguistic contexts. A uniform division of linguistic context amounts to placing same-size linguistic contexts at equal intervals. The method of uniform partitioning can present a data shortage problem, owing to the small amount of data contained in any linguistic context. As a result, it was difficult to infer the clusters’ centroids and fuzzy rules using the CFCM clustering method. Thus, in this paper, the linguistic context was divided stochastically, distributing the data in the output space. Here, the language context division represented the boundary of the fuzzy set, and the linguistic context was generated by the equally distributed trigonometric function using the probabilistic distribution information in the output space. Figure 4 shows the even partitioning context, and Figure 5 shows the flexible partitioning context.
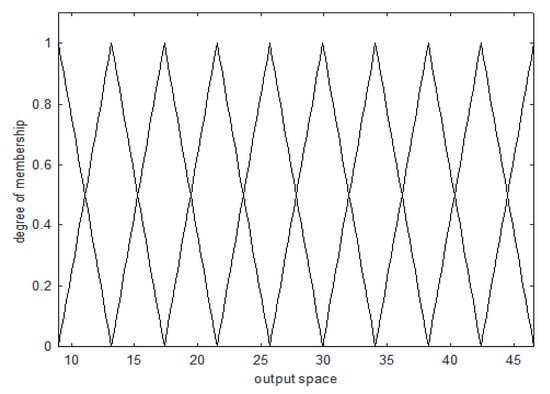
Figure 4.
The method of even partitioning of the linguistic context (case 1).
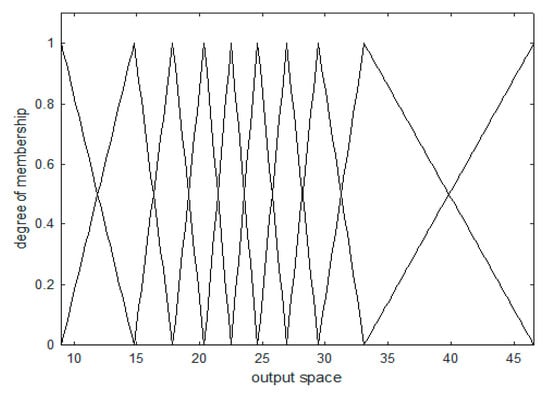
Figure 5.
The method of flexible partitioning of the linguistic context (case 2).
3. Performance Evaluation Method
The accuracy and clarity of the model are essential and important criteria for model evaluation [10]. As described above, the MAE, MAPE, and RMSE methods are widely used for determining the accuracy of predictive models. The MAE metric quantifies the difference between two consecutive variables. Suppose that and are predictive variables that represent the same shape. Examples of versus include prediction time versus observation time, subsequent time versus initial time, and comparison of one measurement technique with an alternative measurement technique. The MAE computes the average vertical distance between predicted and ground truth data points and is used as a general measure for estimating the prediction error in the analysis of time series.
The MAPE metric quantifies the prediction accuracy of a predictive method in statistics and trend estimation. It is also used for evaluating the performance of the loss function for regression problems in the field of machine learning. Typically, the accuracy is expressed as the percentage accuracy, where represents the actual value (ground truth) and represents the predicted value. The difference between and is divided by the ground truth value , and the absolute values are added to obtain the expected value. The result is divided by the number of data points .
The RMSE measures the difference between the predicted values and the ground truth values. This metric is suitable for quantifying precision, and the difference per datum is called the residual. The mean square deviation is used to combine the residuals into one measure. Here, represents the value predicted by the model and is the ground truth value.
3.1. Performance Evaluation Method Suitable for the GM
In this paper, we compared and analyzed performance evaluation methods suitable for the GM, which could evaluate the clarity and analytical ability of the model, instead of the performance evaluation methods, such as the MAE, MAPE, and RMSE. A performance evaluation method suitable for the GM was proposed by Pedrycz and required us to know the coverage and specificity. Coverage is related to the linguistic context and the number of clusters to be created in each context. Specificity is related to the length of the triangular fuzzy number and indicates how specific and detailed the fuzzy number is. Using the coverage and specificity measures, we obtained the PI [26,27,28,29,30,31,32] as the final performance quantifier. In this paper, the predicted performances of different particle models, taken from several studies [26,27,28,29,30,31,32], were compared and analyzed using the performance evaluation method proposed by Hu [30]. The concepts of coverage and specificity are explained in Table 1.

Table 1.
Equations that describe different performance evaluation methods.
3.1.1. Coverage
This is the most basic metric for evaluating the GM performance. Figure 6 illustrates the concept of coverage. Coverage represents the extent to which information granulation is expressed as a result generated by the model. Higher coverage improves a GM’s modeling capabilities. If the actual value is in the range, 1 is returned, otherwise 0 is generated. After calculating the purge water, which is the output of GM, it is confirmed whether the actual output value belongs to the purge water range or not.
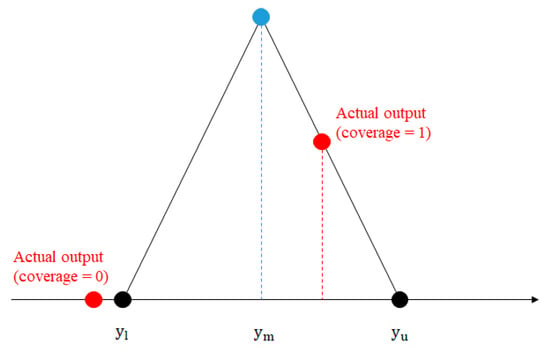
Figure 6.
Schematic of the coverage.
3.1.2. Specificity
Coverage is also important for performance evaluation, but the specificity of detail and characterization also plays an important role. Specificity is the range from the lower value to the upper value. Figure 7 illustrates the concept of specificity. The narrower the range, the higher the specificity and the characteristics. The wider the range, the smaller the detail and the characteristics. In the limit of converged range, specificity attains a maximum of 1.
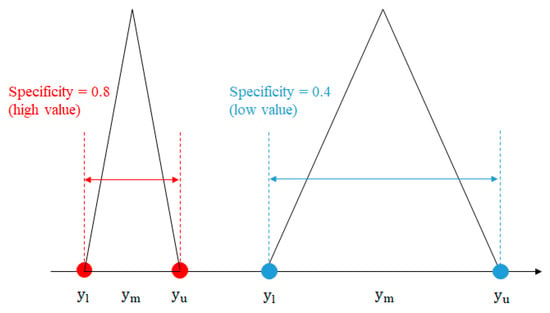
Figure 7.
Schematic of the specificity.
Figure 8 shows the relationship between coverage and specificity. It can be seen that the two quantities exhibit a tradeoff: For higher coverage, the specificity is lower, while for lower coverage, the specificity is higher. The results of the performance evaluation method vary depending on how the above-described coverage and specificity are defined.
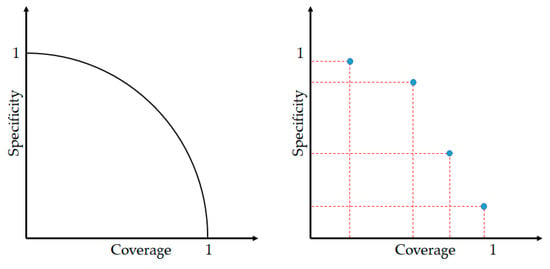
Figure 8.
Relationship between coverage and specificity.
4. Experimental Results
In this section we compare the predictive performances of different GMs using the linguistic context segmentation, using the performance evaluation method proposed by Hu [30] among the performance evaluation methods suitable for the GM, as described in Section 3. To evaluate the predictive performances of different GMs, an experiment was conducted to estimate the vehicle fuel consumption using the auto MPG database.
4.1. Auto MPG Database
In this experiment, we compared and analyzed the predictive performances of different GMs using the auto MPG database. The auto MPG [33] data were obtained for different car types, in terms of the vehicle fuel consumption. The size of the dataset is 392 × 8, with six input variables: number of cylinders, displacement, horsepower, weight, acceleration, and model year. The output variable is the car fuel consumption. Although the car model names were given as a string, this descriptor was not used in this experiment. The data were partitioned by 50:50 into the training set and validation set, and the values were standardized (rescaled to the 0–1 range) for more accurate classification.
4.2. Experiment Method and Analysis of Results
The experimental method was as follows. To evaluate the predictive performance of the GM that divided the linguistic context evenly and the GM that flexibly divided the linguistic context, Hue [30] proposed the use of comparative analysis. The number of the linguistic contexts of the GM varied from 2 to 10, in steps of 1. The number of clusters generated for each linguistic context varied from 2 to 10 in steps of 1, and the fuzzification coefficient was fixed to 2; the experiment was conducted under these conditions. First, the model output of the GM was compared with the output of the auto MPG database. Next, we validated the predictive performance of the GM using the RMSE metric, a general performance evaluation method, and the predictive performance of the GM using the coverage and specificity.
Figure 9 shows the output of the GM that equally divides the output value of the auto MPG validation data and the linguistic context, and the output of the GM that flexibly divides the linguistic context. The figure shows that the values predicted by the model are similar to the ground truth values. Figure 10 and Figure 11 show the performance evaluation results for the GM that flexibly divides the linguistic context, in terms of the RMSE. Table 2 and Table 3 shows the performance evaluation results for each GM, in terms of the RMSE. The performance evaluation in terms of the RMSE show that the GM that flexibly divides the linguistic context and exhibits excellent results, with the RMSE of 3.73.
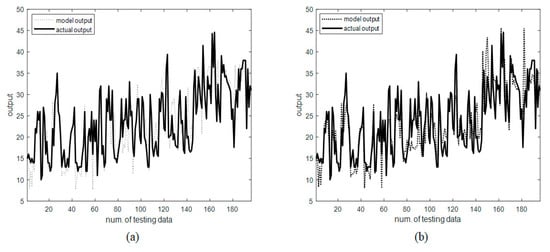
Figure 9.
Predictive performance of different GMs: (a) The GM that evenly divides the linguistic context; (b) the GM that flexibly divides the linguistic context.
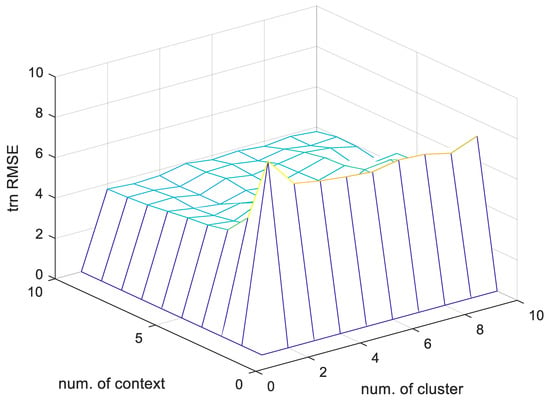
Figure 10.
RMSE performance results on the training dataset for the GM that flexibly splits the linguistic context.
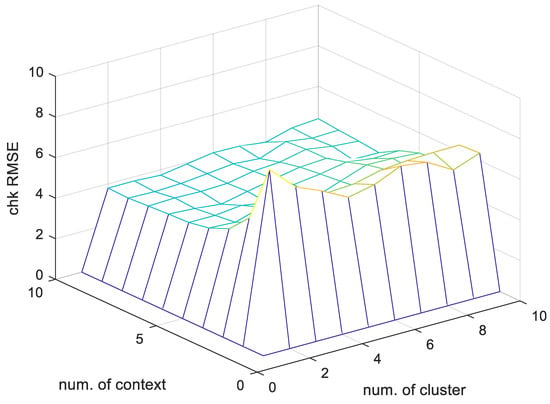
Figure 11.
Root mean square error (RMSE) performance results on the test dataset for the GM that flexibly splits the linguistic context.

Table 2.
RMSE prediction performance results for the GM that evenly divides the linguistic context.

Table 3.
RMSE prediction performance results for the GM that flexibly divides the linguistic context.
Figure 12 and Figure 13 show the predictive performance results for the GM that flexibly segments the linguistic context obtained through the performance evaluation method proposed by Hu [30]. Figure 14 shows the predictive performance results in the form of a line chart.
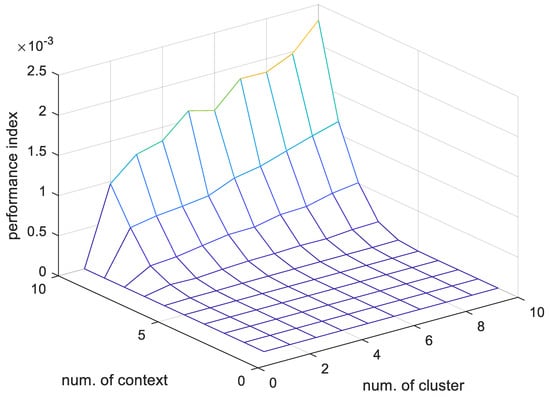
Figure 12.
Predictive performance for the GM that flexibly divides the linguistic context using the method proposed by Hu [30] (using training data).
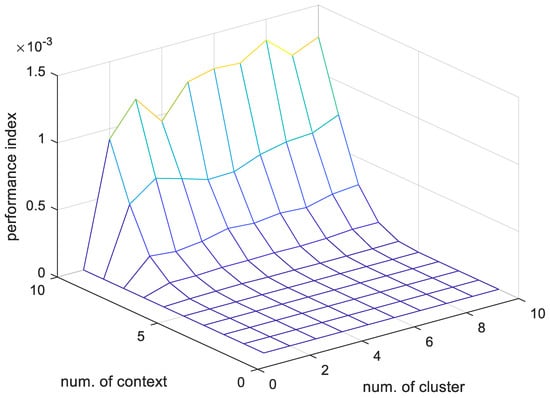
Figure 13.
Performance index of the GM by the variation of the number of contexts and clusters (flexible contexts).
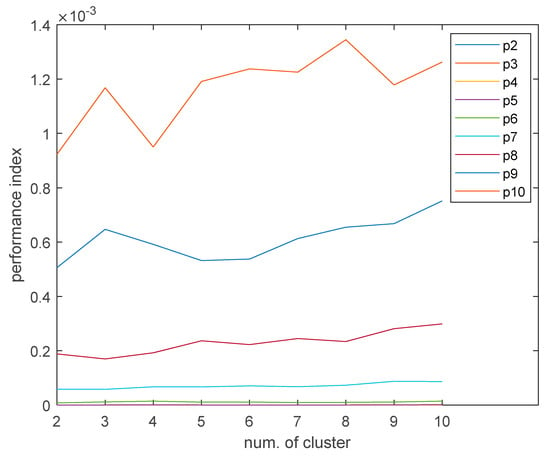
Figure 14.
Performance index of the GM by the variation of the number of contexts (flexible contexts).
Table 4 and Table 5 show the predictive performance of the different GMs by Hu’s [30] method. The GM that evenly divides the linguistic context shows the best results when the number of contexts is 10 and the number of clusters is 10. The GM that flexibly partitions the linguistic context yields the best results when the number of contexts is 10 and the number of clusters is 8.

Table 4.
Predictive performance for the GM that evenly divides the linguistic context using the method proposed by Hu [30].

Table 5.
Predictive performance for the GM that flexibly divides the linguistic context using the method proposed by Hu [30].
5. Discussion
In the case of contexts that are equally spaced in the output space in the design of the GM, the PI value was 1.70 when the number of contexts and clusters per context were 10 and 9, respectively. Here, we obtained the best case as the number of clusters per context increased from 2 to 10. On the other hand, in the case of flexible contexts generated in the output space, the PI value was 13.45 when the number of contexts and clusters per context were 10 and 8, respectively. As a result of comparing the predicted performances of the two GMs, it was confirmed that the GM performance in the case of flexible contexts was excellent, and the predication performance of GMs could be interpreted with the use of coverage and specificity.
6. Conclusions
In this paper, we compared and analyzed the predictive performances of linguistic context segmentation methods of GMs constructed by information granulation. Partitioning of the linguistic context was considered separately for methods that partition evenly and flexibly, and the performance evaluation method proposed by Hu [30] was used, which is suitable for the RMSE and GMs. The experimental results revealed that GM with flexible contexts in the output space showed good prediction performance in comparison to that with equally spaced contexts. In future work, we will consider ways of improving the prediction performance by using optimization algorithms with the linguistic context segmentation method.
Author Contributions
C.-U.Y. suggested the idea of the work and performed the experiments. K.-C.K. designed the experimental method. Both authors wrote and critically revised the paper.
Funding
This research received no external funding.
Acknowledgments
This work was supported by the “Human Resources Program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and was granted financial resources from the Ministry of Trade, Industry & Energy, Republic of Korea. (No. 20194030202410). This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) and funded by the Ministry of Education (No.2018R1D1A1B07044907).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Das, A.K.; Subramanian, K.; Sundaram, S. An evolving interval type-2 neurofuzzy inference system and its metacognitive sequential learning algorithm. IEEE Trans. Fuzzy Syst. 2015, 23, 2080–2093. [Google Scholar]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar]
- Zhang, J.; Deong, Z.; Choi, K.S.; Wang, S. Data-driven elastic fuzzy logic system modeling: Constructing a concise system with human-like inference mechanism. IEEE Trans. Fuzzy Syst. 2017, 26, 2160–2173. [Google Scholar]
- Alizadeh, S.; Kalhor, A.; Jamalabadi, H.; Araabi, B.N.; Ahmadabadi, M.N. Online local input selection through evolving heterogeneous fuzzy inference system. IEEE Trans. Fuzzy Syst. 2016, 24, 1364–1377. [Google Scholar]
- Cervantes, J.; Wu, W.; Salazar, S.; Chairez, I. Takagi-sugeno dynamic neuro-fuzzy controller of uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 2016, 25, 1601–1615. [Google Scholar]
- Juang, C.F.; Chen, C.Y. An interval type-2 neural fuzzy chip with on-chip incremental learning ability for time-varying data sequence prediction and system control. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 216–228. [Google Scholar]
- Deng, Z.; Jiang, K.S.; Choi, K.S.; Chung, F.L.; Wang, S. Knowledge-leverage-based TSK fuzzy system modeling. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1200–1212. [Google Scholar]
- Pedrycz, W.; Vasilakos, V. Linguistic models and linguistic modeling. IEEE Trans. Syst. Man Cybern. 1999, 29, 745–757. [Google Scholar]
- Pedrycz, W.; Kwak, K.C. The development of incremental models. IEEE Trans. Fuzzy Syst. 2007, 15, 507–518. [Google Scholar]
- Kwak, K.C.; Pedrycz, W. A design of genetically oriented linguistic model with the aid of fuzzy granulation. In Proceedings of the IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010; pp. 1–6. [Google Scholar]
- Juneja, K. A fuzzy-filtered neuro-fuzzy framework for software fault prediction for inter-version and inter-project evaluation. Appl. Soft Comput. 2019, 77, 696–713. [Google Scholar]
- Chen, T. Forecasting the yield of a semiconductor product using a hybrid-aggregation and entropy-consensus fuzzy collaborative intelligence approach. Measurement 2019, 142, 60–67. [Google Scholar]
- Sarabakha, A.; Fu, C.; Kayacan, E. Intuit before tuning: Type-1 and type-2 fuzzy logic controllers. Appl. Soft Comput. 2019, 81, 105495. [Google Scholar]
- Yeom, C.U.; Kwak, K.C. Short-term electricity-load forecasting using a TSK-based extreme learning machine with knowledge representation. Energies 2017, 10, 1613. [Google Scholar]
- Maroufpoor, S.; Maroufpoor, E.; Haddad, O.B.; Shiri, J.; Yaseen, Z.M. Soil moisture simulation using hybrid artificial intelligent model: Hybridization of adaptive neuro fuzzy inference system with grey wolf optimizer algorithm. J. Hydrol. 2019, 575, 544–556. [Google Scholar]
- Ali, D.; Yohanna, M.; Ijasini, P.M.; Garkida, M.B. Application of fuzzy-neuro to model weather parameter variability impact on electrical load based on long-term forecasting. Alex. Eng. J. 2018, 57, 223–233. [Google Scholar]
- Bacani, F.; Barros, L.C. Application of prediction models using fuzzy sets: A bayesian inspired approach. Fuzzy Sets Syst. 2017, 319, 104–116. [Google Scholar]
- Tak, N. Meta fuzzy functions: Application of recurrent type-1 fuzzy functions. Appl. Soft Comput. 2018, 73, 1–13. [Google Scholar]
- Carvalho, J.G., Jr.; Costa, C.T., Jr. Non-iterative procedure incorporated into the fuzzy identification on a hybrid method of functional randomization for time series forecasting models. Appl. Soft Comput. 2019, 80, 226–242. [Google Scholar]
- Roy, K.; Mukherjee, A.; Jana, D.K. Prediction of maximum oil-yield from almond seed in a chemical industry: A novel type-2 fuzzy logic approach. S. Afr. J. Chem. Eng. 2019, 29, 1–9. [Google Scholar]
- Khalifa, T.R.; Nagar, A.M.; Brawany, M.A.; Araby, E.A.G.; Bardini, M. A novel fuzzy wiener-based nonlinear modeling for engineering applications. In ISA Transactions; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Naderi, M.; Khamehchi, E. Fuzzy logic coupled with exhaustive search algorithm for forecasting of petroleum economic parameters. J. Pet. Sci. Eng. 2019, 176, 291–298. [Google Scholar]
- Xie, S.; Xie, Y.; Li, F.; Jiang, Z.; Gui, W. Hybrid fuzzy control for the goethite process in zinc production plant combining type-1 and type-2 fuzzy logics. Neurocomputing 2019, 366, 170–177. [Google Scholar]
- Altunkaynak, A.; Kartal, E. Performance comparison of continuous wavelet-fuzzy and discrete wavelet-fuzzy models for water level predictions at northern and southern boundary of Bosphorus. Ocean Eng. 2019, 186, 106097. [Google Scholar]
- Yeom, C.U.; Kwak, K.C. The development of improved incremental models using local granular networks with error compensation. Symmetry 2017, 9, 266. [Google Scholar]
- Tsehayae, A.A.; Pedrycz, W.; Fayek, A.R. Application of granular fuzzy modeling for abstracting labour productivity knowledge bases. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013. [Google Scholar]
- Pedrycz, W.; Hmouz, R.; Balamash, A.S.; Morfeq, A. Hierarchical granular clustering: An emergence of information granules of higher type and higher order. IEEE Trans. Fuzzy Syst. 2015, 23, 2270–2283. [Google Scholar]
- Pedrycz, W.; Wang, X. Designing fuzzy sets with the use of the parametric principle of justifiable granularity. IEEE Trans. Fuzzy Syst. 2015, 24, 489–496. [Google Scholar]
- Zhu, X.; Pedrycz, W.; Li, Z. Granular data description: Designing ellipsoidal information granules. IEEE Trans. Cybern. 2016, 47, 4475–4484. [Google Scholar]
- Hu, X.; Pedrycz, W.; Wang, X. Granular fuzzy rule-based models: A study in a comprehensive evaluation and construction of fuzzy models. IEEE Trans. Fuzzy Syst. 2016, 25, 1342–1355. [Google Scholar]
- Zhu, X.; Pedrycz, W.; Li, Z. Granular models and granular outliers. IEEE Trans. Fuzzy Syst. 2018, 26, 3835–3846. [Google Scholar]
- Galaviz, O.F.R.; Pedrycz, W. Granular fuzzy models: Analysis, design, and evaluation. Int. J. Approx. Reason. 2015, 64, 1–19. [Google Scholar]
- UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets/ (accessed on 4 December 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).