Space–Time Spectral Collocation Method for Solving Burgers Equations with the Convergence Analysis

Abstract

This article deals with a numerical approach based on the symmetric space-time Chebyshev spectral collocation method for solving different types of Burgers equations with Dirichlet boundary conditions. In this method, the variables of the equation are first approximated by interpolating polynomials and then discretized at the Chebyshev–Gauss–Lobatto points. Thus, we get a system of algebraic equations whose solution is the set of unknown coefficients of the approximate solution of the main problem. We investigate the convergence of the suggested numerical scheme and compare the proposed method with several recent approaches through examining some test problems.

1. Introduction

Many phenomena in physics, biology and engineering can be modelled mathematically by partial differential equations (PDEs). The Burgers equation is one of the most important PDEs to be surveyed in the recent years by many researchers [1,2]. This equation describes various kinds of phenomena in plasma physics, solid state physics, optical fibers, fluid dynamics, chemical kinetics, non-linear acoustics, gas dynamics, traffic flow, etc.

Also, the generalized Burgers–Fisher equation is one of the most important classes of non-linear PDEs which has appeared in several categories of applications, such as shockwave formation, turbulence, heat conduction, sound waves in viscous medium, and some other fields of applied branches of science and engineering [3]. Moreover, The Burgers–Huxley equation has been considered to be an evolution equation that describes nerve pulse propagation in biology from which molecular CB properties shall be computed. The generalized Burgers–Huxley equation was investigated to describe the interaction between reaction mechanisms, convection effects, and diffusion transport [4].

Since an analytical in a closed-form solution is generally unavailable for non-linear PDEs, numerical methods are widely used for solving them. There are some effective numerical methods to solve PDEs, especially for the Burgers equation. In [5], a comprehensive review of some techniques is presented. Berger and Kohn in [6] used the med refinement method. Budd et al. in [7] applied mesh movement. Soheili et al. used a moving-mesh PDE (MMPDE) approach [8]. In [9], Ramadan et al. suggested a method based on collocation of septic B-splines over finite elements for numerical solutions of the non-linear Burgers equation. Ramadan and El-Danaf considered the solution of the modified Burgers equation using the collocation method with quintic splines [10]. Haq et al. in [11] formulated simple classical radial basis functions (RBFs) collocation method for the numerical solution of the non-linear dispersive and dissipative Burgers equation. Both Orac et al. in [12] and Lepik in [13] investigated the numerical solutions using Haar wavelet. Inan and Bahadir described implicit exponential difference method in two cases: finite and fully finite [14]. Saka and Dog used quintic B-spline collocation procedure [15]. Irk in [16] used sextic B-spline collocation technique. In [17], Demiray suggested the hyperbolic tangent method and presented travelling wave solution for the perturbed Burgers equation. Hon and Mao in [18] applied the multiquadric (MQ) as a spatial approximation scheme. Schulze-Halberg discussed a linearization method for solving Burgers equation with time dependent coefficients and a non-linear forcing term [19]. In [20], Seydaoglu presented the high-order splitting methods. Guo et al. proposed a high-order finite-volume compact scheme [21]. In [22], Mukundan and Awasthi used new efficient numerical techniques for solving one-dimensional quasi-linear Burgers equation. Hammad and El-Azab solved Burgers–Huxley and Burgers–Fisher equations with discretization in time by a new linear approximation scheme and in space by a high order compact finite difference method in [23]. In [24], Arora and Kumar used a new numerical method entitled “modified cubic B-spline differential quadrature method (MCB-DQM)” to find the approximate solution of the Burgers equations.El-Wakil et al. presented the Burgers equation and some other PDEs with self-similar solutions [25]. Singh et al. in [26] approximated numerical solutions for the generalized Burgers–Huxley (gBH) equation using modified cubic B-spline differential quadrature method (MCB-DQM). The scheme was based on the differential quadrature method in which the weighted coefficients were computed using modified cubic B-splines as a set of basis functions.

The spectral collocation (SC) method is one of the most important methods to solve continuous-time problems including ODEs and PDEs systems in various fields of science and engineering. In this method, an interpolating polynomial is applied to approximate the unknown function. In fact, unknown function in the problem can be expressed in the term of the approximate values at the special nodes. This method shows suitable results in comparison with those of other methods, since it has used the orthogonal polynomials for instance, Legendre and Chebyshev polynomials.

Weinan in [27] analyzed numerical methods for some evolutionary equations which admit semigroup formulations and the author shows the spectral accuracy of the spectral and pseudospectral methods for the Burgers equation. Xiao et al. used the non-linear Petrov–Galerkin method to reduce the order of Navier–Stokes equations and improved the stability of ROM results without tuning parameters. Also, the obtained numerical results show that the proposed POD Petrov–Galerkin method gives more accurate and stable results than the corresponding results obtained by using the POD Bubnov–Galerkin method [28]. In [29], a generalized Langevin equation is investigated and shown that the form of its coefficients depends critically on the assumption of continuity of the reconstructed trajectory. In [30], the two-dimensional unsteady Burgers equation is presented and the authors use the 4-bit lattice Boltzmann model to solve the 2D unsteady Burgers equation. In [31], numerical solutions for the 2D Burgers equation are computed using higher-order accurate finite difference schemes. More precisely, the author used the fourth-order accurate Du Fort Frankel scheme for solving the two-dimensional Burgers equation.

In this paper, we apply the symmetric space-time Chebyshev SC (CSC) method for solving Burgers equation and compare the associated results with those of some other aforementioned well-known methods. Through the numerical examples, we show that CSC method is more effective than other methods and we can achieve to more precise results for the solution of Burgers equations. In fact, we see that the number of discretization points (i.e., the CGL points in CSC method) and also the error of CSC method are less than the others used to solve Burgers equations.

This paper is organized as follows: In Section 2, Burgers equation and its different types are introduced. The CSC method for Burgers equation is implemented in Section 3. In Section 4, the convergence of the CSC method is analyzed. Next, the two-dimensional Burgers equation is introduced in Section 5 and the CSC method is applied to solve the equation. Then, Section 6 contains numerical examples to solve the Burgers equations in both cases of one and two-dimensional. Also, the figures of errors (associated with the proposed method) are depicted in some cases which confirm the efficiency of our suggested numerical scheme. Finally, the paper is concluded with a reasonable conclusion.

2. Burgers Equation

Three important types of Burgers equations are as follows:

• For a field $V(.,.)$ and diffusion coefficient (or viscosity, as in the original fluid mechanical context) $\epsilon$, the general form of viscous Burgers equation is as follows

  $$\begin{array}{c}\hfill V_t+V{V}_x-\epsilon V_{xx}=0,a\le x\le b,t>0.\end{array}$$

  (1)
• The Burgers–Fisher equation is a non-linear PDE of second order of the form

  $$\begin{array}{c}\hfill V_t-V_{xx}+\alpha (t)V{V}_x=\beta (t)V(1-V),a\le x\le b,\end{array}$$

  (2)

  where $\alpha (.)$ and $\beta (.)$ are given functions. It plays an important role in various fields of gas dynamics, traffic flow, physics applications, financial and applied mathematics [23].
• The Burgers–Huxley equation is as follows

  $$\begin{array}{c}\hfill V_t+\alpha V^{\delta }{V}_x-\beta V_{xx}=\gamma V(1-V^{\delta })(V^{\delta }-\eta ),0\le x\le 1,\end{array}$$

  (3)

  where $\alpha ,$$\beta ,$$\delta ,$$\gamma$ and $\eta$ are given constants. The Burgers–Huxley as a non-linear PDE describes the interaction between reaction mechanisms, convection effects, and diffusion transports [23].

In this paper, we represent the Burgers Equations (1)–(3) as the following general form

$$\begin{array}{c}\hfill V_t=\mathsf{\Lambda }(t,V,V_x,V_{xx}).\end{array}$$

(4)

The time initial and space boundary conditions (in Dirichlet form) for Burgers Equation (4) are usually given as follows

$$\begin{array}{c}\hfill V(0,x)=f(x),a\le x\le b,\end{array}$$

(5)

$$\begin{array}{c}\hfill V(t,a)=g_1(t),t\in [T_0,T_1],\end{array}$$

(6)

$$\begin{array}{c}\hfill V(t,b)=g_2(t),t\in [T_0,T_1].\end{array}$$

(7)

3. Implementing the CSC Method

Here, the CSC method for Burgers Equation (4) with conditions (5)–(7) is presented. The CSC method [32,33,34] is one of the most efficient numerical methods to solve continuous-time problems. Recently, some researchers have applied it to solve special problems (see [35,36,37]). One of the most important advantages of CSC method in comparison with other approximate methods is the high degree of accuracy that CSC approximations offer. Also, the CSC underlying polynomial space spanned by Chebyshev orthogonal polynomials on the interval $[-1,1]$ with respect to a weight function $w(t)={\displaystyle \frac{1}{\sqrt{1-t^2}}}$. In the CSC method, we use some points on the interval $[-1,1]$ to discretize the problem. Hence, we first transform the variables of Equation (4) to this interval by the following relations

$$\left\{\begin{array}{cc}t={\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}},\hfill & t\in [T_0,T_1],\overline{t}\in [-1,1],\hfill \\ x={\displaystyle \frac{b-a}{2}}\overline{x}+{\displaystyle \frac{b+a}{2}},\hfill & x\in [a,b],\overline{x}\in [-1,1].\hfill \end{array}\right.$$

(8)

Therefore, Burgers Equation (4)–(7) converted into the following form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{U}_{\overline{t}}=\psi \left(\overline{t},U(\overline{t},\overline{x}),U_{\overline{x}}(\overline{t},\overline{x}),U_{\overline{x}\overline{x}}(\overline{t},\overline{x})\right),\hfill \\ U(-1,\overline{x})=F(\overline{x}),\hfill \\ U(\overline{t},-1)=G_1(\overline{t}),\hfill \\ U(\overline{t},1)=G_2(\overline{t}),\hfill \end{array}\right.\end{array}$$

(9)

where

$$\begin{array}{c}\psi \left(\overline{t},U,U_{\overline{x}},U_{\overline{x}\overline{x}}\right)={\displaystyle \frac{T_1-T_0}{2}}\mathsf{\Lambda }\left({\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}},U,U_{\overline{x}},U_{\overline{x}\overline{x}}\right)\hfill \\ U(\overline{t},\overline{x})=V({\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}},{\displaystyle \frac{b-a}{2}}\overline{x}+{\displaystyle \frac{b+a}{2}}),\hfill \\ U_{\overline{x}}(\overline{t},\overline{x})=\frac{2}{b-a}{V}_x({\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}},{\displaystyle \frac{b-a}{2}}\overline{x}+{\displaystyle \frac{b+a}{2}}),\hfill \\ U_{\overline{x}\overline{x}}(\overline{t},\overline{x})={\left(\frac{2}{b-a}\right)}^2{V}_{xx}({\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}},{\displaystyle \frac{b-a}{2}}\overline{x}+{\displaystyle \frac{b+a}{2}}),\hfill \\ F(\overline{x})=f({\displaystyle \frac{b-a}{2}}\overline{x}+{\displaystyle \frac{b+a}{2}}),\hfill \\ G_1(\overline{t})=g_1({\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}}),\hfill \\ G_2(\overline{t})=g_2({\displaystyle \frac{T_1-T_0}{2}}\overline{t}+{\displaystyle \frac{T_1+T_0}{2}}).\hfill \end{array}$$

To discretize system (9), we use the CGL points on $[-1,1]$ which are defined by the following relations

$$\begin{array}{c}\hfill {\overline{x}}_k={\overline{t}}_k=cos(\frac{N-k}{N}\pi ),k=0,1,...,N,\end{array}$$

(10)

where they are the roots of $(1-\overline{t}{}^2){\displaystyle \frac{d{T}_N}{d\overline{t}}}$ and $T_N(.)$ is the Chebyshev polynomial of order N. It should be noted that the Chebyshev polynomials are expressed by

$$\begin{array}{c}\hfill T_j(\overline{t})=cos(jco{s}^{-1}(\overline{t})),\overline{t}\in [-1,1],j=0,1,\dots ,N,\end{array}$$

(11)

and it is easy to show that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{T}_0(\overline{t})=1,T_1(\overline{t})=\overline{t}\hfill \\ T_{j+1}(\overline{t})=2\overline{t}{T}_j(\overline{t})-T_{j-1}(\overline{t}),j=1,2,\dots .\hfill \end{array}\right.\end{array}$$

For interpolating in the CSC method, the following Lagrange polynomials are used

$$\begin{array}{c}\hfill L_k(\overline{t})=\prod _{\begin{array}{c}j=0\\ j\ne k\end{array}}^N{\displaystyle \frac{\overline{t}-{\overline{t}}_j}{{\overline{t}}_k-{\overline{t}}_j}}=\frac{2}{N{\mu }_k}\sum _{j=0}^N\frac{1}{{\mu }_j}{T}_j({\overline{t}}_k)T_j(\overline{t}),k=0,1,\dots ,N,\overline{t}\in [-1,1],\end{array}$$

where

$$\begin{array}{c}\hfill {\mu }_j=\left\{\begin{array}{cc}2,\hfill & ifj=0,N,\hfill \\ 1,\hfill & if1\le j\le N-1,\hfill \end{array}\right.\end{array}$$

and we have

$$\begin{array}{c}\hfill L_j({\overline{t}}_k)={\delta }_{jk}=\left\{\begin{array}{cc}1,\hfill & ifj=k,\hfill \\ 0,\hfill & ifj\ne k.\hfill \end{array}\right.\end{array}$$

(12)

In the CSC method, to approximate the solution of Burgers Equation (9), we use the following polynomial interpolation

$$U(\overline{t},\overline{x})\approx U^N(\overline{t},\overline{x})=\sum _{i=0}^N\sum _{j=0}^N{\overline{a}}_{ij}^N{L}_i(\overline{t})L_j(\overline{x}).$$

(13)

By (12), we have

$$U^N({\overline{t}}_i,{\overline{x}}_j)={\overline{a}}_{ij}^N.$$

(14)

To express the derivative $U_{\overline{t}}^N(·,·),U_{\overline{x}}^N(·,·)$ and $U_{\overline{x}\overline{x}}^N(·,·)$ in terms of $U^N(·,·)$ at the node points ${\overline{t}}_k$, we can use the matrix multiplication $D=(D_{kj})$ and get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{U}_{\overline{t}}^N({\overline{t}}_p,{\overline{x}}_k)=\sum _{i=0}^N{\overline{a}}_{ik}^N{D}_{pi},\hfill \\ U_{\overline{x}}^N({\overline{t}}_p,{\overline{x}}_k)=\sum _{j=0}^N{\overline{a}}_{pj}^N{D}_{kj},\hfill \\ U_{\overline{x}\overline{x}}^N({\overline{t}}_p,{\overline{x}}_k)=\sum _{j=0}^N{\overline{a}}_{pj}^N{\widehat{D}}_{kj},k,p=0,1,\dots ,N,\hfill \end{array}\right.\end{array}$$

(15)

where

$$\begin{array}{c}\hfill D_{kj}=L_j^{\prime }({\overline{t}}_k)=\left\{\begin{array}{cc}{\displaystyle \frac{{\mu }_k}{{\mu }_j}}{(-1)}^{k+j}{\displaystyle \frac{1}{{\overline{t}}_k-{\overline{t}}_j}},\hfill & ifj\ne k,\hfill \\ -{\displaystyle \frac{{\overline{t}}_k}{2-2{\overline{t}}_k^2}},\hfill & if0\le j=k\le N-1,\hfill \\ -{\displaystyle \frac{2N^2+1}{6}},\hfill & ifj=k=0,\hfill \\ {\displaystyle \frac{2N^2+1}{6}},\hfill & ifj=k=N,\hfill \end{array}\right.\end{array}$$

(16)

$\widehat{D}=D·D=({\widehat{D}}_{kj})$, ${\widehat{D}}_{kj}={\sum }_{l=0}^N{D}_{kl}{D}_{lj},k,j=0,1,\dots ,N$. In fact, multiplication by matrix D transforms a vector of the state variables at the CGL points to the vector of approximate derivatives at these points.

Now, by relations (14) and (15), the system (9) can be converted into the following system of algebraic equations

$$\left\{\begin{array}{c}\sum _{i=0}^N{\overline{a}}_{ik}^N{D}_{pi}-\psi \left({\overline{t}}_p,{\overline{a}}_{pk}^N,\sum _{j=0}^N{\overline{a}}_{pj}^N{D}_{kj},\sum _{j=0}^N{\overline{a}}_{pj}^N{\widehat{D}}_{kj}\right)=0,\hfill \\ {\overline{a}}_{0k}^N=F({\overline{x}}_k);k=0,1,\dots ,N,\hfill \\ {\overline{a}}_{p0}^N=G_1({\overline{t}}_p),{\overline{a}}_{pN}^N=G_2({\overline{t}}_p);p=1,\dots ,N.\hfill \end{array}\right.$$

(17)

Here, by solving above system with respect to $({\overline{a}}_{pk}^N;p,k=0,1,\dots ,N)$, we can obtain continuous and pointwise approximate solutions (13) and (14), respectively.

4. The Convergence of the Method

In this section, first we give definition of the modulus of continuity and then analyze the convergence of the presented method.

Assume that $\overline{\mathsf{\Omega }}=[-1,1]\times [-1,1]$. With $C^r(\overline{\mathsf{\Omega }})$ we denote the space of the continuous functions with continuous derivatives of rth order.

Definition 1.

Function $W:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ with the following properties is called a modulus of continuity [38]

W is increasing,

1.

${lim}_{z\to 0}W(z)=0$,

2.

for any $z_1$ and $z_2\in {\mathbb{R}}^{+}$, $W(z_1+z_2)\le W(z_1)+W(z_2)$,

3.

there exists a constant c such that for all $0<z\le 2,cW(z)\ge z$.

Some important modulus of continuity can be defined as

$$W(z)=z^{\alpha },0<\alpha \le 1.$$

(18)

Now, assume that $B^2$ is a unit circle in ${\mathbb{R}}^2$. We say that a continuous function $f(·,·)$ on $\overline{\mathsf{\Omega }}$ admits $W(·)$ as a modulus of continuity, if the following value is finite

$${\left|f(·,·)\right|}_W=sup\left\{\frac{|f(\overline{t},\overline{x})-f(\tilde{t},\tilde{x})|}{W\left(\parallel (\overline{t},\overline{x})-(\tilde{t},\tilde{x}){\parallel }_{\infty }\right)}:(\overline{t},\overline{x}),(\tilde{t},\tilde{x})\in \overline{\mathsf{\Omega }},(\overline{t},\overline{x})\ne (\tilde{t},\tilde{x})\right\},$$

(19)

where

$$\begin{array}{c}\hfill \parallel (\overline{t},\overline{x})-(\tilde{t},\tilde{x}){\parallel }_{\infty }=max\left\{\right|\overline{t}-\tilde{t}|,|\overline{x}-\tilde{x}\left|\right\};(\overline{t},\overline{x}),(\tilde{t},\tilde{x})\in \overline{\mathsf{\Omega }},(\overline{t},\overline{x})\ne (\tilde{t},\tilde{x}).\end{array}$$

(20)

With $C_W^1(B^2)$ we denote the space of all functions $f(·,·)$ on $B^2$ with continuous first-order partial derivatives, and let it is endowed with the following norm

$${\parallel f(·,·)\parallel }_{1,W}={\parallel f(·,·)\parallel }_{\infty }+\parallel f_{\overline{t}}{(·,·)\parallel }_{\infty }+\parallel f_{\overline{x}}{(·,·)\parallel }_{\infty }+|f_{\overline{t}}{(·,·)|}_W+{\left|f_{\overline{x}}(·,·)\right|}_W·$$

(21)

Next, define

$$\begin{array}{ccc}\hfill C_W^1(\overline{\mathsf{\Omega }})=& \hfill & \{f(·,·)\in C^1(\overline{\mathsf{\Omega }}):\forall (\tilde{t},\tilde{x})\in \overline{\mathsf{\Omega }},\exists map\varphi :B^2\to \overline{\mathsf{\Omega }},s.t.\hfill \\ \hfill & \hfill & (\tilde{t},\tilde{x})\in int(\varphi (B^2))andf\circ \varphi (·,·)\in C_W^1(B^2)\}.\hfill \end{array}$$

(22)

It can be proved that if $\overline{\mathsf{\Omega }}={\bigcup }_{i=1}^{l}int({\varphi }_i(B^2))$ for some ${\varphi }_1,\dots ,{\varphi }_l$, then $f(·,·)\in C_W^1(\overline{\mathsf{\Omega }})$ if and only if $f\circ {\varphi }_i(·,·)\in C_W(B^2)$ for each $i=1,\dots ,l$. Moreover, $C_W^1(\overline{\mathsf{\Omega }})$ with norm

$${\parallel f(·,·)\parallel }_{1,W}=\sum _{i=1}^l{\parallel f\circ {\varphi }_i(·,·)\parallel }_{1,W},$$

(23)

is a Banach space (for more details see [38]). At follows, we show the space of all polynomials of total degree at most $2N$ on $\overline{\mathsf{\Omega }}$ by $Pol(N,N,\overline{\mathsf{\Omega }})$, i.e.,

$$Pol(N,N,\overline{\mathsf{\Omega }})=\{\eta (\tilde{t},\tilde{x})=\sum _{i=0}^N\sum _{j=0}^N{\gamma }_{ij}{\tilde{t}}^i{\tilde{x}}^j:(\tilde{t},\tilde{x})\in \overline{\mathsf{\Omega }},{\gamma }_{ij}\in \mathbb{R}\}.$$

Theorem 1.

For any $f(·,·)\in C_W^1(\overline{\mathsf{\Omega }})$, there is a polynomial $\eta (·,·)\in Pol(N,N,\overline{\mathsf{\Omega }})$ such that

$${\parallel f(·,·)-\eta (·,·)\parallel }_{\infty }\le \frac{c_0{c}_1}{2N}W({\displaystyle \frac{1}{2N}}),$$

(24)

where $c_1={\parallel f(·,·)\parallel }_{1,W}$ and $c_0$ is a constant that depends on $W(·)$, but independent of N.

Proof. 

The proof is a result of Theorem 2.1 in [38]. □

To prove the existence of solutions of the system (17), we convert it in the following form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}|\sum _{i=0}^N{\overline{a}}_{ik}^N{D}_{pi}-\psi \left({\overline{t}}_p,{\overline{a}}_{pk}^N,\sum _{j=0}^N{\overline{a}}_{pj}^N{D}_{kj},\sum _{j=0}^N{\overline{a}}_{pj}^N{\widehat{D}}_{kj}\right)|\hfill \\ \le \frac{\sqrt{N}}{2N-1}W(\frac{1}{2N-1}),p,k=1,2,\dots ,N-1,\hfill \\ |{\overline{a}}_{p0}^N-G_1({\overline{t}}_p)|\le \frac{\sqrt{N}}{2N-1}W(\frac{1}{2N-1}),|{\overline{a}}_{pN}^N-G_2({\overline{t}}_p)|\le \frac{\sqrt{N}}{2N-1}W(\frac{1}{2N-1}),p=0,1,\dots ,N,\hfill \\ |{\overline{a}}_{0k}^N-F({\overline{x}}_k)|\le \frac{\sqrt{N}}{2N-1}W(\frac{1}{2N-1}),k=0,1,\dots ,N,\hfill \end{array}\right.\end{array}$$

(25)

where N is sufficiently big and $W(·)$ is a given modulus of continuity. Since ${lim}_{N\to \infty }\frac{\sqrt{N}}{2N-1}W(\frac{1}{2N-1})=0$, any solution ${\overline{a}}_N=({\overline{a}}_{pk}^N;p,k=0,1,\dots ,N)$ for system of algebraic inequalities (25) is a solution for system of algebraic Equation (17) when N tends to infinity.

We assume that $\psi$ has bounded and continuous derivatives with respect to its arguments. Hence, there exists a constant M such that

$$\begin{array}{c}\hfill |\psi \left(\overline{t},U,U_{\overline{x}},U_{\overline{x}\overline{x}}\right)-\psi \left(\overline{t},\tilde{U},{\tilde{U}}_{\overline{x}},{\tilde{U}}_{\overline{x}\overline{x}}\right)|\le M|U-\tilde{U}|.\end{array}$$

(26)

Now we will show that the system (25) has at least one solution ${\overline{a}}_N$.

Theorem 2.

Let $U(·,·)$ be a solution for system (9) where $U(·,·)$ is in $C_W^1(\overline{\mathsf{\Omega }})$. Then there is a positive integer K such that for any $N\ge K$, system (25) has a solution as

$${\overline{a}}_N=({\overline{a}}_{pk};p,k=0,1,\dots ,N),$$

(27)

which satisfies

$$|U({\overline{t}}_p,{\overline{x}}_k)-{\overline{a}}_{pk}^N|\le \frac{L}{2N-1}W(\frac{1}{2N-1}),p,k=0,1,\dots ,N,$$

(28)

where L is a positive constant independent of N.

Proof of Theorem 2.

Assume that$\eta (·,·)$in$Pol(N-1,N,\overline{\mathsf{\Omega }})$is the best polynomial approximation of$U_{\overline{t}}(·,·)$. By Theorem 1, we get

$$\parallel U_{\overline{t}}(\overline{t},\overline{x})-\eta (\overline{t},\overline{x}){\parallel }_{\infty }\le \frac{\gamma }{2N-1}W(\frac{1}{2N-1}),(\overline{t},\overline{x})\in \overline{\mathsf{\Omega }},$$

(29)

where $\gamma$ is a constant independent of N. We define

$$\tilde{U}(\overline{t},\overline{x})=U(-1,\overline{x})+{\int }_{-1}^{\overline{t}}\eta (\tau ,\overline{x})d\tau ,(\overline{t},\overline{x})\in \overline{\mathsf{\Omega }},$$

(30)

and

$${\overline{a}}_{pk}^N=\tilde{U}({\overline{t}}_p,{\overline{x}}_k);p,k=0,1,\dots ,N.$$

(31)

We will see that ${\overline{a}}_N=({\overline{a}}_{pk}^N;p,k=0,1,\dots ,N)$ satisfies system (25). By (29)–(31), for $(\overline{t},\overline{x})\in \overline{\mathsf{\Omega }}$, we get

$$\begin{array}{c}|U(\overline{t},\overline{x})-\tilde{U}(\overline{t},\overline{x})|=|{\int }_{-1}^{\tau }(U_{\overline{t}}(\tau ,\overline{x})-\eta (\tau ,\overline{x}))d\tau |\le {\int }_{-1}^{\tau }\left|U_{\overline{t}}(\tau ,\overline{x})-\eta (\tau ,\overline{x})\right|d\tau \hfill \\ \le \frac{\gamma }{2N-1}W(\frac{1}{2N-1}){\int }_{-1}^{\tau }d\tau \le \frac{2\gamma }{2N-1}W(\frac{1}{2N-1}).\hfill \end{array}$$

(32)

Now, by the relation (30), the function $\tilde{U}(·,\overline{x})$, $\overline{x}\in [-1,1]$, is a polynomial of total degree at most $2N$. Hence, its derivatives at CGL nodes ${\overline{t}}_0,{\overline{t}}_1,\dots ,{\overline{t}}_N$ are exactly equal to the value of the polynomial at the nodes multiplied by the differential matrix D, defined by (16). Thus, we have

$$\sum _{i=0}^N{\overline{a}}_{ik}^N{D}_{pi}={\tilde{U}}_{\overline{t}}({\overline{t}}_p,{\overline{x}}_k);p,k=0,1,\dots ,N.$$

(33)

Therefore, by the relations (26) and (32), we get

$$\begin{array}{c}\left|\sum _{i=0}^N{a}_{ik}^N{D}_{pi}-\psi \left({\overline{t}}_p,{\overline{a}}_{pk}^N,\sum _{j=0}^N{\overline{a}}_{pj}^N{D}_{kj},\sum _{j=0}^N{\overline{a}}_{pj}^N{\widehat{D}}_{kj}\right)\right|\hfill \\ \le \left|{\tilde{U}}_{\overline{t}}({\overline{t}}_p,{\overline{x}}_k)-U_{\overline{t}}({\overline{t}}_p,{\overline{x}}_k)\right|+\hfill \\ \left|U_{\overline{t}}({\overline{t}}_p,{\overline{x}}_k)-\psi \left({\overline{t}}_p,{\overline{a}}_{pk}^N,\sum _{j=0}^N{\overline{a}}_{pj}^N{D}_{kj},\sum _{j=0}^N{\overline{a}}_{pj}^N{\widehat{D}}_{kj}\right)\right|\hfill \\ =\left|\eta ({\overline{t}}_p,{\overline{x}}_k)-U_{\overline{t}}({\overline{t}}_p,{\overline{x}}_k)\right|+\hfill \\ \left|\psi \left({\overline{t}}_p,U({\overline{t}}_p,{\overline{x}}_k),U_{\overline{x}}({\overline{t}}_p,{\overline{x}}_k),U_{\overline{x}\overline{x}}({\overline{t}}_p,{\overline{x}}_k)\right)-\psi \left({\overline{t}}_p,{\overline{a}}_{pk}^N,\sum _{j=0}^N{\overline{a}}_{pj}^N{D}_{kj},\sum _{j=0}^N{\overline{a}}_{pj}^N{\widehat{D}}_{kj}\right)\right|\hfill \\ \le \left|\eta ({\overline{t}}_p,{\overline{x}}_k)-U_{\overline{t}}({\overline{t}}_p,{\overline{x}}_k)\right|+M\left|U({\overline{t}}_p,{\overline{x}}_k)-{\overline{a}}_{pk}^N\right|\hfill \\ \le \frac{\gamma }{2N-1}W(\frac{1}{2N-1})+M\frac{2\gamma }{2N-1}W(\frac{1}{2N-1})\hfill \\ =\frac{\gamma (2M+1)}{2N-1}W(\frac{1}{2N-1}),p,k=1,\dots ,N-1,\hfill \end{array}$$

(34)

where M is a Lipschitz constant which satisfies the relation (26). Furthermore, for boundary conditions, we get

$$\begin{array}{cc}\hfill \left|\tilde{U}(-1,{\overline{x}}_k)-F({\overline{x}}_k)\right|& \le \left|\tilde{U}(-1,{\overline{x}}_k)-U(-1,{\overline{x}}_k)\right|+\left|U(-1,{\overline{x}}_k)-F({\overline{x}}_k)\right|\hfill \\ \hfill & \le \frac{2\gamma }{2N-1}W(\frac{1}{2N-1}),k=0,1,\dots ,N.\hfill \end{array}$$

(35)

Also, for all $p=0,1,\dots ,N$,

$$\begin{array}{cc}\hfill & \left|\tilde{U}({\overline{t}}_p,-1)-G_1({\overline{t}}_p)\right|=\left|\tilde{U}({\overline{t}}_p,-1)-U({\overline{t}}_p,-1)\right|\le \frac{2\gamma }{2N-1}W(\frac{1}{2N-1}),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & \left|\tilde{U}({\overline{t}}_p,1)-G_2({\overline{t}}_p)\right|=\left|\tilde{U}({\overline{t}}_p,1)-U({\overline{t}}_p,1)\right|\le \frac{2\gamma }{2N-1}W(\frac{1}{2N-1}).\hfill \end{array}$$

(37)

Hence, if we select K such that

$$\begin{array}{c}\hfill max\{\gamma (2M+1),2\gamma \}\le \sqrt{N},\end{array}$$

for $N\ge K$, then by (34)–(37), ${\overline{a}}_N$ satisfies the system (25). This completes the proof. □

Now, we will show that the sequence of the solutions for the system (25) and the sequence of their interpolating polynomials converge to the solution of the system (9).

Theorem 3.

Let ${\{{\overline{a}}_N={\overline{a}}_{pk}^N;p,k=0,1,\dots ,N\}}_{N=K}^{\infty }$ be a sequence of solutions for the system (25) and ${\left\{U^N(·,·)\right\}}_{N=K}^{\infty }$ be their interpolating polynomials sequence defined by (13). Also, we assume that for any $\overline{x}$ in $[-1,1]$, the sequence ${\left\{(U^N(-1,\overline{x}),U_{\overline{t}}^N(·,·))\right\}}_{N=K}^{\infty }$ has a subsequence ${\left\{(U^{N_i}(-1,\overline{x}),U_{\overline{t}}^{N_i}(·,·))\right\}}_{i=0}^{\infty }$ that uniformly converges to $({\varphi }^{\infty }(\overline{x}),\lambda (·,·))$, where $\lambda (·,·)\in C^2(\overline{\mathsf{\Omega }})$, ${\varphi }^{\infty }(·)\in C^2([-1,1])$ and ${lim}_{i\to \infty }{N}_i=\infty$. Then the pair

$$\begin{array}{c}\hfill \tilde{U}(\overline{t},\overline{x})=\underset{i\to \infty }{lim}{U}^{N_i}(\overline{t},\overline{x}),\end{array}$$

(38)

for $(\overline{t},\overline{x})\in \overline{\mathsf{\Omega }}$, is a solution of the system (9).

Proof of Theorem 3.

By our assumptions, we have

$$\tilde{U}(\overline{t},\overline{x})={\varphi }^{\infty }(\overline{x})+{\int }_{-1}^{\overline{t}}\lambda (\tau ,\overline{x})d\tau .$$

(39)

We first show that $\tilde{U}(\overline{t},\overline{x})$ for $\overline{t}\in [-1,1]$ and $\overline{x}=x_k$, $k=0,1,\dots ,N$ satisfy the system (9). Assume that $\tilde{U}(·,{\overline{x}}_k)$ for some $k=1,\dots ,N-1$ does not satisfy the first equation of (9). Then, there is a $\tau$ in $(-1,1)$ such that

$${\tilde{U}}_{\overline{t}}(\tau ,{\overline{x}}_k)-\psi \left({\overline{t}}_p,\tilde{U}(\tau ,{\overline{x}}_k),{\tilde{U}}_{\overline{x}}(\tau ,{\overline{x}}_k),{\tilde{U}}_{\overline{x}\overline{x}}(\tau ,{\overline{x}}_k)\right)\ne 0.$$

Since the CGL nodes ${\left\{{\overline{t}}_p\right\}}_{p=0}^N$ are dense in $[-1,1]$ when $N\to \infty$, there is a sequence ${\left\{{\overline{t}}_{l_{N_i}}\right\}}_{i=1}^{\infty }$ such that $0<l_{N_i}<N_i$ and ${lim}_{i\to \infty }{\overline{t}}_{l_{N_i}}=\tau$. Thus,

$$\begin{array}{c}\underset{i\to \infty }{lim}\left({\tilde{U}}_{\overline{t}}({\overline{t}}_{l_{N_i}},{\overline{x}}_k)-\psi \left({\overline{t}}_p,\tilde{U}({\overline{t}}_{l_{N_i}},{\overline{x}}_k),{\tilde{U}}_{\overline{x}}({\overline{t}}_{l_{N_i}},{\overline{x}}_k),{\tilde{U}}_{\overline{x}\overline{x}}({\overline{t}}_{l_{N_i}},{\overline{x}}_k)\right)\right)\hfill \\ ={\tilde{U}}_{\overline{t}}(\tau ,{\overline{x}}_k)-\psi \left({\overline{t}}_p,\tilde{U}(\tau ,{\overline{x}}_k),{\tilde{U}}_{\overline{x}}(\tau ,{\overline{x}}_k),{\tilde{U}}_{\overline{x}\overline{x}}(\tau ,{\overline{x}}_k)\right)\ne 0.\hfill \end{array}$$

(40)

On the other hand, since ${lim}_{i\to \infty }\frac{\sqrt{N_i}}{2N_i-1}W(\frac{1}{2N_i-1})=0$, by (25) we obtain

$$\underset{i\to \infty }{lim}\left({\tilde{U}}_{\overline{t}}({\overline{t}}_{l_{N_i}},{\overline{x}}_k)-\psi \left({\overline{t}}_p,\tilde{U}({\overline{t}}_{l_{N_i}},{\overline{x}}_k),{\tilde{U}}_{\overline{x}}({\overline{t}}_{l_{N_i}},{\overline{x}}_k),{\tilde{U}}_{\overline{x}\overline{x}}({\overline{t}}_{l_{N_i}},{\overline{x}}_k)\right)\right)=0,$$

which contradicts with (40). Thus, $\tilde{U}(\overline{t},\overline{x})$ (for all $\overline{t}\in [-1,1]$ and $\overline{x}={\overline{x}}_k,k=1,\dots ,N-1$) satisfies the first equation of (9). Also, it can be easily proven that $\tilde{U}(·,{\overline{x}}_k)$, $k=0,1,\dots ,N$, satisfies the boundary conditions. For example, we show that $\tilde{U}(-1,{\overline{x}}_k)=F({\overline{x}}_k)$ for $k=0,1,\dots ,N$. We have

$$\begin{array}{cc}0\hfill & \le |\tilde{U}(-1,{\overline{x}}_k)-F({\overline{x}}_k)|=|\underset{i\to \infty }{lim}{U}^{N_i}(-1,{\overline{x}}_k)-F({\overline{x}}_k)|=\underset{i\to \infty }{lim}|U^{N_i}(-1,{\overline{x}}_k)-F({\overline{x}}_k)|\hfill \\ & =\underset{i\to \infty }{lim}|{\overline{a}}_{0k}^{N_i}-F({\overline{x}}_k)|\le \underset{i\to \infty }{lim}\frac{\sqrt{N_i}}{2N_i-1}W(\frac{1}{2N_i-1})=0.\hfill \end{array}$$

Hence, $\tilde{U}(-1,{\overline{x}}_k)=F({\overline{x}}_k)$ for all $k=0,1,\dots ,N$. Now, we know that the nodes ${\left\{{\overline{x}}_k\right\}}_{k=0}^N$ are dense in $[-1,1]$ when $N\to \infty$. Therefore the pair $\tilde{U}(·,·)$, defined by (38), is a solution of (9) on $\overline{\mathsf{\Omega }}=[-1,1]\times [-1,1]$. This completes the proof. □

5. The Generalization of the CSC Method for Two-Dimensional Burgers Equation

In this section, we introduce the two-dimensional Burgers equation and solve it by using the CSC method. The two-dimensional Burgers equation is as follows

$$\begin{array}{c}\hfill U_t(x,y,t)+U(x,y,t)U_x(x,y,t)+U(x,y,t)U_y(x,y,t)=\epsilon (U_{xx}(x,y,t)+U_{yy}(x,y,t)),\\ \hfill (x,y,t)\in [0,1]\times [0,1]\times [0,T],\end{array}$$

(41)

and the time initial and space boundary conditions are as follows

$$\begin{array}{c}\hfill U(x,y,0)=f(x,y),\end{array}$$

(42)

$$\begin{array}{c}\hfill U(0,y,t)=h_1(y,t),\end{array}$$

(43)

$$\begin{array}{c}\hfill U(1,y,t)=h_2(y,t),\end{array}$$

(44)

$$\begin{array}{c}\hfill U(x,0,t)=h_3(x,t),\end{array}$$

(45)

$$\begin{array}{c}\hfill U(x,1,t)=h_4(x,t).\end{array}$$

(46)

As we explained ${\overline{x}}_k,{\overline{y}}_n$ and ${\overline{t}}_p$ are the CGL points which were defined in the Section 3.

Now, for obtaining the numerical solution of the two-dimensional Burgers Equation (41) by applying the CSC method, the interpolation polynomial is following

$$U(\overline{x},\overline{y},\overline{t})\approx U^N(\overline{x},\overline{y},\overline{t})=\sum _{i=0}^N\sum _{j=0}^N\sum _{l=0}^N{\overline{a}}_{ijl}^N{L}_i(\overline{x})L_j(\overline{y})L_l(\overline{t}).$$

(47)

By (12), we have

$$U^N({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)={\overline{a}}_{knp}^N$$

(48)

To represent the derivatives $U_{\overline{t}}^N(·,·,·),U_{\overline{x}}^N(·,·,·),U_{\overline{y}}^N(·,·,·),U_{\overline{x}\overline{x}}^N(·,·,·)$ and $U_{\overline{y}\overline{y}}^N(·,·,·)$ in terms of $U^N(·,·,·)$ at the node points $({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)$, by using the matrix multiplication $D=(D_{kj})$, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{U}_{\overline{t}}^N({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)=\sum _{l=0}^N{\overline{a}}_{knl}^N{D}_{pl},\hfill \\ U_{\overline{x}}^N({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)=\sum _{i=0}^N{\overline{a}}_{inp}^N{D}_{ki},\hfill \\ U_{\overline{y}}^N({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)=\sum _{j=0}^N{\overline{a}}_{kjp}^N{D}_{nj},\hfill \\ U_{\overline{x}\overline{x}}^N({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)=\sum _{i=0}^N{\overline{a}}_{inp}^N{\widehat{D}}_{kj},\hfill \\ U_{\overline{y}\overline{y}}^N({\overline{x}}_k,{\overline{y}}_n,{\overline{t}}_p)=\sum _{j=0}^N{\overline{a}}_{kjp}^N{\widehat{D}}_{nj},k,n,p=0,1,\dots ,N,\hfill \end{array}\right.\end{array}$$

(49)

where $D_{kj}$ and ${\widehat{D}}_{kj}$ were defined in the Section 3.

Now, by applying relations (48) and (49) Equation (41) can be rewritten as

$$\left\{\begin{array}{c}\sum _{l=0}^N{\overline{a}}_{knl}^N{D}_{pl}+{\overline{a}}_{knp}\left(\sum _{i=0}^N{\overline{a}}_{inp}^N{D}_{ki}+\sum _{j=0}^N{\overline{a}}_{kjp}^N{D}_{nj}\right)-\epsilon \left(\sum _{i=0}^N{\overline{a}}_{inp}^N{\widehat{D}}_{kj}+\sum _{j=0}^N{\overline{a}}_{kjp}^N{\widehat{D}}_{nj}\right)=0\hfill \\ {\overline{a}}_{kn0}=f({\overline{x}}_k,{\overline{y}}_n),k,n=0,1,\dots ,N,\hfill \\ {\overline{a}}_{0np}=h_1({\overline{y}}_n,{\overline{t}}_p),n=0,1,\dots ,N,p=1,\dots ,N,\hfill \\ {\overline{a}}_{Nnp}=h_2({\overline{y}}_n,{\overline{t}}_p),n=0,1,\dots ,N,p=1,\dots ,N,\hfill \\ {\overline{a}}_{k0p}=h_3({\overline{x}}_k,{\overline{t}}_p),k=1,\dots ,N-1,p=1,\dots ,N,\hfill \\ {\overline{a}}_{kNp}=h_4({\overline{x}}_k,{\overline{t}}_p),k=1,\dots ,N-1,p=1,\dots ,N,\hfill \end{array}\right.$$

(50)

Now, we can obtain the numerical solution of the above system with respect to $({\overline{a}}_{knp}^N;k,n,p=0,1,\dots ,N)$.

6. Numerical Examples

In the following examples, we use the Levenberg-Marquardt method (a quasi-Newton method) for FSOLVE command in MATLAB software to solve the algebraic system (17). We calculate $L_2$ and $L_{\infty }$ errors as follows

$$\begin{array}{cc}\hfill L_2& =\Vert U(\overline{t},·)-U^N(\overline{t},·){\Vert }_2=(\sum _{j=0}^N\mid U(\overline{t},x_j)-U^N(\overline{t},x_j){\mid }^2{)}^{\frac{1}{2}},\hfill \\ \hfill L_{\infty }& =\Vert U(\overline{t},·)-U^N(\overline{t},·){\Vert }_{\infty }=\underset{0\le j\le N}{max}\mid U(\overline{t},x_j)-U^N(\overline{t},x_j)\mid ,\hfill \end{array}$$

(51)

where $x_j,j=0,1,\dots ,N$, are the collocation points, $\overline{t}\in [-1,1]$ is a given point and $U(·,·)$ and $U^N(·,·)$ are the analytical and approximate solutions, respectively. Also, the absolute error can be obtained by

$$\begin{array}{c}\hfill E(\overline{t},\overline{x})=\mid U(\overline{t},\overline{x})-U^N(\overline{t},\overline{x})\mid ,(\overline{t},\overline{x})\in [-1,1]\times [-1,1].\end{array}$$

Example 1.

Consider the Burgers–Fisher Equation (2), where $T_0=-0.2$, $T_1=0$, $a=-1$, $b=0$, $\alpha (t)=24$ and $\beta (t)=-48$ for $t\in [T_0,T_1]$. Also, we assume that the boundary conditions are given by

$$\begin{array}{cc}\hfill U(t,-1)& =\frac{1}{2}-\frac{1}{2}tanh\left[6(-1-8t)\right],\hfill \\ \hfill U(t,0)& =\frac{1}{2}-\frac{1}{2}tanh\left[6(-8t)\right],\hfill \end{array}$$

and the initial condition is as follows

$$\begin{array}{c}\hfill U(-0.2,x)=\frac{1}{2}-\frac{1}{2}tanh\left[6(x+1.6)\right].\end{array}$$

Then the exact solution is

$$\begin{array}{c}\hfill U(t,x)=\frac{1}{2}-\frac{1}{2}tanh\left[6(x-8t)\right].\end{array}$$

We gain the numerical results by the CSC method at $t=-0.1$, $-0.05$, $-0.04$, $-0.035$, $-0.03$ for $N=30\times 30$ which are shown in Table 1. We observe that our numerical results are better than the results of MMPDE methods [8], which they are obtained for $\Delta t={10}^{-6}$ and $\Delta x=\frac{1}{60}$ (or N = 200,000 × 60). In Table 1, $L_2$ errors are presented. In Figure 1 and Figure 2, we show the approximate solution and absolute error, respectively. In Figure 3, we represent the exact and approximate solutions for $t=-0.1$, $-0.05$ and $-0.03$. We also illustrate $L_2$ errors in Figure 4.

Table 1. Comparison of the $L_2$ error for Example 1.

Method	N	$\mathit{t}=-0.1$	$\mathit{t}=-0.05$	$\mathit{t}=-0.04$	$\mathit{t}=-0.035$	$\mathit{t}=-0.03$
Presented method	$30\times 30$	$1.8293\times {10}^{-4}$	$1.1920\times {10}^{-4}$	$1.2691\times {10}^{-4}$	$1.4053\times {10}^{-4}$	$1.4187\times {10}^{-4}$
Mesh for optimal M [8]	200,000 × 60	$2.1\times {10}^{-3}$	$2.9\times {10}^{-3}$	$3.4\times {10}^{-3}$	$3.7\times {10}^{-3}$	$4.2\times {10}^{-3}$
Mesh for arc-length M [8]	200,000 × 60	$2.7\times {10}^{-3}$	$8\times {10}^{-3}$	$7.9\times {10}^{-3}$	$7.6\times {10}^{-3}$	$7.1\times {10}^{-3}$
Mesh for curvature M [8]	200,000 × 60	$2.1\times {10}^{-3}$	$2.4\times {10}^{-3}$	$2.4\times {10}^{-3}$	$2.4\times {10}^{-3}$	$2.5\times {10}^{-3}$

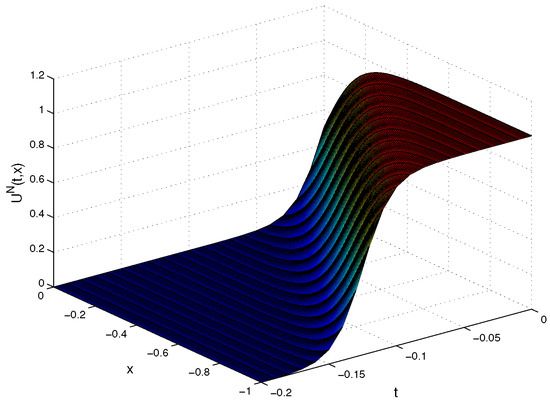
Figure 1. The approximate solution for Example 1.

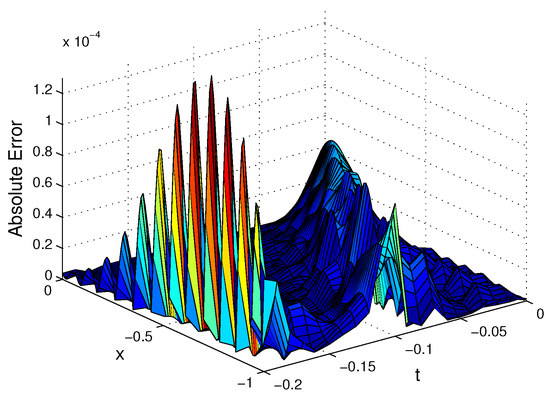
Figure 2. The absolute error $E(.,.)$ for example 1

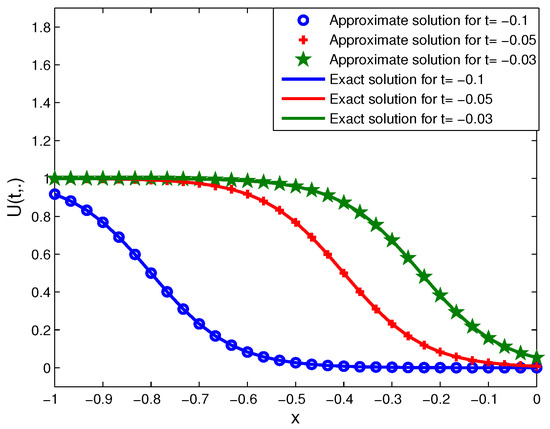
Figure 3. Exact and approximate solutions for $t=-0.1$, $-0.05$ and $-0.03$.

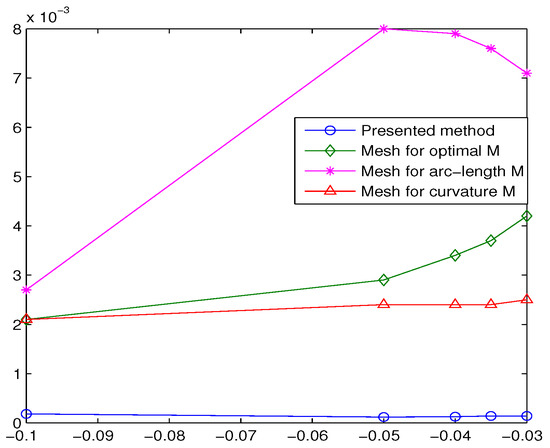
Figure 4. $L_2$ errors for Example 1.

Example 2.

Consider the Burgers–Fisher Equation (2), where $T_0=-0.05$, $T_1=0.05$, $a=-1$, $b=0$, $\alpha (t)=20$ and $\beta (t)=-1+3sint$ for $t\in [T_0,T_1]$. Also, consider the boundary conditions

$$\begin{array}{cc}\hfill U(t,-1)& =\frac{cosh[-1-3cost]+sinh[-1-3cost]-\sqrt{5}}{-4cosh[-1-3cost]+6sinh[-1-3cost]},\hfill \\ \hfill U(t,0)& =\frac{cosh[-3cost]+sinh[-3cost]-\sqrt{5}}{-4cosh[-3cost]+6sinh[-3cost]},\hfill \end{array}$$

and the initial condition

$$\begin{array}{c}\hfill U(-0.05,x)=\frac{cosh[x-3cos(-0.05)]+sinh[x-3cos(-0.05)]-\sqrt{5}}{-4cosh[x-3cos(-0.05)]+6sinh[x-3cos(-0.05)]}.\end{array}$$

By these, the exact solution is as follows

$$\begin{array}{c}\hfill U(t,x)=\frac{cosh[x-3cost]+sinh[x-3cost]-\sqrt{5}}{-4cosh[x-3cost]+6sinh[x-3cost]}.\end{array}$$

We solve the system (17) according to this example. Table 2 shows the $L_2$ errors at $t=-0.05$, $-0.025$, 0, $0.025$ and $0.05$ for CSC method and MMPDE methods [8]. Our numerical results are satisfied $N=10\times 10$ (or equivalently $\Delta x=0.1$ and $\Delta t=0.01$) and results of the MMPDE methods are with $\Delta x=\frac{1}{40}$ and $\Delta t={10}^{-4}$ (or equivalently $N=1000\times 40$). In Figure 5, Figure 6 and Figure 7, we illustrate the approximate solution, absolute error and the $L_2$ error, respectively.

Table 2. Comparison of the $L_2$ error for Example 2.

Method	N	$\mathit{t}=-0.05$	$\mathit{t}=-0.025$	$\mathit{t}=0$	$\mathit{t}=0.025$	$\mathit{t}=0.05$
Presented method	$10\times 10$	$4.8044\times {10}^{-6}$	$2.4602\times {10}^{-4}$	$4.1079\times {10}^{-4}$	$5.3422\times {10}^{-4}$	$6.2951\times {10}^{-4}$
Mesh for optimal M [8]	$1000\times 40$	$2.2\times {10}^{-3}$	$4\times {10}^{-3}$	$5.3\times {10}^{-3}$	$3.5\times {10}^{-3}$	$1.2\times {10}^{-3}$
Mesh for arc-length M [8]	$1000\times 40$	$1.8\times {10}^{-3}$	$4.1\times {10}^{-3}$	$6.6\times {10}^{-3}$	$6.8\times {10}^{-3}$	$2.3\times {10}^{-3}$
Mesh for curvature M [8]	$1000\times 40$	$2.2\times {10}^{-3}$	$4\times {10}^{-3}$	$5.2\times {10}^{-3}$	$3.6\times {10}^{-3}$	$9.6\times {10}^{-4}$

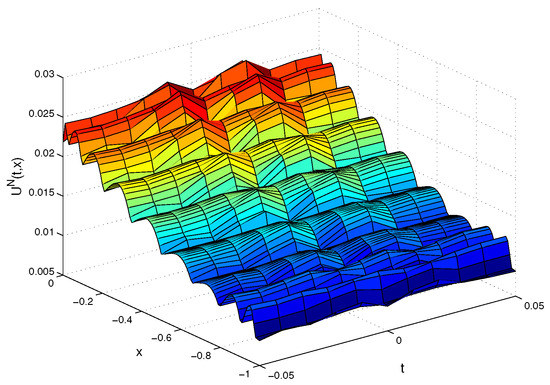
Figure 5. The approximate solution for Example 2.

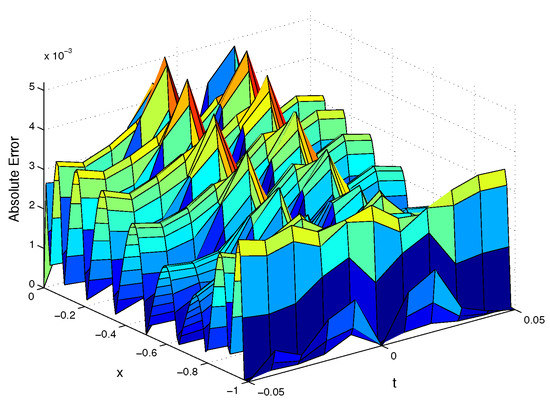
Figure 6. The absolute error $E(.,.)$ for Example 2.

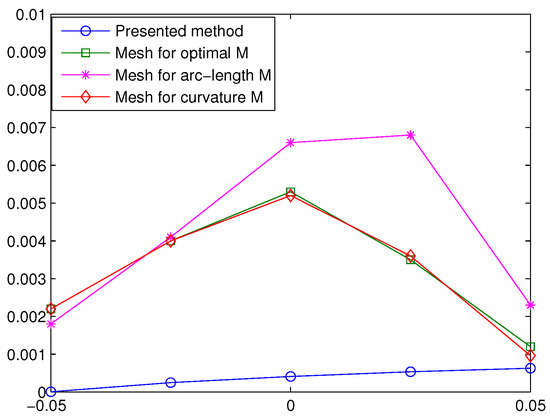
Figure 7. $L_2$ errors for Example 2.

Example 3.

Consider the Burgers–Huxley Equation (3) with $\alpha =1$, $\delta =2$ and $\gamma =0$. Therefore, it can be written as follows

$$\begin{array}{c}\hfill U_t+U^2{U}_x-\beta U_{xx}=0,\end{array}$$

(52)

where $T_0=1$, $T_1=10$, $a=0$ and $b=1$. Also, consider the boundary conditions

$$\begin{array}{cc}\hfill U(t,0)& =0,\hfill \\ \hfill U(t,1)& ={\displaystyle \frac{1}{t+\frac{t\sqrt{t}}{c_0}exp(\frac{1}{4\beta t})}},\hfill \end{array}$$

(53)

and the initial condition

$$\begin{array}{c}\hfill U(1,x)={\displaystyle \frac{x}{1+\frac{1}{c_0}exp(\frac{x^2}{4\beta })}},\end{array}$$

(54)

where $0<c_0<1$. Hence, the exact solution is given by

$$\begin{array}{c}\hfill U(t,x)={\displaystyle \frac{\frac{x}{t}}{1+\frac{\sqrt{t}}{c_0}exp(\frac{x^2}{4\beta t})}}.\end{array}$$

We take $c_0=0.5$ and $\beta =0.01$. Table 3 shows the $L_{\infty }$ errors by using CSC method and given methods in [9,12,15,16] for $t=2$, 4 and 6 and $N=9\times 9$. In Figure 8 and Figure 9, we show the approximate solution and absolute error, respectively. Also, in Figure 10, we represent the exact and approximate solutions for $t=2$, 6 and 10. Moreover, Figure 11 shows the $L_{\infty }$ error.

Table 3. Comparison of the $L_{\infty }$ error for Example 3.

Method	N	$\mathit{T}=2$	$\mathit{T}=6$	$\mathit{T}=10$
Presented method	$9\times 9$	$5.5673\times {10}^{-4}$	$4.4466\times {10}^{-4}$	$3.0034\times {10}^{-4}$
Haar wavelet method [12]	$16\times 900$	$7.5978\times {10}^{-4}$	$4.6335\times {10}^{-4}$	$1.16480\times {10}^{-3}$
QBC method [10]	$200\times 900$	$1.21698\times {10}^{-3}$	$7.2249\times {10}^{-4}$	$1.28124\times {10}^{-3}$
SBC method [9]	$50\times 900$	$1.70309\times {10}^{-3}$	$7.6105\times {10}^{-4}$	$1.80239\times {10}^{-3}$
QBCA1 method [15]	$200\times 900$	$8.1680\times {10}^{-4}$	$5.2579\times {10}^{-4}$	$1.28125\times {10}^{-3}$
QBCA2 method [15]	$200\times 900$	$8.2212\times {10}^{-4}$	$5.2579\times {10}^{-4}$	$1.28125\times {10}^{-3}$
SBC1 method [16]	$200\times 900$	$8.2934\times {10}^{-4}$	…	$1.28127\times {10}^{-3}$
SBC2 method [16]	$200\times 900$	$8.2734\times {10}^{-4}$	…	$1.28127\times {10}^{-3}$

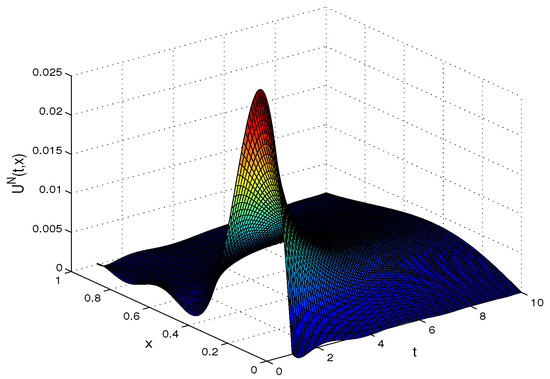
Figure 8. The approximate solution for Example 3.

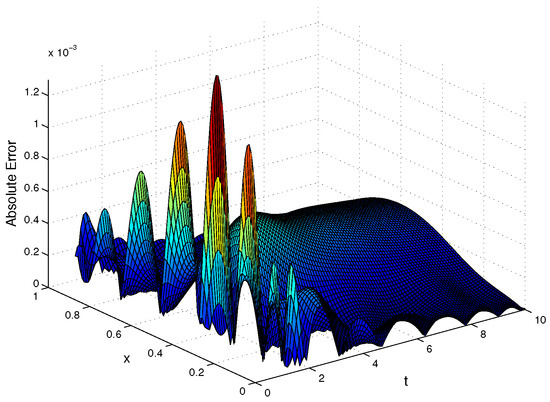
Figure 9. The absolute error $E(.,.)$ for Example 3.

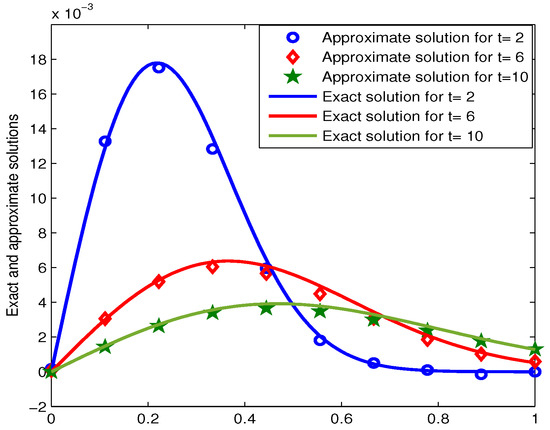
Figure 10. Exact and approximate solutions for $t=2$, 6 and 10.

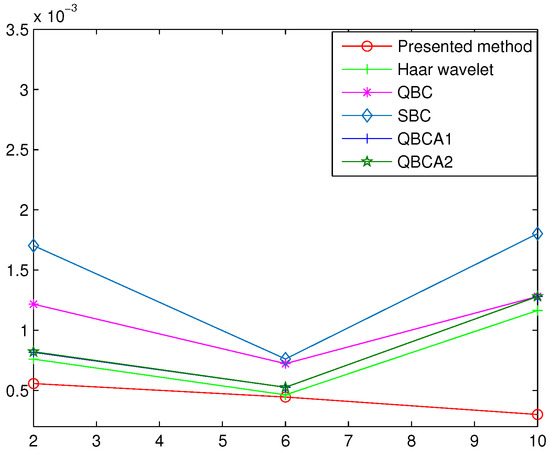
Figure 11. $L_{\infty }$ errors for Example 3.

Example 4.

Consider the Burgers Equation (52) for $x\in [0,1.3]$ and

$$\left\{\begin{array}{c}U(t,0)=0,\hfill \\ U(t,1)={\displaystyle \frac{1.3}{t+\frac{t\sqrt{t}}{c_0}exp(\frac{1.69}{4\beta t})}},\hfill \\ U(1,x)={\displaystyle \frac{x}{1+\frac{1}{c_0}exp(\frac{x^2}{4\beta })}}.\hfill \end{array}\right.$$

The numerical results of our method and other methods [12,16] are displayed in Table 4 for different values of t. The $L_{\infty }$ error results for this example is depicted in Table 4 along with the comparison of the error computed by the present method and other methods. In Figure 12 and Figure 13, the approximate solution and absolute error are shown, respectively. Also, in Figure 14, we represent the exact and approximate solutions for $t=2$, 6 and 10.

Table 4. Comparison of the $L_{\infty }$ error for Example 4.

Method	N	$\mathit{T}=2$	$\mathit{T}=6$	$\mathit{T}=10$
Presented method	$10\times 10$	$5.306\times {10}^{-4}$	$4.294\times {10}^{-4}$	$3.166\times {10}^{-4}$
Haar wavelet method [12]	$16\times 900$	$7.2890\times {10}^{-4}$	$4.5606\times {10}^{-4}$	$3.2374\times {10}^{-4}$
SBC1 method [16]	$260\times 900$	$8.2934\times {10}^{-4}$	…	$3.2723\times {10}^{-4}$
SBC2 method [16]	$260\times 900$	$8.2734\times {10}^{-4}$	…	$3.2337\times {10}^{-4}$

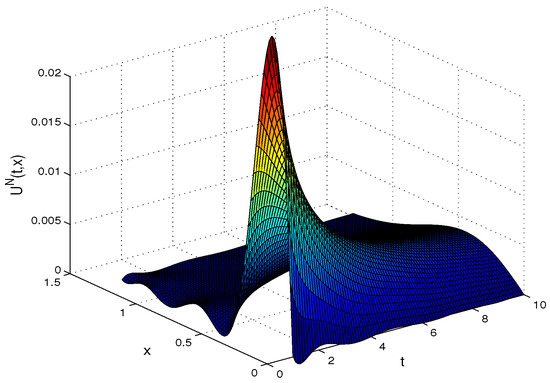
Figure 12. The approximate solution for Example 4.

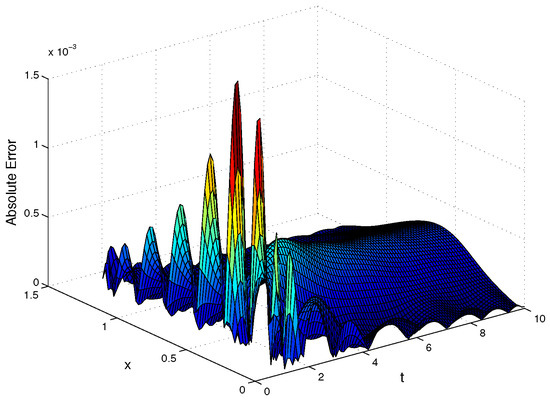
Figure 13. The absolute error $E(.,.)$ for Example 4.

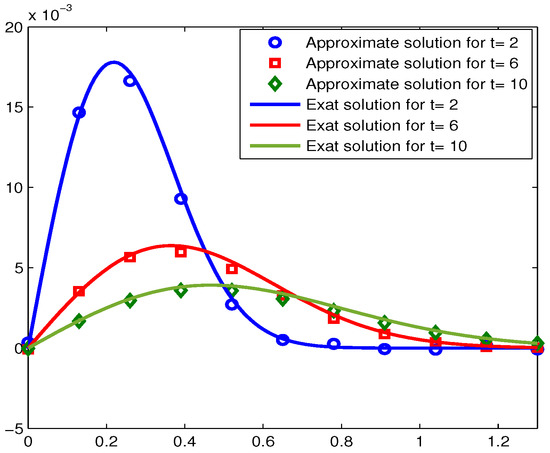
Figure 14. Exact and approximate solutions for $t=2$, 6 and 10.

Example 5.

Consider the Burgers Equation (1), where $T_0=1$, $T_1=5$, $a=0$, $b=8$ and $\epsilon =0.5$. The initial condition for the current problem is

$$\begin{array}{c}\hfill U(1,x)={\displaystyle \frac{x}{1+exp(\frac{1}{4\epsilon }(x^2-\frac{1}{4}))}},\end{array}$$

(55)

and the boundary conditions are

$$\begin{array}{cc}\hfill U(t,0)& =0,\hfill \\ \hfill U(t,8)& ={\displaystyle \frac{8}{t+t{(\frac{t}{exp(\frac{1}{8\epsilon })})}^{\frac{1}{2}}exp(\frac{16}{\epsilon t})}}.\hfill \end{array}$$

(56)

Here, we have the following analytical solution

$$\begin{array}{c}\hfill U(t,x)={\displaystyle \frac{\frac{x}{t}}{1+{(\frac{t}{exp(\frac{1}{8\epsilon })})}^{\frac{1}{2}}exp(\frac{x^2}{4\epsilon t})}}.\end{array}$$

In Figure 15 and Figure 16, we show the approximate solution and absolute error, respectively. Also, Figure 17 illustrates the comparison between the exact solution and numerical solution given by the proposed method. Also, we compare the $L_{\infty }$ and $L_2$ errors which are computed by the present method and other methods [14] in Table 5. We can observe that the results of CSC for $N=30\times 30$ are better than the results of method of Inan and Bahadir [14] for $N=320\times 40,000$.

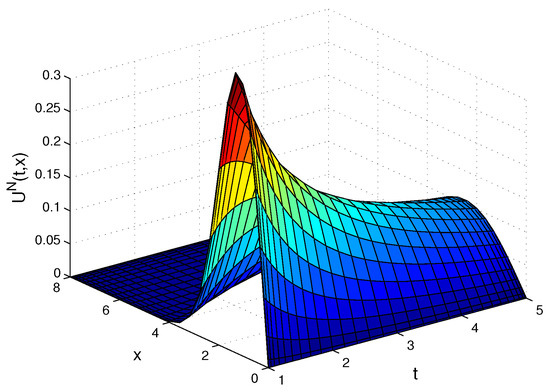
Figure 15. The approximate solution for Example 5.

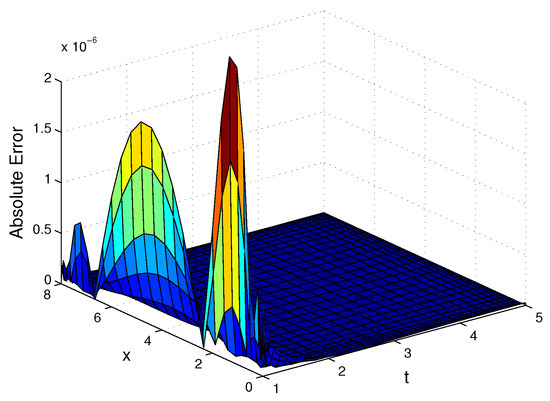
Figure 16. The absolute error $E(.,.)$ for Example 5.

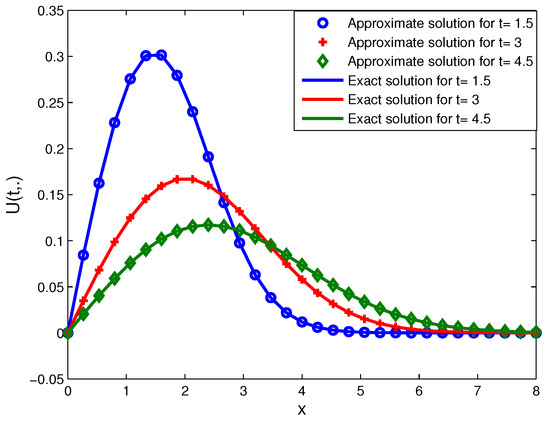
Figure 17. Exact and approximate solutions for Example 5.

Table 5. Comparison of the $L_{\infty }$ and $L_2$ errors for Example 5

Method	T	N	${\mathit{L}}_2$	${\mathit{L}}_{\mathit{\infty }}$
Presented method	$T=1.5$	$30\times 30$	$3.2025\times {10}^{-8}$	$1.2611\times {10}^{-7}$
$I-EFD$ method [14]	$T=1.5$	$320\times$ 40,000	$2.1\times {10}^{-5}$	$1.8\times {10}^{-5}$
$FI-EFD$ method  [14]	$T=1.5$	$320\times$ 40,000	$2.2\times {10}^{-5}$	$1.9\times {10}^{-5}$
Presented method	$T=3$	$30\times 30$	$3.2026\times {10}^{-8}$	$6.9546\times {10}^{-9}$
$I-EFD$ method [14]	$T=3$	$320\times$ 40,000	$2.2\times {10}^{-5}$	$3.8\times {10}^{-5}$
$FI-EFD$ method [14]	$T=3$	$320\times$ 40,000	$2.3\times {10}^{-5}$	$1.8\times {10}^{-5}$
Presented method	$T=4.5$	$30\times 30$	$3.2028\times {10}^{-8}$	$1.6022\times {10}^{-9}$
$I-EFD$ method [14]	$T=4.5$	$320\times$ 40,000	$4.08\times {10}^{-4}$	$7.43\times {10}^{-4}$
$FI-EFD$ method [14]	$T=4.5$	$320\times$ 40,000	$4.08\times {10}^{-4}$	$7.43\times {10}^{-4}$

Example 6.

By considering the two-dimensional Burgers Equation (41) with $T=1$ and $\epsilon =0.1,0.2,0.5$ and 1, the initial condition is as follow [30,31]

$$\begin{array}{c}\hfill U(x,y,0)={\displaystyle \frac{1}{1+exp(\frac{(x+y)}{2\epsilon })}},\end{array}$$

(57)

and the boundary conditions are

$$\begin{array}{cc}\hfill U(0,y,t)& ={\displaystyle \frac{1}{1+exp(\frac{y-t}{2\epsilon })}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill U(1,y,t)& ={\displaystyle \frac{1}{1+exp(\frac{(1+y-t)}{2\epsilon })}},\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill U(x,0,t)& ={\displaystyle \frac{1}{1+exp(\frac{(x-t)}{2\epsilon })}},\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill U(x,1,t)& ={\displaystyle \frac{1}{1+exp(\frac{(x+1-t)}{2\epsilon })}}.\hfill \end{array}$$

(60)

By these considerations, the exact solution is

$$\begin{array}{c}\hfill U(x,y,t)={\displaystyle \frac{1}{1+exp(\frac{(x+y-t)}{2\epsilon })}}.\end{array}$$

We calculate approximate solutions and absolute errors in different $\epsilon =0.1,0.2,0.5$ and 1 with $N=10$. In Figure 18 and Figure 19, we observe the approximate solutions and absolute errors with $\epsilon =0.1$, respectively. Also, Figure 20 and Figure 21 illustrate the numerical solution and absolute error given by the presented method for $\epsilon =0.1$. The approximate solutions and absolute errors with $\epsilon =0.5$ and 1 are expressed in Figure 22, Figure 23, Figure 24 and Figure 25, respectively. Moreover, we computed the $L_{\infty }$ errors for various $\epsilon$ at $t=t_0$ which are shown in Table 6.

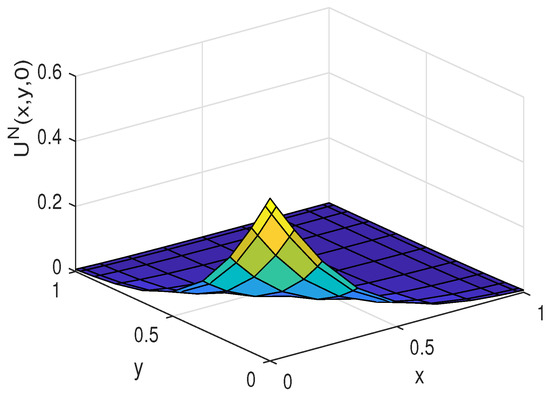
Figure 18. The approximate solution for $\epsilon =0.1$ Example 6.

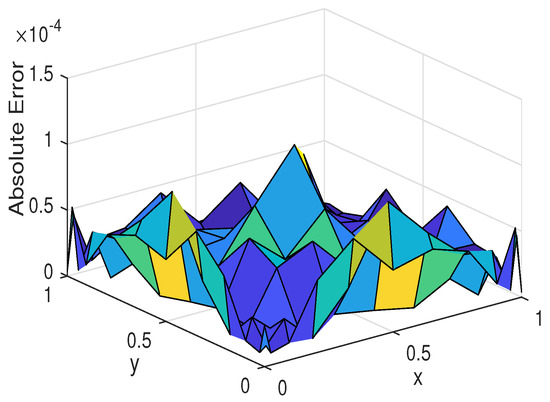
Figure 19. The absolute error for $\epsilon =0.1$ Example 6.

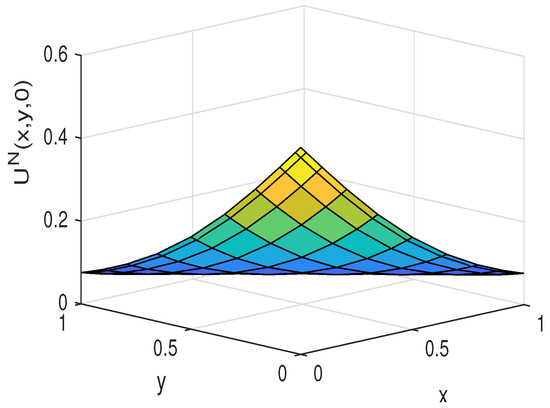
Figure 20. The approximate solution for $\epsilon =0.2$ Example 6.

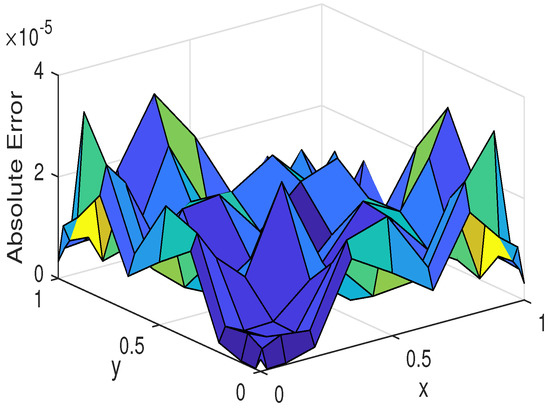
Figure 21. The absolute error for $\epsilon =0.2$ Example 6.

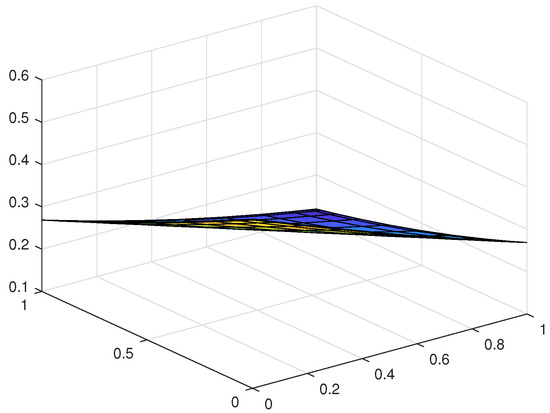
Figure 22. The approximate solution for $\epsilon =0.5$ Example 6.

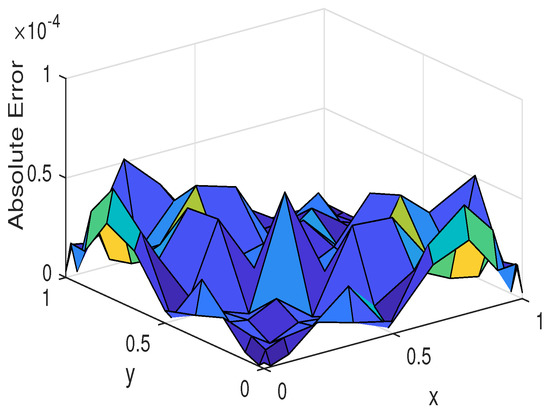
Figure 23. The absolute error for $\epsilon =0.5$ Example 6.

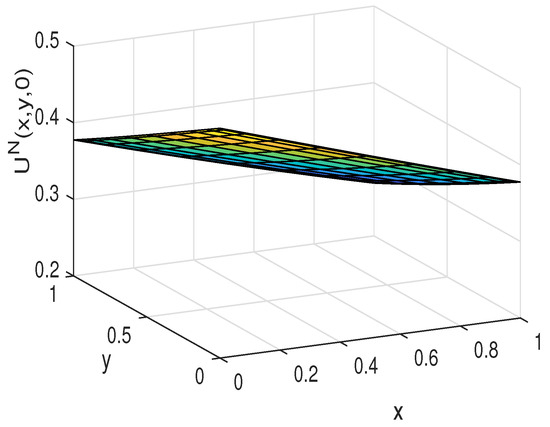
Figure 24. The approximate solution for $\epsilon =1$ Example 6.

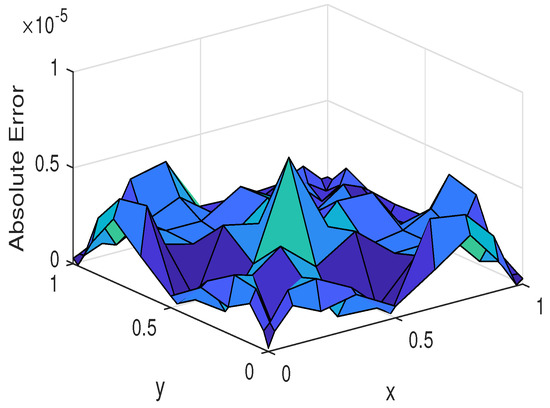
Figure 25. The absolute error for $\epsilon =1$ Example 6.

Table 6. The $L_{\infty }$ error for various $\epsilon$ Example 6.

The CSC Method	$\epsilon =0.1$	$\epsilon =0.2$	$\epsilon =0.5$	$\epsilon =1$
$L_{\infty }$	$1.076\times {10}^{-4}$	$3.421\times {10}^{-5}$	$6.073\times {10}^{-5}$	$7.333\times {10}^{-6}$

7. Conclusions

In this article, we used the Chebyshev spectral collocation method to get numerical solutions for different types of one and two-dimensional Burgers equation. We analyzed the convergence of the CSC method by using the concept of module of continuity and compared the obtained approximate solutions with those of other methods. We showed that the CSC method has very high accuracy and it is more precise with respect to the other numerical methods. Our investigations can be used in the three-dimensional case and we prepare these investigations as a future article.