3. Gravothermal Instability
Let us use the following dimensionless variables to solve the TOV equation
We denote
m as the rest mass of one particle,
as the total mass-energy density at the origin, and
. TOV equation (
2) and mass equation (
4) become, by use of Equations (
3), (
14), and (
15),
where
is given by Equation (
17) and
This forms the system to be solved with initial conditions
,
. To generate the caloric curves, the boundary radius of integration
is chosen for each
, such that the compactness of rest mass, hereafter known as “rest compactness”, to distinguish from the usual compactness
,
is kept constant. The rest compactness controls the intensity of relativistic effects. We denote the total rest mass
and the rest mass-energy density is given by use of (
16):
The pressure and thermal mass-energy density
may be calculated from the expressions
In
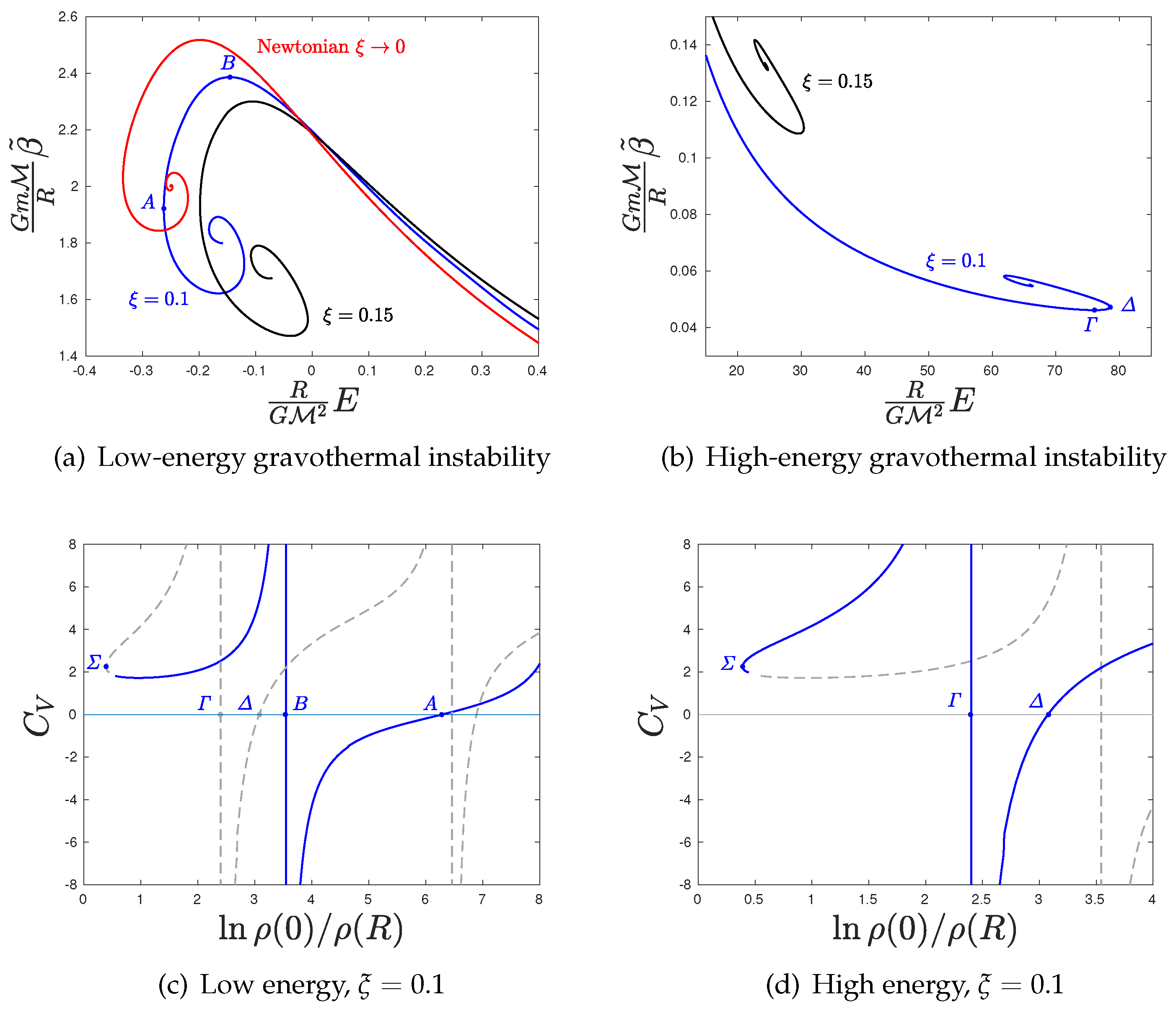
Figure 1a, the spiral of the caloric curve
is depicted, corresponding to the low-energy gravothermal instability. The exact Antonov spiral is recovered for zero rest compactness
. As
increases the low-energy spiral is reformed, moving towards higher temperatures and energies. This means that as the sphere becomes more compact, and therefore relativistic effects more intense, the stability domain is decreasing, and thus the system gets destabilized. This relativistic generalization of gravothermal catastrophe occurs to progressively higher minimum energies, which for
corresponds to point called
A, as in
Figure 1a.
As we move along this caloric curve from point
A to
B, and then to higher energies and temperatures, the total mass-energy density profile becomes more homogeneous, because the dominating rest mass density gets more homogeneously distributed. This is manifested by a decrease of the density contrast
. However, as temperature rises, the thermal energy density profile continuously steepens due to the Tolman–Ehrenfest effect—the weight of heat, at some point, denoted
in
Figure 1c—the gravitation of thermal energy takes over its outward pointing, stabilizing, pressure effect. From that point on, the density profile becomes steeper, i.e., the density contrast increases, and thermal mass gravity dominates over rest mass gravity.
At sufficiently high energies, there appears a second spiral, the high-energy one. At the point of maximum energy, denoted
for
in
Figure 1b, the high-energy or relativistic gravothermal instability sets in.
Figure 1c,d shows that this instability is similar to gravothermal catastrophe, in that it occurs as the system passes from negative to positive specific heat and not the other way around. This indicates that similarly to gravothermal catastrophe, in the high-energy gravothermal instability a self-gravitating core with negative specific heat forms and decouples from the rest of the system. A heat transfer from the core to the halo, i.e., a core–halo structure, leads to a runaway effect as the halo acquires positive specific heat; likewise, the whole system does in the unstable domain. However, the big difference is shown in
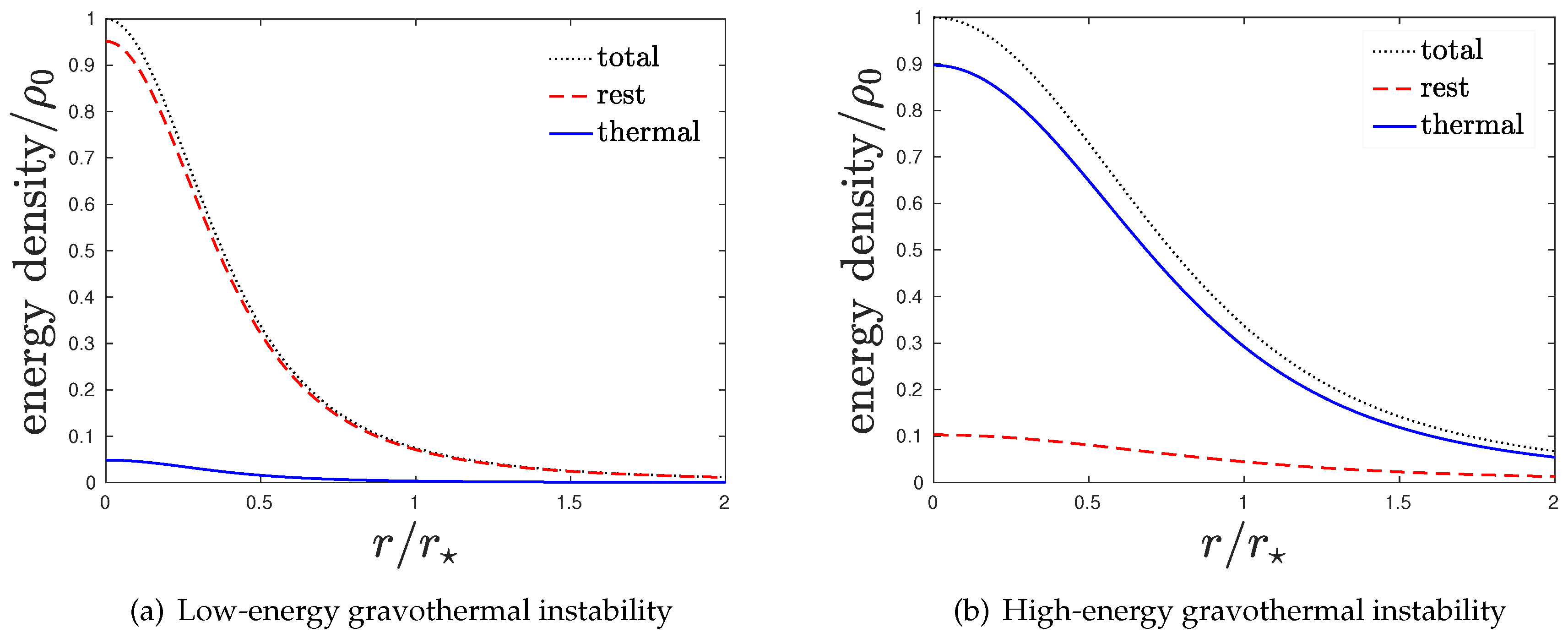
Figure 2a,b. The core at the onset of the high-energy gravothermal instability is dominated by thermal energy density and not rest mass-energy density, which is completely opposite to Antonov instability. The system collapses under the weight of its own heat. The temperature gradient from the core to the outer regions, formed at the onset of the instability, causes the self-gravitating (negative specific heat) core to heat up further, and thus become even heavier because it accumulates more heat. Thus, the system becomes destabilized, as its energy is increasing and not decreasing, unlike the Antonov case. This is evidenced in
Figure 1b.
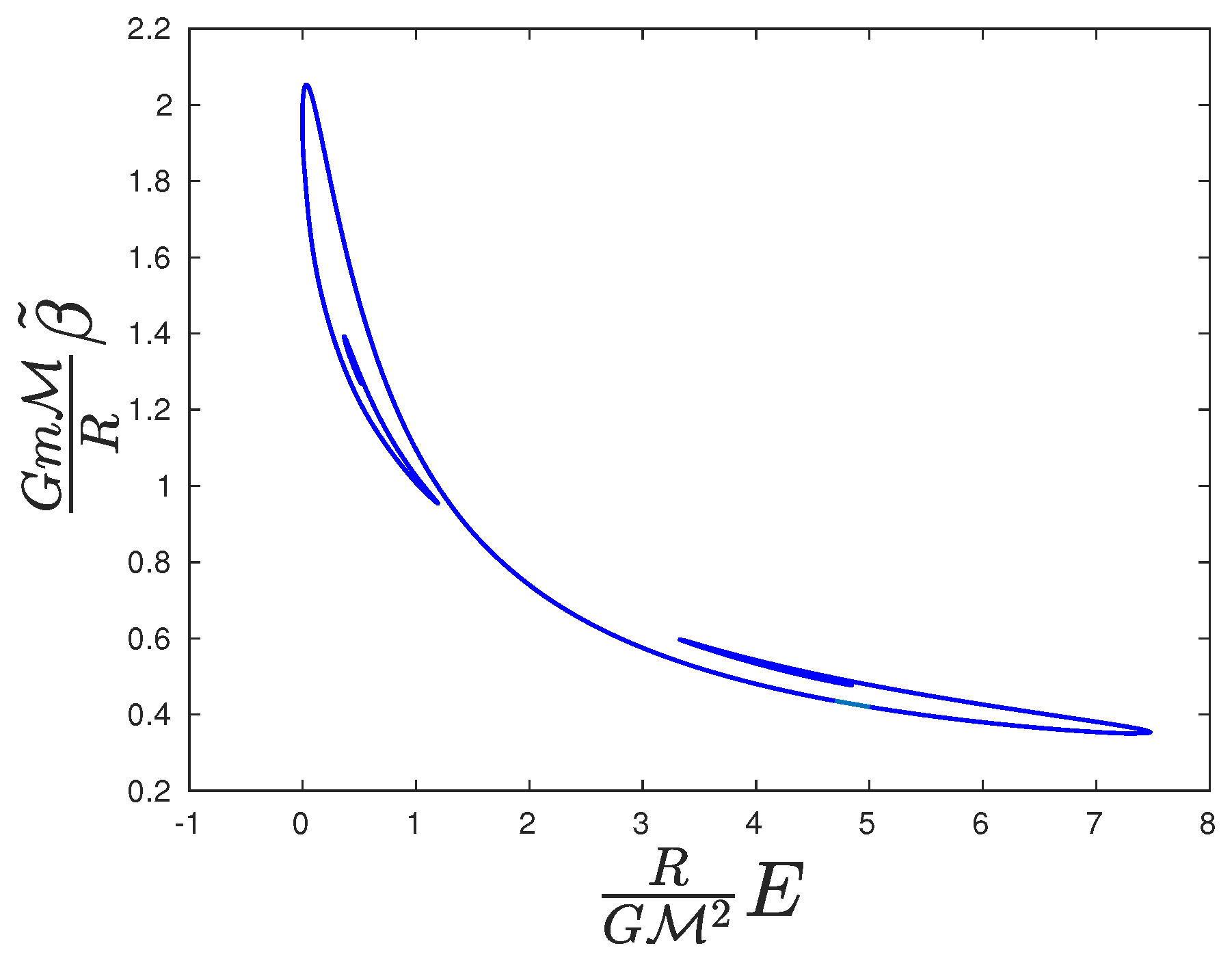
Both spirals, together with the stable branch connecting them, are shown in a single diagram in
Figure 3 for
. As the rest compactification is increasing, i.e., relativistic effects become more intense, the relativistic spiral moves along lower energies, i.e., the stable domain gets smaller. This destabilization adds up to the destabilization caused by the low-energy spiral. The two spirals approach each other with increasing
, and finally merge to a single point for
This is an ultra-maximum limit of rest compactness. No static, stable, relativistic classical ideal gas can exist with rest mass to radius ratio higher than
. Thus, for stable equilibria, it always holds that
Let us now keep the energy fixed along with the number of particles and vary the radius of the system. This means we assume conditions of the microcanonical ensemble. If the gravothermal energy
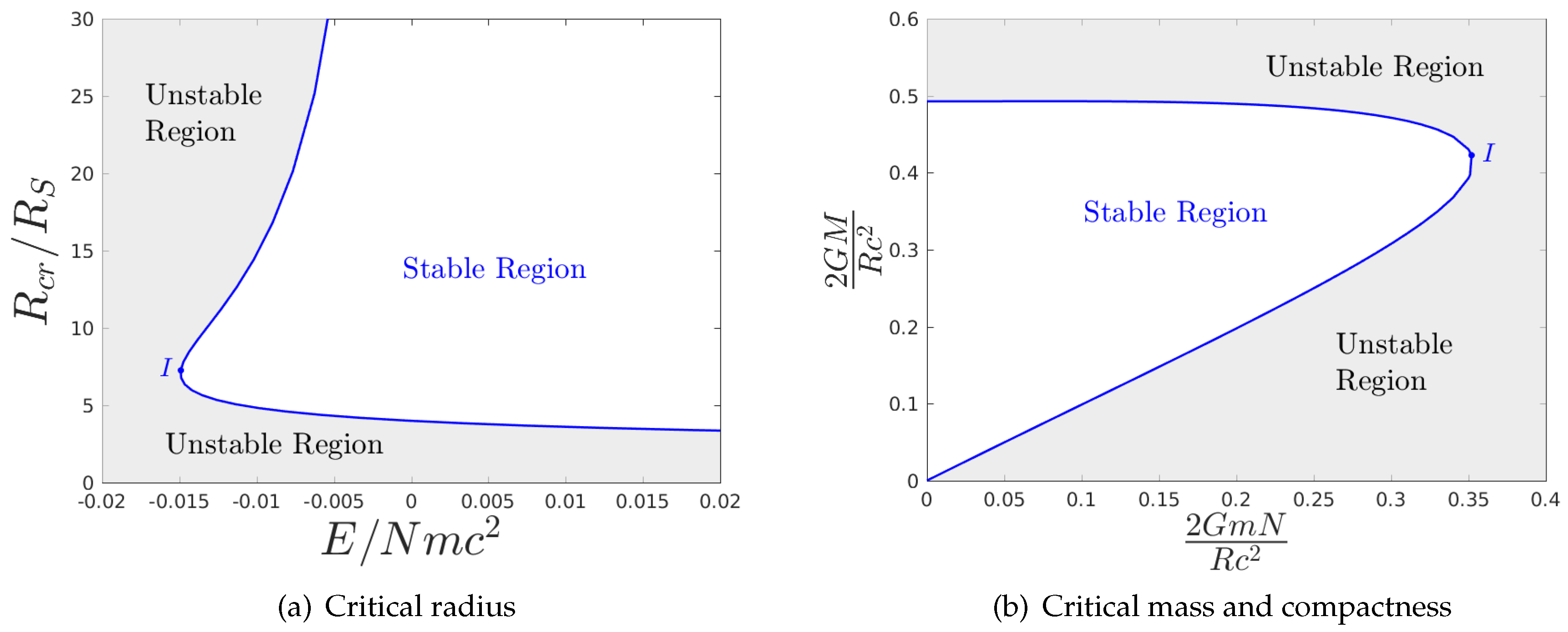
is negative, but sufficiently high so that stable equilibria do exist, there appear two critical radii, which delimit the stable domain shown in
Figure 4a. The maximum radius is a manifestation of the low-energy instability and the minimum radius signifies the high-energy gravothermal instability. Therefore, in the low-energy instability, the gas sphere becomes unstable when it becomes sufficiently large and not small. The expansion causes the cooling of the system, which forces the rest mass towards the center in order to generate a pressure gradient strong enough to halt gravity. Above the critical radius, a runaway heat transfer appears, with direction from the core to the halo and the core collapses. On the other hand if the radius is sufficiently decreased the resulted heating of the system forces thermal energy, and not rest mass, to concentrate on the center in order to generate a pressure gradient of a different origin in this case. Below a critical radius, the high-energy gravothermal instability sets in and the system collapses with a similar core–halo mechanism. However, now the system becomes unstable when it becomes sufficiently small and not large. As relativistic effects becomes more intense, i.e., when the absolute gravothermal energy,
approaches a value closer to
and the system gets destabilized, as the stable domain decreases. The low-energy maximum radius decreases and the high-energy minimum radius increases. They merge at the ultra minimum gravothermal energy
, represented by point
I in
Figure 4a. Therefore, for stable equilibria, it always holds that
This limit corresponds to the limit (
32). For positive gravothermal energy
E, there appears only the high-energy gravothermal instability, and thus the stable domain is bounded only by the minimum radius.
In
Figure 4b, the critical compactness
w.r.t. the rest compactness
is plotted. This plot may also be realized as the critical mass-energy w.r.t. the number of particles for a fixed radius
. For any rest compactness, there appear two critical energies: The lower energy corresponds to the low-energy gravothermal instability and the higher energy to the high-energy gravothermal instability. The maximum rest compactness given in (
32) corresponds to point
I. The total mass compactness cannot be bigger than
.
Note that this analysis applies to the conditions of a microcanonical ensemble. This means that we assume adiabatic boundary conditions where no energy exchange between the system and its environment is allowed. In a canonical ensemble, where the system is allowed to exchange heat with a reservoir, the stability properties are completely different. This highlights the nonequivalence of ensembles in gravity (see, e.g., in [
23]). In the canonical case, both instabilities, in either the low or high energy regime, now called low-
T or high-
T isothermal collapse, respectively, occur below a minimum radius for fixed temperature [
5]. However, in the low-
T regime, the instability sets in below a critical temperature, and, in the high-
T one, above a critical temperature for fixed radius. In the low-
T case, the decrease of temperature reduces the ability of the system to generate a pressure gradient, and, in the high-
T case, the increase of temperature enhances the concentration of thermal energy towards the center increasing its gravitation.
Apparently, the source of gravitational instability is in all of the above cases some heat transfer, either between subsystems of the system or the system and its environment: Gravitational instability manifests the universality of gravity and heat. The origin of gravitational instability, including quantum effects and interactions, will be discussed further in a separate work.
4. Core-Collapse Supernova
In a core-collapse supernova, the collapse of the core of a massive star is initiated by the shift of nuclear statistical equilibrium (some modern reviews include [
24,
25,
26]) when the nuclear fuel is exhausted. During the collapse, the core is heated up. Part of this thermal energy is consumed to dissociate heavy nuclei to nucleons with parallel emission of energetic neutrinos, while electron capture by protons enriches the core with neutrons. Neutrinos become trapped inside the core at densities ∼ 10
gr/cm
, and the collapse of the core may be halted at densities above the normal nuclear density
10
gr/cm
with a bounce. At the bounce, the core consists of an ultra-hot (≳50 MeV) nucleon gas, dominated by neutrons, and trapped neutrinos of energy 100–300 MeV.
If the core at the time of the bounce lies in the unstable domain of
Figure 4b, which defines the stable domain in compactness space, it will be subject to the high-energy gravothermal instability and will not be able to halt collapse. The temperature corresponding to the ultra maximum limit, point
I of
Figure 4b, of relativistic gravothermal instability is
= 0.19 mc
, that is, 178 MeV for neutrons.
Note that the physics of the relativistic gravothermal instability, does not, qualitatively, depend on the equation of state. It is natural to expect that will persist for any equation of state. This is due to the universality of the effects of gravity and heat. Regarding our case of interest, namely, the quantum Fermi gas, this is proved in [
27,
28].
Note, in addition, that a system undergoing a gravothermal instability will be subject to heat transfer from a newly formed core to the outer regions, the “halo”. Due to its negative specific heat, the core will get hotter and contracted. Such a phenomenon resembles the implosion–explosion structure of a supernova. If, at some point, the temperature and compactness values allow for quantum degeneracy pressure to halt the collapse, the system will form a protoneutron star. In this case, the core-collapse supernova may be viewed as a microcanonical gravitational phase transition [
28,
29] from the initial gaseous (gravitational) phase of the massive star to the collapsed (gravitational) phase of the protoneutron star. This may only occur if the system is subject to the low-energy gravothermal instability, i.e., if at the onset of instability it lied below the lower line of
Figure 4b.
5. Conclusions
This paper focused on two fundamental properties of matter: the ability to move and to gravitate. The aim of this paper was to investigate how these phenomena intervene with respect to the stability of systems containing material particles that present only these phenomena. Such a system is called the relativistic, classical, self-gravitating ideal gas.
Although random movement, namely, thermal energy, naturally favors a disordered, homogeneous state, the intriguing, universal character of gravity intervenes, and I propose that there exists a threshold beyond which the heating of the system does not homogenize, but steepens, the total mass-energy density. This is because the thermal energy gravitates. At a critical point of maximum energy and minimum radius, an instability sets in. A self-gravitating core with negative specific heat, dominated by the gravitation of thermal mass, decouples from the outer regions and collapses similarly to Antonov instability. A relativistic generalization of Antonov instability—the low-energy gravothermal instability—also occurs, but, in this case, beyond critical points of minimum energy and maximum radius. As the relativistic effects get more intense, i.e., the compactness of rest mass is increasing, the caloric curve, which has the form of a double spiral, decreases in size. At some point, it reduces to a point where the two types of gravothermal instability, at low and high energy, merge, revealing that they are aspects of a single phenomenon.
Figure 4b depicts the stable domain outside which a gravothermal instability occurs. I argue that if the collapsing ultra-hot core formed during a core-collapse supernova lies inside the unstable domain of
Figure 4b at the time of the bounce (when it achieves densities
10
gr/cm
), it will be subject to the relativistic gravothermal instability. It will not be able to stabilize itself and continue to collapse towards the formation of a black hole. Finally, the current results support the idea that the implosion–explosion structure of supernovae, i.e., the implosion of the core with parallel explosion of outer parts, reflects the core–halo structure of the low-energy gravothermal instability.