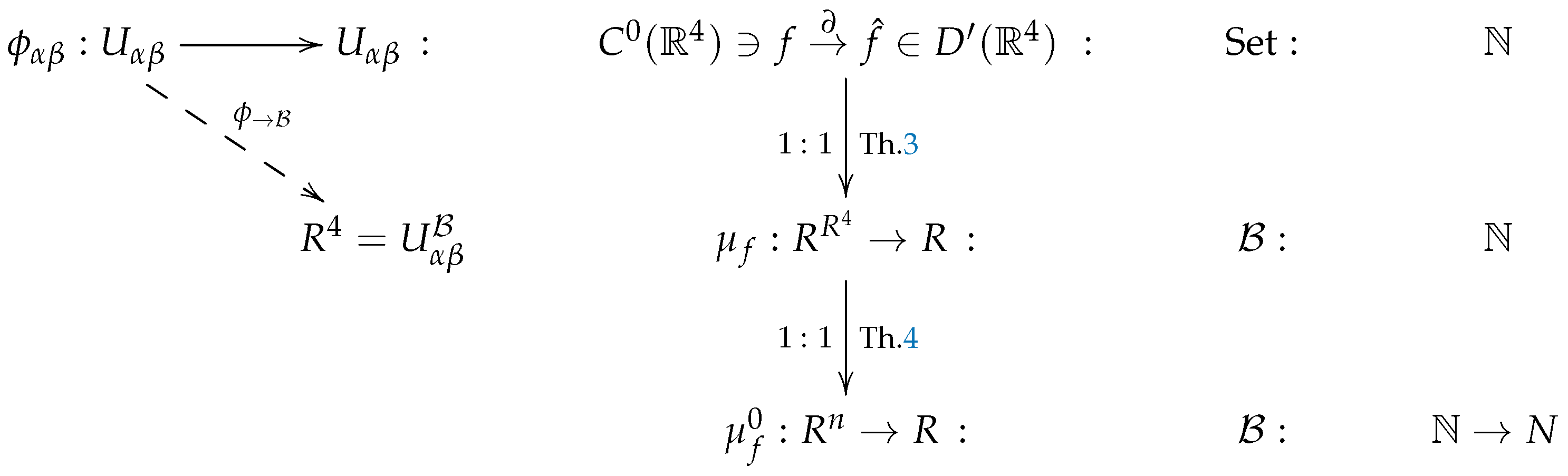Let
be a Grothendieck topos which is a topos of sheaves on a site (e.g., [
13,
22]) with 1. a sub-object classifier as defined in the sheaves toposes, 2. the internal logic is now intuitionistic and internal reasoning is performed without any use of the axiom of choice in set theory and the excluded third low (
), 3. intuitionistic set theory.
is defined in Set but can be embedded to certain toposes e.g., smooth toposes widely analyzed in [
13]. Let
be the Basel topos which is one of the smooth toposes defined in [
13]. Then it holds
In every Grothendieck topos with natural numbers object there exists the canonical representation of NNO given by the so-called constant sheaf . This ’constant sheaf’ is the sheaf corresponding to the constant presheaf . Moreover, given two toposes with the canonical constant sheaves NNO’s , and geometric morphisms , , so thus these canonical NNO’s are preserved by geometric morphisms.
We will see later how to cure these unwanted properties.
2.1. Local Ext/Int Symmetry on Smooth Manifolds
Given a smooth (in Set) and sending to our present aim is to find descriptions of distinguishing its exotic smoothness structure from the standard one. This is well-defined question since the functor sends fully and faithfully all smooth manifolds from Set internally to .
Remark 6. depicts any of nonstandard smoothings on . They are called exotic smooth , i.e., ’s (e.g., [16]). Each such smoothness structure of is a smooth manifold homeomorphic to the topological but nondiffeomorphic to it with the standard smoothing. The standard smooth structure of is such that the product is smooth. There is unique standard smooth . It is known that there exist at least two families, each of cardinality of the continuum, of exotic ’s: Small and large exotic ’s. The later are not smoothly embeddable in the standard , or , as open subsets while the small ’s allow for such embedding. Let A be a smooth ring and the corresponding locus in . We use abbreviation for the sheaf in representing A, i.e., .
Lemma 4. The standard is represented as in .
Proof. The standard smooth
in Set is the global smooth Cartesian product of 4 factors
. It is sent to
in
. This last is
in
by (
2) and (
3).
is
with modified Grothendieck topology hence loci are objects in
and sheaves are representable (Remarks 4 and 5).
Thus, the standard smooth from Set is in .
Lemma 5. Any small exotic is represented in as and large exotic by where is certain non-trivial ideal in and in and .
Proof. Every small exotic
is embeddable smoothly as an open subset of
so the result for small
follows from [
13] (Corollary 2.2, p. 25). Large
’s are not embeddable in
but are still smooth manifolds so they are representable in the claimed form, i.e.,
is finitely presented
where
is finitely generated [
13] (p. 24). The upper bound
follows from the Whitney embedding theorem for the real smooth manifolds. □
Remark 7. It would be interesting to give the explicit description of ideals distinguishing between different exotic ’s. Such task presumably requires making use of complicated boundaries of Casson handless which are infinite geometric constructions. As far as we know such an approach to invariants of ’s have never been carried out.
Here we will follow different strategy without direct referring to Casson handles. We are developing new kind of symmetry for exotic smoothness structures on based on and Set.
Let us consider a smooth manifold M in Set, , with a smooth atlas . We assign to each a map , or the identity (isomorphism in Set, diffeomorphism) in Set. Thus, the following function is defined
Definition 1. (a) -cover of a smooth manifold M is the above assignment (
6)
such that and , i.e., (b) A -local smooth manifold is a smooth manifold M which every atlas has underlying -cover, i.e. Remark 8. When M is certain smooth manifold in Set then to be -local means that for any its smooth cover there exists certain -cover such that every is or . We say that a smooth cover of M derives from a -cover if the smooth cover has underlying -local atlas.
We are going to explore what structures on M are determined by its -local covers. First, let us assume that the structure we are looking for is invariant with respect to the choice of the local maps consisting -covers. Moreover, we want the structure be a smooth structure of a manifold of the same dimension.
Proposition 2. If and is smooth, then .
Proof. The result is a direct consequence of the following fundamental fact. Any smooth atlas of any exotic cannot contain just one local chart. Moreover, if each smooth atlas on is not a single-element one such is diffeomorphic to certain exotic and is not diffeomorphic to the standard smooth . This is simply the consequence of the fact that given a single-element atlas on it is just the standard . □
Thus, the existence of a
-covers for every open cover of
M can change its smoothness structure. We will see in
Section 2.2.3 that indeed one finds an action on smooth functions on
M in Set which derives from existence of
-covers (again for
). This is Definition 4 which makes precise the equivalence of functions modified by
-covers on
with functions from certain smoothness structure on
in Set. This smoothness structure is called Set-invariant
-local smoothness structure in
Section 2.2.3.
Here we use phrase -invariant smoothness structure or -invariant structure for indicating this possibility that -covers can modify smoothness structures on manifolds. The resulting structure is then called -invariant structure.
Corollary 1. Any realization of the -invariant smooth structure on any must be an exotic .
2.2. Is Any Exotic Equivalent to a -Invariant Structure?
We showed that any
-invariant smooth structure on
is an exotic
. Now we are going to approach the reverse problem: Given any exotic
is it generated by the canonical
-invariant smooth structure? If Yes and if there are tools to distinguish different exotic structures in terms of
-invariance, which would mean the equivalence of both constructions. We do not resolve this problem here with all generality. Instead we show that
-covers lead us precisely towards understanding of exotic smooth functions on
. Thus, we will work rather with real-valued functions on
than with handle-bodies underlying known exotic
. Moreover, the
-invariance can be used also for describing exotic smoothings of
with finitely many maps in the smooth atlas. The similar approach, though based more on the structure of Casson handles, was initialized in [
17,
18] and further developed in [
19].
Let be an exotic when working in Set. When switching to is the canonical image of via the embedding . The meaning of will be clear from the context. Given exotic in Set we have the space of exotic smooth functions on it . The space of standard smooth functions is related with . All exotic and all standard smooth functions are continuous
Moreover, if
then
[
23] so for any exotic
there have to exist smooth exotic functions which are merely continuous with respect to the standard smoothness structure. Let
be one of such continuous function which become exotic smooth in some exotic smoothness structure of an exotic
. The subsequent task is to understand and perform infinite many differentiations of this continuous function in the exotic smoothness structure. This kind of problem has been successfully resolved in the theory of distributions. Thus, the question we want to explore further is whether distribution theory can help understanding exotic smoothness on
.
2.2.1. First Comparison of Distributions and Exotic Smoothness Structures on
Let us consider a smooth function
and a test function
with the support in a certain ball in
, hence vanishing at infinity. The space
of test functions is the sum of subspaces
, of test functions with supports in
K, over all compact subsets
[
24] (p. 151). Then it holds
where
is a multi-index and
so that
. This formula, as is well known, serves as a prescription how to extend the differentiation over nondifferentiable functions from
. Then the rich distribution theory has been developed which extends differentiation over non-continuous functions and over proper distributions not-being functions at all.
Remark 9. The important fact which follows from (
7)
is that whenever a distribution is represented by a smooth function then the distributional differentiation coincides with the usual differentiation of the smooth function H and we write for such regular distributions. Thus, differentiation of continuous functions by distributions preserves differentiations of smooth functions. Remark 10. This extension of continuous functions is minimal: One must take the space of all distributions to include all continuous functions with all partial derivatives. If we take any proper subclass of distributions then it follows that not all continuous functions were included. This is the consequence of the two following theorems [24] (pp. 167, 169, Theorems. 6.26, 6.28). Let be the space of distributions on open subset .
Theorem 1 ([
24])
. Suppose , and K is a compact subset of Ω
. Then there is a continuous function f in Ω and there is a multi-index α such thatfor every . This can be made more global ([
24] (p. 169, Th. 6.28).
Theorem 2 ([
24])
. Suppose . There exist continuous functions in Ω, one for each multi-index α, such that- a.
each compact intersects the supports of only finitely many , and
- b.
If h has finite order, then the functions can be chosen so that only finitely many are different from 0.
Let us note that quite analogous situation takes place for exotic smooth functions on
. As we observed before given an exotic
some continuous functions become differentiable and some standard smooth become nondifferentiable but only continuous. To distinguish one exotic smoothness structure from another, one should find a way to distillate the set of continuous functions which become exotic smooth when switching between various
’s. This is currently out of our reach (however, see [
25] where functional subspaces were analyzed from the point of view of trees defining Casson handless).
2.2.2. Distributions in
Distribution theory in the topos
has been presented in [
13]. The choice of the topos
is crucial here. As we noted already in Remark 1 the canonical NNO in
is the constant sheaf
which, however, leads to the variety of problems regarding smooth manifolds in
. The crucial for curing these weaknesses and for the proper representation of distributions in
is to substitute
by another NNO object. The substitution is the object of smooth natural numbers,
N, which is a kind of intuitionistic end-extension of
in
. Such consistent replacement is one of the main topics of [
13].
Remark 11. The object N contains nonstandard big natural numbers [13] and R either. Because of that is non-Archimedean with respect to and becomes Archimedean with respect to N. Moreover, problems stated in (2)
are now cured because of referring to N preserve compactness, e.g., is s-compact (smooth compact, i.e., with respect to N);
s preserves open covers with respect to N;
s preserves partitions of unity subordinated to open covers (with respect to N);
the ring R is a local ring;
Let us follow the description of internal to distributions. As we mentioned above R is a non-Archimedean ring with respect to which becomes Archimedean relating to N. The reason is that N contains infinite big natural numbers which, however, can be inverted, i.e., . Thus, one has the object of invertible infinitesimals as sub-object of R. Since is a model of synthetic differential geometry there exists also the object △ of non-invertible infinitesimals. More precisely, let be a space (sub-object of R in ) of infinitesimals. There are two sub-objects of □
The ring of accessible reals is defined as
Remark 12. Note the appearance of different types, and N, in definitions above. Thinking in Set the accessible reals comprise those which are Archimedean with respect to —the standard natural numbers. Infinitesimals i.e., the object □ can be well presented in terms of the apartness relation # on R: , then So any infinitesimal cannot be apparted from zero by any .
Remark 13. Internal logic of toposes is intuitionistic logic and because of that there exist non-invertible infinitesimals in which cannot exist in Set.
A function is accessible if for every multi-index and , .
has accessible support when .
Definition 2. A test function is an accessible function with accessible support.
Let be the space of all test functions from and be an object of functions with accessible supports.
Definition 3. A distribution on is an R-linear mapwhich for fulfils There is direct
correspondence between distributions from
and Set [
13] (p. 336, Th. 3.15.3).
Theorem 3 ([
13])
. The global sections functor induces a bijection between distributions in and external distributions , and between distributions with compact support, i.e., R-linear maps and external distribution with compact support . Moreover, every distribution in can be represented by a function (predistribution) . Specifically, every function as above defines an R-linear functional by integration in
If
fulfils the continuity rule
it is called a predistribution.
Theorem 4 ([
13], p. 324, Th. 3.6)
. For every distribution μ on there exists a predistribution such that for all Thus, given the correspondence between external and internal to distributions now we have the possibility to represent internally every distribution from Set by regular -internal distribution.
Remark 14. From the proofs of both theorems above in [13] it follows that the facts stated are true only because of the existence of invertible infinitesimals and replacing by N consistently in . 2.2.3. The Construction of -Invariant Functions as Smooth Exotic
Given a smooth -local atlas on M (as in Definition 1), it always contains some local map(s) in (see Remark 8) such that some smooth transition function should be replaced by . How can we define the transitions from Set to and back? Certainly, the obvious choice is to use global section functor and its left adjoint the constant sheaf functor . The pair is a geometric morphism. Additionally, on manifolds there exists full and faithful embedding such that where ≃ is a diffeomorphism of M in Set (see (5)). Thus, given we can embed it by s into and .
Now given a continuous function , we are going to understand it as differentiable or smooth in an exotic smoothness structure on . The crucial ingredient of the approach is the allowed local shift in the -atlas.
Definition 4. -local smoothness structure on is smoothly equivalent to certain smoothness structure on iff every smooth function is also smooth in the structure .
-local smoothness structure on is Set-invariant when it is smoothly equivalent to certain smoothness structure of in Set.
Remark 15. This definition claims that certain continuous functions which are going to be smoothed out by means of -local structures can be smoothed out by the change of smoothness structure on .
Theorem 5. If one begins with a local smooth cover of and make it -local smooth by taking some of its local maps as -local, then Set-invariant smoothness structure equivalent to this -structure, is not diffeomorphic to the initial one.
To prove this result, we need the following observation.
Proposition 3. For every -local smooth cover of which is Set-invariant there exist continuous functions in which become smooth.
Proof. Let
be nondifferentiable. We still differentiate it as distribution
. Then the local transition function
sends
to
via
. The global section functor
determines 1 : 1 correspondence between distributions in
and external distributions in Set (Theorem 3). This correspondence goes as follows [
13] (p. 234). Given a distribution
in Set it defines a natural transformation in
which is the internal
-distribution
. This natural transformation
is defined by components. Let
be an element
and
A is a smooth ring
with
an ideal in
. So
are stages-components. Given a sheaf in
e.g.,
R or
one can consider them on stages
and obtain
correspondingly. Also any natural transformation, e.g.,
, is to be defined by components i.e., on
and then it reads
. Thus, the definition of
on components is as follows (here
is an ideal in
)
Given an external distribution we have the unique R-linear map in which is the internal distribution in . This internal distribution can be marked as which indicates the reverse direction of the correspondence, i.e., the global section functor uniquely retrieves the external distribution .
The change of the local map from Set to
sends
to
and
to
. Next step is to represents
by the predistribution
such that
is continuous [
13] (Remark 3.9.2, p. 311). Moreover, there always exist its differentials of arbitrarily order (for any 4-index
) as follows from the Kock axiom [
13] (p. 303). Thus, the local change of the map into
-internal defines, in terms of
, smoothness of continuous functions on
in Set.
Externally, distributions in Set obtained by differentiating the continuous functions can be represented by continuous functions due to Theorems 1 and 2. More precisely, there exist distributions e.g., from with respect to the test functions as in Theorem 1 which are entirely determined by a continuous functions on . □
The diagram below shows the steps performed in the proof above (See
Figure 1).
Proof of Theorem 5. Given a local map from a smooth atlas on let it be changed into -internal one. It is then possible to find a continuous function on which becomes smooth in the just by repeating the construction from the proof of Proposition 3. Then the Set-invariant -smoothness structure on is not be diffeomorphic to the initial smoothness structure. □
Remark 16. From the construction above it follows that, in principle, one can make locally any continuous function -smooth. To distinguish between smoothness structures on we need some additional global information. This is analogous to exotic smooth manifolds which locally are describable by standard smooth transition functions. The difference between them is written in some topological information given by Casson handles.
Remark 17. The construction of Theorem 5 can be repeated however at this stage of development of the approach we do not know whether obtained smoothness structures are pairwise different and nondiffeomorphic.
2.3. Local -Invariance and General Tovariance
There is, however, a price to pay for the change in : The object of smooth natural numbers N is not preserved by geometric morphisms between topoi ( does) - it does not even exist in general. The consequence would be leaving the class of geometric morphisms and geometric theories when approaching exotic 4-smoothness by -means.
Remark 18. A geometric morphism between toposes is the pair of functors and its left adjoint which preserves finite limits.
Remark 19. Let L be the 1st order language. The set of geometric formulae in L is the smallest set of formulae containing atomic formulae and closed by finite conjunction (∧), arbitrary disjunction (∨), and existential quantification (∃).
A theory is geometric if it can be axiomatized by sentences of the form where ϕ and ψ are geometric formulae and for some .
Proposition 4 ([
11])
. The inverse image part of a geometric morphism preserves any geometric theory. If is a sheaf topos over a site C with the object NNO (e.g., with ), then there is a unique geometric morphism where is the global section functor and the inverse image being the locally constant sheaf functor ( is the sheafification functor of the constant presheaf in ). Then
Proposition 5 ([
22], Lemma A.4.1.14)
. For any geometric morphism between toposes the inverse image functor preserves NNO, i.e., if is a NNO in then is the NNO in . It follows
Corollary 2. The object N of smooth natural numbers in is not preserved by the geometric morphism between and Set.
Proof. N is not isomorphic to in and for the geometric morphism the inverse image part of it, , sends to . □
Similarly, it holds
Corollary 3. Given a topos with NNO and a geometric morphism , then N in is not preserved by g, i.e., .
Remark 20. N is not NNO in . The arithmetic of natural numbers based on N is a weaker form of the arithmetic based on e.g., coherent induction principle holds instead of induction [13]. However, the distinction between N and in remains undecidable and hard to be grasped [13] (p. 307). Let
,
be the topos
with the canonical NNO,
, and with
N the object of smooth natural numbers, respectively. Let the meta-procedure of consistent replacement of
by
N be abbreviated as
. Hence
. In particular,
,
and
is non-Archimedean, nonlocal ring in
while
is Archimedean and local ring. The best way to describe
is via a corresponding shift in axiomatic systems [
13]. Such a shift leads to the weakening of arithmetic. However, as we saw in Corollaries above, smooth
N replacing the canonical NNO might be a source of non-geometricity in theories formulated in
which are based on
N.
For example, the theory of distributions in
and the meta correspondence as in Theorem 3 are non-geometric since they rely essentially on smooth natural numbers
N. If these results have additionally physical implications that would be a way showing the breaking of the tovariance principle [
11]. Below we will show how much we can push forward this program based on the results of this paper.
The original general tovariance principle as in [
11] relies on the free choice of arbitrary topos
with NNO such that any physical quantum theory formulated in the geometric language internally to
is equivalent to any other formulation internal to
, provided the change
is a geometric morphism. It follows that physics does not distinguish between these two representations and hence geometric logic is the language in which physical theories should be formulated. [
11]. Consequently, any quantum theory with the quantum algebra of observables is equivalent to certain commutative algebra of a classical theory. The equivalence is in terms of physical indistinguishability which resembles effects of gravity in GR. They are locally indistinguishable from the acceleration of the physical frame by any physical experiment. This quantum-classical equivalence for toposes is a direct consequence of the fact that for each noncommutative
-algebra
there exists a topos
in which
becomes internally a commutative algebra. However, already in [
11] the authors observed that the construction of a
-algebra is not geometric (the completeness property and the existence of a norm are not geometric in general) and that strong formulation of the tovariance principle may be broken and not giving the strict equivalence of quantum and classical formulations. Consequently the authors themselves quit referring to this principle as general physical rule [
12] (p. 493). However, still the point-free version of
-algebras (localic
-algebras) have been developed [
26] which are applicable to any topos and thus giving rise to the constructive version of the tovariance principle (We are greatly indebted to the anonymous referee for indicating this fact to us.). We are not making any specific use of the quantum-classical equivalence here, which, anyway, was the main reason for considering general tovariance. Rather we consider a theory, eventually in the geometric language, as physically (and mathematically) invariant with respect to the various interpretations in toposes with NNO. Thus, at this stage, we can restrict the class of physical theories to these theories which are formulated in the geometric language. Even this is done the shift
, replacing
by
N, is the source of non-geometricity which cannot be preserved by geometric morphisms. That is why the general tovariance principle gains the following weaker form becoming special tovariance principle
Special tovariance principle. When a physical theory is formulated in the geometric language one cannot experimentally distinguish between their realizations in different toposes with NNO when the change of the toposes is via geometric morphisms.
We thus left in this formulation undecided the question whether all physical theories can be formulated as geometric theories. If they were (in a sufficiently general form) and if we changed toposes by geometric morphisms then QM in the geometric formulation would lead to
-algebras which be physically equivalent to commutative algebras of observables [
11].
Even though this weak form of the tovariance principle were true the approach to exotic smoothness in this paper shows that the original strong general tovariance principle could be broken and the weak form above is too restrictive. Let us indicate two important ingredients of the breaking process.
We follow ‘global-to-local’ pattern known from gauge theories. This means that given local -structure on a smooth manifold one switches between Set and frames without possibility to leave entirely any of them (Definition 1). The Definition 1 can thus serve as an obstruction to the global choice of a topos on M, i.e., Set or . It can be restated as the property of non-existence of any global Set or -sections on M.
Any -invariant structure on M would rely on generalized equivalence between the Set construction with respect to and construction with respect to N. The constructions are not equivalent by geometric morphisms since N is not preserved - it does not exist in general (Corollaries 2 and 3).
Thus, even if a theory is geometrically formulated local -invariance can enforce its non-geometricity and the weak tovariance principle would be too restrictive as allowing only for geometric theories. However, as far as the non-geometric modifications like give rise to no physical implications, the status of the tovariance principle would be still unaffected on this ground.
To decide this problem, we are searching for an exotic
which has clear physical implications. It is
embedded in
and considered in [
15]. It was shown that the curvature of such embedded
is responsible for the realistic value of the cosmological constant [
15] which, moreover, is a topological invariant. This is a really strong connection of a physical quantity and topological structure of this
. If we assume that it is derived as some local
-structure then we can state the following conjecture
Conjecture 1. If the exotic as above is equivalent to certain Set-invariant local -structure (see Definition 4) then the strong general tovariance principle do not hold true and the weak tovariance principle is too restrictive.
The above conjecture in this formulation is true but still we do not know whether the ‘if’ assumption can be skipped. We will address this issue elsewhere.