Novel Fuzzy Clustering Methods for Test Case Prioritization in Software Projects

Abstract

Systematic Regression Testing is essential for maintaining software quality, but the cost of regression testing is high. Test case prioritization (TCP) is a widely used approach to reduce this cost. Many researchers have proposed regression test case prioritization techniques, and clustering is one of the popular methods for prioritization. The task of selecting appropriate test cases and identifying faulty functions involves ambiguities and uncertainties. To alleviate the issue, in this paper, two fuzzy-based clustering techniques are proposed for TCP using newly derived similarity coefficient and dominancy measure. Proposed techniques adopt grouping technology for clustering and the Weighted Arithmetic Sum Product Assessment (WASPAS) method for ranking. Initially, test cases are clustered using similarity//dominancy measures, which are later prioritized using the WASPAS method under both inter- and intra-perspectives. The proposed algorithms are evaluated using real-time data obtained from Software-artifact Infrastructure Repository (SIR). On evaluation, it is inferred that the proposed algorithms increase the likelihood of selecting more relevant test cases when compared to the recent state-of-the-art techniques. Finally, the strengths of the proposed algorithms are discussed in comparison with state-of-the-art techniques.

1. Introduction

The quality of software can be improved through a software testing process. However, a software testing process is a tedious process, and it consumes more testing time. Strenuous efforts need to be vested if testing happens to be in the cycle, which is otherwise known as regression testing (RT) [1,2,3,4]. RT is a continuous process, and it has to be stopped at an apt time, where a reasonable number of bugs have been fixed. During every cycle of testing, bugs are found and fixed. Debugging may impact the lines of code that result in new errors. These new errors are fixed in subsequent iterations. RT ascertains that changes in software during bug fixing will not affect the overall quality and performance of the software product being developed [5].

Chittimalli and Harrold [6] proved that the RT is more expensive, and it requires more than 33% of the cumulative expenses of the software. Yoo and Harman [7] examined various regression test cases and showed the importance of a reduction of time in the test suite in RT. The reduction in time for software testing mainly depends on any one of the following strategies: (i) Test Suite Minimization (TSM)—a methodology of removal of repetitive experiments to reduce the number of tests to run [8], (ii) Test Case Selection (TCS)—another way of reducing the number of tests to run [9] by way of modifications, and (iii) Test Case Prioritization (TCP) [10,11]—the most significant approach to reduce the number of tests to run by way of optimization.

RT should not be obviated because of its substantial impact on a time constraint. Rather, test cases in the test suite should be prioritized. Many ways of prioritizing test cases are based on their fault, exposing potential. The factors towards fault exposure are purely a white-box approach having a focus on branch coverage, and statement coverage [12]. Huang et al. [5] focused on the past data, such as the severity of the fault identified, the time spent for exercising the relevant test case, and the very first test case that identified specific severe fault, which is the backbone for finding the cost-cognizant average of faults detected. Keeping this as a fitness function and applying genetic algorithm resulted in optimized ordering of test cases which was a breakthrough in regression test prioritization.

The historical information about each test case reveals the number of times exercised, code coverage, and the iteration number in which the fault was uncovered, ends up in discovering an innovative equation setting up the priority numbers to the test cases [12]. Further, Huang et al. [13] prioritized test cases for GUI using weighted methods. Dennis Jeffrey et al. [8] viewed the programs written as slices based on their data and control flow. Every slice may represent multiple specifications. A single test case may cover a few of the requirements in a particular slice. Moreover, the output influencing statements of the slice and expressions present in the slice is the area in which attention must be paid. All of these aspects are applied heuristically to achieve prioritization. The workflow of the proposed methodologies is given in Figure 1. Figure 1 shows the various TCP methods used by researchers in RT, and in this paper, we have proposed two methods under the similarity/dominancy category. It is observed that the two clustering methods are developed to tackle two different perspectives. Similarity-based clustering is used in a situation where accuracy is more importance than time. In contrast, dominance-based clustering is used in situations where time is more importance than accuracy. Finally, after clustering, the clusters and the test cases are prioritized using the Weighted Arithmetic Sum Product Assessment (WASPAS) method.

The details of those methods will be discussed in Section 3. The construction of this paper is as follows. Section 2 discusses the previous studies related to TCP techniques. Section 3 provides the proposed methodology where the core contributions are discussed. Further, in Section 4, a numerical example is presented, and Section 5 gives the real case analysis where the strength of the proposed framework is discussed. Finally, in Section 6, concluding remarks are provided along with the future scope of research.

2. Related Studies of Test Case Prioritization (TCP)

Prioritizing test cases is a predominant optimization problem, in which the least prioritized test cases may be ignored to save time, while the quality remains intact [14]. Test case prioritization is an attempt to arrange the test cases, in such a way that highly formidable test cases lead the remaining ones based on the factors such as critical bugs’ coverage and satisfying the customer’s critical requirements. This leads to exemplary permutation of test cases, forming an archetypal test suite. The test cases in such test suites are used to uncover the bugs at the earliest, even though few of the trailing test cases are not exercised. Such prioritization is an optimization effort since it never undermines the power of testing. Several prioritization approaches have been developed for the researchers in the last decade, which is based on coverage, search, fault, risk, requirements, history, similarity, and others. From the survey published by Muhammad Khatibsyarbini et al. [15], more than 70% of the published works deals with STP (Software Testing Prioritization) which is based on search, coverage, faulty, requirement, and history, whereas the other methods occupy the rest of the percentage which is inclusive of similarity-based STP.

Singh [16] presented a detailed review of 65 studies in Regression-based TCP (RTCP) which covers the period of 1997–2011. This study covered the empirical study of eight main approaches and discussed gaps, metrics, and artifact used. Catal and Misha [17] elaborated another review of 120 studies in RTCP from 2001 to 2011, which discusses the trends in TCP approaches, including evaluation metrics. Yoo and Harman [7] conducted a literature review of RTs over 159 studies over the period of 1977–2009. This study covers four important TCP approaches of RTs namely TCP, TSM & TCS.

Similarly, Refs. [18,19] discussed 19 and 90 studies of literature review in RTCP, respectively. Khatibsyarsini et al. [15] presented 80 studies in RTCP from 1998 to 2016. They selected 80 studies from 707 articles collected from the above said period for discussing various quality assessments. This review covers the types of RT, TCP, tools, and evaluation metrics used. The limitations of the above systematic literature review consist of: (i) there is no empirical evidence for other TCP approaches, (ii) gaps have not been identified regarding the usage of artifacts on TCP approaches, and (iii) reasons behind the importance of the evaluation metrics are not clearly stated.

In this paper, similarity-based approaches for TCP have been concentrated. This will provide priority to the test cases that are the most dissimilar from those already selected. Recently, many researchers have derived similarity-based approaches [12,13,20,21,22] for TCP. Thomas et al. [23] proposed text analysis method for static TCP. In this paper, the main objective of the similarity-based techniques is to maximize the commonality and minimize the diversity, which is the opposite to researchers that have been obtaining priority that is based on maximizing the diversity and minimizing the similarity [24,25,26,27]. In general, similarity-based TCP is mainly divided into two types, which are distribution based and ART (Adaptive Random Test) inspired. TCP for the first case is derived from clustered test cases through dissimilarities between test cases [28,29]. ART is used as an improvised methodology of random testing, and in almost all cases, it outperforms all the cases expect when the size of code is less [30]. ART-inspired is an extension method of ART in TCP, the test cases with higher similarity are only considered instead of considering all of them, and this provides better results than ART [26]. Yves Ledru et al. [31] proposed a TCP model using four similarity-based different string distances, and then it was been proved that the proposed method has better Average Percentage Fault Detection (APFD) than randomly ordered test suites.

Zhang et al. [32] and Jiang et al. [33] have proposed adaptive random testing based prioritization techniques guided by code-coverage. Breno Miranda et al. [34] have extended the concepts of [32,33] using FAST approach, and finally, they proved that the FAST method performs better scaling and timing. ART (Adaptive Random Testing) [2] is a variant of random test generation that tries to spread, as evenly as possible, the test inputs in the input domain. In the present experimentation, the FAST approaches have been compared against both [26,35], which are further described in Section 5. Also, the approach proposed by Fang et al. [36] is based on code coverage information, from which they exploit the execution frequency profiles. Among black-box methods, Ledru et al. [31] propose a similarity-based approach solely considering the strings that express the test cases, i.e., the input data or the JUnit test cases. Also, FAST has been compared against this approach (see Section 5). Noor and Hemmati [37] developed a history-based approach in which, among new or modified test cases, those that are the most similar to failing ones are prioritized. FAST does not currently use historical data.

In software testing, diversity is a useful measure for both selecting and prioritizing test cases, and several similarity-based approaches have been proposed [14,24,26,28,35]. In this, clustering plays the role of prioritizing test cases. ARS approach clusters the test cases according to the number of objects and methods using k-means and k-medoids clustering algorithms. Another method which clusters the test cases according to object and method invocation sequence similarity metric uses the k-medoids clustering algorithm [14].

Model-Based Black-Box Techniques

White-box clustering is also profoundly used in clustering. Program entities such as assignment statements and control structures are analyzed. These are categorized based on the frequency of execution with respect to test cases. Clusters are formed having the same amount of frequencies. Inner elements of the cluster are further clustered using a greedy approach. Ultimately, a representative of each cluster gives an ordered sequence of test cases. This methodology uses both similarity and distance measures [36].

Event-oriented graph models and the importance of events lead to the clustering of events using unsupervised neural network and fuzzy c-means clustering in finding the frequently occurring event groups, thus providing high ranking to their respective test cases [38].

Various similarity measures over the test cases based on their code coverage have been studied and analyzed. Subsequently, many prioritization algorithms, such as Adaptive Random Testing and Global similarity-based algorithms, are scrutinized using various similarity measures. The apt prioritization algorithms with the best-fit similarity measures are suggested by [1,2]. The factors, namely, customer priority, implementation complexity, fault proneness, and volatility of the requirements are weighed, and their weight factors paved the way for prioritizing the associated test cases. Yuen Ta Kyu et al. [3] addressed the issues in transforming specifications into code, especially when the logical expressions are prone to drift away from the intended meaning. Different forms of the same expression result in multiple results, which may be undesirable. Test cases must be prioritized to obtain compelling test cases that can resolve such an issue.

Requirement based black box prioritization techniques were enhanced by introducing regression test factors such as the impact of fault in requirements, completeness, and traceability. Apart from the severity of faults detected, test efforts on a total and average basis are also used to discern the weight of test cases in attaining the ordering [22]. A new revolutionized approach in the field of prioritization has been introduced by Stephen W. Thomas et al. [23]. Their work focused on text analysis, wherein keywords, literals, comments, and identifiers were extracted from the documents. The test cases which are associated with the identified phrases or topics are considered, and the similarity among them was measured. The most dissimilar test cases were assigned with high ranking.

A novel method of prioritization was to introduce a mutant version of programs raising faults. These are generated through automation rather than hand seeded. Then the rate of fault detection was measured using block coverage, functional coverage, and random coverage and established that mutation-based prioritization was one of the best approaches [24]. Location services-based applications often suffer into the anomaly of rendering undesired locations. Hence, KeZhai et al. [25] introduced a new set of metrics and classified faults in five different categories. Based on these categories, test cases were prioritized and assessed by the harmonic mean of fault detection.

Li et al. [39] analyzed the search algorithms in prioritization which focused on coding facets, giving a stance over choosing the right algorithm from the greedy, meta-heuristic, or genetic and size up the factors determining the efficiency of the search algorithms. Elberzhager et al. [40] did a comprehensive survey of software testing articles and classified them. These classifications help the test manager in determining the required effort in testing, deciding over the stop point of testing and setting up the quality assurance aspects triggered by inspections and reviews. Furthermore, Elbaum et al. [41] presented a method for selection of test cases in a cost-effective manner.

Studies [11,40] presents a systematic review on TCP techniques and analysis its effects on software testing. Yoo and Harman [7], have also done survey and reviews on various test case optimization research methodologies. Do et al. [42] conducted a study on six different prioritization techniques and figured out the performance of the methods by varying time constraints imposed on them. Shrivathsan et al. [43] have done a substantial survey of test case prioritization techniques.

The advantages of the proposed similarity measures are: (i) similarity measures can be evaluated separately in the test cases, as well as the faulty items which are based on the grouping technology; (ii) it is based on the newly developed similarity measuring formula; and (iii) two-way similarity measures provide better classification accuracy than one-way similarity measures provide.

From the above literature survey, it shows that the improvement may take place by proposing an effective similarity-based TCP which will increase the testing accuracy and for that purpose, the present work proposes two similarity-based TCP and, finally, it is proved that the proposed method provides considerably good coverage of test cases.

From the investigation of the literature, the following challenges are encountered:

• Clustering methods proposed in the literature are single-sided clustering, that is, clustering is done from the perspectives of test cases. This will cause potential information loss, as the interrelationship between test cases and faulty functions is ignored.
• The similarity measures used in literature do not concentrate on the distribution of the data (input), which affects the convergence process. Moreover, literature studies do not provide methods pertaining to accuracy and time separately, and this is an open challenge to address.
• Prioritization methods do not consider inter- and intra-clustering, which eventually causes loss of information.
• Finally, customization on constraints is not dominantly provided in TCP. This would restrict the convergence and cause inaccuracies.

Motivated from these open challenges and to overcome them, the following contributions are made in this paper:

• Challenge one is resolved by proposing a novel two-way clustering that clusters both test cases and faulty functions for better understanding the interrelationship among them.
• Challenge two is addressed by proposing a new similarity measure that utilizes the power of exponent measure and provides smoothening of data for effective convergence. Further, the distribution of the data is also taken into consideration, and dominancy measure is proposed along with similarity measure for properly managing accuracy time trade-off.
• The WASPAS method is extended for inter- and intra-clustering prioritization, which effectively prioritizes test cases.
• Finally, the programming model is put forward for better customization of parameters to obtain an optimal test case for the set of faulty functions.

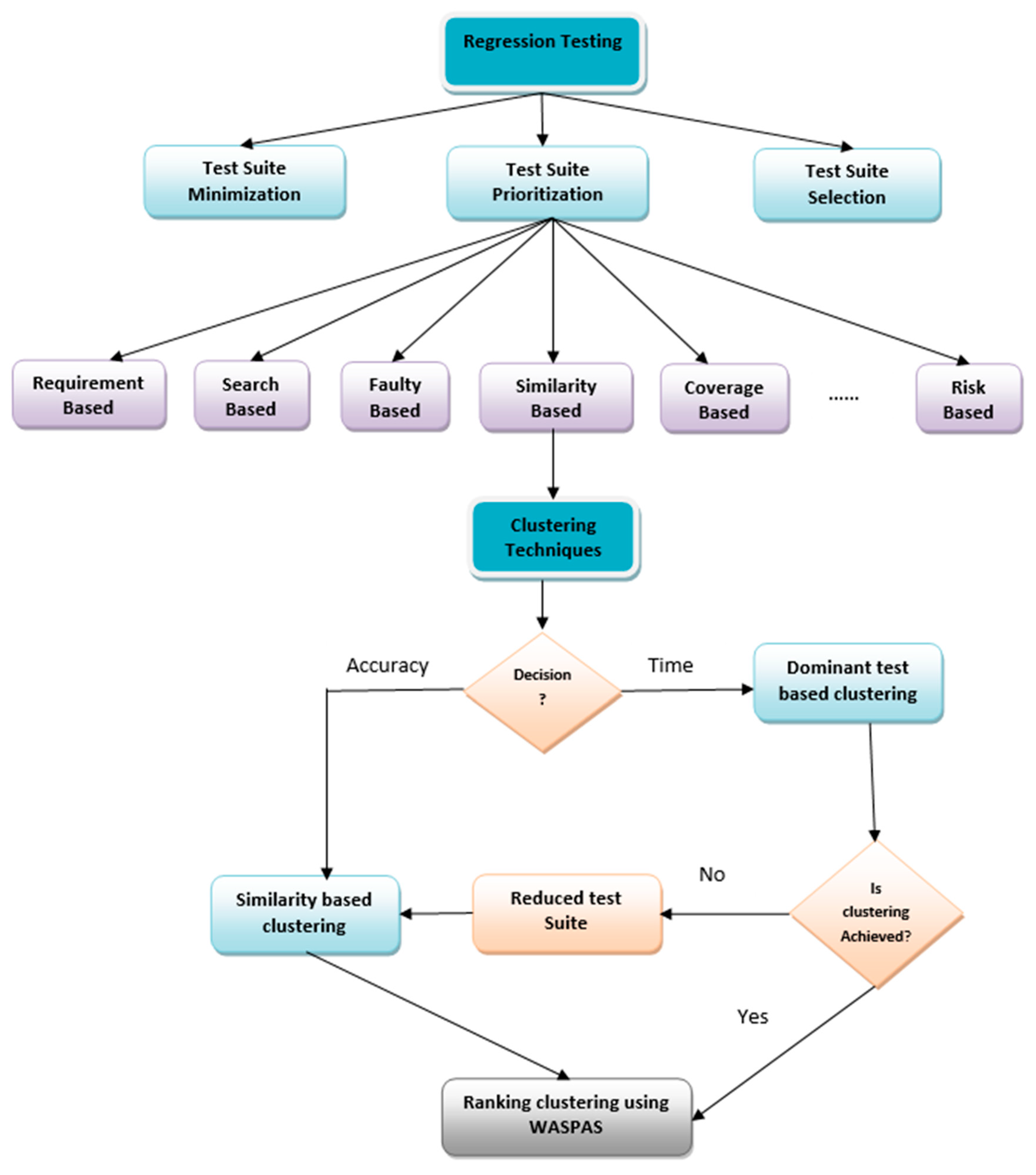
3. Proposed Methodology

Practically, in the context of Regression testing for software quality assurance, test case prioritization is a crucial aspect. In this paper, a fuzzy similarity-based test case prioritization model is proposed to improve the performance of regression testing compared to the existing literature. AbdurRahman et al. [44] proposed Call Dependency Graph (CDG) method, which uses the measure based on the similarity, wherein the degree of relationship between two test cases is measured through similarity. Boolean values are used to find the presence and absence of connectivity.

3.1. Proposed Fuzzy-Similarity Test Case Prioritization (TCP) Model (FSTPM)

All requirements are not equally important to the clients. Therefore, a software technique needs to be developed for selecting the requirements which are important to the clients. Hence, specific requirements need more attention from testers. Thus, the requirements clusters are prioritized, and their priority information is used to select test cases from each cluster, obtaining a complete set of reordered test cases. That is, the clusters with higher priority can be visited at an earlier time, and several test cases could be selected from it.

Proposed Fuzzy-Similarity Test Case Prioritization (TCP) Model (FSTPM) is a clustering model, and its solution procedure is based on grouping. Optimal clustering is obtained by using optimal grouping between the test cases and the faulty functions. The solution procedure for FSTPM is given below:

Given the fuzzy linguistic matrix F = [L_ij], where the values of L_ij are linguistic and for the sake of convenience, the following linguistic levels are identified. The linguistic levels are low (LL), low-high (LH), medium (MM), medium-high (MH), high (HH), and very high (VH). Here, L_ij is represented as the fault f_j, which is identified by the test case TC_i. The Gaussian membership function is used to associate the truth value to the linguistic levels.

Modify the linguistic matrix F into fuzzy matrix F1 = [b_ij] where b_ij is the fuzzified value of the given linguistic levels in F. All the entries of the fuzzy matrix F1 lies within 0 and 1. This value is the degree of relationship between the test cases and the fault.

To convert the given fuzzy matrix F1 into 0–1 adjacency matrix F2 = [a_ij], whose elements are defined by:

$$a_{ij}= \{\begin{array}{c} 0 if b_{ij}\le \vartheta \\ 1 if b_{ij}>\vartheta \end{array},$$

(1)

where the value of $\vartheta$ is chosen based on the testing-time constraint. If higher the testing-time then lower the $\vartheta$ value and lesser testing-time leads to higher $\vartheta$ value. The value of $\vartheta$ is calculated by:

$$\vartheta =min\left\{\frac{1}{\rho }, \frac{G_c}{N}\right\},$$

(2)

where $\rho$ = maximum number of permissible test cases in a group; G_C = number of permissible grouping and N = number of test-cases (or) a maximum number of faults identified by a test case. The value of $\rho$ must satisfy the condition: $\rho = \frac{N+1}{G_c}$.

After finding the 0–1 adjacency matrix F2, grouping between the test cases is identified. The following procedure is used to find the grouping of similar test cases.

Construct a lower triangular similarity matrix for the given test cases from the 0–1 adjacency matrix F2 by using:

TC_sim $= \{S_{ij}; i>j and \forall i, j=1, 2, 3, \dots , N\},$ where N = total number of test cases and

$$S_{ij}= \left(\frac{a\left(\frac{a}{n{e}^{\left(\frac{n-a}{n+a}\right)}} +d\right)}{\left[a\left(\frac{a}{n{e}^{\left(\frac{n-a}{n+a}\right)}}\right)+ b+c+ad\right]}\right).$$

(3)

Here, a is the number of faults that exists on both the test cases TC_i and TC_j; b is the number of faults that exists only on TC_i; c is the number of faults that exists only on TC_j and d is the number of faults that do not exist on test cases TC_i and TC_j.

When test cases uncover faulty function, repetition of test cases may occur; if such a scenario exists, then any of the repeated test cases is removed before applying the grouping techniques. Suppose $S_{ij}=1$, then TC_i and TC_j have the same faulty functions, and either TC_i or TC_j is removed, and these two test cases are tagged into one, namely TC_ij. This will reduce the processing time of the problem.

After modifying the similarity matrix, all dominant similarity coefficients are swapped into the first ${\mathrm{G}}_{\mathrm{c}}$ columns (G_c—number of groups), because of the maximum number of clusters is ${\mathrm{G}}_{\mathrm{c}}$. For this purpose, the similarity matrix is further modified as follows: (i) if larger similarity coefficient value appears between the test cases in the first ${\mathrm{G}}_{\mathrm{c}}$ column of each row, then all the values are retained as such; (ii) if the largest similarity value appears after ${\mathrm{G}}_{\mathrm{c}}$ column, then that column is interchanged to any one of the first ${\mathrm{G}}_{\mathrm{c}}$ columns; and (iii) if the largest similarity value occurs in various places including the first ${\mathrm{G}}_{\mathrm{c}}$ column, then ε quantity is added to the highest similarity appeared in the first ${\mathrm{G}}_{\mathrm{c}}$ column and this quantity lies typically between 0.001 and 0.005. The nature of the problem is not affected by this. A few problems require this modification.

For finding the optimal grouping of the test cases, the following 0–1 optimization problem is constructed:

The optimal clustering problem for grouping test cases which maximizes the sum of similarities $S_{ij}$ is given by:

$$Max Z= {{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^N{S}_{ij}{y}_{ij} for i>j,$$

(4)

where $y_{ij}= \{\begin{array}{c}1; both the test cases T{C}_i and T{C}_{j}are mutually inclusive\\ 0; both the test cases T{C}_i and T{C}_{j}are mutually exclusive\end{array}$

Subject to the constraints:

$${\displaystyle {\displaystyle \sum }_{i=1}^N}{y}_{ij}=1 for j=1, 2, \dots , N and i\ge j,$$

(5)

$${\displaystyle {\displaystyle \sum }_{\begin{array}{c}j=1\\ i=j\end{array}}^N}{y}_{ij}= G_c for j=1, 2, \dots , N,$$

(6)

$$\rho y_{jj}+ {\displaystyle {\displaystyle \sum }_{i=1}^N}{y}_{ij}\ge 0 for j=1, 2, \dots , N and i>j,$$

(7)

$$and y_{ij}=0 or 1 for i, j=1, 2, 3, \dots , N.$$

(8)

Using similarity values obtained from 4(d) the optimization problem is derived as per Equations (4) through (8) and using MATLAB^® software, the optimal grouping between the test cases is obtained. Optimization toolbox is used that adopts linear programming solver with a dual-simplex algorithm. Further, the parameters are set according to the application, and they are discussed below.

After finding the 0–1 adjacency matrix F2, there is the need to find grouping between the faultiness. The following procedure is used to find the grouping of the similarity values between the faulty functions, which are similar to step (4) with minor modifications.

Construct a lower triangular similarity matrix for the given faulty functions from the 0–1 adjacency matrix F2 from:

FAULT_sim $= \{S_{ij}; i>j and \forall i, j=1, 2, 3, \dots , M\},$ where M = total number of faultiness identified by all the test cases and:

$$S_{ij}= \left(\frac{a\left(\frac{a}{n{e}^{\left(\frac{n-a}{n+a}\right)}} +d\right)}{\left[a\left(\frac{a}{n{e}^{\left(\frac{n-a}{n+a}\right)}}\right)+ b+c+ad\right]}\right).$$

(9)

Here, a is the number of faulty functions exists on both the faulty functions FAULT_i and FAULT_j; b is the number of faults exists only on FAULT_i c is the number of faults exists only on FAULT_j and d is the number of faults does not exist on faulty functions FAULT_i and FAULT_j.

When faulty function uncovered by test cases, repetition of faulty functions may occur; if such a scenario exists, then any of the faulty function is removed before applying grouping techniques. Suppose S_ij = 1, then FAULT_i and FAULT_j have the same faulty functions, and either FAULT_i or FAULT_j is removed, and these two test cases are tagged into one, namely FAULT_ij. This will reduce the time complexity of the problem.

For finding the optimal grouping of the test cases, the following 0–1 optimization problem has been constructed:

The optimal clustering problem for grouping test cases, which maximizes the sum of similarities $S_{ij}$ and it is derived as:

$$Max Z= {{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{j=1}^M{S}_{ij}{x}_{ij} for i>j,$$

(10)

where $x_{ij}= \{\begin{array}{c}1; both the faulty items are mutually inclusive\\ 0; both the faulty items are mutually exclusive\end{array}$ and M = number of faulty functions identified by the test cases.

Subject to the constraints:

$${\displaystyle {\displaystyle \sum }_{j=1}^M}{x}_{ij}=1 for i=1, 2, \dots , M and i\ge j,$$

(11)

$${\displaystyle {\displaystyle \sum }_{j=1}^M}{x}_{jj}= G_c for j=1, 2, \dots , M,$$

(12)

$$\rho x_{jj}+ {\displaystyle {\displaystyle \sum }_{i=1}^M}{x}_{ij}\ge 0 for j=1, 2, \dots , M and i>j,$$

(13)

$$and x_{ij}=0 or 1 for i, j=1, 2, 3, \dots , M.$$

(14)

Using similarity values, the optimization problem is derived as per Equations (10) through (14) and solved by using MATLAB^® software (MathWorks, Natick, MA, USA) with linear programming solver and dual-simplex algorithm. As mentioned earlier, parameter values are application-specific, and they are discussed below. Finally, the optimal grouping between the faultiness is obtained

Using the optimal grouping between the test cases and faultiness, the incidence matrix F₂ is rearranged as per the grouping got from steps (4) and (5) and then finally, optimal clustering is obtained.

For ease of understanding Algorithm 1 is presented, which clearly describes the working of fuzzy-similarity test case prioritization model.

Algorithm 1: Pseudo code for fuzzy-similarity test case prioritization model (FSTPM)

Input: Given F = [Lij], for i = 1, 2, …, n and j = 1, 2, …, m are the linguistic relationship matrix between the set of n-test cases and m-faulty items.

Output: F1 = [aij], for i = 1, 2, …, n and j = 1, 2, …, m, with clustering partition between the set of test cases and faultiness.

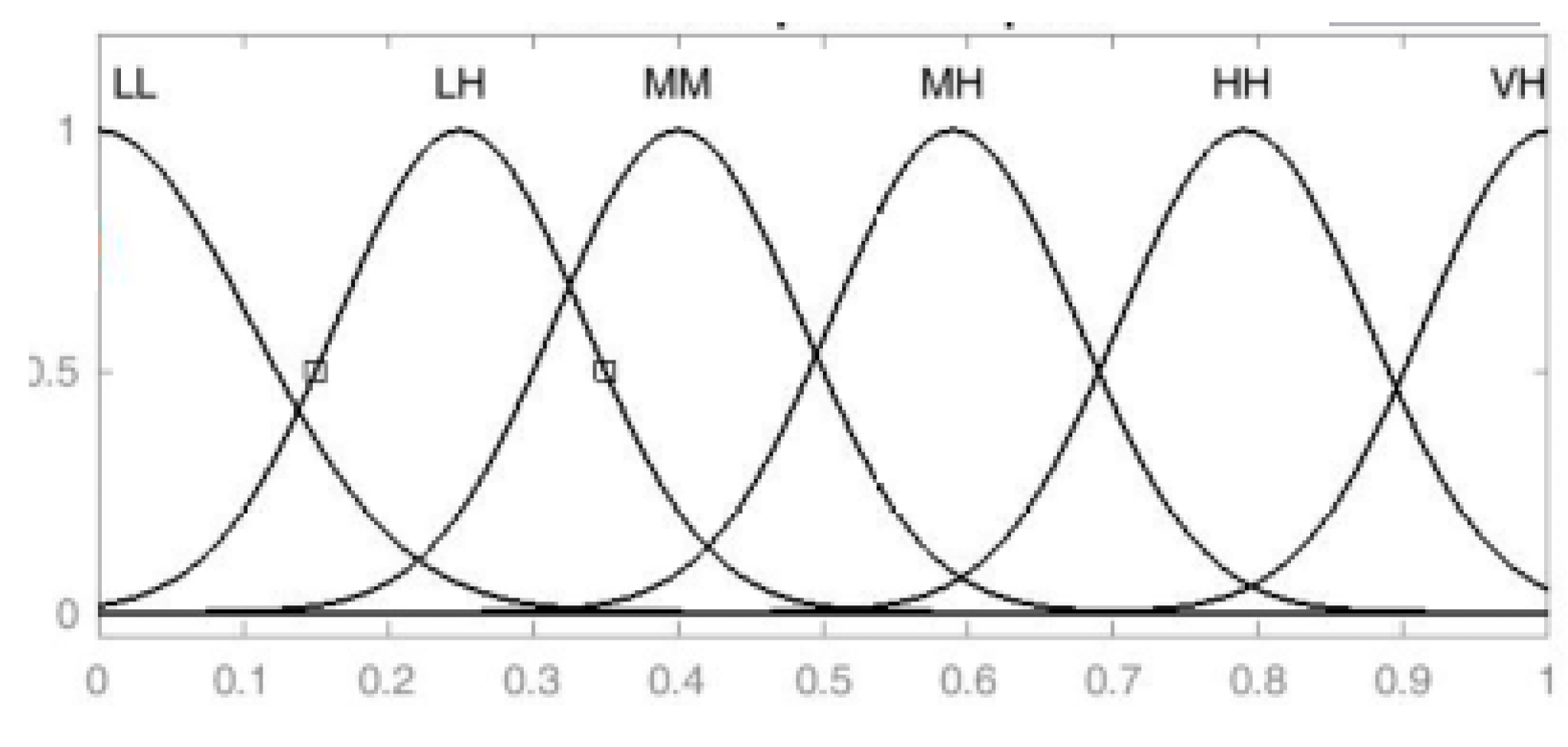
1. Using Gaussian membership function, convert the given F-linguistic relationship matrix into F1 = [bij] for i = 1, 2, …, n and j = 1, 2, …, m as fuzzy matrix

2. To compute fuzzy 0–1 matrix F2 = [aij] for i = 1, 2, …, n and j = 1, 2, …, m from F1 by using the relation $a_{ij}\leftarrow \{\begin{array}{c} 0 if b_{ij}\le \vartheta \\ 1 if b_{ij}>\vartheta \end{array}$ where $\vartheta \leftarrow min\left\{\frac{1}{\rho }, \frac{G_c}{N}\right\}$

3. for i = 1 to n do

{

for j = 1 to n do

{

i. to compute a, b, c and d values between the ith and jth row

ii. to compute the similarity between the test cases by using the relation $S_{ij}\leftarrow \left(\frac{a\left(\frac{a}{n{e}^{\left(\frac{n-a}{n+a}\right)}} +d\right)}{\left[a\left(\frac{a}{n{e}^{\left(\frac{n-a}{n+a}\right)}}\right)+ b+c+ad\right]}\right)$

}

}

4. using the similarity index Sij as obtained from step-3, to solve the following 0–1 programming: $$Max Z= {{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^N{S}_{ij}{y}_{ij} for i>j$$

where $y_{ij}= \{\begin{array}{c}1; both the test cases T{C}_i and T{C}_{j}are mutually inclusive\\ 0; both the test cases T{C}_i and T{C}_{j}are mutually exclusive\end{array}$

subject to the constraints

${\displaystyle {\displaystyle \sum }_{i=1}^N}{y}_{ij}=1 for j=1, 2, \dots , N and i\ge j$

${\displaystyle {\displaystyle \sum }_{\begin{array}{c}j=1\\ i=j\end{array}}^N}{y}_{ij}= G_c for j=1, 2, \dots , N$

$\rho y_{jj}+ {\displaystyle {\displaystyle \sum }_{i=1}^N}{y}_{ij}\ge 0 for j=1, 2, \dots , N and i>j$$and y_{ij}=0 or 1 for i, j=1, 2, 3, \dots , N$

5. Apply steps 3 and 4 for faultiness and based on the yij, values, group/cluster the faultiness

6. Based on the group of test cases and the faultiness, rearrange the rows and columns of F2, then we got the clustering. This will be the given input of an inter and intra ranking of clusters

3.2. Dominancy Test Based Clustering for Test Case Prioritization (DTTCP)

The limitation of FSTPM is the random assumption of many terms, namely (i). The number of clustering, (ii). The maximum number of test cases accommodated in a group, (iii) Fixation of the threshold value, and so on. Again, if the number of groups varies, then the clustering accuracy also varies. In the above example, if the number of groups is fixed as 3, then the clustering accuracy is above 60%, whereas for the same problem if we fix the number of groups as 2, then the clustering accuracy exceeds 85%. The limitation of the FSTPM is that they cannot handle clusters of varying numbers between test cases and faculty functions. To overcome these limitations, a new clustering method based on the dominancy test for test case prioritization (DTTCP) has been proposed.

The advantages of the DTTCP are: (1) based on the nature of the problem, the number of clusters can be calculated systematically and (2) if the number of grouping between the test cases and faulty items mismatch, then the resultant matrix is used to find the clustering, which requires very less computational time when compared to its counterpart. Once the dominancy test is applied, the size of the problem will reduce drastically. The following is the procedure for DTTCP:

Start with the matrix F2 derived from Section 3.1. T1, T2 …, Tn is the set of test cases (given in rows) and F1, F2, …, Fm is the set of faulty items (given in columns).

Compare the dominance between the rows. If the row vector Ta contains the row vector Tb then row Tb is removed and re-designate row Ta by Tab. If Ta $\supseteq$ Tb $\supseteq$ Tc then remove rows Tb and Tc and re-designate row Ta by Tabc. Similarly, if Ta $\supseteq$ Tb $\dots \supseteq$ Tk then removes rows Tb, Tc, … Tk and re-designate row Ta by Tab…k.

For the ease of understanding, Algorithm 2 is presented, which describes the working of DTTCP.

Algorithm 2: Pseudo code for dominancy test for test case prioritization (DTTCP)

Input: Given F = [Lij], for i = 1, 2, …, n and j = 1, 2, …, m are the linguistic relationship matrix between the set of n-test cases and m-faulty items. Output: F2 = [aij], for i = 1, 2, …, n and j = 1, 2, …, m, with clustering partition between the set of test cases and faultiness (or) Recommended to move to FSTPM with reduced F2 fuzzy 0–1 matrix Using Gaussian membership function, convert the given F-linguistic relationship matrix into F1 = [bij] for i = 1, 2, …, n and j = 1, 2, …, m as fuzzy matrix To compute fuzzy 0–1 matrix F2 = [aij] for i = 1, 2, …, n and j = 1, 2, …, m from F1 by using the relation $a_{ij}\leftarrow \{\begin{array}{c} 0 if b_{ij}\le \vartheta \\ 1 if b_{ij}>\vartheta \end{array}$ where $\vartheta \leftarrow min\left\{\frac{1}{\rho }, \frac{G_c}{N}\right\}$ To apply the following steps to find the cluster or the reduced F2 matrix: If the row vector Ta contains ($\supseteq )$ the row vector Tb, then row Tb is removed and re-designate row Ta by Tab. If no more rows are contains with other rows, then stop the process Apply steps 3a and 3b for columns also, and do the same process If the size of the matrix is a square matrix then stop the process. The resulting matrix is partitioned accordingly. Otherwise, the size of the matrix of F2 is drastically reduced and then performs steps 3 to 6 as FSTPM.

In the previous example, TC₁ $\supseteq$ TC₈ and TC₆ $\supseteq$ TC₅, then remove rows TC₅ and TC₈, then the resultant F2 matrix is modified as follows:

$$\mathrm{F}2=Testcases\{\begin{array}{c}\begin{array}{cccccccccc}& 1& 2& 3& 4& 5& 6& 7& 8& 9\end{array}\\ \begin{array}{c}18\\ 2\\ 3\\ 4\\ 65\\ 7\\ 9\end{array}\left[\begin{array}{ccccccccc}1& 0& 0& 1& 1& 1& 1& 0& 0\\ 0& 1& 1& 1& 1& 1& 0& 0& 0\\ 0& 1& 1& 1& 0& 0& 1& 1& 0\\ 0& 1& 1& 0& 0& 0& 1& 1& 1\\ 1& 0& 0& 0& 1& 1& 1& 0& 1\\ 1& 1& 1& 1& 0& 0& 0& 1& 0\\ 1& 1& 1& 1& 0& 1& 0& 0& 0\end{array}\right]\end{array}.$$

Similarly, perform step-2 for columns also. Here, F₂ $\supseteq$ F₃$\supseteq$ F₈, then remove columns three & eight and re-designate column F₂ by F₂₃₈. Likewise, F₆ $\supseteq$ F₅, then remove columns five and re-designate column F₆ by F₆₅. Again, F₇ $\supseteq$ F₉, then remove column 9 and re-designate column F₇ by F₇₉. Hence, the resultant F₂ is given by:

$$\mathrm{F}2=Testcases\{\begin{array}{c}\begin{array}{cccccc}& 1& 238& 4& 65& 79\end{array}\\ \begin{array}{c}18\\ 2\\ 3\\ 4\\ 65\\ 7\\ 9\end{array}\left[\begin{array}{rrrrr}1& 0& 0& 1& 1\\ 0& 1& 1& 1& 1\\ 0& 1& 1& 1& 0\\ 0& 1& 1& 0& 0\\ 1& 0& 0& 0& 1\\ 1& 1& 1& 1& 0\\ 1& 1& 1& 1& 0\end{array}\right]\end{array}.$$

Apply steps 2 and 3 until the number of groups of rows and columns is equal in number.

From step 2 we get, F₁₈ $\supseteq$ F₆₅, then remove row 65 and re-designate column F₁₈ by F₁₈₆₅. Again TC₃$\supseteq$ TC₄ and TC₉ $\supseteq$ TC₇, then remove rows TC₄ and TC₇, then the resultant F2 matrix is modified as follows:

$$\mathrm{F}2=Testcases\{\begin{array}{c}\begin{array}{cccccc}& 1& 238& 4& 65& 79\end{array}\\ \begin{array}{c}1865\\ 2\\ 34\\ 97\end{array}\left[\begin{array}{rrrrr}1& 0& 0& 1& 1\\ 0& 1& 1& 1& 1\\ 0& 1& 1& 1& 0\\ 0& 1& 1& 0& 0\end{array}\right]\end{array}.$$

Similarly, it is applied to columns and rows, and finally, the matrix F2 is reduced as:

$$\mathrm{F}2=Testcases\{\begin{array}{c}\begin{array}{ccc}651& 238& 784\end{array}\\ \begin{array}{c}1865\\ 972\\ 34\end{array}\left[\begin{array}{rrr}1& 0& 0\\ 0& 1& 1\\ 0& 1& 1\end{array}\right]\end{array}.$$

Expanding the above matrix, the required clustering is obtained, which is the output of the final clustering for dominancy test. The APFD measure of the above two methods, along with non-prioritization, is given in the following Figure 2a–c.

Clearly, from the above Figure 2a–c, it is concluded that cluster based on the similarity coefficient performs better than the other methods.

3.3. Discussion

As per the client’s requirement, not all the requirements are equally important, and some requirements are used frequently when the software is deployed. Hence, those frequently addressed requirements are more important during the clustering process. For this purpose, we have taken input as linguistic, and it provides the degree of relationship between the test cases and the faulty functions. The uniqueness of the proposed clustering methodology is that the identical properties among the test-cases and the faulty functions are identified separately and then combined. The proposed methodology performs better than the other clustering algorithms suggested in the recent state-of-the-art techniques by Gokce et al. [38], Mohammed et al. [44], Chaurasia et al. [45], and Mohammed and Do [46]. Grouping accuracy is based on: (i) the number of clusters to select and (ii) the number of test cases accommodated in each cluster.

Three different measures are used for measuring the performance of the proposed method. The first one is an accuracy, which is based on how many 1’s are accommodated in the clusters. For optimal $\mathsf{\rho },{ \mathrm{G}}_{\mathrm{c}}, \mathrm{and} \vartheta$, the proposed method achieved nearly 71% accuracy, whereas the other state-of-the-art techniques achieved a maximum of 62% with regards to the final clustering. In the above example, in cluster-1, the detected faults are f₂, f₃, and f₄, and the undetected fault is f₅. Similarly, in cluster-2, detected faults are f₇ and f₉; and in this case, no fault is being undetected. In cluster-3, detected faults are f₁ and f₆, and fault f₈ is undetected. The advantage of this clustering methodology is that applying grouping technology for test cases separately and faults separately, so that the number of undetected faults is very less, compared to the other clustering algorithms.

Depending on the clusters set, the clustering accuracy varies. In the same example, if the number of cluster set is assumed to be two, then the clustering accuracy will be 87.5%. Hence, the assumption of cluster sets is critical while applying clustering techniques for prioritization.

The performance analysis, before and after clustering is ascertained through Average Percentage Fault Detection (APFD) measure. APFD achieves a better result of 51.34% through the clustering method than other methods (without clustering) with an APFD score of 48.76%. Hence, the clustering method of prioritization gives a relatively better result. The following session discusses the variously estimated clustering, and the ranking among the clustering, which is calculated through the Weighted Arithmetic Sum and Product Assessment (WASPAS) method.

3.4. An Inter and Intra Ranking of Clusters

Consider the procedure for ranking the clusters and then selecting desirable order in which test cases must be utilized for better performance.

Step 1:

Obtain k clusters each having an evaluation matrix of order m by n where m denotes the number of test cases, and n denotes the number of criteria.

Step 2:

The values in these matrices are linguistic. These are converted into fuzzy values by using Gaussian membership function.

Step 3:

Initially, the dominant cluster is estimated by using the weighted arithmetic method given in Equation (15). The weight of each test case is considered to be equal, and this helps the procedure to pay equal attention to each test case.

$${\mathsf{\zeta }}_{\mathrm{i}}={\displaystyle {\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}}{\mathrm{w}}_{\mathrm{j}}{\mathsf{\mu }}_{\mathrm{ij}},$$

(15)

where n is the number of criteria, ${\mathrm{w}}_{\mathrm{j}}$ is the weight of the criteria with $0\le {\mathrm{w}}_{\mathrm{j}}\le 1$, and ${\displaystyle \sum }_{\mathrm{j}}{\mathrm{w}}_{\mathrm{j}}=1$ and ${\mathsf{\mu }}_{\mathrm{ij}}$ is the fuzzy value.

Step 4:

Using step 3, the weighted arithmetic value of each test case pertaining to a particular cluster is obtained. The average is calculated for each cluster, and these values are normalized to obtain the weight of the cluster. They are given by Equations (16) and (17):

$${\mathrm{c}}_{\mathrm{p}}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{m}}{\mathsf{\zeta }}_{\mathrm{i}}}{\mathrm{m}},$$

(16)

$${\mathsf{\phi }}_{\mathrm{p}}=\frac{{\mathrm{c}}_{\mathrm{p}}}{{{\displaystyle \sum }}_{\mathrm{p}=1}^{\mathrm{k}}{\mathrm{c}}_{\mathrm{p}}},$$

(17)

where p is the number of clusters taken for the study.

Step 5:

From step 4, the weight of each cluster is obtained, and using these values dominant cluster can be determined.

Step 6:

The matrix of order m by n is chosen from the dominant cluster, and the test cases are ranked using the WASPAS method. The formulations are given by Equations (18)–(20):

$${\mathrm{Q}}_1={\displaystyle {\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}}{\mathrm{w}}_{\mathrm{j}}{\mathsf{\mu }}_{\mathrm{ij}},$$

(18)

$${ \mathrm{Q}}_2={\displaystyle {\displaystyle \prod }_{\mathrm{j}=1}^{\mathrm{n}}}{\left({\mathsf{\mu }}_{\mathrm{ij}}\right)}^{{\mathrm{w}}_{\mathrm{j}}},$$

(19)

$${\mathrm{Q}}_3={\mathsf{\lambda }\mathrm{Q}}_1+\left(1-\mathsf{\lambda }\right){\mathrm{Q}}_2,$$

(20)

where ${\mathrm{Q}}_1$ is the weighted sum method (WSM), ${\mathrm{Q}}_2$ is the weighted product method (WPM), ${\mathrm{Q}}_3$ is the final rank value ${\mathrm{w}}_{\mathrm{j}}$ is the weight of the j^th criterion with $0\le {\mathrm{w}}_{\mathrm{j}}\le 1$ and ${\displaystyle \sum }_{\mathrm{j}}{\mathrm{w}}_{\mathrm{j}}=1$ and $\mathsf{\lambda }$ is the strategy value with $0\le \mathsf{\lambda }\le 1$.

Step 7:

The ${\mathrm{Q}}_3$ value is obtained for each test case and the test case, which has the highest value is a highly preferred test case and so on.

4. Numerical Example

4.1. Illustration of Clustering of Test Cases

The proposed algorithm is illustrated with nine test cases, which uncovers nine faults and the scenario of uncovering is as shown below:

TC₁ = { f1, f4, f5, f6, f7}, TC₂ = { f2, f3, f4, f5, f6}, TC₃ = {f1, f2, f3, f4, f7, f8}, TC₄ = { f2, f3, f7, f8, f9}, TC₅ = { f1, f4, f6, f7, f9}, TC₆ = { f1, f3, f5, f6, f7, f9 }, TC₇ = { f1, f2, f3, f4, f8}, TC₈ = { f1, f6, f8}, TC₉ = { f1, f2, f3, f4, f6}.

From the available information, the fuzzy-linguistic matrix F is constructed as shown below:

By applying appropriate value to their concerned Gaussian Membership Function, the following fuzzy-matrix F1 is derived. The input membership function for the given problem is defined in Figure 3.

In the sample problem, the number of test-cases (N = 9) and the number of faults identified by all the test-cases (M = 9) are equal. Let us assume that the number of groups G_c = 3. Therefore, $\vartheta =min\left\{\frac{1}{\rho }, \frac{G_c}{N}\right\}=min\left\{\frac{1}{4}, \frac{3}{9}\right\}=0.25$. Hence, modify the fuzzy matrix F1 into 0–1 incidence matrix, namely F2 using Equation (2) as:

From F2, construct a lower or upper triangular similarity index matrix for test cases TC_sim = $\{S_{ij}; i>j and \forall i, j=1, 2, 3, \dots , 9\}$ using Equation (3) as:

Substitute TC_sim(S_ij) value in the optimization function given in (4) and expand the constraints given in Equations (5)–(8). Then by using MATLAB^® software (optimization toolbox, with solver as linear programming) solve the 0–1 programming, to obtain the following result. (Since G_c is 3, by applying Equation (2), the maximum number of test cases accommodated in a single group will be $\rho =4$ and the remaining indices not mentioned below (varying between i = 1–9 and j = 1–9) are zero. Hence, relating the above, three clusters among test cases have been obtained, namely Cluster-1 = {1, 5, 6, 8}, Cluster-2 = {2, 9, 7} and Cluster-3 = {3, 4}.

y66 = y77 = y44 = y16 = y29 = y34 = y56 = y85 = y97 = 1

In a similar mechanism, grouping technology concepts are applied to faulty functions using step (5) in the solution procedure from F2, construct a lower or upper triangular similarity index matrix for faulty functions FAULT_sim = $\{S_{ij}; i>j and \forall i, j=1, 2, 3, \dots , 9\}$ using Equation (3) as:

Substitute FAULT_sim (S_ij) value in the optimization function given in (9) and expanding the constraints given in Equations (10)–(13), and then using MATLAB^® software to solve the 0–1 programming, the following results were obtained (Assumed G_c is 3, then using (2), the maximum number of test cases accommodated in a single group will be $\vartheta =4)$.

x66 = x22 = x77 = x15 = x34 = x42 = x56 = x87 = x98 = 1

The indices not mentioned in Equation (15) (varying for i = 1–9, and j = 1–9) are zero. Hence, relating the above, three clusters have been obtained for faulty functions, namely Cluster-1 = {1, 5, 6}, Cluster-2 = {2, 3, 4} and Cluster-3 = {7, 8, 9}. Here also, if we set G_c as 2, then test case numbered 8 is either added to the first cluster or the second cluster. Rearrange the matrix F2 as per the equality constraints given above, the resultant matrix is a clustering matrix and is given in (16).

4.2. An illustrative Example for Inter and Intra Test Case Prioritization

Form matrices of order $m\times n$ where m represents the test cases and n represents the faults. Based on the clustering process, these matrices are formed of order $4\times 3$, $3\times 3$, and $2\times 2$, respectively.

$$\mathrm{Matrix}1= \left[\begin{array}{ccc}0.89& 0.92& 0.71\\ 0.7& 0& 0.88\\ 0.56& 0.74& 0.85\\ 0.76& 0& 0.89\end{array}\right]\mathrm{Matrix} 2= \left[\begin{array}{ccc}0.81& 0.89& 0.74\\ 0.67& 0.95& 0.78\\ 0.96& 0.66& 0.74\end{array}\right] \mathrm{Matrix} 3= \left[\begin{array}{ccc}0.34& 0.92& 0\\ 0.75& 0.73& 0.83\end{array}\right]$$

Calculate the WASPAS parameters using Equations (20)–(22) and they are shown in

Table 1. Rank value analysis for cluster-1.

Alternative	Sum	Product	Rank
A1	0.84	0.834	0.83
A2	0.526	0	0.26
A3	0.716	0.706	0.711
A4	0.55	0	0.275

.

From Table 1, the intra ranking is given by TC₁ > TC₅ > TC₆ > TC₈ for cluster-1, TC₂ > TC₉ > TC₇ for cluster 2 and TC₃ > TC₄ for cluster 3, respectively. The inter ranking is given by C3 > C1 > C2 with values 3.59, 2.63, and 2.4, respectively. A similar idea is adopted for

Table 2. Value analysis for cluster-2.

Alternative	Sum	Product	Rank
A1	0.813	0.81	0.81
A2	0.8	0.79	0.7959
A3	0.786	0.77	0.781

and

Table 3. Rank value analysis for cluster-3.

Alternative	Sum	Product	Rank
A1	0.42	0	0.21
A2	0.776	0.7749	0.7758

as well.

5. A Real Case Study Analysis

The proposed technique is tested with the programs developed by researchers and is extracted from the local software company, which is collaborated with some group of students in the university, and it is available in (https://sir.unl.edu). The programs chosen for testing purpose are illustrated with descriptions in

Table 4. Software projects tested.

Objects	Language	Req.	Versions	Size (KLoC)	Classes	# Faulty Versions	Fault Types	Bug Type	Bug Description
Pool 1	Java	19	2	3.62	28	36	Real	Race	Thread execution order and execution speed problem
Pool 2	Java	59	2	18.66	88	114	Real	Deadlock	Resource allocation contention problem
Pool 3	Java	123	3	38.09	124	136	Real	Deadlock	Resource allocation contention problem
Pool 4	Java	84	4	20.43	94	112	Real	Deadlock	Resource allocation contention problem

. The chosen programs belong to the category of concurrency. These programs inherently have the quality of multithreaded activities requiring arbitration.

In Table 4, each of the objects is associated with the programming languages which are used to create an object, the number of lines of code in the program, number of classes used in an object, number of faulty versions, the number of versions, number of requirements and its types, and the types of bugs based on the given requirements. The test case studied in this work is a functional test case associated with requirements. The performance analysis of the proposed methods with the following ten popular prioritization techniques is given below.

Total statement coverage prioritization (P1): Test cases are ordered with respect to the number of statements covered by them. The greater the number of statements covered, the higher the prioritization. When more than one test case covers the same number of statements, then they are assigned priority randomly, being next to each other.

Additional statement coverage prioritization (P2): Test cases are ordered based on their higher number of statements coverage. Then, this ordering is adjusted based on which test case covers the uncovered statements.

Total branch coverage prioritization (P3): It is very similar to the total statement coverage prioritization, except that the coverage is for branches, rather than for the statements.

Additional branch coverage prioritization (P4): It is very similar to the additional statement coverage prioritization, except that the coverage is for branches, rather than for the statements.

Total function coverage prioritization (P5): It is very similar to the total statement coverage prioritization, except that the coverage is for functions, rather than for the statements.

Additional function coverage prioritization (P6): It is very similar to the additional statement coverage prioritization, except that the coverage is for functions, rather than for the statements.

Total fault exposing potential prioritization (P7): This technique considers the identification of a fault in two dimensions. The first dimension is that the test covers a faulty statement. Another dimension is that the fault of a statement failing a test case means that the test case does not expose the fault. Based on both dimensions, a test case will be awarded value. This awarded value is computed by considering three factors. 1) Statement execution probability. 2) Probability in a change of state (computed through statement mutation) when mutants are exposed and or are not exposed 3) The subsequent state changes due to the preceding factor. For a test case, this awarded value is found for each of the statements covered by it. Moreover, the summation of these values will be the Total Fault Exposing Potential value of that test case. The test cases of the suite are reordered according to the descending order of total Fault Exposing Potential (FEP) value, yielding prioritization.

Total FEP-function level prioritization (P8): This technique is analogous to total FEP statement-level prioritization, and a function is considered for coverage in lieu of statements.

Additional fault exposing potential prioritization (P9): It is an extension of Total fault exposing potential prioritization. The Fault Exposing Potential (FEP) value of a test case with respect to a statement is adjusted, by lowering the award values of all other test cases covering the same statement. The rationale behind this is the correctness of the statement is very first ascertained by the test case covering it first. This value is estimated by means of a factor called “confidence”, ranging between 0 and 1. When a test case exercises a statement and not finding any fault, then the confidence value of that statement increases. The confidence of a statement is influenced by the FEP of the test case too. Additional confidence of a statement is obtained by finding the difference between prior confidence value and posterior confidence value of that statement. If a test case “TCi” covers ‘m’ statements, then the additional confidence values of all ‘m’ statements covered by TCi is summed up to figure out Additional fault exposing the potential of the test case TCi. Finally, the test cases are arranged in descending order of Additional fault exposing potential values.

Additional FEP-function level prioritization (P10): This technique is analogous to additional FEP statement-level prioritization. And, a function is considered for coverage in lieu of statements.

From the literature, it is highly evident that the performances of the prioritization techniques are improving the performance of software testing in terms of Average Percentage of Faults Detected (APFD) measure and Code Complexity Measure (CCM) measures. Hence, these two metrics are used in software testing to validate the test case prioritization. The details of the performance metrics are given below.

Various runs are made for the programs mentioned in Table 4 as per coverage techniques stated above, and their efficiency is analyzed in terms of Average Percentage of Faults Detected (APFD) measure. The APFD measure is given in Equation (21).

$$\mathrm{APFD}=1-\frac{{\mathrm{FCP}}_{\mathrm{I}}+{\mathrm{FCP}}_2+\dots +{\mathrm{FCP}}_{\mathrm{tf}}}{\mathrm{ttc}\times \mathrm{tf}}+\frac{1}{2\times \mathrm{ttc}}$$

(21)

In Equation (21), ‘FCP’ signifies the fault covered in its very first position among the test cases, ‘ttc’ refers a total number of test cases considered, and ‘tf’ refers a total number of faults. This is one of the performance measurement metrics, and during the execution of the test suite, the APFD measure is obtained, and this value lies typically between 0 and 100. A higher APFD measure signifies higher prioritization and a lesser APFD value implies lesser prioritization. Depending on LoC, the number of clusters is taken. In this study, the performance is tested with three different cluster sizes, namely 3, 6, and 9. Then the performance of the test case prioritization is estimated with different cluster sizes and is given in Table 2.

The second performance measure, the Code Complexity Measure (CCM) depends on three pieces of information, lines of code (LOC), Nested block depth (NBD), and McCabe cyclomatic complexity (MCC). The LOC is the total number of lines in a class, NBD is the number of nested statements used in a class and MCC is the number of linearly independent paths to reach the goal of a method. CMM is obtained from the relation:

$$CMM= \frac{1}{3}\left(\frac{LOC}{max\left(LOC\right)}+ \frac{NBD}{max\left(NBD\right)}+ \frac{MCC}{max\left(MCC\right)}\right).$$

(22)

Figure 4a–d summarizes the performance analysis of the proposed methods and others with respect to the percentage of APFD scores after having applied prioritization techniques for the programs extracted from sources given above with respect to the generated random test cases. Here, N1 and N2 represents the two proposed methods namely clustering based prioritization with similarity coefficient and clustering based prioritization with dominancy. The performance analyses of the proposed methods with 3, 6, and 9 clusters are tested and Table 2 shows the percentage of APFD score below.

Table 5. APFD score values in different number of clusters.

Proposed Methods	Pool 1 No. of Clusters			Pool 2 No. of Clusters			Pool 3 No. of Clusters			Pool 4 No. of Clusters
	3	6	9	3	6	9	3	6	9	3	6	9
N1	73.21	72.56	69.23	73.48	78.36	75.86	74.16	77.12	73.57	73.31	74.67	71.78
N2	71.97	71.64	70.05	74.51	76.43	74.09	74.82	76.07	75.66	66.85	70.96	68.32

shows that the optimal groupings for Pool 1 to Pool 4 are 3, 6, 6, and 6, respectively. From the box plots, Figure 4a–d indicates that the proposed method performs better than the other state-of-the-art techniques available in the literature. By applying various rounds of prioritization techniques, the standard deviation of N1 and N2 are better than many of the other techniques and comparing mean and median values with other methods are always better. In Pool 3, one data of N1 is moving to the outlier and this may easily be corrected by using any of the removals of outlier methods.

6. Conclusions

This paper proposes and demonstrates two fuzzy based clustering techniques, FSTPM and DTCTP, which are based on the newly developed similarity coefficient and the dominancy test, respectively. These proposed methods are implemented, tested, and analyzed using an empirical study that accesses requirement based fuzzy clustering techniques in test case prioritization. The results show that the requirements-based-fuzzy-clustering-approach which incorporates traditional code analysis information can improve the effectiveness of test case prioritization techniques, but the results vary based on the cluster size. Finally, it is concluded that, by grouping test cases associated with a similarity or dominancy related set of requirements, regression testing processes can be managed more effectively.