Three-Way Decisions with Interval-Valued Intuitionistic Fuzzy Decision-Theoretic Rough Sets in Group Decision-Making

Abstract

In this article, we demonstrate how interval-valued intuitionistic fuzzy sets (IVIFSs) can function as extended intuitionistic fuzzy sets (IFSs) using the interval-valued intuitionistic fuzzy numbers (IVIFNs) instead of precision numbers to describe the degree of membership and non-membership, which are more flexible and practical in dealing with ambiguity and uncertainty. By introducing IVIFSs into three-way decisions, we provide a new description of the loss function. Thus, we firstly propose a model of interval-valued intuitionistic fuzzy decision-theoretic rough sets (IVIFDTRSs). According to the basic framework of IVIFDTRSs, we design a strategy to address the IVIFNs and deduce three-way decisions. Then, we successfully extend the results of IVIFDTRSs from single-person decision-making to group decision-making. In this situation, we adopt a grey correlation accurate weighted determining method (GCAWD) to compute the weights of decision-makers, which integrates the advantages of the accurate weighted determining method and grey correlation analysis method. Moreover, we utilize the interval-valued intuitionistic fuzzy weighted averaging (IIFWA) operation to count the aggregated scores and the accuracies of the expected losses. By comparing these scores and accuracies, we design a simple and straightforward algorithm to deduce three-way decisions for group decision-making. Finally, we use an illustrative example to verify our results.

1. Introduction

Three-way decision-making, which is a decision-making model based on human cognition, has a very unique function in dealing with uncertainty. It can offer three strategies (acceptance, non-commitment, and rejection) in dealing with uncertainty problems. It has a very wide application background, such as investment, risk decision, government decision, information filtering, text classification, cluster analysis, etc. [1]. Three-way decisions theory is first proposed in the framework of rough sets [2,3]. Yao [1,4,5,6,7] developed rules for three-way decisions, which include positive, boundary, and negative rules. Yao also proposed decision-theoretic rough sets (DTRSs), which greatly enriched and developed three-way decisions [5,6,8,9,10,11].

In the present study, how to confirm the loss functions of DTRSs is always the heart of the matter. Under the influence of a realistic decision-making environment, some factors, such as limited knowledge, finite intelligence, and the different risk preference of decision-makers, limited time, and limited budgets often make decision-makers fail to make precise decisions [12]. Therefore, many researchers construct different kinds of loss functions based on the simulation and evaluation of a decision-making environment, characterized by uncertainty, to adapt to a realistic decision environment, which greatly enriches the determination of the loss function. Zadeh [13] found that fuzzy sets are effective methods to deal with vague, imprecise, and uncertainty problems. Mishra et al. [14] showed that the fuzzy information boundaries tend to be better at accurate information, which makes decision-makers perform better in realistic decision-making environments. Liang et al. [15,16,17,18,19] successfully used triangular fuzzy numbers, hesitant fuzzy sets, interval numbers, intuitionistic fuzzy sets, and typical stochastic functions to determine the loss function.

The IVIFSs also play an important role in describing uncertainty [20]. Atanassov and Gargov [20] extended the intuitionistic fuzzy sets (IFSs) to the interval-valued intuitionistic fuzzy sets (IVIFSs), which use interval-valued intuitionistic fuzzy numbers (IVIFNs), instead of precise numbers, to describe the membership and non-membership function. Then, the IVIFSs began to get a lot of attention of researchers [21,22,23,24,25,26,27,28,29]. Atanassov [21] has studied basic properties and put forward some relationships and the operational rules of the IVIFSs. Xu [26] designed a method based on a distance measure for IVIFSs under a group decision-making environment. Xu [27] gave some aggregation operators and defined the score and accuracy function of IVIFSs for ordering the IVIFSs. Liu et al. [28] extended the entropy and subsethood from IFSs to general IVIFSs. Xu et al. [29] introduced the clustering technique of IVIFSs. The IVIFSs, which use the interval-valued intuitionistic fuzzy numbers instead of precision numbers to describe the membership and non-membership function, are more flexible and practical in dealing with ambiguity and uncertainty.

Unlike the existing works, presented in [15,16,17,18], this article uses IVIFNs, instead of precise numbers, to describe the loss functions of the DTRSs and construct a new framework of interval-valued intuitionistic fuzzy decision-theoretic rough sets (IVIFDTRSs). We also design a strategy and infer rules for three-way decisions for IVIFDTRSs in a single-person decision-making environment. In dealing with complex problems, group decision-making tends to be more scientific and rational than individual decision-making because it can focus on the wisdom of decision-makers in different fields, take advantage of more information to form more feasible methods, and it is usually easy for it to gain universal recognition. In order to avoid the incomprehensiveness of individual decisions, we extend IVIFDTRSs from single-person decision-making to group decision-making. It is common knowledge that the determination of the weight of decision-makers is crucial in group decision-making. Hence, there are a lot of researchers introduced the correlation and aggregation method of interval-valued intuitionistic fuzzy sets [30,31,32,33,34,35,36,37]. Thus, we provided the grey correlation accurate weighted determining method (GCAWD) to confirm the weight of decision-makers, which integrated the advantages of the accurate weighted determining method [30] and grey correlation analysis method [31]. Then, we adopted the interval-valued intuitionistic fuzzy weighted averaging (IIFWA) operation to aggregate the group opinions and compute the scores and accuracies of the expected losses. By comparing these scores and accuracies, we develop a simple and straightforward algorithm to deduce three-way decisions.

This paper extends IFDTRSs to IVIFDTRSs, and extends IVIFDTRSs from single-person decision-making to group decision-making, which provides a more scientific and rational way to deal with the uncertainty of decision-making. This paper also provides a new method, named GCAWD, to confirm the weights of experts. This method first gives the expert a greater initial weight if the expert has larger IVIFNs in relation to the membership degree of attributes, because such an expert knows more about the attribute, and then determines the final weight of decision-makers by considering two aspects of group ideas and information distribution. Finally, it establishes a planning model according to the principle of entropy.

The remainder of the article contains the following: Section 2 introduces some basic concepts of Bayesian decision procedures and IVIFNs. Section 3 designs the basic model of IVIFDTRSs. Section 4 designs a strategy and infers the rules of three-way decisions for IVIFDTRSs in single-person decision-making. Section 5 provides the GCAWD to calculate the weights of decision-makers and studies the decision analysis of IVIFDTRSs in relation to group decision-making. Section 6 gives an illustrative example. Section 7 concludes the paper and introduces future research prospects.

2. Preliminaries

The model of DTRSs based on Bayesian decision procedure, the basic concepts, relations, and operations of IVIFSs and IVIFNs are briefly introduced as follows [5,7,10,11].

2.1. Decision-Theoretic Rough Sets Model

Let the set of states $\Omega =\left\{{\omega }_1,{\omega }_2,\cdots ,{\omega }_s\right\}$ denote a finite set of $s$ states, and the set of states $A=\left\{a_1,a_2,\cdots ,a_n\right\}$ be a finite set of $n$ possible actions. $\mathrm{Pr}({\omega }_j|\mathrm{x})$ is the conditional probability of an object $x$ being in state ${\omega }_j$, given that the object $x$ is described by $\mathrm{x}$. Here, $\mathrm{x}$ is the equivalence class of $x$. $\lambda (a_i|{\omega }_j)$ is the loss or cost for taking action $a_i$ in the state ${\omega }_j$. For object $x$, suppose to take the action $a_i$. According to the method of minimum-risk Bayesian decision [11,38], the expected loss associated with action $a_i$ is given below:

$$R(a_i|\mathrm{x})={\displaystyle \sum _{j=1}^s\lambda (a_i|{\omega }_j)}P({\omega }_j|\mathrm{x})$$

(1)

Generally, $\mathrm{x}$ is a description of the object $x$, $\tau (\mathrm{x})$ is a decision rule function that represents which action to take, and $R$ is the overall risk, which can be calculated as follows [16]:

$$R={\displaystyle \sum _{\mathrm{x}}^{}R(\tau (\mathrm{x})|\mathrm{x})}\mathrm{Pr}(\mathrm{x})$$

(2)

Let $\Omega =\left\{X,{}^{\neg }X\right\}$ denote the set of states indicating that an object is in $X$ and not in $X$. Let $A=\left\{a_P,a_B,a_N\right\}$ be the set of actions, where $a_P$, $a_B$, and $a_N$ represent the three actions in classifying an object, deciding $POS(X)$, $NEG(X)$, and $BND(X)$, respectively. ${\lambda }_{PP}$, ${\lambda }_{BP}$, and ${\lambda }_{NP}$ represent the cost of taking actions $a_P$, $a_B$, and $a_N$ when the object $x$ is in $X$, respectively. Similarly, ${\lambda }_{PN}$, ${\lambda }_{BN}$, and ${\lambda }_{NN}$ represent the cost of taking actions $a_P$, $a_B$, and $a_N$ when the object $x$ is not in $X$. For an object with the description $[x]$, suppose an action $a_i(i=P,B,N)$ is taken, then we can calculate the expected loss $R(a_i|[x])(i=P,B,N)$ associated with taking the individual actions as follows:

$$R(a_P|[x])={\lambda }_{PP}\mathrm{Pr}(X|[x])+{\lambda }_{PN}\mathrm{Pr}({}^{\neg }X|[x])$$

(3)

$$R(a_B|[x])={\lambda }_{BP}\mathrm{Pr}(X|[x])+{\lambda }_{BN}\mathrm{Pr}({}^{\neg }X|[x])$$

(4)

$$R(a_N|[x])={\lambda }_{NP}\mathrm{Pr}(X|[x])+{\lambda }_{NN}\mathrm{Pr}({}^{\neg }X|[x])$$

(5)

Here, $\mathrm{Pr}(X|[x])$ and $\mathrm{Pr}({}^{\neg }X|[x])$ are the probabilities that an object in the equivalence class $[x]$ belongs to $X$ and ${}^{\neg }X$, respectively.

According to the minimum-risk decision of Bayesian decision procedure, the decision rules can be expressed as follows:

$$\begin{array}{c}(P)\mathrm{if}R(a_P|[x])\le R(a_B|[x])\mathrm{and}R(a_P|[x])\le R(a_B|[x]),\mathrm{decide}x\in POS(C)\\ (B)\mathrm{if}R(a_B|[x])\le R(a_P|[x])\mathrm{and}R(a_B|[x])\le R(a_N|[x]),\mathrm{decide}x\in BND(C)\\ (N)\mathrm{if}R(a_N|[x])\le R(a_P|[x])\mathrm{and}R(a_N|[x])\le R(a_B|[x]),\mathrm{decide}x\in NEG(C)\end{array}$$

2.2. Interval-Valued Intuitionistic Fuzzy Sets (IVIFSs)

The concept of IVIFSs was first introduced by Atanassov and Gargov [12,20]. It is composed of an interval-valued membership degree and an interval-valued non-membership degree. In this subsection, we review some basic concepts and operations of IVIFSs [27].

Definition 1.

Let anon-null set$X=\left\{x_1,x_2,\cdots ,x_n\right\}$be fixed, then an IVIFS$\tilde{E}$over$X$ is an object having the form [3]:

$$\tilde{E}=\left\{<x_i,{\tilde{\mu }}_{\tilde{E}}(x_i),{\tilde{v}}_{\tilde{E}}(x_i)>|x_i\in X\right\}$$

(6)

Here,${\tilde{\mu }}_{\tilde{E}}(x_i)\subseteq [0，1]$and${\tilde{\nu }}_{\tilde{E}}(x_i)\subseteq [0,1]$are the membership and non-membership degrees of$x$to$\tilde{E}$, respectively. Additionally, both${\tilde{\mu }}_{\tilde{E}}(x_i)$and${\tilde{\nu }}_{\tilde{E}}(x_i)$are intervals, and for all$x_i\in X$:

$$\sup {\tilde{\mu }}_{\tilde{E}}(x_i)+\sup {\tilde{v}}_{\tilde{E}}(x_i)\le 1$$

(7)

Especially, if$\inf {\tilde{\mu }}_{\tilde{E}}(x)=\sup {\tilde{\mu }}_{\tilde{E}}(x)$and$\inf {\tilde{\nu }}_{\tilde{E}}(x)=\sup {\tilde{\nu }}_{\tilde{E}}(x)$then the IVIFS$\tilde{E}$ reduces to an intuitionistic fuzzy set (IFS).

2.3. Interval-Valued Intuitionistic Fuzzy Numbers (IVIFNs)

For an IVIFS $\tilde{E}$ [20,27], the pair $({\tilde{\mu }}_{\tilde{E}}(x_i)，{\tilde{\nu }}_{\tilde{E}}(x_i))$ is called an interval-valued intuitionistic fuzzy number (IVIFN). We denote an IVIFN by $\tilde{\alpha }=([a,b],[c,d])$ for convenience, where:

$$[a,b]\subseteq [0,1],[c,d]\subseteq [0,1],b+d\le 1$$

Meanwhile, $S(\alpha )$ and $H(\alpha )$ are the score and accuracy functions of $\tilde{\alpha }$, respectively. They can be computed as follows:

$$S(\alpha )=\frac{1}{2}\left(a-c+b-d\right),S(\alpha )\in [-1,1]$$

(8)

$$H(\alpha )=\frac{1}{2}\left(a+b+c+d\right),H(\alpha )\in [0,1]$$

(9)

In particular, if $a=b$ and $c=d$ then the IVIFN $\tilde{\alpha }$ reduces to an intuitionistic fuzzy number (IFN).

Definition 2.

Let${\tilde{\alpha }}_1=([a_1,b_1],[c_1,d_1])$and${\tilde{\alpha }}_2=([a_2,b_2],[c_2,d_2])$ be any two IVIFNs, we define their relations and operations as follows [9,10]:

(O1)${\tilde{\alpha }}_1+{\tilde{\alpha }}_2=([a_1+a_2-a_1{a}_2,b_1+b_2-b_1{b}_2],[c_1{c}_2,d_1{d}_2])$

(O2)${\tilde{\alpha }}_1\cdot {\tilde{\alpha }}_2=([a_1{a}_2,b_1{b}_2],[c_1+c_2-c_1{c}_2,d_1+d_2-d_1{d}_2])$

(O3)$\lambda {\tilde{\alpha }}_1=([1-{(1-a_1)}^{\lambda },1-{(1-b_1)}^{\lambda }],[c_1{}^{\lambda },d_1{}^{\lambda }])$

(O4)${\tilde{\alpha }}^{\lambda }{}_1=([a_1{}^{\lambda },b_1{}^{\lambda }],[1-{(1-c_1)}^{\lambda },1-{(1-d_1)}^{\lambda }])$

Additionally, the$S(\alpha )$and$H(\alpha )$of${\tilde{\alpha }}_1$and${\tilde{\alpha }}_2$ can be computed as:

(O5)$S({\alpha }_1)=\frac{1}{2}\left(a_1-c_1+b_1-d_1\right)$

(O6)$S({\alpha }_2)=\frac{1}{2}\left(a_2-c_2+b_2-d_2\right)$

(O7)$H({\alpha }_1)=\frac{1}{2}\left(a_1+b_1+c_1+d_1\right)$

(O8)$H({\alpha }_2)=\frac{1}{2}\left(a_2+b_2+c_2+d_2\right)$

(O9)$d({\tilde{\alpha }}_1,{\tilde{\alpha }}_2)=\frac{1}{4}(\left|a_1-a_2\right|+\left|b_1-b_2\right|+\left|c_1-c_2\right|+\left|d_1-d_2\right|)$

Then, we can use the$S(\alpha )$and$H(\alpha )$to contrast${\tilde{\alpha }}_1$and${\tilde{\alpha }}_2$ as follows:

(R1) if$S({\alpha }_1)<S({\alpha }_2)$, then${\tilde{\alpha }}_1<{\tilde{\alpha }}_2$.

(R2) if$S({\alpha }_1)>S({\alpha }_2)$, then${\tilde{\alpha }}_1>{\tilde{\alpha }}_2$.

(R3) if$S({\alpha }_1)=S({\alpha }_2)$and$H({\alpha }_1)<H({\alpha }_2)$, then${\tilde{\alpha }}_1<{\tilde{\alpha }}_2$.

(R4) if$S({\alpha }_1)=S({\alpha }_2)$and$H({\alpha }_1)>H({\alpha }_2)$, then${\tilde{\alpha }}_1>{\tilde{\alpha }}_2$.

(R5) if$S({\alpha }_1)=S({\alpha }_2)$and$H({\alpha }_1)=H({\alpha }_2)$, then${\tilde{\alpha }}_1={\tilde{\alpha }}_2$.

3. Interval-Valued Intuitionistic Fuzzy Decision-Theoretic Rough Sets Model

In this section, we introduce the IVIFNs, instead of precise numbers, to describe the loss functions of DTRSs and construct a new model of interval-valued intuitionistic fuzzy decision-theoretic rough sets (IVIFDTRSs) according to the Bayesian decision procedure [11,15,16,17,18,38].

Following the results in Ref. [17], the IVIFDTRS model is composed of two states and three actions. Let $\Omega =\left\{C,{}^{\neg }C\right\}$ denote the set of states indicating that an object is in $C$ and not in $C$. Let ${\rm A}=\left\{a_P,a_B,a_N\right\}$ be the set of actions, $a_P$, $a_B$ and $a_N$ are three actions which represent deciding to classify object $x\in POS(C)$, $x\in BND(C)$ and $x\in NEG(C)$, respectively. The loss function matrix represented by IVIFNs is supplied in

Table 1. The loss function matrix represented by interval-valued intuitionistic fuzzy sets (IVIFNs).

Action	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\tilde{E}({\lambda }_{PP})=([a_{PP},b_{PP}],[c_{PP},d_{PP}])$	$\tilde{E}({\lambda }_{PN})=([a_{PN},b_{PN}],[c_{PN},d_{PN}])$
$a_B$	$\tilde{E}({\lambda }_{BP})=([a_{BP},b_{BP}],[c_{BP},d_{BP}])$	$\tilde{E}({\lambda }_{BN})=([a_{BN},b_{BN}],[c_{BN},d_{BN}])$
$a_N$	$\tilde{E}({\lambda }_{NP})=([a_{NP},b_{NP}],[c_{NP},d_{NP}])$	$\tilde{E}({\lambda }_{NN})=([a_{NN},b_{NN}],[c_{NN},d_{NN}])$

.

In Table 1, $\tilde{E}$ is an interval-valued intuitionistic fuzzy concept of loss, and the loss functions $\tilde{E}({\lambda }_{••})$ $(•=P,B,N)$ are IVIFNs. $\tilde{E}({\lambda }_{PP})$, $\tilde{E}({\lambda }_{BP})$ and $\tilde{E}({\lambda }_{NP})$ represent the cost degrees of taking actions $a_P$, $a_B$ and $a_N$ when the object $x$ is in $C$, respectively. Additionally, $\tilde{E}({\lambda }_{PN})$, $\tilde{E}({\lambda }_{BN})$ and $\tilde{E}({\lambda }_{NN})$ represent the cost of taking actions $a_P$, $a_B$ and $a_N$ when the alternation $x$ belongs to ${}^{\neg }C$. There are some deserved relationships, which are as follows:

$$a_{PP}<a_{BP}<a_{NP},b_{PP}<b_{BP}<b_{NP},c_{PP}>c_{BP}>c_{NP},d_{PP}>d_{BP}>d_{NP},$$

$$a_{PN}>a_{BN}>a_{NN},b_{PN}>b_{BN}>b_{NN},c_{PN}<c_{BN}<c_{NN},d_{PN}<d_{BN}<d_{NN}.$$

For Table 1, we denote that ${\tilde{\mu }}_E({\lambda }_{••})(•=P,B,N)$ and ${\tilde{\nu }}_E({\lambda }_{••})(•=P,B,N)$ are the membership and non-membership degree of $x$ to $\tilde{E}$, respectively. They are described as follows:

$${\tilde{\mu }}_E({\lambda }_{PP})=[a_{PP},b_{PP}],{\tilde{v}}_E({\lambda }_{PP})=[c_{PP},d_{PP}],{\tilde{\mu }}_E({\lambda }_{PN})=[a_{PN},b_{PN}],{\tilde{v}}_E({\lambda }_{PN})=[c_{PN},d_{PN}],$$

$${\tilde{\mu }}_E({\lambda }_{BP})=[a_{BP},b_{BP}],{\tilde{v}}_E({\lambda }_{PN})=[c_{BP},d_{BP}],{\tilde{\mu }}_E({\lambda }_{BN})=[a_{BN},b_{PN}],{\tilde{v}}_E({\lambda }_{BN})=[c_{BN},d_{BN}],$$

$${\tilde{\mu }}_E({\lambda }_{NP})=[a_{NP},b_{NP}],{\tilde{v}}_E({\lambda }_{NP})=[c_{NP},d_{NP}],{\tilde{\mu }}_E({\lambda }_{NN})=[a_{NN},b_{NN}],{\tilde{v}}_E({\lambda }_{NN})=[c_{NN},d_{NN}].$$

Proposition 1.

Based on above operations, the following relationships are implied:

$$\begin{array}{l}\begin{array}{l}{a}_{PP}<a_{BP}<a_{NP}\\ b_{PP}<b_{BP}<b_{NP}\end{array}\}\Rightarrow {\tilde{\mu }}_E({\lambda }_{PP})<{\tilde{\mu }}_E({\lambda }_{BP})<{\tilde{\mu }}_E({\lambda }_{NP})\\ \begin{array}{l}{c}_{PP}>c_{BP}>c_{NP}\\ d_{PP}>d_{BP}>d_{NP}\end{array}\}\Rightarrow {\tilde{\nu }}_E({\lambda }_{NP})<{\tilde{\nu }}_E({\lambda }_{BP})<{\tilde{\nu }}_E({\lambda }_{PP})\end{array}\}\Rightarrow \tilde{E}({\lambda }_{PP})<\tilde{E}({\lambda }_{BP})<\tilde{E}({\lambda }_{NP}),$$

(10)

$$\begin{array}{l}\begin{array}{l}{a}_{PN}>a_{BN}>a_{NN}\\ b_{PN}>b_{BN}>b_{NN}\end{array}\}\Rightarrow {\tilde{\mu }}_E({\lambda }_{NN})<{\tilde{\mu }}_E({\lambda }_{BN})<{\tilde{\mu }}_E({\lambda }_{PN})\\ \begin{array}{l}{c}_{PN}<c_{BN}<c_{NN}\\ d_{PN}<d_{BN}<d_{NN}\end{array}\}\Rightarrow {\tilde{\nu }}_E({\lambda }_{PN})<{\tilde{\nu }}_E({\lambda }_{BN})<{\tilde{\nu }}_E({\lambda }_{NN})\end{array}\}\Rightarrow \tilde{E}({\lambda }_{NN})<\tilde{E}({\lambda }_{BN})<\tilde{E}({\lambda }_{PN}).$$

(11)

For Proposition 1, (10) and (11) illustrate that the loss from taking the action $a_P$ is less than that from taking the action $a_B$, and the combined loss from taking the action $a_P$ and $a_B$ is less than the loss from taking the action $a_N$ when the classifying object $x$ belongs to $C$. Meanwhile, the reverse orders of these losses are set up when the classifying object $x$ is in ${}^{\neg }C$. It must be emphasized that $\stackrel{\sim }{{\mu }_{•}}=[a_{••},b_{••}](•=P,B,N)$ and $\stackrel{\sim }{{\nu }_{•}}=[c_{••},d_{••}](•=P,B,N)$ are the prerequisites of IVIFDTRSs. $\mathrm{Pr}(C|[x])$ and $\mathrm{Pr}({}^{\neg }C|[x])$ are the probabilities that an object $x$ in the equivalence class $[x]$ belongs to $C$ and ${}^{\neg }C$, i.e., $\mathrm{Pr}(C|[x])+\mathrm{Pr}({}^{\neg }C|[x])=1$. For an object $x$, the expected losses $R(a_{•}|[x])(•=P,B,N)$ are described as follows:

$$R(a_P|[x])=\tilde{E}({\lambda }_{PP})\mathrm{Pr}(C|[x])\oplus \tilde{E}({\lambda }_{PN})\mathrm{Pr}({}^{\neg }C|[x]),$$

(12)

$$R(a_B|[x])=\tilde{E}({\lambda }_{BP})\mathrm{Pr}(C|[x])\oplus \tilde{E}({\lambda }_{BN})\mathrm{Pr}({}^{\neg }C|[x]),$$

(13)

$$R(a_N|[x])=\tilde{E}({\lambda }_{NP})\mathrm{Pr}(C|[x])\oplus \tilde{E}({\lambda }_{NN})\mathrm{Pr}({}^{\neg }C|[x]).$$

(14)

Here, $R(a_{•}|[x])(•=P,B,N)$ are also IVIFNs. According to the operation rule (O3) of IVIFNs proposed in Definition 2, the $R(a_{•}|[x])(•=P,B,N)$ are calculated as:

$$\begin{array}{ll}R(a_P|[x])=& ([1-{(1-a_{PP})}^{\mathrm{Pr}(C|[x])},1-{(1-b_{PP})}^{\mathrm{Pr}(C|[x])}],[c_{PP}{}^{\mathrm{Pr}(C|[x])},d_{PP}{}^{\mathrm{Pr}(C|[x])}])\\ & \oplus ([1-{(1-a_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])},1-{(1-b_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])}],[c_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])},d_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}])\end{array},$$

(15)

$$\begin{array}{ll}R(a_B|[x])=& ([1-{(1-a_{BP})}^{\mathrm{Pr}(C|[x])},1-{(1-b_{BP})}^{\mathrm{Pr}(C|[x])}],[c_{BP}{}^{\mathrm{Pr}(C|[x])},d_{BP}{}^{\mathrm{Pr}(C|[x])}])\\ & \oplus ([1-{(1-a_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])},1-{(1-b_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])}],[c_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])},d_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}])\end{array},$$

(16)

$$\begin{array}{ll}R(a_N|[x])=& ([1-{(1-a_{NP})}^{\mathrm{Pr}(C|[x])},1-{(1-b_{NP})}^{\mathrm{Pr}(C|[x])}],[c_{NP}{}^{\mathrm{Pr}(C|[x])},d_{NP}{}^{\mathrm{Pr}(C|[x])}])\\ & \oplus ([1-{(1-a_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])},1-{(1-b_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])}],[c_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])},d_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}])\end{array}.$$

(17)

Proposition 2.

According to the operation rule (O1) of IVIFNs, proposed in Definition 2, the$R(a_{•}|[x])(•=P,B,N)$can be calculated as:

$$\begin{array}{l}R(a_P|[x])=([1-{(1-a_{PP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])},1-{(1-b_{PP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])}],\\ [c_{PP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])},d_{PP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}])\end{array}$$

(18)

$$\begin{array}{l}R(a_B|[x])=([1-{(1-a_{BP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])},1-{(1-b_{BP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])}],\\ [c_{BP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])},d_{BP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}])\end{array}$$

(19)

$$\begin{array}{l}R(a_N|[x])=([1-{(1-a_{NP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])},1-{(1-b_{NP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])}],\\ [c_{NP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])},d_{NP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}])\end{array}$$

(20)

According to the minimum-risk decision of the Bayesian decision procedure, the decision rules can be expressed as follows:

$$\begin{array}{c}\left(P\right)ifR(a_P|[x])\le R(a_B|[x])\mathrm{and}R(a_P|[x])\le R(a_B|[x]),\mathit{decide}x\in POS(C)\\ \left(B\right)ifR(a_B|[x])\le R(a_P|[x])\mathrm{and}R(a_B|[x])\le R(a_N|[x]),\mathit{decide}x\in BND(C)\\ \left(N\right)ifR(a_N|[x])\le R(a_P|[x])\mathrm{and}R(a_N|[x])\le R(a_B|[x]),\mathit{decide}x\in NEG(C)\end{array}$$

4. Decision Analysis of IVIFDTRSs for Single-Person Decision-Making

From Section 3, we use IVIFNs to describe the loss functions and propose a strategy to deduce the rules of three-way decisions (P)–(N). Additionally, we know that the expected losses $R(a_{•}|[x])=([A_{•},B_{•}],[C_{•},D_{•}](•=P,B,N)$ are IVIFNs too. Under single-person decision-making, we can directly use the score and accuracy functions of IVIFNs to compare the expected losses $R(a_P|[x])=([A_P,B_P],[C_P,D_P]$, $R(a_B|[x])=([A_B,B_B],[C_B,D_B]$ and $R(a_N|[x])=([A_N,B_N],[C_N,D_N]$.

In light of (8) and (9), the score functions of $R(a_{•}|[x])=([A_{•},B_{•}],[C_{•},D_{•}](•=P,B,N)$ can be expressed as follows:

$$\begin{array}{ll}S(R(a_P|[x]))=& (2-{(1-a_{PP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])}-{(1-b_{PP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])}\\ & -c_{PP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}-d_{PP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])})/2\end{array}$$

(21)

$$\begin{array}{ll}S(R(a_B|[x]))=& (2-{(1-a_{BP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])}-{(1-b_{BP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])}\\ & -c_{BP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}-d_{BP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])})/2\end{array}$$

(22)

$$\begin{array}{ll}S(R(a_N|[x]))=& (2-{(1-a_{NP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])}-{(1-b_{NP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])}\\ & -c_{NP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}-d_{NP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])})/2\end{array}$$

(23)

At the same time, the accuracy functions are deduced as follows:

$$\begin{array}{ll}H(R(a_P|[x]))=& (2-{(1-a_{PP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])}-{(1-b_{PP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{PN})}^{\mathrm{Pr}({}^{\neg }C|[x])}\\ & +c_{PP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}+d_{PP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{PN}{}^{\mathrm{Pr}({}^{\neg }C|[x])})/2\end{array}$$

(24)

$$\begin{array}{ll}H(R(a_B|[x]))=& (2-{(1-a_{BP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])}-{(1-b_{BP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{BN})}^{\mathrm{Pr}({}^{\neg }C|[x])}\\ & +c_{BP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}+d_{BP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{BN}{}^{\mathrm{Pr}({}^{\neg }C|[x])})/2\end{array}$$

(25)

$$\begin{array}{ll}H(R(a_N|[x]))& =(2-{(1-a_{NP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-a_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])}-{(1-b_{NP})}^{\mathrm{Pr}(C|[x])}\cdot {(1-b_{NN})}^{\mathrm{Pr}({}^{\neg }C|[x])}\\ & +c_{NP}{}^{\mathrm{Pr}(C|[x])}\cdot c_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])}+d_{NP}{}^{\mathrm{Pr}(C|[x])}\cdot d_{NN}{}^{\mathrm{Pr}({}^{\neg }C|[x])})/2\end{array}$$

(26)

For the rule (P) of Section 3, the conditions based on the IVIFN contrast rules (R1)–(R4) imply the following prerequisites:

$$(C_{P1})S(R(a_P|[x]))<S(R(a_B|[x]))$$

$$(C_{P2})S(R(a_P|[x]))=S(R(a_B|[x]))\cap H(R(a_P|[x]))<H(R(a_B|[x]))$$

$$(C_{P3})S(R(a_P|[x]))<S(R(a_N|[x]))$$

$$(C_{P4})S(R(a_P|[x]))=S(R(a_N|[x]))\cap H(R(a_P|[x]))<H(R(a_N|[x]))$$

Similarly, for the rule (B), the conditions based on the IVIFN contrast rules (R1)–(R4) imply the following prerequisites:

$$(C_{B1})S(R(a_B|[x]))<S(R(a_P|[x]))$$

$$(C_{B2})S(R(a_B|[x]))=S(R(a_P|[x]))\cap H(R(a_B|[x]))<H(R(a_P|[x]))$$

$$(C_{B3})S(R(a_B|[x]))<S(R(a_N|[x]))$$

$$(C_{B4})S(R(a_B|[x]))=S(R(a_N|[x]))\cap H(R(a_B|[x]))<H(R(a_N|[x]))$$

Additionally, for the rule (N), the conditions based on the IVIFN contrast rules (R1)–(R4) imply the following prerequisites:

$$(C_{N1})S(R(a_N|[x]))<S(R(a_P|[x]))$$

$$(C_{N2})S(R(a_N|[x]))=S(R(a_P|[x]))\cap H(R(a_N|[x]))<H(R(a_P|[x]))$$

$$(C_{N3})S(R(a_N|[x]))<S(R(a_B|[x]))$$

$$(C_{N4})S(R(a_N|[x]))=S(R(a_B|[x]))\cap H(R(a_N|[x]))<H(R(a_B|[x]))$$

On the basis of $(C_{P1})–(C_{P4})$, $(C_{B1})–(C_{B4})$ and $(C_{N1})–(C_{N4})$, the decision rules (P)–(N) can be re-described as follows:

$$\begin{array}{c}\left(P\right)if((C_{P1})\cup (C_{P2}))\cap ((C_{P3})\cup (C_{P4})),\mathit{decide}x\in POS(C)\\ \left(B\right)if((C_{B1})\cup (C_{B2}))\cap ((C_{B3})\cup (C_{B4})),\mathit{decide}x\in BND(C)\\ \left(N\right)if((C_{N1})\cup (C_{N2}))\cap ((C_{N3})\cup (C_{N4})),\mathit{decide}x\in NEG(C)\end{array}$$

5. Decision Analysis of IVIFDTRSs for Group Decision-Making

In Section 4, we deduce the decision rules of IVIFDTRSs for single-person decision-making, where all the relevant evaluation information is supplied by only one person. However, due to the limitations of personal knowledge and ability, as well as the complexity of the decision environment, the original decision information, provided by only one person, is not enough. We need more persons to provide the evaluation information. In order to adapt to this scenario, we develop the IVIFDTRSs for group decision-making.

5.1. Basic Notations

Suppose there are $m$ decision-makers $D=\left\{d_1,d_2,\cdots ，d_k，\cdots ，d_m\right\}$, whose weight vector is $\omega =({\omega }_1,{\omega }_2,\cdots ,{\omega }_k,\cdots ,{\omega }_m)$, ${\omega }_k\ge 0$ and ${\displaystyle \sum _{k=1}^m{\omega }_k}=1$. For the decision-maker $d_k(k=1,2,\cdots ,m)$, the interval-valued intuitionistic fuzzy loss functions are given in

Table 2. The loss function matrix represented by IVIFNs with the decision-maker $d_k$.

${\mathit{d}}_{\mathit{k}}$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(k)}}({\lambda }_{PP})=([a_{PP}^{(k)},b_{PP}^{(k)}],[c_{PP}^{(k)},d_{PP}^{(k)}])$	$\widetilde{E^{(k)}}({\lambda }_{PN})=([a_{PN}^{(k)},b_{PN}^{(k)}],[c_{PN}^{(k)},d_{PN}^{(k)}])$
$a_B$	$\widetilde{E^{(k)}}({\lambda }_{BP})=([a_{BP}^{(k)},b_{BP}^{(k)}],[c_{BP}^{(k)},d_{BP}^{(k)}])$	$\widetilde{E^{(k)}}({\lambda }_{BN})=([a_{BN}^{(k)},b_{BN}^{(k)}],[c_{BN}^{(k)},d_{BN}^{(k)}])$
$a_N$	$\widetilde{E^{(k)}}({\lambda }_{NP})=([a_{NP}^{(k)},b_{NP}^{(k)}],[c_{NP}^{(k)},d_{NP}^{(k)}])$	$\widetilde{E^{(k)}}({\lambda }_{NN})=([a_{NN}^{(k)},b_{NN}^{(k)}],[c_{NN}^{(k)},d_{NN}^{(k)}])$

.

In Table 2, $[a_{••}^{(k)},b_{••}^{(k)}]\subseteq [0,1]$, $[c_{••}^{(k)},d_{••}^{(k)}]\subseteq [0,1](•=P,B,N)$ and $b_{••}^{(k)}+d_{••}^{(k)}\le 1$. There are also some reasonable relationships with respect to loss functions for the decision-maker $d_k$, which are as follows:

$$a_{PP}^{(k)}<a_{BP}^{(k)}<a_{NP}^{(k)},b_{PP}^{(k)}<b_{BP}^{(k)}<b_{NP}^{(k)},c_{PP}^{(k)}>c_{BP}^{(k)}>c_{NP}^{(k)},d_{PP}^{(k)}>d_{BP}^{(k)}>d_{NP}^{(k)},$$

$$a_{PN}^{(k)}>a_{BN}^{(k)}>a_{NN}^{(k)},b_{PN}^{(k)}>b_{BN}^{(k)}>b_{NN}^{(k)},c_{PN}^{(k)}<c_{BN}^{(k)}<c_{NN}^{(k)},d_{PN}^{(k)}<d_{BN}^{(k)}<d_{NN}^{(k)}.$$

5.2. The Determination of Decision-Maker Weights

In group decision-making, the determination of the weight of decision-makers is the heart of the matter. Zhou et al. [30] obtained the weight of decision-makers by the accurate weighted determining method, and Li et al. [31] determined the weight of decision-makers by the grey related analytical method. We provided the grey correlation accurate weighted determining method (GCAWD) to confirm the weight of decision-makers, which integrated the advantages of the accurate weighted determining method and grey correlation analysis method. The grey correlation accurate weighted determining method (GCAWD) first confirmed the different classification decisions of attribute weights by the accurate weighted determining method. This gave greater weight to the attributes that have larger intuitionistic fuzzy numbers and maintained the original internal relationship between different classification decision attribute values. Then, the grey correlation accurate weighted determining method (GCAWD) determined the weight of decision-makers by the grey related analytical method, which established the model to find the weight of each decision-maker based on the grey relation degree between the individual expert and the expert group, as well as the principle of entropy maximization.

5.2.1. The Determination of the Different Classification Decision Attribute Weights

To facilitate the calculation of the decision attribute weights, we construct a new score function $s(\alpha )=\frac{1}{4}[2+\left(a-c+b-d\right)]$ which has a consistent relationship with the original score function $S(\alpha )=\frac{1}{2}\left(a-c+b-d\right)$. It is obvious that the new score function $s(\alpha )\in [0,1]$

It is common knowledge that $E_{({\lambda }_{PP})}^{(k)}=(E_{({\lambda }_{PP})}^{(1)},E_{({\lambda }_{PP})}^{(2)},\cdot \cdot \cdot ,E_{({\lambda }_{PP})}^{(k)},\cdot \cdot \cdot E_{({\lambda }_{PP})}^{(m)})$ are group interval-valued intuitionistic fuzzy numbers. Let $E_{({\lambda }_{PP})}^{(k)\prime }=(E_{({\lambda }_{PP})}^{(1)\prime },E_{({\lambda }_{PP})}^{(2)\prime },\cdot \cdot \cdot ,E_{({\lambda }_{PP})}^{(k)\prime },\cdot \cdot \cdot E_{({\lambda }_{PP})}^{(m)\prime })$ be a substitute for $E_{({\lambda }_{PP})}^{(k)}=(E_{({\lambda }_{PP})}^{(1)},E_{({\lambda }_{PP})}^{(2)},\cdot \cdot \cdot ,E_{({\lambda }_{PP})}^{(k)},\cdot \cdot \cdot E_{({\lambda }_{PP})}^{(m)})$, which satisfies $E_{({\lambda }_{PP})}^{(k-1)\prime }\ge E_{({\lambda }_{PP})}^{(m)\prime }$.

According to the accurate weighted determining method, we can calculate the accurate weight vectors ${\omega }_{E_{{\lambda }_{PP}}^{(k)\prime }}=({\omega }_{E_{{\lambda }_{PP}}^{(1)\prime }},{\omega }_{E_{{\lambda }_{PP}}^{(1)\prime }},\cdot \cdot \cdot ,{\omega }_{E_{{\lambda }_{PP}}^{(k)\prime }},\cdot \cdot \cdot {\omega }_{E_{{\lambda }_{PP}}^{(m)\prime }})$ of the attribute $E_{({\lambda }_{PP})}^{(k)\prime }$ as follows:

$${\omega }_{E_{{\lambda }_{PP}}^{(k)\prime }}=T_{E_{({\lambda }_{PP})}^{(k)\prime }}/{\displaystyle \sum _k^m{T}_{E_{({\lambda }_{PP})}^{(k)\prime }}}$$

(27)

where:

$$T_{E_{({\lambda }_{PP})}^{(k)\prime }}=S(E_{({\lambda }_{PP})}^{(k)\prime })\cdot I(E_{({\lambda }_{PP})}^{(k)\prime })\cdot L(E_{({\lambda }_{PP})}^{(k)\prime })\cdot R(E_{({\lambda }_{PP})}^{(k)\prime })$$

(28)

where:

$$S(E_{({\lambda }_{PP})}^{(k)\prime })=s(E_{({\lambda }_{PP})}^{(k)\prime }),S(E_{({\lambda }_{PP})}^{(k)\prime })|(s(E_{({\lambda }_{PP})}^{(k)\prime })=0)\to 0^{+}$$

$$I(E_{({\lambda }_{PP})}^{(k)\prime })=\{\begin{array}{l}h(E_{({\lambda }_{PP})}^{(k)\prime }),{\displaystyle \prod _{j=1,j\ne k}^m(s(E_{({\lambda }_{PP})}^{(k)\prime })-s(E_{({\lambda }_{PP})}^{(j)\prime }))}=0\\ 1,\mathrm{else}\end{array}$$

$$L(E_{({\lambda }_{PP})}^{(k)\prime })={\displaystyle \prod _{j=1}^{k-1}l(E_{({\lambda }_{PP})}^{(j)\prime })},k=2,3,\cdot \cdot \cdot ,m;$$

$$l(E_{({\lambda }_{PP})}^{(j)\prime })=\{\begin{array}{l}h(E_{({\lambda }_{PP})}^{(j)\prime }),\{\begin{array}{l}s(E_{({\lambda }_{PP})}^{(j-1)\prime })-s(E_{({\lambda }_{PP})}^{(j)\prime })=0\\ s(E_{({\lambda }_{PP})}^{(j)\prime })-s(E_{({\lambda }_{PP})}^{(j+1)\prime })>0\end{array}\\ 1,\mathrm{else}\end{array}$$

$$R(E_{({\lambda }_{PP})}^{(k)\prime })={\displaystyle \prod _{j=k+1}^{m}r(E_{({\lambda }_{PP})}^{(j)\prime })},k=1,2,\cdot \cdot \cdot ,m-1;$$

$$r(E_{({\lambda }_{PP})}^{(j)\prime })=\{\begin{array}{l}h(E_{({\lambda }_{PP})}^{(j)\prime }),\{\begin{array}{l}s(E_{({\lambda }_{PP})}^{(j-1)\prime })-s(E_{({\lambda }_{PP})}^{(j)\prime })>0\\ s(E_{({\lambda }_{PP})}^{(j)\prime })-s(E_{({\lambda }_{PP})}^{(j+1)\prime })=0\end{array}\\ 1,\mathrm{else}\end{array}$$

Here, $l(E_{({\lambda }_{PP})}^{(1)\prime })=l(E_{({\lambda }_{PP})}^{(m)\prime })=r(E_{({\lambda }_{PP})}^{(1)\prime })=r(E_{({\lambda }_{PP})}^{(m)\prime })=1$, $L(E_{({\lambda }_{PP})}^{(1)\prime })=1$, $R(E_{({\lambda }_{PP})}^{(m)\prime })=R(E_{({\lambda }_{PP})}^{(m-1)\prime })$, $j=2,3,\cdot \cdot \cdot ,m-1$.

Then, we can easily obtain the accurate weight vectors ${\omega }_{E_{{\lambda }_{PP}}^{(k)}}=({\omega }_{E_{{\lambda }_{PP}}^{(1)}},{\omega }_{E_{{\lambda }_{PP}}^{(1)}},\cdot \cdot \cdot ,{\omega }_{E_{{\lambda }_{PP}}^{(k)}},\cdot \cdot \cdot {\omega }_{E_{{\lambda }_{PP}}^{(m)}})$ of the decision attribute $E_{({\lambda }_{PP})}^{(k)}$.

By parity of reasoning, we can calculate the accurate weight vectors ${\omega }_{E_{{\lambda }_{PN}}^{(k)}}$, ${\omega }_{E_{{\lambda }_{BP}}^{(k)}}$, ${\omega }_{E_{{\lambda }_{BN}}^{(k)}}$, ${\omega }_{E_{{\lambda }_{NP}}^{(k)}}$ and ${\omega }_{E_{{\lambda }_{NN}}^{(k)}}$ of the decision attributes $E_{({\lambda }_{PN})}^{(k)}$, $E_{({\lambda }_{BP})}^{(k)}$, $E_{({\lambda }_{BN})}^{(k)}$, $E_{({\lambda }_{NP})}^{(k)}$ and $E_{({\lambda }_{NN})}^{(k)}$.

5.2.2. The Determination of Decision-Maker Weights

According to the principle of decision-maker consensus, and the accurate weights of the decision attributes, which are calculated in Section 5.2.1, we can concentrate each decision solution to get a comprehensive evaluation value for each decision solution in the determination of expert weights. We can calculate the grey correlation degree by putting the comprehensive evaluation value of group decision as the reference sequence and letting the appraisal value, which every expert gave to each decision solution, be the compared sequence.

(1) The comprehensive index value of each decision solution for decision-maker $d_k$ can be calculated as follows:

$$\begin{array}{ll}\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}}& ={\omega }_{E_{({\lambda }_{PP})}^{(k)}}\cdot {\tilde{E}}_{E_{({\lambda }_{PP)}}^{(k)}}+{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}\cdot {\tilde{E}}_{E_{({\lambda }_{PN)}}^{(k)}}\\ & =([1-{(1-a_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-a_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}},1-{(1-b_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-b_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}}],\\ & [c_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot c_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}},d_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot d_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}}])\end{array}$$

(29)

$$\begin{array}{ll}\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}}& ={\omega }_{E_{({\lambda }_{BP})}^{(k)}}\cdot {\tilde{E}}_{E_{({\lambda }_{BP)}}^{(k)}}+{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}\cdot {\tilde{E}}_{E_{({\lambda }_{BN)}}^{(k)}}\\ & =([1-{(1-a_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-a_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}},1-{(1-b_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-b_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}}],\\ & [c_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot c_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}},d_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot d_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}}])\end{array}$$

(30)

$$\begin{array}{ll}\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}}& ={\omega }_{E_{({\lambda }_{NP})}^{(k)}}\cdot {\tilde{E}}_{E_{({\lambda }_{NP)}}^{(k)}}+{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}\cdot {\tilde{E}}_{E_{({\lambda }_{NN)}}^{(k)}}\\ & =([1-{(1-a_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-a_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}},1-{(1-b_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-b_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}}],\\ & [c_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot c_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}},d_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot d_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}}])\end{array}$$

(31)

(2) The comprehensive evaluation average value of the decision-makers group with respect to each decision solution can be counted as follows:

$$\begin{array}{ll}\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}}& =\frac{1}{m}{\displaystyle \sum _{k=1}^m\stackrel{}{{\tilde{Z}}_{a_P}^{(k)}}}\\ & =([\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-a_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-a_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}})},\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-b_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-b_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})}],\\ & [\frac{1}{m}{\displaystyle \sum _{k=1}^m(c_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot c_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}})},\frac{1}{m}{\displaystyle \sum _{k=1}^m(d_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot d_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}}})])\end{array}$$

(32)

$$\begin{array}{ll}\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}}& =\frac{1}{m}{\displaystyle \sum _{k=1}^m\stackrel{}{{\tilde{Z}}_{a_B}^{(k)}}}\\ & =([\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-a_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-a_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})},\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-b_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-b_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})}],\\ & [\frac{1}{m}{\displaystyle \sum _{k=1}^m(c_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot c_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}})},\frac{1}{m}{\displaystyle \sum _{k=1}^m(d_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot d_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}}})])\end{array}$$

(33)

$$\begin{array}{ll}\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}}& =\frac{1}{m}{\displaystyle \sum _{k=1}^m\stackrel{}{{\tilde{Z}}_{a_N}^{(k)}}}\\ & =([\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-a_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-a_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}})},\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-b_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-b_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}})}],\\ & [\frac{1}{m}{\displaystyle \sum _{k=1}^m(c_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot c_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}})},\frac{1}{m}{\displaystyle \sum _{k=1}^m(d_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot d_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}}})])\end{array}$$

(34)

(3) The grey correlation coefficient between the opinion of the individual decision-maker and the opinions of the group decision-makers with respect to each decision solution can be calculated as follows:

$$\xi (\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})=\frac{\underset{k}{{\displaystyle \min }}\underset{a_P}{{\displaystyle \min }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})+\rho \underset{k}{{\displaystyle \min }}\underset{a_P}{{\displaystyle \min }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})}{d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})+\rho \underset{k}{{\displaystyle \max }}\underset{a_P}{{\displaystyle \max }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})}$$

(35)

$$\xi (\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})=\frac{\underset{k}{{\displaystyle \min }}\underset{a_P}{{\displaystyle \min }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})+\rho \underset{k}{{\displaystyle \min }}\underset{a_P}{{\displaystyle \min }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})}{d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})+\rho \underset{k}{{\displaystyle \max }}\underset{a_P}{{\displaystyle \max }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})}$$

(36)

$$\xi (\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{(k)}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}})=\frac{\underset{k}{{\displaystyle \min }}\underset{a_P}{{\displaystyle \min }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}})+\rho \underset{k}{{\displaystyle \min }}\underset{a_P}{{\displaystyle \min }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}})}{d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}})+\rho \underset{k}{{\displaystyle \max }}\underset{a_P}{{\displaystyle \max }}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}})}$$

(37)

Here,

$$\begin{array}{ll}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})=& \frac{1}{4}(\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-a_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-a_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}})}-(1-{(1-a_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-a_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}})\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-b_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-b_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}})}-(1-{(1-b_{PP}^{(k)})}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot {(1-b_{PN}^{(k)})}^{{\omega }_{E_{({\lambda }_{PN)}}^{(k)}}})\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(c_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot c_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}})}-c_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot c_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}}\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(d_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot d_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}})}-d_{PP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PP})}^{(k)}}}\cdot d_{PN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{PN})}^{(k)}}}\right|)\end{array}$$

$$\begin{array}{ll}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})=& \frac{1}{4}(\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-a_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-a_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})}-(1-{(1-a_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-a_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-b_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-b_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})}-(1-{(1-b_{BP}^{(k)})}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot {(1-b_{BN}^{(k)})}^{{\omega }_{E_{({\lambda }_{BN)}}^{(k)}}})\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(c_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot c_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}})}-c_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot c_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}}\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(d_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot d_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}})}-d_{BP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BP})}^{(k)}}}\cdot d_{BN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{BN})}^{(k)}}}\right|)\end{array}$$

$$\begin{array}{ll}d(\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}})=& \frac{1}{4}(\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-a_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-a_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}})}-(1-{(1-a_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-a_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}})\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(1-{(1-b_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-b_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}})}-(1-{(1-b_{NP}^{(k)})}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot {(1-b_{NN}^{(k)})}^{{\omega }_{E_{({\lambda }_{NN)}}^{(k)}}})\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(c_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot c_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}})}-c_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot c_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}}\right|\\ & +\left|\frac{1}{m}{\displaystyle \sum _{k=1}^m(d_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot d_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}})}-d_{NP}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NP})}^{(k)}}}\cdot d_{NN}^{(k)}{}^{{\omega }_{E_{({\lambda }_{NN})}^{(k)}}}\right|)\end{array}$$

(4) The grey correlation degree between the opinion of the individual decision-maker and the opinions of the group decision-makers can be reckoned as follows:

$${\gamma }_{ok}=\frac{1}{3}(\xi (\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{P}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_P}^{(k)}}})+\xi (\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{B}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_B}^{(k)}}})+\xi (\stackrel{}{{\displaystyle {\tilde{Z}}_{a_{N}o}^{}}},\stackrel{}{{\displaystyle {\tilde{Z}}_{a_N}^{(k)}}}))$$

(38)

(5) In order to ensure the consistency of the expert opinion, we set up the decision-maker weight solution model according to the maximum relevance principle of the comprehensive index value of expert weight and the group comprehensive evaluation value.

$$\begin{array}{l}\max {\displaystyle \sum _{k=1}^m{({\omega }_k{\gamma }_{ok})}^2}\\ s.t.{\displaystyle \sum _{k=1}^m{\omega }_k}=1\\ {\omega }_k\ge \eta ,k=1,2,\cdot \cdot \cdot ,m\end{array}$$

(39)

According to the maximal entropy principle, we set up the decision-maker weight solution model as follows:

$$\begin{array}{l}\max H(\omega )=-{\displaystyle \sum _{k=1}^m{\omega }_k\ln {\omega }_k}\\ s.t.{\displaystyle \sum _{k=1}^m{\omega }_k}=1\\ {\omega }_k\ge \eta ,k=1,2,\cdot \cdot \cdot ,m\end{array}$$

(40)

Overall considering the consistency of the opinions of each decision-makers with the maximizing principle of entropy, the solving model of decision-maker weights can be built as follows:

$$\begin{array}{l}\max [\mu {\displaystyle \sum _{k=1}^m{({\omega }_k{\gamma }_{ok})}^2}-(1-\mu ){\displaystyle \sum _{k=1}^m{\omega }_k\ln {\omega }_k}]\\ s.t.{\displaystyle \sum _{k=1}^m{\omega }_k}=1\\ {\omega }_k\ge \eta ,k=1,2,\cdot \cdot \cdot ,m\end{array}$$

(41)

Here, $\mu$ and $1-\mu$ are the weight distribution between maximum correlation and maximum entropy, $0<\mu <1$, generally, $\mu =0.5$. ${\omega }_k$ are the weights of decision-makers, ${\omega }_k\ge \eta$ to ensure that all decision-makers are involved in decision-making, and $\eta$ is critical value. Generally, $\eta >0$, and the value is suggested to be $\eta =\frac{1}{2m}$.

5.3. The Aggregation of Group Decision-Making Loss Functions

Xu and Chen [25] provided an interval-valued intuitionistic fuzzy weighted averaging (IIFWA) operation, which can be used to aggregate the interval-valued intuitionistic fuzzy loss functions and obtain the aggregation loss functions in group decision-making. The aggregation loss functions are:

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{••})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{••}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{••}))={\omega }_1{\tilde{E}}_{}^{\left(1\right)}({\lambda }_{••})\oplus {\omega }_2{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{••})\oplus \cdots \oplus {\omega }_m{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{••})$$

(42)

where $(•=P,B,N)$, according to the calculation rules of IVIFNs, and the aggregation loss functions are computed as follows:

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{••})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{••}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{••}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{••}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{••}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{••}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{••}^{(k)}{}^{{\omega }_k}}])$$

(43)

So, the aggregation of the loss functions $\tilde{E}({\lambda }_{PP})$, $\tilde{E}({\lambda }_{PN})$, $\tilde{E}({\lambda }_{BP})$, $\tilde{E}({\lambda }_{BN})$, $\tilde{E}({\lambda }_{NP})$ and $\tilde{E}({\lambda }_{NN})$ are calculated as:

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{PP})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{PP}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{PP}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{PP}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{PP}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{PP}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{PP}^{(k)}{}^{{\omega }_k}}])$$

(44)

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{PN})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{PN}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{PN}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{PN}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{PN}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{PN}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{PN}^{(k)}{}^{{\omega }_k}}])$$

(45)

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{BP})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{BP}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{BP}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{BP}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{BP}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{BP}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{BP}^{(k)}{}^{{\omega }_k}}])$$

(46)

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{BN})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{BN}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{BN}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{BN}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{BN}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{BN}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{BN}^{(k)}{}^{{\omega }_k}}])$$

(47)

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{NP})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{NP}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{NP}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{NP}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{NP}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{NP}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{NP}^{(k)}{}^{{\omega }_k}}])$$

(48)

$$IIFW{A}_{\omega }({\tilde{E}}_{}^{\left(1\right)}({\lambda }_{NN})，{\tilde{E}}_{}^{\left(2\right)}({\lambda }_{NN}),\cdots ,{\tilde{E}}_{}^{\left(m\right)}({\lambda }_{NN}))=([1-{\displaystyle \prod _{k=1}^m{(1-a_{NN}^{(k)})}^{{\omega }_k},}1-{\displaystyle \prod _{k=1}^m{(1-b_{NN}^{(k)})}^{{\omega }_k}}],[{\displaystyle \prod _{k=1}^m{c}_{NN}^{(k)}{}^{{\omega }_k},}{\displaystyle \prod _{k=1}^m{d}_{NN}^{(k)}{}^{{\omega }_k}}])$$

(49)

5.4. The Decision Rules and Method for Group Decision-Making

In light of the results (18)–(20) and (44)–(49), we can calculate the $R(a_{•}|[x])(•=P,B,N)$ as follows:

$$\begin{array}{ll}R(a_P|[x])=& ([1-{\displaystyle \prod _{k=1}^m{(1-a_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{PN}^{(k)})}^{{\omega }_k}{}^{\cdot \mathrm{Pr}({}^{\neg }C|[x])}},}1-{\displaystyle \prod _{k=1}^m{(1-b_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{PN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}],\\ & [{\displaystyle \prod _{k=1}^m{c}_{PP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{PN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}},}{\displaystyle \prod _{k=1}^m{d}_{PP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{PN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}])\end{array}$$

(50)

$$\begin{array}{ll}R(a_B|[x])=& ([1-{\displaystyle \prod _{k=1}^m{(1-a_{BP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{BN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}},}1-{\displaystyle \prod _{k=1}^m{(1-b_{BP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{BN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}],\\ & [{\displaystyle \prod _{k=1}^m{c}_{BP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{BN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}},}{\displaystyle \prod _{k=1}^m{d}_{BP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{BN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}])\end{array}$$

(51)

$$\begin{array}{ll}R(a_N|[x])=& ([1-{\displaystyle \prod _{k=1}^m{(1-a_{NP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{NN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}},}1-{\displaystyle \prod _{k=1}^m{(1-b_{NP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{NN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}],\\ & [{\displaystyle \prod _{k=1}^m{c}_{NP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{NN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}},}{\displaystyle \prod _{k=1}^m{d}_{NP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{NN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}])\end{array}$$

(52)

According to the results (50)–(52), the scores of $R(a_{•}|[x])(•=P,B,N)$ are calculated as follows:

$$\begin{array}{ll}S(R(a_P|[x]))=& (2-{\displaystyle \prod _{k=1}^m{(1-a_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{PN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}-{\displaystyle \prod _{k=1}^m{(1-b_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{PN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}\\ & -{\displaystyle \prod _{k=1}^m{c}_{PP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{PN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}-}{\displaystyle \prod _{k=1}^m{d}_{PP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{PN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])})/2}\end{array}$$

(53)

$$\begin{array}{ll}S(R(a_B|[x]))=& (2-{\displaystyle \prod _{k=1}^m{(1-a_{BP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{BN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}-{\displaystyle \prod _{k=1}^m{(1-b_{BP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{BN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}\\ & -{\displaystyle \prod _{k=1}^m{c}_{BP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{BN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}-}{\displaystyle \prod _{k=1}^m{d}_{BP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{BN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])})/2}\end{array}$$

(54)

$$\begin{array}{ll}S(R(a_N|[x]))=& (2-{\displaystyle \prod _{k=1}^m{(1-a_{NP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{NN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}-{\displaystyle \prod _{k=1}^m{(1-b_{NP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{NN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}\\ & -{\displaystyle \prod _{k=1}^m{c}_{NP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{NN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}-}{\displaystyle \prod _{k=1}^m{d}_{NP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{NN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])})/2}\end{array}$$

(55)

Also, the accuracies of $R(a_{•}|[x])(•=P,B,N)$ are calculated as:

$$\begin{array}{ll}H(R(a_P|[x]))=& (2-{\displaystyle \prod _{k=1}^m{(1-a_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{PN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}-{\displaystyle \prod _{k=1}^m{(1-b_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{PN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}\\ & +{\displaystyle \prod _{k=1}^m{c}_{PP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{PN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}+}{\displaystyle \prod _{k=1}^m{d}_{PP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{PN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])})/2}\end{array}$$

(56)

$$\begin{array}{ll}H(R(a_B|[x]))=& (2-{\displaystyle \prod _{k=1}^m{(1-a_{BP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{BN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}-{\displaystyle \prod _{k=1}^m{(1-b_{PP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{PN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}\\ & +{\displaystyle \prod _{k=1}^m{c}_{BP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{BN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}+}{\displaystyle \prod _{k=1}^m{d}_{BP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{BN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])})/2}\end{array}$$

(57)

$$\begin{array}{ll}H(R(a_N|[x]))=& (2-{\displaystyle \prod _{k=1}^m{(1-a_{NP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-a_{NN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}-{\displaystyle \prod _{k=1}^m{(1-b_{NP}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{(1-b_{NN}^{(k)})}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}}\\ & +{\displaystyle \prod _{k=1}^m{c}_{NP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}\cdot {\displaystyle \prod _{k=1}^m{c}_{NN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])}}+}{\displaystyle \prod _{k=1}^m{d}_{NP}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}(C|[x])}}\cdot {\displaystyle \prod _{k=1}^m{d}_{NN}^{(k)}{}^{{\omega }_k\cdot \mathrm{Pr}({}^{\neg }C|[x])})/2}\end{array}$$

(58)

Finally, we designed a simple and straightforward algorithm for IVIFDTRSs in group decision-making, which is as follows:

Step 1: Choose $m$ decision-makers $D=\left\{d_1,d_2,\cdots ，d_k，\cdots ，d_m\right\}$ $(k=1,2,\cdots ,m)$.

Step 2: Let $X=\left\{x_1,x_2,\cdots ,x_n\right\}$ be a finite set of objects. Confirm the $\mathrm{Pr}(C|x)$ and $\mathrm{Pr}({}^{\neg }C|x)$, which are the conditional probabilities of an object $x$ being in state $C$ and ${}^{\neg }C$, respectively, where $\mathrm{Pr}(C|x)+\mathrm{Pr}({}^{\neg }C|x)=1$.

Step 3: The decision-makers provided their interval-valued intuitionistic fuzzy loss functions for each object, and we collect the original information of the loss functions provided by all decision-makers, the loss functions are provided in Table 2.

Step 4: Calculate the weight vector $\omega =({\omega }_1,{\omega }_2,\cdots ，{\omega }_k，\cdots ，{\omega }_m)$ by the grey correlation accurate weighted determining method (GCAWD) for each decision-maker, where ${\omega }_k\ge 0$ and ${\displaystyle \sum _{k=1}^m{\omega }_k}=1$.

Step 5: According to the operation of IIFWA, we calculate the scores $S(R(a_P|[x]))$, $S(R(a_B|[x]))$, $S(R(a_N|[x]))$ and the accuracies $H(R(a_P|[x]))$, $H(R(a_B|[x]))$, $H(R(a_N|[x]))$ of the expected losses based on (53)–(58).

Step 6: Rank all the scores $S(R(a_P|[x]))$, $S(R(a_B|[x]))$ and $S(R(a_N|[x]))$. Obviously, we select the minimum score of the excepted loss. If there is only one minimum score, we take the action which has the minimum score and go to Step 9. If not, we go to Step 7.

Step 7: Since there are two or more minimum scores, we continue to rank the accuracies $H(R(a_P|[x]))$, $H(R(a_B|[x]))$, $H(R(a_N|[x]))$. If there is only one minimum accuracy, we take the action that has the minimum accuracy and go to Step 9. If not, we go to Step 8.

Step 8: If there are two or more actions that have the same minimum score and accuracy, we select the action supported by more experts according to the minority is subject to majority rule and then go to Step 9.

Step 9: End.

6. An Illustrative Example

In this section, we use the decision-making process of IVIFDTRSs to deal with the E-commerce development decisions of the regional economy of Sichuan Province of China and exhibit the decision process of individual three-way decisions. According to the 11th five-year plan of the Sichuan national economic and social development, the regional economy of the Sichuan Province is constituted by five regions: (1) $x_1$: Chengdu economic region; (2) $x_2$: Northeast of Sichuan economic region; (3) $x_3$: Panxi economic region; (4) $x_4$: Southern Sichuan economic region; (5) $x_5$: Northwest of Sichuan economic region. Because of resource constraints, we choose the region appropriate to the development of E-commerce or step-up development efforts. At the same time, we also consider that different choices will result in different degrees of loss. Therefore, the E-commerce development decisions of the regional economy of the Sichuan Province are consistent with three-way decisions.

6.1. The Decision Analysis of IVIFDTRSs for Group Decision-Making

For the E-commerce development decisions of the regional economy of the Sichuan Province, there are two states $\Omega =\left\{C,{}^{\neg }C\right\}$, $C$ represents that one region is prosperous and ${}^{\neg }C$ represents that one region is behindhand. The set of actions for each region $x_i(i=1,2,\dots ,5)$ is given by ${\rm A}=\{a_P,a_B,a_N\}$. Here, $a_P$ represents to take the action of developing E-commerce, $a_B$ represents to take the action of creating conditions to develop E-commerce, $a_N$ represents to take the action of refuse to develop E-commerce, respectively. We also set up a group, which consists of five experts $e_i(i=1,2,\dots ,5)$, to evaluate the five regions. Hence, we use the algorithm of IVIFDTRSs for group decision-making.

Step 1: We suppose that the conditional probabilities of the regions to $C$ are shown in

Table 3. The conditional probabilities of regions belong to $C$.

Region	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$
$\mathrm{Pr}(C|[x])$	1	0.8	0.3	0.6	0.1

.

Step 2: The values of the losses corresponding to every expert are listed in

Table 4. The loss function matrix represented by IVIFNs with the expert $e_1$.

${\mathit{e}}_1$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(1)}}({\lambda }_{PP})=([a_{PP}^{(1)},b_{PP}^{(1)}],[c_{PP}^{(1)},d_{PP}^{(1)}])=([0.01,0.01],[0.99,0.99])$	$\widetilde{E^{(1)}}({\lambda }_{PN})=([a_{PN}^{(1)},b_{PN}^{(1)}],[c_{PN}^{(1)},d_{PN}^{(1)}])=([0.99,0.99],[0.01,0.01])$
$a_B$	$\widetilde{E^{(1)}}({\lambda }_{BP})=([a_{BP}^{(1)},b_{BP}^{(1)}],[c_{BP}^{(1)},d_{BP}^{(1)}])=([0.2,0.4],[0.5,0.6])$	$\widetilde{E^{(1)}}({\lambda }_{BN})=([a_{BN}^{(1)},b_{BN}^{(1)}],[c_{BN}^{(1)},d_{BN}^{(1)}])=([0.6,0.7],[0.2,0.3])$
$a_N$	$\widetilde{E^{(1)}}({\lambda }_{NP})=([a_{NP}^{(1)},b_{NP}^{(1)}],[c_{NP}^{(1)},d_{NP}^{(1)}])=([0.8,0.9],[0.01,0.1])$	$\widetilde{E^{(1)}}({\lambda }_{NN})=([a_{NN}^{(1)},b_{NN}^{(1)}],[c_{NN}^{(1)},d_{NN}^{(1)}])=([0.01,0.05],[0.9,0.95])$

,

Table 5. The loss function matrix represented by IVIFNs with the expert $e_2$.

${\mathit{e}}_2$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(2)}}({\lambda }_{PP})=([a_{PP}^{(2)},b_{PP}^{(2)}],[c_{PP}^{(2)},d_{PP}^{(2)}])=([0.05,0.1],[0.8,0.9])$	$\widetilde{E^{(2)}}({\lambda }_{PN})=([a_{PN}^{(2)},b_{PN}^{(2)}],[c_{PN}^{(2)},d_{PN}^{(2)}])=([0.85,0.95],[0.01,0.05])$
$a_B$	$\widetilde{E^{(2)}}({\lambda }_{BP})=([a_{BP}^{(2)},b_{BP}^{(2)}],[c_{BP}^{(2)},d_{BP}^{(2)}])=([0.5,0.6],[0.2,0.4])$	$\widetilde{E^{(2)}}({\lambda }_{BN})=([a_{BN}^{(2)},b_{BN}^{(2)}],[c_{BN}^{(2)},d_{BN}^{(2)}])=([0.2,0.3],[0.6,0.7])$
$a_N$	$\widetilde{E^{(2)}}({\lambda }_{NP})=([a_{NP}^{(2)},b_{NP}^{(2)}],[c_{NP}^{(2)},d_{NP}^{(2)}])=([0.9,0.95],[0.01,0.05])$	$\widetilde{E^{(2)}}({\lambda }_{NN})=([a_{NN}^{(2)},b_{NN}^{(2)}],[c_{NN}^{(2)},d_{NN}^{(2)}])=([0.01,0.1],[0.8,0.9])$

,

Table 6. The loss function matrix represented by IVIFNs with the expert $e_3$.

${\mathit{e}}_3$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(3)}}({\lambda }_{PP})=([a_{PP}^{(3)},b_{PP}^{(3)}],[c_{PP}^{(3)},d_{PP}^{(3)}])=([0.01,0.05],[0.9,0.95])$	$\widetilde{E^{(3)}}({\lambda }_{PN})=([a_{PN}^{(3)},b_{PN}^{(3)}],[c_{PN}^{(3)},d_{PN}^{(3)}])=([0.82,0.95],[0.01,0.05])$
$a_B$	$\widetilde{E^{(3)}}({\lambda }_{BP})=([a_{BP}^{(3)},b_{BP}^{(3)}],[c_{BP}^{(3)},d_{BP}^{(3)}])=([0.2,0.4],[0.3,0.6])$	$\widetilde{E^{(3)}}({\lambda }_{BN})=([a_{BN}^{(3)},b_{BN}^{(3)}],[c_{BN}^{(3)},d_{BN}^{(3)}])=([0.4,0.5],[0.3,0.4])$
$a_N$	$\widetilde{E^{(3)}}({\lambda }_{NP})=([a_{NP}^{(3)},b_{NP}^{(3)}],[c_{NP}^{(3)},d_{NP}^{(3)}])=([0.7,0.9],[0.05,0.1])$	$\widetilde{E^{(3)}}({\lambda }_{NN})=([a_{NN}^{(3)},b_{NN}^{(3)}],[c_{NN}^{(3)},d_{NN}^{(3)}])=([0.05,0.1],[0.7,0.8])$

,

Table 7. The loss function matrix represented by IVIFNs with the expert $e_4$.

${\mathit{e}}_4$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(4)}}({\lambda }_{PP})=([a_{PP}^{(4)},b_{PP}^{(4)}],[c_{PP}^{(4)},d_{PP}^{(4)}])=([0.1,0.2],[0.7,0.8])$	$\widetilde{E^{(4)}}({\lambda }_{PN})=([a_{PN}^{(4)},b_{PN}^{(4)}],[c_{PN}^{(4)},d_{PN}^{(4)}])=([0.85,0.9],[0.01,0.1])$
$a_B$	$\widetilde{E^{(4)}}({\lambda }_{BP})=([a_{BP}^{(4)},b_{BP}^{(4)}],[c_{BP}^{(4)},d_{BP}^{(4)}])=([0.4,0.5],[0.45,0.5])$	$\widetilde{E^{(4)}}({\lambda }_{BN})=([a_{BN}^{(4)},b_{BN}^{(4)}],[c_{BN}^{(4)},d_{BN}^{(4)}])=([0.45,0.55],[0.4,0.45])$
$a_N$	$\widetilde{E^{(4)}}({\lambda }_{NP})=([a_{NP}^{(4)},b_{NP}^{(4)}],[c_{NP}^{(4)},d_{NP}^{(4)}])=([0.7,0.8],[0.1,0.2])$	$\widetilde{E^{(4)}}({\lambda }_{NN})=([a_{NN}^{(4)},b_{NN}^{(4)}],[c_{NN}^{(4)},d_{NN}^{(4)}])=([0.1,0.15],[0.8,0.85])$

and

Table 8. The loss function matrix represented by IVIFNs with the expert $e_5$.

${\mathit{e}}_5$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(5)}}({\lambda }_{PP})=([a_{PP}^{(5)},b_{PP}^{(5)}],[c_{PP}^{(5)},d_{PP}^{(5)}])=([0.1,0.3],[0.6,0.7])$	$\widetilde{E^{(5)}}({\lambda }_{PN})=([a_{PN}^{(5)},b_{PN}^{(5)}],[c_{PN}^{(5)},d_{PN}^{(5)}])=([0.7,0.8],[0.1,0.2])$
$a_B$	$\widetilde{E^{(5)}}({\lambda }_{BP})=([a_{BP}^{(5)},b_{BP}^{(5)}],[c_{BP}^{(5)},d_{BP}^{(5)}])=([0.3,0.5],[0.4,0.5])$	$\widetilde{E^{(5)}}({\lambda }_{BN})=([a_{BN}^{(5)},b_{BN}^{(5)}],[c_{BN}^{(5)},d_{BN}^{(5)}])=([0.6,0.7],[0.2,0.3])$
$a_N$	$\widetilde{E^{(5)}}({\lambda }_{NP})=([a_{NP}^{(5)},b_{NP}^{(5)}],[c_{NP}^{(5)},d_{NP}^{(5)}])=([0.75,0.9],[0.01,0.1])$	$\widetilde{E^{(5)}}({\lambda }_{NN})=([a_{NN}^{(5)},b_{NN}^{(5)}],[c_{NN}^{(5)},d_{NN}^{(5)}])=([0.1,0.2],[0.6,0.8])$

, which consists of IVIFNs.

Step 3: According to (27)–(28), we can compute the accurate weight vectors of the decision attributes. The results are shown in the following matrices:

$$\begin{array}{l}{\omega }_1=\left(\begin{array}{l}0.0154,0.2170\\ 0.1571,0.2511\\ 0.2043,0.0758\end{array}\right),{\omega }_2=\left(\begin{array}{l}0.1731,0.2049\\ 0.2618,0.1067\\ 0.2157,0.1480\end{array}\right),{\omega }_3=\left(\begin{array}{l}0.0808,0.2033\\ 0.1780,0.1973\\ 0.1964,0.2347\end{array}\right)\\ {\omega }_4=\left(\begin{array}{l}0.3077,0.1995\\ 0.2042,0.1928\\ 0.1821,0.2166\end{array}\right),{\omega }_5=\left(\begin{array}{l}0.4231,0.1753\\ 0.1990,0.2516\\ 0.2015,0.3249\end{array}\right)\end{array}$$

Based on (29)–(31), we can calculate the comprehensive index value of each decision solution for each expert. The results are shown in the following matrices:

$$\begin{array}{l}{d}_1=\left(\begin{array}{l}[0.6319,0.6319],[0.3681,0.3681]\\ [0.2329,0.3179],[0.5987,0.6821]\\ [0.2808,0.3777],[0.3872,0.6223]\end{array}\right),d_2=\left(\begin{array}{l}[0.3281,0.4686],[0.3744,0.5314]\\ [0.1857,0.2429],[0.6211,0.7571]\\ [0.3924,0.4841],[0.3583,0.5159]\end{array}\right)，\\ d_3=\left(\begin{array}{l}[0.2949,0.4584],[0.3888,0.5416]\\ [0.1311,0.2036],[0.6364,0.7621]\\ [0.2200,0.3793],[0.5107,0.6038]\end{array}\right),d_4=\left(\begin{array}{l}[0.3369,0.4102],[0.3576,0.5898]\\ [0.1971,0.2558],[0.7120,0.7442]\\ [0.2150,0.2799],[0.6264,0.7201]\end{array}\right)，\\ d_5=\left(\begin{array}{l}[0.2256,0.3515],[0.5380,0.6485]\\ [0.2600,0.3561],[0.5563,0.6439]\\ [0.2691,0.4152],[0.3349,0.5848]\end{array}\right)\end{array}$$

Based on (32)–(34), we can calculate the average value of the comprehensive evaluation of group decision-makers with respect to each decision solution. The results are shown in the following matrix:

$$d_e=\left(\begin{array}{l}[0.3035,0.4641],[0.4054,0.5359]\\ [0.2014,0.2753],[0.6249,0.7179]\\ [0.2755,0.3872],[0.4435,0.6094]\end{array}\right)$$

Based on (35)–(37), we can calculate the grey correlation coefficient between the opinion of the individual decision-maker and the opinions of the group decision-makers for each decision solution. The results are shown in the following matrices:

$$k_1=\left(\begin{array}{l}0.4709\\ 0.6103\\ 0.8605\end{array}\right),k_1=\left(\begin{array}{l}0.9062\\ 0.7141\\ 0.5106\end{array}\right),k_1=\left(\begin{array}{l}0.8696\\ 0.5094\\ 0.7713\end{array}\right),k_1=\left(\begin{array}{l}0.7715\\ 0.6083\\ 0.4680\end{array}\right),k_1=\left(\begin{array}{l}0.5373\\ 0.4151\\ 0.7260\end{array}\right)$$

Based on (38), we can calculate the grey correlation degree between the opinion of the individual decision-maker and the opinions of the group decision-makers. The results are shown in the following matrix:

$${\gamma }_{ok}=({\gamma }_{o{k}_1},{\gamma }_{o{k}_2},{\gamma }_{o{k}_3},{\gamma }_{o{k}_4},{\gamma }_{o{k}_5})=\left(0.6472,0.7103,0.7168,0.6159,0.5595\right)$$

Based on (41), we can calculate the decision-maker weights. The results are shown in the following matrix:

$$\omega =({\omega }_1,{\omega }_2,{\omega }_3,{\omega }_4,{\omega }_5)=(0.1987,0.2158,0.2176,0.1907,0.1771)$$

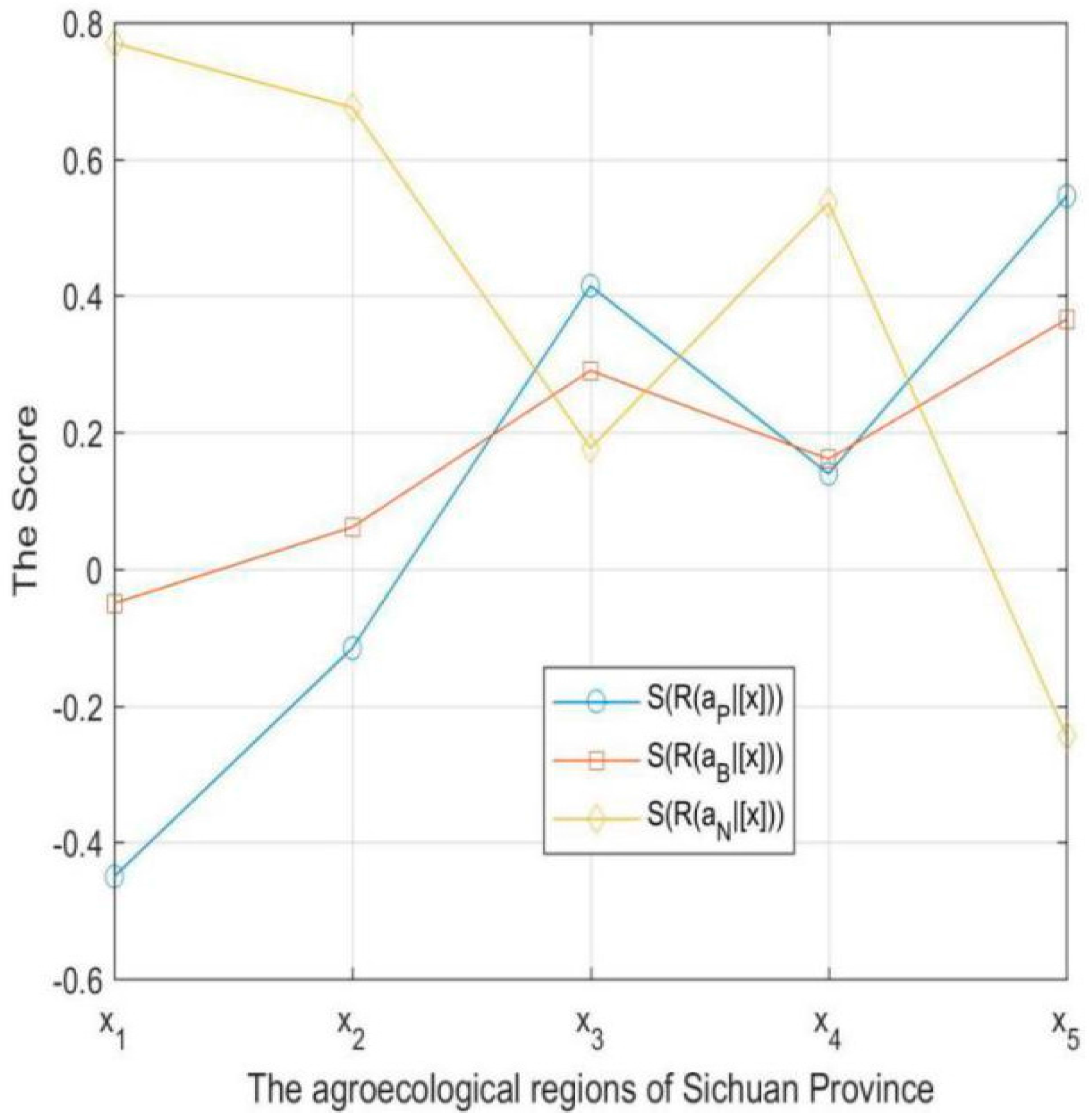
Step 4: Based on (53)–(58), we can calculate the scores and accuracies of $R(a_{•}|[x])(•=P,B,N)$ for each region with the group experts. The results are exhibited in

Table 9. The computation results list of the scores with the group experts.

Region	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$
$S(R(a_P|[\mathrm{x}]))$	−0.7383	0.0204	0.7524	0.4401	0.8544
$S(R(a_B|[\mathrm{x}]))$	−0.0212	0.0152	0.1004	0.0503	0.1323
$S(R(a_N|[\mathrm{x}]))$	0.7850	0.6829	0.1147	0.5269	−0.3728

and

Table 10. The computation results list of the accuracies with the group experts.

Region	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$
$H(R(a_P|[\mathrm{x}]))$	0.9229	0.8755	0.9245	0.8862	0.9649
$H(R(a_B|[\mathrm{x}]))$	0.8388	0.8474	0.8672	0.8555	0.8746
$H(R(a_N|[\mathrm{x}]))$	0.9053	0.8792	0.8274	0.8515	0.8496

and Figure 1.

Here, we take $x_2$ as an example to illustrate the calculation procedure. According to Table 3, the conditional probability $\mathrm{Pr}(C|[x_2])$ is 0.8. Hence, $\mathrm{Pr}({}^{\neg }C|[x_2])=0.2$. For the region $x_2$, the scores of $R(a_{•}|[x])(•=P,B,N)$ are calculated based on (53)–(55):

$$\begin{array}{ll}S(R(a_P|[x_2]))=& (2-{\displaystyle \prod _{k=1}^5{(1-a_{PP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-a_{PN}^{(k)})}^{0.2{\omega }_k}}}-{\displaystyle \prod _{k=1}^5{(1-b_{PP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-b_{PN}^{(k)})}^{0.2{\omega }_k}}}\\ & -{\displaystyle \prod _{k=1}^5{c}_{PP}^{(k)}{}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{c}_{PN}^{(k)}{}^{0.2{\omega }_k}}-}{\displaystyle \prod _{k=1}^5{d}_{PP}^{(k)}{}^{0.8{\omega }_k}}\cdot {\displaystyle \prod _{k=1}^5{d}_{PN}^{(k)}{}^{0.8{\omega }_k})/2}=0.0204\end{array}$$

$$\begin{array}{ll}S(R(a_B|[x_2]))=& (2-{\displaystyle \prod _{k=1}^5{(1-a_{BP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-a_{BN}^{(k)})}^{0.2{\omega }_k}}}-{\displaystyle \prod _{k=1}^5{(1-b_{BP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-b_{BN}^{(k)})}^{0.2{\omega }_k}}}\\ & -{\displaystyle \prod _{k=1}^5{c}_{BP}^{(k)}{}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{c}_{BN}^{(k)}{}^{0.2{\omega }_k}}-}{\displaystyle \prod _{k=1}^5{d}_{BP}^{(k)}{}^{0.8{\omega }_k}}\cdot {\displaystyle \prod _{k=1}^5{d}_{BN}^{(k)}{}^{0.8{\omega }_k})/2}=0.0152\end{array}$$

$$\begin{array}{ll}S(R(a_N|[x_2]))=& (2-{\displaystyle \prod _{k=1}^5{(1-a_{NP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-a_{NN}^{(k)})}^{0.2{\omega }_k}}}-{\displaystyle \prod _{k=1}^5{(1-b_{NP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-b_{NN}^{(k)})}^{0.2{\omega }_k}}}\\ & -{\displaystyle \prod _{k=1}^5{c}_{NP}^{(k)}{}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{c}_{NN}^{(k)}{}^{0.2{\omega }_k}}-}{\displaystyle \prod _{k=1}^5{d}_{NP}^{(k)}{}^{0.8{\omega }_k}}\cdot {\displaystyle \prod _{k=1}^5{d}_{NN}^{(k)}{}^{0.8{\omega }_k})/2}=0.6829\end{array}$$

The accuracies of $R(a_{•}|[x])(•=P,B,N)$ are calculated based on (56)–(58):

$$\begin{array}{ll}H(R(a_P|[x_2]))=& (2-{\displaystyle \prod _{k=1}^5{(1-a_{PP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-a_{PN}^{(k)})}^{0.2{\omega }_k}}}-{\displaystyle \prod _{k=1}^5{(1-b_{PP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-b_{PN}^{(k)})}^{0.2{\omega }_k}}}\\ & +{\displaystyle \prod _{k=1}^5{c}_{PP}^{(k)}{}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{c}_{PN}^{(k)}{}^{0.2{\omega }_k}}+}{\displaystyle \prod _{k=1}^5{d}_{PP}^{(k)}{}^{0.8{\omega }_k}}\cdot {\displaystyle \prod _{k=1}^5{d}_{PN}^{(k)}{}^{0.8{\omega }_k})/2}=0.8755\end{array}$$

$$\begin{array}{ll}H(R(a_B|[x_2]))=& (2-{\displaystyle \prod _{k=1}^5{(1-a_{BP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-a_{BN}^{(k)})}^{0.2{\omega }_k}}}-{\displaystyle \prod _{k=1}^5{(1-b_{BP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-b_{BN}^{(k)})}^{0.2{\omega }_k}}}\\ & +{\displaystyle \prod _{k=1}^5{c}_{BP}^{(k)}{}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{c}_{BN}^{(k)}{}^{0.2{\omega }_k}}+}{\displaystyle \prod _{k=1}^5{d}_{BP}^{(k)}{}^{0.8{\omega }_k}}\cdot {\displaystyle \prod _{k=1}^5{d}_{BN}^{(k)}{}^{0.8{\omega }_k})/2}=0.8388\end{array}$$

$$\begin{array}{ll}H(R(a_N|[x_2]))=& (2-{\displaystyle \prod _{k=1}^5{(1-a_{NP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-a_{NN}^{(k)})}^{0.2{\omega }_k}}}-{\displaystyle \prod _{k=1}^5{(1-b_{NP}^{(k)})}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{(1-b_{NN}^{(k)})}^{0.2{\omega }_k}}}\\ & +{\displaystyle \prod _{k=1}^5{c}_{NP}^{(k)}{}^{0.8{\omega }_k}\cdot {\displaystyle \prod _{k=1}^5{c}_{NN}^{(k)}{}^{0.2{\omega }_k}}+}{\displaystyle \prod _{k=1}^5{d}_{NP}^{(k)}{}^{0.8{\omega }_k}}\cdot {\displaystyle \prod _{k=1}^5{d}_{NN}^{(k)}{}^{0.8{\omega }_k})/2}=0.8792\end{array}$$

Step 4: In light of the results calculated in Figure 1, we find that $S(R(a_P|{[\mathrm{x}}_1]))$, $S(R(a_B|{[\mathrm{x}}_2]))$, $S(R(a_B{|[\mathrm{x}}_3]))$, $S(R(a_B{|[\mathrm{x}}_4]))$ and $S(R(a_N{|[\mathrm{x}}_5]))$ are the only minimum scores in the regions $x_1$, $x_2$, $x_3$, $x_4$ and $x_5$, respectively. Hence, we classify the regions $x_1$, $x_2$, $x_3$, $x_4$ and $x_5$ into $POS(C)$, $BND(C)$, $BND(C)$, $BND(C)$ and $NEG(C)$, respectively. Thus, we decide to vigorously develop E-commerce in region $x_1$, named $a_P$, take the non-commitment decision in the region $x_2$, $x_3$ and $x_4$, named $a_B$, and reduce investment to develop E-commerce in region $x_5$, named $a_N$. Finally, the decision results of each are shown in

Table 11. The final decision to select the regions in which to develop E-commerce in the Sichuan Province with the group of experts.

Region	The Minimum Score	The Selected Action	The Development Decision
$x_1$	$S(R(a_P|{[\mathrm{x}}_1]))$	$a_P$	$POS(C)$
$x_2$	$S(R(a_B{|[\mathrm{x}}_2]))$	$a_B$	$BND(C)$
$x_3$	$S(R(a_B{|[\mathrm{x}}_3]))$	$a_B$	$BND(C)$
$x_4$	$S(R(a_B{|[\mathrm{x}}_4]))$	$a_B$	$BND(C)$
$x_5$	$S(R(a_N{|[\mathrm{x}}_5]))$	$a_N$	$NEG(C)$

.

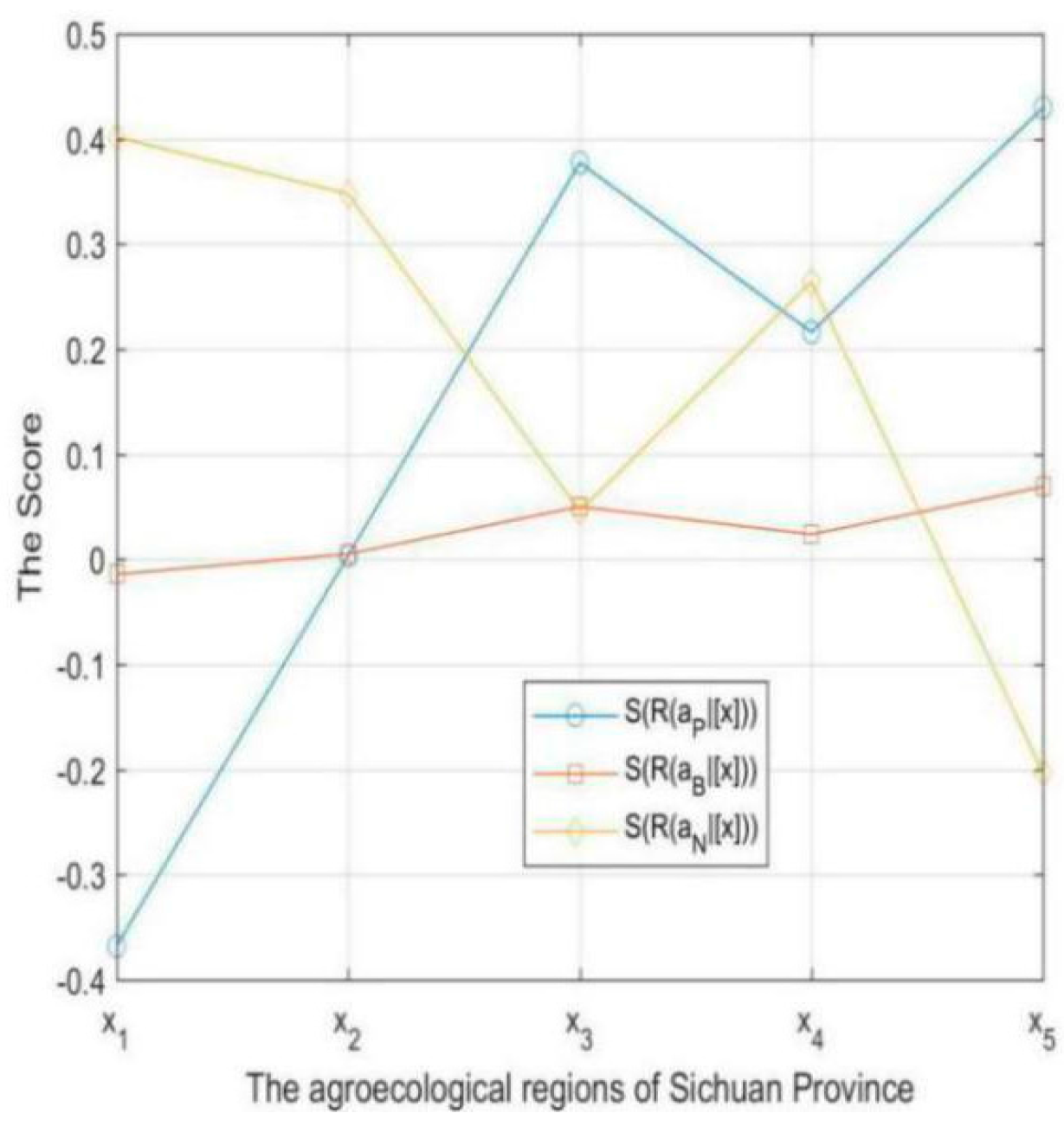
6.2. The Contrastive Analysis of IVIFDTRSs between Group Decision-Making and Single-Expert Decision-Making

For the sake of contrasting the effectiveness of IVIFDTRSs for group decision-making and single-expert decision-making, we count the scores of $R(a_{•}|[x])(•=P,B,N)$ for each region with the expert $e_5$ based on (21)–(23). The results are shown in

Table 12. The computation results list of the scores with the expert $e_5$.

Region	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$
$S(R(a_P|[\mathrm{x}]))$	−0.4500	−0.1157	0.4146	0.1394	0.5461
$S(R(a_B|[\mathrm{x}]))$	−0.0500	0.0615	0.2906	0.1610	0.3656
$S(R(a_N|[\mathrm{x}]))$	0.7700	0.6756	0.1770	0.5359	−0.2449

and Figure 2.

The decision results for expert $e_5$ are show in

Table 13. The final decision to select the regions in which to develop E-commerce in the Sichuan Province with the expert $e_5$.

Region	The Minimum Score	The Selected Action	The Development Decision
$x_1$	$S(R(a_P|{[\mathrm{x}}_1]))$	$a_P$	$POS(C)$
$x_2$	$S(R(a_P{|[\mathrm{x}}_2]))$	$a_P$	$POS(C)$
$x_3$	$S(R(a_B{|[\mathrm{x}}_3]))$	$a_N$	$NEG(C)$
$x_4$	$S(R(a_B{|[\mathrm{x}}_4]))$	$a_P$	$POS(C)$
$x_5$	$S(R(a_B{|[\mathrm{x}}_5]))$	$a_N$	$NEG(C)$

.

Comparing Table 11 and Table 13, the group of experts and the expert $e_5$ make different decisions in regions $x_2$, $x_3$ and $x_4$: the experts group tend to take the non-commitment decision in regions $x_2$, $x_3$ and $x_4$, but the expert $e_5$ decides to develop E-commerce in regions $x_2$, $x_4$ and to reduce investment in, or abstain from, developing E-commerce in region $x_3$. From the different decisions, the results in Table 11 are more authoritative and reasonable, because they are more cautious and synthetically utilize all the decision information of the five experts.

6.3. The Contrastive Analysis between IVIFDTRSs and IFDTRSs

In order to illustrate that the IVIFDTRSs more effectively characterize the risk attitude of decision-makers than IFDTRSs, we also asked the group of five experts to give the values of the loss functions with intuitionistic fuzzy numbers. The values with intuitionistic fuzzy numbers (IFNs) of the losses with the group experts are listed in

Table 14. The loss function matrix represented by IFNs with the expert $e_1$.

${\mathit{e}}_1$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(1)}}({\lambda }_{PP})=({\mu }_{PP}^{(1)},{\nu }_{PP}^{(1)})=(0.01,0.99)$	$\widetilde{E^{(1)}}({\lambda }_{PN})=({\mu }_{PN}^{(1)},{\nu }_{PN}^{(1)})=(0.99,0.01)$
$a_B$	$\widetilde{E^{(1)}}({\lambda }_{BP})=({\mu }_{BP}^{(1)},{\nu }_{BP}^{(1)})=(0.4,0.6)$	$\widetilde{E^{(1)}}({\lambda }_{BN})=({\mu }_{BN}^{(1)},{\nu }_{BN}^{(1)})=(0.7,0.3)$
$a_N$	$\widetilde{E^{(1)}}({\lambda }_{NP})=({\mu }_{NP}^{(1)},{\nu }_{NP}^{(1)})=(0.9,0.1)$	$\widetilde{E^{(1)}}({\lambda }_{NN})=({\mu }_{NN}^{(1)},{\nu }_{NN}^{(1)})=(0.05,0.95)$

,

Table 15. The loss function matrix represented by IFNs with the expert $e_2$.

${\mathit{e}}_2$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(2)}}({\lambda }_{PP})=({\mu }_{PP}^{(2)},{\nu }_{PP}^{(2)})=(0.1,0.9)$	$\widetilde{E^{(2)}}({\lambda }_{PN})=({\mu }_{PN}^{(2)},{\nu }_{PN}^{(2)})=(0.95,0.05)$
$a_B$	$\widetilde{E^{(2)}}({\lambda }_{BP})=({\mu }_{BP}^{(2)},{\nu }_{BP}^{(2)})=(0.6,0.4)$	$\widetilde{E^{(2)}}({\lambda }_{BN})=({\mu }_{BN}^{(2)},{\nu }_{BN}^{(2)})=(0.3,0.7)$
$a_N$	$\widetilde{E^{(2)}}({\lambda }_{NP})=({\mu }_{NP}^{(2)},{\nu }_{NP}^{(2)})=(0.95,0.05)$	$\widetilde{E^{(2)}}({\lambda }_{NN})=({\mu }_{NN}^{(2)},{\nu }_{NN}^{(2)})=(0.1,0.9)$

,

Table 16. The loss function matrix represented by IFNs with the expert $e_3$.

${\mathit{e}}_3$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(3)}}({\lambda }_{PP})=({\mu }_{PP}^{(3)},{\nu }_{PP}^{(3)})=(0.05,0.95)$	$\widetilde{E^{(3)}}({\lambda }_{PN})=({\mu }_{PN}^{(3)},{\nu }_{PN}^{(3)})=(0.95,0.05)$
$a_B$	$\widetilde{E^{(3)}}({\lambda }_{BP})=({\mu }_{BP}^{(3)},{\nu }_{BP}^{(3)})=(0.4,0.6)$	$\widetilde{E^{(3)}}({\lambda }_{BN})=({\mu }_{BN}^{(3)},{\nu }_{BN}^{(3)})=(0.5,0.4)$
$a_N$	$\widetilde{E^{(3)}}({\lambda }_{NP})=({\mu }_{NP}^{(3)},{\nu }_{NP}^{(3)})=(0.9,0.1)$	$\widetilde{E^{(3)}}({\lambda }_{NN})=({\mu }_{NN}^{(3)},{\nu }_{NN}^{(3)})=(0.1,0.8)$

,

Table 17. The loss function matrix represented by IFNs with the expert $e_4$.

${\mathit{e}}_4$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(4)}}({\lambda }_{PP})=({\mu }_{PP}^{(4)},{\nu }_{PP}^{(4)})=(0.2,0.8)$	$\widetilde{E^{(4)}}({\lambda }_{PN})=({\mu }_{PN}^{(4)},{\nu }_{PN}^{(4)})=(0.9,0.1)$
$a_B$	$\widetilde{E^{(4)}}({\lambda }_{BP})=({\mu }_{BP}^{(4)},{\nu }_{BP}^{(4)})=(0.5,0.5)$	$\widetilde{E^{(4)}}({\lambda }_{BN})=({\mu }_{BN}^{(4)},{\nu }_{BN}^{(4)})=(0.55,0.45)$
$a_N$	$\widetilde{E^{(4)}}({\lambda }_{NP})=({\mu }_{NP}^{(4)},{\nu }_{NP}^{(4)})=(0.8,0.2)$	$\widetilde{E^{(4)}}({\lambda }_{NN})=({\mu }_{NN}^{(4)},{\nu }_{NN}^{(4)})=(0.1,0.85)$

and

Table 18. The loss function matrix represented by IFNs with the expert $e_5$.

${\mathit{e}}_5$	$\mathit{C}(\mathit{P})$	${}^{\neg }\mathit{C}(\mathit{N})$
$a_P$	$\widetilde{E^{(5)}}({\lambda }_{PP})=({\mu }_{PP}^{(5)},{\nu }_{PP}^{(5)})=(0.3,0.7)$	$\widetilde{E^{(5)}}({\lambda }_{PN})=({\mu }_{PN}^{(5)},{\nu }_{PN}^{(5)})=(0.8,0.2)$
$a_B$	$\widetilde{E^{(5)}}({\lambda }_{BP})=({\mu }_{BP}^{(5)},{\nu }_{BP}^{(5)})=(0.5,0.5)$	$\widetilde{E^{(5)}}({\lambda }_{BN})=({\mu }_{BN}^{(5)},{\nu }_{BN}^{(5)})=(0.7,0.3)$
$a_N$	$\widetilde{E^{(5)}}({\lambda }_{NP})=({\mu }_{NP}^{(5)},{\nu }_{NP}^{(5)})=(0.9,0.1)$	$\widetilde{E^{(5)}}({\lambda }_{NN})=({\mu }_{NN}^{(5)},{\nu }_{NN}^{(5)})=(0.2,0.8)$

.

Based on the operational rules (46)–(48) of IFDTRSs, and Liang and Liu [1], we count the scores of the $R(a_{•}|[x])(•=P,B,N)$ for each region. The results are exhibited in

Table 19. The computation results list of the scores with the group experts.

Region	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$
$S(R(a_P|[\mathrm{x}]))$	−0.3680	0.0038	0.3774	0.2163	0.4299
$S(R(a_B|[\mathrm{x}]))$	−0.0141	0.0052	0.0503	0.0238	0.0672
$S(R(a_N|[\mathrm{x}]))$	0.4017	0.3478	0.0459	0.2643	−0.2031

and Figure 3.

The decision results for IFNSs are shown in

Table 20. The final decision to select the regions in which to develop E-commerce in the Sichuan Province with the group of experts for IFNSs.

Region	The Minimum Score	The Selected Action	The Development Decision
$x_1$	$S(R(a_P|{[\mathrm{x}}_1]))$	$a_P$	$POS(C)$
$x_2$	$S(R(a_P{|[\mathrm{x}}_2]))$	$a_P$	$POS(C)$
$x_3$	$S(R(a_N{|[\mathrm{x}}_3]))$	$a_N$	$NEG(C)$
$x_4$	$S(R(a_B{|[\mathrm{x}}_4]))$	$a_B$	$BND(C)$
$x_5$	$S(R(a_N{|[\mathrm{x}}_5]))$	$a_N$	$NEG(C)$

.

Comparing Table 11 and Table 20, the decisions of IVIFNSs and IFNSs are different in region $x_2$ and $x_3$: the decision process of IVIFNSs tend toward the non-commitment decision in region $x_2$ and $x_3$, but the decision process of IFNSs tend toward the decision to develop E-commerce in region $x_2$ and reduce investment in, or abstain from, developing E-commerce in region $x_3$. As we know, the loss of delayed decision is usually less than the loss of putting an object into $POS(C)$ when the object does not belong to $C$. Additionally, the loss of delayed decision is usually less than the loss of putting an object into $NEG(C)$ when the object does not belong to ${}^{\neg }C$. From the difference in the decisions between Table 11 and Table 20, it can be deduced that the decision process of IVIFNSs can more effectively reduce the loss caused by wrong decision-making than can the decision process of IFNSs, and it can help individuals make more scientific and reasonable decisions in fuzzy environments.

7. Conclusions

In this paper, we construct a new IVIFDTRSs model by introducing IVIFNs into DTRSs, which can extend the DTRSs and IFDTRSs. Based on the IVIFDTRSs model, we also expand three-way decisions from single-person decision-making to group decision-making. Under the single-person decision-making, we design a strategy to deduce the decision rules. With respect to group decision-making, we adopt GCAWD to confirm the weight of each expert and use an IIFWA-integrated operator to aggregate the losses of every expert as well as deduce the rules of three-way decisions with respect to IVIFDTRSs.

This research discusses the IVIFDTRSs model by considering IVIFSs and deduces its decision rules, which is a very important form of uncertainty, and expands the classical model of DTRSs. This research also adopts GCAWD method to confirm the weight of each expert, which offers a more scientific way to determine the weight of experts in group decision-making. We will continue to research the generalization IVIFDTRSs model, expand the IVIFDTRSs model to Multi-classification problem, and use in practical applications based on the IVIFDTRSs model.