1. Introduction
Along with advances in transportation infrastructure, more and more underwater tunnels have been under construction. During the construction process, the initial equilibrium of groundwater is broken. Water ingress may seriously influence the behavior of tunnels in the construction stage as well as in the operation stage. The safety of underwater tunnels during the construction and operation stages is threatened by the groundwater flow. Therefore, it is important and meaningful to investigate the seepage field of underwater tunnels [
1,
2,
3] and predict the water ingress into tunnels in advance [
4,
5].
Nowadays, the commonly used methods to obtain analytical solutions of seepage fields for underwater tunnels are the complex variable method, mirror image method, and axisymmetric modeling method [
6]. Based on the complex variable method, Kolymbas and Wagner [
7] used the conformal mapping technique and obtained exact analytical solutions of groundwater ingress into a circular tunnel with deep or shallow buried depth. Considering the different boundary conditions at the tunnel perimeter, constant total hydraulic head and constant water pressure, Park et al. [
8] and Huangfu et al. [
9] derived analytical solutions of seepage field for steady water inflow into a drained circular tunnel in a semi-infinite aquifer. Zhang et al. [
10] investigated analytical solutions for tunnel leakage–induced ground and tunnel responses considering the grouting effect. Ying et al. [
11] derived a semi-analytical solution for groundwater ingress into lined tunnels using a conformal mapping technique. Using the mirror image method, Harr [
12] presented the pore pressure distribution of a circular tunnel. Using the axisymmetric modeling method, Wang et al. [
13] conducted a theoretical and experimental study to analyze the influence of controlled drainage on the external water pressure of lining for deep tunnels. In addition, Li et al. [
14] investigated analytical solutions for steady water inflow into a subsea grouted tunnel using the complex variable method, mirror image method, and axisymmetric modeling method. However, all the research mentioned above focused on single underwater tunnels. The analytical solutions of seepage field for symmetrical underwater tunnels have had little research. For symmetrical underwater tunnels, the boundary conditions are more complex than they are for single underwater tunnels. It is too hard to find an appropriate conformal mapping function, which makes it difficult to apply the complex variable method to analyze the seepage field for symmetrical underwater tunnels. When it comes to the axisymmetric modeling method, it is often used to analyze the analytical solutions of seepage field for single underwater tunnels because of the simple boundary conditions. However, due to the property of superposition for the potential function, the mirror image method can be used to analyze the seepage field for symmetrical underwater tunnels with complex boundary conditions.
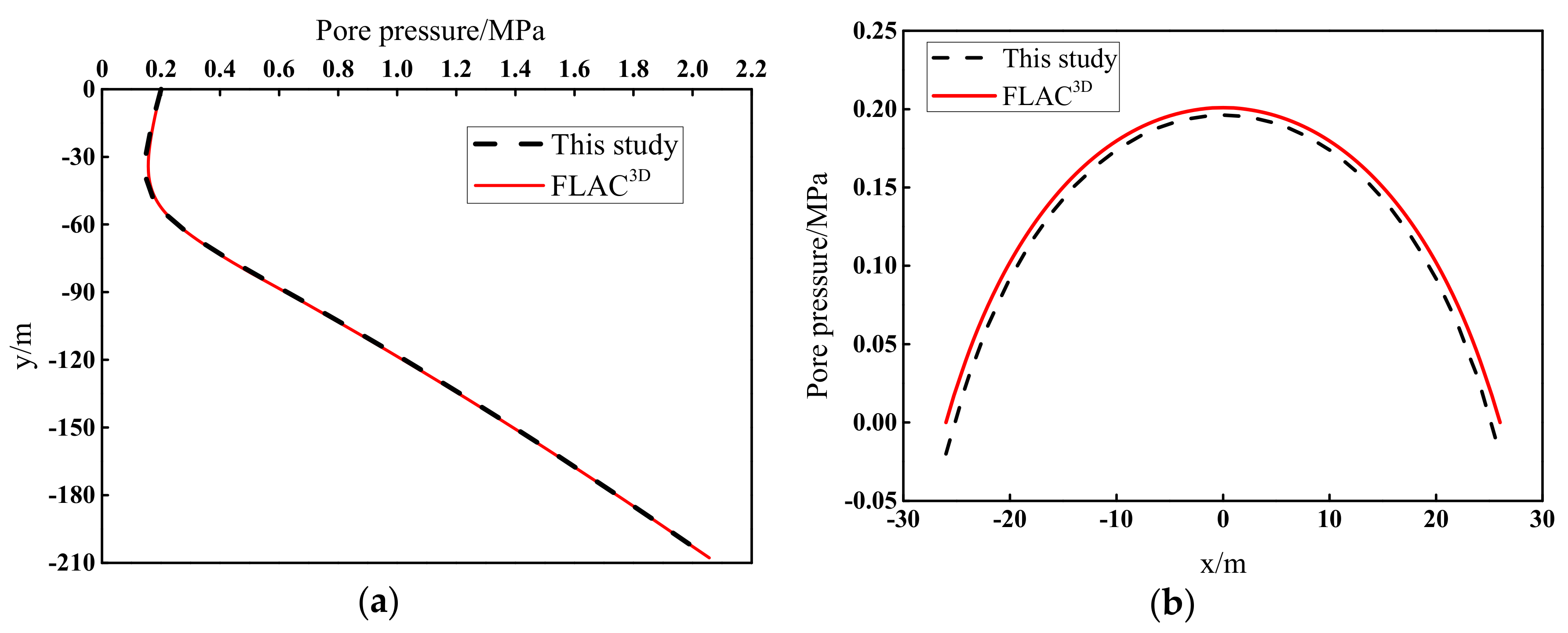
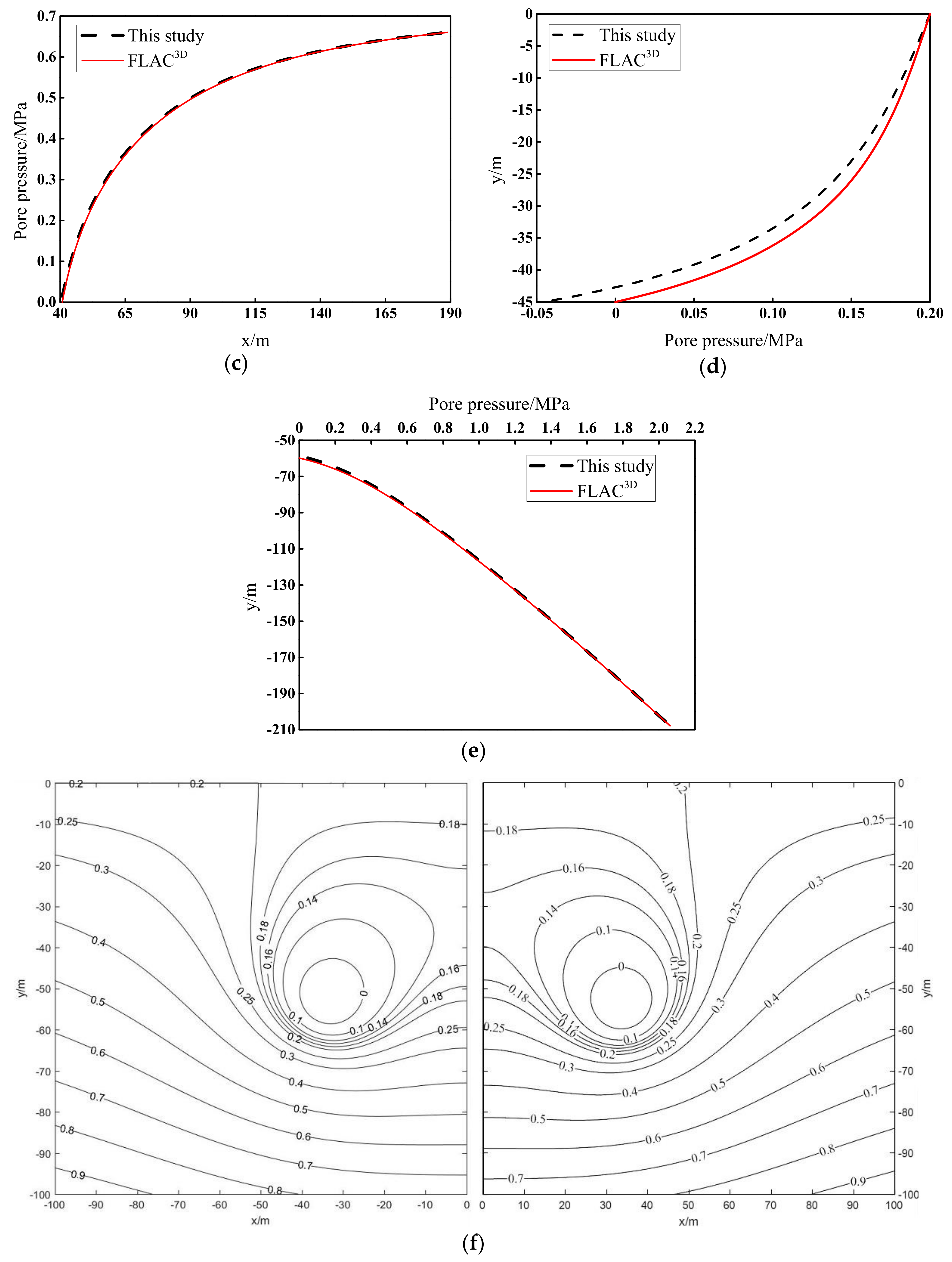
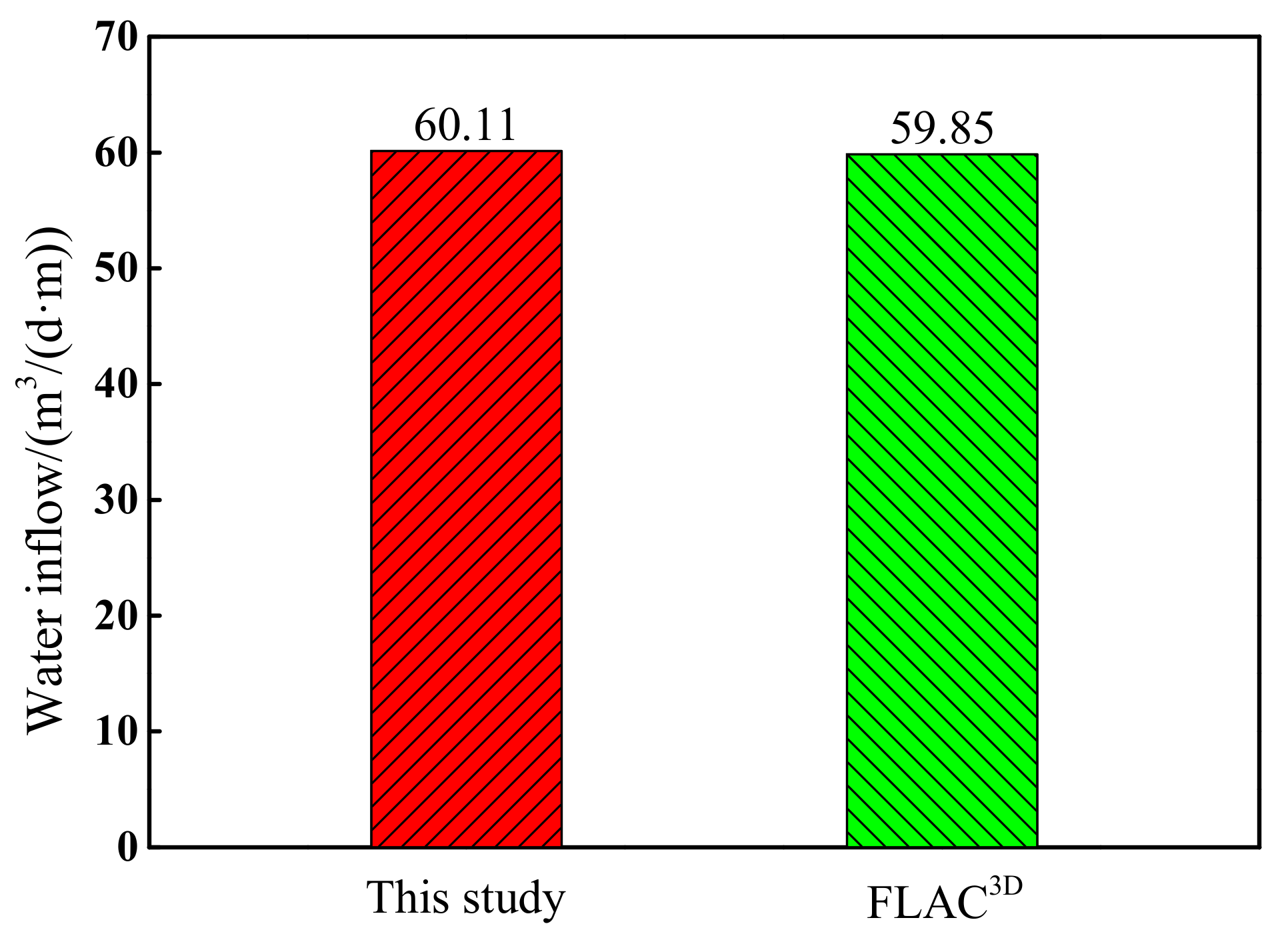
This paper focuses on the analytical solutions of steady seepage field for symmetrical underwater tunnels. An analytical model of seepage field is proposed. The analytical solutions are obtained based on the mirror image method and superposition principle. A series of numerical simulations are conducted to validate the analytical solutions.
2. Problem Description
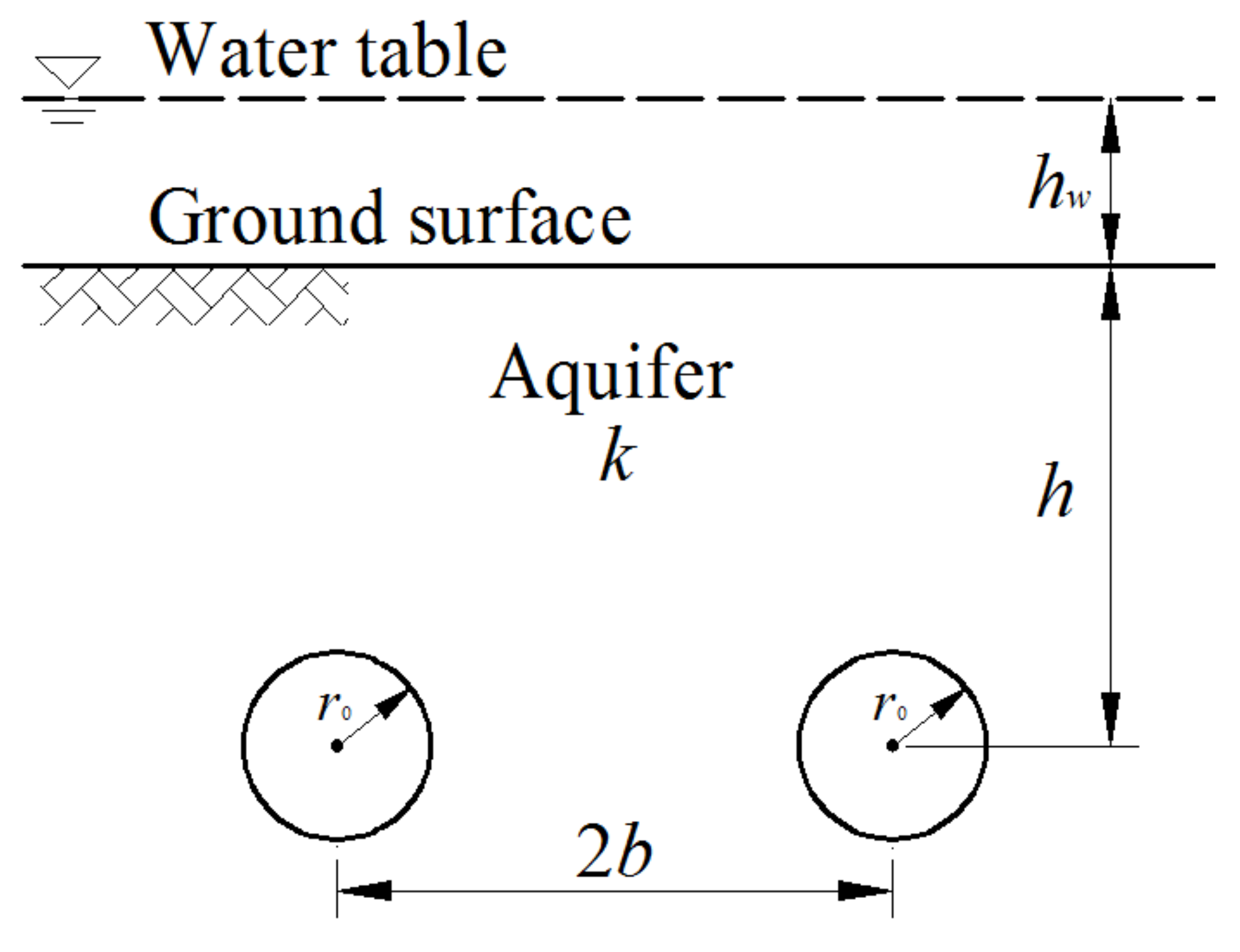
Figure 1 shows the model for analyzing the steady seepage field of symmetrical underwater tunnels in a semi-infinite aquifer. In this model,
r0 represents the radius of the tunnels. The distance between the two tunnel centers is 2
b. The tunnel depth from the center to the ground surface is
h. The water table is above the ground surface. The water depth from the water table to the ground surface is
hw. The permeability of the aquifer is expressed as
k.
In order to obtain the analytical solutions of steady seepage field, several simplified assumptions are made, as follows:
- (1)
Symmetrical underwater tunnels are circular and are located in a fully saturated, homogeneous, isotropic, and semi-infinite aquifer.
- (2)
A state of steady flow is assumed.
- (3)
The fluid is incompressible.
- (4)
The water table above the ground surface is horizontal and remains unchanged.
According to Darcy’s law and conservation of mass, in fully saturated, homogeneous, isotropic media, the differential equation for two-dimensional steady-state groundwater flow is given by the Laplace equation:
where
H is the total hydraulic head and is equal to the sum of the pressure head and elevation head, that is
where
p is water pressure,
γw is the unit weight of water, and
y is the elevation head.
3. Analytical Solutions
Equation (1) cannot be solved directly to obtain the analytical solutions of seepage field due to the complex boundary conditions. The mirror image method is widely used in analyzing steady seepage field. By mirroring the prototype semi-infinite seepage field into a virtual one, the problem of obtaining analytical solutions of steady seepage field in a semi-infinite aquifer is converted into a problem of obtaining such solutions in an infinite aquifer.
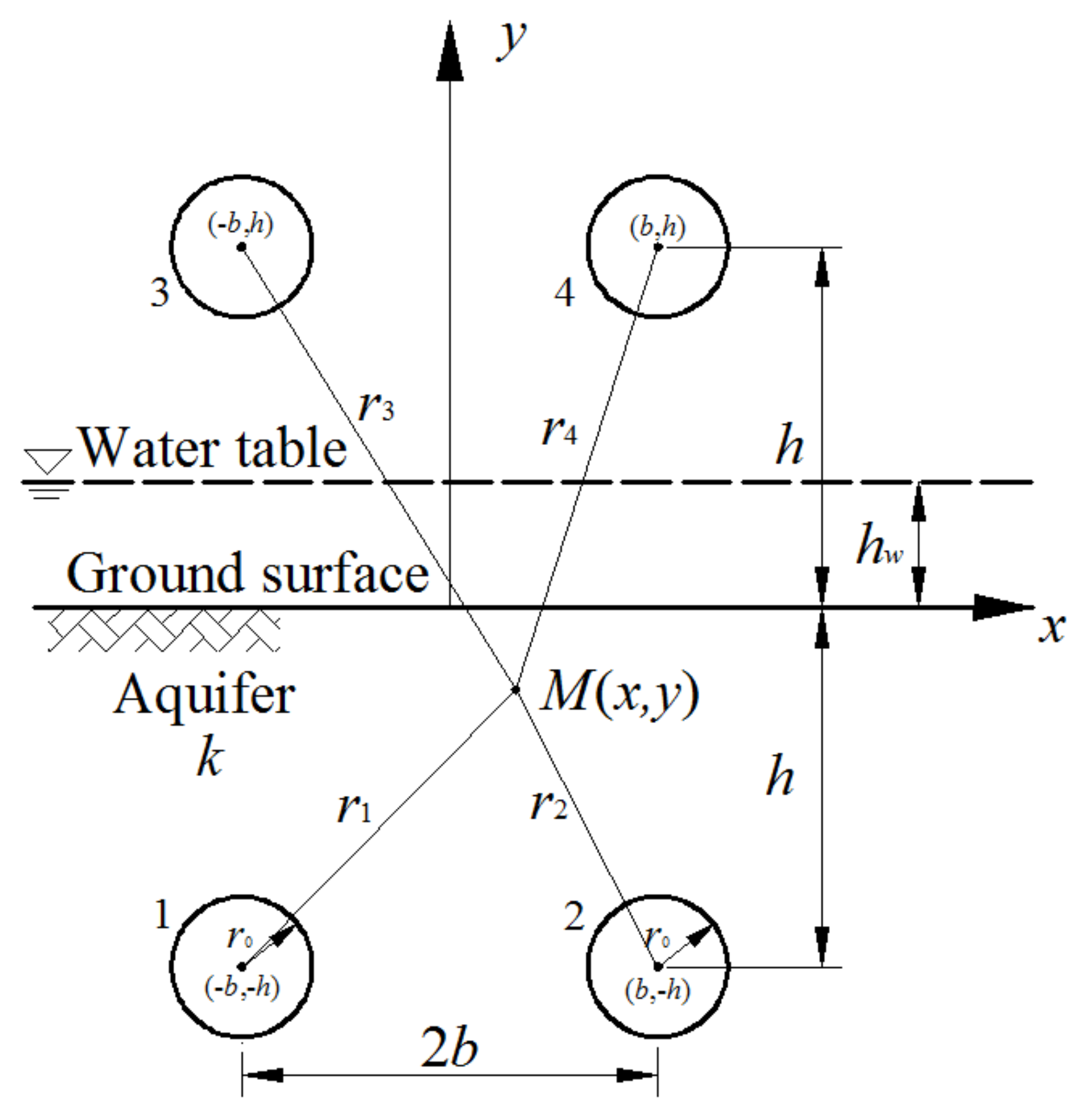
Figure 2 describes the model to obtain the analytical solutions of steady seepage field for symmetrical underwater tunnels using the mirror image method. The ground surface is considered as the mirror face. The prototype semi-infinite steady seepage field is equivalent to a steady seepage field formed by two pumping wells, while the virtual steady seepage field is equivalent to a steady seepage field generated by two injection wells. Furthermore, the seepage velocity and water inflow of the prototype seepage field are equal to those of the virtual seepage field. The steady seepage field in an infinite aquifer composed of four tunnels is formed.
In
Figure 2, tunnel 3 is the mirror image of tunnel 1, while tunnel 4 is the mirror image of tunnel 2. Because of symmetry, the water inflow for both tunnel 1 and tunnel 2 is assumed to be
Q. Supposing that water inflow is positive and water outflow is negative, the water inflow for both tunnel 3 and tunnel 4 is −
Q. A Cartesian coordinate system is applied (see
Figure 2).
M(
x,
y) is a certain point in the semi-infinite aquifer;
r1,
r2 represent the distance from the point
M(
x,
y) to the centers of tunnels 1 and 2, respectively; and
r3,
r4 represent the distance from the point
M(
x,
y) to the centers of tunnels 3 and 4, respectively. According to geometric properties,
r1,
r2,
r3, and
r4 can be denoted as:
According to Bear [
15], Equation (1) can be converted into an equation in the polar coordinate system, as follows:
where
r is the seepage radius and
H is the total hydraulic head.
According to Darcy’s law, the water inflow per meter of a circular tunnel can be denoted as
By integrating,
H can be expressed as
where
C is the integral constant.
According to the superposition principle [
15], the total hydraulic head
HM of point
M(
x,
y) in the infinite aquifer composed of four tunnels can be written as
When the point M(x,y) is on the ground surface (i.e., r1 = r3 and r2 = r4), the total hydraulic head is equal to hw. Substituting this boundary condition into Equation (10), the integral constant C can be obtained as C = hw.
When the point M(x,y) is at the perimeter of tunnel 1 (i.e., r1 = r0), r2, r3, and r4 can be denoted as , , and . Here, x and y represent the abscissa and ordinate values at the perimeter of tunnel 1. Thus, x and y follow the relationships and . If r0 is small enough relative to b and r0 is small enough relative to h, x and y can be approximately denoted as x = −b and y = −h. r2, r3, and r4 can be approximately rewritten as , , and .
When the point M(x,y) is at the perimeter of tunnel 2 (i.e., r2 = r0), r1, r3, and r4 can be denoted as , , and . Here, x and y represent the abscissa and ordinate values at the perimeter of tunnel 2. Thus, x and y follow the relationships and . If r0 is small enough relative to b and r0 is small enough relative to h, x and y can be approximately denoted as x = b and y = −h. r1, r3, and r4 can be approximately rewritten as , , and .
In the next sections, two kinds of boundary conditions are discussed to obtain the analytical solutions of steady seepage field for symmetrical underwater tunnels: (1) constant total hydraulic head H0 at the perimeter of the tunnel and (2) constant water pressure p0 at the perimeter of the tunnel.
3.1. Considering Constant Total Hydraulic Head H0 at the Perimeter of a Symmetrical Tunnel
Substituting the boundary conditions into Equation (10), the total hydraulic head
H0 can be written as
The water inflow of a symmetrical tunnel can be obtained as
Substituting Equation (12) into Equation (10), the total hydraulic head
HM of point
M(
x,
y) in the semi-infinite aquifer is denoted as
According to Equation (2), the pore pressure
pM in the semi-infinite aquifer can be written as
3.2. Considering Constant Water Pressure p0 at the Perimeter of a Symmetrical Tunnel
When gravity is neglected and the elevation head is not taken into account, the water pressure
p0 at the perimeter of a symmetrical tunnel is described as
p0 =
γwH0, and the total hydraulic head at the perimeter of the tunnel is constant. Therefore, according to the derived equation in
Section 3.1, the pore pressure
pM of point
M(
x,
y) in the semi-infinite aquifer can be written as
Actually, the pore pressure is related to the unit weight and elevation head. Thus, referring to Huang et al. [
9], the real expression of the pore pressure
pM should be assumed as
where
X(
x,
y) and
Y(
x,
y) are determined by the boundary conditions.
Considering the unit weight and elevation head, the boundary conditions are described as follows: when the point
M(
x,
y) is at the perimeter of a symmetrical tunnel,
pM =
p0; when the point
M(
x,
y) is on the ground surface,
. Substituting the boundary conditions above into Equation (16), the solutions to
X(
x,
y) and
Y(
x,
y) can be found with
and
Substituting Equations (17) and (18) into Equation (16), the pore pressure
pM of point
M(
x,
y) in the semi-infinite aquifer can be written as
According to Equation (2), the total hydraulic head
HM of point
M(
x,
y) in the semi-infinite aquifer is denoted as
Substituting Equation (20) into Equation (10) and considering the boundary conditions at the perimeter of a symmetrical tunnel, the water inflow of a symmetrical tunnel is calculated as