On Eccentricity-Based Topological Indices and Polynomials of Phosphorus-Containing Dendrimers
Abstract
:1. Introduction
2. Definitions and Notations
3. The Eccentricity-Based Indices and Polynomials for the Molecular Graph
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adronov, A.; Frechet, J.M.J. Light-harvesting dendrimers. Chem. Commun. 2000, 33, 1701–1710. [Google Scholar] [CrossRef]
- Naka, K.; Tanaka, Y.; Chujo, Y. Effect of anionic starburst dendrimers on the crystallization of CaCO3 in aqueous solution, Size control of spherical vaterite particles. Langmuir 2002, 18, 3655–3658. [Google Scholar] [CrossRef]
- Suresh, R.; Singh, C.; Rewar, P. Dendrimers as carriers and its application in therapy. Int. J. Anal. Pharm. Biomed. Sci. 2015, 4, 15–23. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Goswami, R.; Madan, A.K. Eccentric-connectivity index: A novel highly discriminating topological descriptor for structure–property and structure–activity studies. J. Chem. Inf. Comput. Sci. 1997, 37, 273–282. [Google Scholar] [CrossRef]
- Dureja, H.; Madan, A.K. Topochemical models for prediction of cyclin-dependent kinase 2 inhibitory activity of indole-2-ones. J. Mol. Model. 2005, 11, 525–531. [Google Scholar] [CrossRef] [PubMed]
- Ilic, A.; Gutman, I. Eccentric-connectivity index of chemical trees. MATCH Commun. Math. Comput. Chem. 2011, 65, 731–744. [Google Scholar]
- Kumar, V.; Madan, A.K. Application of graph theory: Prediction of cytosolic phospholipase A(2) inhibitory activity of propan-2-ones. J. Math. Chem. 2006, 39, 511–521. [Google Scholar] [CrossRef]
- Zhou, B. On eccentric-connectivity index. MATCH Commun. Math. Comput. Chem. 2010, 63, 181–198. [Google Scholar]
- Ashrafi, A.R.; Ghorbani, M.; Hossein-Zadeh, M.A. The eccentric-connectivity polynomial of some graph operations. Serdica J. Comput. 2011, 5, 101–116. [Google Scholar]
- Ghorbani, M.; Hosseinzadeh, M.A. A new version of Zagreb indices. Filomat 2012, 26, 93–100. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, M.; Madan, A. K Connective eccentricity index: A novel topological descriptor for predicting biological activity. J. Mol. Graph. Model. 2000, 18, 18–25. [Google Scholar] [CrossRef]
- De, N. Relationship between augmented eccentric-connectivity index and some other graph invariants. Int. J. Adv. Math. 2013, 1, 26–32. [Google Scholar] [CrossRef]
- Doślić, T.; Saheli, M. Augmented eccentric-connectivity index. Miskolc Math. Notes 2011, 12, 149–157. [Google Scholar]
- Alaeiyan, M.; Asadpour, J.; Mojarad, R. A numerical method for MEC polynomial and MEC index of one-pentagonal carbon nanocones. Fuller. Nanotub. Carbon Nanostruct. 2013, 21, 825–835. [Google Scholar] [CrossRef]
- Aslam, A.; Jamil, M.K.; Gao, W.; Nazeer, W. Topological aspects of some dendrimer structures. Nanotechnol. Rev. 2018, 7, 123–129. [Google Scholar] [CrossRef]
- Aslam, A.; Bashir, Y.; Ahmad, S.; Gao, W. On Topological Indices of Certain Dendrimer Structures. Z. Naturforschung A 2017, 72, 559–566. [Google Scholar] [CrossRef]
- Bashir, Y.; Aslam, A.; Kamran, M.; Qureshi, M.I.; Jahangir, A.; Rafiq, M.; Bibi, N.; Muhammad, N. On forgotten topological indices of some dendrimers structure. Molecules 2017, 22, 867. [Google Scholar] [CrossRef] [PubMed]
- Soleimania, N.; Bahnamirib, S.B.; Nikmehr, M.J. Study of dendrimers by topological indices. ACTA CHEMICA IASI 2017, 25, 145–162. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, B.; Gao, W. Distance indices calculating for two classes of dendrimer. Geol. Ecol. Landsc. 2017, 1, 133–142. [Google Scholar] [CrossRef]
- Yang, J.; Xia, F. The eccentric connectivity index of dendrimers. Int. J. Contemp. Math. Sci. 2010, 5, 2231–2236. [Google Scholar]
- Badetti, E.; Lloveras, V.; Muñoz-Gómez, J.L.; Sebastián, R.M.; Camimade, A.M.; Majoral, J.P.; Veciana, J.; Vidal-Gancedo, J. Radical dendrimers: A family of five generations of phosphorus dendrimers functionalized with TEMPO radicals. Macromolecules 2014, 47, 7717–7724. [Google Scholar] [CrossRef]
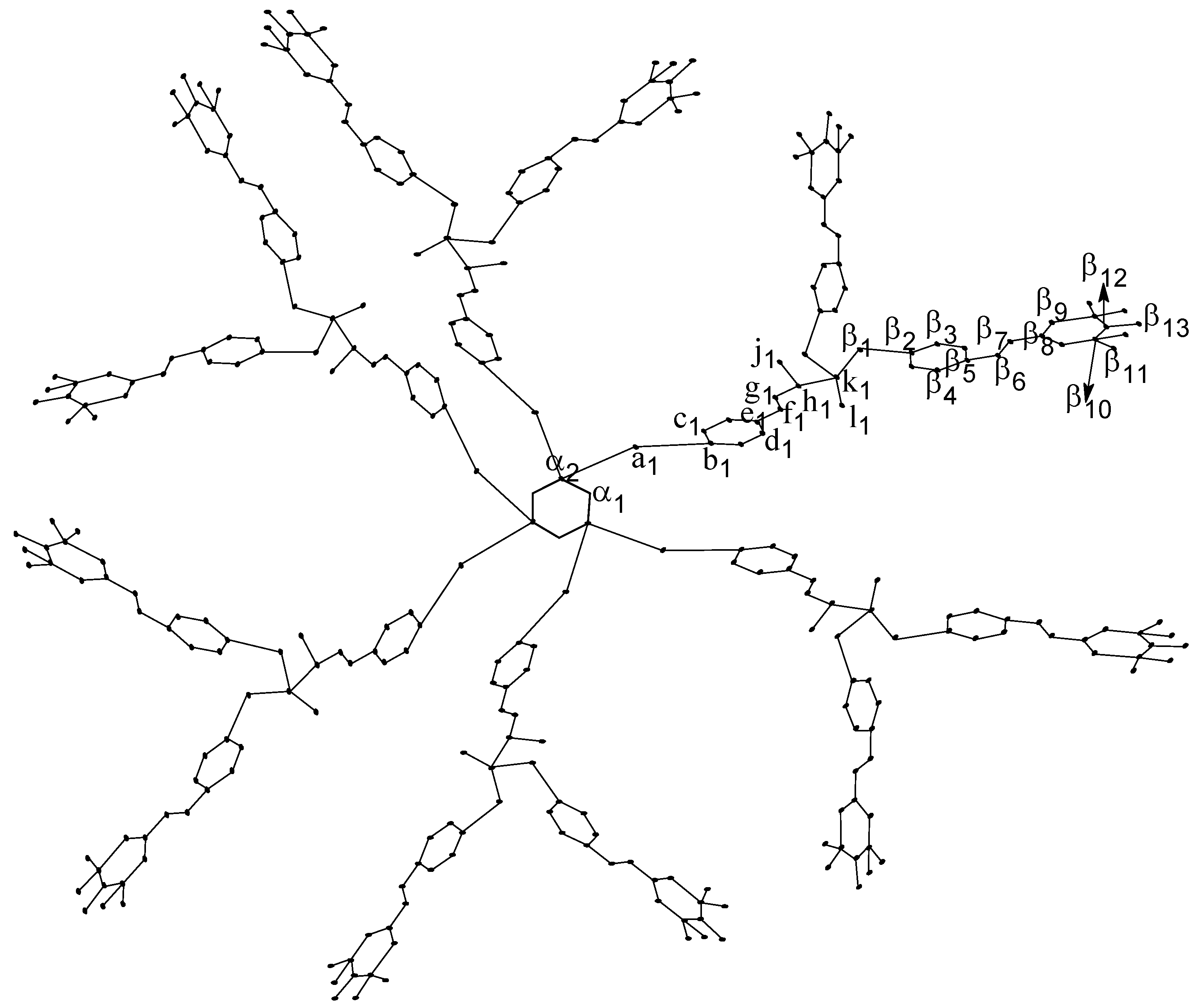
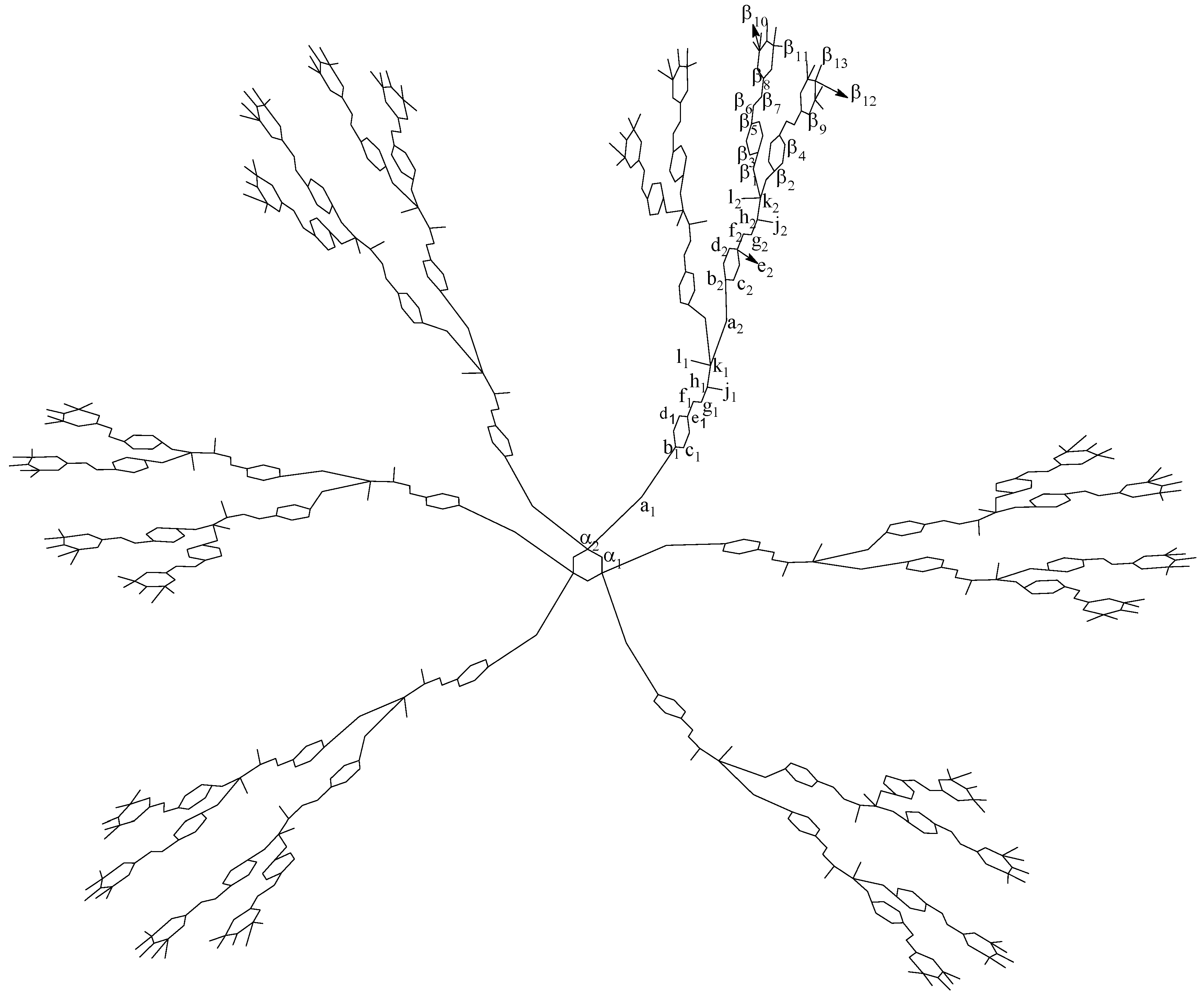
| Representative | Degree | Eccentricity | Frequency | ||
|---|---|---|---|---|---|
| 2 | 8 | 16 | 3 | ||
| 4 | 8 | 16 | 3 | ||
| 2 | 7 | 12 | |||
| 3 | 6 | 8 | |||
| 2 | 5 | 6 | |||
| 2 | 5 | 6 | |||
| 3 | 6 | 8 | |||
| 2 | 5 | 6 | |||
| 2 | 5 | 6 | |||
| 3 | 6 | 8 | |||
| 2 | 7 | 12 | |||
| 4 | 7 | 6 | |||
| 1 | 4 | 4 | |||
| 3 | 9 | 16 | |||
| 1 | 3 | 3 |
| Representative | Degree | Eccentricity | Frequency | ||
|---|---|---|---|---|---|
| 2 | 7 | 12 | |||
| 3 | 6 | 8 | |||
| 2 | 5 | 6 | |||
| 2 | 5 | 6 | |||
| 3 | 6 | 8 | |||
| 2 | 5 | 6 | |||
| 2 | 5 | 6 | |||
| 3 | 7 | 8 | |||
| 1 | 3 | 3 | |||
| 4 | 8 | 12 | |||
| 1 | 4 | 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.M.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aslam, A.; Nazeer, W. On Eccentricity-Based Topological Indices and Polynomials of Phosphorus-Containing Dendrimers. Symmetry 2018, 10, 237. https://doi.org/10.3390/sym10070237
Kang SM, Iqbal Z, Ishaq M, Sarfraz R, Aslam A, Nazeer W. On Eccentricity-Based Topological Indices and Polynomials of Phosphorus-Containing Dendrimers. Symmetry. 2018; 10(7):237. https://doi.org/10.3390/sym10070237
Chicago/Turabian StyleKang, Shin Min, Zahid Iqbal, Muhammad Ishaq, Rabia Sarfraz, Adnan Aslam, and Waqas Nazeer. 2018. "On Eccentricity-Based Topological Indices and Polynomials of Phosphorus-Containing Dendrimers" Symmetry 10, no. 7: 237. https://doi.org/10.3390/sym10070237
APA StyleKang, S. M., Iqbal, Z., Ishaq, M., Sarfraz, R., Aslam, A., & Nazeer, W. (2018). On Eccentricity-Based Topological Indices and Polynomials of Phosphorus-Containing Dendrimers. Symmetry, 10(7), 237. https://doi.org/10.3390/sym10070237





