Abstract
In the study of the quantitative structure–activity relationship and quantitative structure-property relationships, the eccentric-connectivity index has a very important place among the other topological descriptors due to its high degree of predictability for pharmaceutical properties. In this paper, we compute the exact formulas of the eccentric-connectivity index and its corresponding polynomial, the total eccentric-connectivity index and its corresponding polynomial, the first Zagreb eccentricity index, the augmented eccentric-connectivity index, and the modified eccentric-connectivity index and its corresponding polynomial for a class of phosphorus containing dendrimers.
Keywords:
eccentric-connectivity index; augmented eccentric-connectivity index; molecular graph; phosphorus containing dendrimers MSC:
05C90
1. Introduction
Dendrimers are synthetic polymers with highly branched structures, consisting of multiple branched monomers radiating from a central core. Layers of monomers are attached stepwise during synthesis, with the number of branch points defining the generation of a dendrimer [1]. Different kinds of experiments have proved that these polymers with well-defined dimensional structures and topological architectures have an array of applications in medicine [2]. Nowadays, dendrimers are currently attracting the interest of a great number of scientists because of their unusual physical and chemical properties and their wide range of potential applications in different fields, such as physics, biology, chemistry, engineering, and medicine [3]. A topological index, sometimes known as a graph theoretic index, is a numerical invariant of a chemical graph. Topological indices are the mathematical measures associated with molecular graph structures that correlate a chemical structure with various physical properties, biological activities or chemical reactivities. A topological index is an invariant of a graph, ; that is, if denotes a topological index of graph , and if is another graph such that , then . In chemistry, biochemistry and nanotechnology, distance-based topological indices of graphs are useful in isomer discrimination, structure–property relationships and structure–activity relationships.
2. Definitions and Notations
Let G be a connected and simple molecular graph with vertex set, , and edge set, . The vertices of G correspond to atoms, and an edge between two vertices corresponds to the chemical bond between these vertices. In graph G, two vertices, u and v, are adjacent, if and only if, they are the end vertices of an edge, , and we write or . For a vertex, u, the set of neighbor vertices is denoted by and is defined as . The degree of vertex is denoted by and is defined as . Let denote the sum of the degrees of all neighbors of vertex u, that is . A -path on n vertices is defined as a graph with vertex set, , and edge set, . The distance, , between two vertices, , is defined as the length of the shortest -path in G. For a given vertex, , the eccentricity, , is defined as the largest distance between v and any other vertex, u in G. In 1947, Harold Wiener published a paper entitled “Structural Determination of Paraffin Boiling Points” [4]. In this work, the quantity, , eventually named the Wiener index or Wiener number, was introduced for the first time, and he showed that there are excellent correlations between and a variety of physico-chemical properties of organic compounds. Another distance-based topological index of the graph G is the eccentric-connectivity index, , which is defined as [5]
Different applications and mathematical properties of this index were discussed in [6,7,8,9]. For a graph, G, the eccentric-connectivity polynomial in variable y is defined as [10]
The total eccentricity index of a graph, G, is expressed as follows:
The total eccentric-connectivity polynomial in variable y of a graph, G, is defined as [10]
The first Zagreb index of a graph, G, in terms of eccentricity was given by Ghorbani and Hosseinzadeh [11], as follows:
Gupta and his co-authors [12] introduced the augmented eccentric-connectivity index of a graph, G, and it is defined as
where denotes the product of degrees of all neighbors of vertex u. Various properties of this index have been studied in [13,14]. For a graph, G, the modified versions of the eccentric-connectivity index and its polynomial are defined as follows
Several mathematical and chemical properties of the modified eccentric-connectivity index and its polynomial were studied in [10,15]. Some major types of topological indices of graphs are degree-based, distance-based, and counting-related. Some degree-based topological indices have been computed for some classes of dendrimers, see for instance [16,17,18]. For a study of distance-based topological indices, see [19,20,21]. In this paper, we compute several distance-based indices, namely, the eccentric-connectivity index, the total eccentric-connectivity index, and the modified eccentric-connectivity index for the phosphorus-containing dendrimer Cyclotriphosphazene [22]. We also compute the corresponding polynomials of these indices for the same dendrimer. We also compute the first Zagreb eccentricity index and the augmented eccentric-connectivity index for the said dendrimer.
3. The Eccentricity-Based Indices and Polynomials for the Molecular Graph
Let the molecular graph of this dendrimer be , where the generation stage of is represented by n. The first and second generations are shown in Figure 1 and Figure 2 respectively.
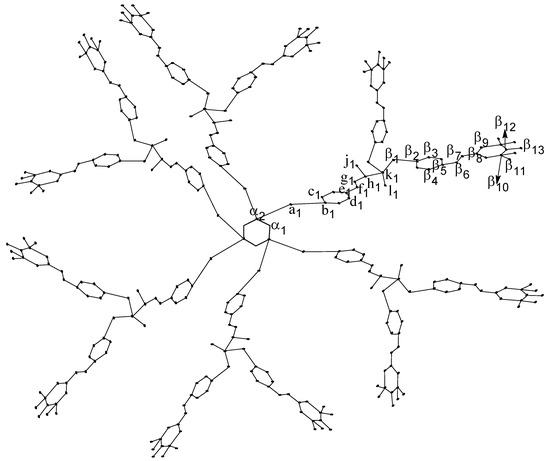
Figure 1.
First generation.
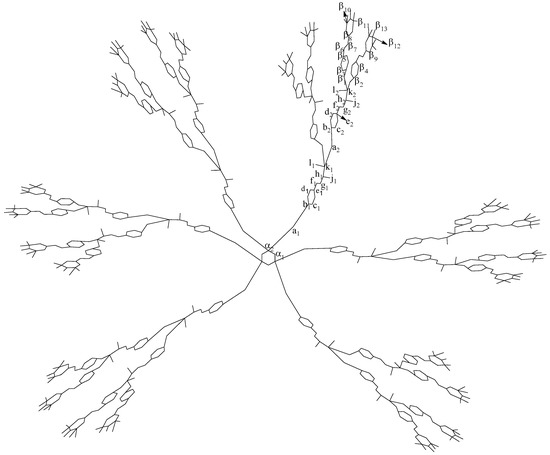
Figure 2.
Second generation.
The size and order of graph are and , respectively. To compute the eccentricity-based indices and polynomials of , it is enough to compute the required information for a set of representatives of . We will compute the required information by using computational arguments. We make three sets of representatives of , say and where , as shown in Figure 1 and Figure 2. The degree, , , and eccentricity for each u for the sets A, B, and C are shown in Table 1 and Table 2. For simplicity, we assume throughout the paper. By using Table 1 and Table 2, we calculate the different eccentricity-based indices and their corresponding polynomials. In the following theorem, we determine the eccentric-connectivity index of .

Table 1.
Sets A and B with their degrees, , , eccentricities, and frequencies.

Table 2.
Set C with degrees, , , eccentricities, and frequencies.
Theorem 1.
For graph , the eccentric-connectivity index is given by
Proof.
By putting the values of Table 1 and Table 2 into Equation (1), the eccentric-connectivity index of can be written as follows:
After some calculations, we get
which completes the theorem. ☐
When the degrees of vertices are not taken into account, then by using the values of Table 1 and Table 2 in (3), we have the following result.
Corollary 1.
For graph , the total eccentric-connectivity index is given by
In the next theorem, the eccentric-connectivity polynomial for the molecular graph is derived.
Theorem 2.
For graph , the eccentric-connectivity polynomial is given by
Proof.
After some calculations, we get the required result. ☐
Corollary 2.
For graph , the total eccentric-connectivity polynomial is given by
In the next theorem, we compute the closed formula for the first Zagreb eccentricity index.
Theorem 3.
For graph , the first Zagreb eccentricity index is given by
Proof.
By using the values of Table 1 and Table 2 in (5), we compute the first Zagreb eccentricity index of as follows:
After some calculations, we obtain
which finishes the theorem. ☐
We determine the augmented eccentric-connectivity index in the next theorem.
Theorem 4.
For graph , the augmented eccentric-connectivity index is given by
Proof.
By using the values of Table 1 and Table 2 in (6), we compute the augumented eccentric-connectivity index of in the following way:
After some calculations, we obtain the required result. ☐
Now, we compute the closed formula for the modified eccentric-connectivity index.
Theorem 5.
For graph , the modified eccentric-connectivity index is given by
Proof.
By using the values of Table 1 and Table 2 in (7), we compute the modified eccentric-connectivity index of in the following way:
After some calculations, we obtain
which completes the proof. ☐
Finally, we compute the closed formula for the modified eccentric-connectivity polynomial.
Theorem 6.
For graph , the modified eccentric-connectivity polynomial is given by
4. Conclusions
In this paper we discussed the theoretical topics in molecular science and computed the eccentric topological indices for a class of phosphorus-containing dendrimers in regard to their molecular structure analysis, distance computing and mathematical derivation. Phosphorus-containing dendrimers have various applications in nanomedicine and materials science; therefore, these theoretical results could have applications in medical science.
Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was supported by Higher Education Commission Pakistan.
Conflicts of Interest
The authors declare no conflict of interest. We are thankful to both reviewers and editor for positive suggestions that improve the quality of this paper.
References
- Adronov, A.; Frechet, J.M.J. Light-harvesting dendrimers. Chem. Commun. 2000, 33, 1701–1710. [Google Scholar] [CrossRef]
- Naka, K.; Tanaka, Y.; Chujo, Y. Effect of anionic starburst dendrimers on the crystallization of CaCO3 in aqueous solution, Size control of spherical vaterite particles. Langmuir 2002, 18, 3655–3658. [Google Scholar] [CrossRef]
- Suresh, R.; Singh, C.; Rewar, P. Dendrimers as carriers and its application in therapy. Int. J. Anal. Pharm. Biomed. Sci. 2015, 4, 15–23. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Goswami, R.; Madan, A.K. Eccentric-connectivity index: A novel highly discriminating topological descriptor for structure–property and structure–activity studies. J. Chem. Inf. Comput. Sci. 1997, 37, 273–282. [Google Scholar] [CrossRef]
- Dureja, H.; Madan, A.K. Topochemical models for prediction of cyclin-dependent kinase 2 inhibitory activity of indole-2-ones. J. Mol. Model. 2005, 11, 525–531. [Google Scholar] [CrossRef] [PubMed]
- Ilic, A.; Gutman, I. Eccentric-connectivity index of chemical trees. MATCH Commun. Math. Comput. Chem. 2011, 65, 731–744. [Google Scholar]
- Kumar, V.; Madan, A.K. Application of graph theory: Prediction of cytosolic phospholipase A(2) inhibitory activity of propan-2-ones. J. Math. Chem. 2006, 39, 511–521. [Google Scholar] [CrossRef]
- Zhou, B. On eccentric-connectivity index. MATCH Commun. Math. Comput. Chem. 2010, 63, 181–198. [Google Scholar]
- Ashrafi, A.R.; Ghorbani, M.; Hossein-Zadeh, M.A. The eccentric-connectivity polynomial of some graph operations. Serdica J. Comput. 2011, 5, 101–116. [Google Scholar]
- Ghorbani, M.; Hosseinzadeh, M.A. A new version of Zagreb indices. Filomat 2012, 26, 93–100. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, M.; Madan, A. K Connective eccentricity index: A novel topological descriptor for predicting biological activity. J. Mol. Graph. Model. 2000, 18, 18–25. [Google Scholar] [CrossRef]
- De, N. Relationship between augmented eccentric-connectivity index and some other graph invariants. Int. J. Adv. Math. 2013, 1, 26–32. [Google Scholar] [CrossRef]
- Doślić, T.; Saheli, M. Augmented eccentric-connectivity index. Miskolc Math. Notes 2011, 12, 149–157. [Google Scholar]
- Alaeiyan, M.; Asadpour, J.; Mojarad, R. A numerical method for MEC polynomial and MEC index of one-pentagonal carbon nanocones. Fuller. Nanotub. Carbon Nanostruct. 2013, 21, 825–835. [Google Scholar] [CrossRef]
- Aslam, A.; Jamil, M.K.; Gao, W.; Nazeer, W. Topological aspects of some dendrimer structures. Nanotechnol. Rev. 2018, 7, 123–129. [Google Scholar] [CrossRef]
- Aslam, A.; Bashir, Y.; Ahmad, S.; Gao, W. On Topological Indices of Certain Dendrimer Structures. Z. Naturforschung A 2017, 72, 559–566. [Google Scholar] [CrossRef]
- Bashir, Y.; Aslam, A.; Kamran, M.; Qureshi, M.I.; Jahangir, A.; Rafiq, M.; Bibi, N.; Muhammad, N. On forgotten topological indices of some dendrimers structure. Molecules 2017, 22, 867. [Google Scholar] [CrossRef] [PubMed]
- Soleimania, N.; Bahnamirib, S.B.; Nikmehr, M.J. Study of dendrimers by topological indices. ACTA CHEMICA IASI 2017, 25, 145–162. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, B.; Gao, W. Distance indices calculating for two classes of dendrimer. Geol. Ecol. Landsc. 2017, 1, 133–142. [Google Scholar] [CrossRef]
- Yang, J.; Xia, F. The eccentric connectivity index of dendrimers. Int. J. Contemp. Math. Sci. 2010, 5, 2231–2236. [Google Scholar]
- Badetti, E.; Lloveras, V.; Muñoz-Gómez, J.L.; Sebastián, R.M.; Camimade, A.M.; Majoral, J.P.; Veciana, J.; Vidal-Gancedo, J. Radical dendrimers: A family of five generations of phosphorus dendrimers functionalized with TEMPO radicals. Macromolecules 2014, 47, 7717–7724. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).