A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making
Abstract
1. Introduction
- (1)
- The evaluation of surgical treatments involves several criteria including subjective and objective criteria. Some scholars have used several objective criteria to evaluate surgical treatments quantitatively [6,11,12]. Subjective criteria such as severity of the side effects and severity of the complications were utilized in Chenabc’s study [9]. Thus, the subjective criteria combined with objective criteria are applied in the index system of the proposed model.
- (2)
- With regard to the partial use of information, it is appropriate to apply fuzzy logic to describe evaluation information regarding surgical treatments. The evaluation information from hospital cases mainly involves crisp numbers and interval numbers. Zhang et al. [13] presented that a neutrosophic set is an effective tool for reflecting the fuzziness in text evaluation because the evaluation information from patients is text information that represents sentiment values, and every sentiment value has not only a certain degree of truth, but also a falsity degree and an indeterminacy degree [14]. So, it needs to be transformed into neutrosophic numbers with positive, medium, and passive values. For example, when asked to assess whether medical equipment would be “good”, from the sentiment value of a patient we may deduce that the membership degree of truth is 0.6, the membership degree of indeterminacy is 0.2, and the membership degree of falsity is 0.2. Pang et al. [15] stated that probabilistic linguistic term sets (PLTS) are more convenient for the DMs to provide their preference as they may have hesitancy among several possible linguistic terms when expressing their evaluation information, so the PLTS need to be applied to express experts’ linguistic terms more accurately. For example, when asked to assess whether a surgical treatment would be appropriate for a particular patient based on the patient’s conditions, an expert may deduce that the probability of “high” is 0.7, the probability of “medium high” is 0.2, and the probability of “medium” is 0.1. Therefore, evaluation information, including crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels, needs to be considered in the selection model.
- (3)
- To deal with the priority order of surgical treatments based on heterogeneous MCGDM, a systematic approach need to be used in the proposed model. Shih et al. [16] hold that TOPSIS is a practical and useful technique for the ranking and selection of a number of externally determined alternatives through distance measures, and it has been connected to multiple-criteria decision-making (MCDM) [17]. Lourenzutti et al. [18] and Li et al. [19] presented heterogeneous TOPSIS for multicriteria group decision-making. Thus, the TOPSIS method is applied in the proposed model to solve the surgical treatment selection.
2. Literature Review
3. Preliminaries
3.1. Interval Numbers
3.2. Neutrosophic Set Theory
3.3. Probabilistic Linguistic Term Sets and Their Basic Concepts
- (1)
- If, then by Equation (3), we can compute, i = 1, 2.
- (2)
- If, then we add some elements to the one with the smaller number of elements according to Definition 13.
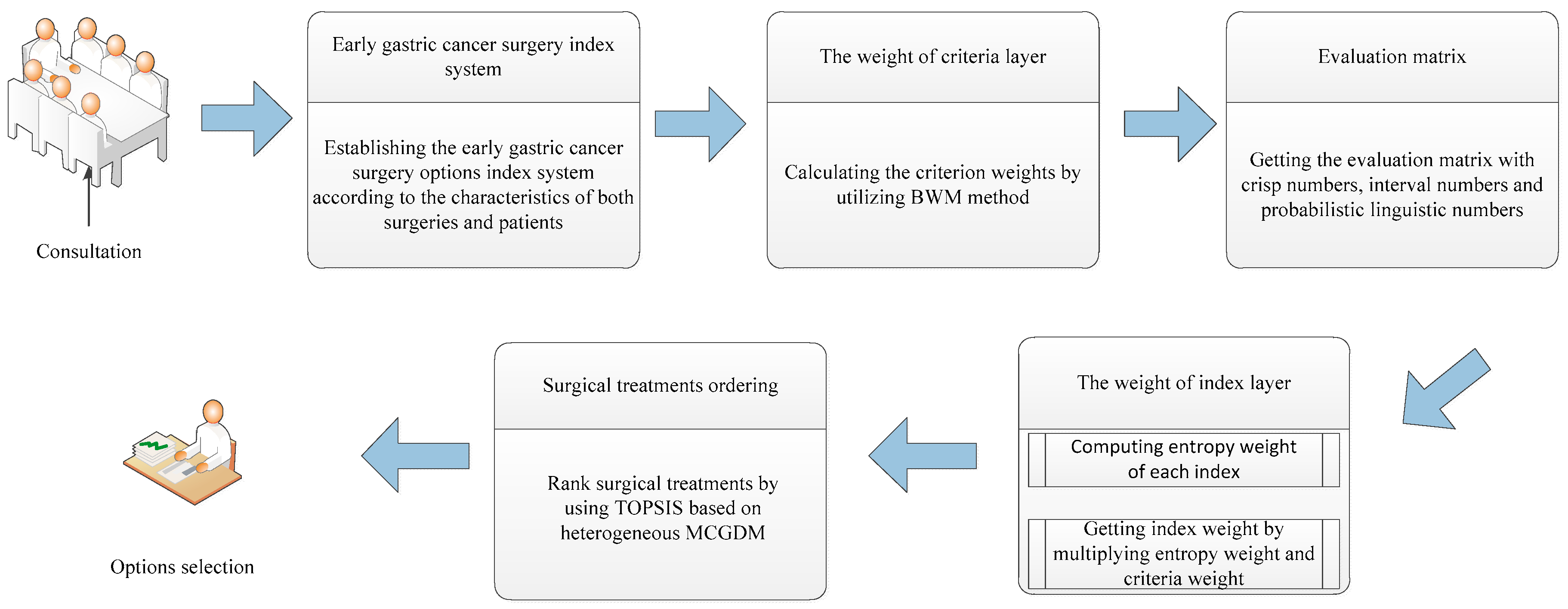
4. The Proposed Selection Model of Surgical Treatment for Early Gastric Cancer
4.1. The Establishment of the Early Gastric Cancer Surgery Index System
4.2. The Estimation of Criteria Weights with BWM
- Step 1.
- Determine a set of decision criteria.In this step, we consider the criteria that should be used to arrive at a decision.
- Step 2.
- Determine the best (e.g., most desirable, most important) and the worst (e.g., least desirable, least important) criterion.
- Step 3.
- Determine the preference of the best criterion over all the other criteria, using a number between 1 and 9. The resulting best-to-others vector would be where indicates the preference of the best criterion B over criterion j. It is clear that = 1.
- Step 4.
- Determine the preference of all the criteria over the worst criterion, using a number between 1 and 9. The resulting others-to-worst vector would be: where indicates the preference of the criterion j over the worst criterion W. It is clear that = 1.
- Step 5.
- Find the optimal weights .
4.3. The Evaluation Matrix of Early Gastric Cancer Surgery
4.4. The Calculation of Index Weight
4.5. TOPSIS and Its Application in Heterogeneous MCGDM
- Step 1.
- Define and normalize the decision matrix .
- Step 2.
- Aggregate the weights to the decision matrix by making .
- Step 3.
- Define the positive ideal solution (PIS), , and the negative ideal solution (NIS), , for each criterion. Usually, and for benefit criteria, and and for cost criteria.
- Step 4.
- Calculate the separation measures for each alternative.
- Step 5.
- Calculate the closeness coefficients to the ideal solution for each alternative.
- Step 6.
- Rank the alternatives according to . The bigger is, the better alternative will be.
- Step 1.
- Normalize evaluation matrix R [18].
- Step 2.
- Construct the positive ideal solution (PIS) and the negative ideal solution (NIS) for experts.
- Step 3.
- Step 4.
- Calculate relative closeness degree of surgical treatments to the PIS for experts.
- Step 5.
- Compute the weights of experts.
- Step 6.
- Compute relative closeness degrees of surgical treatments with respect to the PIS for the group.
- Step 7.
- Rank the surgical treatments by using .
5. Empirical Study
5.1. Early Gastric Cancer Surgery Criteria Weight
5.2. Evaluation Matrix
5.3. Weight of Gastric Cancer Surgery Index
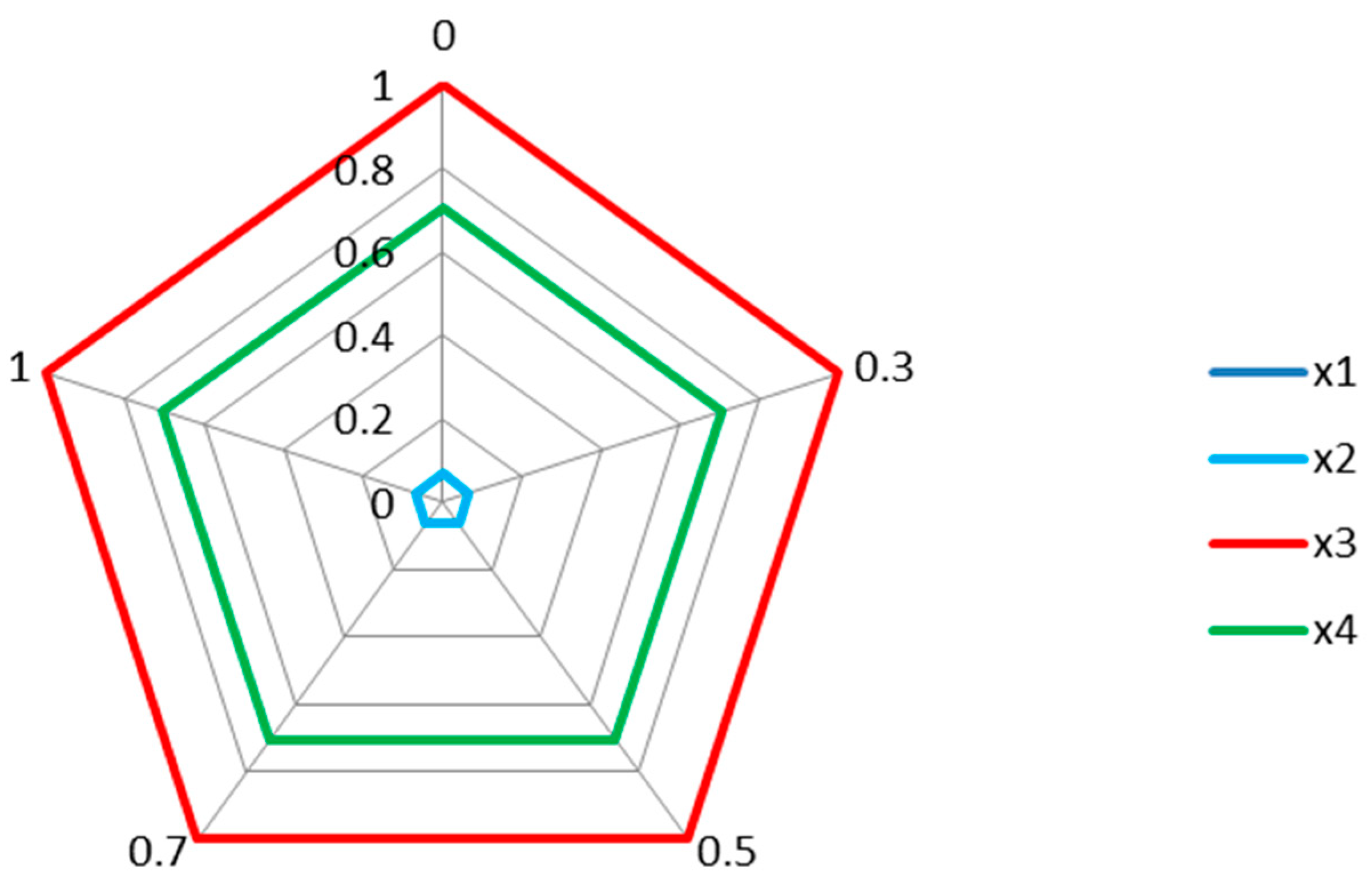
5.4. Selecting Result of Surgical Treatments
5.5. Sensitivity Analysis
5.6. Comparison Analysis
- (1)
- The proposed model considers both subjective and objective criteria comprehensively in the index system for early gastric cancer, which combines fuzzy theory with quantitative data analysis. This enables the surgical treatment selection to be solved more realistically.
- (2)
- The evaluation information is evaluated from medical records, patient’s sentiment, and experts based on the patient’s conditions, the surgery, and the hospital’s medical status, etc., including crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic term sets; this makes the surgical treatment selection more accurate and reliable.
- (3)
- With the proposed model, the prioritization of alternative surgical treatment methods is determined by using TOPSIS, which is more flexible and simple in solving MGCDM problem [18]. Thus, the proposed selection model of surgical treatments for early gastric cancer patients can provide the most appropriate surgical treatment reliably.
6. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kamangar, F.; Dores, G.M.; Anderson, W.F. Patterns of cancer incidence, mortality, and prevalence across five continents: Defining priorities to reduce cancer disparities in different geographic regions of the world. J. Clin. Oncol. 2006, 24, 2137–2150. [Google Scholar] [CrossRef] [PubMed]
- Torre, L.A.; Bray, F.; Siegel, R.L.; Ferlay, J.; Lortettieulent, J.; Jemal, A. Global cancer statistics, 2012. CA Cancer J. Clin. 2015, 65, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, S.; Tada, M.; Kawai, K. Early gastric cancer: Its surveillance and natural course. Endoscopy 1995, 27, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.Y. The effect of patient’s asymmetric information problem on elderly use of medical care. Appl. Econ. 2007, 39, 2133–2142. [Google Scholar] [CrossRef]
- Wu, T.H.; Chen, C.H.; Mao, N.; Lu, S.T. Fishmeal supplier evaluation and selection for aquaculture enterprise sustainability with a fuzzy MCDM approach. Symmetry 2017, 9, 286. [Google Scholar] [CrossRef]
- Pisanu, A.; Montisci, A.; Piu, S.; Uccheddu, A. Curative surgery for gastric cancer in the elderly: Treatment decisions, surgical morbidity, mortality, prognosis and quality of life. Tumori 2007, 93, 478–484. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Choi, I.J.; Kim, C.G.; Cho, S.J.; Kook, M.C.; Ryu, K.W.; Kim, Y.W. Therapeutic decision-making using endoscopic ultrasonography in endoscopic treatment of early gastric cancer. Gut Liver 2016, 10, 42–50. [Google Scholar] [CrossRef] [PubMed]
- Noh, S.H.; Hyung, W.J.; Cheong, J.H. Minimally invasive treatment for gastric cancer: Approaches and selection process. J. Surg. Oncol. 2005, 90, 188–193. [Google Scholar] [CrossRef] [PubMed]
- Chenabc, T.Y. The extended QUALIFLEX method for multiple criteria decision analysis based on interval type-2 fuzzy sets and applications to medical decision making. Eur. J. Oper. Res. 2013, 226, 615–625. [Google Scholar]
- Ji, P.; Zhang, H.; Wang, J. Fuzzy decision-making framework for treatment selection based on the combined QUALIFLEX–TODIM method. Int. J. Syst. Sci. 2017, 48, 3072–3086. [Google Scholar] [CrossRef]
- Kim, S.; Lee, M.; Kim, S.W.; Lee, B.S.; Nam, E.J.; Kim, Y.T. Feasibility and surgical outcomes of laparoscopic metastasectomy in the treatment of ovarian metastases from gastric cancer. J. Minim. Invasive Gynecol. 2013, 21, 1306–1311. [Google Scholar] [CrossRef]
- Hu, Y.F.; Deng, Z.W.; Liu, H.; Mou, T.Y.; Chen, T.; Lu, X.; Wang, D.; Yu, J.; Li, G.-X. Staging laparoscopy improves treatment decision-making for advanced gastric cancer. World J. Gastroenterol. 2016, 22, 1859–1868. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-Y.; Ji, P.; Wang, J.-Q.; Chen, X.-H. A novel decision support model for satisfactory restaurants utilizing social information: A case study of TripAdvisor.com. Tour. Manag. 2017, 59, 281–297. [Google Scholar] [CrossRef]
- Rivieccio, U. Neutrosophic logics: Prospects and problems. Fuzzy Sets Syst. 2008, 159, 1860–1868. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z. Probabilistic Linguistic Term Sets in Multi-Attribute Group Decision Making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Shih, H.S.; Shyur, H.J.; Lee, E.S. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Afshar, A.; Mariño, M.A.; Saadatpour, M.; Afshar, A. Fuzzy TOPSIS multi-criteria decision analysis applied to Karun Reservoirs System. Water Resour. Manag. 2011, 25, 545–563. [Google Scholar] [CrossRef]
- Lourenzutti, R.; Krohling, R.A. A generalized TOPSIS method for group decision making with heterogeneous information in a dynamic environment. Inf. Sci. 2016, 330, 1–18. [Google Scholar] [CrossRef]
- Li, D.-F.; Huang, Z.-G.; Chen, G.-H. A systematic approach to heterogeneous multiattribute group decision making. Comput. Ind. Eng. 2010, 59, 561–572. [Google Scholar] [CrossRef]
- Ma, Y.X.; Wang, J.Q.; Wang, J.; Wu, X.H. An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options. Neural Comput. Appl. 2017, 28, 2745–2765. [Google Scholar] [CrossRef]
- Hu, J.; Yang, Y.; Chen, X. A novel TODIM method-based three-way decision model for medical treatment selection. Int. J. Fuzzy Syst. 2018, 20, 1240–1255. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.-Q.; Tian, Z.-P.; Zhao, D.-Y. A multihesitant fuzzy linguistic multicriteria decision-making approach for logistics outsourcing with incomplete weight information. Int. Trans. Oper. Res. 2018, 25, 831–856. [Google Scholar] [CrossRef]
- Zhao, X.; Hwang, B.-G.; Gao, Y. A fuzzy synthetic evaluation approach for risk assessment: A case of Singapore’s green projects. J. Clean. Prod. 2016, 115, 203–213. [Google Scholar] [CrossRef]
- Mangla, S.K.; Kumar, P.; Barua, M.K. Risk analysis in green supply chain using fuzzy AHP approach: A case study. Resour. Conserv. Recycl. 2015, 104, 375–390. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- You, X.; Chen, T.; Yang, Q. Approach to multi-criteria group decision-making problems based on the best-worst-method and ELECTRE method. Symmetry 2016, 8, 95. [Google Scholar] [CrossRef]
- Tian, Z.-P.; Wang, J.-Q.; Zhang, H.-Y. An integrated approach for failure mode and effects analysis based on fuzzy best-worst, relative entropy and VIKOR methods. Appl. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Ali, M.; Minh, N.V.; Le, H.S. A neutrosophic recommender system for medical diagnosis based on algebraic neutrosophic measures. Appl. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Zhai, Y.; Xu, Z.; Liao, H. Probabilistic linguistic vector-term set and its application in group decision making with multi-granular linguistic information. Appl. Soft Comput. 2016, 49, 801–816. [Google Scholar] [CrossRef]
- Tsaur, R.C. Decision risk analysis for an interval TOPSIS method. Appl. Math. Comput. 2011, 218, 4295–4304. [Google Scholar] [CrossRef]
- Liu, H.-W. Ranking fuzzy numbers based on a distance measure. J. Shandong Uuiv. 2004, 39, 30–36. [Google Scholar]
- Dymova, L.; Sevastjanov, P.; Tikhonenko, A. A direct interval extension of TOPSIS method. Expert Syst. Appl. 2013, 40, 4841–4847. [Google Scholar] [CrossRef]
- Wang, H.; Smarandache, F.; Zhang, Y.-Q.; Sunderraman, R. Interval neutrosophic sets and logic: Theory and applications in computing. Comput. Sci. 2005, 65, 87. [Google Scholar]
- Wu, X.-H.; Wang, J.-Q.; Peng, J.J.; Qian, J. A novel group decision-making method with probability hesitant interval neutrosphic set and its application in middle level manager’s selection. Int. J. Uncertain. Quantif. 2018, 8, 291–319. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistruct. 2012, 4, 410–413. [Google Scholar]
- Majumdar, P.; Samanta, S. On similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar]
- Huang, H.L. New distance measure of single-valued neutrosophic sets and its application. Int. J. Intell. Syst. 2016, 31, 1021–1032. [Google Scholar] [CrossRef]
- Tan, R.; Zhang, W.; Chen, L. Study on emergency group decision making method based on VIKOR with single valued neutrosophic sets. J. Saf. Sci. Technol. 2017, 13, 79–84. [Google Scholar]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Wei, G.-W. Some generalized aggregating operators with linguistic information and their application to multiple attribute group decision making. Comput. Ind. Eng. 2011, 61, 32–38. [Google Scholar] [CrossRef]
- Nie, R.-X.; Tian, Z.-P.; Wang, X.-K.; Wang, J.-Q.; Wang, T.-L. Risk evaluation by FMEA of supercritical water gasification system using multi-granular linguistic distribution assessment. Knowl. Based Syst. 2018. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A sequential selection process in group decision making with a linguistic assessment approach. Inf. Sci. 1995, 85, 223–239. [Google Scholar] [CrossRef]
- Liu, P.; You, X. Probabilistic linguistic TODIM approach for multiple attribute decision-making. Granul. Comput. 2017, 2, 333–342. [Google Scholar] [CrossRef]
- Gao, J.; Yi, R. Cloud generalized power ordered weighted average operator and its application to linguistic group decision-making. Symmetry 2017, 9, 156. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Feng, X.Q. Method for interval multi-attribute decision making based on entropy. Comput. Eng. Appl. 2010, 46, 236–238. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Zhang, H.Y.; Chen, X.H. An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets. Appl. Soft Comput. 2014, 25, 236–246. [Google Scholar] [CrossRef]
- Wei, H. A Study on multi-index evaluation model based on synthetic weighting for the problem of technology innovation capability of enterprises. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007; pp. 5823–5826. [Google Scholar]
- Hwang, C.L.; Yoon, K.P. Multiple Attributes Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Bortolussi, L.; Sgarro, A. Hamming-Like Distances for Ill-Defined Strings in Linguistic; University of Trieste: Trieste, Italy, 2007; pp. 105–118. [Google Scholar]
- Li, D.F. Compromise ratio method for fuzzy multi-attribute group decision making. Appl. Soft Comput. 2007, 7, 807–817. [Google Scholar] [CrossRef]
- Chen, S.J.; Krelle, W. Fuzzy Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1992. [Google Scholar]
- Zhou, J.; Su, W.; Baležentis, T.; Streimikiene, D. Multiple criteria group decision-making considering symmetry with regards to the positive and negative ideal solutions via the pythagorean normal cloud model for application to economic decisions. Symmetry 2018, 10, 140. [Google Scholar] [CrossRef]
- Lourenzutti, R.; Krohling, R.A. TODIM based method to process heterogeneous information. Procedia Comput. Sci. 2015, 55, 318–327. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L.; Gao, J.; Chu, H.; Xu, C. An extended VIKOR-based approach for pumped hydro energy storage plant site selection with heterogeneous information. Information 2017, 8, 106. [Google Scholar] [CrossRef]

| Evaluation | Very Bad | Bad | Slightly Bad | OK | Slightly Good | Good | Very Good |
|---|---|---|---|---|---|---|---|
| Sentiment degree | −0.95459 | −0.75 | −0.10607 | 0 | 0.106066 | 0.75 | 0.954594 |
| Criteria | Indices | Definition | Index Type |
|---|---|---|---|
| Tumor characteristics (A1) | Suitability of tumor size (a11) | The degree of suitability that tumor size is suitable for this surgery | Benefit |
| Suitability of differentiated degree (a12) | The degree of suitability that tumor differentiation is suitable for this surgery | Benefit | |
| Suitability of depth of invasion (a13) | The degree of suitability that the depth of invasion is suitable for this surgery | Benefit | |
| Surgical situation (A2) | Complexity of surgery (a21) | The more complicated the operation is, the higher the risk becomes | Cost |
| Blood loss (a22) | The amount of bleeding in the surgery | Cost | |
| Survival rate (a23) | The survival probability in surgery | Benefit | |
| Operating time (a24) | The time spent in surgery | Cost | |
| Oncological clearance (a25) | The condition of oncological clearance | Benefit | |
| Operative wound (a26) | The wound size of surgery | Cost | |
| Surgical outcomes (A3) | Wound infection (a31) | Wound infections after surgery | Cost |
| Probability of a cure (a32) | The probability of curing early gastric cancer | Benefit | |
| Severity of the complications (a33) | The possibility of complications like wound dehiscence, fever | Cost | |
| Severity of the side effects (a34) | The possibility of side effects after surgery | Cost | |
| Probability of a recurrence (a35) | The probability of a recurrence because of unsuccessful surgery | Cost | |
| Hospital stays (a36) | Length of hospital stay | Cost | |
| Recovery time (a37) | The postoperative recovery time | Cost | |
| Degree of dysfunction (a38) | The function of gastric system for patients after the surgery | Cost | |
| Medical technology (A4) | Medical technical level (a41) | The technical force and medical standards in the hospital | Benefit |
| Teamwork Capacity (a42) | The teamwork capacity of medical team | Benefit | |
| Medical resources (a43) | Available medical resources in the hospital | Benefit | |
| Proficiency (a44) | Skill degree of medical professionals | Benefit | |
| Medical equipment (A5) | Advanced equipment (a51) | The performance of medical equipment | Benefit |
| Perfection level (a52) | Complete supporting facilities in medical | Benefit | |
| Disinfecting technical (a53) | The equipment for disinfection and sterilization | Benefit | |
| Emergency facilities (a54) | The perfection of emergency medical facilities | Benefit |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Consistency Index (max ξ) | 0.00 | 0.44 | 1.00 | 1.63 | 2.30 | 3.00 | 3.73 | 4.47 | 5.23 |
| Criteria | A1 | A2 | A3 | A4 | A5 |
|---|---|---|---|---|---|
| Best criterion: A1 | 1 | 3 | 4 | 6 | 8 |
| Criteria | A1 | A2 | A3 | A4 | A5 |
|---|---|---|---|---|---|
| Worst criterion: A5 | 8 | 7 | 6 | 4 | 1 |
| Tumor Characteristics | Tumor Size | Differentiated Degree | Depth of Invasion |
|---|---|---|---|
| Condition | 6.5 × 4.5 × 2 (cm) | Middle differentiation | Invading serosa |
| Indices | Alternatives | |||
|---|---|---|---|---|
| x1 | x2 | x3 | x4 | |
| a22 | [3.28, 5.36] | [2.58, 5.7] | [25, 80] | [80, 180] |
| a23 | 0.978 | 0.993 | 0.959 | 0.949 |
| a24 | [20, 30] | [60, 90] | [270, 302] | [263, 314] |
| a25 | <0.4280, 0, 0> | <0.6036, 0, 0> | <0.3207, 0, 0> | <0.2671, 0, 0> |
| a26 | <0.5621, 0, 0> | <0.8523, 0, 0> | <0.8182, 0, 0> | <0.1597, 0, 0> |
| a35 | 0.0835 | 0.004 | 0.0122 | 0.0135 |
| a36 | [5.8, 8] | [2, 10] | [9.6, 12] | [8.6, 16.2] |
| a37 | [13.12, 17.44] | [16.29, 20.06] | [25.69, 31.39] | [41.33, 47.97] |
| a41 | <0.8112, 0, 0> | <0.6656, 0, 0> | <0.7591, 0, 0> | <0.5927, 0, 0> |
| a42 | <0.8129, 0, 0> | <0.7995, 0, 0> | <0.7397, 0, 0> | <0.7035, 0, 0> |
| a43 | <0.6611, 0, 0> | <0.6784, 0, 0> | <0.7706, 0, 0> | <0.7727, 0, 0> |
| a44 | <0.6469, 0, 0> | <0.6913, 0, 0> | <0.7851, 0, 0> | <0.8134, 0, 0> |
| a51 | <0.7851, 0, 0> | <0.8626, 0, 0> | <0.7914, 0, 0> | <0.6776, 0, 0> |
| a52 | <0.6157, 0, 0> | <0.6873, 0, 0> | <0.7133, 0, 0> | <0.7848, 0, 0> |
| a53 | <0.7648, 0, 0> | <0.7897, 0, 0> | <0.8127, 0, 0> | <0.7876, 0, 0> |
| a54 | <0.7442, 0, 0> | <0.7533, 0, 0> | <0.7194, 0, 0> | <0.8072, 0, 0> |
| Indices | Experts | Alternatives | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x1 | ||
| a11 | e1 | {s2(0.5), s3(0.4)} | {s3(0.4), s4(0.3)} | {s3(0.2), s4(0.3), s5(0.5)} | {s1(0.6), s2(0.4)} |
| e2 | {s2(0.3), s3(0.4)} | {s3(0.4), s4(0.6)} | {s3(0.2), s4(0.3), s5(0.4)} | {s1(0.5), s2(0.3) | |
| e3 | {s2(0.4), s3(0.5)} | {s3(0.3), s4(0.4)} | {s3(0.3), s4(0.3), s5(0.4)} | {s1(0.6), s2(0.2) | |
| a12 | e1 | {s1(0.3), s2(0.4)} | {s1(0.3), s2(0.2)} | {s3(0.2), s4(0.4), s5(0.4)} | {s4(0.4), s5(0.6)} |
| e2 | {s1(0.3), s2(0.4), s3(0.2)} | {s1(0.3), s2(0.4)} | {s4(0.4), s5(0.5)} | {s3(0.2), s4(0.4), s5(0.4)} | |
| e3 | {s1(0.3), s2(0.3), s3(0.2)} | {s1(0.3), s2(0.4), s3(0.1)} | {s4(0.4), s5(0.3), s6(0.2)} | {s3(0.2), s4(0.4), s5(0.3)} | |
| a13 | e1 | {s1(0.3), s2(0.5) } | {s1(0.3), s2(0.7) } | {s4(0.4), s5(0.3), s6(0.3)} | {s4(0.4), s5(0.3), s6(0.2)} |
| e2 | {s1(0.6), s2(0.4) } | {s1(0.5), s2(0.3) } | {s4(0.4), s5(0.6) } | {s4(0.3), s5(0.4), s6(0.3)} | |
| e3 | {s1(0.4), s2(0.2), s3(0.1)} | {s1(0.3), s2(0.6) } | {s5(0.3), s6(0.4)} | { s5(0.5), s6(0.2)} | |
| a21 | e1 | {s2(0.1), s3(0.5), s4(0.3)} | {s2(0.1), s3(0.4), s4(0.2)} | {s2(0.1), s3(0.3), s4(0.4)} | {s2(0.2), s3(0.3), s4(0.3)} |
| e2 | {s2(0.2), s3(0.4), s4(0.3)} | {s4(0.2), s5(0.3), s6(0.1)} | {s3(0.2), s4(0.4), s5(0.1)} | {s4(0.4), s5(0.1)} | |
| e3 | {s4(0.3), s5(0.2)} | {s3(0.4), s4(0.2), s5(0.3)} | {s4(0.6), s5(0.3)} | {s4(0.3), s5(0.2), s6(0.2)} | |
| a31 | e1 | {s0(0.3), s1(0.3), s2(0.1)} | {s0(0.3), s1(0.3), s2(0.2)} | {s1(0.3), s2(0.3), s3(0.3)} | {s1(0.2), s2(0.3), s3(0.3)} |
| e2 | {s2(0.1), s3(0.2), s4(0.2)} | {s2(0.2), s3(0.3), s4(0.1)} | {s2(0.1), s3(0.3), s4(0.3)} | {s3(0.3), s4(0.3), s5(0.3)} | |
| e3 | {s0(0.4), s1(0.3)} | {s0(0.4), s1(0.2)} | {s1(0.3), s2(0.2) } | {s2(0.4), s3(0.3)} | |
| a32 | e1 | {s2(0.1), s3(0.4), s4(0.4)} | {s2(0.1), s3(0.5), s4(0.1)} | {s3(0.1), s4(0.4), s5(0.4)} | {s2(0.2), s3(0.1), s4(0.3)} |
| e2 | {s3(0.2), s4(0.4), s5(0.3)} | {s3(0.5), s4(0.1), s5(0.3)} | {s4(0.4), s5(0.3), s6(0.2)} | {s4(0.2), s5(0.3), s6(0.3)} | |
| e3 | {s3(0.4), s4(0.4), s5(0.2)} | {s3(0.6), s4(0.3) } | {s4(0.5), s5(0.4)} | {s5(0.4), s6(0.3)} | |
| a33 | e1 | {s1(0.5), s2(0.1), s3(0.2)} | {s1(0.5), s2(0.2), s3(0.2)} | {s1(0.2), s2(0.3), s3(0.2)} | {s1(0.3), s2(0.2), s3(0.1)} |
| e2 | {s2(0.1), s3(0.2), s4(0.1)} | {s1(0.5), s2(0.2)} | {s2(0.4), s3(0.2)} | {s2(0.3), s3(0.2), s4(0.4)} | |
| e3 | {s1(0.6), s2(0.2)} | {s2(0.1), s3(0.2), s4(0.2)} | {s2(0.3), s3(0.2), s4(0.2)} | {s4(0.2), s5(0.4)} | |
| a34 | e1 | {s1(0.3), s2(0.3), s3(0.4)} | {s1(0.5), s2(0.2), s3(0.3)} | {s1(0.4), s2(0.3), s3(0.2)} | {s2(0.2), s3(0.2), s4(0.6)} |
| e2 | {s2(0.3), s3(0.2), s4(0.4)} | {s2(0.4), s3(0.2), s4(0.1)} | {s2(0.1), s3(0.3), s4(0.4)} | {s3(0.3), s4(0.2), s5(0.2)} | |
| e3 | {s3(0.3), s4(0.3)} | {s3(0.3), s4(0.1)} | {s3(0.4), s4(0.2)} | {s3(0.2), s4(0.4)} | |
| a38 | e1 | {s0(0.2), s1(0.3), s2(0.1)} | {s1(0.3), s2(0.3)} | {s1(0.2), s2(0.3), s3(0.3)} | {s1(0.2), s2(0.2), s3(0.4)} |
| e2 | {s2(0.1), s3(0.2), s4(0.3)} | {s0(0.2), s1(0.2), s2(0.2)} | {s2(0.4), s3(0.4)} | {s2(0.2), s3(0.4), s4(0.2} | |
| e3 | {s1(0.4), s2(0.2)} | {s2(0.2), s3(0.2), s4(0.2} | {s3(0.3), s4(0.2), s5(0.2)} | {s2(0.3), s3(0.6)} | |
| Indices | Alternatives | |||
|---|---|---|---|---|
| x1 | x2 | x3 | x4 | |
| a22 | [0.9702, 0.9818] | [0.9683, 0.9857] | [0.5556, 0.8611] | [0, 0.5556] |
| a23 | 0.659090909 | 1 | 0.227272727 | 0 |
| a24 | [0.9045, 0.9363] | [0.7134, 0.8089] | [0.0382, 0.1401] | [0, 0.1624] |
| a25 | <0.4280, 0, 0> | <0.6036, 0, 0> | <0.3207, 0, 0> | <0.2671, 0, 0> |
| a26 | <0.5621, 0, 0> | <0.8523, 0, 0> | <0.8182, 0, 0> | <0.1597, 0, 0> |
| a35 | 0 | 1 | 0.896855346 | 0.880503145 |
| a36 | [0.5062, 0.6420] | [0.3827, 0.8765] | [0.2593, 0.4074] | [0, 0.4691] |
| a37 | [0.6364, 0.7265] | [0.5631, 0.6604] | [0.3456, 0.4645] | [0, 0.1384] |
| a41 | <0.8112, 0, 0> | <0.6656, 0, 0> | <0.7591, 0, 0> | <0.5927, 0, 0> |
| a42 | <0.8129, 0, 0> | <0.7995, 0, 0> | <0.7397, 0, 0> | <0.7035, 0, 0> |
| a43 | <0.6611, 0, 0> | <0.6784, 0, 0> | <0.7706, 0, 0> | <0.7727, 0, 0> |
| a44 | <0.6469, 0, 0> | <0.6913, 0, 0> | <0.7851, 0, 0> | <0.8134, 0, 0> |
| a51 | <0.7851, 0, 0> | <0.8626, 0, 0> | <0.7914, 0, 0> | <0.6776, 0, 0> |
| a52 | <0.6157, 0, 0> | <0.6873, 0, 0> | <0.7133, 0, 0> | <0.7848, 0, 0> |
| a53 | <0.7648, 0, 0> | <0.7897, 0, 0> | <0.8127, 0, 0> | <0.7876, 0, 0> |
| a54 | <0.7442, 0, 0> | <0.7533, 0, 0> | <0.7194, 0, 0> | <0.8072, 0, 0> |
| Indices | Alternatives | |||
|---|---|---|---|---|
| x1 | x2 | x3 | x4 | |
| a11 | {s0.95, s1.57, s0} | {s1.4, s2.13, s0} | {s0.72, s1.24, s2.25} | {s0.66, s0.68, s0} |
| a12 | {s0.38, s0.93, s0.48} | {s0.47, s0.98, s0.13} | {s1.39, s2.02, s1.11} | {s0.95, s2.13, s1.22} |
| a13 | {s0.51, s0.88, s0.14} | {s0.42, s1.16, s0} | {s1.78, s2.64, s0.65} | {s2.18, s1.8, s1.04} |
| a21 | {s0.84, s1.14, s0.44} | {s0.86, s0.88, s0.33} | {s0.91, s0.86, s0.38} | {s1.17, s0.53, s0.25} |
| a31 | {s2.27, s1.83, s0.45} | {s1.92, s1.68, s0.45} | {s1.74, s1.41, s0.63} | {s1.46, s1.25, s0.44} |
| a32 | {s0.69, s1.57, s1.48} | {s1.32, s1.31, s0.74} | {s1.44, s1.89, s1.19} | {s1.50, s1.65, s1.43} |
| a33 | {s2.62, s1.01, s0.42} | {s2.38, s1.08, s0.49} | {s1.94, s1.18, s0.48} | {s1.49, s0.82, s0.47} |
| a34 | {s1.44, s0.95, s0.7} | {s2.34, s0.72, s0.39} | {s1.59, s1.03, s0.55} | {s1.02, s0.84, s0.50} |
| a38 | {s2.00, s1.60, s0.56} | {s1.93, s1.55, s0.68} | {s1.51, s1.19, s0.47} | {s1.19, s1.50, s0.67} |
| Criteria | Weights | Indices | Weights |
|---|---|---|---|
| A1 | 0.5333 | a11 | 0.263315 |
| a12 | 0.319028 | ||
| a13 | 0.417657 | ||
| A2 | 0.1778 | a21 | 0.153238 |
| a22 | 0.023316 | ||
| a23 | 0.270952 | ||
| a24 | 0.06846 | ||
| a25 | 0.194089 | ||
| a26 | 0.289945 | ||
| A3 | 0.1333 | a31 | 0.205559 |
| a32 | 0.228812 | ||
| a33 | 0.172388 | ||
| a34 | 0.108363 | ||
| a35 | 0.088117 | ||
| a36 | 0.003831 | ||
| a37 | 0.007015 | ||
| a38 | 0.185916 | ||
| A4 | 0.0889 | a41 | 0.241684 |
| a42 | 0.26108 | ||
| a43 | 0.246315 | ||
| a44 | 0.250921 | ||
| A5 | 0.0667 | a51 | 0.257649 |
| a52 | 0.231559 | ||
| a53 | 0.260798 | ||
| a54 | 0.249994 |
| Indices | Experts | Alternatives | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||
| a11 | e1 | {s2(0.56), s3(0.44), s2(0)} | {s3(0.57), s4(0.43), s3(0)} | {s3(0.2), s4(0.3), s5(0.5)} | {s1(0.6), s2(0.4), s1(0)} |
| e2 | {s2(0.43), s3(0.57), s2(0)} | {s3(0.4), s4(0.6), s3(0)} | {s3(0.22), s4(0.33), s5(0.45)} | {s1(0.63), s2(0.37), s1(0)} | |
| e3 | {s2(0.44), s3(0.56), s2(0)} | {s3(0.43), s4(0.57), s3(0)} | {s3(0.3), s4(0.3), s5(0.4)} | {s1(0.75), s2(0.25), s1(0)} | |
| a12 | e1 | {s1(0.43), s2(0.57), s1(0)} | {s1(0.6), s2(0.4), s1(0)} | {s3(0.2), s4(0.4), s5(0.4)} | {s4(0.4), s5(0.6), s4(0)} |
| e2 | {s1(0.33), s2(0.45), s3(0.22)} | {s1(0.43), s2(0.57), s1(0)} | {s4(0.44), s5(0.56), s4(0)} | {s3(0.2), s4(0.4), s5(0.4)} | |
| e3 | {s1(0.37), s2(0.37), s3(0.26)} | {s1(0.37), s2(0.5), s3(0.13)} | {s4(0.45), s5(0.33), s6(0.22)} | {s3(0.22), s4(0.45), s5(0.33)} | |
| a13 | e1 | {s1(0.37), s2(0.63), s1(0)} | {s1(0.3), s2(0.7), s1(0)} | {s4(0.4), s5(0.3), s6(0.3)} | {s4(0.45), s5(0.33), s6(0.22)} |
| e2 | {s1(0.6), s2(0.4), s1(0)} | {s1(0.63), s2(0.37), s1(0)} | {s4(0.4), s5(0.6), s4(0)} | {s4(0.3), s5(0.4), s6(0.3)} | |
| e3 | {s1(0.57), s2(0.29), s3(0.14)} | {s1(0.33), s2(0.67), s1(0)} | {s5(0.43), s6(0.57), s5(0)} | {s5(0.71), s6(0.29), s5(0)} | |
| a21 | e1 | {s4(0.11), s3(0.56), s2(0.33)} | {s4(0.14), s3(0.57), s2(0.29)} | {s4(0.13), s3(0.37), s2(0.5)} | {s4(0.26), s3(0.37), s2(0.37)} |
| e2 | {s4(0.22), s3(0.45), s2(0.33)} | {s2(0.33), s1(0.5), s0(0.17)} | {s3(0.29), s2(0.57), s1(0.14)} | {s2(0.8), s1(0.2), s1(0)} | |
| e3 | {s2(0.6), s1(0.4), s1(0)} | {s3(0.45), s2(0.22), s1(0.33)} | {s2(0.67), s1(0.33), s1(0)} | {s2(0.43), s1(0.28), s0(0.29)} | |
| a31 | e1 | {s6(0.43), s5(0.43), s4(0.14)} | {s6(0.37), s5(0.38), s4(0.25)} | {s5(0.33), s4(0.33), s3(0.34)} | {s5(0.22), s4(0.45), s3(0.33)} |
| e2 | {s4(0.2), s3(0.4), s2(0.4)} | {s4(0.33), s3(0.5), s2(0.17)} | {s4(0.14), s3(0.43), s2(0.43)} | {s3(0.33), s2(0.33), s1(0.34)} | |
| e3 | {s6(0.57), s5(0.43), s5(0)} | {s6(0.67), s5(0.33), s5(0)} | {s5(0.6), s4(0.4), s4(0)} | {s4(0.57), s3(0.43), s3(0)} | |
| a32 | e1 | {s2(0.11), s3(0.44), s4(0.45)} | {s2(0.14), s3(0.72), s4(0.14)} | {s3(0.11), s4(0.44), s5(0.45)} | {s2(0.33), s3(0.17), s4(0.5)} |
| e2 | {s3(0.22), s4(0.45), s5(0.33)} | {s3(0.56), s4(0.11), s5(0.33)} | {s4(0.45), s5(0.33), s6(0.22)} | {s4(0.25), s5(0.37), s6(0.38)} | |
| e3 | {s3(0.4), s4(0.4), s5(0.2)} | {s3(0.67), s4(0.33), s3(0)} | {s4(0.55), s5(0.45), s4(0)} | {s5(0.57), s6(0.43), s5(0)} | |
| a33 | e1 | {s5(0.62), s4(0.13), s3(0.25)} | {s5(0.56), s4(0.22), s3(0.22)} | {s5(0.29), s4(0.42), s3(0.29)} | {s5(0.5), s4(0.33), s3(0.17)} |
| e2 | {s4(0.25), s3(0.5), s2(0.25)} | {s5(0.71), s4(0.29), s4(0)} | {s4(0.67), s3(0.33), s3(0)} | {s4(0.33), s3(0.22), s2(0.45)} | |
| e3 | {s5(0.75), s4(0.25), s4(0)} | {s4(0.2), s3(0.4), s2(0.4)} | {s4(0.42), s3(0.29), s2(0.29)} | {s2(0.33), s1(0.47), s1(0)} | |
| a34 | e1 | {s5(0.3), s4(0.3), s3(0.4)} | {s5(0.5), s4(0.2), s3(0.3)} | {s5(0.45), s4(0.33), s3(0.22)} | {s4(0.2), s3(0.2), 2(0.6)} |
| e2 | {s4(0.33), s3(0.22), s2(0.45)} | {s4(0.57), s3(0.29), s2(0.14)} | {s4(0.13), s3(0.37), s2(0.5)} | {s3(0.42), s2(0.29), s1(0.29)} | |
| e3 | {s3(0.5), s2(0.5), s2(0)} | {s3(0.75), s2(0.25), s2(0)} | {s3(0.67), s2(0.33), s2(0)} | {s3(0.33), s2(0.67), s2(0)} | |
| a38 | e1 | {s6(0.33), s5(0.5), s4(0.17)} | {s5(0.5), s4(0.5), s4(0)} | {s5(0.25), s4(0.37), s3(0.38)} | {s5(0.25), s4(0.25), s3(0.5)} |
| e2 | {s4(0.17), s3(0.33), s2(0.5)} | {s6(0.33), s5(0.33), s4(0.34)} | {s4(0.5), s3(0.5), s3(0)} | {s4(0.25), s3(0.5), s2(0.25)} | |
| e3 | {s5(0.67), s4(0.33), s4(0)} | {s4(0.33), s3(0.33), s2(0.34)} | {s3(0.43), s2(0.29), s1(0.28)} | {s4(0.33), s3(0.67), s3(0)} | |
| Different Values of | The Ranking of Surgical Treatments | Ranking Orders | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||
| 0 | 0.067280513 | 1 | 0.704819514 | ||
| 0 | 0.067280513 | 1 | 0.704819514 | ||
| 0 | 0.067280513 | 1 | 0.704819514 | ||
| 0 | 0.067280513 | 1 | 0.704819514 | ||
| 0 | 0.067280513 | 1 | 0.704819514 | ||
| Different Values of | The Ranking of Surgical Treatments | Ranking Orders | |||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | ||
| 0 | 0.069246088 | 1 | 0.703826118 | ||
| 0.131619756 | 0 | 1 | 0.804240841 | ||
| 0 | 0.067280513 | 1 | 0.704819514 | ||
| 0 | 0.531275419 | 1 | 0.213842101 | ||
| 0 | 0.510492538 | 1 | 0.219962121 | ||
| Alternatives | Heterogeneous TODIM | Heterogeneous VIKOR | ||||
|---|---|---|---|---|---|---|
| Ranking | Ranking | |||||
| 0.131573 | 3 | 0.702564564 | 0.222736429 | 1 | 4 | |
| 0.324262 | 2 | 0.62637026 | 0.216910241 | 0.901839 | 3 | |
| 1 | 1 | 0.240544451 | 0.037226276 | 0 | 1 | |
| 0 | 4 | 0.516377929 | 0.138206602 | 0.570677 | 2 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.-P.; He, J.-Q.; Cheng, P.-F.; Wang, J.-Q.; Zhang, H.-Y. A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making. Symmetry 2018, 10, 223. https://doi.org/10.3390/sym10060223
Li D-P, He J-Q, Cheng P-F, Wang J-Q, Zhang H-Y. A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making. Symmetry. 2018; 10(6):223. https://doi.org/10.3390/sym10060223
Chicago/Turabian StyleLi, Dan-Ping, Ji-Qun He, Peng-Fei Cheng, Jian-Qiang Wang, and Hong-Yu Zhang. 2018. "A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making" Symmetry 10, no. 6: 223. https://doi.org/10.3390/sym10060223
APA StyleLi, D.-P., He, J.-Q., Cheng, P.-F., Wang, J.-Q., & Zhang, H.-Y. (2018). A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making. Symmetry, 10(6), 223. https://doi.org/10.3390/sym10060223





