Fuzzy Association Rule Based Froth Surface Behavior Control in Zinc Froth Flotation
Abstract
1. Introduction
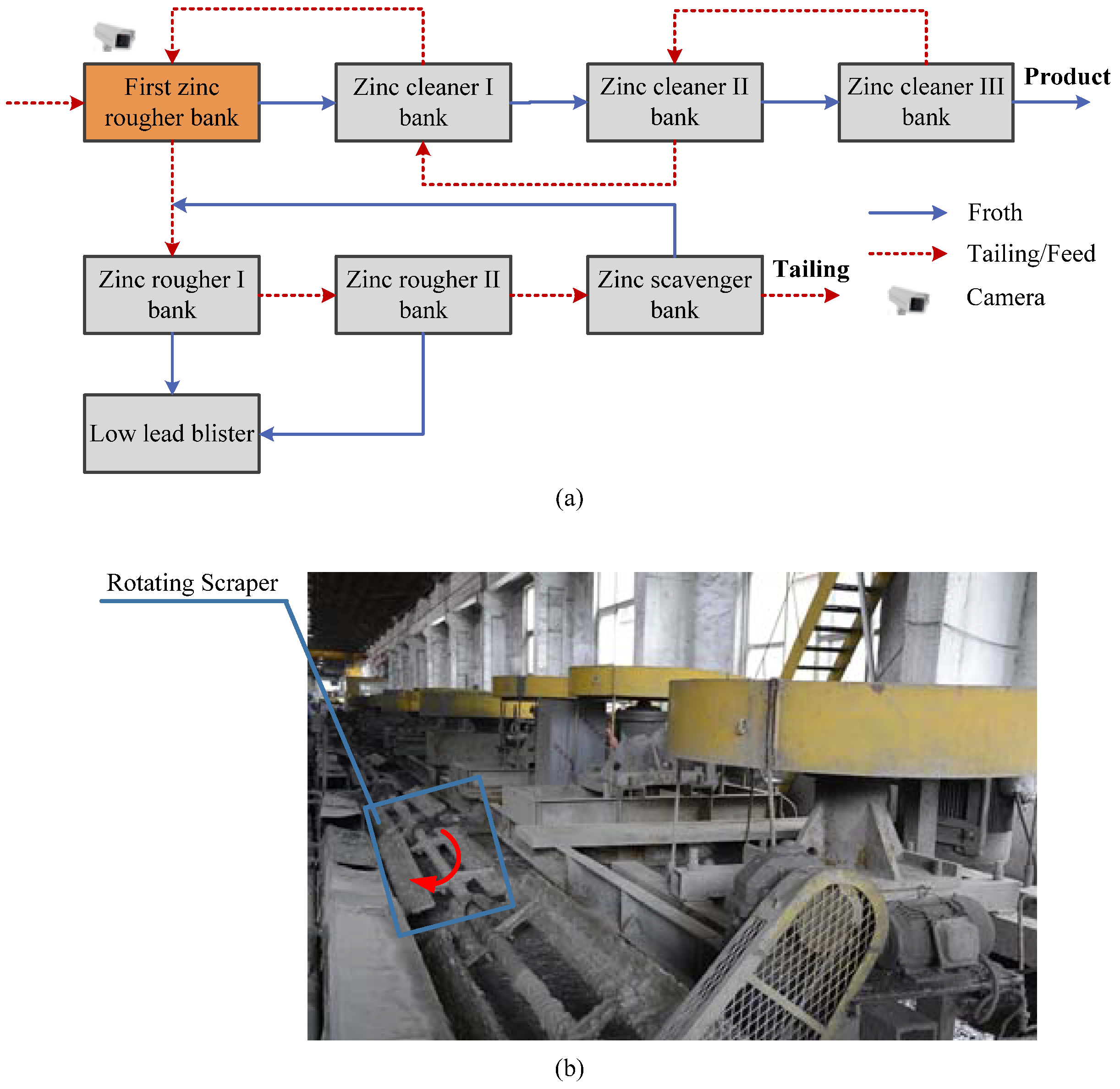
2. Process Description
3. Methods
3.1. Froth Surface Behavior Representation
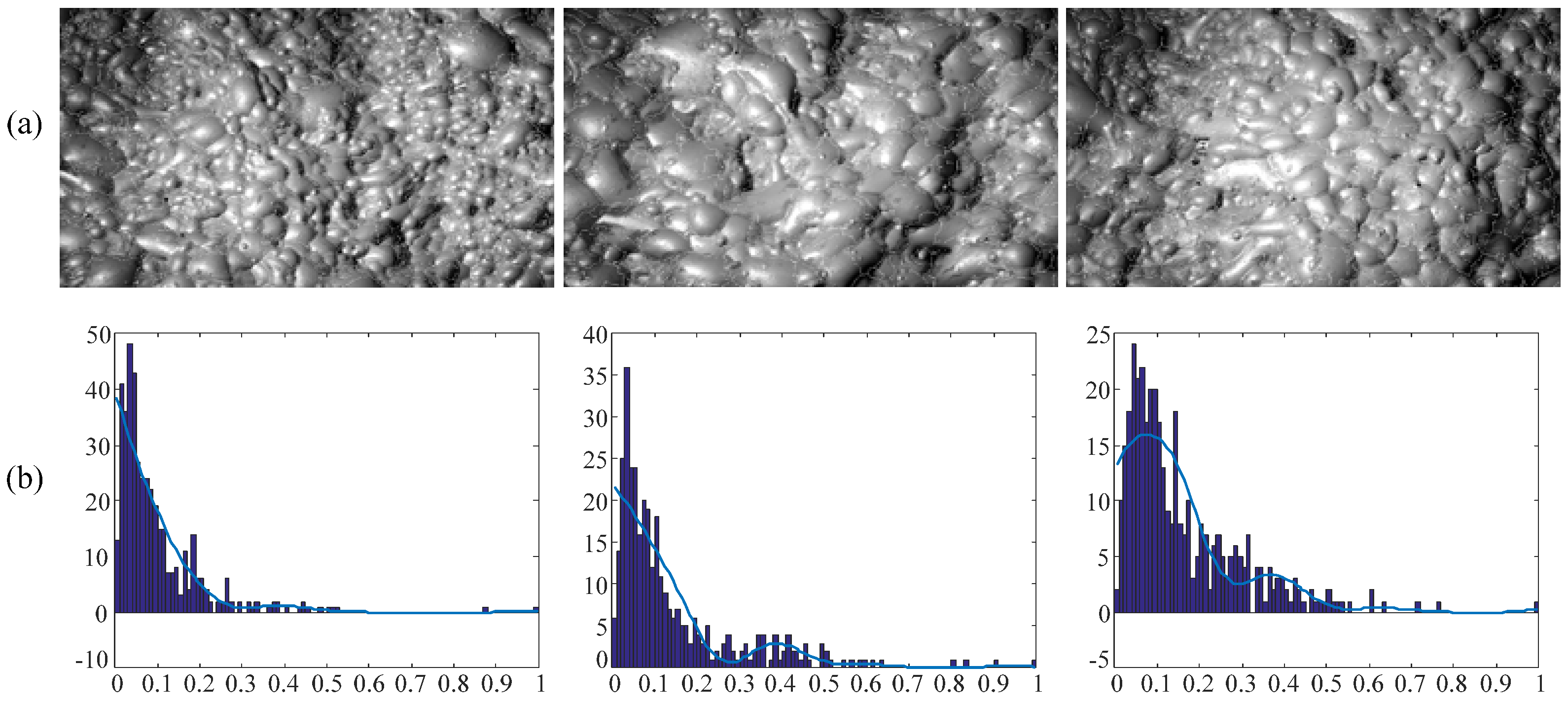
3.1.1. Bubble Size Distribution
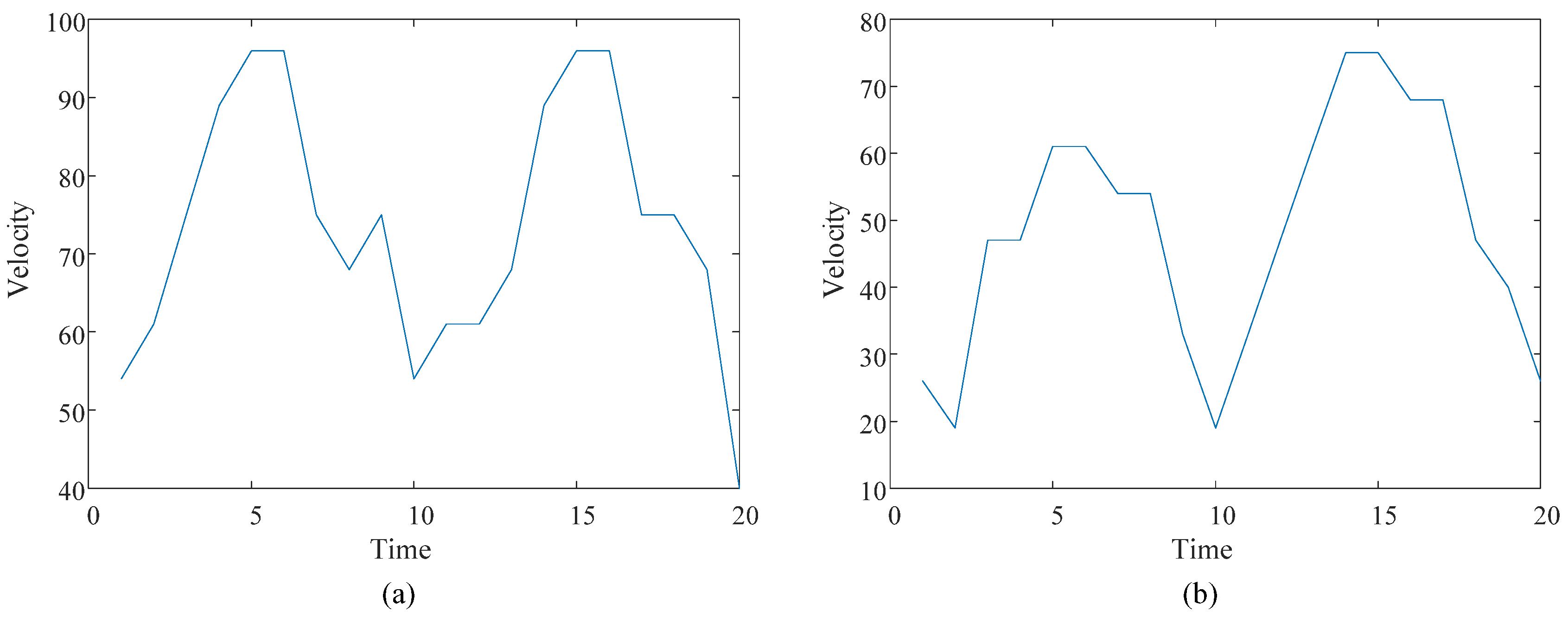
3.1.2. Froth Velocity Distribution
3.2. Rule Base Construction
3.2.1. Association Rule Mining
| Algorithm I: Fuzzy Apriori-Based Setpoint Association Rule Mining. |
| Input: A collection of froth behavior data at reagent adjusting time, |
| their corresponding froth behavior data captured after reagent adjustment, |
| and XRF grade analysis result of collected froth after reagent adjustment |
| Output: |
|
3.2.2. Fuzzy Inference System
3.3. Reagent Control
3.3.1. Flotation Causal Inference Model Construction
3.3.2. Distance Metric
- (i)
- ;
- (ii)
- ;
- (iii)
- ; and
- (iv)
- .
3.3.3. Reagent Control Based on Receding Horizon Optimization
4. Results and Discussion
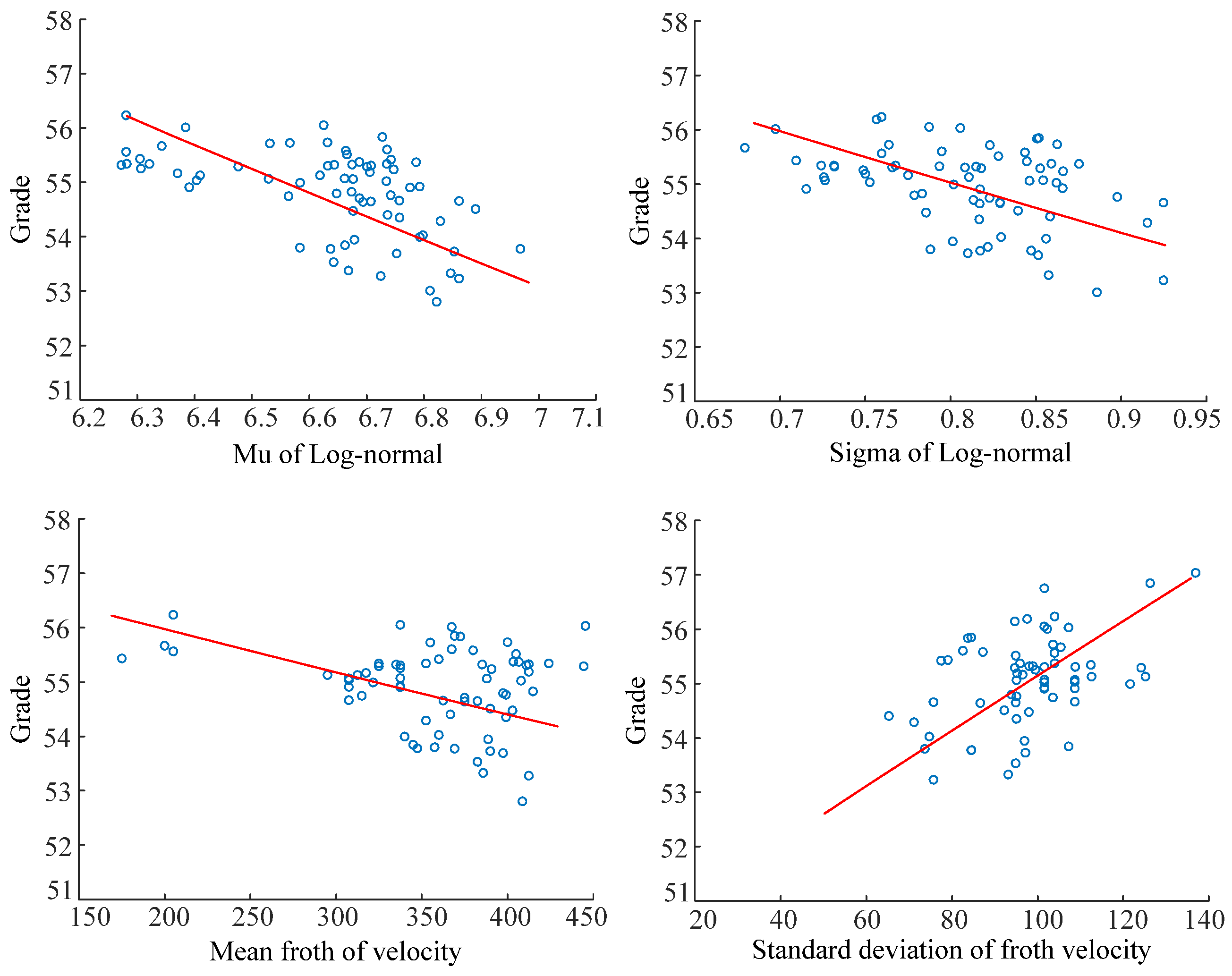
4.1. Relationship between Visual Features and Process Variables
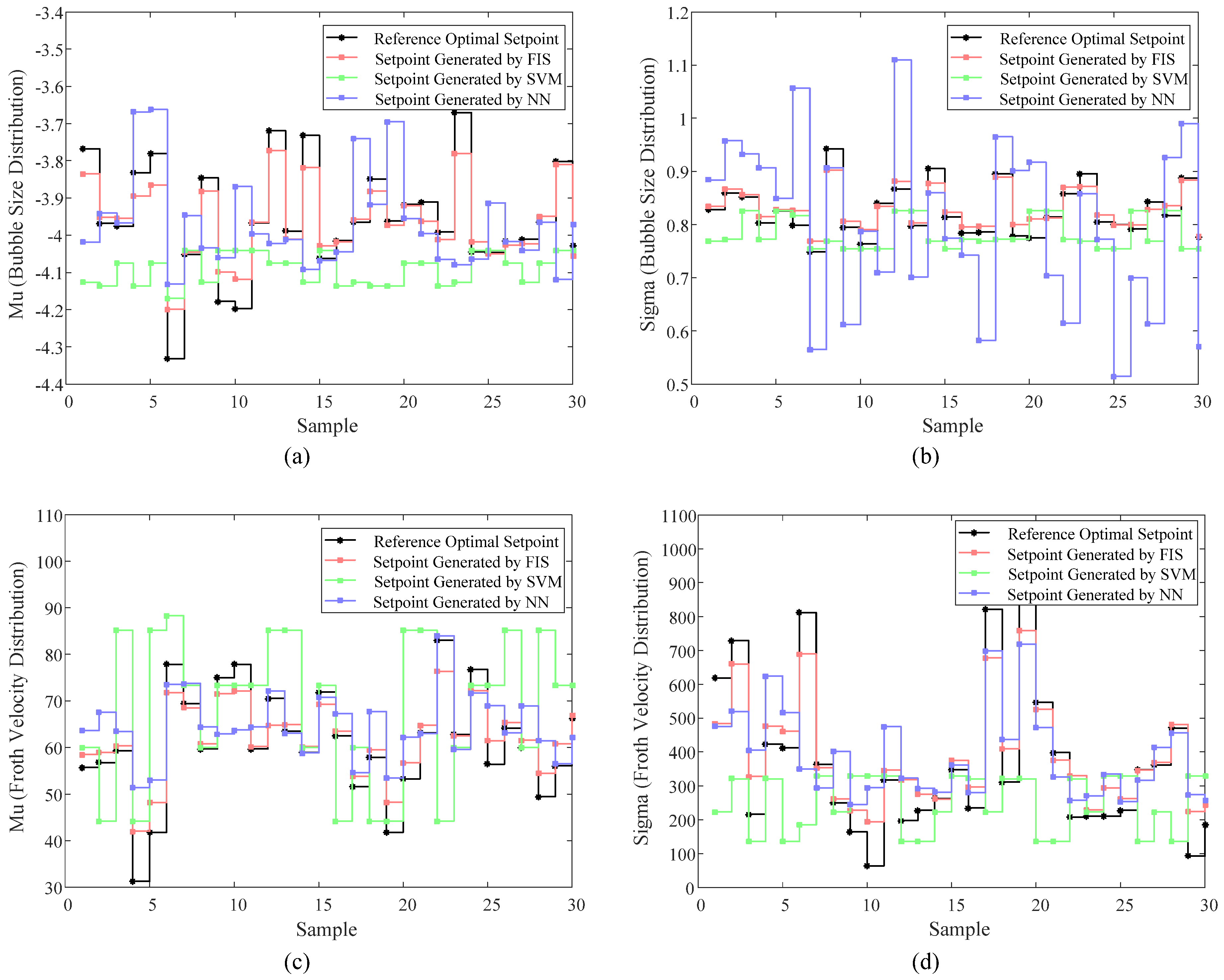
4.2. Validation of the Fuzzy A Priori Association Rule Mining
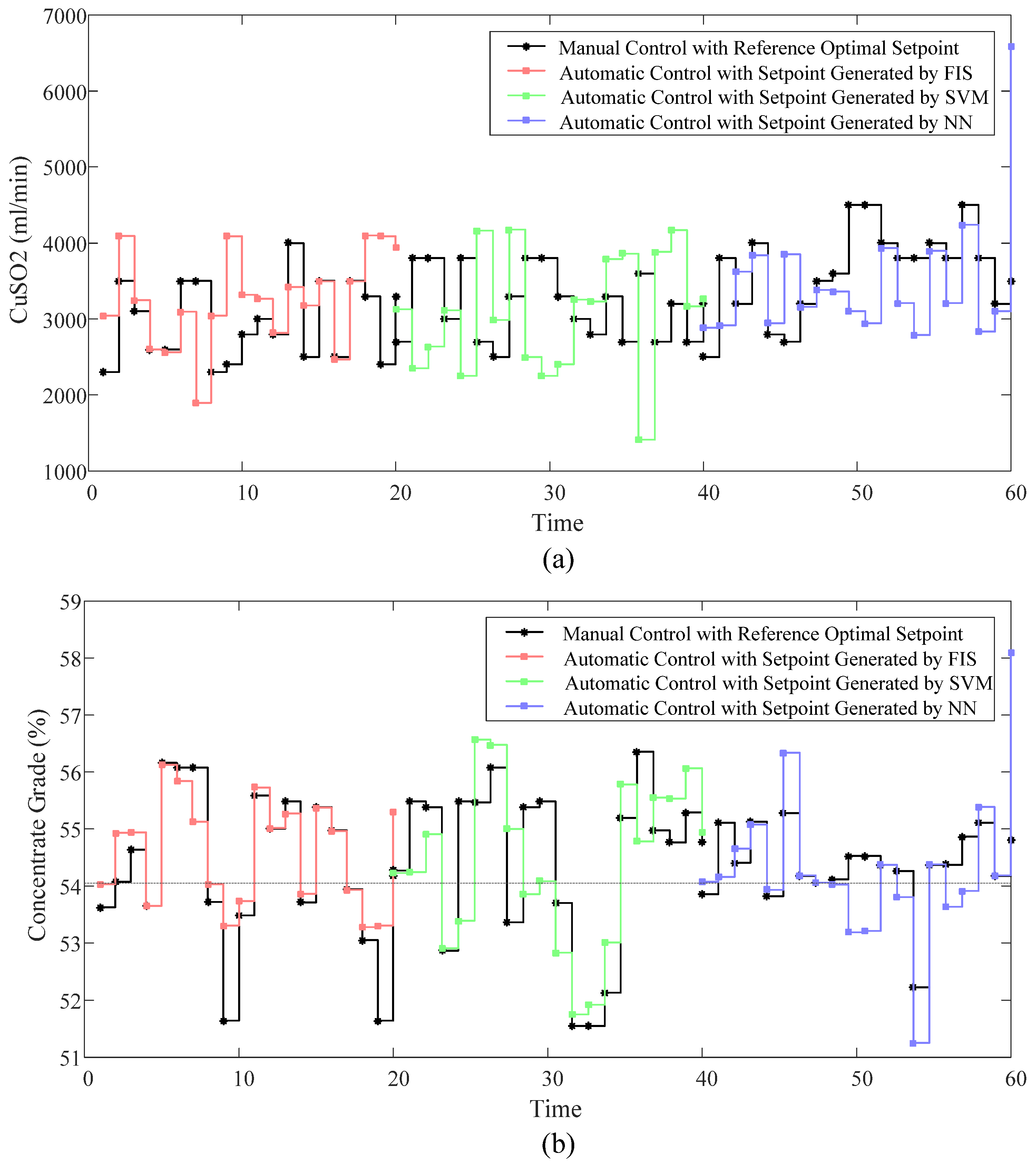
4.3. Industrial Experiments
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Park, H.; Wang, L. Experimental studies and modeling of surface bubble behaviour in froth flotation. Chem. Eng. Res. Des. 2015, 101, 98–106. [Google Scholar] [CrossRef]
- Aldrich, C.; Marais, C.; Shean, B.; Cilliers, J. Online monitoring and control of froth flotation systems with machine vision: A review. Int. J. Miner. Process. 2010, 96, 1–13. [Google Scholar] [CrossRef]
- Symonds, P.J.; De Jager, G. A technique for automatically segmenting images of the surface froth structures that are prevalent in industrial flotation cells. In Proceedings of the 1992 South African Symposium on Communications and Signal Processing. COMSIG ‘92, Cape Town, South Africa, 11 September 1992. [Google Scholar]
- Moolman, D.W.; Aldrich, C.; Deventer, J.S.J.V.; Stange, W.W. Digital image processing as a tool for on-line monitoring of froth in flotation plants. Miner. Eng. 1994, 7, 1149–1164. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Z.; Liu, J.; Tan, Z.; Xu, P. Recognition of flotation working conditions through froth image statistical modeling for performance monitoring. Miner. Eng. 2016, 86, 116–129. [Google Scholar] [CrossRef]
- Jahedsaravani, A.; Massinaei, M.; Marhaban, M. Application of image processing and adaptive neuro-fuzzy system for estimation of the metallurgical parameters of a flotation process. Chem. Eng. Commun. 2016, 203, 1395–1402. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Z.; Ai, M.; Gui, G. Nonlinear modeling of the relationship between reagent dosage and flotation froth surface image by hammerstein-wiener model. Miner. Eng. 2018, 120, 19–28. [Google Scholar] [CrossRef]
- Ai, M.; Xie, Y.; Xu, D.; Gui, W.; Yang, C. Data-driven flotation reagent changing evaluation via union distribution analysis of bubble size and shape. Can. J. Chem. Eng. 2018. [Google Scholar] [CrossRef]
- Contreras, F.; Yianatos, J.; Vinnett, L. On the froth transport modelling in industrial flotation cells. Miner. Eng. 2013, 41, 17–24. [Google Scholar] [CrossRef]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Soille, P. Morphological image analysis: Principles and applications. Sens. Rev. 2003, 28, 800–801. [Google Scholar]
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE Trans. Image Process. 1993, 2, 176–201. [Google Scholar] [CrossRef] [PubMed]
- Núñez, F.; Cipriano, A. Visual information model based predictor for froth speed control in flotation process. Miner. Eng. 2009, 22, 366–371. [Google Scholar] [CrossRef]
- Jinping, L.; Weihua, G.; Zhaohui, T. Flow velocity measurement and analysis based on froth image SIFT features and Kalman filter for froth flotation. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 2378–2396. [Google Scholar]
- Jahedsaravani, A.; Marhaban, M.H.; Massinaei, M. Prediction of the metallurgical performances of a batch flotation system by image analysis and neural networks. Miner. Eng. 2014, 69, 137–145. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Xie, Y.; Wu, J.; Xu, D.; Yang, C.; Gui, W. Reagent addition control for stibium rougher flotation based on Sensitive Froth Image Features. IEEE Trans. Ind. Electron. 2016, 64, 4199–4206. [Google Scholar] [CrossRef]
- Bergh, L.; Yianatos, J. The long way toward multivariate predictive control of flotation processes. J. Process Control 2011, 21, 226–234. [Google Scholar] [CrossRef]
- Hong, T.-P.; Kuo, C.-S.; Chi, S.-C. Trade-off between computation time and number of rules for fuzzy mining from quantitative data. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2001, 9, 587–604. [Google Scholar] [CrossRef]
- Massinaei, M.; Sedaghati, M.R.; Rezvani, R.; Mohammadzadeh, A.A. Using data mining to assess and model the metallurgical efficiency of a copper concentrator. Chem. Eng. Commun. 2014, 201, 1314–1326. [Google Scholar] [CrossRef]
- Mohanty, S. Artificial neural network based system identification and model predictive control of a flotation column. J. Process Control. 2009, 19, 991–999. [Google Scholar] [CrossRef]
- Shean, B.; Cilliers, J. A review of froth flotation control. Int. J. Miner. Process. 2011, 100, 57–71. [Google Scholar] [CrossRef]
- Maldonado, M.; Desbiens, A.; Poulin, É.; del Villar, R.; Riquelme, A. Automatic control of bubble size in a laboratory flotation column. Int. J. Miner. Process. 2015, 141, 27–33. [Google Scholar] [CrossRef]
- Yoon, R.-H.; Soni, G.; Huang, K.; Park, S.; Pan, L. Development of a turbulent flotation model from first principles and its validation. Int. J. Miner. Process. 2016, 156, 43–51. [Google Scholar] [CrossRef]
- Kistner, M.; Jemwa, G.T.; Aldrich, C. Monitoring of mineral processing systems by using textural image analysis. Miner. Eng. 2013, 52, 169–177. [Google Scholar] [CrossRef]
- Morar, S.H.; Forbes, G.; Heinrich, G.S.; Bradshaw, D.J. The use of a colour parameter in a machine vision system, Smartfroth, to evaluate copper flotation performance At Rio Tinto’s Kennecott Utah copper concentrator. In Proceedings of the Centenary of Flotation Symposium, Brisbane, Australia, 6–9 June 2005; pp. 147–151. [Google Scholar]
- Wu, Y.; Peng, X.; Ruan, K.; Hu, Z. Improved image segmentation method based on morphological reconstruction. Multimedia Tools Appl. 2016, 76, 19781–19793. [Google Scholar] [CrossRef]
- Riquelme, A.; Desbiens, A.; del Villar, R.; Maldonado, M. Predictive control of the bubble size distribution in a two-phase pilot flotation column. Miner. Eng. 2016, 89, 71–76. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, May 7–13 2006; pp. 430–443. [Google Scholar]
- Kaartinen, J.; Hätönen, J.; Hyötyniemi, H.; Miettunen, J. Machine-vision-based control of zinc flotation—A case study. Control Eng. Pract. 2006, 14, 1455–1466. [Google Scholar] [CrossRef]
- Liu, J.J.; MacGregor, J.F. Froth-based modeling and control of flotation processes. Miner. Eng. 2008, 21, 642–651. [Google Scholar] [CrossRef]
- Agrawal, R.; Imielinski, T.; Swami, A.N. Mining Association Rules Between Sets of Items in Large Databases. In Proceedings of the SIGMOD Conference, Washington, DC, USA, 25–28 May 1993; pp. 207–216. [Google Scholar]
- Kalia, H.; Dehuri, S.; Ghosh, A.; Taniar, D. A survey on fuzzy association rule mining. Int. J. Data Warehous. Min. 2013, 9, 1–27. [Google Scholar] [CrossRef]
- Hong, T.P.; Lin, K.Y.; Chien, B.C. Mining fuzzy multiple-level association rules from quantitative data. Appl. Intell. 2003, 18, 79–90. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.S.; Chen, Y.C. A Hammerstein-Wiener recurrent neural network with universal approximation capability. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1832–1837. [Google Scholar]
- Tohkura, Y. A weighted cepstral distance measure for speech recognition. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1414–1422. [Google Scholar] [CrossRef]
- Belattar, K.; Mostefai, S. Similarity measures for Content-Based Dermoscopic Image Retrieval: A comparative study. In Proceedings of the First International Conference on New Technologies of Information and Communication, Ahmedabad, India, 28–29 November 2015. [Google Scholar]
- Maldonado, M.; Desbiens, A.; Del Villar, R. Potential use of model predictive control for optimizing the column flotation process. Int. J. Miner. Process. 2009, 93, 26–33. [Google Scholar] [CrossRef]
- Grne, L.; Pannek, J. Nonlinear Model Predictive Control: Theory and Algorithms; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]


| Procedures for Keypoint Detector |
|---|
|
| Procedures for Keypoint Description |
|---|
| 1. Define a binary test of image patch |
| Define the feature as a vector of binary tests |
| 2. For any feature set of , define the matrix |
| 3. Use the patch orientation and the corresponding rotation matrix to construct a “steered” version of as , thus |
| Feature | Bubble size Distribution | Froth Velocity Distribution | ||
|---|---|---|---|---|
| Mu | Sigma | Mu | Sigma | |
| Grade | −0.47 | −0.42 | −0.32 | 0.51 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Tang, Z.; Ai, M.; Gui, W. Fuzzy Association Rule Based Froth Surface Behavior Control in Zinc Froth Flotation. Symmetry 2018, 10, 216. https://doi.org/10.3390/sym10060216
Zhang J, Tang Z, Ai M, Gui W. Fuzzy Association Rule Based Froth Surface Behavior Control in Zinc Froth Flotation. Symmetry. 2018; 10(6):216. https://doi.org/10.3390/sym10060216
Chicago/Turabian StyleZhang, Jin, Zhaohui Tang, Mingxi Ai, and Weihua Gui. 2018. "Fuzzy Association Rule Based Froth Surface Behavior Control in Zinc Froth Flotation" Symmetry 10, no. 6: 216. https://doi.org/10.3390/sym10060216
APA StyleZhang, J., Tang, Z., Ai, M., & Gui, W. (2018). Fuzzy Association Rule Based Froth Surface Behavior Control in Zinc Froth Flotation. Symmetry, 10(6), 216. https://doi.org/10.3390/sym10060216





