Some Results on Neutrosophic Triplet Group and Their Applications
Abstract
:1. Introduction
1.1. Generalized Group
- (i)
- for all .
- (ii)
- For each there is a unique such that (existence and uniqueness of identity element).
- (iii)
- For each , there is such that (existence of inverse element).
- (i)
- For each , there is a unique .
- (ii)
- and if .
- (iii)
- If X is commutative, then X is a group.
1.2. Neutrosophic Triplet Group
2. Main Results
- 1.
- X is a generalized group if it satisfies the left (or right) cancellation law or X is a left (or right) quasigroup.
- 2.
- X is a generalized group if and only if each element has a unique .
- 3.
- Whenever X has the cancellation laws (or is a quasigroup), then X is a loop and group.
- Let x have at least two neutral elements, say . Then . Therefore, X is a generalized group. Similarly, X is a generalized group if it is has the right cancellation law or if it is a right quasigroup.
- This follows by definition.
- This is straightforward because every associative quasigroup is a loop and group.
2.1. Algebraic Properties of Neutrosophic Triplet Group
- (i)
- H is a neutrosophic triplet subgroup of X.
- (ii)
- For all , .
- (iii)
- For all , , and .
- (i)⇒ (ii)
- If H is an NTSG of X and , then . Therefore, by closure property, .
- (ii)⇒ (iii)
- If , and , then we have , , and , i.e., .
- (iii)⇒ (i)
- , so H is associative since X is associative. Obviously, for any , . Let , then . Therefore, . Thus, H is an NTSG of X.
2.2. Neutrosophic Triplet Group Homomorphism
- 1.
- for all .
- 2.
- for all .
- 3.
- If H is a neutrosophic triplet subgroup of X, then is a neutrosophic triplet subgroup of Y.
- 4.
- If K is a neutrosophic triplet subgroup of Y, then is a neutrosophic triplet subgroup of X.
- 5.
- If X is a normal neutrosophic triplet group and the set with the productis a neutrosophic triplet group.
- Place in to obtain . Additionally, place in to obtain . Thus, for all .
- Place in to obtain . Additionally, place in to obtain . Thus, for all .
- If H is an NTSG of G, then . We shall prove that is an NTSG of Y by Lemma 2.Since for , . Let . Then and . Thus, . Therefore, is an NTSG of Y.
- If K is a neutrosophic triplet subgroup of Y, then . We shall prove that is an NTSG of Y by Lemma 2.Let . Then such that and . Thus, . Therefore, is an NTSG of X.
- Given the neutrosophic triplet group X and the set with the product . is a groupoid.For let . Then . Additionally, let . Then .Thus, and similarly, .On the other hand, , and similarly, .Therefore, is a neutrosophic triplet group. ☐
- 1.
- .
- 2.
- .
- 3.
- is a normal neutrosophic triplet group.
- 4.
- .
- 5.
- for all .
- 6.
- If X is finite, for all where is the index of in , i.e., the number of distinct left cosets of in .
- 7.
- .
- 8.
- If X is finite, .
- . Let , then . We shall use Lemma 2..Thus, is a neutrosophic triplet subgroup of X. For the a-normality, let , then . Therefore, for all . Therefore, .
- . . Therefore, . Let . Then . , and . Therefore, .. Thus, is a neutrosophic triplet subgroup of X.. Therefore, , and . Thus, . Therefore, .
- Let . Then . Therefore, . Thus, is a normal NTG.
- For all , . Therefore, based on Point 3 and Theorem 3, .
- Define a relation ≍ on as follows: if for all . . Therefore, ≍ is reflexive.. Therefore, ≍ is symmetric.. Therefore, ≍ is transitive and ≍ is an equivalence relation.The equivalence class . Therefore, .Thus, for all .
- If X is finite, then for all . Thus, for all where is the index of in , i.e., the number of distinct left cosets of in .
- Define a relation ∼ on X: if . ∼ is an equivalence relation on X, so and, therefore, .
- Hence, based on Point 7, if X is finite, then
- 1.
- f is a monomorphism if and only if for all ;
- 2.
- the factor set is a neutrosophic triplet group (neutrosophic triplet factor group) under the operation defined by
- Let and let . If , this implies thatSimilarly,Conversely, if f is mono, then . Let . Then . Therefore, for all .
- Let .
- Groupoid:
- Based on the multiplication , the factor set is a groupoid.
- Semigroup:
- .
- Neutrality:
- Let . Then and similarly, .
- Opposite:
- Let . Then . Similarly, .
is an NTG. ☐
2.3. Construction of Bol Algebraic Structures
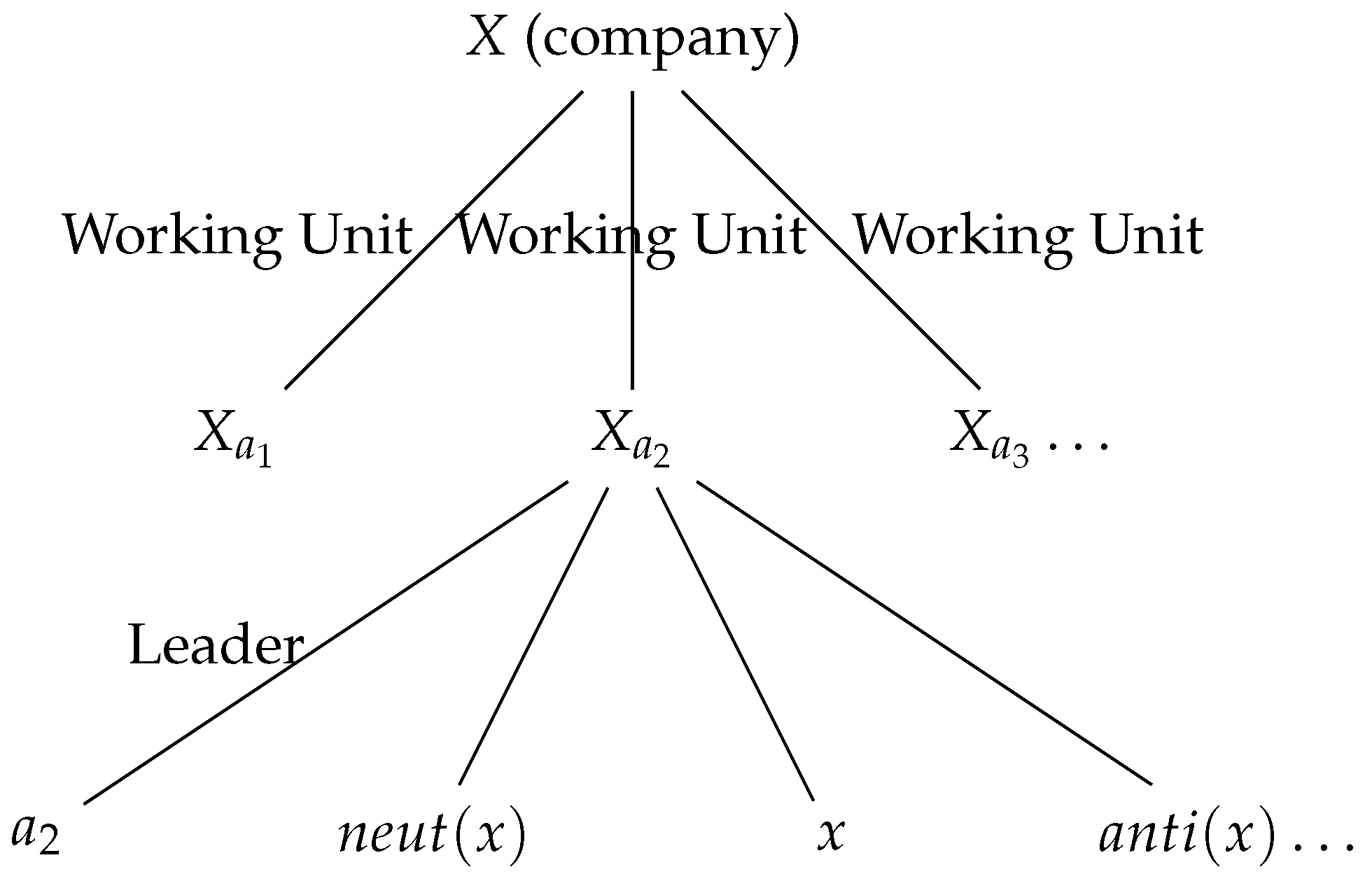
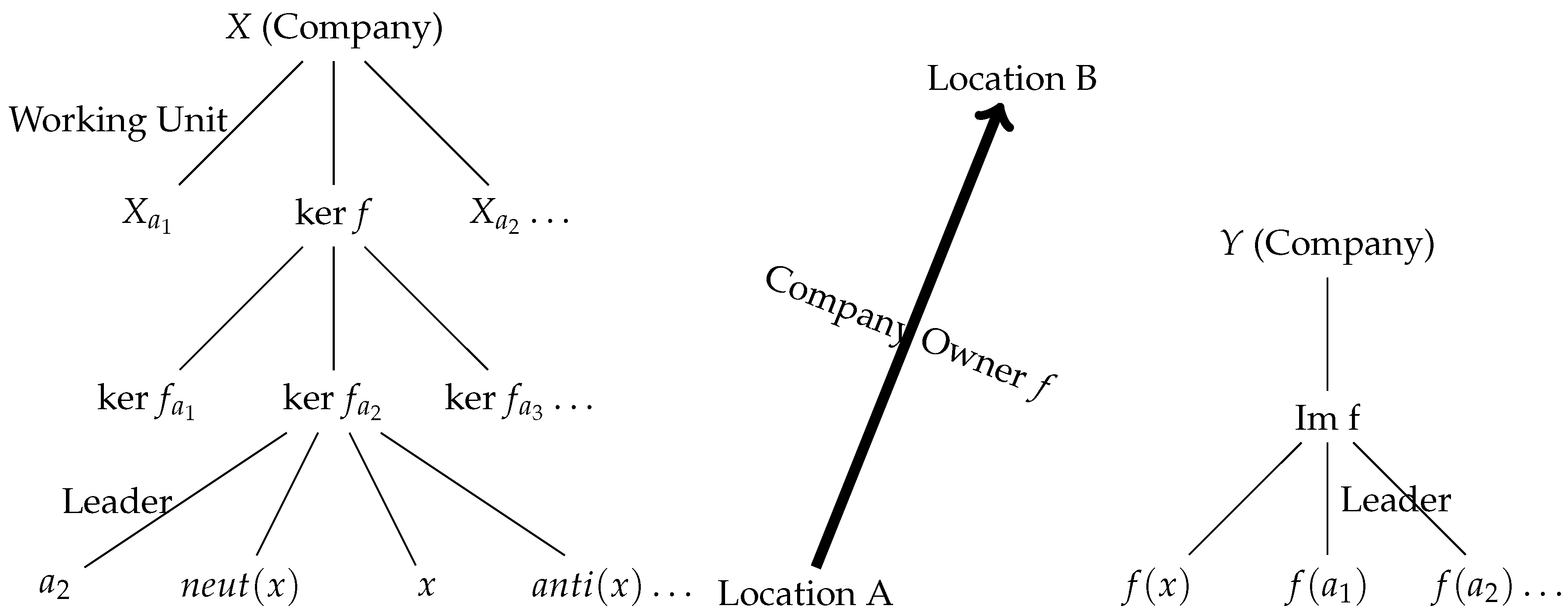
3. Applications in Management and Sports
3.1. One-Way Management and Division of Labor
3.2. Two-Way Management Division of Labor
3.3. Sports
Author Contributions
Conflicts of Interest
References
- Araujo, J.; Konieczny, J. Molaei’s Generalized Groups are Completely Simple Semigroups. Bul. Inst. Polytech. Jassy Sect. I Mat. Mec. Teor. Fiz. 2002, 48, 1–5. [Google Scholar]
- Adeniran, J.O.; Akinmoyewa, J.T.; Solarin, A.R.T.; Jaiyeola, T.G. On some algebraic properties of generalized groups. Acta Math. Acad. Paedagog. Nyhazi. 2011, 27, 23–30. [Google Scholar]
- Agboola, A.A.A. Smooth generalized groups. J. Niger. Math. Soc. 2004, 23, 6–76. [Google Scholar]
- Agboola, A.A.A. Smooth generalized subgroups and homomorphisms. Adv. Stud. Contemp. Math. 2004, 9, 183–193. [Google Scholar]
- Molaei, M.R. Topological generalized groups. Int. J. Appl. Math. 2000, 2, 1055–1060. [Google Scholar]
- Molaei, M.R.; Tahmoresi, A. Connected topological generalized groups. Gen. Math. 2004, 12, 13–22. [Google Scholar]
- Maleki, H.; Molaei, H. On the quotient space of a generalized action of a generalized group. arXiv, 2014; arXiv:1402.3408. [Google Scholar]
- Jaiyéọlá, T.G. A Study of New Concepts in Smarandache Quasigroups and Loops; Books on Demand, ProQuest Information and Learning: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Shcherbacov, V. Elements of Quasigroup Theory and Applications; Monographs and Research Notes in Mathematics; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4987-2155-4. [Google Scholar]
- Chein, O.; Pflugfelder, H.O.; Smith, J.D.H. Quasigroups and Loops: Theory and Applications; Sigma Series in Pure Mathematics 8; Heldermann: Berlin, Germany, 1990; ISBN 3-88538-008-0. [Google Scholar]
- Pflugfelder, H.O. Quasigroups and Loops: Introduction; Sigma Series in Pure Math. 7; Heldermann: Berlin, Germany, 1990. [Google Scholar]
- Smith, J.D.H. An introduction to Quasigroups and Their Representations; Studies in Advanced Mathematics; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007; ISBN 978-1-58488-537-5, 1-58488-537-8. [Google Scholar]
- Smith, J.D.H. Poset Loops. Order 2017, 34, 265–285. [Google Scholar] [CrossRef]
- Glukhov, M.M. On the multiplicative groups of free and free commutative quasigroups. J. Math. Sci. (New York) 2017, 223, 508–517. [Google Scholar] [CrossRef]
- Greer, M. Semiautomorphic inverse property loops. Comm. Algebra 2017, 45, 2222–2237. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press (ARP): Rehoboth, NM, USA, 2003; ISBN 1-879585-76-6. [Google Scholar]
- Smarandache, F. Neutrosophic set, a generalization of the intuitionistic fuzzy set. In Proceedings of the 2006 IEEE International Conference on Granular Computing, Atlanta, GA, USA, 10–12 May 2006; pp. 38–42. [Google Scholar] [CrossRef]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Atanassov, A.K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, P.; Liu, J.; Chen, S.M. Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 2018, 69, 1–24. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.M. Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans. Cybern. 2017, 47, 2514–2530. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Chen, S.M. Multiattribute Group Decision Making Based on Intuitionistic 2-Tuple Linguistic Information. Inf. Sci. 2018, 430–431, 599–619. [Google Scholar] [CrossRef]
- Liu, P. Multiple attribute group decision making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput. Ind. Eng. 2017, 108, 199–212. [Google Scholar] [CrossRef]
- Liu, P.; Li, H. Interval-valued intuitionistic fuzzy power Bonferroni aggregation operators and their application to group decision making. Cognit. Comput. 2017, 9, 494–512. [Google Scholar] [CrossRef]
- Liu, P.; Liu, J.; Merigo, J.M. Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl. Soft Comput. 2018, 62, 395–422. [Google Scholar] [CrossRef]
- Liu, P.; Shi, L. Some Neutrosophic uncertain linguistic number Heronian mean operators and their application to multi-attribute group decision making. Neural Comput. Appl. 2017, 28, 1079–1093. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, L.; Liu, X.; Wang, P. Multi-valued Neutrosophic number Bonferroni mean operators and their application in multiple attribute group decision making. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 1181–1210. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Jaiyéọlá, T.G.; Smarandache, F. Inverse Properties in Neutrosophic Triplet Loop and their Application to Cryptography. Algorithms 2018, 11, 32. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaíyéolá, T.G.; Smarandache, F. Some Results on Neutrosophic Triplet Group and Their Applications. Symmetry 2018, 10, 202. https://doi.org/10.3390/sym10060202
Jaíyéolá TG, Smarandache F. Some Results on Neutrosophic Triplet Group and Their Applications. Symmetry. 2018; 10(6):202. https://doi.org/10.3390/sym10060202
Chicago/Turabian StyleJaíyéolá, Tèmítópé Gbóláhàn, and Florentin Smarandache. 2018. "Some Results on Neutrosophic Triplet Group and Their Applications" Symmetry 10, no. 6: 202. https://doi.org/10.3390/sym10060202
APA StyleJaíyéolá, T. G., & Smarandache, F. (2018). Some Results on Neutrosophic Triplet Group and Their Applications. Symmetry, 10(6), 202. https://doi.org/10.3390/sym10060202





