Abstract
Hamacher operation is a generalization of the algebraic and Einstein operation and expresses a family of binary operation in the unit interval [0,1]. Heronian mean can deal with correlations of different criteria or input arguments and does not bring out repeated calculation. The normal intuitionistic fuzzy numbers (NIFNs) can depict normal distribution information in practical decision making. A decision-making problem was researched under the NIFN environment in this study, and a new multi-criteria group decision-making (MCGDM) approach is herein introduced on the basis of Hamacher operation. Firstly, according to Hamacher operation, some operational laws of NIFNs are presented. Secondly, it is noted that Heronian mean not only takes into account mutuality between the attribute values once, but also considers the correlation between input argument and itself. Therefore, in order to aggregate NIFN information, we developed some operators and studied their properties. These operators include Hamacher Heronian mean (NIFHHM), Hamacher weighted Heronian mean (NIFHWHM), Hamacher geometric Heronian mean (NIFHGHM), and Hamacher weighted geometric Heronian mean (NIFHWGHM). Furthermore, we applied the proposed operators to the MCGDM problem and developed a new MCGDM approach. The characteristics of this new approach are that: (1) it is suitable for making a decision under the NIFN environment and it is more reasonable for aggregating the normal distribution data; (2) it utilizes Hamacher operation to provide an effective and powerful MCGDM algorithm and to make more reliable and more flexible decisions under the NIFN circumstance; (3) it uses the Heronian mean operator to deal with interrelations between the attributes or input arguments, and it does not bring about repeated calculation. Therefore, the proposed method can describe the interaction of the different criteria or input arguments and offer some reasonable and reliable MCGDM aggregation operators, which can open avenues for decision making and broaden perspectives of the decision experts. Lastly, an application is given for showing the effectiveness and feasibility of the approach presented in this paper.
1. Introduction
In the MCGDM procedure, because a lot of problems are uncertain or fuzzy, the value of the input argument is not always a real number and may be more effectively described as a fuzzy value. Zadeh’s fuzzy set (FS) plays an important role in dealing with fuzzy number information [1], and the FS theory has been a good tool which is suitable for various fields, including decision analysis, machine learning, information retrieval, among others.
However, the FS theory only defines a membership function in a domain of discourse, so it is very difficult to describe the vagueness and uncertainty of the objective elements in real society [2]. The intuitionistic fuzzy set (denoted as IFS) theory [3] involves a non-membership function besides a membership function. Recently, the IFS theory has been applied to the MCGDM field. Xu presented some aggregation methods under an intuitionistic fuzzy number circumstance to settle MCGDM problems [4,5]. The IFS was generalized to the interval-valued IFS (denoted as IVIFS) by Gargov [6] and Atanassov [7]. Xu and Yager [8] proposed a new measurement method similar to the IVIFSs for dealing with the MCGDM problem. Tan and Zhang [9] gave a new TOPSIS approach which can deal with a decision-making problem with interval-valued intuitionistic fuzzy number (IVIFN) data. Wang et al. [10] utilized the prospect value function to introduce a score method which can settle the MCGDM problem under the IVIFN environment. Gomathi Nayagam et al. [11] defined an accuracy function of the IVIFNs. Fuzzy number IFS (denoted as FNIFS) theory was proposed by Liu and Yuan [12], where some basic operational laws were defined and the relationships among the FNIFS, the IFS, and interval-valued fuzzy set (IVFS) were discussed. Shu et al. [13] introduced the triangular IFNs (TriIFNs) and presented the operational rules which are utilized in fault-tree analysis. Lin et al. [14] proposed some prioritized operators for the FNIF data. Furthermore, they presented a method to deal with fuzzy number intuitionistic fuzzy MCGDM problems. Wang [15] extended the TriIFNs and originally defined the TriIFNs and IVTriIFNs. The trapezoidal intuitionistic fuzzy numbers (TraIFNs) [16,17,18,19,20,21] are other types of the IFNs. Some MCGDM processes were studied for the TriIFNs or TraIFNs information [22,23,24,25,26,27,28,29,30].
In nature, a lot of social and economic phenomena involve some normal distribution factors, such as random measurement error, average annual rainfall in a region, and others. Yang and Ko [31] proposed the concept with respect to the normal fuzzy numbers (NFNs), which are very suitable for depicting normal distribution information. Wang et al. [32,33] gave the definition of the normal intuitionistic (NIFNs), and they introduced some operations and score function of the NIFNs. Some MCGDM problems were discussed in order to deal with NIFN information [34,35], and some new operators were developed. Nevertheless, these aggregation operators only focus on the impact of input data and ordered result, and they cannot present the interrelationship of input data. Some normal intuitionistic fuzzy Bonferroni mean operators were proposed by Liu and Liu [36] for describing the correlation of input data. Bonferroni originally proposed the Bonferroni mean (BM) in 1950, which considers mutuality of attribute values [37,38]. The BM operators were studied in regard to the circumstance under which the criterion values may be other types, such as NIFNs, HFNs [39], IFNs [40], IVIFNs [41], and IVNs [42].
Heronian mean (denoted as HM) [43,44,45] is another type of decision-making operator which can also objectively express the interrelations between input data. The significant characteristics of the HM operator are that (1) it can account for the interaction of the different criteria or input arguments, which is very desirable in decision making; (2) it pays close attention to the aggregated input data, and it is not the same as power operator or integral aggregation operator, which focus on the importance of the attributes or input data; (3) it can capture the interrelation between an attribute and itself, and take into account the correlation between an input argument and itself. From the definition of the BM and HM operators, the BM operator indicates the correlation between the criteria and (). However, the correlation between and is equal to the correlation between and (). Namely, the BM operator results in the redundant computation. Furthermore, it ignores the correlation between criterion and itself. Although the HM decision operator is similar to the BM aggregation operator, it can settle the aforementioned shortcoming of the BM aggregation operator. At present, the HM has been applied to aggregate the input information with the IFNs [46], the hesitant fuzzy set (HFS) information [47] and the IVIFN [48].
However, the HM is not applied to aggregate the normal intuitionistic fuzzy number (NIFN) arguments. The above aggregation operators only take into account the algebraic operation of the IFNs, hesitant fuzzy set (HFS), IVIFNs, or NIFNs where the algebraic product and sum are important, and they can define union and intersection of the NIFNs, IVIFNs, or HFS. In conclusion, a generalized t-conorm or t-norm can simulate union and intersection between the IFNs or IVIFNs [49,50]. According to Archimedean t-conorm or t-norm, Xia et al. [50] generalized the Hamacher and Frank operational laws and presented some operational laws of the IFNs. Furthermore, they introduced the weighted average and geometric operator for the intuitionistic fuzzy MCGDM problem. Because these operators do not integrate the weight of the attribute and order, they cannot be utilized for IVIFNs. Wang and Liu [51,52] applied the Einstein operation to develop some operators.
Hamacher operation generalizes the algebraic and Einstein operation, and it also plays an important role in studying aggregation method for the MCGDM problem [53]. Hamacher operation depends on Hamacher t-norm and Hamacher t-conorm, which are a pair of dual triangular norms. In other words, Hamacher t-norm or Hamacher t-conorm are binary operations in the unit interval [0,1] which satisfy boundary, monotonicity, associativity, and symmetry, and they are broadly applicable in the FS theory, fuzzy logic, and information aggregation. Especially, as for any hot research topic, Hamacher operation has been applied to aggregate the IFN information, IVIFN information [54], or hesitant fuzzy information.
First of all, in the practical MCGDM procedure, there are many natural phenomena which approximately obey normal distribution. Furthermore, the criteria or input arguments are often stochastic values or fuzzy values, and sometimes the stochastic and fuzzy values exist simultaneously. Under these special circumstances, the IFNs cannot accurately express random information. As an expansion of the IFNs and NFNs, the NIFNs can better describe fuzzy MCGDM problems with normal distribution. Besides this, in the MCGDM process, there is an interaction among the different criteria or input arguments, especially, and some unreasonable information values are determined by the decision maker. Therefore, it is very important to determine how to depict simultaneously stochastic and fuzzy information and how to capture the interaction of the different criteria or input arguments in order to make a reasonable decision by more general and more flexible MCGDM approach.
According to the aforementioned analysis, we note that there are no methods aggregating NIFNs with respect to Hamacher operation and considering the interrelationship between NIFN arguments at the same time. The NIFNs can simultaneously describe the fuzzy and random information, and the HM operator can better capture and handle the correlation between the different criteria or input data and relieve the redundant computation at the same time. Hamacher operation can offer more flexible operation or more general operation for a reasonable MCGDM procedure. Therefore, in this paper, the motivation of the research is (1) to present some new operational laws of the NIFNs on the basis of the Hamacher t-norm and Hamacher t-conorm; (2) to propose some new HM operators and study some of their desirable properties; (3) to develop a new MCGDM approach which can deal with the NIFNs information.
This paper is presented as follows. In Section 2, we review the normal intuitionistic fuzzy number, Hamacher operation, and Heronian mean operators. In Section 3, we establish Hamacher operational rules and their characteristics with respect to the normal intuitionistic fuzzy numbers, furthermore, we describe the normal intuitionistic fuzzy Heronian mean aggregation operators based on Hamacher operation of NIFNs and study their properties. According to the new Hamacher operations, the geometric Heronian mean is extended to the NIFNs, and its weighted version is presented in Section 4. In Section 5, we utilize new operators to make a MCGDM procedure for the NIFN information and introduce the decision steps. In Section 6, an application is introduced to show the new approach and the evidence of the effectiveness. We make a conclusion and present some remarks in Section 7.
2. Preliminaries
Some notions and operational rules with respect to NIFNs are introduced in this section, and the definition of Heronian mean operator is given.
2.1. Normal Intuitionistic Fuzzy Number
Definition 1.
[31] Ifis a real number set, and,is a normal fuzzy number (NFN) whose membership function is presented
Definition 2.
[33] Ifis a finite nonempty set, a normal intuitionistic fuzzy number (NIFN)is presented in the following, whereis the membership function andis the non-membership function, and they satisfy,,.
Compared with the classical IFNs, the non-membership function of the NIFNs can more synthetically capture the fuzziness and uncertainty of objects. From the definition of NIFNs, its universe of discourse is expanded from discrete to continuous, and it can effectively describe a large number of normal distributions under the socioeconomic environment. In the following, some operational rules of the NIFNs were defined in [33].
Let , and , , then
The score and accuracy function with respect to NIFNs are given as follows [33]:
In order to rank any two NIFNs, the following method was introduced by Wang and Li [33].
If , then ;
If , and , then ;
If and , then;
If then ;
If and then ;
If and then .
2.2. Hamacher t-Norm and Hamacher t-Conorm
In FS theory, t-conorm () and t-norm () are very important to the generalization of intersection or union of fuzzy sets [34,42,46,55,56,57,58,59,60,61].
Definition 3.
[46] Ifandare IFSs, then the union and intersection ofandare expressed
Hamacher defined the Hamacher t-norm and Hamacher t-conorm [10,56]:
Especially, when , Hamacher t-norm and Hamacher t-conorm transform into the algebraic t-norm and t-conorm:
If , Hamacher t-norm and Hamacher t-conorm are respectively equal to the Einstein t-norm and t-conorm [39].
2.3. Heronian Mean
Definition 4.
[43] Let, which is greater than zero. The basic Heronian mean (BHM) is defined as follows
Based on the BHM, Yu and Wu [48] applied the parameters and to the BHM and obtained a more general HM version, and they proposed the geometric Heronian mean.
Definition 5.
[48] Letand, then the HM aggregation operator is presented in the following
It is easy to notice that the HM reduces to the BHM when .
Definition 6.
[48] Ifandare not equal to zero at the same time,, then the geometric Heronian mean (denoted as GHM) has the following form
3. Normal Intuitionistic Fuzzy Hamacher Heronian Mean Operator and Its Weighted Form
3.1. Hamacher Operational Laws of the NIFNs
From Definition 3—Hamacher t-norm and Hamacher t-conorm—Hamacher intersection and sum between NIFNs are introduced.
Suppose that , , . The Hamacher operational rules of the NIFNs are presented as follows:
Furthermore, according to Definition 3 and the properties of Hamacher t-norm and t-conorm, the above operation results are all NIFNs. Especially, when , the above operational rules reduce to the operational laws of Definition 2. Therefore, the Hamacher operational laws of NIFNs extend the algebraic operational rules of NIFNs.
Theorem 1.
If,and, then
According to the Hamacher operational rules of NIFNs, Theorem 1 is easily proved, so the proof is omitted.
3.2. Normal Intuitionistic Fuzzy Hamacher Heronian Mean Operator and Its Weighted Form
Definition 7.
Letbe the NIFNs, and, then the normal intuitionistic fuzzy Hamacher Heronian mean (NIFHHM) operator is defined in the following formula
Lemma 1.
Letbe NIFNs, then
Lemma 2.
If,are NIFNs, then
Lemma 3.
Letbe a set of NIFNs, then
Theorem 2.
Ifis a set of NIFNs, then the aggregation result of Formula (32) is still a NIFN, and it has the following expression
With respect to the parameter , some cases of the NIFHHM operator are discussed.
(1) If , then
We call (43)–(45), (48), and (49) the normal intuitionistic fuzzy Heronian mean (NIFHM) operator.
(2) When ,
We call (43)–(45), (50), and (51) the normal intuitionistic fuzzy Einstein Heronian mean (NIFEHM) operator.
The NIFHHM operator is generalization of the above operators and has some properties as follows.
Theorem 3.
If all, then
Theorem 4.
Ifis any permutation ofthen
Theorem 5.
Letandare not simultaneously equal to the value of zero,,, are two sets of NIFNs if the following conditions hold
then, for
for
Theorem 6.
Letbe a set of NIFNs, and
then, when , holds, and when , is right.
From the aforementioned analysis, we can see that the NIFHHM operator does not consider the significance of the input data. However, the importance of the attributes should be considered in a real MCGDM procedure. So, the weighted form of the NIFHHM operator is defined.
Definition 8.
Ifis a collection of NIFNs andis the weight of,,, then normal intuitionistic fuzzy Hamacher weighted Heronian mean operator (NIFHWHM) is defined
Theorem 7.
Ifis a collection of NIFNs and, then the aggregation result of Equation (56) is an NIFN and
It is likely to be noticed that the NIFHWHM operator involves monotonicity and boundedness, but not the properties of commutativity and idempotency.
Theorem 8.
Letandis not simultaneously equal to zero,,are NIFNs, andis the weight of,,. If the following conditions are satisfied
then, for
for
Theorem 9.
Letbe a set of NIFNs, andis the weight of,,
then, when ,
when ,
The NIFHWHM operator also has some cases.
(1) When the parameter ,
We call (57)–(59), (66), and (67) the normal intuitionistic fuzzy weighted Heronian mean (NIFWHM) operator.
(2) If , then
We call (57)–(59), (68), and (69) the normal intuitionistic fuzzy Einstein weighted Heronian mean (NIFEWHM) operator.
4. Normal Intuitionistic Fuzzy Hamacher Geometric Heronian Mean Operator and Its Weighted Form
In this section, the GHM is extended to contain the position where the attribute values are NIFNs, and we introduce the normal intuitionistic fuzzy Hamacher geometric Heronian mean (NIFHGHM) aggregation operator and its weighted form.
Definition 9.
Letbe a collection of NIFNs, andcannot take the value of zero at the same time, a normal intuitionistic fuzzy Hamacher geometric Heronian mean operator (NIFHGHM) is defined
Theorem 10.
Ifis a set of NIFNs, andcannot take the value of zero at the same time, then the aggregation value of Equation (70) is an NIFN and
Especially,
(1) When , the NIFHGHM reduces to normal intuitionistic fuzzy geometric Heronian mean (NIFGHM), which is presented by Formulas (71)–(73) and (76).
(2) If , then
So, the NIFHGHM operator reduces to Formulas (71)–(73), (77), and (78), and it is called the normal intuitionistic fuzzy Einstein geometric Heronian mean (NIFEGHM).
The NIFHGHM operator has some properties considered in the following.
Theorem 11.
If all, then
Theorem 12.
Ifis any permutation of, then
Theorem 13.
Let,do not simultaneously take the value of zero, and,, are NIFNs which satisfy the following conditions
then, for
for
Theorem 14.
Letbe a set of NIFNs, and
then, when , is right, and when , holds.
Similarly, the weighted form of the NIFHGHM operator is defined in the following.
Definition 10.
Ifis a collection of NIFNs,is the weight ofwith, then the normal intuitionistic fuzzy Hamacher weighted geometric Heronian mean (NIFHWGHM) operator is presented as follows
Theorem 15.
Letbe a set of NIFNs andwhich cannot simultaneously take the value of zero, the aggregation result of Equation (83) is an NIFN and
From the above, the NIFHWGHM operator has monotonicity and boundedness.
Theorem 16.
Let,do not simultaneously equal zero, and,are NIFNs, and the following conditions are in place
then, for
for
Theorem 17.
Letbe a set of NIFNs, andis the weight of,,
then, when ,
when ,
The NIFHWGHM operator has also some special cases, discussed in the following.
(1) When , Formulas (87) and (88) reduce to the following equations.
So, the normal intuitionistic fuzzy weighted geometric Heronian mean (NIFWGHM) operator can be defined by Formulas (84)–(86), (93), and (94).
(2) When , then
We can see that the NIFHWGHM operator transforms into the normal intuitionistic fuzzy Einstein weighted geometric Heronian mean (NIFEWGHM) operator, which is defined by Formulas (84)–(86), (95), and (96).
5. New Methods Based on Hamacher Heronian Mean Operator for Normal Intuitionistic Fuzzy Information
Here, we apply the developed operators to the MCGDM problem where the input arguments are some NIFNs.
(1) Description of an MCGDM problem.
We take into account an MCGDM problem with the NIFN information and suppose the following:
a collection of decision makers ;
a collection of alternatives: ;
attributes set: ;
weight of attributes set: ;
weight of decision makers: ;
a NIFNs decision matrix given by for with respect to :
Consequently, the proposed operators are applied to solve the above MCGDM problem, alternatives are ranked in descending order, and the best one is determined.
(2) The new method based on the developed operators (including NIFHHM, NIFHWHM, NIFHGHM, and NIFHWGHM operators).
Step 1. Normalization of decision-making information.
In nature, the bigger values of some benefit attributes () are better and the smaller values of some cost attributes () are better, therefore, decision-making information should be normalized for the unity of input data. Hence, the NIFN decision matrices can be transformed into matrices by Wang’s method [31], where
Step 2. Determine weight vector of the criteria and decision makers and select the aggregation operator.
The weights of the criteria are determined by decision expert or manager, who are experienced in the corresponding field. Generally, if the weights of the criteria and decision maker are given, we utilize the NIFHWHM operator or NIFHWGHM operator, however, if the weights are unknown, the NIFHHM operator or NIFHGHM operator can be applied.
Step 3. Choose the values of the parameters , , and .
On the whole, if decision experts are pessimistic, the bigger parameter values are chosen, while the smaller parameter values are used when decision experts take an optimistic view of the decision results. For convenience, or is selected, especially, when , calculation can decrease.
Step 4. For any pair , apply the selected operator to integrate into the collection of the matrix , where
Step 5. For any value , apply the chosen operator to integrate and get the value of alternative , i.e., aggregate each line of each NIFN decision matrix, where
Step 6. Utilize the ranking method of the NIFNs to rank in descending order and derive the priority of each alternative according to the score function value . If , then the best one of all the alternatives is .
6. An Application Example
A real MCGDM problem will be introduced to show the practical application of the new method in this paper (a stock value evaluation problem), which is adapted from [47]. In the intricate stock market, a real problem is how to analyze the stock investment value and choose the stock. Therefore, an effective stock evaluation approach is very significant. However, most of the financial indicators approximately obey normal distribution, and the NIFNs can effectively describe the phenomenon of normal distribution and evaluate the stock investment value information. To evaluate the stock alternatives, we suppose that there are four stocks (alternatives) denoted as , and we extract the four key financial attributes described as undistributed profits per share , net asset value per share , earnings per share , and equity ratio , whose weight vector is .
Obviously, these attributes are all benefit attributes under which three decision workers utilize NIFNs to evaluate the four alternatives. Three decision makers can evaluate the four alternatives under the four attributes , and three decision matrices are set out in the following tables (see Table 1, Table 2 and Table 3).

Table 1.
Decision matrix E1 from e1.

Table 2.
Decision matrix E2 from e2.

Table 3.
Decision matrix E3 from e3.
6.1. An MCGDM Procedure Related to the NIFHWHM and NIFHWGHM Operators
According to the following steps, all of the alternatives are ranked in order to get the best alternative.
Step 1. Normalizing the input data with the NIFN information, which is shown in Table 1, Table 2 and Table 3.
Considering that all the criteria are benefit criteria, Equation (97) is utilized to integrate the NIFN decision matrix into the normalized matrix (shown in Table 4, Table 5 and Table 6).

Table 4.
Normalization matrix R1 given by e1.

Table 5.
Normalization matrix R2 given by e2.

Table 6.
Normalization matrix R3 given by e3.
Step 2. Decision expert provides that weights of the criteria are and weights of decision makers are , and the NIFHWHM operator and NIFHWGHM operator are chosen.
Step 3. Without the loss of generality, choose the parameter values γ = 2, p = q = 1. From Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, data values are not equal to zero. Thus, according to Formulas (84)–(88), the NIFHWHM operator and NIFHWGHM operator have the following formulas in this example:
Step 4. Apply the NIFHWHM operator to integrate normalization matrices (k = 1,2,3) into a matrix (see Table 7).

Table 7.
The collective decision matrix R of the Hamacher weighted Heronian mean (NIFHWHM) operator.
Step 5. Apply the NIFHWGHM operator to aggregate normalized matrices (k = 1,2,3) into a matrix (see Table 8).

Table 8.
The collective decision matrix R of the Hamacher weighted geometric Heronian mean (NIFHWGHM) operator.
Step 6. Utilizing the NIFHWHM operator to obtain preference values of , get the collection preference value ri (i = 1,2,3,4) of alternative Ai (i = 1,2,3,4) (see Table 9).

Table 9.
Aggregation result of the NIFHWHM operator.
Step 7. Utilizing the NIFHWGHM operator to get the preference values of , obtain the collection preference value ri (i = 1,2,3,4) of alternative Ai (i = 1,2,3,4) (see Table 10).

Table 10.
Aggregation result of the NIFHWGHM operator.
6.2. Sensitivity Analysis
In the method proposed in this paper, three parameters (, , and ) are involved and influence the aggregation result. Therefore, we performed a sensitivity analysis for studying the influence of generalized parameters with respect to the ordering results of the above example. In other words, we chose different parameters , and in Step (3) to rank all the alternatives and to investigate the effect of parameter value changes on the ordering results. The aggregation results are provided in Table 11 and Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5.

Table 11.
Sensitivity analysis with respect to γ in the NIFHWHM operator.
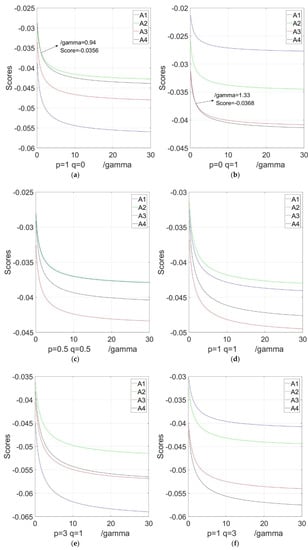
Figure 1.
Sensitivity analysis with respect to in NIFHWHM operator based on different : (a) variation tendency of score function value when ; (b) variation tendency of score function value when ; (c) variation tendency of score function value when ; (d) variation tendency of score function value when ; (e) variation tendency of score function value when ; (f) variation tendency of score function value when .
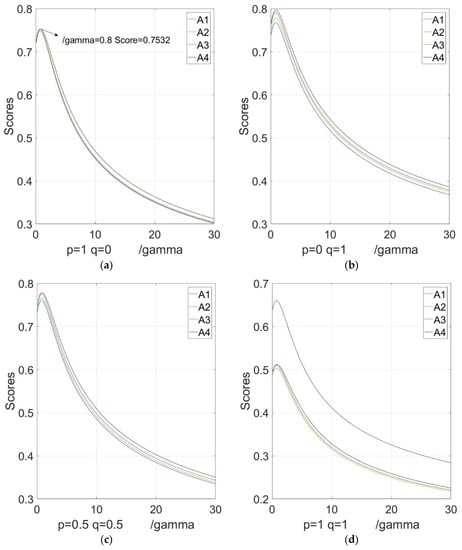
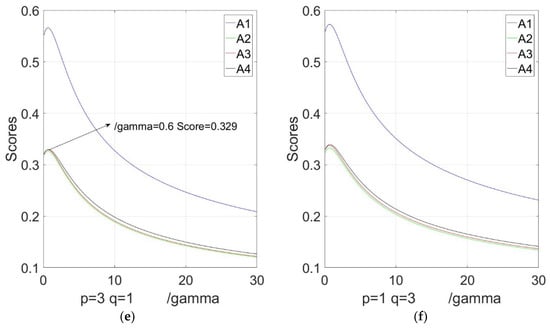
Figure 2.
Sensitivity analysis with respect to in the NIFHWGHM operator based on different : (a) variation tendency of score function value when ; (b) variation tendency of score function value when ; (c) variation tendency of score function value when ; (d) variation tendency of score function value when ; (e) variation tendency of score function value when ; (f) variation tendency of score function value when .
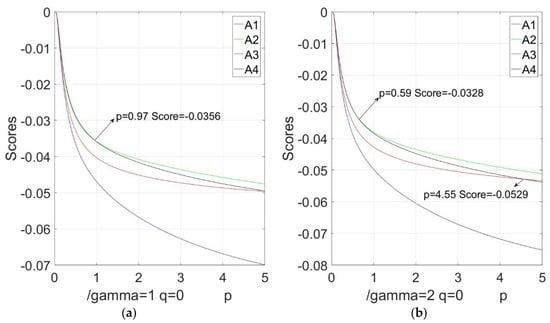
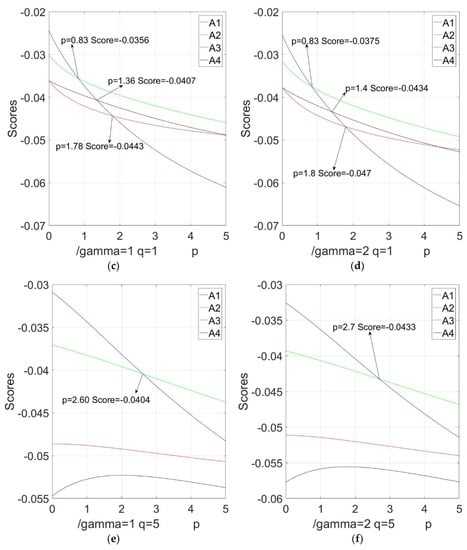
Figure 3.
Sensitivity analysis with respect to in the NIFHWHM operator based on different : (a) variation tendency of score function value when ; (b) variation tendency of score function value when ; (c) variation tendency of score function value when ; (d) variation tendency of score function value when ; (e) variation tendency of score function value when ; (f) variation tendency of score function value when .
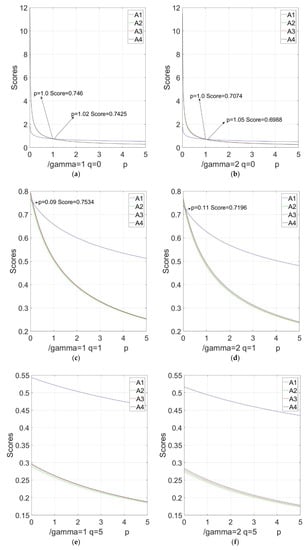
Figure 4.
Sensitivity analysis with respect to in the NIFHWGHM operator based on different : (a) variation tendency of score function value when ; (b) variation tendency of score function value when ; (c) variation tendency of score function value when ; (d) variation tendency of score function value when ; (e) variation tendency of score function value when ; (f) variation tendency of score function value when .
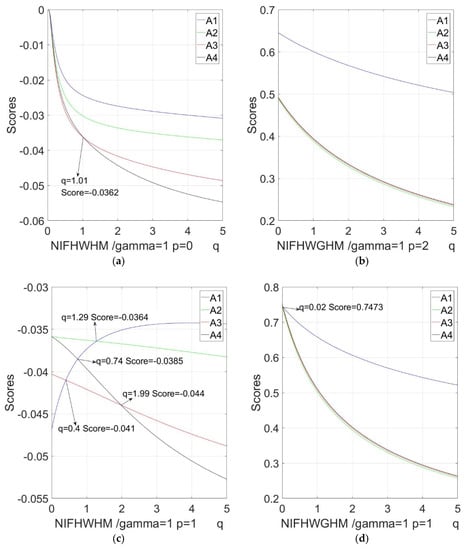
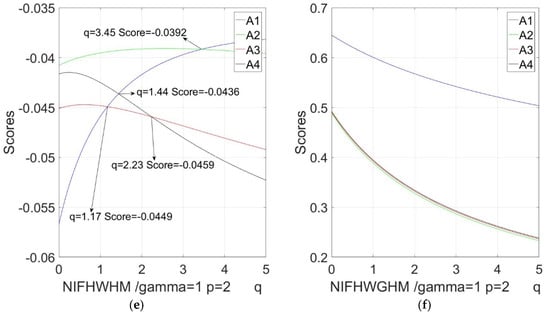
Figure 5.
Sensitivity analysis with respect to in the NIFHWHM and NIFHWGHM operators based on different : (a) variation tendency of score function value when in the NIFHWHM operator; (b) variation tendency of score function value when in the NIFHWGHM operator; (c) variation tendency of score function value when in the NIFHWHM operator; (d) variation tendency of score function value when in the NIFHWGHM operator; (e) variation tendency of score function value when in the NIFHWHM operator; (f) variation tendency of score function value when in the NIFHWGHM operator.
From Table 11 and Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, we can observe that different parameter values have a certain influence on the ordering results. In general, the best alternative is with respect to the NIFWHM operator, while is the best one with respect to the NIFHWGHM operator.
(1) From Table 11 and Figure 1 and Figure 2, the best resolution and ordering results of the alternatives are concordant when and are given in the NIFHWHM or NIFHWGHM operators. When and there is a zero in and , the ordering results are different.
(2) From Figure 3 and Figure 4, we can see that when are given in the NIFHWHM or NIFHWGHM operators and takes the values of the different intervals, the best resolution and the orderings are different. For example, with the NIFHWHM operator, when , , the ranking is ; when , the ranking is ; when , the ranking is ; and when , the ranking is . Additionally, we notice that when , the best one is ; when , the best one is .
(3) Figure 5 shows that sensitivity of the parameter is similar to the parameter , but the influence of the value of is less in the NIFHWGHM operator. As long as , the rankings are concordant .
(4) From Table 11 and Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, on the whole, the score function values of the NIFHWHM or NIFHWGHM operators become smaller when the parameters , , and increase. Therefore, the parameters , , and play crucial roles in the MCGDM procedure. In practical cases, the decision makers can take different values of the parameter, for example, the bigger parameter values are chosen by decision experts who are pessimistic, while smaller parameter values are adopted when decision experts take an optimistic view of the decision results. For convenience, we can assign or ; especially, when , the mathematical calculation can be simplified.
In a word, based on the generalized parameters , , and in the NIFHWHM operator and NIFHWGHM operator, the new method in this paper can offer more flexible or reliable decision-making resolutions. Moreover, the reasonable and best alternative can be properly obtained on the basis of the practical MAGDM problems, namely, the new method can offer a powerful and effective mathematic tool for the MAGDM under uncertainty.
6.3. Comparison Analysis
6.3.1. A Comparison with Decision-Making Methods Using Triangular and Trapezoidal Intuitionistic Fuzzy Information
For further comparison of the rationality and comprehensiveness of the new MCGDM approach in this paper, a prospect value determination method with the TraIFNs [17] and a method with TriIFNs [25] are applied in this section to deal with the aforementioned example. Thus, we need transform the TraIFNs and TriIFNs by the transformation method in [33], which is shown in Table 12. According to Table 12, the information from each expert is also transformed into the TraIFNs and the TriIFNs. Moreover, the normalization method of the TraIFN and TriIFN decision matrix is presented as follows.
where is benefit attributes set.

Table 12.
Transformation method of the normal intuitionistic fuzzy number (NIFN), trapezoidal IFN (TraIFN), and triangular IFN (TriIFN).
From Table 13, it can be seen that the best resolution of the three methods is , but the ordering results are different for these methods. The proposed method of this paper takes into account the interrelations between input data, and it is more practical than the methods in [17,25,30]. The reason is that there are many normal random factors under the social and economic environment. Furthermore, in light of central limit theorem, the limit distribution of the sum of random variables is a normal distribution. However, the TriIFNs and TraIFNs cannot better depict the laws of normal distribution and accurately express corresponding normal random phenomena. Therefore, compared with the TriIFNs and TraIFNs, the NIFNs can better describe the decision problems with normal distribution information and can more realistically express the uncertainty information, and the MCGDM approach in this paper is more reliable and reasonable to aggregate the normal distribution information than the methods in [17,25,30].

Table 13.
Comparison of the ranking results by methods in [17,25,30].
6.3.2. A Comparison with Decision-Making Methods Using the NIFNs
In order to study the advantages of the MCGDM approach in this paper, three methods were applied to deal with the problem in the aforementioned example, and the aggregation results can be seen in Table 14.

Table 14.
Comparison of the ranking results by methods in [34,36,62].
From Table 14, we can observe that the best alternatives are all , but the solution ordering results are completely different for four methods, which can all tackle NIF information. We consider that there are wide interrelationships among the attributes or relationships between input argument and itself in practical MAGDM problems. Moreover, the new method in this paper considers the interrelationship factor between input arguments or between input argument and itself. Therefore, compared with two methods in [34,62], the ranking results from the new method in this paper is more effective and more reasonable.
In addition, if or , then the interrelationships did not exist in the new method in this paper. In the aforementioned example, we can obtain the aggregation ordering results, namely, the relationships between arguments or among the attributes are not considered in the method proposed in this paper. The solution ordering result is the same as that using the methods in [34,62], consequently, this verifies the different ordering results.
Furthermore, for a group of attributes and a collection of input arguments , the method in [36] also takes into account the relationships between any pair of attributes and or between any pair of input arguments and , but it neglects the correlation between input argument and itself or between the attribute and itself. Considering that the correlation between and or between and is equal to the correlation between and or between and , the method in [36] deals with it separately and brings about redundancy. Therefore, compared with the method in [36], the new method in this paper not only considers relationships between the input arguments or the attributes, but also takes into account the correlation between input argument and itself. Furthermore, interrelationships between input arguments are tackled once.
7. Conclusions
In this work, enlightened by Heronian mean, we significantly investigated a family of generalized fuzzy HM operators based on Hamacher operation for NIFNs, including NIFHHM, NIFHWHM, NIFHGHM, and NIFHWGHM operators, and we discuss various properties of the proposed operators which have the desirable quality of not only dealing with the normal intuitionistic fuzzy information, but also considering the correlations of two input arguments once. Therefore, the new proposed operators do not result in redundancy, and these operators also take into account the interrelationship between input argument and itself at the same time. Furthermore, we have manifested that the operators related to Hamacher operation generalize the operators based on the algebraic or Einstein operational rules, and they are more flexible to extend the choice scope of decision makers. On the basis of the developed operators, a new MCGDM approach is introduced in order to deal with normal intuitionistic fuzzy number information. The advantages of this new method are that: (1) it is more reliable and reasonable to aggregate the normal distribution information under the normal intuitionistic fuzzy numbers environment; (2) it offers an effective and powerful mathematic tool for the MAGDM under uncertainty and can provide more reliable and flexible aggregation results in decision making; (3) it not only considers relationships between the input arguments or the attributes, but also takes into account the correlation between input argument and itself or the interrelations between the attribute and itself, furthermore, interrelationships between input arguments or the attributes are tackled once. The new methods provide some reasonable and reliable MCGDM aggregation operators, which broaden the selection scope of the decision makers and offer theory evidence for the MCGDM methods. Meanwhile, the proposed methods solve the interaction of the different criteria or input arguments and do not bring about redundancy of the mathematical calculation. Lastly, an application example revealed that the developed approach is effective and practical by the comparison with other methods. In further research, it is important to investigate how to determine the weights and how to transform other types of fuzzy numbers into the NIFNs, and it is essential to study the application of the proposed operators in wide fields, such as uncertain programming, cluster analysis, pattern recognition, and so on.
Author Contributions
G.Z. accomplishes the whole paper and data analysis is provided by Z.Z. and H.K.
Acknowledgments
This work was supported by the Key Research Foundation of Education Bureau of Hebei Province (No. ZD2015069) and Natural Science Foundation of Hehei Province (No. 2018201172).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Ostaks, A.S. Mathematics in the context of fuzzy sets: Basic ideas, concepts, and some remarks on the history and recent trends of development. Math. Model. Anal. 2011, 16, 173–198. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Genet. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 3, 343–349. [Google Scholar] [CrossRef]
- Atanassov, K.T. Operators over interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 64, 159–174. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group. Fuzzy Optim. Decis. Mak. 2009, 8, 123–139. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, Q. Fuzzy multiple attribute decision making based on interval valued intuitionistic fuzzy sets. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006. [Google Scholar]
- Wang, J.Q.; Li, K.J.; Zhang, H.Y. Interval-valued intuitionistic fuzzy multi-criteria decision-making approach based on prospect score function. Knowl. Based Syst. 2012, 27, 119–125. [Google Scholar] [CrossRef]
- Gomathi Nayagam, V.L.; Muralikrishnan, S.; Sivaraman, G. Multi-criteria decision making method based on interval-valued intuitionistic fuzzy sets. Expert Syst. Appl. 2011, 38, 1464–1467. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, X. Fuzzy number intuitionistic fuzzy set. Fuzzy Syst. Math. 2007, 21, 88–91. (In Chinese) [Google Scholar]
- Shu, M.H.; Cheng, C.H.; Chang, J.R. Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly. Microelectron. Reliab. 2006, 46, 2139–2148. [Google Scholar] [CrossRef]
- Lin, R.; Zhao, X.; Wei, G. Fuzzy number intuitionistic fuzzy prioritized operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2013, 24, 879–888. [Google Scholar] [CrossRef]
- Wang, J.Q. Overview on fuzzy multi-criteria decision-making approach. Control Decis. 2008, 23, 601–606. (In Chinese) [Google Scholar] [CrossRef]
- Kahraman, C.; Cebi, S.; Ona, S.C.; Oztaysi, B. A novel trapezoidal intuitionistic fuzzy information axiom approach: An application to multicriteria landfill site selection. Eng. Appl. Artif. Intell. 2018, 67, 157–172. [Google Scholar] [CrossRef]
- Li, X.H.; Chen, X.H. Value determination method based on multiple reference points under a trapezoidal intuitionistic fuzzy environment. Appl. Soft Comput. 2018, 63, 39–49. [Google Scholar] [CrossRef]
- Wan, S.P.; Yi, Z.H. Power Average of Trapezoidal Intuitionistic Fuzzy Numbers Using Strict t-Norms and t-Conorms. IEEE Trans. Fuzzy Syst. 2016, 24, 1035–1047. [Google Scholar] [CrossRef]
- Ye, J.F. Aggregation operators of trapezoidal intuitionistic fuzzy sets to multicriteria decision making. Int. J. Intell. Inf. Technol. 2017, 13, 1–22. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wu, J.; Liang, C.Y. Some Einstein aggregating operators for trapezoidal intuitionistic fuzzy MAGDM and application in investment evolution. J. Intell. Fuzzy Syst. 2017, 32, 63–74. [Google Scholar] [CrossRef]
- Liang, C.Y.; Zhao, S.P.; Zhang, J.L. Multi-criteria group decision making method based on generalized intuitionistic trapezoidal fuzzy prioritized aggregation operators. Int. J. Mach. Learn. Cybern. 2017, 8, 597–610. [Google Scholar] [CrossRef]
- Wan, S.P.; Zhu, Y.J. Triangular intuitionistic fuzzy triple bonferroni harmonic mean operators and application to multi-attribute group decision making. Iran. J. Fuzzy Syst. 2016, 13, 117–145. [Google Scholar] [CrossRef]
- Saini, N.; Bajaj, R.K.; Gandotra, N.; Dwivedi, R.P. Multi-criteria Decision Making with Triangular Intuitionistic Fuzzy Number based on Distance Measure & Parametric Entropy Approach. Procedia Comput. Sci. 2018, 125, 34–41. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, F.; Lin, L.L.; Dong, J.Y. Some new generalized aggregation operators for triangular intuitionistic fuzzy numbers and application to multi-attribute group decision making. Comput. Ind. Eng. 2016, 93, 286–301. [Google Scholar] [CrossRef]
- Qin, Q.D.; Liang, F.Q.; Li, L.; Chen, Y.W.; Yu, G.F. A TODIM-based multi-criteria group decision making with triangular intuitionistic fuzzy numbers. Appl. Soft Comput. 2017, 55, 93–107. [Google Scholar] [CrossRef]
- Chen, Z.S.; Chin, K.S.; Ding, H.; Li, Y.L. Triangular intuitionistic fuzzy random decision making based on combination of parametric estimation, score functions, and prospect theory. J. Intell. Fuzzy Syst. 2016, 30, 3567–3581. [Google Scholar] [CrossRef]
- Dong, J.Y.; Wan, S.P. A new method for prioritized multi-criteria group decision making with triangular intuitionistic fuzzy numbers. J. Intell. Fuzzy Syst. 2016, 30, 1719–1733. [Google Scholar] [CrossRef]
- Wan, S.P.; Lin, L.L.; Dong, J.Y. MAGDM based on triangular Atanassov’s intuitionistic fuzzy information aggregation. Neural Comput. Appl. 2016, 28, 1–16. [Google Scholar] [CrossRef]
- Lian, T.; Yu, C.; Wang, Z.; Hou, Z. The evaluation study on tourism websites: From the perspective of triangular intuitionistic fuzzy multiple attribute group decision making. J. Appl. Stat. 2017, 44, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.J.; Nan, J.X.; Li, D.F.; Li, Y.X. TOPSIS for MADM with triangular intuitionistic fuzzy numbers. Oper. Res. Manag. Sci. 2012, 21, 96–101. (In Chinese) [Google Scholar]
- Yang, M.S.; Ko, C.H. On a class of fuzzy c-numbers clustering procedures for fuzzy data. Fuzzy Sets Syst. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Wang, J.Q.; Zhou, P.; Li, K.J.; Zhang, H.Y.; Chen, X.H. Multi-criteria decision-making method based on normal intuitionistic fuzzy-induced generalized aggregation operator. TOP 2014, 22, 1103–1122. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, K.J.; Zhang, H.Y. Multi-criteria decision- making method based on induced intuitionistic normal fuzzy related aggregation operators. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2012, 20, 559–578. [Google Scholar] [CrossRef]
- Liu, P.D. Multiple Attribute Decision-Making Methods Based on Normal Intuitionistic Fuzzy Interaction Aggregation Operators. Symmetry 2017, 9, 261. [Google Scholar] [CrossRef]
- Yang, Z.L.; Han, W. A Vertical Projection Distance-Based Method for Multi-Attribute Decision Making with Intuitionistic Normal Fuzzy Numbers. J. Resid. Sci. Technol. 2016, 13. [Google Scholar] [CrossRef]
- Liu, Z.M.; Liu, P.D. Normal intuitionistic fuzzy Bonferroni mean operators and their applications to multiple attribute group decision making. J. Intell. Fuzzy Syst. 2015, 29, 2205–2216. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Intuitionistic fuzzy Bonferroni means. IEEE Trans. Syst. Man. Cybern. 2011, 41, 568–578. [Google Scholar] [CrossRef]
- Bonferroni, C. Sulle medie multiple di potenze. Boll. Mat. Italiana 1950, 5, 267–270. [Google Scholar]
- Zhu, B.; Xu, Z.; Xia, M. Hesitant fuzzy geometric Bonferroni means. Inf. Sci. 2012, 205, 72–85. [Google Scholar] [CrossRef]
- Liu, P.D.; Hen, S.M.; Liu, J.L. Multiple attribute group decision making based on intuitionistic fuzzy interaction partitioned Bonferroni mean operators. Inf. Sci. 2017, 411, 98–121. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Q. A multi-criteria decision making procedure based on interval-valued intuitionistic fuzzy Bonferroni means. J. Syst. Sci. Syst. Eng. 2011, 20, 217–228. [Google Scholar] [CrossRef]
- Li, B.L.; Wang, J.R.; Yang, L.H.; Li, X.T. Multiple Criteria Decision Making Approach with Multivalued Neutrosophic Linguistic Normalized Weighted Bonferroni Mean Hamacher Operator. Math. Probl. Eng. 2018, 2018, 1–23. [Google Scholar] [CrossRef]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions, Aggregation Functions: A Guide for Practitioners; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; pp. 39–122. [Google Scholar]
- Liu, P.D.; Liu, J.L.; Merigó, J.M. Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl. Soft Comput. 2018, 62, 395–422. [Google Scholar] [CrossRef]
- Liu, P.D. Multiple attribute group decision making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput. Ind. Eng. 2017, 108, 199–212. [Google Scholar] [CrossRef]
- Yu, D.J. Intuitionistic fuzzy geometric Heronian mean aggregation operators. Appl. Soft Comput. 2013, 13, 1235–1246. [Google Scholar] [CrossRef]
- Yu, D.J. Hesitant fuzzy multi-criteria decision making methods based on Heronian mean. Technol. Econ. Dev. Econ. 2015. [Google Scholar] [CrossRef]
- Yu, D.J.; Wu, Y.Y. Interval-valued intuitionistic fuzzy Heronian mean operators and their application in multi-criteria decision making. Afr. J. Bus. Manag. 2012, 6, 4158–4168. [Google Scholar] [CrossRef]
- Yu, D.J. Group Decision Making Based on Generalized Intuitionistic Fuzzy Prioritized Geometric Operator. In. J. Intell. Syst. 2012, 27, 635–661. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Zhu, B. Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm. Knowl. Based Syst. 2012, 31, 78–88. [Google Scholar] [CrossRef]
- Wang, W.Z.; Liu, X.W. Intuitionistic Fuzzy Geometric Aggregation Operators Based on Einstein Operations. Int. J. Intell. Syst. 2011, 26, 1049–1075. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Trans. Fuzzy Syst. 2012, 20, 923–938. [Google Scholar] [CrossRef]
- Wu, Q.; Wu, P.; Zhou, L.G.; Chen, H.Y.; Guan, X.J. Some new Hamacher aggregation operators under single-valued neutrosophic 2-tuple linguistic environment and their applications to multi-attribute group decision making. Comput. Ind. Eng. 2018, 116, 144–162. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. A generalization of operators on intuitionistic fuzzy sets using triangular norms and conforms. Notes Intuit. Fuzzy Sets 2002, 8, 19–27. [Google Scholar]
- Tian, J.F.; Pedrycz, W. New refinements of generalized Hölder’s inequality and their applications. Math. Inequal. Appl. 2016, 19, 805–822. [Google Scholar] [CrossRef]
- Tian, J.; Ha, M.H. Properties and refinements of Aczél-type inequalities. J. Math. Inequal. 2018, 12, 175–189. [Google Scholar] [CrossRef]
- Tian, J.; Yang, Z.H. Generalizations of Hu-type inequalities and their applications. J. Nonlinear Sci. Appl. 2017, 11, 1971–1985. [Google Scholar] [CrossRef]
- Tian, J.F. Triple Diamond-Alpha integral and Hölder-type inequalities. J. Inequal. Appl. 2018, 2018, 111. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.F.; Ha, M.H.; Wang, C. Improvements of generalized Hölder’s inequalities and their applications. J. Math. Inequal. 2018, 12, 459–471. [Google Scholar] [CrossRef]
- Tian, J.F.; Ha, M.H. Properties of generalized sharp Hölder’s inequalities. J. Math. Inequal. 2017, 11, 511–525. [Google Scholar] [CrossRef]
- Tian, J.F.; Ha, M.H. Extensions of Hölder-type inequalities on time scales and their applications. J. Nonlinear Sci. Appl. 2017, 11, 937–953. [Google Scholar] [CrossRef]
- Yang, Z.L.; Li, J.Q.; Huang, L.C.; Shi, Y.Y. Developing dynamic intuitionistic normal fuzzy aggregation operators for multi-attribute decision-making with time sequence preference. Expert Syst. Appl. 2017, 82, 344–356. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).