1. Introduction
Cellular automata (CA) [
1] are computational model which consists of a grid of cells where each of the cells acts as a finite automaton. The neighborhood of a cell
in a two dimensional CA is the set of surrounding cells on which the updation of
depends upon. The updation of each cell is based on a transition function, which is called a rule of the CA. Data are represented as states of the cell in a CA. The states of each cell get updated in unit time steps in parallel, based on rules which are characterized by the neighborhood in synchronous fashion. The states of the CA get updated by the application of rules uniformly in each cell in the CA and it produces patterns at each time step. The output pattern of the CA shows the dynamic and complex behavior. One of the reasons for the complex behavior of the CA is due to the various properties exists in the CA rules. The pattern generated by the CA is the cumulative observation of the output of the CA in successive time steps.
Cellular automata have enormous applications in various domains such as engineering, physics, biology, etc. CA are used for modeling complex systems [
2,
3,
4,
5,
6]. This has motivated the interest to do the research on the structure of cellular automata. The major components of the CA are its rules that vary according to the number of states, the size of the neighborhood and the geometric structure of the lattice. Since, CA is used as a computational model to model complex problems; the underlying lattices of the CA are different in shape. The primary objective of this work is to propose a model which can represent various types of symmetric lattices and find out the behavior of the rules characterized by the proposed neighborhood structure. Here the neighborhood of a CA is viewed as a type of star graph, so the rules of the model vary according to the lattice structure and size of the neighborhood. In this proposed work, we classify the rules based on the internal symmetric behavior that exists in the rules, which are leading to a symmetric pattern.
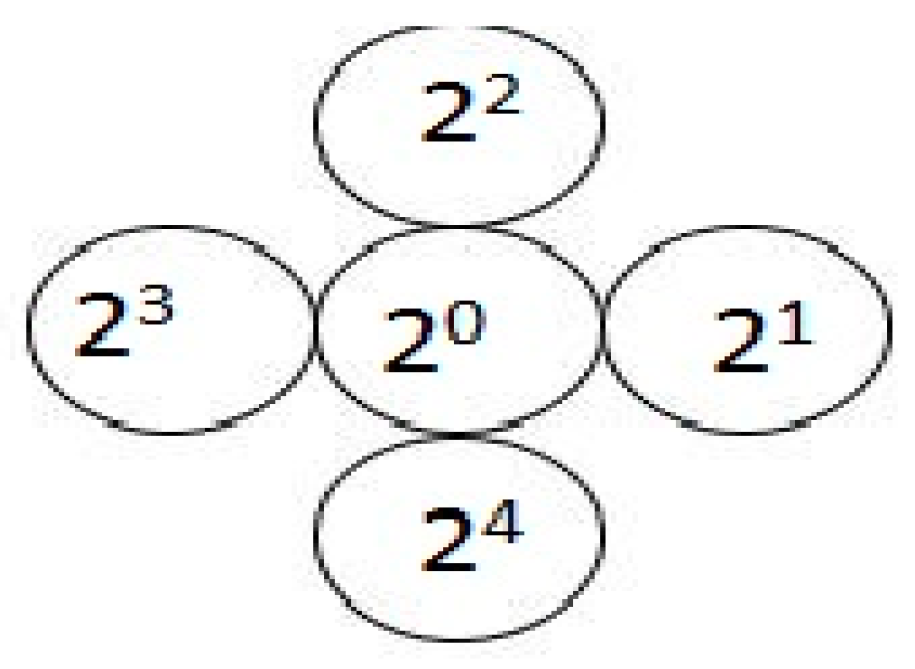
The existing neighborhood structures used in CA are using a fixed neighborhood structure for a specific lattice. Major neighboring structures such as vonNeumann neighborhood [
7] contains five neighborhood cells and the Moore neighborhood [
8] contains nine neighborhood cells for each cell in a two dimensional CA. Wolfram has done an extensive study on totalistic CA [
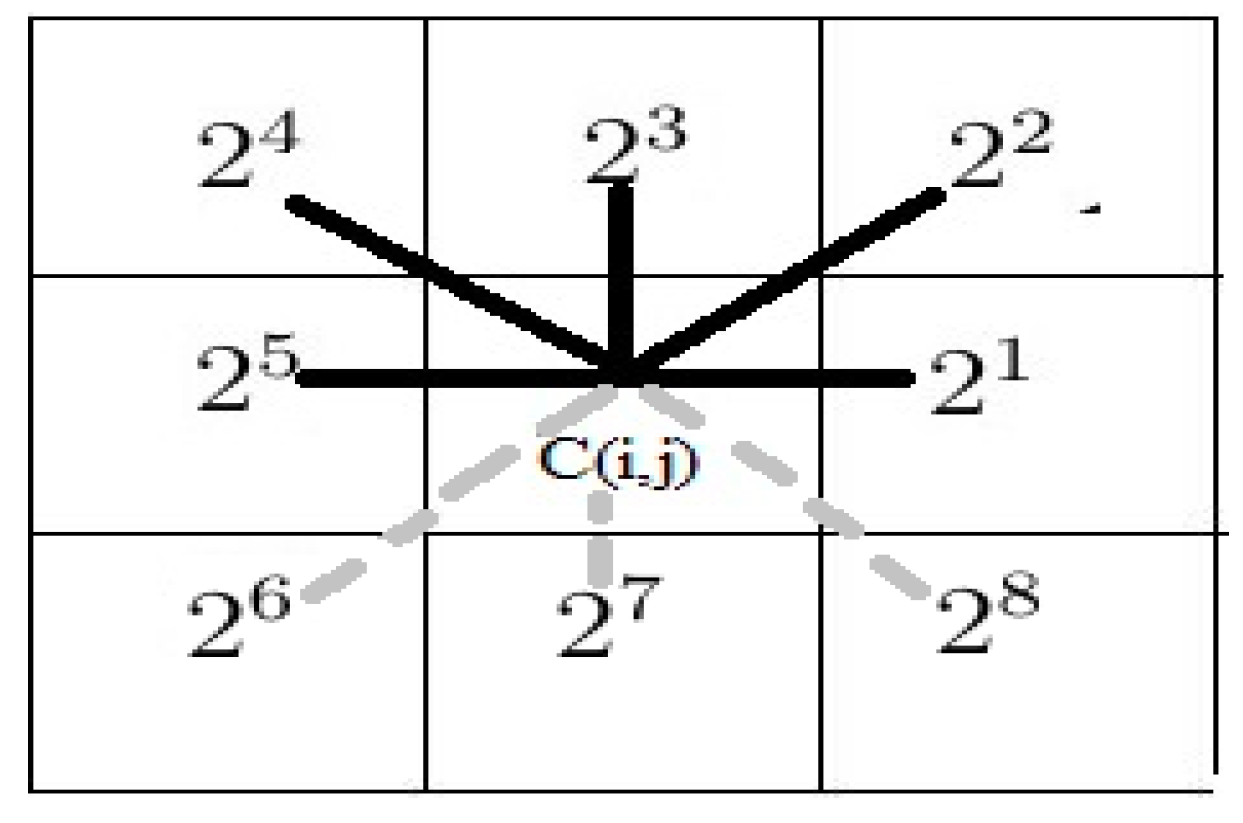
9] based on two dimensional cellular automata with the Moore neighborhood structure, where the updation of every cell in a CA is based on the sum of the state values of the neighborhood of every cell. A.R. Khan [
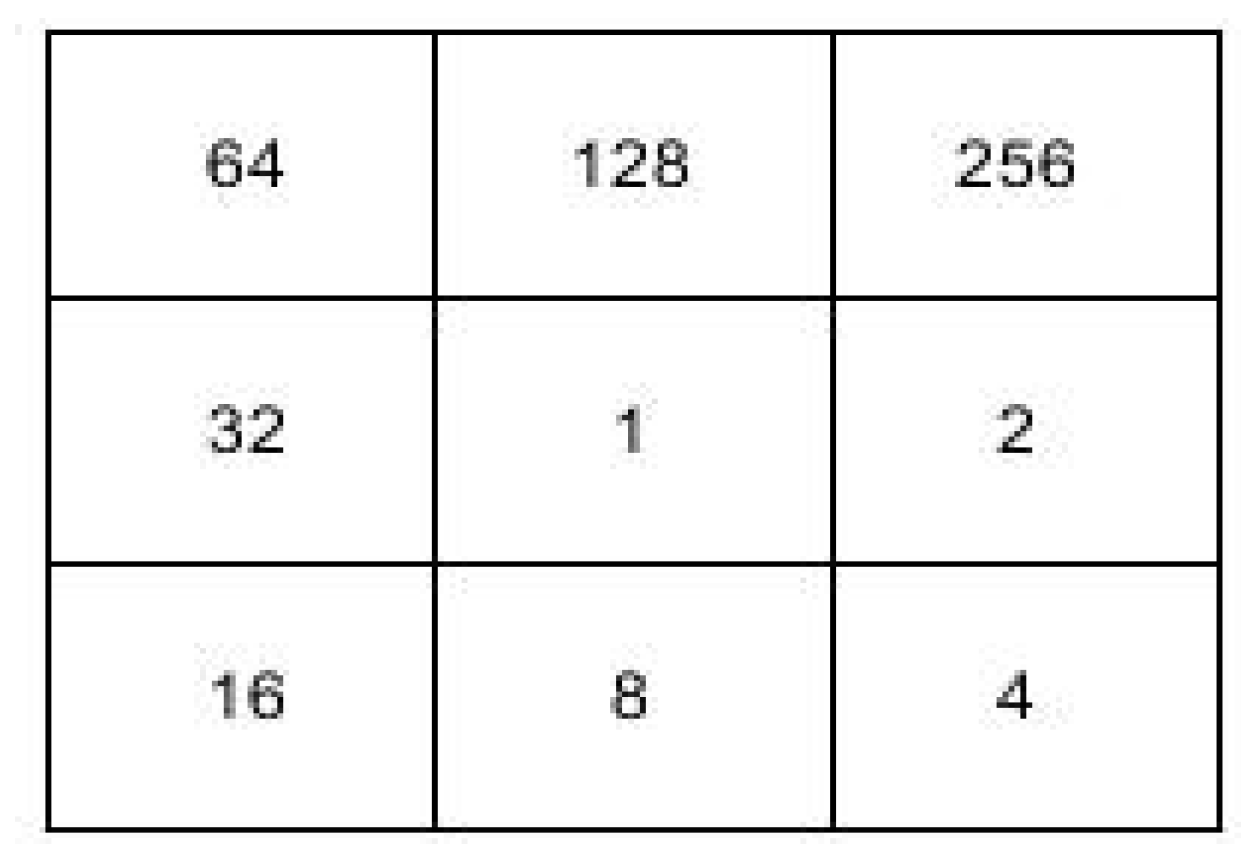
10] used a different approach to represent rules in a rectangular nine neighborhood CA. In a nine neighborhood CA, fixed positional weight is assigned [
10] to each cell in the neighborhood of a cell
to indicate the dependency of the neighborhood with the cell
to update the cell
. In Ref. [
10] rule 1 indicates the dependency of the cell
on itself. Rule 2 indicates the dependency of the cell
on its right neighborhood and rule 4 indicate the dependency of the cell
on its bottom diagonal cell; rule 8 indicates the dependency of the cell
on its bottom cell, etc. in such a way that the nine neighboring cells are considered as nine distinct rules.
Figure 1 refers to the two dimensional CA model described in [
10] shows the dependency of the neighborhood cells to the cell to be updated,
. In another approach, two dimensional CA is viewed as a tree [
11] with
cell structure where each cell has
neighbors. In Ref. [
11] the nodes are indexed by numbers
and the root node is indexed by
, the rules are defined based on the traditional approach [
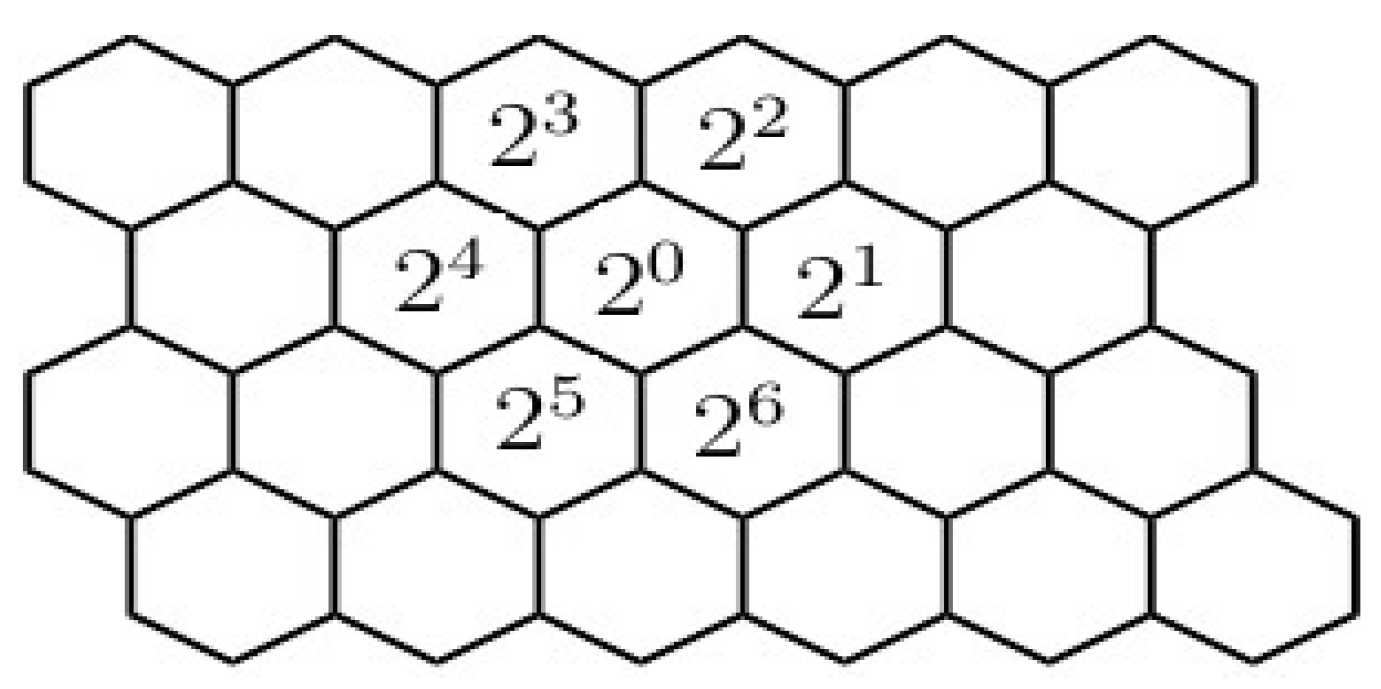
1]. In order to represent a hexagonal lattice, a seven neighborhood [
12] structure is used analogously to a CA model described in [
10]. To update a cell in a hexagonal lattice, the dependency of the six surrounding cells [
12] on the cell to be updated is considered. In Ref. [
12] analogous to the two dimensional model described in [
10] positional weight is assigned to each cell in clockwise direction to indicate the dependency of the neighborhood cells on the cells to be updated.
Cellular automata rules have the immense computation power. Depending upon the structure of the neighborhood and the nature of the operations used to define rules [
13], the characteristics of the rule may change. In order to find out an exact CA rule for a particular application, we need to classify the CA rules according to its properties. One such property that exists in the CA rule is the internal symmetry exists in it. The output pattern of CA at any iteration varies according to the rule of the CA. The various ways of classification of the rules are discussed in Ref. [
14], classification of CA rules into reversible rules, self-symmetric rules and symmetry on pair rules are using matrix algebra on a hexagonal neighborhood model. Linear CA rules are classified based on the patterns generated at
iteration [
15] using fixed positional weight 2D-CA model [
10]. Two dimensional CA rules are classified into symmetric rules and nonequivalent rules under black and white
transformations [
11] on the possible permutations in the rule table. Uniform group rules in a two dimensional cellular automata [
14] are classified into four classes based on the characteristic matrix called T matrix. Totalistic rules, outer totalistic rules [
9] are classified on a 2D-CA based on the number of neighborhoods considered for the updating of each cell.
Symmetry is a property existing in objects; it has a lot of applications [
16,
17,
18,
19] in day to day life in various fields. CA is used for modeling complex systems in various domains, in various types of underlying lattices. So a CA model which is capable of generating symmetric patterns helps to model lots of applications [
20] in various fields such as architecture, biology, human body, etc. where symmetry plays a vital role. Based on the symmetric nature of the CA rules, one can decide that whether the CA can generate symmetric patterns or not. Various studies exist on symmetry in CA rules based on various methods. Internal symmetries of CA rules based on permutation states [
21], β-calculus, and a universal map derived based on β-calculus [
22], discrete Walsh analysis [
23], and polynomial representation of one dimensional CA [
24] symmetropy [
25] are the various methods that exist to measure the symmetry of CA rules. If the rule possesses symmetry, it reflects in the output pattern. By modeling symmetric objects in a CA, one can identify the anomalies present in the objects easily based on the symmetric patterns generated from the objects. So, the main objectives of this paper are as follows.
In the absence of a generic CA model to represent various types of lattices, the main objective of this paper is to propose an angle-based CA model to accommodate various types of symmetric lattices and propose a generic mathematical equation to represent CA rules for any symmetric lattice. In this paper, we propose the classification of CA rules based on the amount of the internal symmetries that exists in the CA rules, which will lead to symmetric patterns generated by a CA.
3. Generic Rule Convention of nSG-CA Model
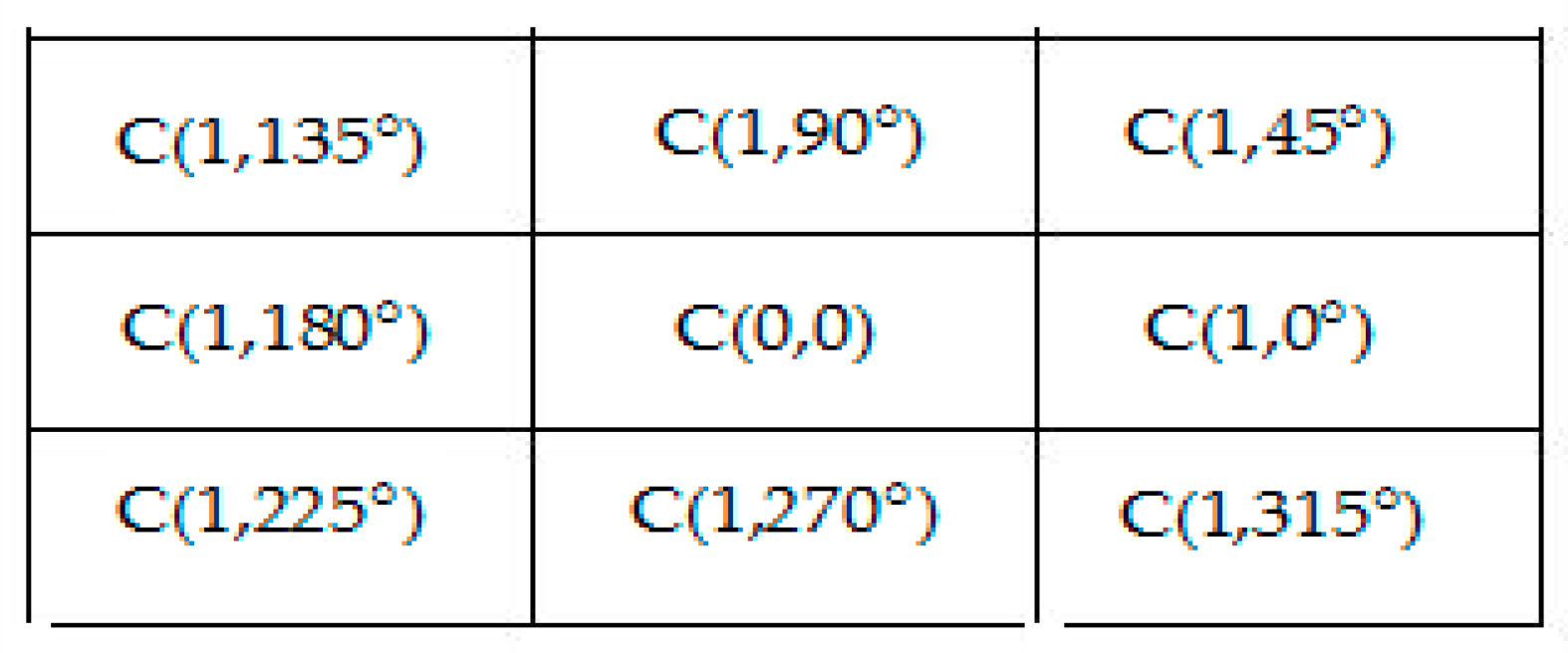
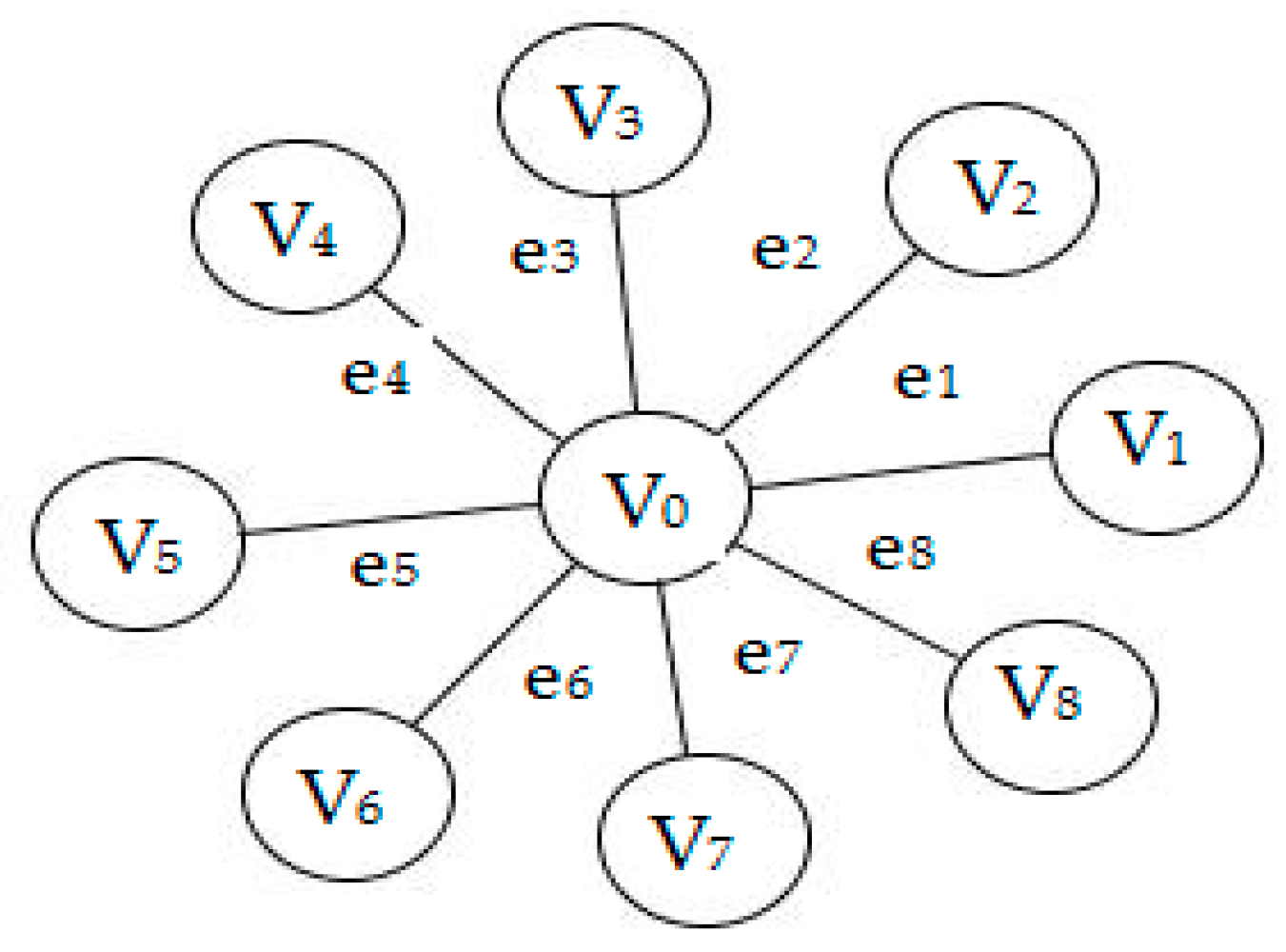
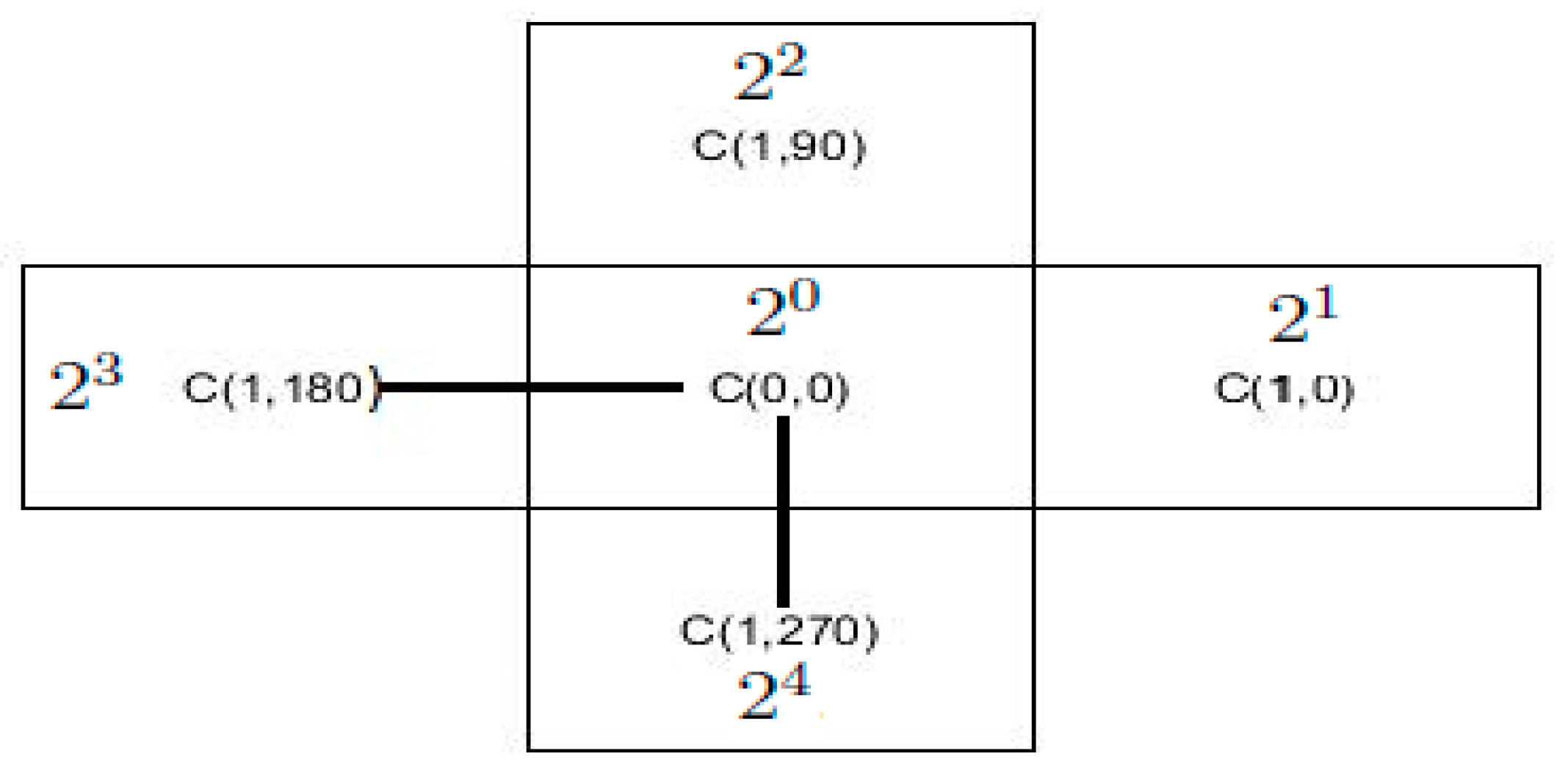
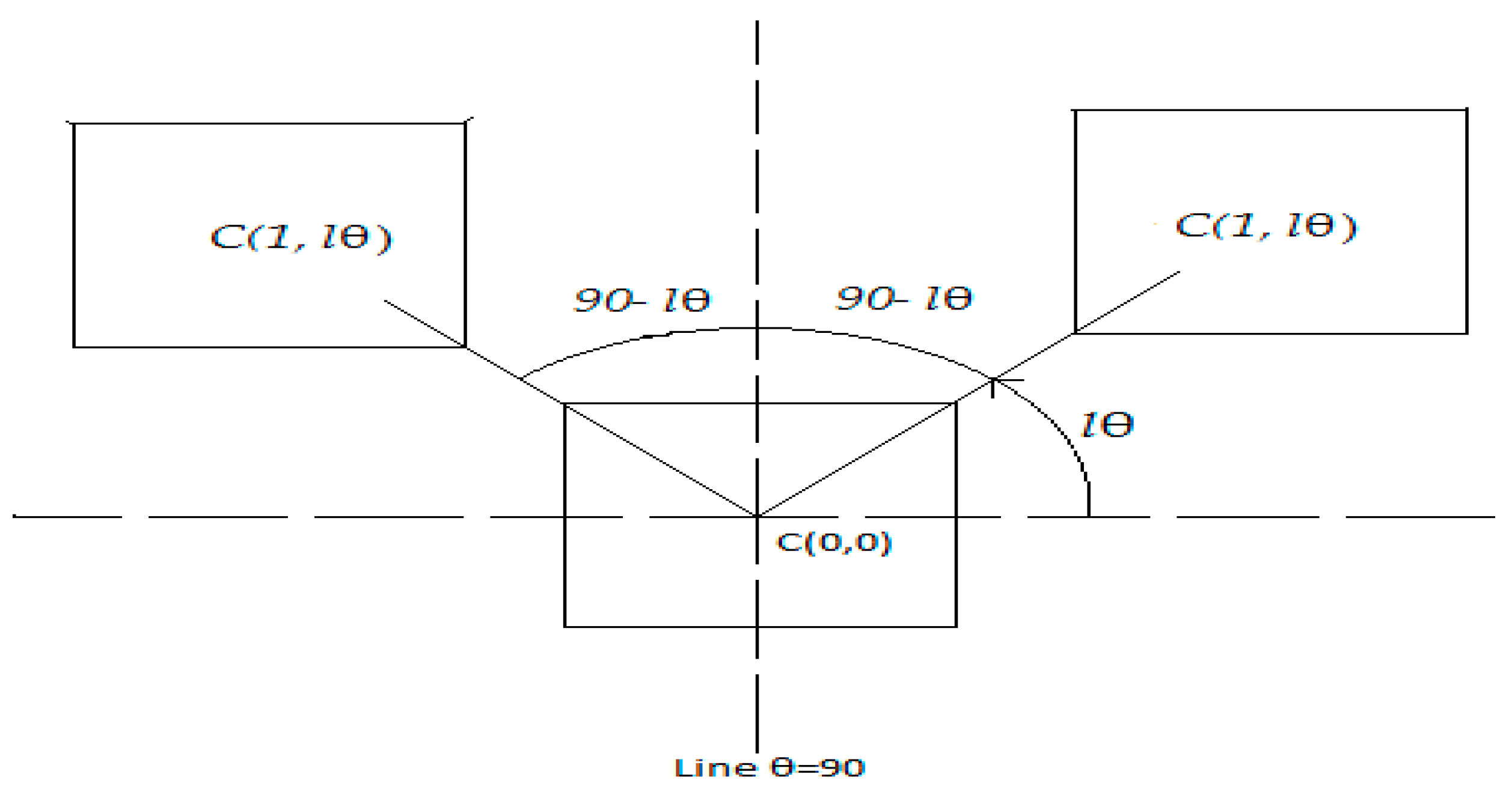
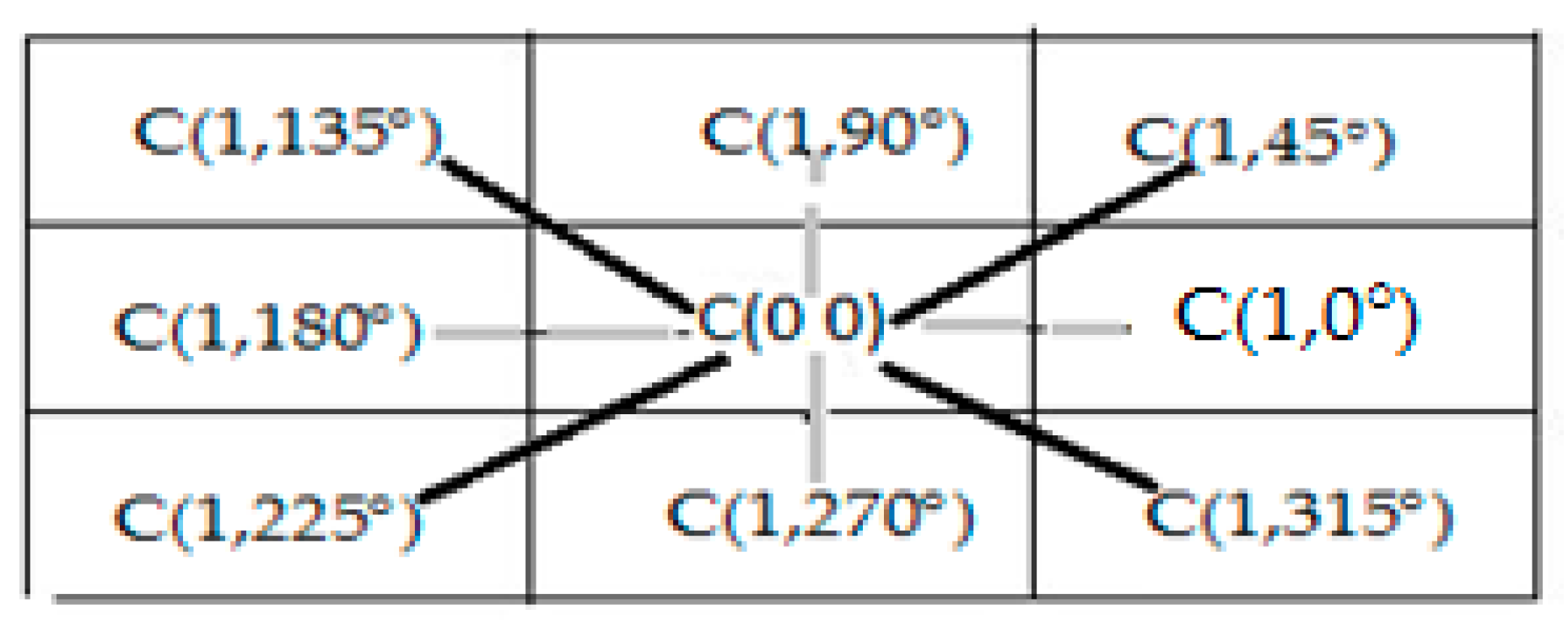
In a star graph CA, the state of each cell gets updated at every time step based on a rule, which is characterized by the neighborhood. A cell in the neighborhood of is indicated as , where is unit distance and is , the polar angle of the neighborhood cell. The CA rules are defined based on the dependency of the cell to be updated with the neighboring cells, i.e., the dependency of , the cell to be updated with , any cell in the neighborhood of is defined as that, the state of at every time step take part in the updation of The rule may depend on a maximum of cells in a neighborhood structure, which include the cell , and its N neighborhood in the unit distance. Different rules are used to update a cell , based on the dependency of with its neighbourhood cells.
Since rules are characterized by the neighborhood, every rule can also be represented as a star graph.
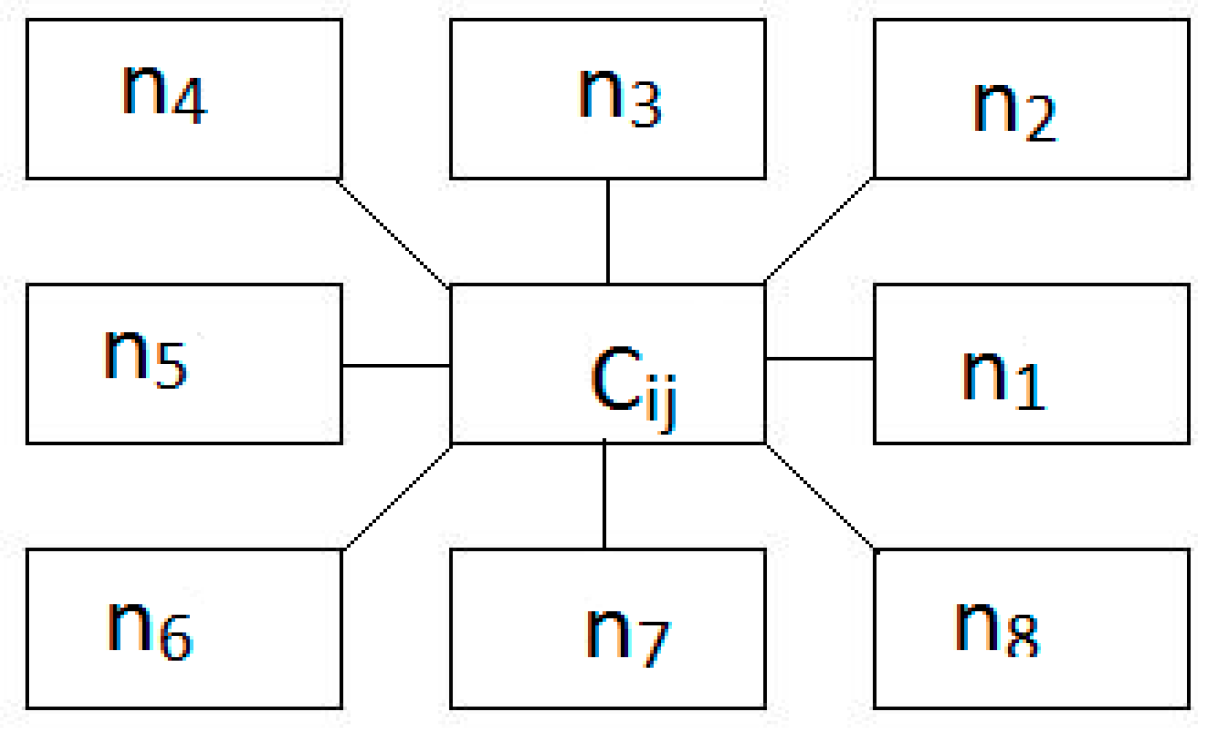
In order to distinguish the rules, a positional weight,
is assigned to each cell in the neighborhood. The positional weight of each cell
in the neighborhood w.r.t the
, the cell to be updated is determined by the equation,
where
is the polar angle of each neighborhood cells,
with the
the cell to be updated. The positional weight,
of the cell to be updated, is
. The positional weight of each cell varies according to the cell to be updated. In Equation (1), the positional weight,
, of each cell represents the rule number characterizing the dependency of the cell to be updated,
to each element
of its neighborhood cell. The
has got dependency only on itself, referred as rule 1. If the cell
has dependency on two or more cells, the rule number is calculated by the arithmetic sum of the rule numbers of the relevant cells.
For example, for a circular lattice shown in
Figure 5, five neighborhood structures are used. nSG-CA rule
refers to the three neighborhood dependency of the cell
to its three neighbors is calculated by the formulae
, where
is the positional weight of the cell to be updated (
). The total number of rules for a two dimensional CA depends on the value of neighborhood,
. The total number of rules of the nSG-CA model is
, which includes the rule characterizing no dependency. For an nSG-CA with a hexagonal lattice has 7 neighborhoods and its positional weight with respect to the cell to be updated (
) is shown in
Figure 6.
In this paper, X-OR is the operation used to update a cell based on its rule number. X-OR is a binary operator and it is commutative.
The total number of rules for different types of two dimensional lattice is different. For a hexagonal lattice, the size of the neighborhood for each cell || is 7, so the total rules are 27 = 128, in a square lattice, for each cell with five neighborhood has 32 rules and for each cell in a rectangular lattice with nine neighborhood can generate 512 rules. A variant of hexagonal lattice, where a cell is placed at every 30 w.r.t the cell to be updated has || = 13. So the total number of rules are 213. So in order to find out a rule for a particular application, classification of cellular automata is required.
4. Classification of Two Dimensional Cellular Automata Rules
One principal direction of research in cellular automata is to study the CA dynamics (patterns) which evolves in successive time steps. A detailed analysis of CA dynamics will enable us to understand the emergent behavior of a pattern and the computational capacity of a CA. In other words, CA classification based on the study of its dynamics has been the major focus of researchers. The CA dynamics vary according to the CA rules. To comprehend the behavior of the rules in the proposed model, it is necessary to have a classification based on their properties. Symmetry is a property exists in CA rules. If a CA rule is symmetric its equivalent pattern is also symmetric. Based on this property, classification of CA rules of nSG-CA model for any heterogeneous symmetric lattice is discussed. Since the nSG-CA model is a type of star graph representation of the neighborhood structure, rules are characterized by the neighborhood, each rule in an nSG-CA can also be represented as a star graph. In order to distinguish the neighborhood structure and rule, the star graph representation of a rule is denoted as r-star graph, where r denote rule.
Definition 7 (r-star graph). It is a subgraph of n-star graph, in which all the vertices and edges are the subsets of nSG-CA.
In order to measure the symmetry in a star graph, graph automorphism [
26] can be used.
Definition 8 (Isomorphic graph). Two graphsandare isomorphic graphs ifstructure preserving vertex bijection.
Definition 9 (Vertex bijection in a graph). A vertex bijectionbetween two graphsandif, the total number of edges between every pair of verticesandin graphis equal to the total number of edges between their imagesand) in graph G2. A vertex bijectionis structure preserving ifandare adjacent in⇔andare adjacent in.
Definition 10 (Graph automorphism). An automorphism of a graph G is the isomorphism [26] with itself, i.e., structure preserving vertex bijection . The set of automorphisms defines a permutation group known as the automorphisms group. A permutation
of
is an automorphism of
if for all
,
then,
. The set of automorphisms of a graph
under the operation, composition of functions, forms a subgroup of the symmetric group of
called the automorphism group [
26,
27] of G. For example, the total number of automorphism for a star graph (
) is
. In Ref. [
28], graph automorphism is used to find the symmetries in a cellular automata, where the global dynamics of a CA are viewed as a graph. So, the concept of graph automorphism can be used as a transformation in an r-star graph to measure the symmetry in a rule.
4.1. CA Rules Based on Symmetry
The r-star graph representation of rule 62 in a rectangular lattice with nine neighborhood nSG-CA is shown in
Figure 7. In rule 62, the cell
depends on five neighborhood cells among nine neighborhoods for its updation. The dependant cells of
are marked using bold line and the nondependant cells are marked using a dotted line in the r-star graph representation of rule 62.
4.1.1.Representation of a given rule
A rule
can be represented as
where
is coefficient and
,
is the multiplication operator.
For example, Rule 25 in a rectangular lattice with five neighborhoods can be represented as shown in
Figure 8.
Automorphisms of a graph is a permutation of its vertex set that preserves incidences of vertices and edges. Since automorphism of a graph is a structure preserving vertex bijection, a transformation is required for the possible mapping of vertices in the r-star graph. So a transformation called -transformation is defined as follows.
Definition 11 (-transformation). Letbe a rule in nSG-CA, where, letbe a transform on the rule, where.
The
-transform on
is defined as,
The set of all -transformations of the rule are the set of automorphisms of the r-star graph; that is . It is equivalent to the total automorphisms of the star graph.
Definition 12 (Symmetric rule). A ruleis said to be symmetric rule, if ∃ a bijectivetransformation such that.
One of the major focus of this work is to find out the symmetric rules (local internal symmetry), which generate symmetric patterns w.r.t. the line . The following theorem supports to define the symmetry in rules w.r.t vertical axis, line .
Theorem 1. In a two state two dimensional nSG-CA, the reflection of the edgew.r.t linein the r-star graph of any ruleis.
Proof. Without loss of any generality, we assume a rectangular lattice for two dimensional nSG-CA. Let
be a cell in the neighborhood of
. By the description of our nSG-CA model, the polar angle(
, between the edge
with the initial line is
. Then the angle between the edge
with the axis of reflection
is
. In a reflection of a line w.r.t an axis, the axis of reflection should bisect the angle between the original line and the reflected line. The only line which will make an angle
with the axis of reflection
is the edge of the star graph which will have a polar angle of
=
, as shown in
Figure 9, i.e. in our nSG-CA model, edge,
can have an angle of
with the pole. Further, we observe that line
is the perpendicular bisector of the angle between the edges (
and (
. Hence the reflection of the edge (
w.r.t line
is (
. This completes the proof.
Based on the above Theorem 1, the symmetry in rules w.r.t. the line , which is denoted as self symmetry is defined.
Definition 13 (Self-symmetry in a rule). A ruleis said to be self symmetric in the r-star graph, if it satisfies the following conditions:
- 1.
is a symmetric rule, whereis a bijective transform of
- 2.
if and only if
Definition 14 (Pairwise symmetric rules). Letbe a rule in an r-star graph, where. Let a transformon the rule. The rulesandare said to be pairwise symmetric rules if.
4.2. Algorithm to Identify the Nature of Symmetry in CA Rules
The following algorithm (Algorithm 1) is used to identify the nature of symmetry in CA rules.
| Algorithm 1. Identification of type of symmetry in a rule. |
Input: Rule number, or Conclude that
Output: Returns the pairwise symmetric pair rules of f or
Conclude that f is self-symmetric |
| Initialization | 1 Let be a partition of with coefficient 1
2 Let be a horizontal line passing through the cell to be updated on -Axis.
3 Initialize variables, , and as 0 |
| Iteration for partition checking | 4 for each in
5 case 1:
6 Let and be two partitions coincide with such that is on the left side and is on the right side w.r.t the cell to be updated.
7 Assign |
| Partition is in upper half | 8 If
9 If
10
11
12
13
14
15
16 case 2: |
| Partition is in the lower half | 17 where
18
19
20
21
22
23
24 case 3:
25
26
27 |
| Partition checking iteration | 28 |
| Nature of rule | 29 given rule is self-symmetric
30 else
31 rules are pairwise symmetric |
4.2.1. Description of Algorithm
The algorithm to identify the nature of symmetry for a given rule is shown in Algorithm1. In order to identify the nature of symmetry exists in a rule, the given rule is partitioned into powers of 2 based on the Equation (2). Assuming that a horizontal line L is passed through the cell to be updated and it contains two partitions such as in the left side of cell to be updated and in the right side of the cell to be updated. Each partition of a rule is either at the top or bottom of the line L. Thus, two cases are considered. Case 1 checks whether the partition is in the top of the line L or not and find out the equivalent reflection of each partition. Case 2 checks for the partitions which are in the bottom of the line L and find out its equivalent reflections. Case 3 checks whether the partition includes the cell to be updated or not and find out the reflection. If the sum of the reflections of a rule is same as the given rule number, then conclude that the given rule is self-symmetric and the sum of the reflections of its partitions of the given rule differs from the given rule, then conclude that they are pairwise symmetric rules. The Algorithm 1 takes polynomial time complexity only to check the nature of the rules.
4.2.2. Illustration
Consider a rule 25 in a hexagonal lattice with seven neighborhoods. The partitions of the rule 25 with coefficient 1 are , , and . Consider each of the partitions, as , then equals so, the image is . The second partition is , so consider as which is lesser than , then , i.e., 1. Then the image is i.e., . The third partition is , then the image is itself. So the sum of , , and is 7, which is not equal to 25. So conclude that rule 7 and rule 25 are pairwise symmetric rules in a hexagonal lattice with seven neighborhoods.
4.3. Global Symmetry (Symmetry in Pattern)
The local internal symmetry of the rule
is discussed in the session 4.2. The connection between local internal symmetries and the dynamics of nSG-CA is provided by global symmetries, which are obtained as concatenations of local internal symmetries.
Figure 10 shows the r-star graph of a self-symmetric rule, in the figure 10, the edges present in the r-star graph is marked as bold. If the rule is self symmetric, the cell state set of the rule is partitioned into three disjoint sets w.r.t. the vertical line. They are as follows:
- (a)
State set in the left side of the vertical line;
- (b)
State set on the right side of the vertical line;
- (c)
State set is on the vertical line.
To illustrate this, let us consider a rule
,
is a transform of the rule
since
and
is a symmetric rule,
are local internal symmetries of the rule
as shown in the
Figure 10. The cell state set of
is
can be divided into three sets. They are,
is on the left side of the vertical line
is in the right side of the vertical line
is the cell on the vertical line.
nSG-CA is a dynamical system x, where evolution is the state space x, is obtained in discrete steps by the repeated iteration of the global evolution rule.
x, → x, , where . The global evolution rule is induced by a local rule x, , is the number of neighbors of the central cell. If is self symmetric, then the rule set can be partitioned into three disjoint sets. Let is the cells of the left side, is the cells on the right side of the vertical line, , and is on the vertical line. For the input configuration , the evolving state set of and the evolving state of are symmetric, because of the internal symmetry of each cell. The evolving state set of are also symmetric since, cells of are on the vertical line. Therefore, the self-symmetric rule generates symmetric pattern , which is symmetric w.r.t. line obtained by , and act on an input configuration .
5. Results
There are two types of symmetric rules with respect to line
in an nSG-CA model. They are pairwise symmetric rules and self-symmetric rules. The nSG-CA model is based on null boundary conditions. X-OR is considered as the operator for the experiments. Consider a rectangular lattice with five neighborhood cells.
Figure 11 shows the initial seed image, where
represents 1 and space represents 0. In order to generate a pattern, X-OR operation is applied to all the cells in the neighborhood with the cell to be updated. The uniform rule is applied to all the cells w.r.t the cell to be updated at each time step in parallel. Null boundary conditions are applied. The symmetry axis is a vertical line passing through 90
.
Figure 12 shows the pattern of rule 19 and rule 25 in a rectangular lattice with five neighborhood structure. The evolving pattern in four iterations are shown in the
Figure 12. From the figure, it is observed that both the patterns are pairwise symmetric. i.e., symmetric with respect to axis,
.
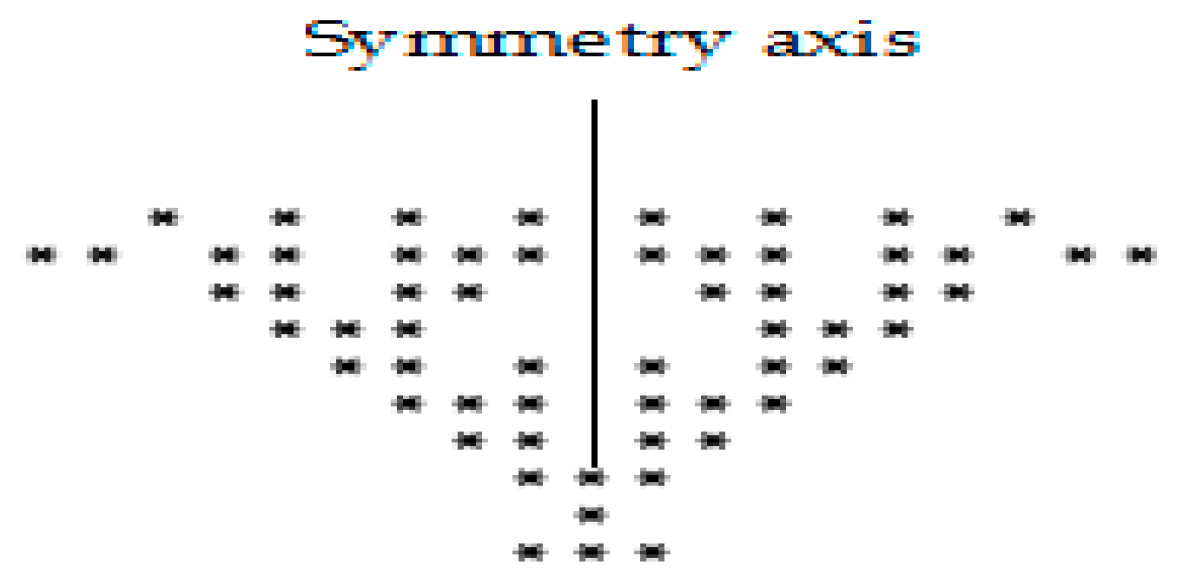
Figure 13 shows the pattern of the rule 31 in a rectangular lattice with five neighborhoods at 8th iteration, which shows a self-symmetric pattern.
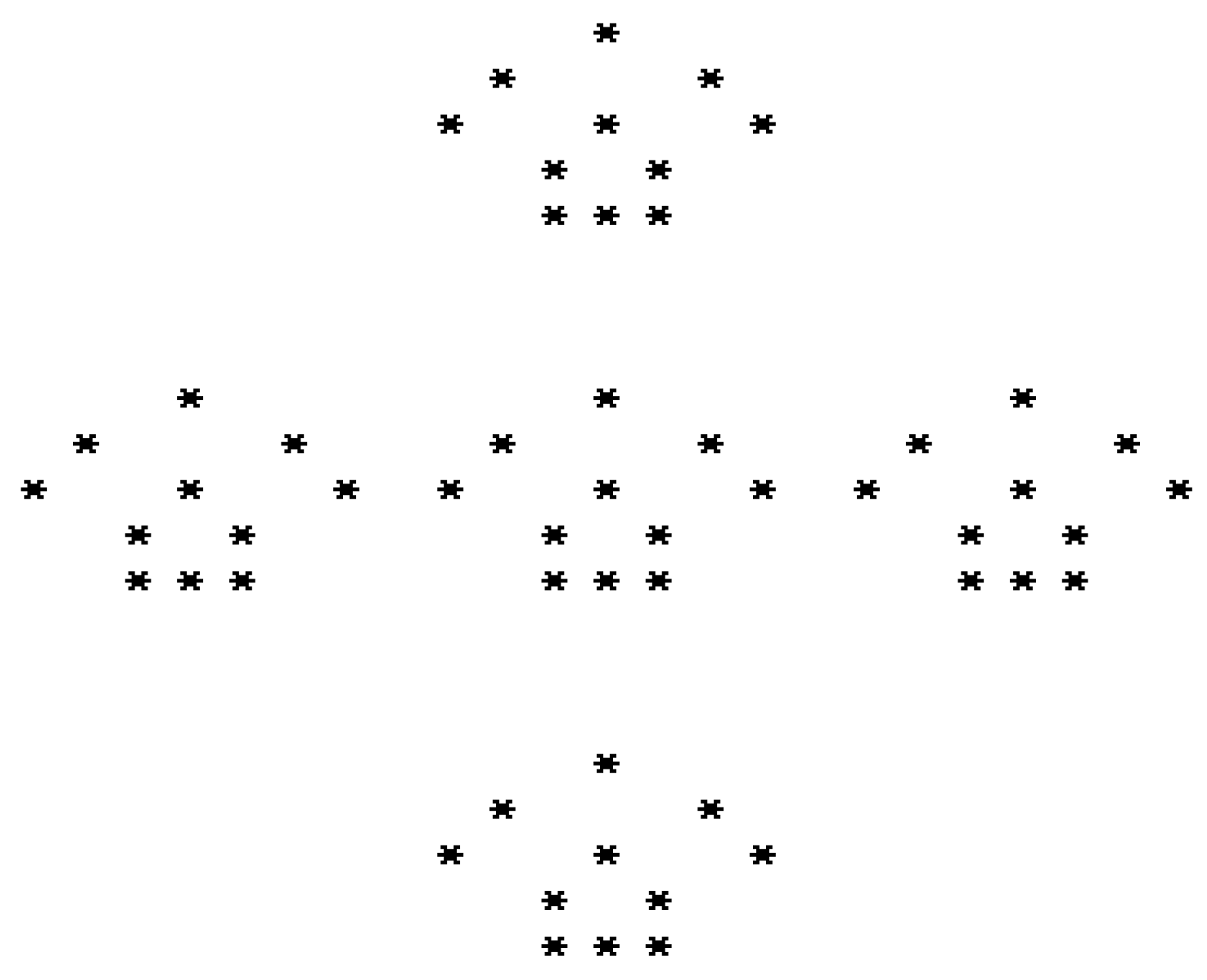
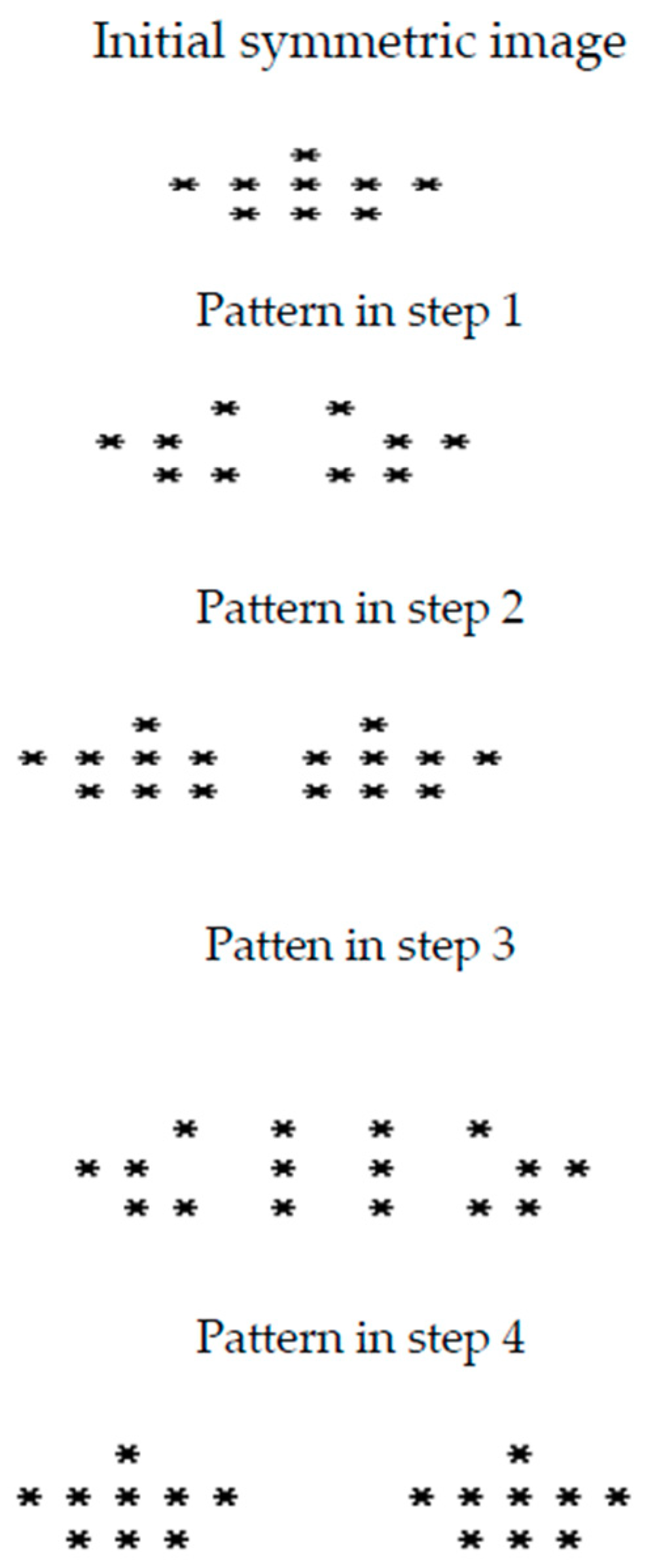
In order to understand the behavior of the X-OR rule, an evolution of X-OR for four iterations on a symmetric initial seed is shown in
Figure 14. From this, one can observe that if the input is symmetric and if we apply a symmetric rule it generates a symmetric pattern at every time step.
The classification of symmetric rules in a rectangular lattice with five neighborhood is shown in
Table 1. The total 31 rules are classified into five classes based on the number of cells dependent on the cells to be updated among the five neighborhood cells. Thus
5C
1 indicates dependency of one neighborhood to the cell to be updated among five neighborhoods;
5C
2,
5C
3,
5C
4,
5C
5 indicates the dependency of two, three, four, and five neighborhood cells to the cell to be updated, respectively.
Consider a hexagonal lattice with seven neighborhoods and an initial seed image shown in
Figure 11. Then,
Figure 15 and
Figure 16 indicate two pair rules which are generating pairwise symmetric patters.
Figure 16 indicates the pattern of rule 28 in a hexagonal lattice for six iterations. The Pattern generated for Rule 14 in a hexagonal lattice for six iterations is shown in
Figure 16. Self-symmetric pattern of rule 97 for eight iterations is shown in
Figure 17.
The classification of symmetric rules in a hexagonal lattice with seven neighborhood cells are shown in
Table 2. There are 128 rules in a two dimensional CA with hexagonal lattice including rule 0. These rules are classified into seven classes based on the number of cells dependent on the cells to be updated among the seven neighborhood cells. Thus
7C
1 indicates dependency of one neighborhood to the cell to be updated among seven neighborhoods cells;
7C
2,
7C
3,
7C
4,
7C
5,
7C
6,
7C
7 indicates the dependency of two, three, four, five, six, and seven neighborhood cells to the cell to be updated respectively. PR denote pairwise symmetric rules, which are mentioned in brackets and self-denote the self-symmetric rules in a two dimensional CA with hexagonal lattice. There are no pairwise symmetric rules in
7C
7 category.
6. Discussion
In order to simulate various complex systems, where the underlying lattices may be different in nature using cellular automata, the angle based model is used. nSG-CA model can be used to accommodate various types of neighborhood structures with the angle() concept. The generic rule convention used in nSG-CA generates unique rules for each symmetric lattice. Every rule in an nSG-CA model with a specific lattice gets a unique number i.e., no two rules have the same number in a lattice.
The algorithm proposed in this paper can be used to check the symmetric nature of each rule in a specific lattice. In order to measure the symmetry in a rule, which is represented as r-star graph, a -transform based on graph automorphism is used. A rule is said to be symmetric if .
Self-symmetric rule is defined based on subset of -transform, i.e., a rule is self-symmetric w.r.t the line , if the reflection of all the vertices in the r-star graph w.r.t line is a vertex in the r-star graph if self. The self-symmetric rules generate self-symmetric patterns if the input data are symmetric. A mechanism is discussed in this paper to reflect the self-symmetry exists in a rule to the output pattern (global symmetry). Pairwise symmetric rules are also defined based on -transformation. Two pairwise symmetric rules together generate a bilateral symmetric pattern if the input is symmetric.
The angle concept used in this work is as follows, the polar angle and input angle () are the key parameters of this work. With the input angle, we can accommodate any two dimensional symmetric lattices in a CA. A generic rule convention, which suits for any symmetric lattice could derive with relationship between the polar angle and input angle of cells in a two dimensional CA. In order to find the symmetry in rules, -transform is used based on the angle. So, with one parameter, all the concepts discussed in this work are covered.
6.1. Applications of the Proposed nSG-CA Model
Symmetry is a property observed in many objects in our day to day life, such as architectures, arts, natural objects, human body, etc. has a lot of applications in our day to day life [
29]. Bilateral symmetry i.e., vertical symmetry computation of shapes and images is a basic problem in computer vision, image processing, and mathematics. The work, such as the use of bilateral symmetry in facial recognition [
30,
31], 3D face authentication, and recognition based on bilateral symmetry analysis [
32,
33], bilateral symmetry in modeling the human body to recognize an automated person [
34], and in feature restoration to recover features that are invisible [
34], has used bilaterally symmetry analysis of the pattern generated from the models; CA is used for image processing [
35] applications.
The main application of the nSG-CA model is to find out the asymmetry in symmetric images such as brain anomaly detection, anomaly detection in mammograms, etc. The brain exhibits a high level of bilateral symmetry and it gets violated in the presence of an anomaly. So with the pairwise symmetric rules, one can find out the anomaly in brain images. Similarly like any other objects which exhibits symmetry with respect to line .
Since CA is used for modeling complex systems [
36], the nSG-CA model is suitable for modeling different types of symmetric regular lattices such as the square lattice, rectangular lattice, hexagonal lattice, etc. In crashworthy applications, in order to absorb more crash energy, different variants hexagonal lattice such as honeycomb structures [
37,
38] where cells are placed in
etc. are used. Since cellular automata can be used as a platform to simulate crash worthy applications [
39], using the nSG-CA model, one can simulate any applications with honeycomb structures because, the representation of honeycomb structure is easy with this proposed model. Moreover, all the rules of the proposed model are bilaterally symmetric. Since the symmetric rules are capable of generating symmetric patterns, using this nSG-CA model, one can generate symmetric patterns based on various types of lattice to model various complex systems.
6.2. Comparison with Existing Models
The existing two dimensional CA models such as the Moore neighborhood [
1] and von Neumann neighborhood [
8] are used for the representation of rectangular lattices with nine neighborhoods and five neighborhoods. Other fixed weight neighborhood models [
10] and the seven neighborhood hexagonal model [
12], which is based on the fixed weight neighborhood model, also exist. Instead of multiple models, one can represent any symmetric lattice such as a rectangular lattice, hexagonal lattice, circular lattice, square lattice, etc. using the nSG-CA model based on an angle itself.
In many of the applications, in order to generate bilateral symmetric patterns i.e., vertical symmetric patterns, pairwise symmetrical CA rules are required. The classification of symmetric rules discussed in [
14,
15,
16] requires exponential time complexity to identify a pairwise symmetric rules which can generate a bilateral symmetric pattern, because they are defined based on a permutation approach. However in this work an algorithm is proposed to find the self-symmetric rule and a pairwise symmetric rule in polynomial time, which generates bilateral symmetric patterns.