Geometrical Information Flow Regulated by Time Lengths: An Initial Approach
Abstract
1. Introduction
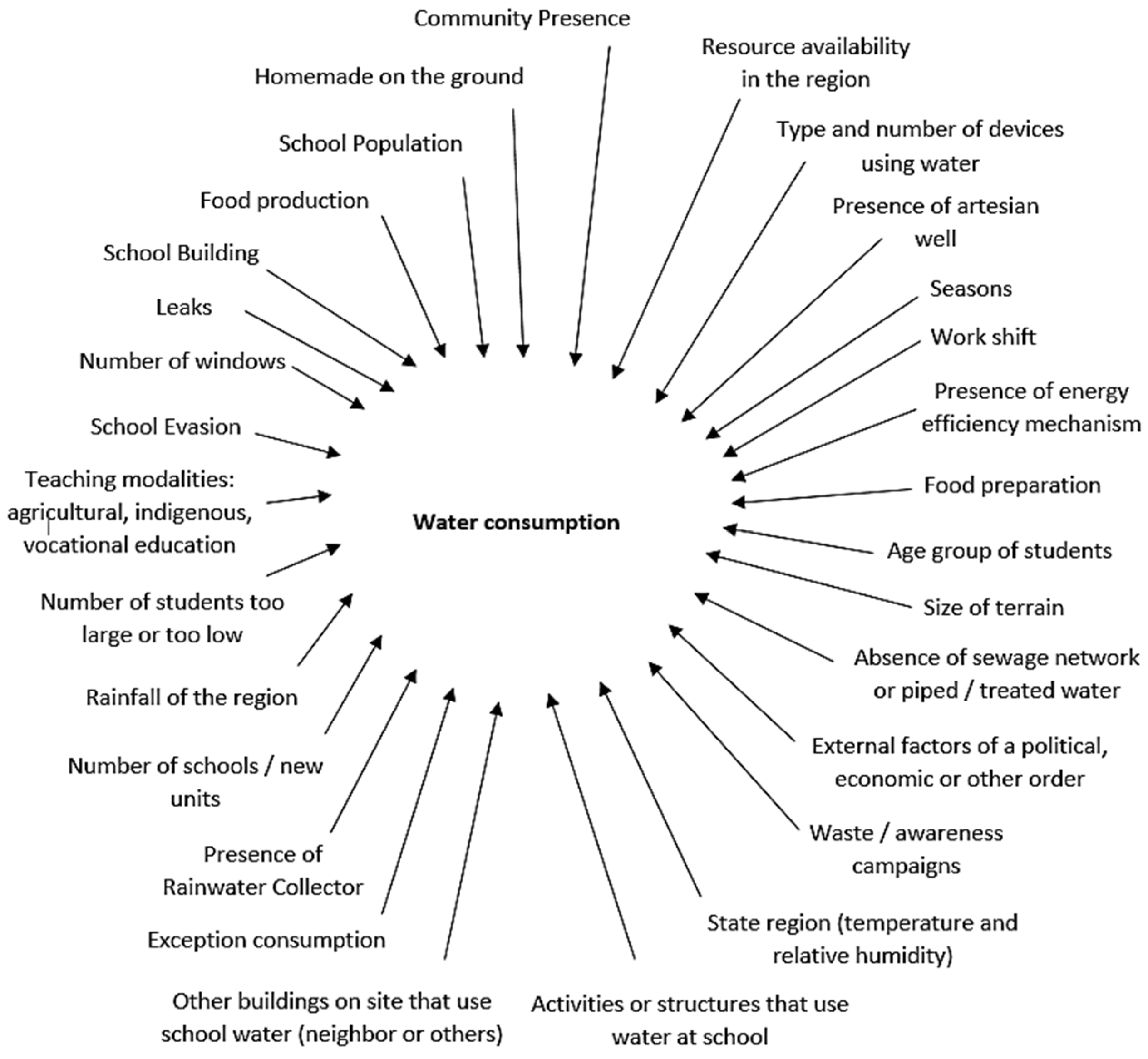
2. Methodology
2.1. Theoretical Framework of Experiment
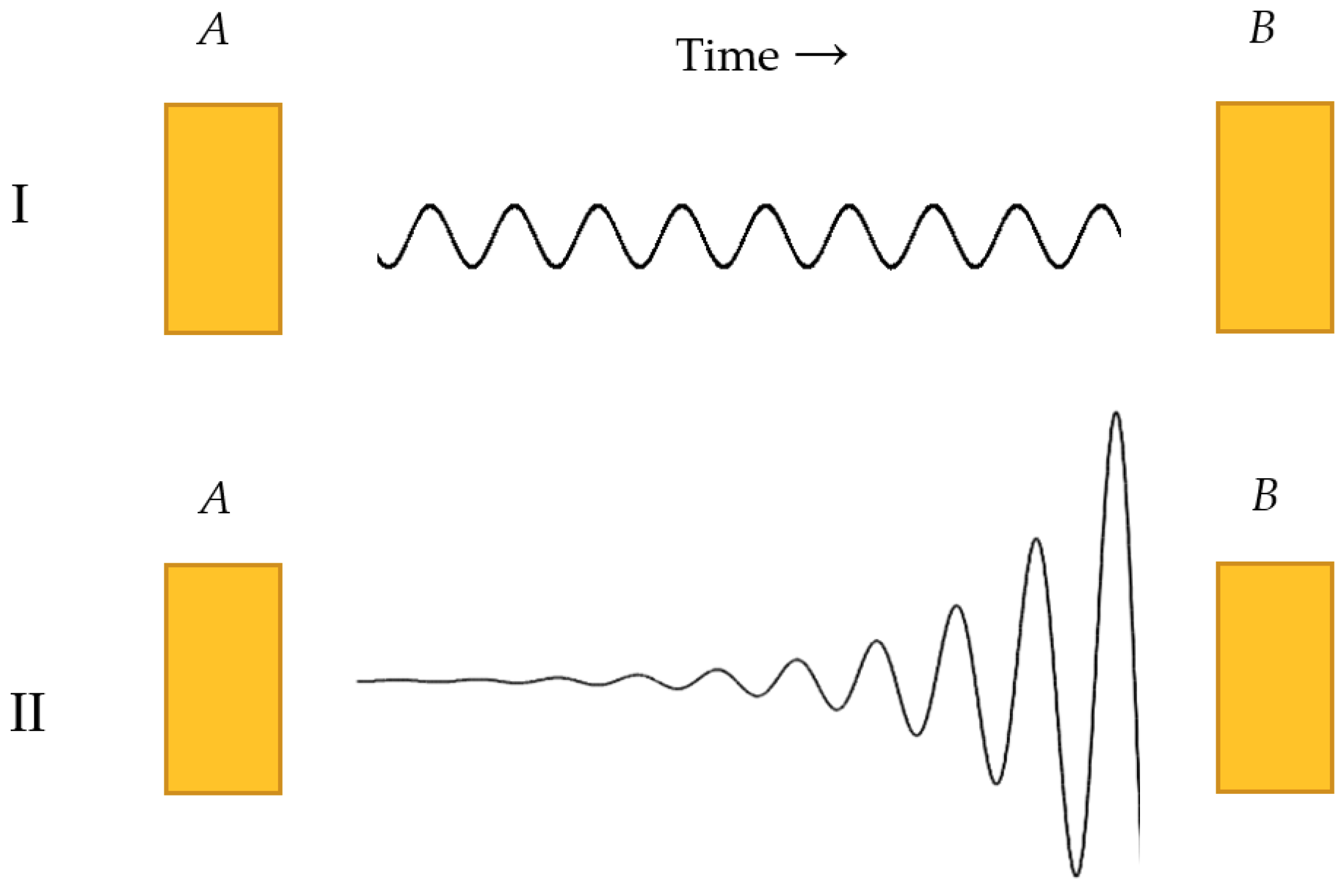
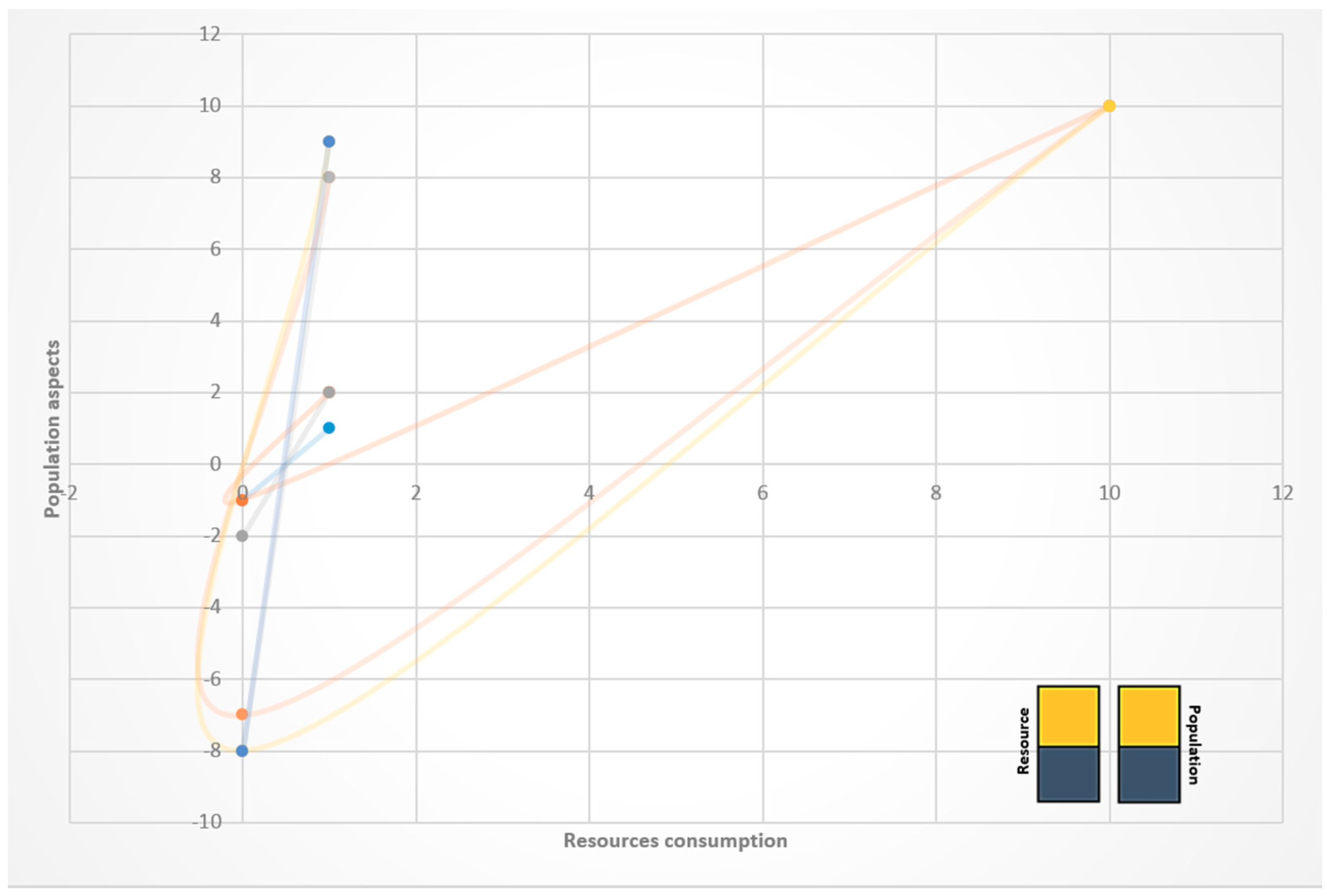
2.1.1. Information Flow and Ergodic Properties
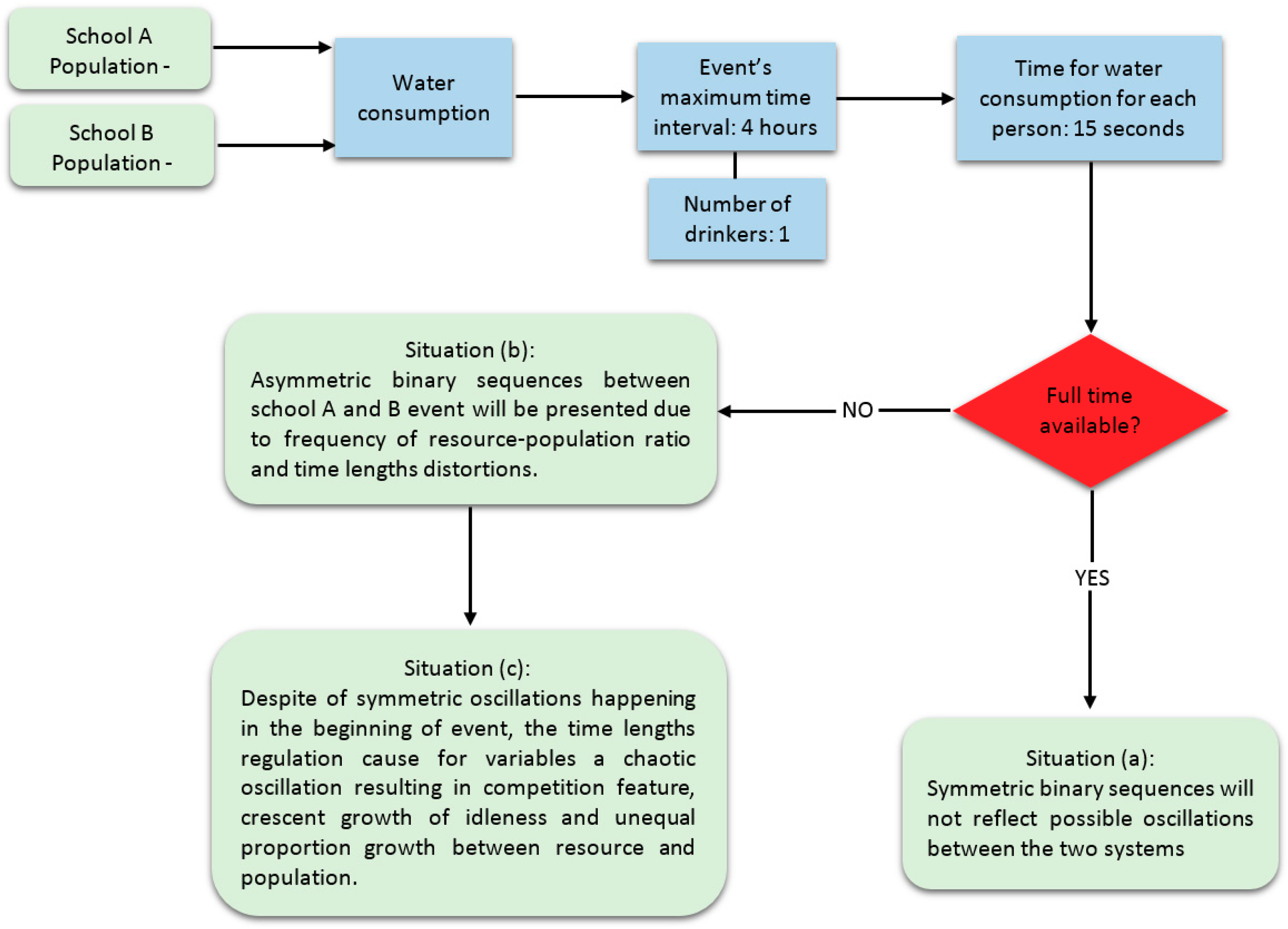
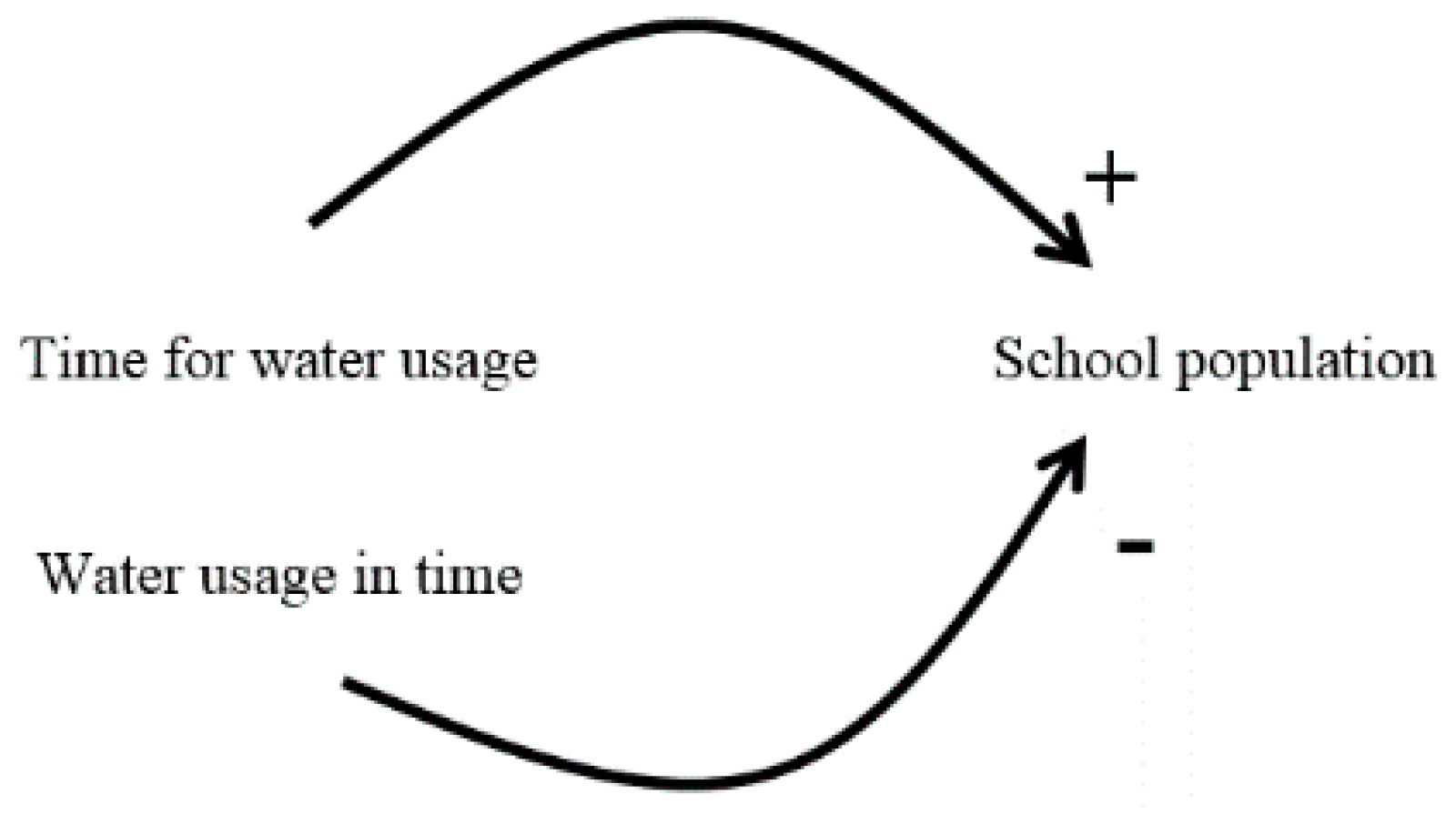
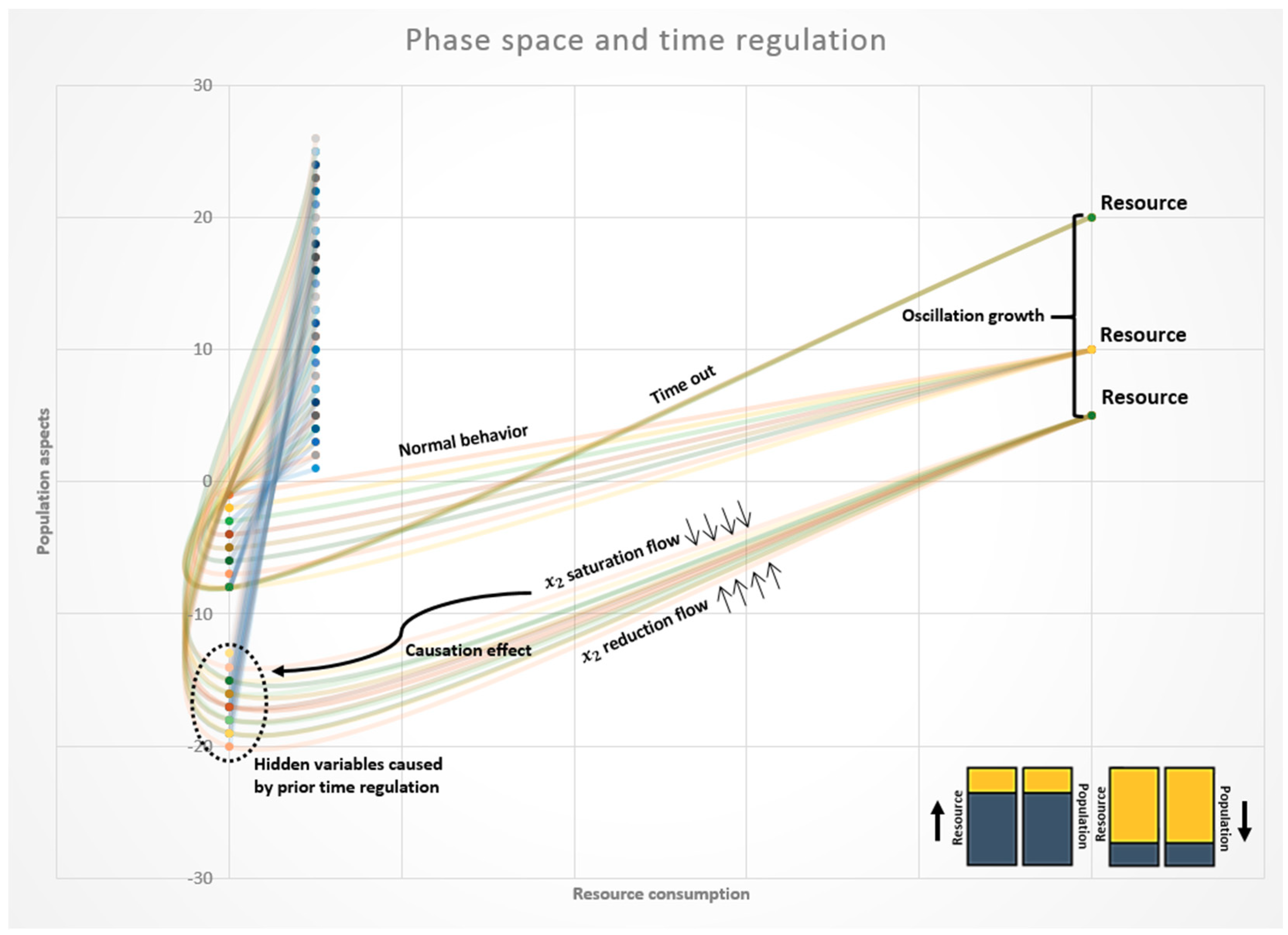
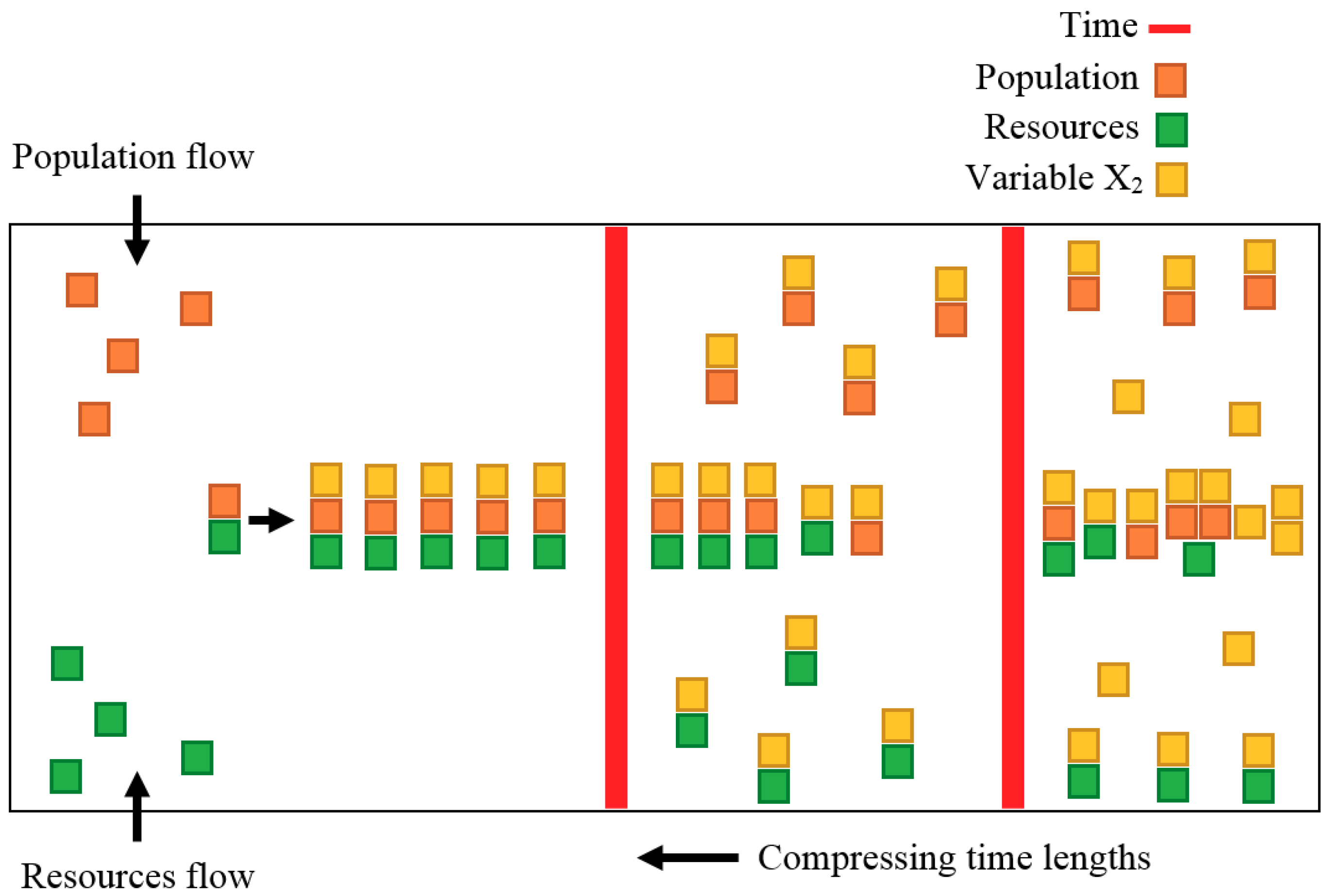
2.1.2. Information Flow and Time as the Cause of Oscillations
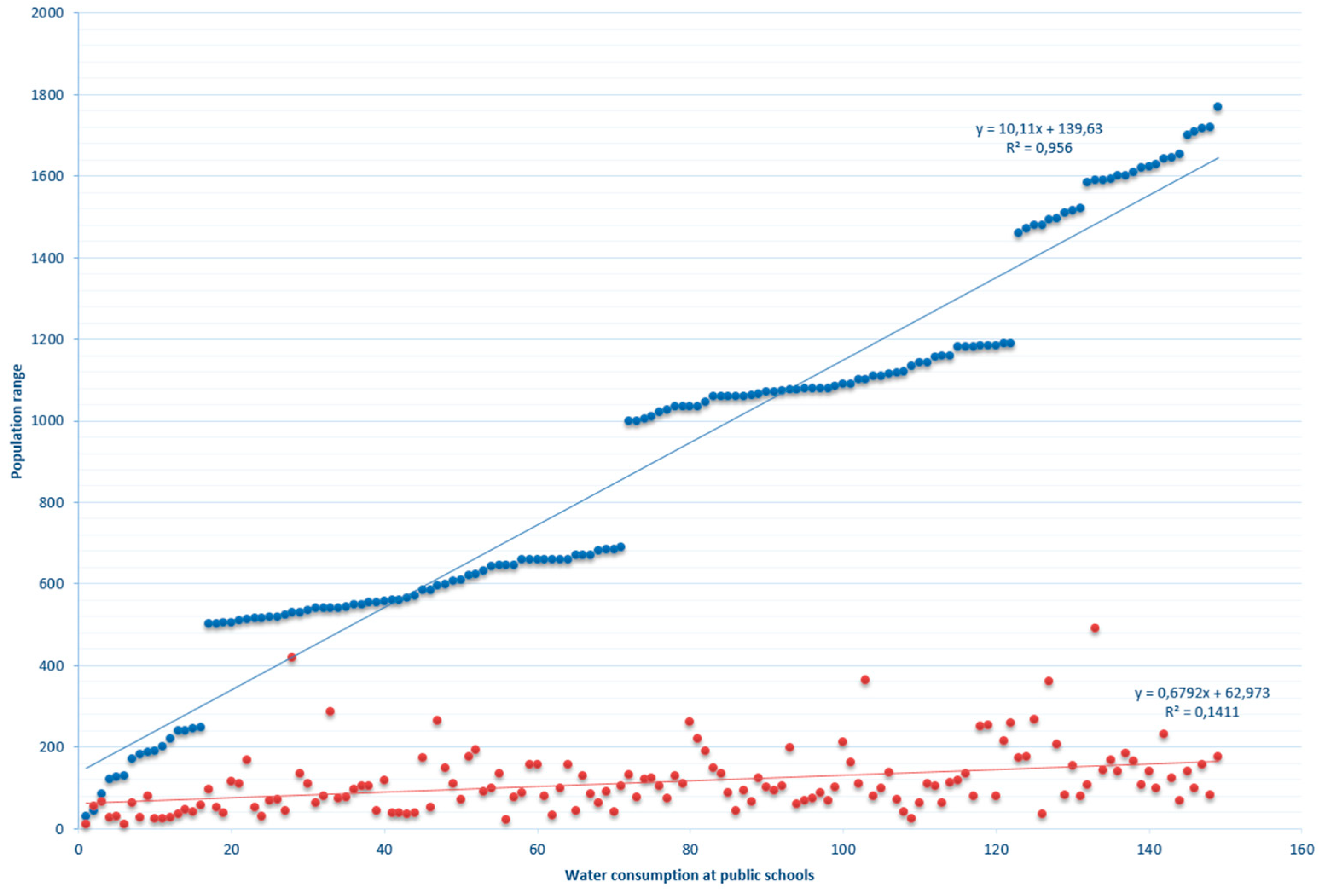
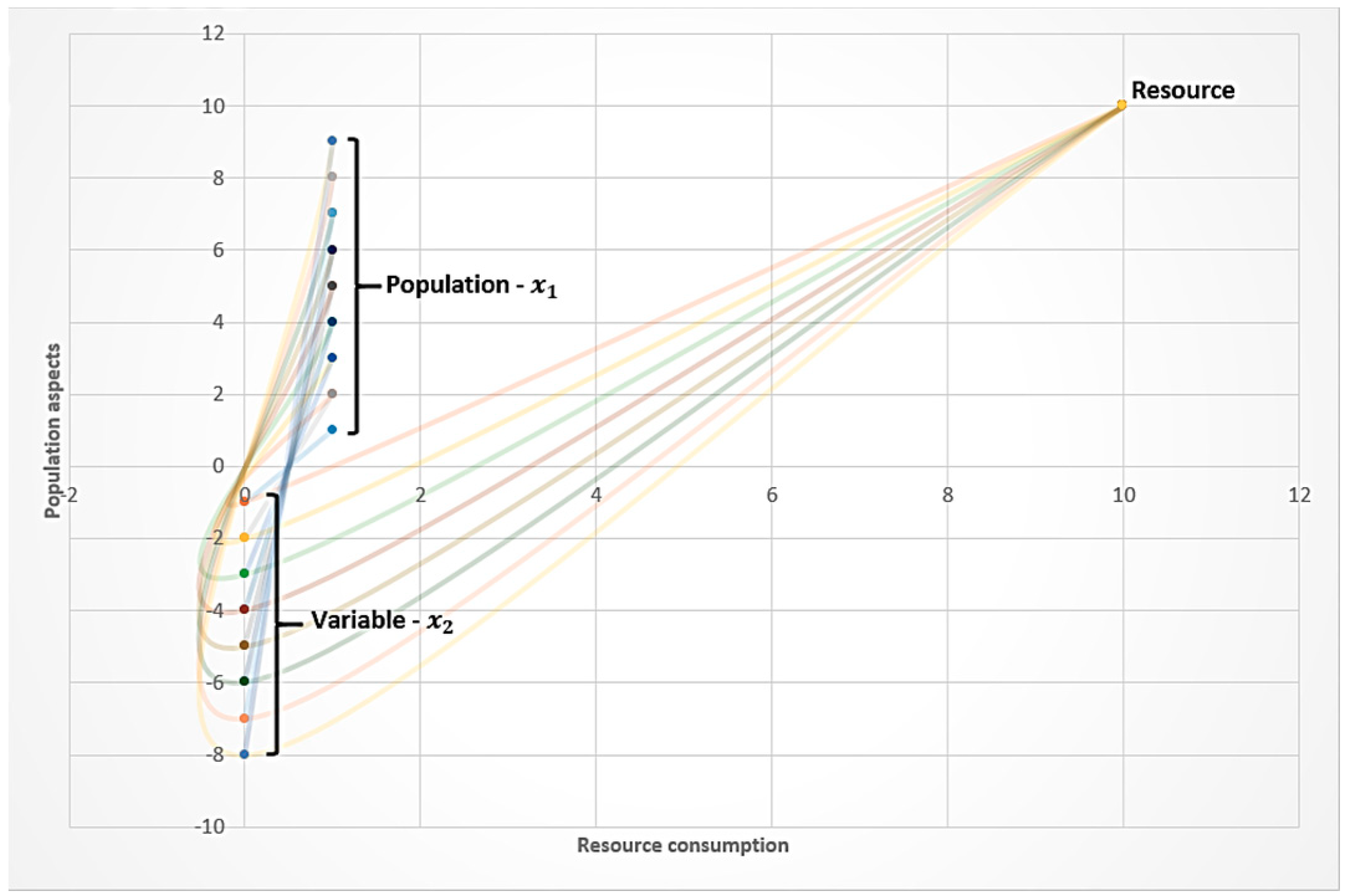
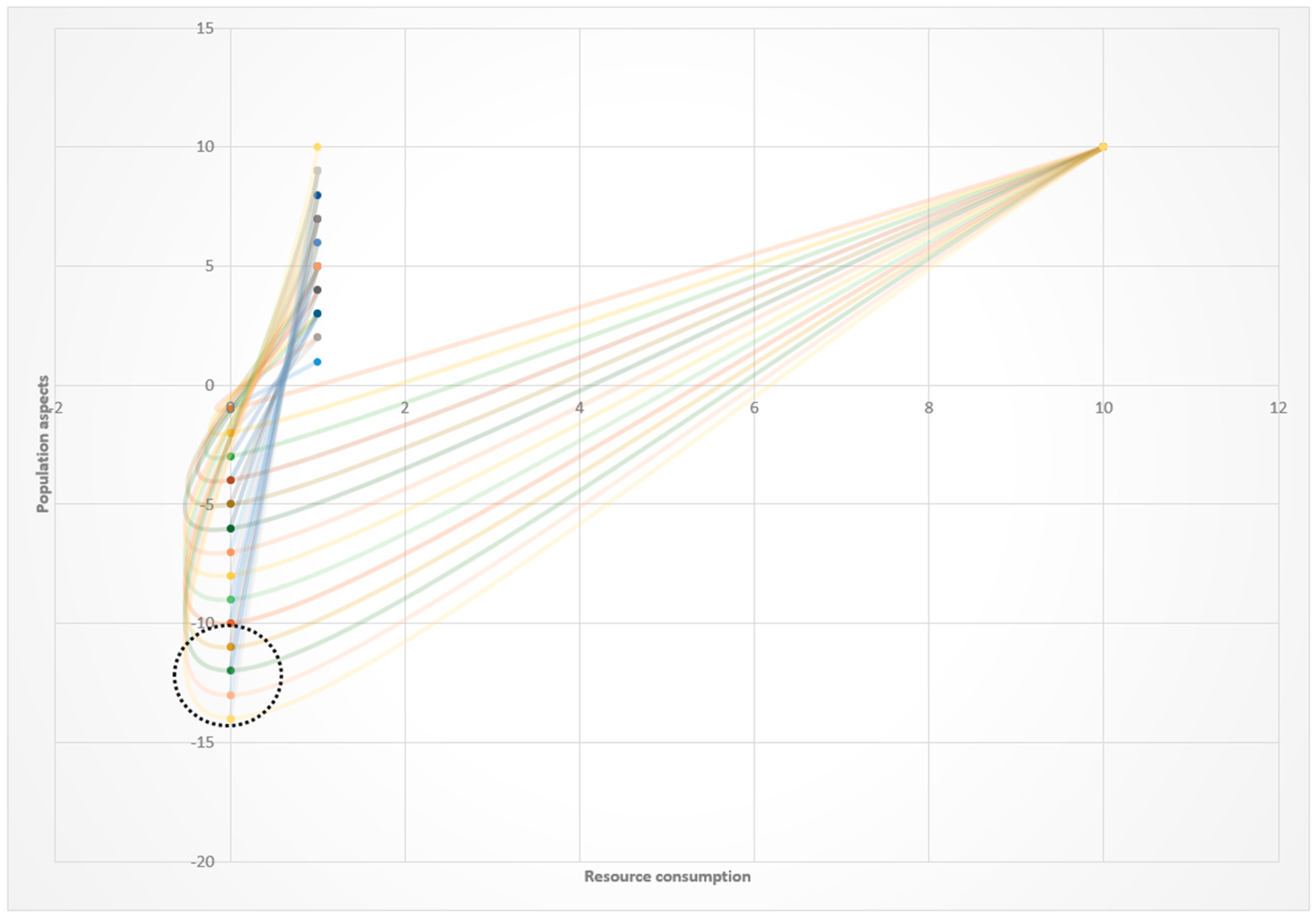
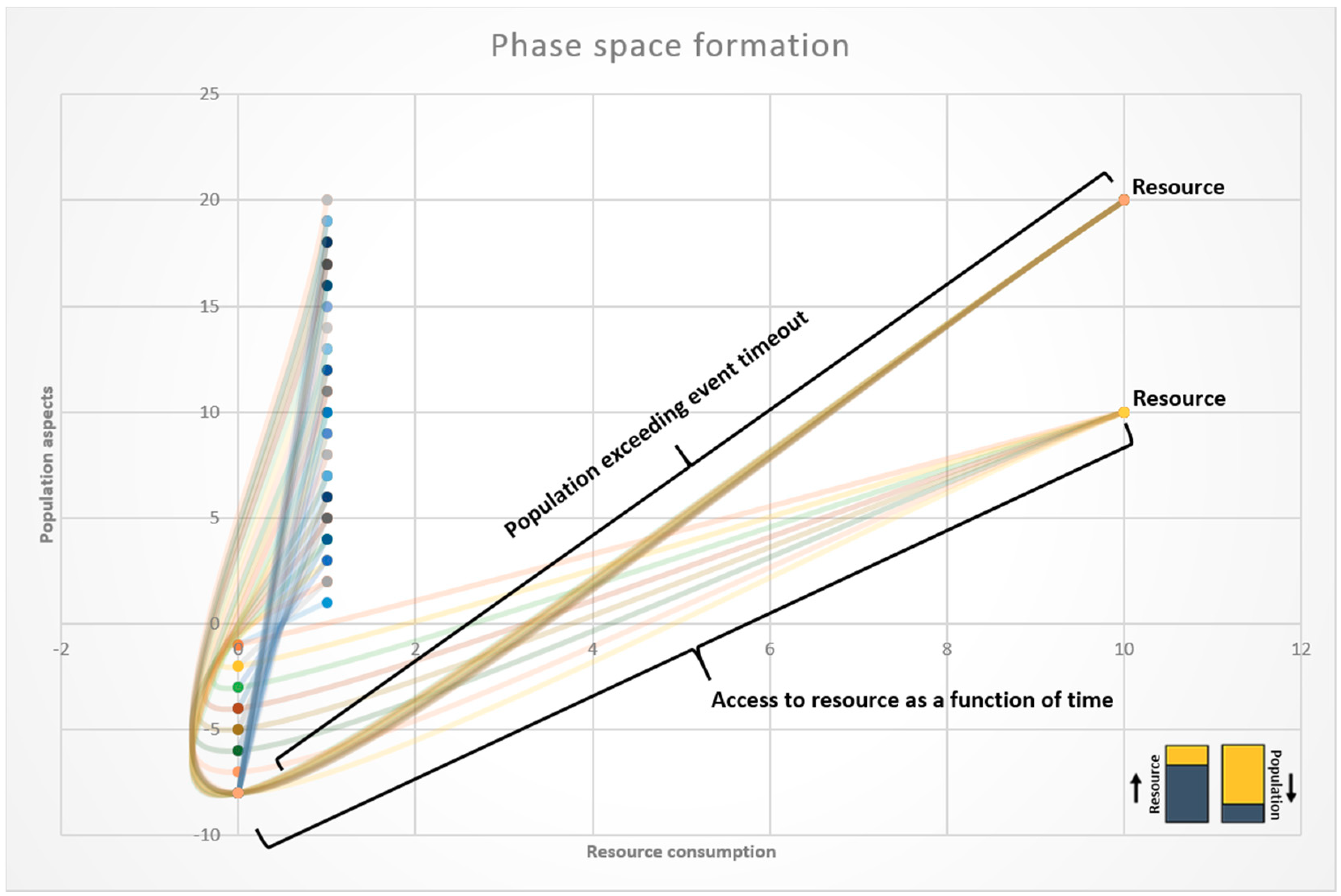
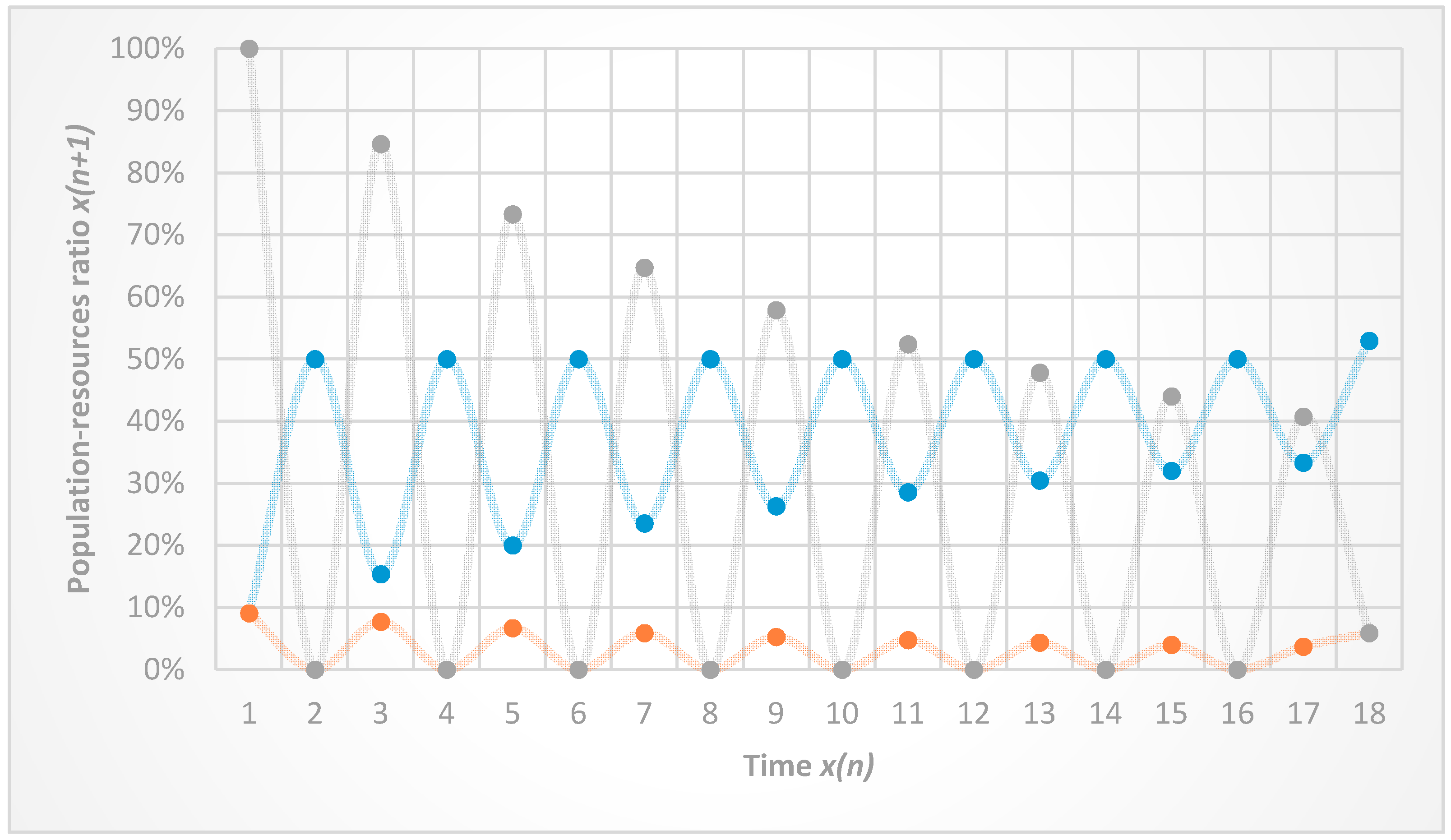
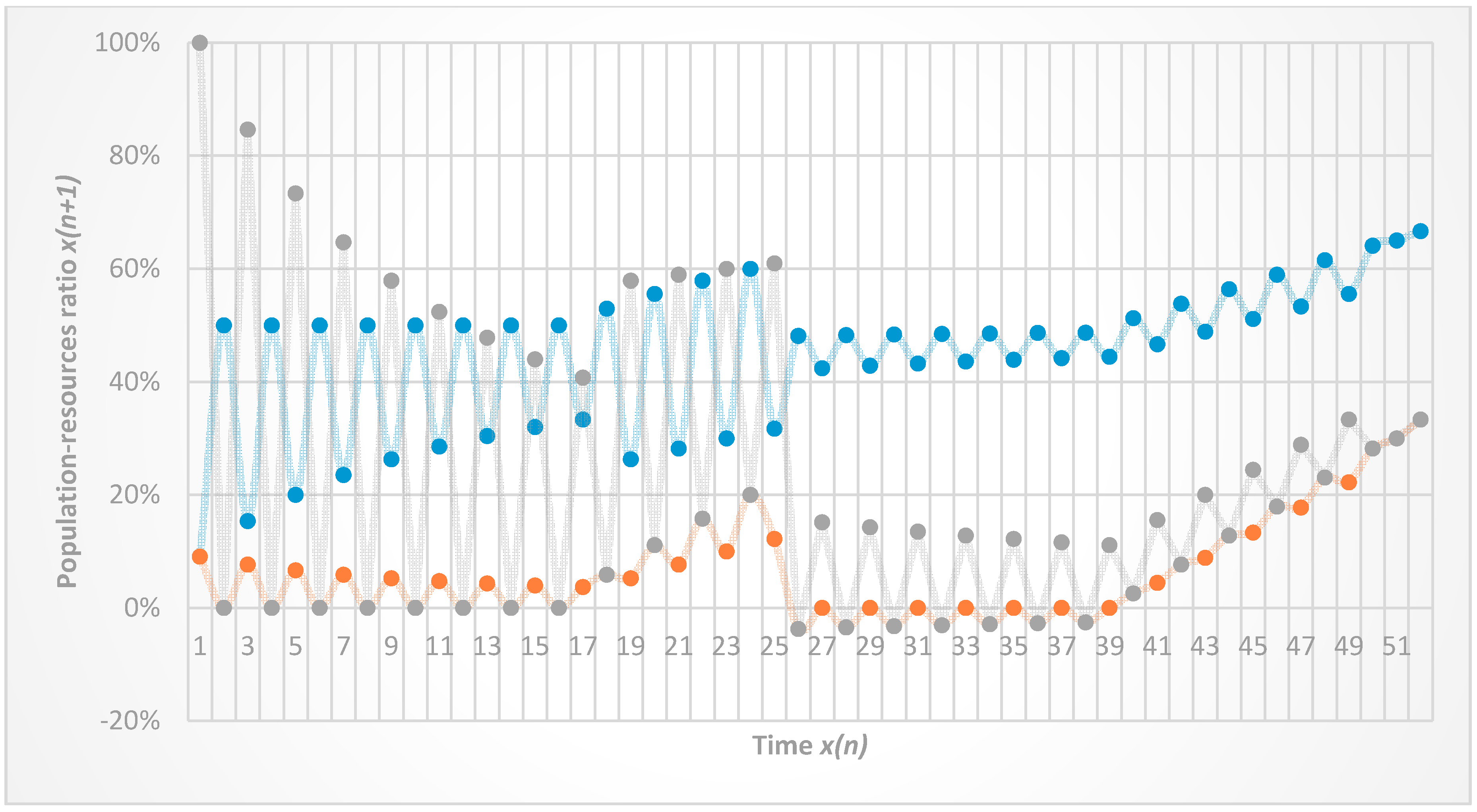
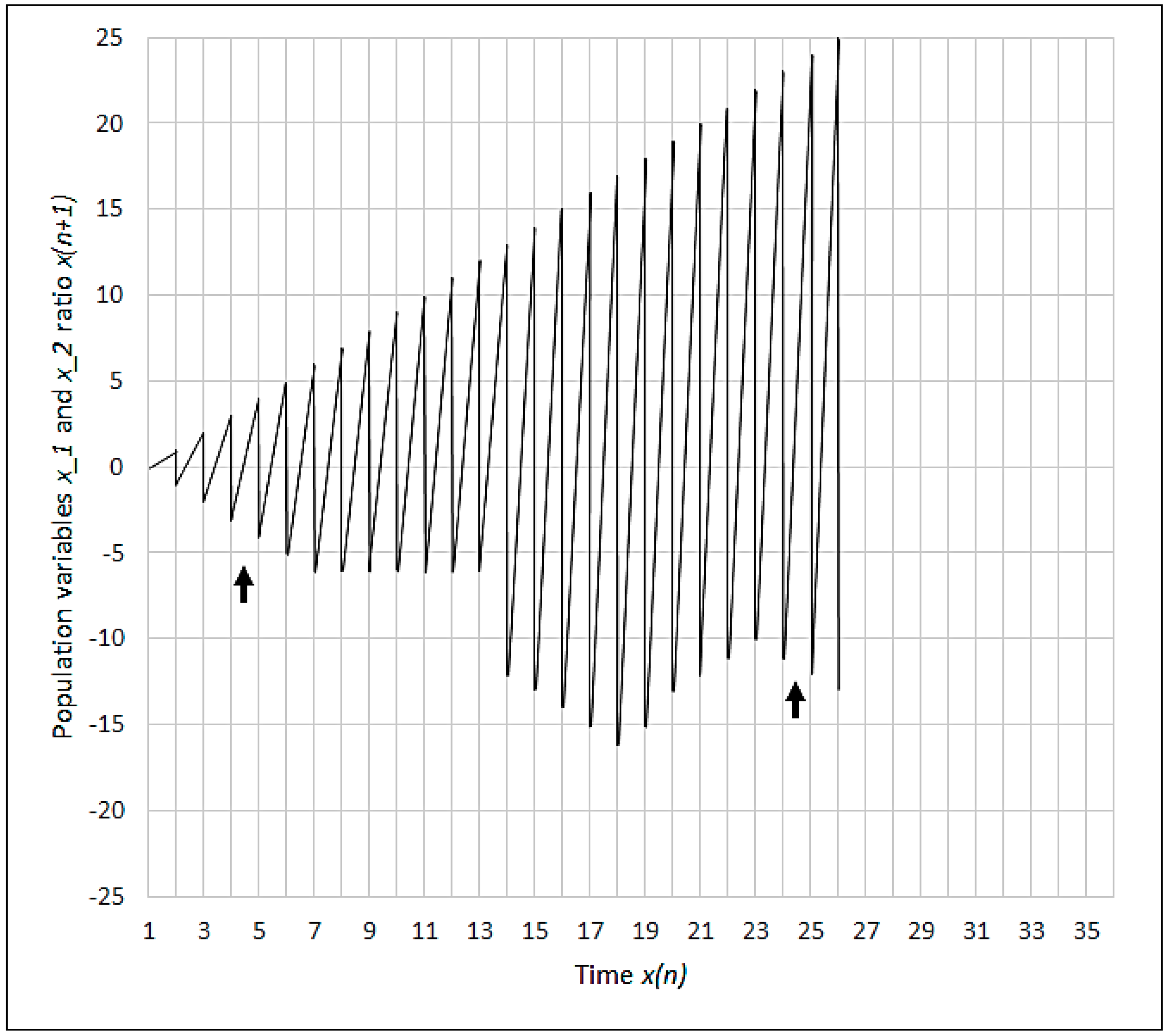
3. Results
Non-Ergodicity
4. Discussion
- -
- -
- vector based diseases [35];
- -
- -
- -
- -
- logistics aspects of administration and commerce flow [36];
- -
- -
- engineering of materials [37];
- -
- -
- language processing regarding space and time accelerations or other biological aspects [22];
- -
- -
- -
- duality based and quantum based phenomena, such as economics and particles and other fields of knowledge related to the issue [30]; and,
- -
- computing, networking, and communications [38].
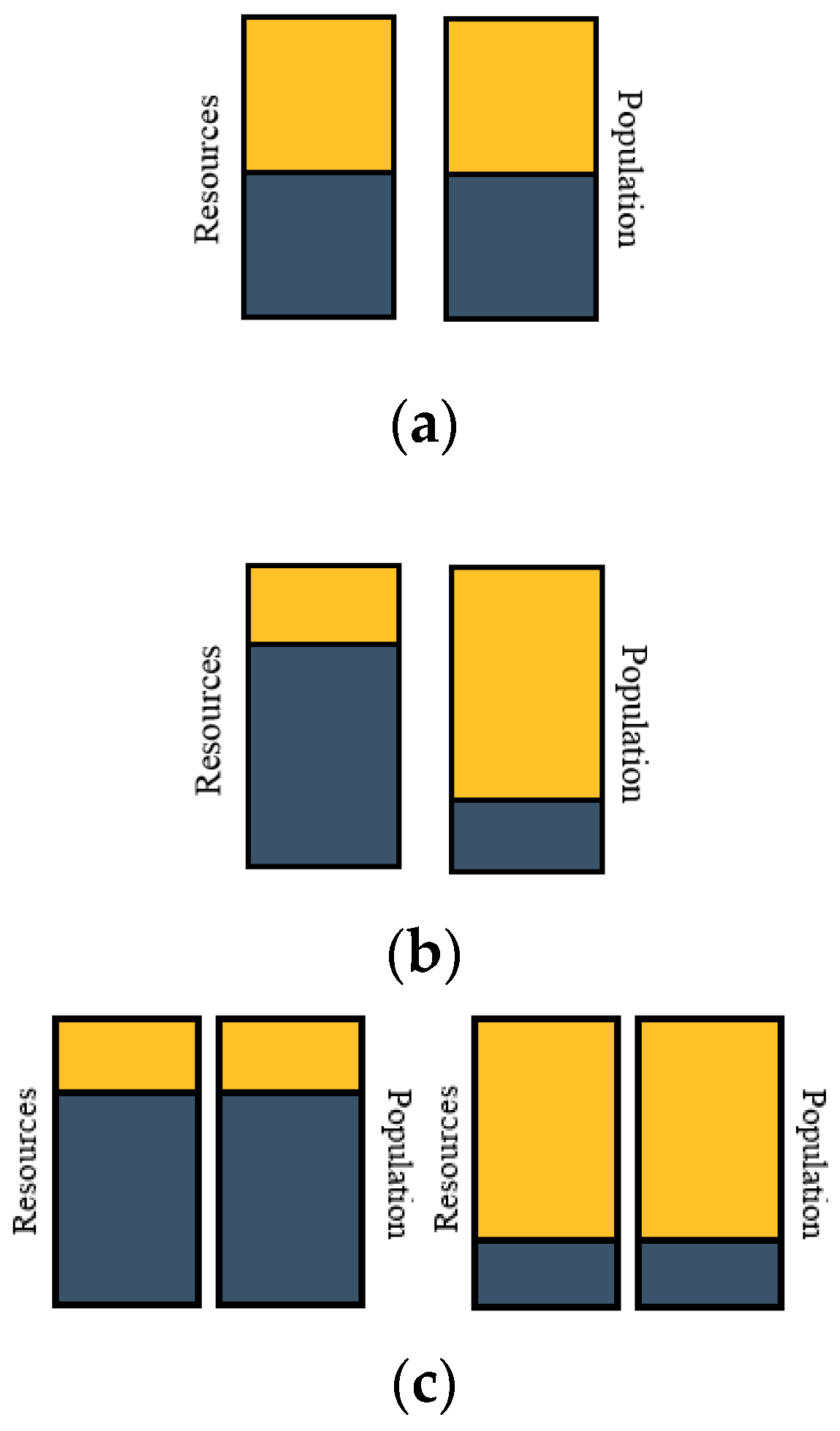
- (a)
- proportionality between/among variable’s distribution (for open/closed system)—linearity
- -
- General management of deterministic flows methods; and,
- (b)
- disproportionality between/among variable’s distribution (open system)—nonlinearity
- -
- Time regulated dynamics.
5. Conclusions
Funding
Conflicts of Interest
References
- Eppel, E.A.; Rhodes, M.L. Complexity theory and public management: A ‘becoming’ field. Public Manag. Rev. 2018, 20, 949–959. [Google Scholar] [CrossRef]
- Telles, C.R.; Cunha, A.R.B.D.; Chueiri, A.M.S.; Kuromiya, K. Analysis of oscillations in continuous expenditures and their multiple causalities: A case study. J. Econ. Adm. Sci. 2018, 34. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Wu, L. Model for instantaneous residential water demands. J. Hydraul. Eng. 1995, 121, 232–246. [Google Scholar] [CrossRef]
- Guercio, R.; Magini, R.; Pallavicini, I. Instantaneous residential water demand as stochastic point process. WIT Trans. Ecol. Environ. 2001, 48, 10. [Google Scholar] [CrossRef]
- Telles, C.R. Metodologia para Análise do Consumo de Água em Edificações Escolares. Parana J. Sci. Educ. 2017, 3, 1–10. (In Portuguese) [Google Scholar]
- Blokker, E.J.M.; Vreeburg, J.H.G.; Van Dijk, J.C. Simulating residential water demand with a stochastic end-use model. J. Water Resour. Plan. Manag. 2009, 136, 19–26. [Google Scholar] [CrossRef]
- Balacco, G.; Carbonara, A.; Gioia, A.; Iacobellis, V.; Piccinni, A.F. Investigation of peak water consumption variability at local scale in Puglia (Southern Italy). Proceedings 2018, 2, 674. [Google Scholar] [CrossRef]
- Yarnold, P.R. Minimize usage of binary measurement scales in rigorous classical research. Optim. Data Anal. 2018, 7, 3–9. [Google Scholar]
- Dahl, C. A survey of energy demand elasticities for the developing world. J. Energy Dev. 1994, 18, 1–47. [Google Scholar]
- Bertsimas, D.; Thiele, A. Robust and data-driven optimization: Modern decision-making under uncertainty. Model. Methods Appl. Innov. Decis. Mak. 2006, 3, 95–122. [Google Scholar]
- Bhattacharyya, S.C.; Timilsina, G.R. Energy Demand Models for Policy Formulation: A Comparative Study of Energy Demand Models; The World Bank: Washington, DC, USA, 2009. [Google Scholar]
- Secretaria de Estado da Educação do Paraná (PARANÁ). Excel, Work Sheet about Water Consumption at 149 Public Schools at Paraná State; Continuous Service Sector: Curitiba, Brazil, 2013. [Google Scholar] [CrossRef]
- Arditi, R.; Ginzburg, L.R. Coupling in predator-prey dynamics: Ratio-dependence. J. Theor. Biol. 1989, 139, 311–326. [Google Scholar] [CrossRef]
- Aven, T. Risk assessment and risk management: Review of recent advances on their foundation. Eur. J. Oper. Res. 2016, 253, 1–13. [Google Scholar] [CrossRef]
- Gibbins, P. Particles and Paradoxes: The Limits of Quantum Logic; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Harush, U.; Barzel, B. Dynamic patterns of information flow in complex networks. Nat. Commun. 2017, 8, 2181. [Google Scholar] [CrossRef] [PubMed]
- Butucea, C.; Delmas, J.F.; Dutfoy, A.; Fischer, R. Maximum entropy distribution of order statistics with given marginals. Bernoulli 2018, 24, 115–155. [Google Scholar] [CrossRef]
- Fried, R.; Didelez, V.; Lanius, V. Partial correlation graphs and dynamic latent variables for physiological time series. In Innovations in Classification, Data Science, and Information Systems; Springer: Berlin/Heidelberg, Germany, 2004; pp. 259–266. [Google Scholar]
- Martin-Löf, P. Complexity oscillations in infinite binary sequences. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1971, 19, 225–230. [Google Scholar] [CrossRef]
- Gencaga, D.; Knuth, K.H.; Rossow, W.B. A recipe for the estimation of information flow in a dynamical system. Entropy 2015, 17, 438–470. [Google Scholar] [CrossRef]
- Donner, R.V.; Small, M.; Donges, J.F.; Marwan, N.; Zou, Y.; Xiang, R.; Kurths, J. Recurrence-based time series analysis by means of complex network methods. Int. J. Bifurc. Chaos 2011, 21, 1019–1046. [Google Scholar] [CrossRef]
- Li, M.; Xie, K.; Kuang, H.; Liu, J.; Wang, D.H.; Fox, G.E.; Shi, Z.F.; Chen, L.; Zhao, F.; Mao, Y.; et al. Neural coding of cell assemblies via spike-timing self-information. Cereb. Cortex 2018, 28, 2563–2576. [Google Scholar] [CrossRef] [PubMed]
- Baran, T.; Harmancioglu, N.B.; Cetinkaya, C.P.; Barbaros, F. An extension to the revised approach in the assessment of informational entropy. Entropy 2017, 19, 634. [Google Scholar] [CrossRef]
- Mézard, M.; Montanari, A. Information, Physics and Computation; Oxford University Press: Corby, UK, 2009. [Google Scholar]
- Tsitsiklis, J. Bernoulli Process: Probabilistic Systems Analysis and Applied Probability, Lecture 13. MIT Opencourseware, 2011. Available online: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-041-probabilistic-systems-analysis-and-applied-probability-fall-2010/video-lectures/lecture-13-bernoulli-process/ (accessed on 25 September 2018).
- Cauchy, A.L.B. Cours d’Analyse de l’École Royale Polytechnique; Debure: De L’ Imprimerie Royale, France, 1821. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Willey-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ha, J.; Tan, P.P.; Goh, K.L. Linear and nonlinear causal relationship between energy consumption and economic growth in China: New evidence based on wavelet analysis. PLoS ONE 2018, 13, e0197785. [Google Scholar] [CrossRef] [PubMed]
- Telles, C.R.; Chueiri, A.M.S.; Cunha, A.R.B. Pesquisa Operacional do Setor de Serviços Contínuos: Economia, Meio Ambiente e Educação, 2nd ed.; Secretaria de Estado da Educação do Paraná: Curitiba, Brazil, 2018; 146p. [Google Scholar] [CrossRef]
- Licata, I.; Chiatti, L. Timeless approach to quantum jumps. Quanta 2015, 4, 10–26. [Google Scholar] [CrossRef]
- Weijs, S. Information Theory for Risk-based Water System Operation. Ph.D Thesis, Water Resources Management, Faculty of Civil Engineering & Geosciences of Technische Universiteit, Delft, The Netherlands, 2011. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2011, 5, 3–55. [Google Scholar] [CrossRef]
- Pekkonen, M.; Ketola, T.; Laakso, J.T. Resource availability and competition shape the evolution of survival and growth ability in a bacterial community. PLoS ONE 2013, 8, e76471. [Google Scholar] [CrossRef] [PubMed]
- Duncan, C.J.; Duncan, S.R.; Scott, S. The dynamics of scarlet fever epidemics in England and Wales in the 19th century. Epidemiol. Infect. 1996, 117, 493–499. [Google Scholar] [CrossRef] [PubMed]
- Giannoula, A.; Gutierrez-Sacristán, A.; Bravo, Á.; Sanz, F.; Furlong, L.I. Identifying temporal patterns in patient disease trajectories using dynamic time warping: A population-based study. Sci. Rep. 2018, 8, 4216. [Google Scholar] [CrossRef] [PubMed]
- Afy-Shararah, M.; Rich, N. Operations flow effectiveness: A systems approach to measuring flow performance. Int. J. Oper. Prod. Manag. 2018. [Google Scholar] [CrossRef]
- Klug, M.J.; Scheurer, M.S.; Schmalian, J. Hierarchy of information scrambling, thermalization, and hydrodynamic flow in graphene. Phys. Rev. B 2018, 98, 045102. [Google Scholar] [CrossRef]
- Tao, Y.; Yu, S.; Zhou, J. Information Flow Queue Optimization in EC Cloud. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 5–8 March 2018; pp. 888–892. [Google Scholar]
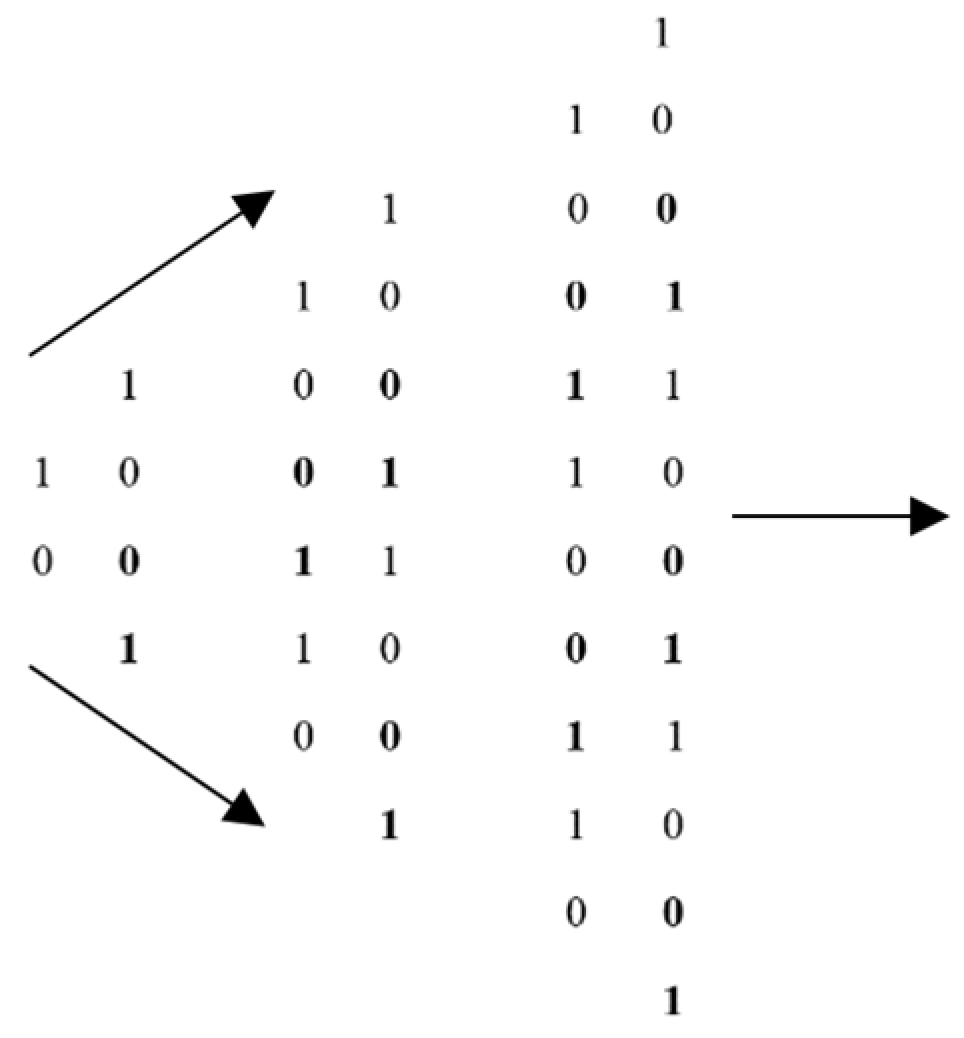

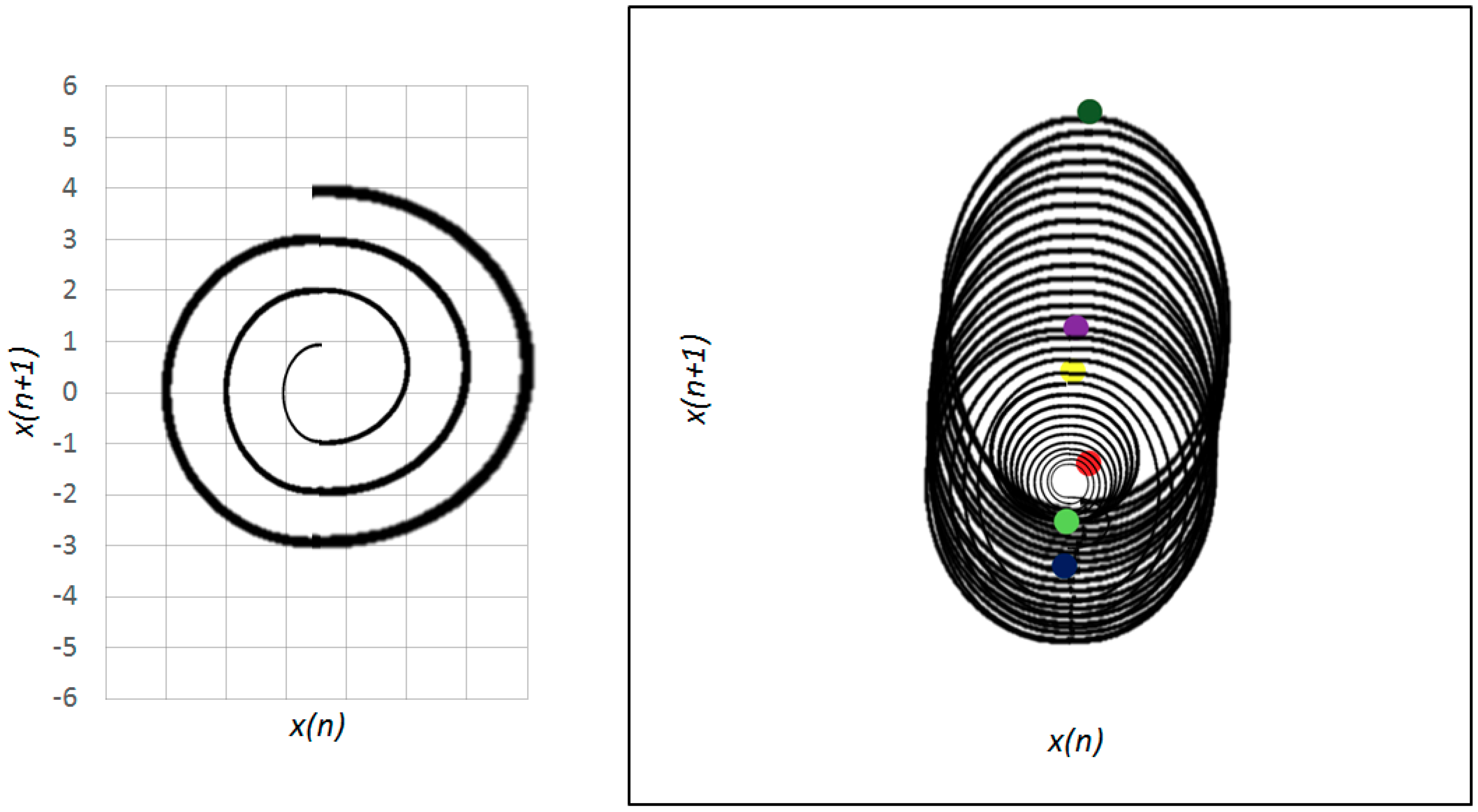
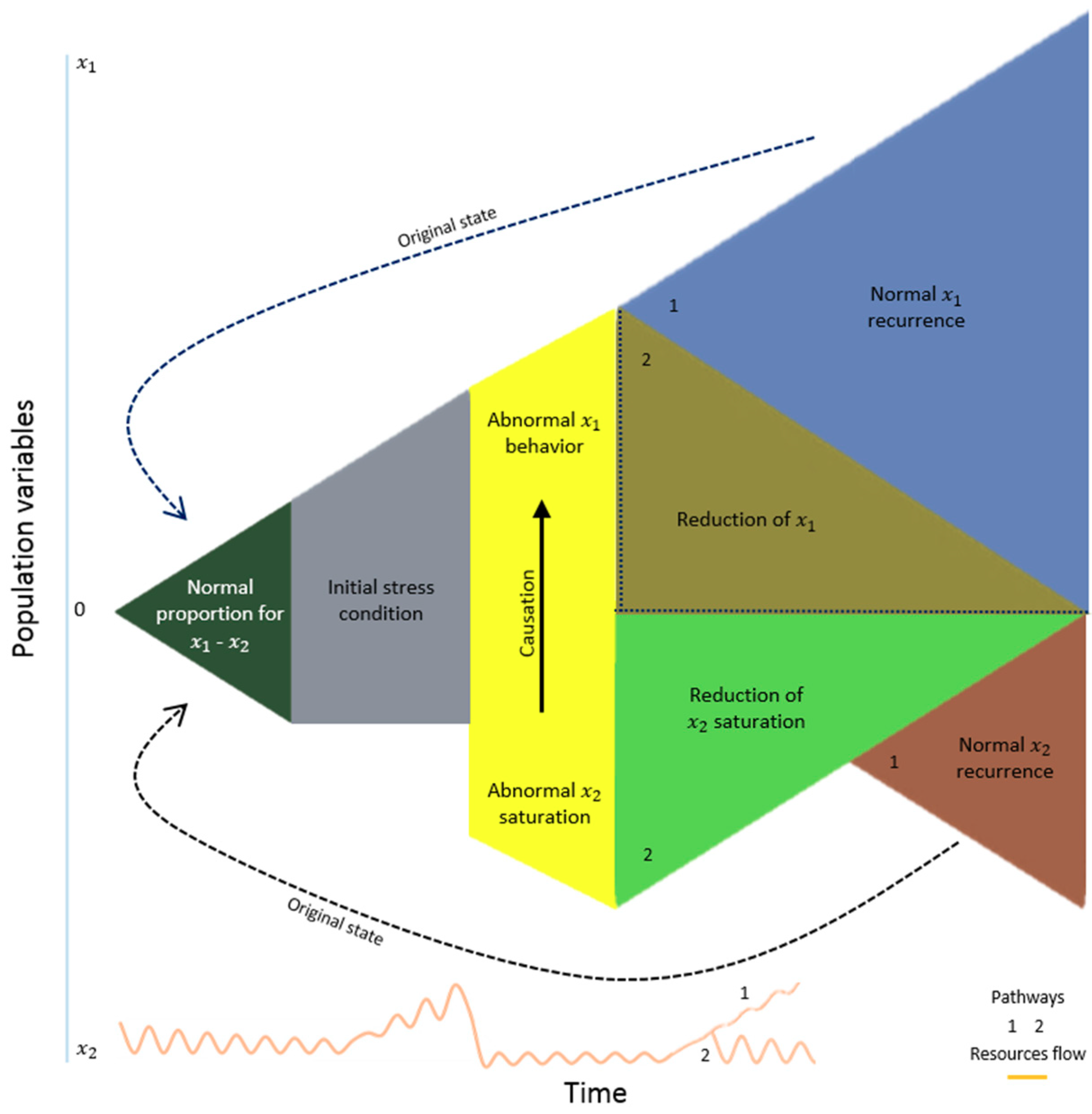
| Time. | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | |
|---|---|---|---|---|---|---|---|---|---|
| Variables | X1 | X2 | X1 | X2 | X1 | X2 | X1 | X2 | |
| Bits | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberto Telles, C. Geometrical Information Flow Regulated by Time Lengths: An Initial Approach. Symmetry 2018, 10, 645. https://doi.org/10.3390/sym10110645
Roberto Telles C. Geometrical Information Flow Regulated by Time Lengths: An Initial Approach. Symmetry. 2018; 10(11):645. https://doi.org/10.3390/sym10110645
Chicago/Turabian StyleRoberto Telles, Charles. 2018. "Geometrical Information Flow Regulated by Time Lengths: An Initial Approach" Symmetry 10, no. 11: 645. https://doi.org/10.3390/sym10110645
APA StyleRoberto Telles, C. (2018). Geometrical Information Flow Regulated by Time Lengths: An Initial Approach. Symmetry, 10(11), 645. https://doi.org/10.3390/sym10110645





