Construction and Simulation of Composite Measures and Condensation Model for Designing Probabilistic Computational Applications
Abstract
1. Introduction
Motivation
- A generalized computational model of composite discrete measures on arbitrary smooth functions is formulated in real and complex metric spaces.
- It is illustrated that the model can operate on linear, non-linear and arbitrary smooth functions.
- The operational modes and properties of the measures on z-plane are constructed.
- The construction of composite measures on a real 2-D surface is proposed.
- The concept of condensation measure of uniform contraction map and the associated properties are presented.
2. Related Work
3. Formulation of Model
3.1. Composite Measures in Real Metric Space
3.2. Composite Measures in Complex Metric Space
3.3. Properties of Composite Measure in Algebra
4. Computing Probability-Metric Product
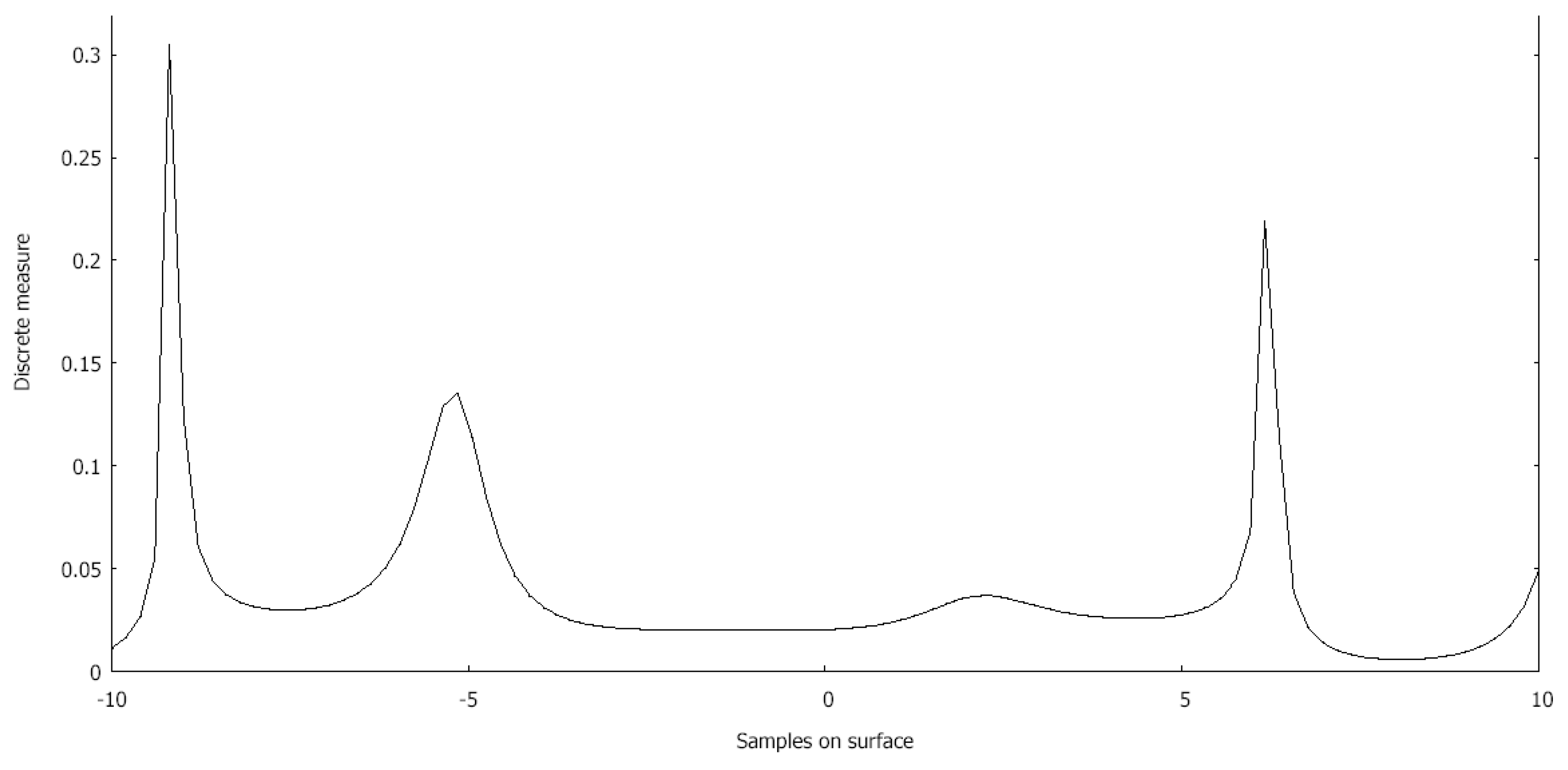
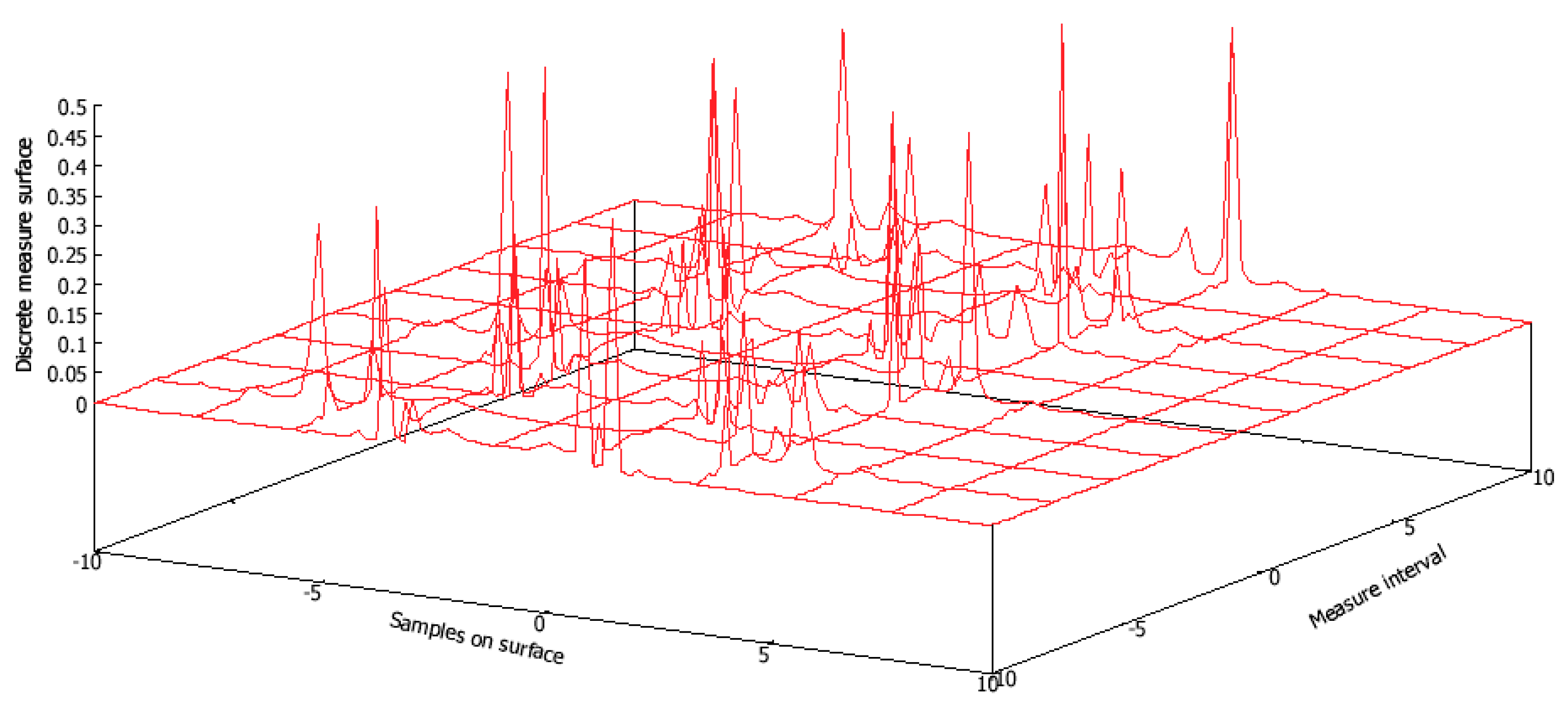
5. Discrete Measure on 2-D Real Surface
Contraction and Condensation Measure
6. Computational Evaluation
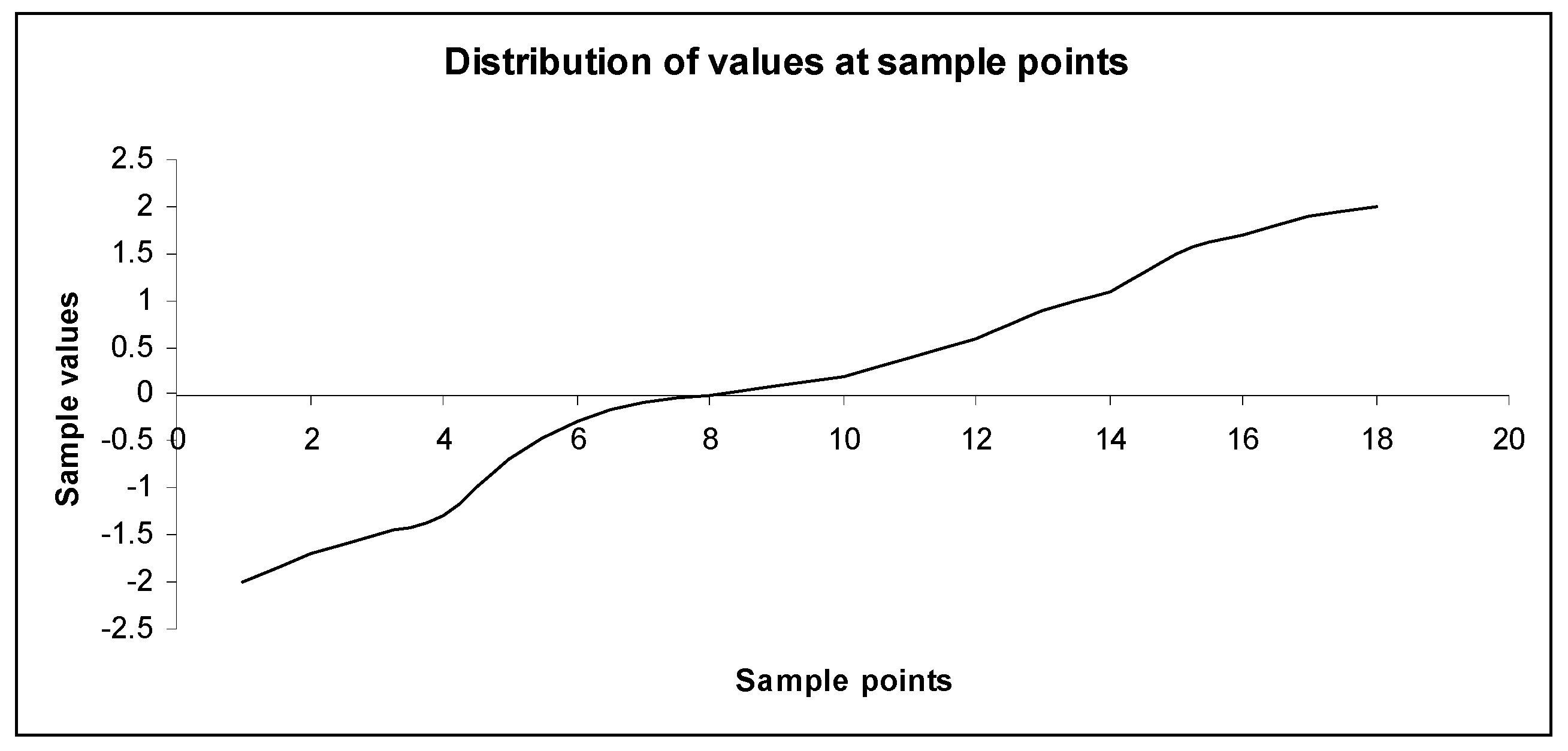
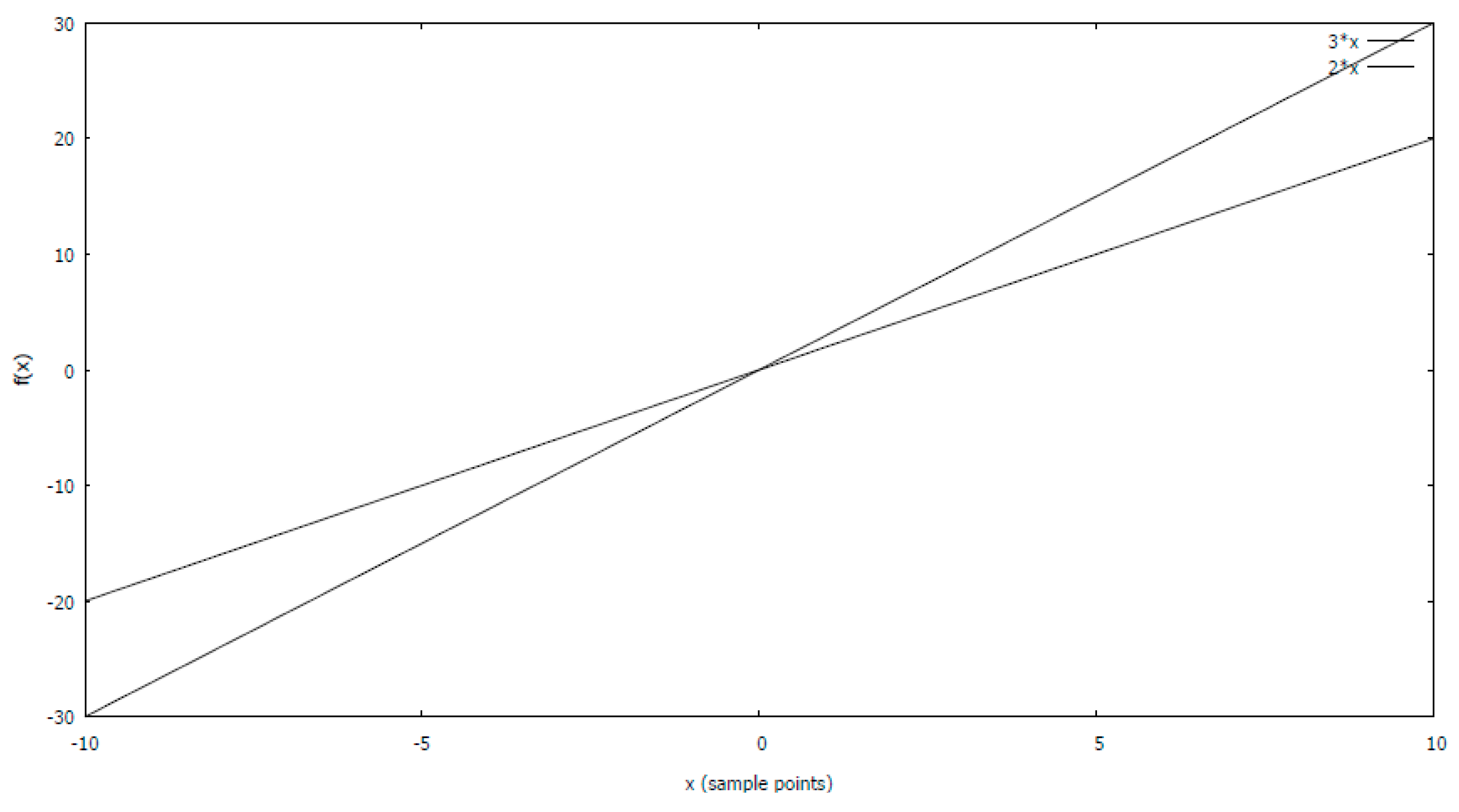
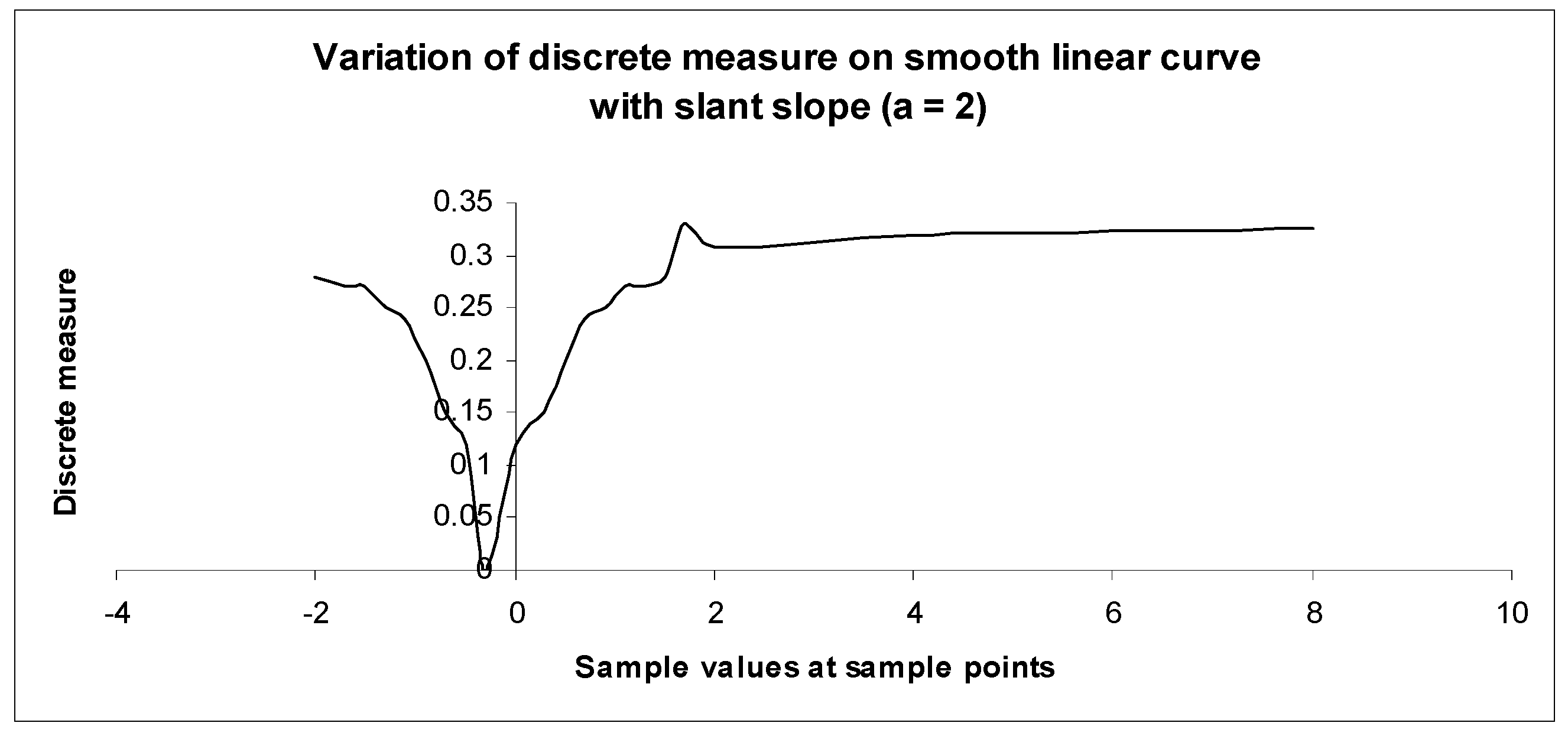
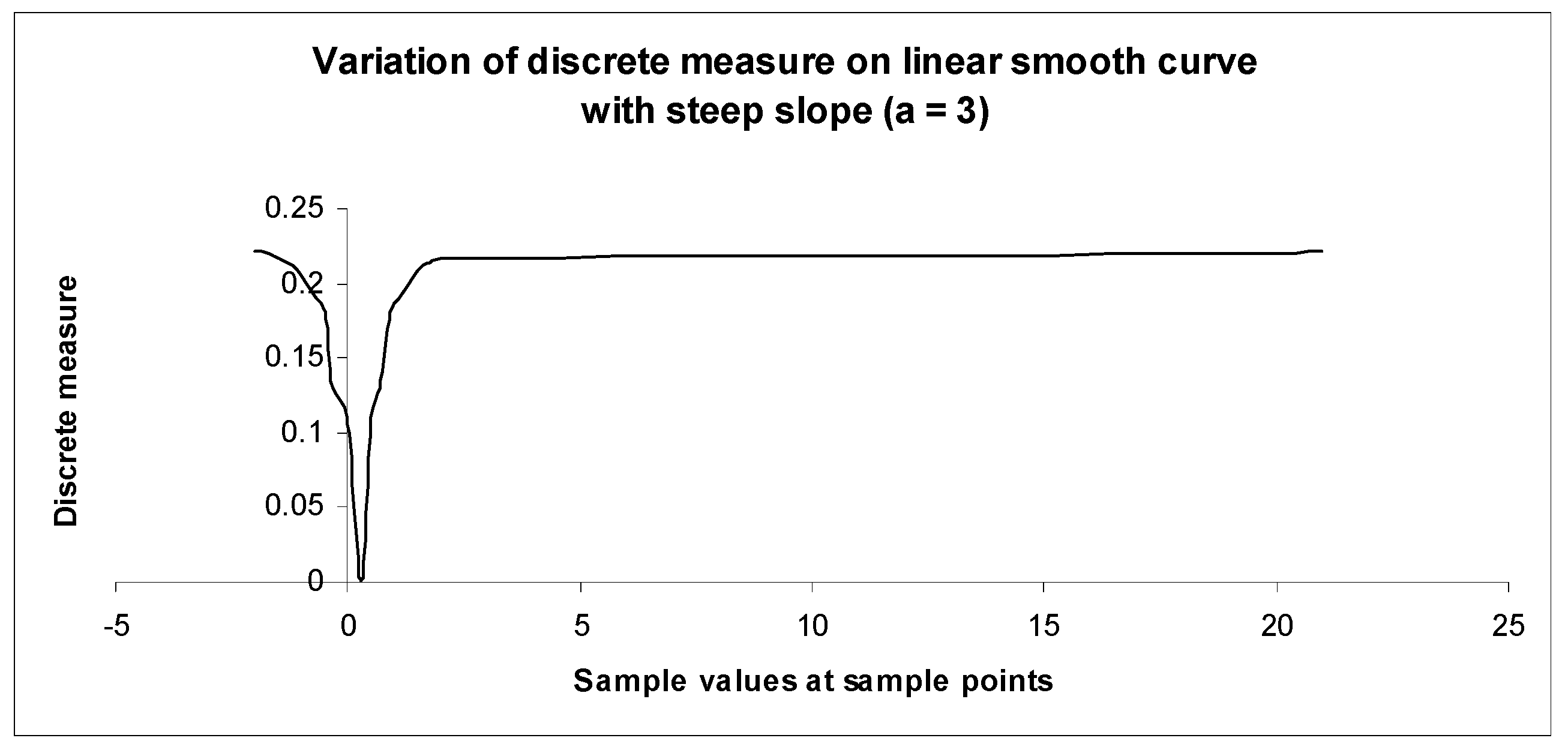
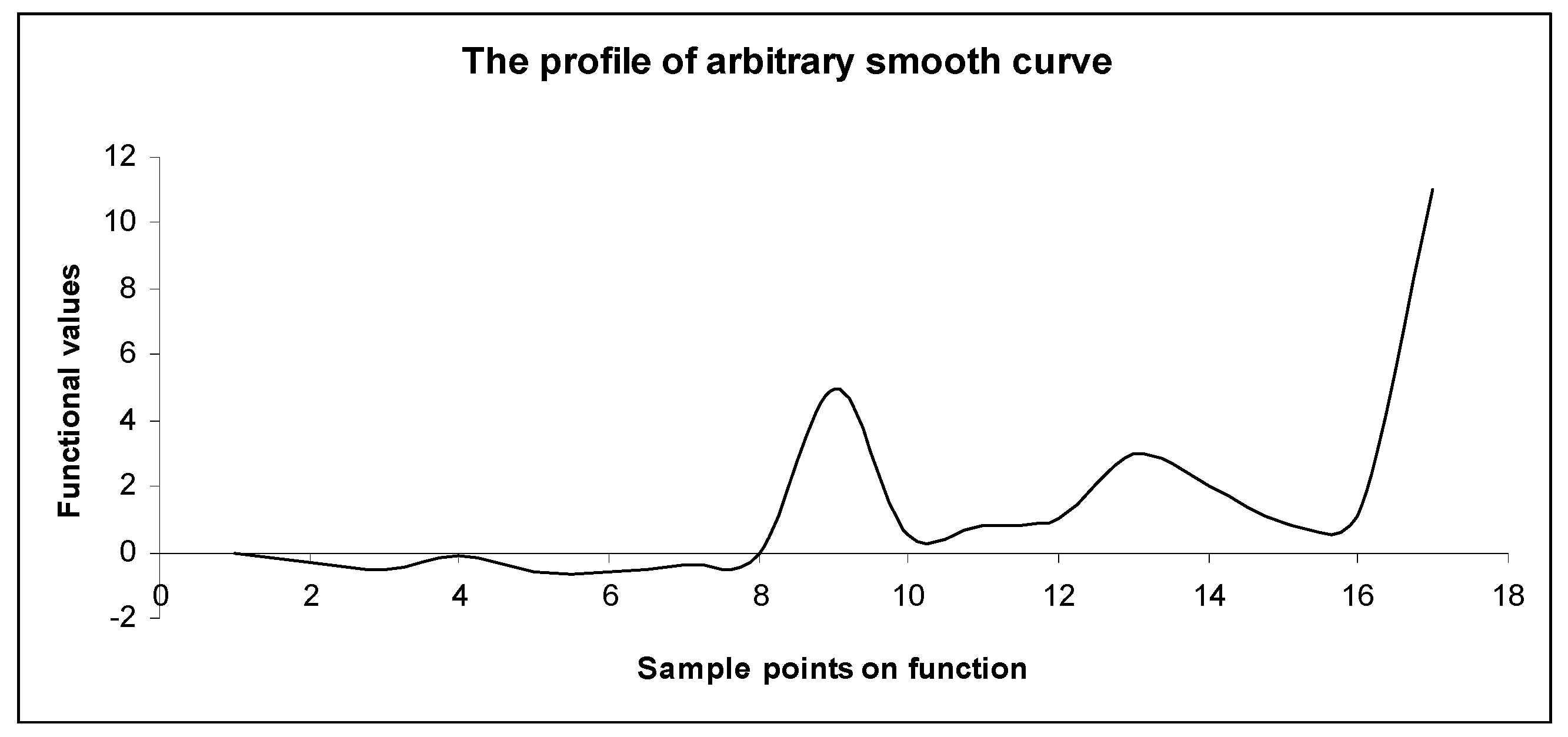
6.1. Evaluation on Linear Smooth Curve
6.2. Evaluation on Non-Linear Curves
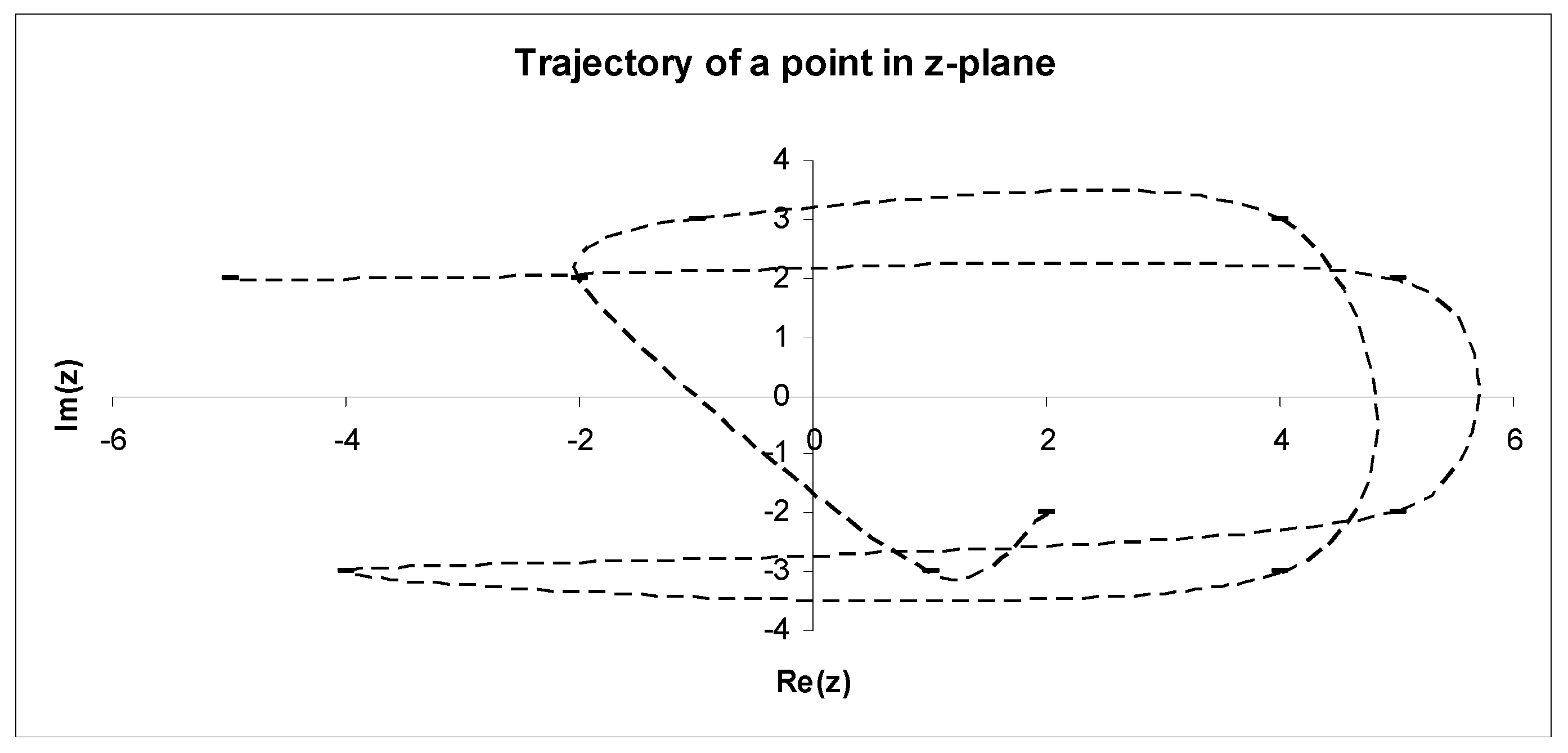
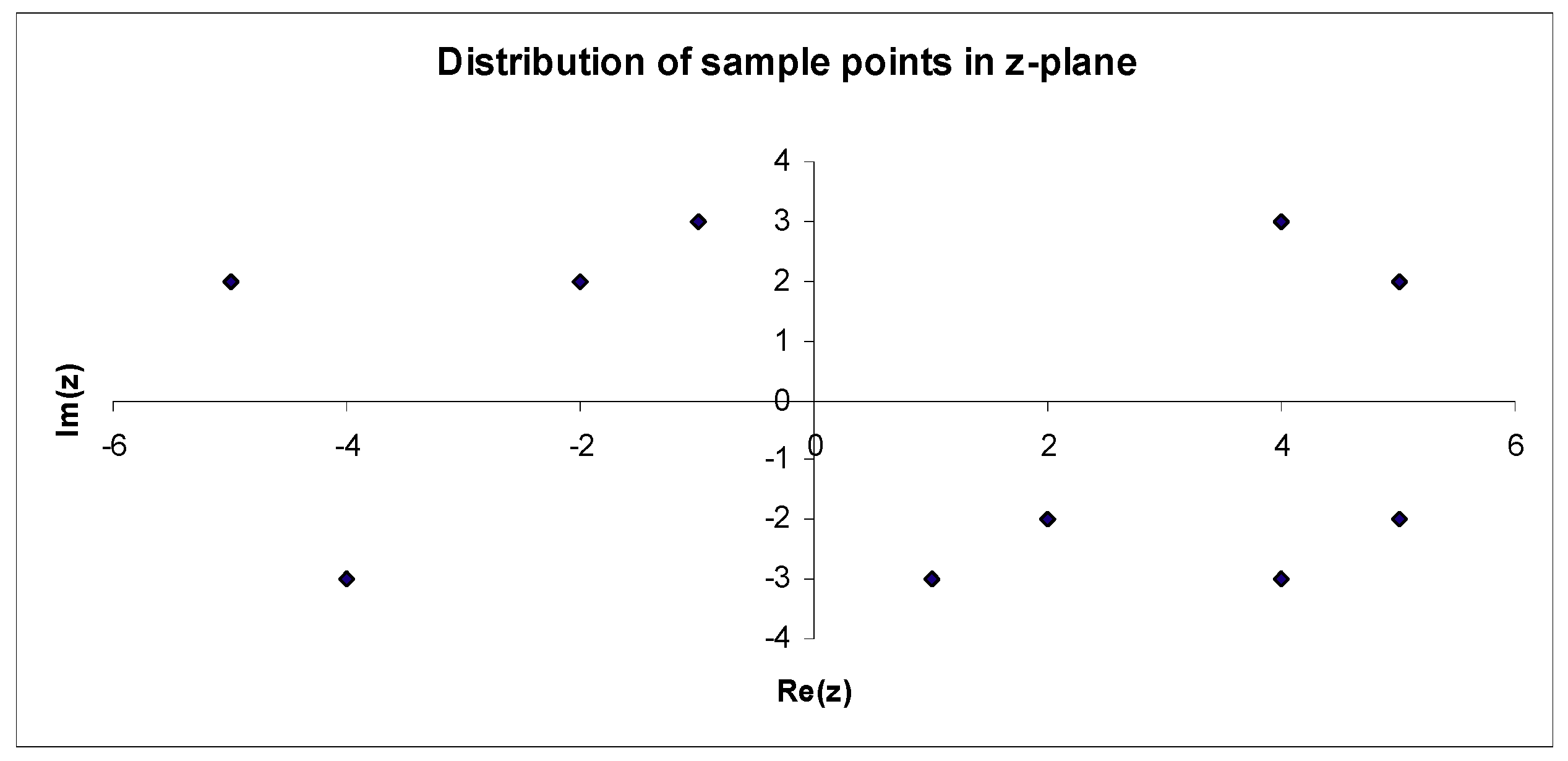
6.3. Evaluation in z-Plane
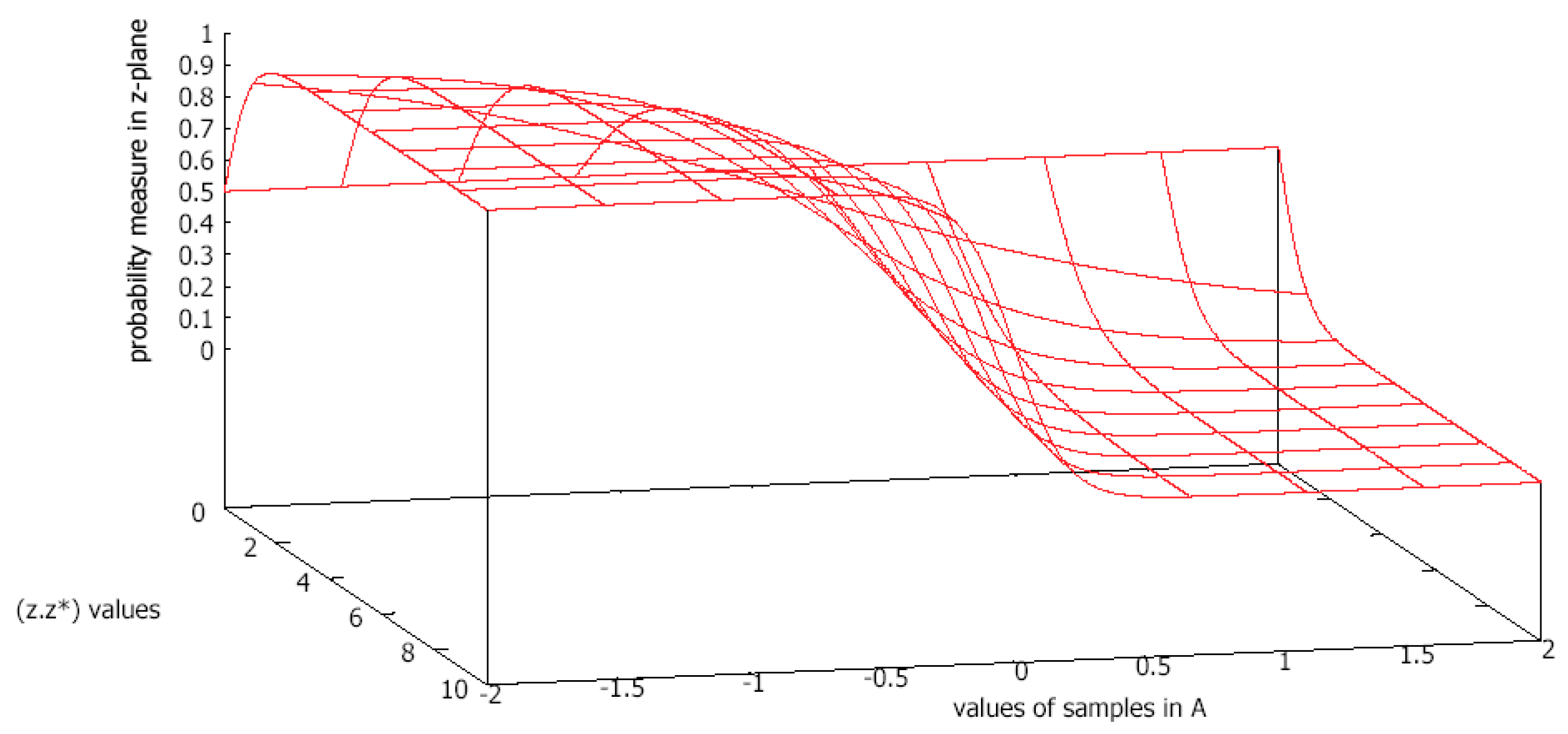
6.4. Measure on Real Surface
7. Comparative Analysis
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Hassin, Y.; Peleg, D. Distributed Probabilistic Polling and Applications to Proportionate Agreement. In Lecture Notes in Computer Science; Wiedermann, J., van Emde Boas, P., Nielsen, M., Eds.; Springer: Berlin, Germany, 1999; Volume 1644, pp. 402–411. [Google Scholar]
- Benjelloun, O.; Sarma, A.; Halevy, A.; Widom, J. ULDBs: Databases with uncertainty and lineage. In Proceedings of the 32nd International Conference on Very Large Data Bases, Seoul, Korea, 12–15 September 2006; pp. 953–964. [Google Scholar]
- Jampani, R.; Xu, F.; Wu, M.; Perez, L.; Jermaine, C. MCDB: A monte carlo approach to managing uncertain data. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 9–12 June 2008. [Google Scholar]
- Kent, P.; Jensen, R.K.; Kongsted, A. A comparison of three clustering methods for finding subgroups in MRI, SMS or clinical data: SPSS TwoStep Cluster analysis, Latent Gold and SNOB. BMC Med. Res. Methodol. 2014, 14, 113. [Google Scholar] [CrossRef] [PubMed]
- Norman, G. Analyzing Randomized Distributed Algorithms. In Validation of Stochastic Systems; Baier, C., Haverkort, B.R., Hermanns, H., Katoen, J.P., Siegle, M., Eds.; Springer: Berlin, Germany; Volume 2925, pp. 384–418.
- Wigderson, A. Do probabilistic algorithms outperform deterministic ones? In Lecture Notes in Computer Science; Larsen, K.G., Skyum, S., Winskel, G., Eds.; Springer: Berlin, Germany, 1998; Volume 1443, pp. 212–214. [Google Scholar]
- Calafiore, G.C.; Dabbene, F.; Tempo, R. Randomized algorithms for probabilistic robustness with real and complex structured uncertainty. IEEE Trans. Autom. Control 2000, 45, 2218–2235. [Google Scholar] [CrossRef]
- Chung, K.M.; Pettie, S.; Su, H.H. Distributed Algorithms for the Lovasz Local Lemma and Graph Colouring. In Proceedings of the ACM Symposium on Principles of Distributed Computing, Paris, France, 15–18 July 2014. [Google Scholar]
- Jibrin, S.; Boneh, A.; Caron, R.J. Probabilistic algorithms for extreme point identification. J. Interdiscip. Math. 2007, 10, 131–142. [Google Scholar] [CrossRef]
- Richard, M.K. An Introduction to Randomized Algorithms. Discret. Appl. Math. 1991, 34, 165–201. [Google Scholar]
- Dubhashi, D.; Grable, D.A.; Panconesi, A. Near-optimal, distributed edge colouring via the nibble method. Theor. Comput. Sci. 1998, 203, 225–251. [Google Scholar] [CrossRef]
- Barenboim, L.; Elkin, M.; Pettie, S.; Schneider, J. The Locality of Distributed Symmetry Breaking. J. ACM 2016, 63. [Google Scholar] [CrossRef]
- Lassaigne, R.; Peyronnet, S. Probabilistic verification and approximation. Ann. Pure Appl. Logic 2008, 152, 122–131. [Google Scholar] [CrossRef]
- Repovš, D.; Savchenko, A.; Zarichnyi, M. Fuzzy Prokhorov metric on the set of probability measures. Fuzzy Sets Syst. 2011, 175, 96–104. [Google Scholar] [CrossRef]
- Hoyrup, M.; Rojas, C. Computability of probability measures and Martin-Löf randomness over metric spaces. Inf. Comput. 2009, 207, 830–847. [Google Scholar] [CrossRef]
- Tian, Y.; Yin, Z.; Huang, M. Missing data probability estimation-based Bayesian outlier detection for plant-wide processes with multisampling rates. Symmetry 2018, 10, 475. [Google Scholar] [CrossRef]
- Shao, S.; Zhang, X.; Li, Y.; Bo, C. Probabilistic single-valued (interval) neutrosophic hesitant fuzzy set and its application in multi-attribute decision making. Symmetry 2018, 10, 419. [Google Scholar] [CrossRef]
- Ercan, S. On the statistical convergence of order α in paranormed space. Symmetry 2018, 10, 483. [Google Scholar] [CrossRef]
- Breugel, F.; Worrell, J. A behavioural pseudometric for probabilistic transition systems. Theor. Comput. Sci. 2005, 331, 115–142. [Google Scholar] [CrossRef]
- Kurtz, T.G.; Manber, U. A probabilistic distributed algorithm for set intersection and its analysis. Theor. Comput. Sci. 1987, 49, 267–282. [Google Scholar] [CrossRef]
- Hind, I.; Ali, D. Probabilistic distributed algorithm for uniform election in polyo-triangular grid graphs. In Proceedings of the 2014 Second World Conference on Complex Systems (WCCS), Agadir, Morocco, 10–12 November 2014. [Google Scholar]
- Anashin, V.; Khrennikov, A. Applied Algebraic Dynamics; Walter de Gruyter: Berlin, Germany, 2009. [Google Scholar]
- Eifler, L. Open mapping theorems for probability measures on metric spaces. Pac. J. Math. 1976, 66, 89–97. [Google Scholar] [CrossRef]
- Parthasarathy, K.R. Probability measures in a metric space. In Probability and Mathematical Statistics; Academic Press: New York, NY, USA, 1967; pp. 26–55. [Google Scholar]
- Horvath, A.G. Normally Distributed Probability Measure on the Metric Space of Norms. Acta Math. Sci. 2013, 33, 1231–1242. [Google Scholar] [CrossRef]
- Vovk, V.; Shen, A. Prequential randomness and probability. Theor. Comput. Sci. 2010, 411, 2632–2646. [Google Scholar] [CrossRef]
- Hertling, P.; Weihrauch, K. Randomness spaces. In Lecture Notes in Computer Science; Larsen, K.G., Skyum, S., Winskel, G., Eds.; Springer: Berlin, Germany, 1998; Volume 1443, pp. 796–807. [Google Scholar]
- Edalat, A. The Scott topology induces the weak topology. In Proceedings of the 11th Annual IEEE Symposium on Logic in Computer Science, Washington, DC, USA, 27–30 July 1996. [Google Scholar]
- Gács, P. Uniform test of algorithmic randomness over a general space. Theor. Comput. Sci. 2005, 341, 91–137. [Google Scholar] [CrossRef]
- Calude, C.S.; Hertling, P.H.; Jurgensen, H.; Weihrauch, K. Randomness on full shift spaces. Chaos Solitons Fractals 2001, 12, 491–503. [Google Scholar] [CrossRef]
- Willis, G.A. Probability measures on groups and some related ideals in group algebras. J. Funct. Anal. 1990, 92, 202–263. [Google Scholar] [CrossRef]





| Models | Locally Compactness | Haar Measurability Condition | Norm Closure | Amenability |
|---|---|---|---|---|
| PMG | Yes | Yes | Finite | Integrable (convergent to 0) |
| DCM | Yes | No | Finite | Summable (convergent in positive interval) |
| LM | No | No | Possibly infinite | Integrable (may not be convergent) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagchi, S. Construction and Simulation of Composite Measures and Condensation Model for Designing Probabilistic Computational Applications. Symmetry 2018, 10, 638. https://doi.org/10.3390/sym10110638
Bagchi S. Construction and Simulation of Composite Measures and Condensation Model for Designing Probabilistic Computational Applications. Symmetry. 2018; 10(11):638. https://doi.org/10.3390/sym10110638
Chicago/Turabian StyleBagchi, Susmit. 2018. "Construction and Simulation of Composite Measures and Condensation Model for Designing Probabilistic Computational Applications" Symmetry 10, no. 11: 638. https://doi.org/10.3390/sym10110638
APA StyleBagchi, S. (2018). Construction and Simulation of Composite Measures and Condensation Model for Designing Probabilistic Computational Applications. Symmetry, 10(11), 638. https://doi.org/10.3390/sym10110638




