Feedforward Neural Networks with a Hidden Layer Regularization Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Neural Network Structure and Batch Gradient Method without Regularization Term
2.2. A Batch Gradient Method with Hidden Layer Regularization Terms
2.2.1. Batch Gradient Method with Lasso Regularization Term
2.2.2. Batch Gradient Method with Group Lasso Regularization Term
2.3. Datasets
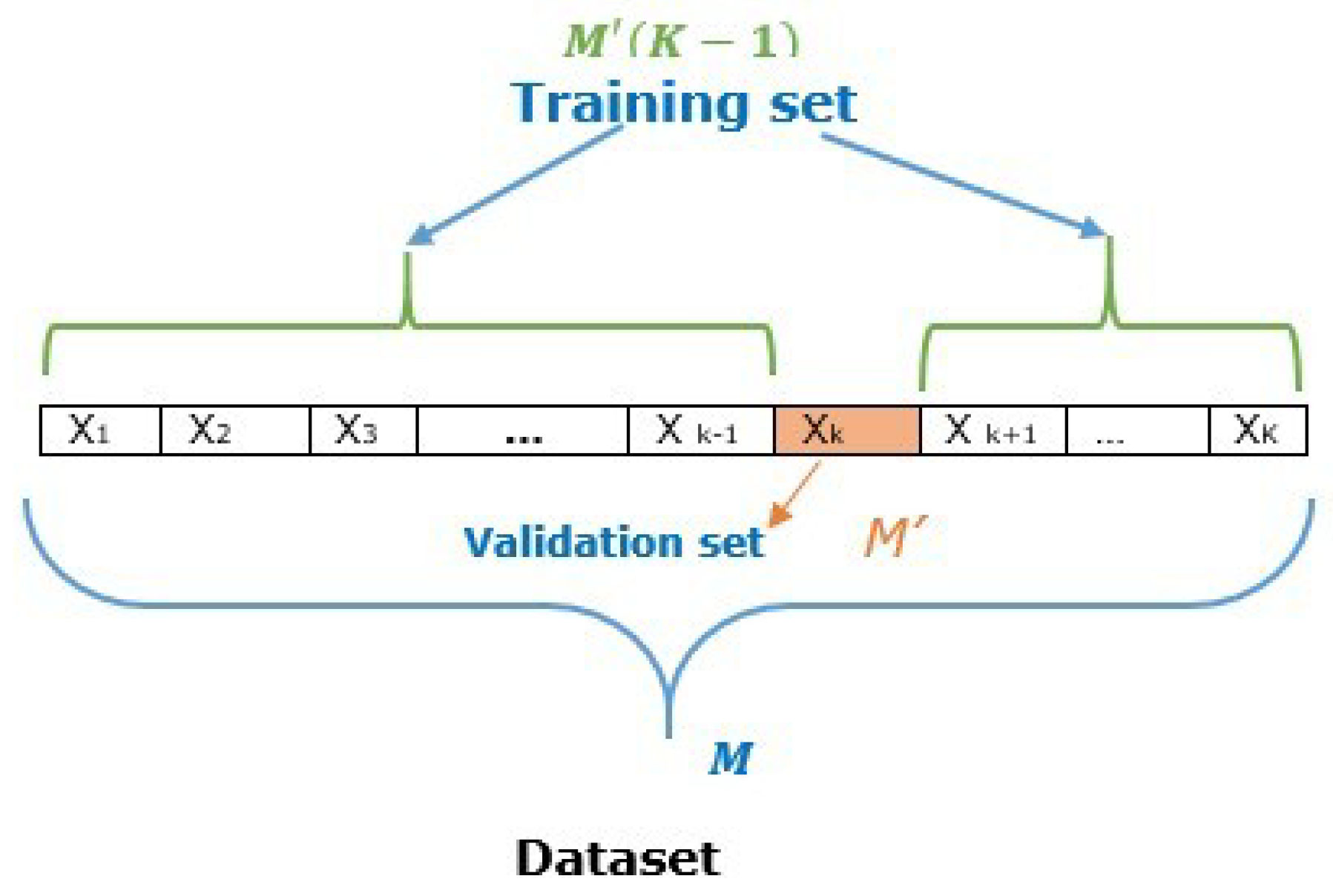
2.3.1. K-fold Cross-Validation Method
2.3.2. Data Normalization
2.3.3. Activation Function
2.4. Hidden Neuron Selection Criterion
- Use a K-fold cross-validation method to split the dataset into a training set and validation set.
- Pick large fully connected FNNs with structure , where is neuron number in the input layer, is neuron number in the hidden layer, and r is neuron number in the output layer (including bias neuron). The number of the input layer and output layer neurons are set equal to the numbers of attributes and classes for each dataset, respectively. Likewise, the number of hidden layer neurons initially is set randomly in a way that it needs to be remarkably bigger than the numbers of attributes and classes.
- Randomly initialize network weights w and in .
- For each train the network using a training set with the standard batch gradient method without any regularization term (i.e., ) as a function learning rate and pick the best that gives the best learning.
- Use the best learning rate obtained from step 3 and start the training process further by increasing the regularization coefficient up to too many numbers of hidden layer neurons are removed, and the accuracy of the network is degraded.
- Compute the norm of the total outgoing weights from each neuron j in the hidden layer; if the norm of total outgoing weights from neuron j in the hidden layer is less or equal to the threshold value, then remove the neuron j from the network else the neuron j will survive.
- Compute the training accuracy using Equation (23).
- Evaluate the trained network using a validation set.
- Compute the testing accuracy using Equation (24).
- Compute the average training and average testing accuracy of the overall results of K using Equations (25) and (26), respectively.
- Compute the average number of redundant or unnecessary hidden layer neurons.
- Select the best regularization parameter that gives the best average results.
3. Results
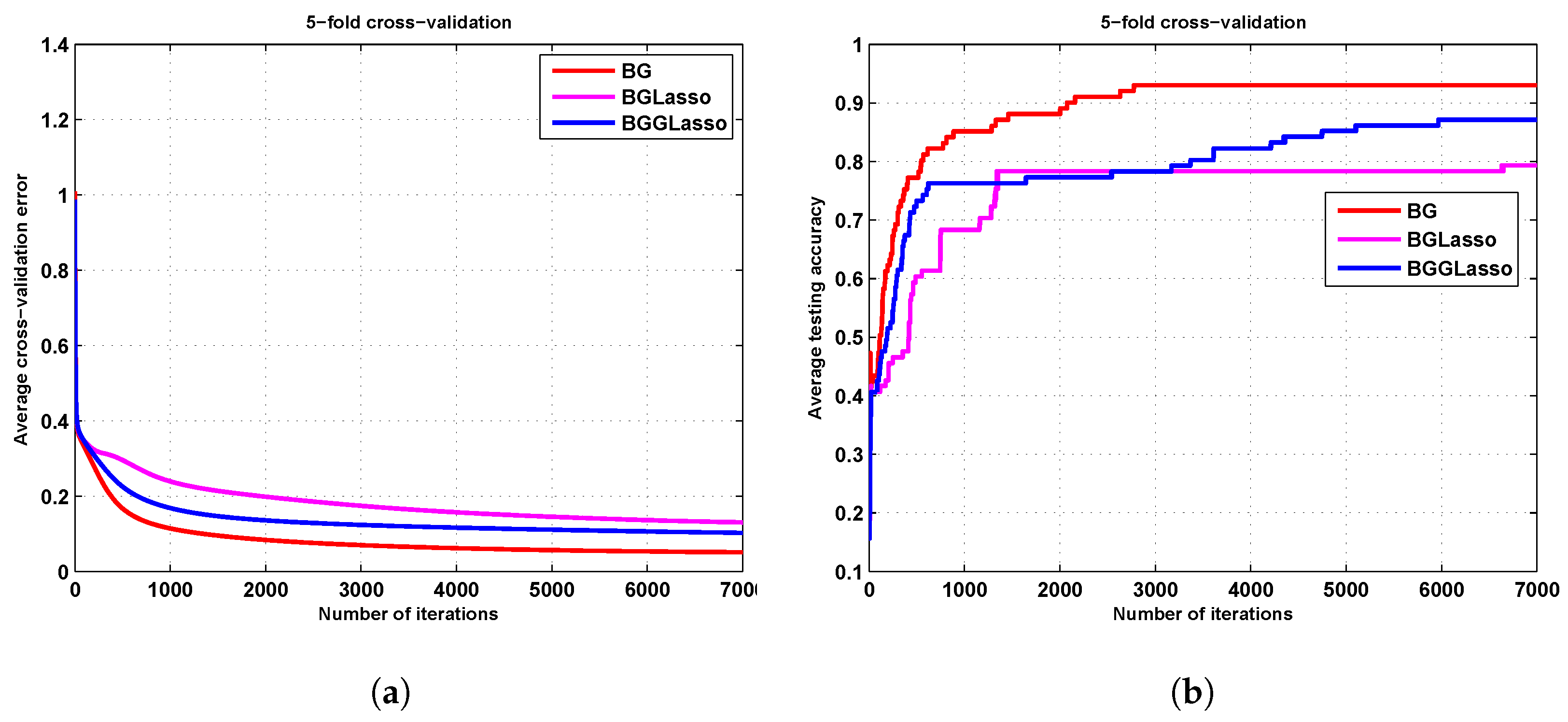
3.1. The Iris Results
3.2. The Zoo Results
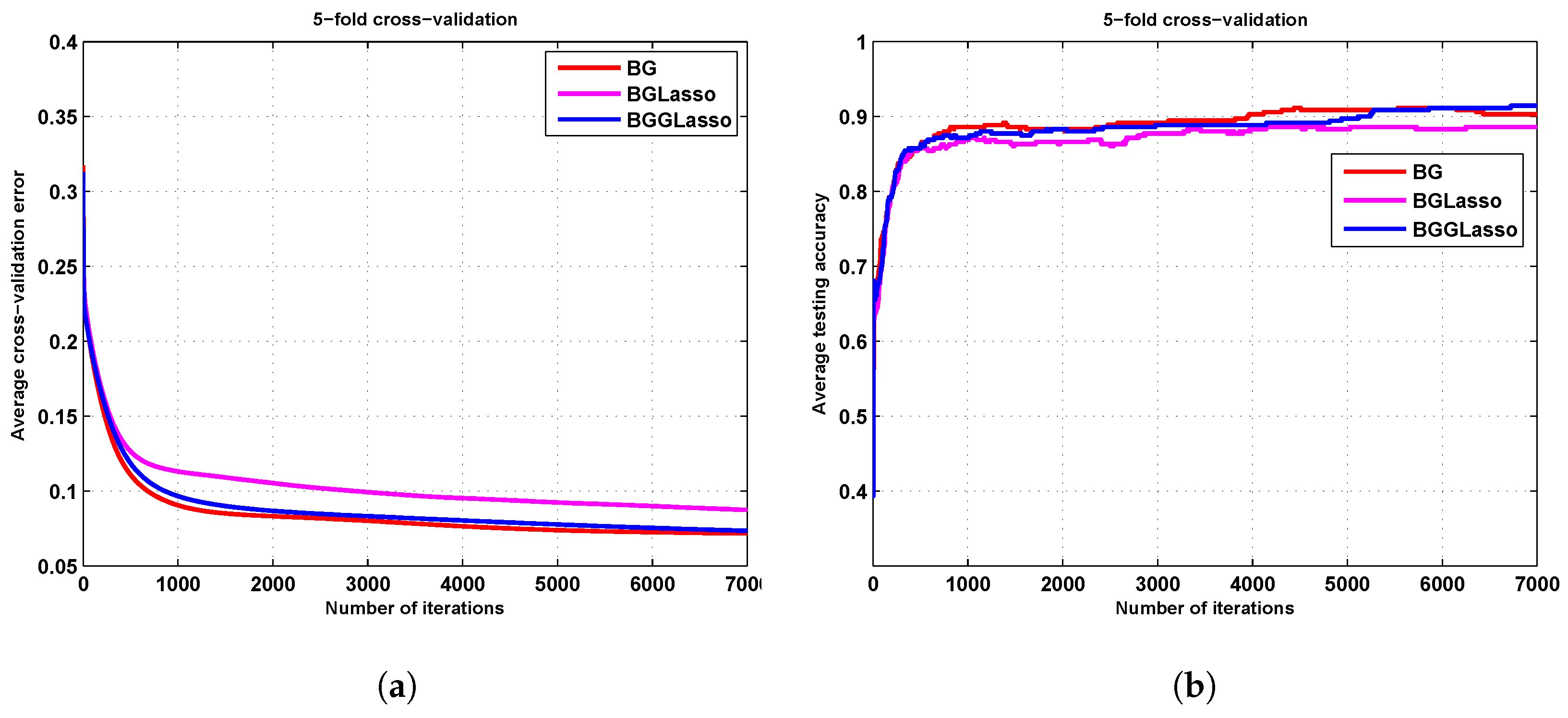
3.3. The Seed Results
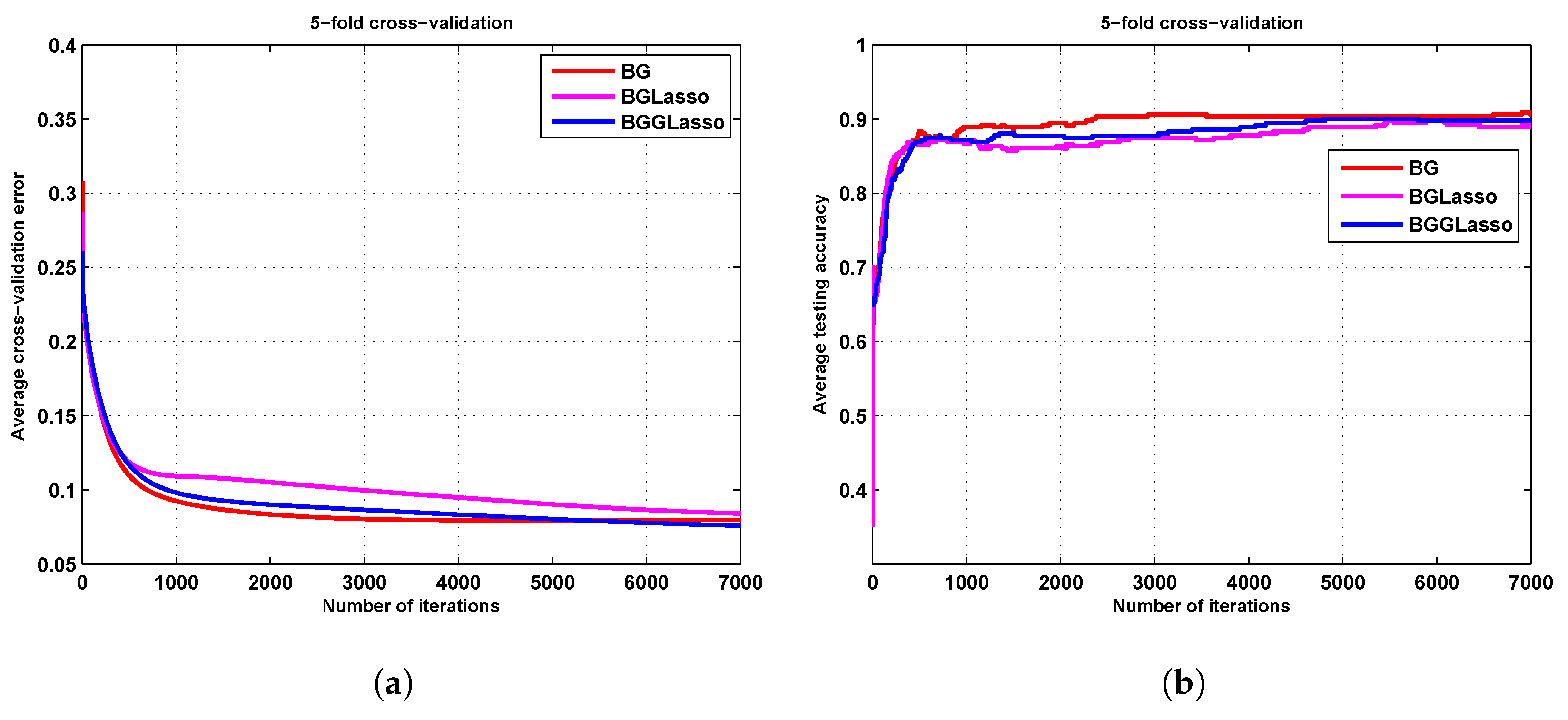
3.4. The Ionosphere Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Lippmann, R. An introduction to computing with neural nets. IEEE ASSP Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Plawiak, P.; Tadeusiewicz, R. Approximation of phenol concentration using novel hybrid computational intelligence methods. Int. J. Appl. Math. Comput. Sci. 2014, 24, 165–181. [Google Scholar] [CrossRef]
- Hinton, G.E. Connectionist learning procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef]
- Pławiak, P.; Rzecki, K. Approximation of phenol concentration using computational intelligence methods based on signals from the metal-oxide sensor array. IEEE Sens. J. 2015, 15, 1770–1783. [Google Scholar]
- Plagianakos, V.P.; Sotiropoulos, D.G.; Vrahatis, M.N. An Improved Backpropagation Method with Adaptive Learning Rate. In Proceedings of the 2nd International Conference on: Circuits, Systems and Computers, Iraeus, Greece, 26–28 October 1998. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533. [Google Scholar] [CrossRef]
- Wilson, D.R.; Martinez, T.R. The general inefficiency of batch training for gradient descent learning. Neural Netw. 2003, 16, 1429–1451. [Google Scholar] [CrossRef]
- Sietsma, J.; Dow, R.J. Neural net pruning-why and how. In Proceedings of the IEEE International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; Volume 1, pp. 325–333. [Google Scholar]
- Setiono, R. A penalty-function approach for pruning feedforward neural networks. Neural Comput. 1997, 9, 185–204. [Google Scholar] [CrossRef] [PubMed]
- Aran, O.; Yildiz, O.T.; Alpaydin, E. An Incremental Framework Based on Cross-Validation for Estimating the Architecture of a Multilayer Perceptron. IJPRAI 2009, 23, 159–190. [Google Scholar] [CrossRef]
- Augasta, M.G.; Kathirvalavakumar, T. A Novel Pruning Algorithm for Optimizing Feedforward Neural Network of Classification Problems. Neural Process. Lett. 2011, 34, 241–258. [Google Scholar] [CrossRef]
- Augasta, M.G.; Kathirvalavakumar, T. Pruning algorithms of neural networks, a comparative study. Cent. Eur. J. Comput. Sci. 2013, 3, 105–115. [Google Scholar] [CrossRef]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal brain damage. Adv. Neural Inf. Process. Syst. 1990, 2, 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G.; Wolff, G.J. Optimal brain surgeon and general network pruning. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 293–299. [Google Scholar]
- Chang, X.; Xu, Z.; Zhang, H.; Wang, J.; Liang, Y. Robust regularization theory based on Lq(0 < q < 1) regularization: The asymptotic distribution and variable selection consistence of solutions. Sci. Sin. Math. 2010, 40, 985–998. [Google Scholar]
- Xu, Z.; Zhang, H.; Wang, Y.; Chang, X.; Liang, Y. L1/2 Regularizer. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Wu, W.; Fan, Q.; Zurada, J.M.; Wang, J.; Yang, D.; Liu, Y. Batch gradient method with smoothing L1/2 regularization for training of feedforward neural networks. Neural Netw. 2014, 50, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, Z.; Yang, D.; Mohamed, K.S.; Wang, J.; Wu, W. Convergence of batch gradient learning algorithm with smoothing L1/2 regularization for Sigma–Pi–Sigma neural networks. Neurocomputing 2015, 151, 333–341. [Google Scholar] [CrossRef]
- Fan, Q.; Wu, W.; Zurada, J.M. Convergence of batch gradient learning with smoothing regularization and adaptive momentum for neural networks. SpringerPlus 2016, 5, 295. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zurada, J.M.; Liu, Y.; Wu, W. Input Layer Regularization of Multilayer Feedforward Neural Networks. IEEE Access 2017, 5, 10979–10985. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Meier, L.; Van De Geer, S.; Bühlmann, P. The group lasso for logistic regression. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2008, 70, 53–71. [Google Scholar] [CrossRef]
- Alvarez, J.M.; Salzmann, M. Learning the number of neurons in deep networks. In Advances in Neural Information Processing Systems, Proceedings of the Annual Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Neural Information Processing Systems Foundation, Inc.: La Jolla, CA, USA, 2016; pp. 2270–2278. [Google Scholar]
- Dua, D.; Taniskidou, E.K.; UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences. Available online: http://archive.ics.uci.edu/ml (accessed on 14 October 2018).
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: New York, NY, USA, 2011. [Google Scholar]
- Zhang, H.; Tang, Y.; Liu, X. Batch gradient training method with smoothing L0 regularization for feedforward neural networks. Neural Comput. Appl. 2015, 26, 383–390. [Google Scholar] [CrossRef]
- Reed, R. Pruning algorithms—A survey. IEEE Trans. Neural Netw. 1993, 4, 740–747. [Google Scholar] [CrossRef] [PubMed]


| Datasets | No. of Examples | No. of Attributes | No. of Class |
|---|---|---|---|
| Iris | 150 | 4 | 3 |
| Zoo | 101 | 17 | 7 |
| Seeds | 210 | 7 | 3 |
| Ionosphere | 351 | 34 | 2 |
| Methods | Sparsity | Accuracy | |||||
|---|---|---|---|---|---|---|---|
| AVGNPWs | AVGNPHNs | Training Acc. (%) | Testing Acc. (%) | ||||
| BG | 0.000 | 0.050 | 0.000 | 0.000 | 0.010 | 98.500 | 98.000 |
| BGLasso | 0.010 | 0.050 | 53.200 | 0.000 | 0.060 | 97.800 | 93.300 |
| BGGLasso | 0.010 | 0.050 | 18.400 | 6.000 | 0.020 | 98.300 | 97.300 |
| Methods | Sparsity | Accuracy | |||||
|---|---|---|---|---|---|---|---|
| AVGNPWs | AVGNPHNs | Training Acc .(%) | Testing Acc. (%) | ||||
| BG | 0.000 | 0.040 | 0.000 | 0.000 | 0.0200 | 99.800 | 93.100 |
| BGLasso | 0.030 | 0.040 | 314.400 | 0.000 | 0.200 | 86.600 | 79.300 |
| BGGLasso | 0.030 | 0.040 | 47.800 | 6.800 | 0.030 | 93.600 | 87.100 |
| Methods | Sparsity | Accuracy | |||||
|---|---|---|---|---|---|---|---|
| AVGNPWs | AVGNPHNs | Training Acc. (%) | Testing Acc. (%) | ||||
| BG | 0.000 | 0.080 | 0.000 | 0.000 | 0.0200 | 92.500 | 91.400 |
| BGLasso | 0.009 | 0.080 | 101.600 | 0.000 | 0.060 | 89.500 | 89.100 |
| BGGLasso | 0.009 | 0.080 | 24.600 | 8.200 | 0.040 | 91.700 | 90.900 |
| Methods | Sparsity | Accuracy | |||||
|---|---|---|---|---|---|---|---|
| AVGNPWs | AVGNPHNs | Training Acc. (%) | Testing Acc. (%) | ||||
| BG | 0.000 | 0.050 | 0.000 | 0.000 | 0.020 | 98.800 | 92.000 |
| BGLasso | 0.007 | 0.050 | 1327.800 | 0.000 | 0.090 | 94.000 | 88.900 |
| BGGLasso | 0.007 | 0.050 | 45.600 | 22.800 | 0.040 | 97.100 | 91.400 |
| Methods | Sparsity | Accuracy | |||||
|---|---|---|---|---|---|---|---|
| AVGNPWs | AVGNPHNs | Training Acc. (%) | Testing Acc. (%) | ||||
| BG | 0.000 | 0.050 | 0.000 | 0.000 | 0.020 | 98.000 | 90.900 |
| BGLasso | 0.007 | 0.050 | 1646.400 | 0.000 | 0.100 | 94.500 | 89.800 |
| BGGLasso | 0.007 | 0.050 | 60.400 | 30.200 | 0.050 | 96.900 | 90.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemu, H.Z.; Wu, W.; Zhao, J. Feedforward Neural Networks with a Hidden Layer Regularization Method. Symmetry 2018, 10, 525. https://doi.org/10.3390/sym10100525
Alemu HZ, Wu W, Zhao J. Feedforward Neural Networks with a Hidden Layer Regularization Method. Symmetry. 2018; 10(10):525. https://doi.org/10.3390/sym10100525
Chicago/Turabian StyleAlemu, Habtamu Zegeye, Wei Wu, and Junhong Zhao. 2018. "Feedforward Neural Networks with a Hidden Layer Regularization Method" Symmetry 10, no. 10: 525. https://doi.org/10.3390/sym10100525
APA StyleAlemu, H. Z., Wu, W., & Zhao, J. (2018). Feedforward Neural Networks with a Hidden Layer Regularization Method. Symmetry, 10(10), 525. https://doi.org/10.3390/sym10100525





