New Soft Set Based Class of Linear Algebraic Codes

Abstract

In this paper, we design and develop a new class of linear algebraic codes defined as soft linear algebraic codes using soft sets. The advantage of using these codes is that they have the ability to transmit m-distinct messages to m-set of receivers simultaneously. The methods of generating and decoding these new classes of soft linear algebraic codes have been developed. The notion of soft canonical generator matrix, soft canonical parity check matrix, and soft syndrome are defined to aid in construction and decoding of these codes. Error detection and correction of these codes are developed and illustrated by an example.

1. Introduction

Shannon [1,2] published an historic paper that marked the beginning of both error correcting codes and information theory. Since then, several researchers have developed and designed codes like BCH codes [3,4], self-dual codes [5], maximum distance codes [6], Hamming distance of linear codes [7], and codes over Z_m [8,9]. However fuzzy codes and distance properties was developed by [10]. For literature used in this paper on coding theory, see Reference [11].

In this paper, we define soft linear codes using soft sets. Soft sets [12] are generalization of fuzzy sets introduced in [13]. Fuzzy sets work on membership degree whose range varies from Reference [0, 1] and soft sets deal with uncertainty in a parametric way. Thus, a soft set is a parameterized family of sets and the boundary of the set depends on the parameters. Since then, soft sets [14] have been developed to neutrosophic soft sets [15], soft neutrosophic groups [16], soft neutrosophic algebraic structures, and their generalization [17,18,19,20]. Relationship among soft sets and fuzzy sets was studied in Reference [20,21]. Here, for the first time, soft set theory has been used in the construction of algebraic codes, which we choose to call as soft algebraic linear codes.

This paper is organized into six sections. Section 1 is introductory in nature. All basic concepts to make this paper a self-contained one are given in Section 2. Section 3 introduces the new notion of algebraic soft codes and defines and describes some related properties of them. Soft parity check matrix and soft generator matrix are introduced in Section 3. Section 4 describes decoding, error detection and error correction of the soft linear algebraic codes. Section 5 gives the soft communication model and brings out the difference between the linear algebraic codes and soft linear algebraic codes. Section 6 gives the conclusions based on our study and probable future research for any researcher.

2. Fundamental Notions

In this section the basic concepts needed to make this paper a self-contained one is given. This section is divided into two subsections. Section 2.1 describes the basic concepts about the linear algebraic codes and their related properties and Section 2.2 gives the definition and a few properties of soft sets.

2.1. Algebraic Linear Codes and Their Properties

All the basic concepts, definition and properties of algebraic linear codes are taken from Reference [11]. The fundamental algebraic structure used in the definition of linear algebraic codes are vector spaces and vector subspaces defined over a finite field F. Throughout this paper, we only consider the finite field Z₂ = {0, 1}, the finite field of characteristic two. We use F to denote Z₂.

Definition 1.

Let V be a set of elements on which a binary operation called addition, ‘+’ is defined. Let F be a field. An operation product or multiplication, denoted by ‘.’, between the elements in F and the elements in V is defined. The set V is called a vector space over the field F if it satisfies the following conditions:

1.

V is a commutative group under addition.

2.

For any element a in F and any element v in V, a.v = v.a is in V.

3.

Distributive law: For any u and v in V and for any a,b ∈ F

a.(u + v) = a.u + a.v; (a + b).v = a.v + b.v.

4.

Associative law: For any v in V and any a and b in F; (a.b).v = a.(b.v).

5.

Let 1 be the unit element of F. Then for any v in V, 1.v = v and 0.v = 0 for 0 ∈ F and ‘$\overline{0}$’ is the zero vector of V.

We call a proper subset U of V (U ⊂ V) to be a vector subspace of V over F if U itself is a vector space over F.

Definition 2.

A block code of length n with 2^k codewords is called a linear code, denoted by C (n, k), if and only if its 2^k codewords form a k-dimensional subspace of the vector space Vⁿ of all the n tuples over the field GF(2).

The method for generating these C(n, k) codes using the generator matrix G is as follows. G is given in the following:

$$G=\left[\begin{array}{ccccc}{g}_{00}& g_{01}& g_{02}& \dots & g_{0,n-1}\\ g_{10}& g_{11}& g_{12}& \dots & g_{1,n-1}\\ ⋮& ⋮& & & \\ g_{k-1,0}& g_{k-1,1}& g_{k-1,2}& & g_{k-1,n-1}\end{array}\right]$$

g_i,j ∈ Z₂ = F; for 0 ≤ i ≤ k − 1 and 0 ≤ j ≤ n − 1. Consider u = (u₀ u₁ … u_k−1), the message to be encoded, the corresponding codeword v is given by v = u.G. Every codeword v in C (n, k) is a linear combination of k codewords.

The error detection and error correction of these codes is given in Reference [11]. If the generator matrix G in the standard form is G = (A; I_{k × k}), then parity check matrix H can be got in the standard form as H = (I_{n−k × n−k}; A^T). The generator matrix can be in any other form, and then the parity check matrix can be found out by the usual methods given in Reference [11].

The syndrome of the received codeword y, denoted by s(y) = yH^T is obtained from the parity check matrix H. Thus, the parity check matrix H of a code helps to detect the error from the received word. The error correcting capacity of a code depends on the metric that is used over the code. The most basic metric, namely the Hamming metric of the code is defined as follows:

Definition 3.

For any two vectors x = (x₁ … x_n) and y = (y₁ … y_n) in Vⁿ, the n dimensional vector space over the field F = Z₂, the Hamming distance d(x, y) and the Hamming weight w(x) are defined as follows:

d(x, y) = |{x_i:x_i ≠ y_i; x_i ∈ x; y_i ∈ y}|

w(x) = |{x_i:x_i ≠ 0; x_i ∈ x}|.

Definition 4.

The minimum distance d_min of a code C(n, k) is defined as

$$d_{min}=\underset{\begin{array}{c}x,y\in C\\ x\ne y\end{array}}{min}d(x,y).$$

The coset leader method used for error correction, makes use of the standard array for syndrome decoding as described in Reference [11].

2.2. Soft Set Theory

The soft set theory which is a generalization of fuzzy set theory was proposed by Reference [12].

While this part X concerns to an inceptive domain, P(X) is the power set of X, V is called a set of parameters, or D ⊂ V. The soft set theory defined by Reference [12] is given below.

Definition 5.

The set (f, D) is said to be a soft set of X where a mapping of f is given by f:D → P(X).

In other words, a soft set over X is a parameterized family of subsets of the universe X. For d ∈ D, f(d) can be considered as the set of d-elements of the soft set (f, D), or as the set of d-approximate elements of the soft set.

Let (f, D) and (g, E) be two soft sets over X, (f, D) is called a soft subset of (g, E) if D ⊆ E and f(s) ⊆ g(s), for all s ∈ D. This relationship is denoted by (f, D) ⊂ (g, E). Similarly, (f, D) is called a soft superset of (g, E) if (g, E) is a soft subset of (f, D) which is denoted by (f, D) ⊃ (g, E). If (f, D) ⊆ (g, E) and (g, E) ⊆ (f, D), the two soft sets are said to be equal.

3. Algebraic Soft Linear Codes and Their Properties

In this section the concept of soft linear code and algebraic soft linear code of type 1 are proposed and notion of soft generator matrix and soft parity check matrix are introduced.

Definition 6.

Let F = Z₂; be the field of characteristic two. Let W = F × … × F = F^m, be a vector space over the field F of dimension m. P(W) be the power set of W. (f, D) is said to be a soft algebraic linear code over F if and only if f(d) is a linear algebraic code of W for all d ∈ D; D ⊂ V, where V is the set of parameters.

It is to be noted that not all vector subspaces of W, forms a linear algebraic code. Further, the soft algebraic linear code does not in general include all linear algebraic codes of W.

Example 1.

Let W = F³ be a vector space over the field F. (f, D) is a soft linear code over W where f(D) = {f(d₁), f(d₂)} with

f(d₁) = {000, 111} and f(d₂) = {000, 110, 101, 011}.

Clearly {000, 111} and {000, 110, 101, 011} are linear algebraic codes. {{000, 000}, {000, 110}, {000, 101}, {000, 011}, {111, 000}, {111, 110}, {111, 101}, and {111, 011}} is the set of soft codewords of (f, D). There are 8 soft codewords for the soft code (f, D).

In view of this example we define soft codeword as follows:

Definition 7.

Let W = F × … × F = F^m, be a vector space over the field F of dimension m. P(W) be the power set of W. (f, D) be a soft algebraic linear code over F. Let f(D) = {f(d₁), …, f(d_t)} where each f(d_i); 1 ≤ i ≤ t is a linear algebraic code of W. Each t-tuple {x₁, x₂, …, x_t}; x_i ∈ f(d_i); 1 ≤ i ≤ t is defined as the soft codeword of the soft algebraic code (f, D). We have |f(d₁)| × |f(d₂)|× … × |f(d_t)| number of soft codewords for this (f, D).

In the above example, the soft dimension (f, D) = {1, 2}, that is the number of linearly independent codewords of the linear algebraic code associated with f(d₁) and f(d₂), respectively.

We have the following definition in view of this.

Definition 8.

Let W = F^m, be a vector space over the field F of dimension m. (f, D) be a soft algebraic linear code over F. Let f(D) = {f(d₁), …, f(d_t)} where each f(d_i); 1 ≤ i ≤ t is a linear algebraic code of W. Here each f(d_i) ∈ f(D) is a linear algebraic code and dimension of f(d_i) is n_i where n_i is the number of linear independent elements of f(d_i). The soft dimension of (f, D) = {n₁, …, n_t} and the number of soft codewords of (f, D) is |f(d₁)| × |f(d₂)| × … × |f(d_t) |where 1 ≤ i ≤ t.

Definition 9.

Let (f, D) be the same as in above Definition 8. (f, D) is called soft code of type 1, if the dimension of (f, D) = {n₁, n₂, …, n_t} is such that n₁ = n₂ = … = n_t.

In the following we give an example of soft code of type 1.

Example 2.

Let (f, D) be a soft code in W = F × … × F = F⁵ over the field F. Consider

f(d₁) = {00000, 11111, 10110, 01001},
f(d₂) = {00000, 11111, 11001, 00110},
f(d₃) = {00000, 11111, 00111, 11000}, and
f(d₄) = {00000, 11111, 11100, 00011}.

The soft dimension of (f, D) is {2, 2, 2, 2}. Hence (f, D) is a soft code of type 1.

Theorem 1.

Every soft algebraic linear code of type 1 is trivially a soft algebraic linear code but the converse is not true.

Proof. 

The result follows from the definition of soft code of type 1. For the converse, result follows from Example 1, where the dimensions of f(d₁) and f(d₂) are different. □

Now we proceed on to define the soft generator matrix for soft linear algebraic code (f, D).

Definition 10.

Let (f, D) be a soft linear algebraic code as in Definition 8, where f(D) = {f(d₁), …, f(d_t)}. We know that associated with each f(d_i) we have an algebraic code of dimension n_i. Let G_i; 1 ≤ i ≤ t be the generator matrix associated with this algebraic code associated with f(d_i). Then we define the soft generator matrix G_s as the t-matrix given by G_s = [G₁|G₂| … |G_t]. If the each generator matrix G_i of the soft generator matrix G_s is represented in the standard form then the soft generator matrix G_s is known as soft canonical generator matrix and is denoted by G_s*.

Example 3.

The soft generator matrix of the soft linear code of type 1 given in Example 2 is as follows:

$$G_s=\left[G_1\left|G_2\right|G_3|G_4\right]=\left[\left[\begin{array}{ccccc}1& 0& 1& 1& 0\\ 0& 1& 0& 0& 1\end{array}\right]|\left[\begin{array}{ccccc}1& 1& 0& 0& 1\\ 0& 0& 1& 1& 0\end{array}\right]|\left[\begin{array}{ccccc}0& 0& 1& 1& 1\\ 1& 1& 0& 0& 0\end{array}\right]|\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 0& 0& 0& 1& 1\end{array}\right]\right]$$

where G_i is the generator matrix of the algebraic code associated with f(d_i); i = 1, 2, 3, 4; clearly this G_S is not the soft canonical generator matrix.

The following example gives the soft canonical generator matrix for the soft linear code.

Example 4.

Suppose (f, D) be a soft code over W = F⁵, where

f(d₁) = {00000, 10010, 01001, 00110, 11011, 10100, 01111, 11101};
f(d₂) = {00000, 11111, 10110, 01001}

are algebraic linear codes with standard generator matrix G₁ and G₂ where

$$G_1=\left[\begin{array}{ccccc}1& 0& 1& 1& 0\\ 0& 1& 0& 0& 1\end{array}\right],\hspace{1em}{G}_2=\left[\begin{array}{ccccc}1& 0& 0& 1& 0\\ 0& 1& 0& 0& 1\\ 0& 0& 1& 1& 0\end{array}\right].$$

The soft canonical generator bi-matrix of (f, D) is:

$$G_s^{*}=\left[\left[\begin{array}{ccccc}1& 0& 1& 1& 0\\ 0& 1& 0& 0& 1\end{array}\right]|\left[\begin{array}{ccccc}1& 0& 0& 1& 0\\ 0& 1& 0& 0& 1\\ 0& 0& 1& 1& 0\end{array}\right]\right].$$

Now we proceed onto to define soft parity check matrix and soft canonical parity check matrix for a soft linear algebraic code.

Definition 11.

Consider (f, D) as in Definition 8. Let f(D) = {f(d₁), …, f(d_t)} where each f(d_i) is linear algebraic code, let H_i (1 ≤ i ≤ t) be the parity check matrix associated with each linear algebraic code. Then H_S = {H₁|H₂| … |H_t} is the soft parity check matrix associated with the soft linear algebraic code.

If each H_i is taken in the standard form then the corresponding soft parity check matrix$H_s^{*}$is defined as the soft canonical parity check matrix of the soft algebraic linear code.

Now, in the following section, we give a method to determine soft errors in received codewords and how the soft error corrections are carried out.

4. Soft Linear Algebraic Decoding Algorithms

During transmission over any medium, the transmitted codeword can get corrupted with errors. The process of identifying these errors from the received codeword is known as error detection and the process of correcting the errors and obtaining the correct codeword is known as error correction. In this section, we introduce the notion the soft decoding algorithm, error detection, and error correction for soft linear algebraic codes. The method of soft syndrome decoding is proposed.

First, we proceed on to define the notion of coset and soft coset leader. The definition of coset and coset leader for any linear algebraic code can be had from Reference [11].

We now define the coset leaders as elements in each of the cosets with the least weight. For any code, C = C(n, k) is as follows as the algebraic code is a subspace of W so is a subgroup of W.

$$\begin{array}{ccc}CosetLeaders& CodewordsascosetsofC& Syndromes\\ e_0=0& x_1,\dots ,x_m& s=0\\ e_1& e_1+x_1,\dots ,e_1+x_m& e_1{H}^T\\ e_2& e_2+x_1,\dots ,e_2+x_m& e_2{H}^T\\ ⋮& ⋮& ⋮\\ e_p& e_p+x_1,\dots ,e_p+x_m& e_p{H}^T\end{array}$$

where e_i’s are coset leaders. Syndrome of e_i, s(e_i) = e_iH^T; 0 ≤ i ≤ t.

H is the parity check matrix of the linear algebraic code C. The coset leader method is used for error correction by making use of the standard array for syndrome decoding [11].

Definition 12.

Let (f, D) be the soft linear code as given in Definition 8. Let H_s = (H₁|H₂| … |H_t) be the soft parity check matrix of (f, D). Suppose y is the received soft message, the soft syndrome of y is defined as s(y) = y$H_s^T$; if s(y) ≠ (o) then we say the soft codeword has soft error.

Now, we proceed on to analogously describe the syndrome decoding method for soft linear algebraic codes.

Let W = F^m be a vector space of dimension n over F = Z₂. Let (f, D) be a soft algebraic code with f(D) = (f(d₁), …, f(d_t)) where each f(d_i); 1 ≤ i ≤ t; is a linear algebraic code over W. Any soft codeword in (f, D) will be of the form x = (x₁, x₂, …, x_t) where x_i ∈ f(d_i) and x_i = $\left(y_1^i,\dots ,y_m^i\right)$ a m-tuple for which it will have k_i message symbols; 1 ≤ i ≤ t.

If z is a received message we have to first find out if z has any error and if z has error we have to correct it. Now to check for error we find the soft syndrome s(z) = zH^T = $z\left(H_1^T|H_2^T|\dots |H_t^T\right)$ where each H_i is the parity check matrix of the linear algebraic code associated with f(d_i); 1 ≤ i ≤ t.

If s(z) ≠ (0) we have an error. This error is defined as the soft error and s(z) is defined as soft syndrome of the soft codeword z received. This procedure of finding out whether the received soft codeword is correct or not; it is termed as soft error detection.

Now, we proceed on to correct the soft error as s(z) ≠ (0); some soft error has occurred during transmission. We can build an analogous table for error correction or standard array for soft syndrome decoding. Soft coset leaders in the case of soft codes will be carried out in an analogous way, which will be described by an example.

Example 5.

Let (f, D) be a soft code defined in Example 1. The soft parity check matrix of (f, D) be

$$H=\left[H_1|H_2\right]=\left[\left[\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\end{array}\right]|\left[\begin{array}{ccc}1& 1& 1\end{array}\right]\right].$$

The transpose of H is as follows,

$$H^T=\left[\left[\begin{array}{cc}1& 0\\ 1& 1\\ 0& 1\end{array}\right]|\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\right].$$

And the soft coset leaders of (f, D) are

e₀ = {000, 000}, e₁ = {100, 100}, e₂ = {010, 010} and e₃ = {001, 001}

The

Table 1. Soft Syndrome Coding.

Soft Coset Leaders	Soft Codewords as Cosets of (f, D)	Soft Syndromes
e0 = {000, 000}	{000, 000}, (000, 110}, {000, 101}, {000, 011}, {111, 000}, {111, 110}, {111, 101}, {111, 011}	e0HT = {00, 0}
e1 = {100, 100}	{100, 100}, (100, 010}, {100, 001}, {100, 111}, {011, 100}, {111, 010}, {011, 001}, {011, 111}	e1HT = {10, 1}
e2 = {010, 010}	{010, 010}, (010, 100}, {010, 111}, {010, 001}, {101, 010}, {101, 100}, {101, 111}, {101, 001}	e2HT = {11, 1}
e3 = {001, 001}	{001, 001}, (001, 111}, {001, 100}, {001, 010}, {110, 001}, {110, 111}, {110, 100}, {110, 010}	e3HT = {01, 1}

of soft syndrome decoding is as follows:

Using this table for the soft code (f, D) given in the example, we can correct any received soft codeword which has error.

For instance, let y = {110, 010} be the received soft codeword.

We see

$${\mathit{yH}}^T=\{110,010\}\left[\left[\begin{array}{cc}1& 0\\ 1& 1\\ 0& 1\end{array}\right]|\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\right]=\left[(110)\left[\begin{array}{cc}1& 0\\ 1& 1\\ 0& 1\end{array}\right]|(010)\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\right]=\{01,1\}\ne \{00, 0\}.$$

It is clear that error has occurred.

Clearly y ∉ (f, D) so we have to correct the soft error, we use the Table 1. We have found yH^T = {01, 1} using the table, it corresponds to soft coset leader e₃. This y = {110, 010} appears as the last one in the table in the middle column. Thus, the error term is e₃ = {001, 001}, which should be added with y. Now, y + e₃ = {110, 010} + {001, 001} = {111, 011} ∈ f(D), which is the correct codeword.

Theorem 2.

Suppose (f, D) be a soft linear algebraic code over a field F, given in Definition 8, any element received codeword, which has some error y = (y₁, …, y_t); y_i ∈ W = F^m; 1 ≤ i ≤ t; then there is a soft codeword nearest to y given by x = y + soft coset leader e_i of the soft code (f, D).

Proof. 

Let (f, D) be a soft linear algebraic code over a field F with H as the soft parity check matrix. Let y = (y₁, …, y_t) be the received codeword, we find the soft syndrome;

$$s\left(y\right)={\mathit{yH}}^T=(y_1\dots y_t)\left[H_1^T|H_2^T|\dots |H_t^T\right]$$

where s(y) = (0) implies that there is no error, so y is the correct codeword. If s(y) ≠ (0), then we work as follows: First, we find all the soft linear algebraic coset of the soft linear algebraic code (f, D) for soft set-based syndrome decoding, and then find the appropriate soft linear algebraic coset leaders e_i from the collection of coset leaders using the one analogues Table 1. Then, for all soft coset leaders we calculate the soft set-based syndrome and make a table of soft linear algebraic coset leaders with their soft set-based syndromes. For decoding a soft linear algebraic codeword y, we can merely find the soft set-based syndrome of the soft linear algebraic codeword and then compare soft coset leader syndrome with their soft set-based syndrome. After the comparison, we add the soft decoded word to the soft linear algebraic coset leader. Thus, y is soft decoded as x = y + e_i; e_i is the soft coset leader and x is the corrected word. □

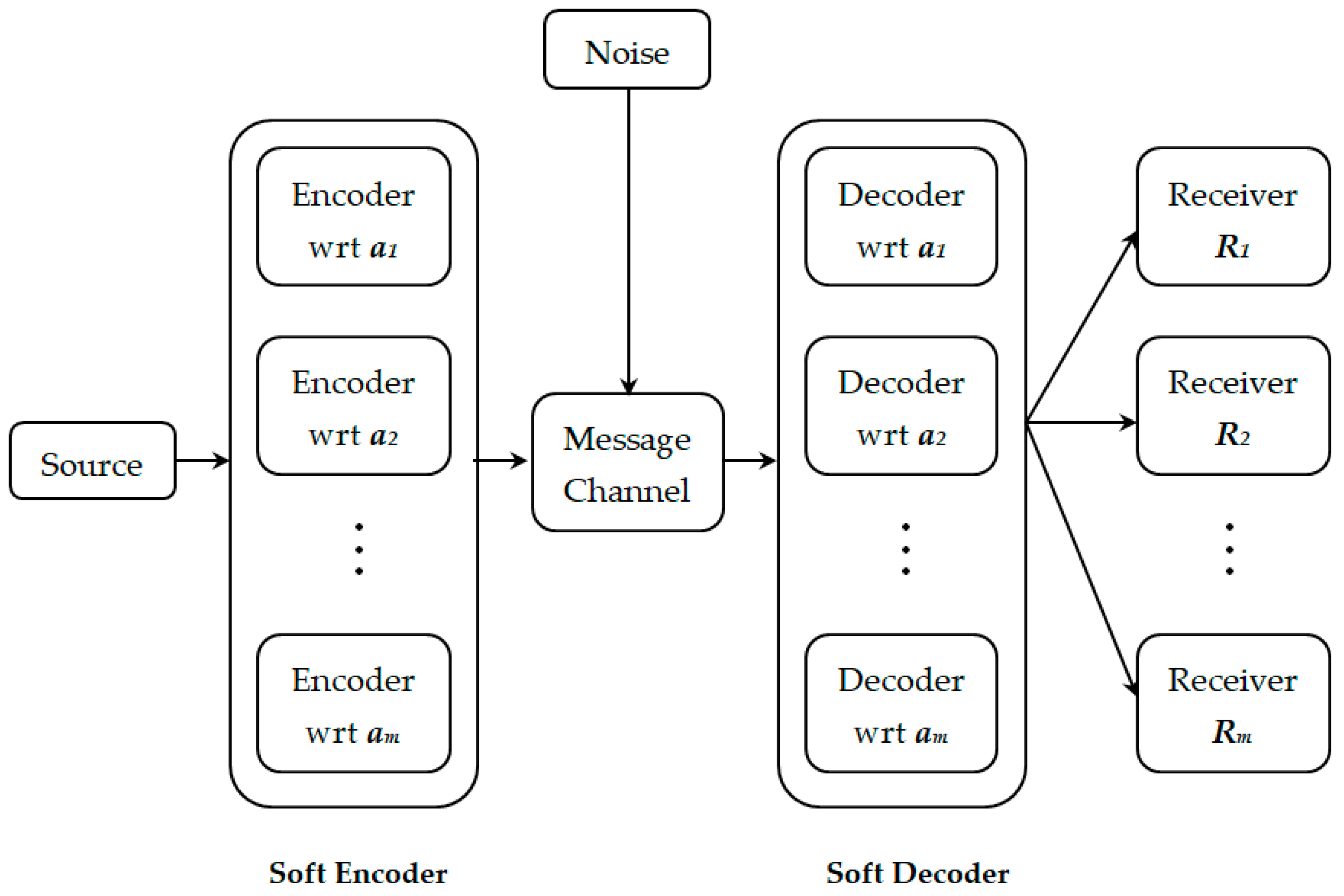
5. Soft Set-Based Communication Transmission and Comparison of Soft Linear Algebraic Codes and Linear Algebraic Codes

In this section, we propose a soft set-based communication transmission. The following proposed model comprises of a soft linear algebraic encoder that is an approximated collection of encoders. Hence, if (f, D) is a soft code; in D corresponding to each parameter d, in the soft encoder we have an encoder. Moreover, we have a soft linear algebraic decoder that is the collection of decoders; hence, to each parameter in D, we have a decoder in the soft linear algebraic decoder. In parameter set A = (a₁, …, a_m), there are m parameters. A soft set-based communication transmission reduces to classical communication transmission if we have m = 1. The model of soft set-based communication transmission is given in the following Figure 1.

The major difference among linear code and soft linear code is that for the soft linear code every soft code word has some attributes or concept, i.e., each soft code word is distinguished by some attributes, but the linear algebraic codes do not enjoy this property. Thus, one can work on the attributes of soft code words, for example an attribute “d_i” can have some attribute that can trick the hackers. Therefore, the soft linear codes can be more secure as compared to the classical linear codes due to the parameterization. The soft linear codes have a different distinct structure. Soft linear code is a collection of subspaces, whereas a linear code is only one subspace. Each subspace relies on the set of parameters that are used. Hence, soft linear codes are more generalized in comparison to the linear codes.

Linear codes can transfer only one message to a receiver whereas soft linear codes can simultaneously transmit m-well defined messages to m-set of receivers. The time taken for transmitting m-messages to m-receivers will take at least m unit of time in case of linear algebraic codes, whereas in case of soft algebraic codes the time taken will be only the time taken to transmit a single message, since the m-messages are transmitted simultaneously. The latest methodology makes use of bi-matrices and is more generalized uses with the perception of m-matrices. Clearly, this concept of soft algebraic code saves time. In soft decoding procedure, one can decode a set of code words (soft code word) at a time while it is not feasible in case of linear algebraic codewords decoding procedure.

6. Conclusions

There is an important role of algebraic codes in the minimization of data delinquency, which is generated by deficiencies, i.e., inference, noise channel, and crosstalk. In this paper, we have proposed the latest notions of soft linear algebraic codes for the first time by using the soft set. This latest class of codes can remit simultaneously m-messages to the m-people. Therefore, these new codes can save both time and economy. Soft parity check matrix (parity check m-matrix) and soft generator matrix (generator m-matrix) were defined. Decoding of soft linear codes was done using soft syndrome decoding techniques. The channel transmission is also illustrated. Finally, the major difference and comparison of soft linear codes with classical linear codes are presented.

Even though the proposed code has some advantages over the classical ones, it still has limitations in dealing with the multichannel coding problem, rank metrics, etc. Therefore, for future study, we wish to implement neutrosophic soft sets in algebraic linear codes. Further introduction of soft code with rank metric [22] and construction of T-direct soft codes [23] may be helpful to tackle the multichannel coding problem, which is left for researchers in coding theory. The general case based on N-soft sets and others [24,25,26,27,28,29,30,31,32,33,34,35,36] will be developed as well.