A Semi-Supervised Model for Top-N Recommendation
Abstract
:1. Introduction
- We made an assumption about users’ relative preferences among unrated items and put forward an approach to build an intermediate set and optimize the AUC metric.
- We used the intermediate set as a teaching set and designed a semi-supervised self-training model.
- We conducted extensive experiments on three popular datasets, and the experimental results demonstrated the effectiveness of our approach.
2. Related Work
2.1. Top-N Recommendation
2.2. Semi-Supervised Recommendation
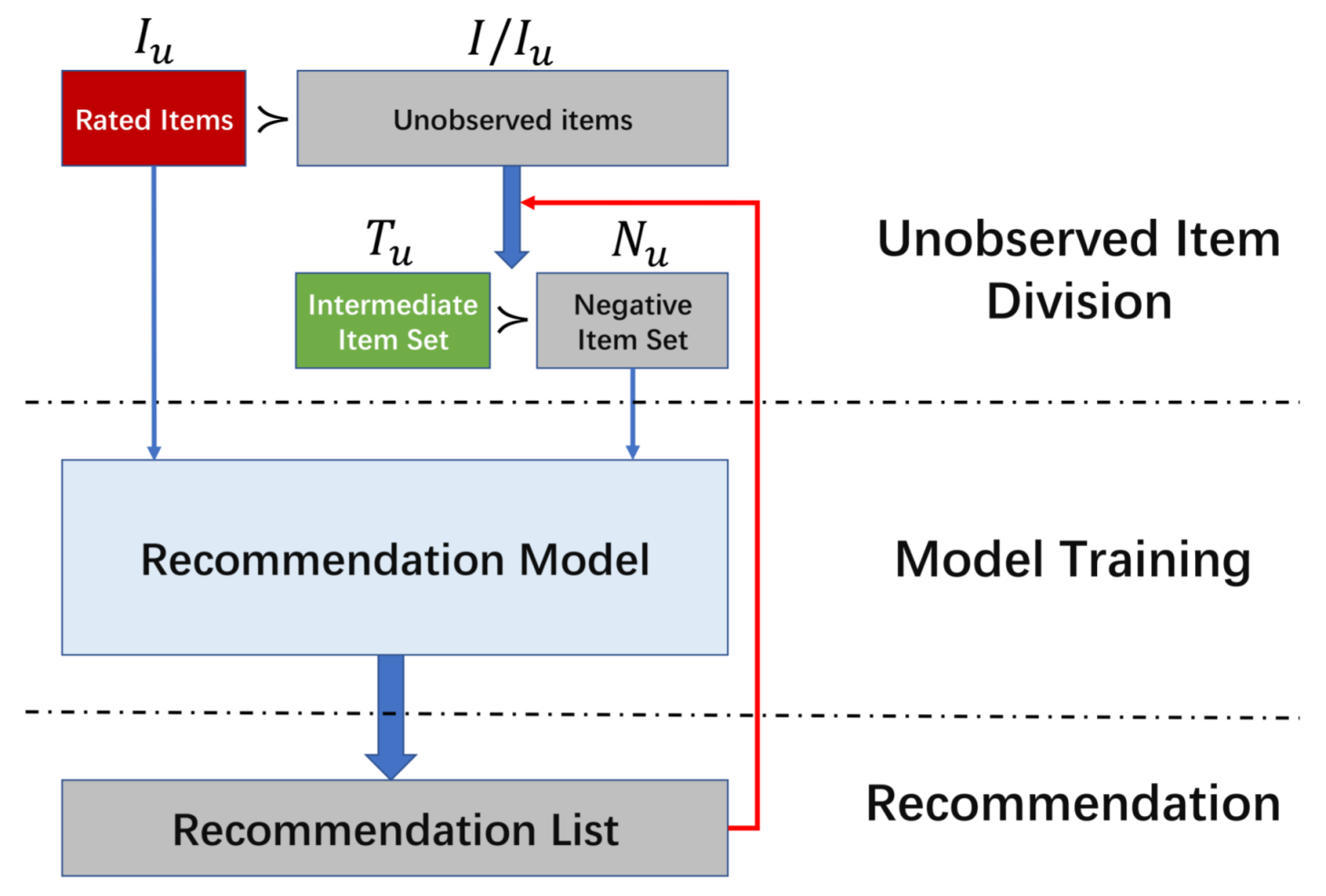
3. Our Approach
3.1. Problem Definition
3.2. Overview
3.3. Objective Function
3.4. Model Learning
| Algorithm 1: Semi-supervised Bayesian personalized ranking. |
 |
3.5. Matrix Factorization Model with Semi-BPR
3.6. Complexity Analysis
4. Experiments
4.1. Experimental Setup
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.2. Impacts of Parameters
4.3. Performance Comparison
4.3.1. Baselines
4.3.2. Parameter Settings
4.3.3. Recommendation Performance
- MostPop was the worst of all compared approaches, which implies that generating personalized recommendations for each user is very necessary.
- UserKNN, ItemKNN approaches are popular in recommender systems. Their performance depends on the choice of a heuristic similarity measure. In most cases, neighborhood approaches were shown to be worse than pointwise or pairwise approaches.
- WRMF is the state-of-the-art pointwise approach for top-N recommendation tasks. However, WRMF cannot directly optimize the ranking-oriented metrics and is slightly worse than the BPR-MF pairwise approach. This demonstrates that pairwise assumptions are more reasonable than pointwise assumptions.
- In all three datasets, the proposed Semi-BPR-MF model outperformed the other baselines in all evaluation metrics. For sparse datasets, like the Ciao dataset, only considering user preference between the observed feedback and unobserved feedback can not achieve a satisfactory level of performance. Compared with the best baseline BPR-MF model, our approach can obtain a significant performance improvement.
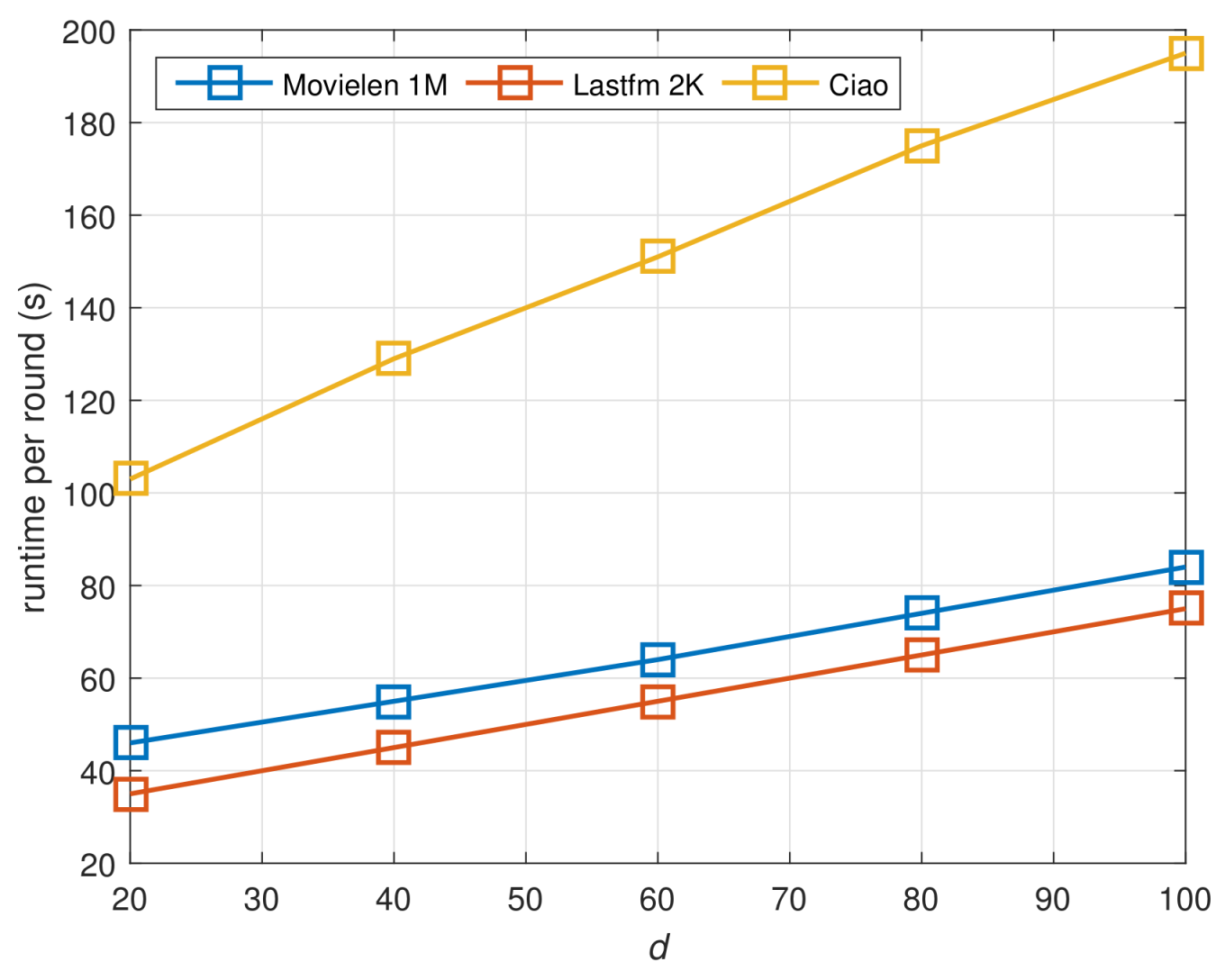
4.4. Scalability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bell, R.M.; Koren, Y. Lessons from the netflix prize challenge. ACM SIGKDD Explor. Newsl. 2007, 9, 75–79. [Google Scholar] [CrossRef]
- Linden, G.; Smith, B.; York, J. Amazon.com recommendations: Item-to-item collaborative filtering. IEEE Int. Comput. 2003, 7, 76–80. [Google Scholar] [CrossRef]
- Pan, R.; Zhou, Y.; Cao, B.; Liu, N.; Lukose, R.; Scholz, M.; Yang, Q. One-class collaborative filtering. In Proceedings of the 2008 8th IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 502–511. [Google Scholar]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 8th IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Ning, X.; Karypis, G. SLIM: Sparse linear methods for top-N recommender systems. In Proceedings of the 2011 11th IEEE International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011; pp. 497–506. [Google Scholar]
- Kabbur, S.; Ning, X.; Karypis, G. FISM: Factored item similarity models for top-n recommender systems. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 659–667. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the 23th Conference on Uncertainty in Artificial Intelligence (UAI 2009), Montreal, QC, Cananda, 18–21 June 2009; pp. 452–461. [Google Scholar]
- Pan, W.; Chen, L. GBPR: Group preference based bayesian personalized ranking for one-class collaborative filtering. In Proceedings of the 23th International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 2691–2697. [Google Scholar]
- Shi, Y.; Karatzoglou, A.; Baltrunas, L.; Larson, M.; Oliver, N.; Hanjalic, A. CLiMF: Collaborative less-is-more filtering. In Proceedings of the 23th International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 3077–3081. [Google Scholar]
- Shi, Y.; Karatzoglou, A.; Baltrunas, L.; Larson, M.; Hanjalic, A.; Oliver, N. TFMAP: Optimizing map for top-n context-aware recommendation. In Proceedings of the 35th ACM Special Interest Group on Information Retrieval (SIGIR), Portland, OR, USA, 12–16 August 2012; pp. 155–164. [Google Scholar]
- Zhao, T.; Mcauley, J.; King, I. Leveraging social connections to improve personalized ranking for collaborative filtering. In Proceedings of the 23th ACM International Conference on Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014; pp. 261–270. [Google Scholar]
- Song, D.; Meyer, D.A. Recommending positive links in signed social networks by optimizing a generalized AUC. In Proceedings of the 29th AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 290–296. [Google Scholar]
- Liu, H.; Wu, Z.; Zhang, X. CPLR: Collaborative pairwise learning to rank for personalized recommendation. Knowl.-Based Syst. 2018, 148, 31–40. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, C.; Pei, S.; Sun, G.; Zhang, X. Walkranker: A unified pairwise ranking model with multiple relations for item recommendation. In Proceedings of the 32th AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Hady, M.F.A.; Schwenker, F. Semi-supervised learning. J. R. Stat. Soc. 2006, 172, 530. [Google Scholar]
- Zhang, M.; Tang, J.; Zhang, X.; Xue, X. Addressing cold start in recommender systems: a semi-supervised co-training algorithm. In Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval, Gold Coast, Australia, 6–11 July 2014; pp. 73–82. [Google Scholar]
- Zhang, X. Utilizing tri-training algorithm to solve cold start problem in recommender system. Comput. Sci. 2016, 12, 108–114. [Google Scholar]
- Hao, Z.; Cheng, Y.; Cai, R.; Wen, W.; Wang, L. A semi-supervised solution for cold start issue on recommender systems. In Proceedings of the Asia-Pacific Web Conference, Guangzhou, China, 18–20 September 2015; pp. 805–817. [Google Scholar]
- Usunier, N.; Amini, M.R.; Goutte, C. Multiview Semi-supervised Learning for Ranking Multilingual Documents. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Athens, Greece, 4–8 September 2011. [Google Scholar]
- Truong, T.V.; Amini, M.R.; Gallinari, P. A self-training method for learning to rank with unlabeled data. In Proceedings of the European Symposium on Artificial Neural Networks–Advances in Computational Intelligence and Learning, Bruges, Belgium, 22–24 April 2009. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. IEEE Comput. J. 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, J.; Sun, Z.; Yorke-Smith, N. Librec: A java library for recommender systems. In Proceedings of the 23th Conference on User Modeling, Posters, Demos, Late-breaking Results and Workshop Adaptation and Personalization (UMAP 2015), Dublin, Ireland, 29 June–3 July 2015. [Google Scholar]






| Symbol | Description |
|---|---|
| U | User set |
| I | Item set |
| User number | |
| Item number | |
| Used to index a user | |
| Used to index an item | |
| Users that have rated item i | |
| Items that user u has rated | |
| Rating matrix. , if the feedback is observed; otherwise, . | |
| The scoring function of user u. refers to the predicted scoring value of item i. |
| Dataset | User# | Item# | Feedback# | Density |
|---|---|---|---|---|
| Movielens 1M | 6040 | 3706 | 1,000,209 | 4.47% |
| Lastfm 2K | 1892 | 17,632 | 92,834 | 0.28% |
| Ciao | 7267 | 11,211 | 147,987 | 0.18% |
| Method | Movielens 1M | Lastfm 2K | Ciao |
|---|---|---|---|
| MostPop | - | - | - |
| UserKNN | |||
| ItemKNN | |||
| WRMF | , , | , , | , , |
| , | |||
| BPR-MF | , | , | , |
| , | |||
| BPR-KNN | |||
| Semi-BPR-MF | , r = 0.1, | , , | , , |
| , | , | , , | |
| , , | , , | , , |
| Dataset | Models | Pre@5 | Rec@5 | MAP@5 | MRR@5 | AUC@5 | NDCG@5 |
|---|---|---|---|---|---|---|---|
| MostPop | 0.2088 | 0.0405 | 0.1499 | 0.3525 | 0.7626 | 0.2181 | |
| UserKNN | 0.3895 | 0.0982 | 0.3087 | 0.6088 | 0.8975 | 0.4118 | |
| ItemKNN | 0.3311 | 0.0772 | 0.2579 | 0.5390 | 0.8624 | 0.3514 | |
| Movielens 1M | WRMF | 0.4138 | 0.1059 | 0.3292 | 0.6330 | 0.9092 | 0.4359 |
| BPR-KNN | 0.4018 | 0.1002 | 0.3223 | 0.6166 | 0.9005 | 0.4245 | |
| BPR-MF | 0.4172 | 0.1032 | 0.3382 | 0.6262 | 0.9055 | 0.4387 | |
| Semi-BPR-MF | 0.4345 | 0.1080 | 0.3560 | 0.6464 | 0.9129 | 0.4571 | |
| MostPop | 0.0857 | 0.0448 | 0.0567 | 0.1888 | 0.6458 | 0.0952 | |
| UserKNN | 0.2002 | 0.1044 | 0.1542 | 0.4233 | 0.7848 | 0.2300 | |
| ItemKNN | 0.2373 | 0.1234 | 0.1844 | 0.4897 | 0.8246 | 0.2714 | |
| Lastfm 2K | WRMF | 0.2458 | 0.1278 | 0.1823 | 0.4807 | 0.8365 | 0.2727 |
| BPR-KNN | 0.2459 | 0.1263 | 0.1836 | 0.4910 | 0.8381 | 0.2750 | |
| BPR-MF | 0.2544 | 0.1312 | 0.1886 | 0.4948 | 0.8469 | 0.2813 | |
| Semi-BPR-MF | 0.2678 | 0.1387 | 0.2075 | 0.5230 | 0.8509 | 0.3007 | |
| MostPop | 0.0281 | 0.0289 | 0.0251 | 0.0665 | 0.5533 | 0.0385 | |
| UserKNN | 0.0422 | 0.0421 | 0.0369 | 0.0963 | 0.5767 | 0.0562 | |
| ItemKNN | 0.0362 | 0.0325 | 0.0294 | 0.0772 | 0.5642 | 0.0453 | |
| Ciao | WRMF | 0.0448 | 0.0433 | 0.0365 | 0.0972 | 0.5817 | 0.0573 |
| BPR-KNN | 0.0425 | 0.0415 | 0.0351 | 0.0942 | 0.5790 | 0.0551 | |
| BPR-MF | 0.0443 | 0.0466 | 0.0383 | 0.1013 | 0.5847 | 0.0594 | |
| Semi-BPR-MF | 0.0478 | 0.0506 | 0.0415 | 0.1095 | 0.5908 | 0.0642 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Peng, Y. A Semi-Supervised Model for Top-N Recommendation. Symmetry 2018, 10, 492. https://doi.org/10.3390/sym10100492
Chen S, Peng Y. A Semi-Supervised Model for Top-N Recommendation. Symmetry. 2018; 10(10):492. https://doi.org/10.3390/sym10100492
Chicago/Turabian StyleChen, Shulong, and Yuxing Peng. 2018. "A Semi-Supervised Model for Top-N Recommendation" Symmetry 10, no. 10: 492. https://doi.org/10.3390/sym10100492
APA StyleChen, S., & Peng, Y. (2018). A Semi-Supervised Model for Top-N Recommendation. Symmetry, 10(10), 492. https://doi.org/10.3390/sym10100492





