1. Introduction
A graph comprising vertices and edges is a discrete structure in which each edge joins only two different vertices. In this paper, we consider graphs with only finitely many vertices. Several graph classes model various problems wherein one can observe a lot of variance in their properties. Graph chromatic number is a pertinent parameter in graph theory. A coloring of a graph
G can be deemed as a mapping that allots colors to elements in it. A usual type of coloring is a proper vertex coloring, where we color the vertices of
G in such a way that two vertices joined by an edge receive different colors. The chromatic number
of
G is the least number of colors needed to properly color the vertices of
G. Finding the
of a given graph is a computationally hard task. Garey et al. [
1], showed that the determination of
is an NP-complete problem unless it is 1 or 2 where NP stands for Non-Deterministic Polynomial time. That is no polynomial-time algorithm could correctly find it. However, several practical algorithms that approximate the
in polynomial time exist in literature [
2,
3].
An interesting instance where graph coloring is applied is the open-shop scheduling problem. It kindles us to find the least time to produce a set of products that has to pass through a sequence of processes on several machines. If all of them consume equal time where there is no compulsion of order, then this problem can be modeled using a bipartite graph. Here products and processes both act as vertices. We introduce an edge between them if and only if the product go through that process. The least time required to finish all processes is the least colors required in a proper edge-coloring of the respective graph. In the case of only two machines or only two products, the problem of finding the least time can be resolved in polynomial time. However, when we have three or more machines and three or more products to be produced then a best known algorithm is exponential as of now.
computation finds its use also in communication through mobile phones. Global System for mobile communication (GSM) network is the most commonly used cellular network. It means that the land area is partitioned into hexagonal cells with transceiver for each cell joining the mobile devices within the cell. To keep away from doing signal interference two neighboring cells should not share the same channel. The famous Four Color Theorem for maps provides four different channels independently of the shape of the cells. However, in real life instances the network is not that simple. This is because the users first should be able to shift from a given cell area to another without experiencing any signal loss. Next there are several phone carriers. Then, the same frequency using cells must be separated by a distance at least two or three to avoid interference. So such a conceivable model is highly complicated. To be precise, the respective graph will be non planar and hence not feasible for a four-coloring. This problem can be dealt with another method of graph coloring, named list coloring. Here each vertex has a list of available colors associated with it. On can assign to each vertex a color from its list without violating the concept of proper coloring. For the problem of the cellular network, every vertex is a transceiver and a list of its available colors are a list of frequencies available for assignment at that transceiver. To find the number of frequencies required one has to find the minimum cardinality of the lists that allows the vertices of the graph colored without violating proper coloring concept. This number is named as the list chromatic number and its computation is much more hard to find than the usual
. For more, one can refer to [
4,
5,
6].
Another interesting application of graph coloring related to interference is register allocation. Here a computer program has huge number of variables, but a processor has only a limited number say 32, of registers for basic operations. So a compiler has to decide how to provide the registers these variables. Several variables can be allotted to a given register, but variables that are in use at a given time cannot be allotted to the same register without spoiling their values. When we model this by means of a graph, vertices stand for temporary variables and two of them are joined by an edge if they are involved concurrently at some point in the program. The number of registers required to make the program run is then equal to the least number of colors in a proper vertex coloring of this interference graph. It may be the case that this number is more than the fixed number of registers. However, then it amounts to the fact that there exist variables which cannot be allotted to any register. Such extra variables can be shifted to Random Acces Memory (RAM) after each operation by a method named spilling. As RAM access speed is very low the aim is to optimize the number of spills. Chaitin’s noteworthy algorithm [
7] applies interference graph coloring in both register allocations and spilling. To begin, an interference graph is designed. Such a graph is sparse in reality, so in the place of adjacency matrix, an adjacency vector is placed for at each vertex. Then, get rid of unwanted register copy operations by combining vertices. To finish, all vertices of degree less than 32 are removed in succession. Also it leads to null graph at the end of the process, in the case of which it is possible to allot colors for vertices by reversing the adopted method and including the omitted vertices back in place. Now to probe the other possibility where each vertex in the modified graph has at least 32 neighbors, one also adds a spill code. To identify which node to spill, the procedure maintains a table of guessed costs of spills for vertices, and resolve to spill a vertex whose cost is least as dictated by its current degree. For more see [
8].
A distance graph is a simple graph with vertex set V and any two elements of V are said to form an edge if the absolute euclidean distance between them is a member of D. If D happens to be a singleton set with the element 1 and the set V happens to be the euclidean two dimensional space then the computation of of such a distance graph is the famous HNP (Hadwiger-Nelson Problem). For this distance graph the best known lower bound is 4 and the best known upper bound is 7. These bound are due to Nelson and Isbell respectively.
If instead of
if we consider
with the same distance set {1} then Raiskii [
9] showed that
and later it was modified to 6 in [
10]. A lot of efforts were made to obtain an upper bound of 21 for this graph in [
11] and it was modified to 18 in [
12]. It was further modified into 15 in [
13]. For higher dimensions of the form
n-times the lower and upper bound for the
are
and
in [
14] and [
15] respectively.
7. Computation of of Catalan Number Distance Set
Consider the distance graph
. Such objects were dealt in [
27]. Suppose that
is a set of first 10 distinct Catalan numbers. Form
where
consists of the Catalan numbers. A minimal graph to realize each element of
as a distance between any two of its vertices exactly once is the simplest graph
A coloring of the elements of
is deemed proper if any two adjacent elements in it are colored distinctly. The smallest number of colors used in such a process named as the chromatic number
Let Set As is bipartite, Hence,
Proposition 1. Let be any Catalan number distance graph. Let and Then as provided with
Recall the following two results of Yegnanarayanan from [
28].
Proposition 2. if the elements of D are odd integers.
Proposition 3. If for a given positive integer n, consists all those elements of D built by integers divisible by then .
Theorem 1. Consider where denotes the distance set of first 15 distinct Catalan numbers. Then where is that subset of built by integers divisible by
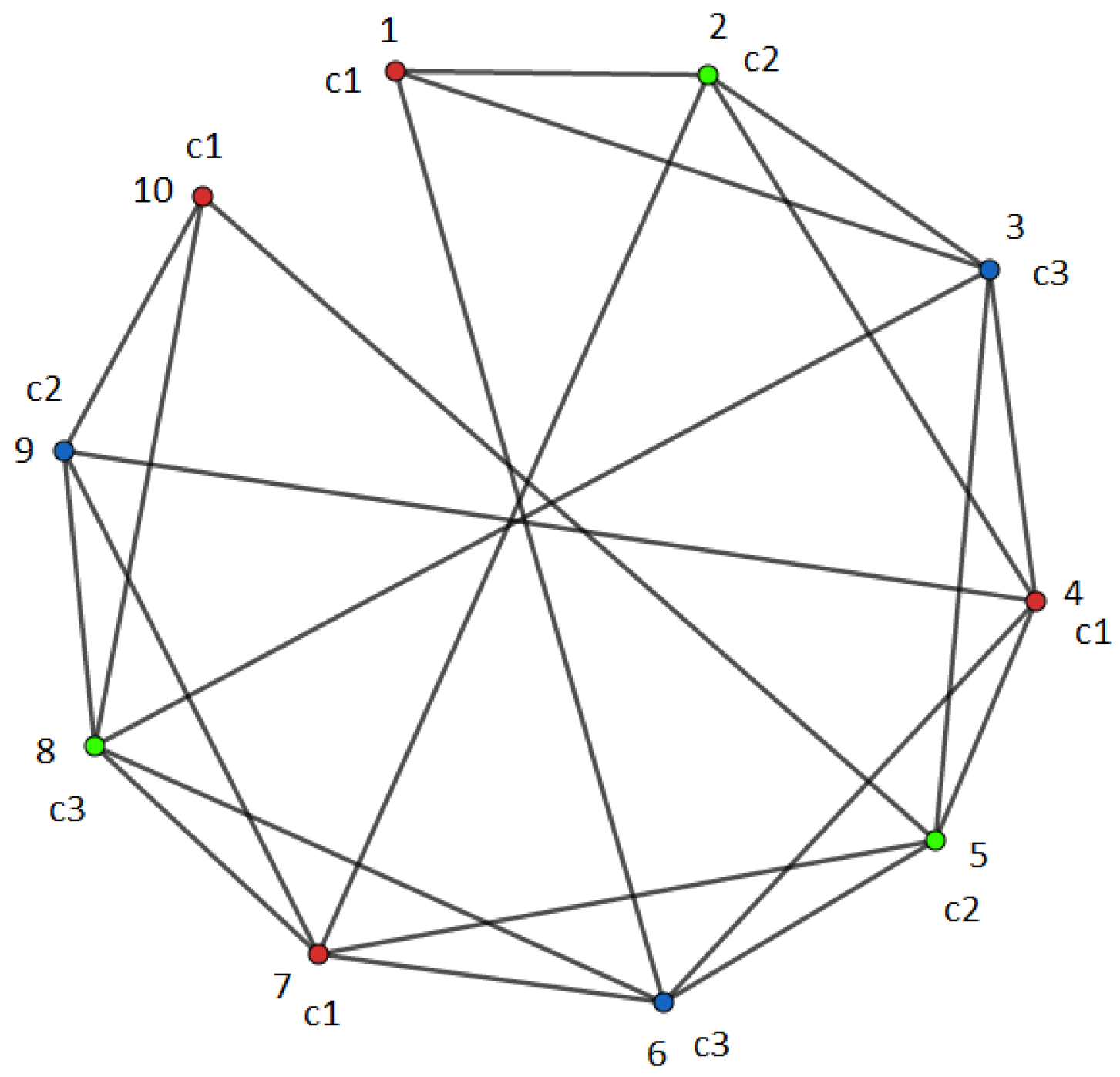
Proof. The graph
shown in
Figure 3 namely
is a subgraph of
We show in the next section that
Therefore,
≤
as
is a monotone function. We now determine the upper bound as follows using Proposition 3. Clearly,
For
we get
For
For
. For
5,6,7,9 to 15 are not improving the above bounds. Also
yields a bound same as that for
Hence we conclude that
□
In general, in view of Theorem 1, we raise the following problem:
Problem 1. What is for any
Note 1. An easy upper bound for is that
Theorem 2. Consider with where are the sum of the ith and th Catalan numbers. Then .
Proof. Voigt et al. in [
29,
30] have proved that if the elements of
D includes two coprime elements of distinct parity then
As
and
we infer that
is more than or equal to 3. Now the upper bound can be found by using the Proposition 3. For
n = 1,
For
n = 2,
It is easy to check that
to 16 has not improved the upper bound 16 provided by
Therefore
□
Theorem 3. Consider with where are the values of the Hankel transform of first 8 of Theorem 2. Then .
Proof. The lower bound follows from the same reasoning of what is said in Theorem 2. We now find the upper bound by using the Proposition 3. For we get For we get For we get Therefore □
Problem 2. What is where D consists of any finite list of n of Theorem 2.
Problem 3. What is where D consists of any finite list of n of Theorem 3.
Note 2. In a similar manner as in Theorem 1 one can determine bounds ( both lower and upper) for the chromatic number of generalized
k-Catalan number distance graphs listed in
Table 1. However finding the bounds (both lower and upper) of
whose distance set elements are finite list of
n such
k-Catalan number is an open question.
Note 3. Presume that the vertex set of a Catalan number distance graph is labelled arbitrarily and an element from the Catalan distance set is allowed to repeat in the graph then we get several other non trivial graphs. For instance,
Figure 3 shows a Catalan number distance graph whose
is 3. This raises an interesting question: what is the
of such an arbitrarily formed Catalan number distance graph?
8. Graph Coloring for Interference Networks
The problem of minimization of interference in wireless communication pose enormous challenges. If a vertex interference range includes another vertex y then one can say x may interfere with This means the magnitude of interference on a vertex y can be measured by the magnitude of interference produced by all those vertices whose transmission area embraces It is known that in frequency division multiplexing of mobile networks the minimization of interference is directly related to the bringing down of number of channels which then leads to the increasing of bandwidth of the frequency channels. A small interference is useful to code overhead in systems where code division multiplexing is employed. However, in the case of networks employing battery driven devices it is better to minimize the interference to increase the longevity of the network. Interference can be kept to a minimum by keeping vertices with limited transmission power. In such a case, the area covered by such vertices result in low interference. However, then this action may lead to the disconnection of communication links. So, it is prudent to estimate the amount of reduction of transmission power of the vertices so that the connectivity characteristic of the network is preserved. Minimization of Interference in networks results in non-collisions and packet retransmissions and this factor saves power consumption and improves the longevity of the network.
Interference can be represented in the form of an Interference graph of a wireless network. Here the edges denote the interference occurring in their respective end points. The problem of minimizing the vertex collisions and signal clashes can be thought of as allotment of color to vertex task of the associated graph of interference. Distinctly colored vertices are assigned distinct channel of radio frequency. Robust graph vertex coloring methods suggest effective or correct channel picking ways that decreases wireless interference. The graph vertex coloring method is useful as it bars vertices from getting connected with other conflicting ones via radio frequency. These methods are pertinent as it conforms to mathematical rigidity. Prudent allotment of channels aligns allotment of color to vertex task and interference minimizing task in wireless network [
31].
Suppose that is the greatest number of vertices of equal degree j in a simple graph G with . Let and be the degree sequence of If then clearly . If then for . That is . However, then this means that the G is r-degenerate or any subgraph of G includes in it a vertex of degree < Further it is known that at most r colors are needed to color any r-degenerate G properly. Hence,
Theorem 4. If G is simple then is at most .
Discussion. Consider the task of assignment of wi-fi channel in the language of graph theory. If G has k-colors as spectrum (also called k-channels). Let W be a matrix of interferences associated with each vertex of The aim is to find a minimum threshold in such a way that accepts a k-coloring f (allotment of channels) with reference to which for all is called least k-chromatic threshold of denoted by
Consider the graph
in
Figure 3 with
Let
be such that
for
for
for
Then
f is a 3-chromatic coloring for
Let
Then Now Similarly, for So here and the least 3-chromatic threshold of written as
In view of Theorem 4, the graph
of
Figure 3 has an upper bound for its
as 5. Moreover the presence of a
in
indicates
This along with the fact that
f is a 3-chromatic coloring shows
.
As the problem of determination of fixes the parameter k and focus on minimizing it would be interesting to look at its complementary problem where the threshold is fixed. The focus is on minimizing the number of colors k (channels) by allowing the size of the spectrum to be the cardinality of in such a manner that accepts a color function f with k-colors (allotmentt of channels) where at any vertex the interference is is called as -interference of written as A main feature of this determination lies in finding the least number of colors (or frequencies) to realize minimum throughput in the network for all users. Hence one can also think of deeming it as a task of finding to ensure quality of service the actual resources requirement.
Suppose that for a given a color specific interference at a vertex u is defined as follows: Then if then We call a k-coloring f of G as W-concrete if Let , Then one can clearly visualize that Also if for some specific coloring then it will be W-concrete. If for some then one can attempt to recolor again and again to achieve Please note that each step in the process contributes to and decrements This procedure results in the reduction of by a quantity and terminates by achieving a W-concrete coloring of G. So
Theorem 5. A W-concrete coloring for with color spectrum cardinality atleast 2 exists. For the graph in Figure 3, ;
;
;
;
;
;
;
;
;
.
It is easy to see that for and hence f is not a W-concrete coloring for Moreover, for
Suppose that
is fixed and
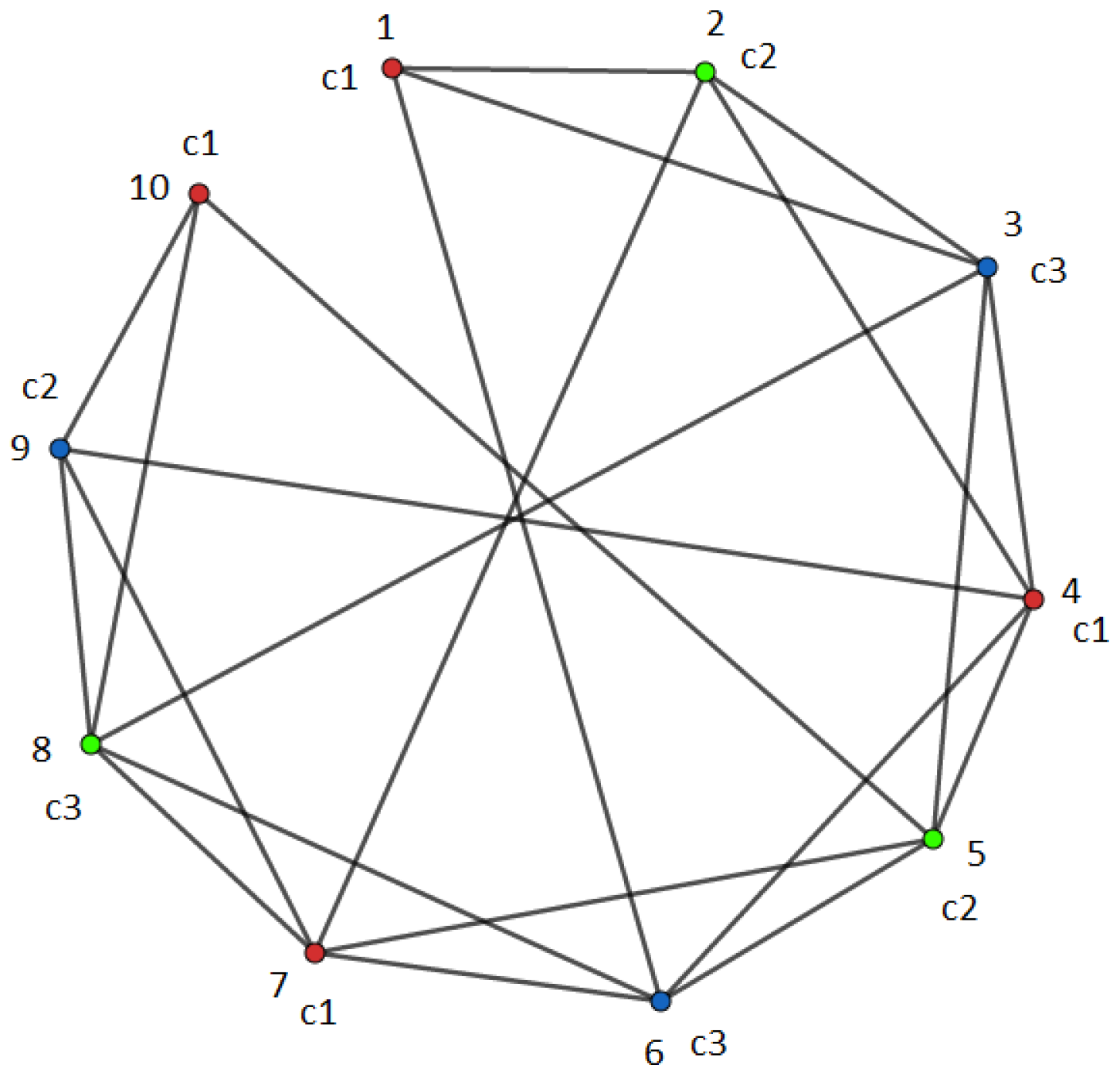
be a set of first two distinct Catalan numbers. Let
and
Then the graph
is shown in
Figure 4.
Clearly the matrix associated with is the distance between the elements of
That is and Define as Then f is a 3-chromatic coloring for Now, Effortlessly for Hence, is the 4-interference chromatic number.
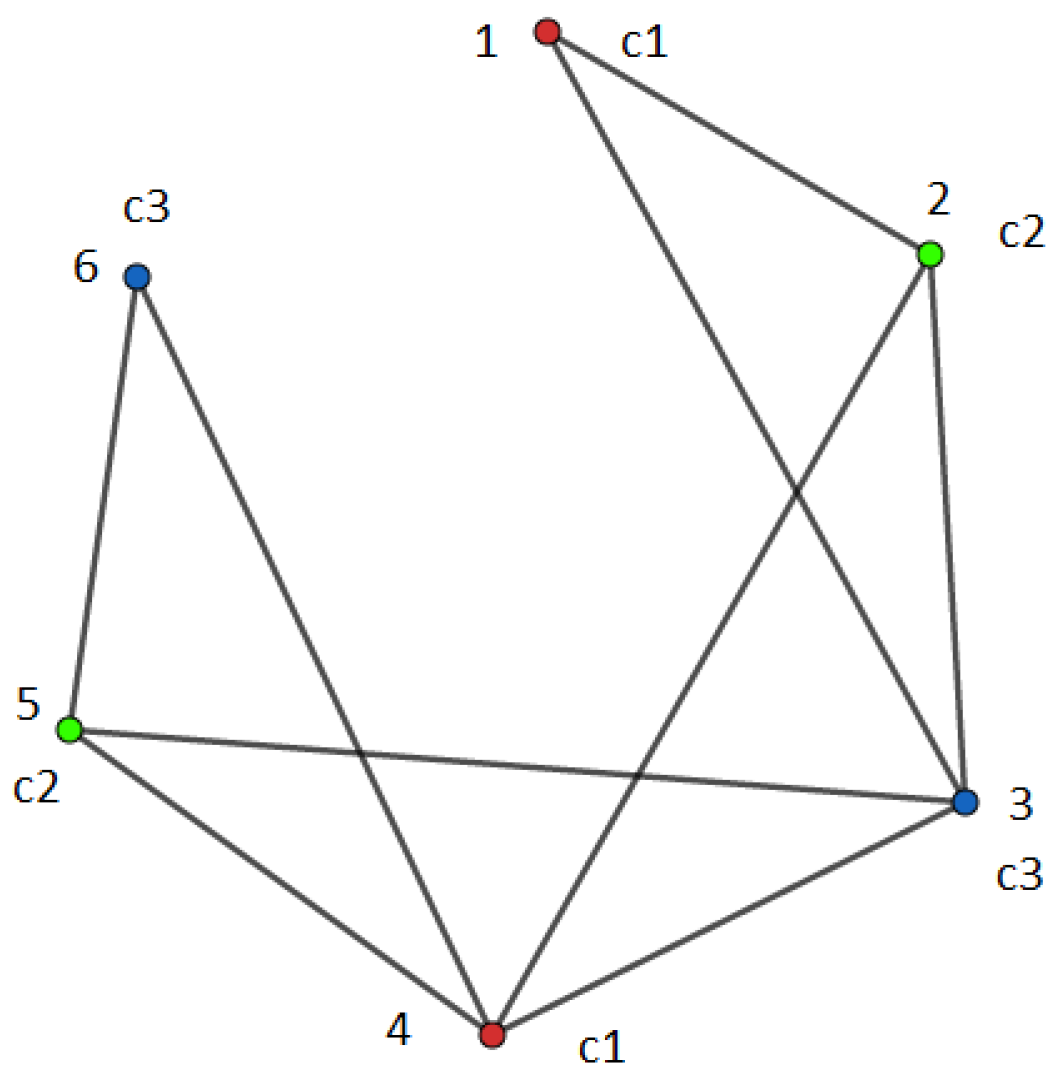
If we alter
to
then we can alter the size of
from 6 to 4 as
Then the resulting graph turns out to be
the complete graph on 4 vertices.
is shown in
Figure 5.
and Define as Then f is a 4-chromatic coloring for Now So, Hence, is the 3-interference chromatic number.