Statistical Inference for the Information Entropy of the Log-Logistic Distribution under Progressive Type-I Interval Censoring Schemes

Abstract

In recent years, information entropy has been studied and developed rapidly across disciplines as a measure of information value. In this article, the maximum likelihood estimation and EM algorithm are used to estimate the parameters of the log-logistic distribution for progressive type-I interval censored data, and the hypothesis testing algorithm of information entropy is proposed. Finally, Monte Carlo numerical simulations are conducted to justify the feasibility of the algorithm.

1. Introduction

The log-logistic distribution, which is also known as the Fisk distribution in economics, is a continuous probability distribution for a non-negative random variable. The works in [1,2] first studied the characteristics of the log-logistic distribution in detail. The work in [3] introduced a new survival model based on logistic and log-logistic distributions. The work in [4] considered the best linear unbiased estimators of the unknown parameters of the log-logistic distribution. When the product’s failure density model is a log-logistic distribution, the acceptance test based on the life test was studied by [5].

The log-logistic distribution is widely and extensively applied in survival analysis as a parametric model for events in which the rate initially increases and then decreases, such as cancer mortality after treatment in medical research, simple models for wealth or income distribution in economics, etc.

In order to improve the reliability of industrial products, many statisticians have begun to study various types of lifetime data. In the industrial life inspection and medical survival analysis, it was usually impossible for the experimenters to observe the lifetime of all individuals due to time and cost. That is, the complete sample is unpractical and unrealistic. The censored sample is common in practice.

Typically, the unit enters a failure or death before the loss, withdrawal or one only knows the lifetime of the units in a range of circumstances. The most popular censoring schemes mainly include type-I censorship, conventional type-II censorship and progressive censoring.

For the type-I censoring scheme, the product life testing is terminated at an advance planned time; see [6,7,8,9]. As for the conventional type-II censored scheme, the product life testing is finished whenever the pre-specified life time is reached; see [10,11,12]. Both type-I and type-II censoring schemes allow the test item to be withdrawn simply at the end of the life test. However, the progressive censored scheme allows test items to be deleted and removed sometime before the end of the life test.

In this article, we mainly focus on the inference of the entropy of the log-logistic distribution under the progressive type-I interval censoring scheme. The progressively censored method for obtaining data is proposed, that is observation is performed within two consecutive predetermined time periods, and the items are only allowed to be withdrawn at specific time points. Then, the statistical analysis is studied on the data obtained under this censored method.

Suppose n items are put on a life testing at the initial time $t_0=0$ and they will be checked and inspected at m predetermined times $0<t_1<t_2<\cdots <t_m$, where $t_m$ is the pre-specified time to end the experiment. At the $i^{\mathrm{th}}$ checking time $t_i$, the amount of failures $X_i$ in $(t_{i-1},t_i]$ is counted, and $R_i$ surviving items $i=1,\dots ,m$ are randomly taken out and deleted from the life testing. The amount, $S_i$, of surviving units is a random variable at a predetermined time $t_i$, and $R_i$ is no larger than $S_i$. Furthermore, $R_i$ is determined by a predetermined percentage of the surviving items remaining at $t_i$, $i=1,\dots ,m$. For instance, if the pre-specified percentage values are $p_1,\dots ,p_{m-1}$ and $p_m=1$, $R_i$ can be determined by using $R_i=floor\left[p_i{S}_i\right]$ at each checking time $t_i$, where $floor\left[x\right]$ gives the largest positive integer not exceeding x. Thus, progressive type-I interval censored data of size n can be expressed as $Y_i=(X_i,R_i,t_i)$, $i=1,\dots ,m$. If $R_i=0$, $i=1,2,\dots ,m-1$ and ${\displaystyle R_m=n-\sum _{n=1}^m{X}_i}$, and the progressive type-I interval censored data becomes the known type-I interval censored data.

Let $R=(R_1,R_2,\dots ,R_m)$, $X=(X_1,X_2,\dots ,X_m)$, $B(a,b)$ represent the binomial distribution with the number of trials a and the probability of success b and $F(t;\beta )$ be the distribution function of the inspection times. Let $v_1=n$, ${\delta }_1\left(\beta \right)=F(t_1;\beta )$, ${\displaystyle v_i=n-\sum _{j=1}^{i-1}(X_j+R_j)}$ and ${\delta }_i\left(\beta \right)=\frac{F(t_i|\beta )-F(t_{i-1}|\beta )}{1-F(t_{i-1}|\beta )}$ $i=2,\cdots ,m$.

It can be shown that:

$$X_1\sim B(v_1,{\delta }_1\left(\beta \right))$$

$$X_i|X_{i-1},\dots ,X_1;R_{i-1},\dots ,R_1\sim B(v_i,{\delta }_i\left(\beta \right))$$

The rest of the article is organized as follows. In Section 2, the information entropy of the log-logistic distribution is proposed and introduced. In Section 3, the maximum likelihood estimation and EM algorithm are used to derive the parameter estimation and Fisher information of information entropy. The asymptotic normal distribution is also obtained. In Section 4, we develop a hypothesis testing algorithm on information entropy to test whether the amount of information can eliminate the average uncertainty. The power function analysis of the proposed algorithm is also conducted in this section. We use Monte Carlo simulation to justify and illustrate the algorithm in Section 5. Finally, the conclusions about our proposed algorithm are presented in Section 6.

2. Information Entropy

A random variable T is said to have the log-logistic distribution, if its cumulative distribution function (cdf) is:

$$\begin{array}{cc}\hfill F_T\left(t\right)=1-{(1+t^{\beta })}^{-1},& t\ge 0,\beta >0\end{array}$$

(1)

The probability density function (pdf) is as follows:

$$\begin{array}{cc}\hfill f_T\left(t\right)=\frac{\beta t^{\beta -1}}{{(1+t^{\beta })}^2}& t\ge 0,\beta >0\end{array}$$

(2)

In 1948, the statistician Shannon proposed the definition of information entropy. He successfully solved the problem of quantitative measurement of information and first explained the relationship between probability and information redundancy in mathematical language. Entropy is especially used to measure the uncertainty of objects in information theory, which is a perfect mathematical theory supporting all modern digital communications.

The physical meaning of information entropy has the following three aspects:

(1)

Indicating the average amount of information provided by each message or symbol after the source is output;

(2)

Indicating the average uncertainty of the source after the source is output;

(3)

Measuring the uncertainty on a random variable T.

Let T be a random variable having distribution function $F\left(t\right)=P(T\le t)$, and its probability density function is $f\left(t\right)$. The Shannon’s entropy can be defined as:

$$\begin{array}{c}\hfill H\left(f\right)={\int }_0^{\infty }f\left(t\right)[-lnf\left(t\right)]dt\end{array}$$

(3)

For the log-logistic distribution, the entropy can be calculated as:

$$\begin{array}{c}\hfill H\left(f\right)={\int }_0^{\infty }f\left(t\right)[-lnf\left(t\right)]dt=2-ln\beta \end{array}$$

(4)

3. Parameter Estimations

3.1. Maximum Likelihood Estimation

Considering the progressively type-I censored data, $Y_i=(X_i,R_i,t_i)$, $i=1,2,\cdots ,n$, from a continuous log-logistic distribution with cdf $F(t;\beta )$ based on progressive type-I interval censoring, the likelihood function is defined as (see [13]):

$$L(Y|\beta )\propto {\left[F(t_1;\beta )\right]}^{X_1}{[1-F(t_1;\beta )]}^{R_1}\times {[F(t_2;\beta )-F(t_1;\beta )]}^{X_2}{[1-F(t_2;\beta )]}^{R_2}$$

$$\times \dots \times {[F(t_m;\beta )-F(t_{m-1};\beta )]}^{X_m}{[1-F(t_m;\beta )]}^{R_m}$$

$$=\prod _{i=1}^m{[F(t_i;\beta )-F(t_{i-1};\beta )]}^{X_i}{[1-F(t_i;\beta )]}^{R_i}$$

where $t_0=0$ and $\beta$ is the parameter vector. For the log-logistic distribution proposed as above, the likelihood function can be given as:

$$\begin{array}{cc}\hfill L\left(\beta \right)& =\prod _{i=1}^m{[F_T\left(t_i\right)-F_T\left(t_{i-1}\right)]}^{X_i}{[1-F_T\left(t_i\right)]}^{R_i}\hfill \\ & =\prod _{i=1}^m{[{(1+t_{i-1}^{\beta })}^{-1}-{(1+t_i^{\beta })}^{-1}]}^{X_i}{(1+t_i^{\beta })}^{-R_i}\hfill \end{array}$$

(5)

The calculation of the maximum likelihood estimator for a single parameter function is given by [13]. If $X_1=n$, then $ln\left(L\right(\beta \left)\right)$ is maximized when $\beta$ approaches zero.

$$\begin{array}{c}\hfill {\displaystyle lnL\left(\beta \right)=\sum _{i=1}^m[X_{i}ln[{(1+t_{i-1}^{\beta })}^{-1}-{(1+t_i^{\beta })}^{-1}]-R_{i}ln(1+t_i^{\beta })]}\end{array}$$

(6)

Set the derivative of the log-likelihood function with respect to $\beta$ to be zero, and the maximum likelihood estimate (MLE) of $\beta$ is the solution of Equation (7). The log-likelihood function is given by:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{d\beta }lnL\left(\beta \right)=\sum _{i=1}^m[X_i\frac{{(1+t_i^{\beta })}^{-2}{t}_i^{\beta }ln{t}_i-{(1+t_{i-1}^{\beta })}^{-2}{t}_{i-1}^{\beta }ln{t}_{i-1}}{{(1+t_{i-1}^{\beta })}^{-1}-{(1+t_i^{\beta })}^{-1}}-R_i\frac{t_i^{\beta }ln{t}_i}{1+t_i^{\beta }}]\equiv 0}\end{array}$$

(7)

Under fairly weak regular conditions, the maximum likelihood estimator is consistent. Under a slightly stronger assumption, MLE is asymptotically normal. The work in [14] discussed the asymptotic properties of the maximum likelihood estimator under the left truncated and right censored data and have proven that the MLE are asymptotic normal. Fisher’s information is $I\left(\beta \right)=-E[\frac{d^{2}lnL\left(\beta \right)}{d{\beta }^2}]$. From (7), we have:

$$\begin{array}{c}\hfill {\displaystyle \frac{d^2}{d{\beta }^2}lnL(\beta )=-\sum _{i=1}^m[X_i\frac{A^{\prime }B-A{B}^{\prime }}{{[{(1+t_{i-1}^{\beta })}^{-1}-{(1+t_i^{\beta })}^{-1}]}^2}-R_i\frac{(1+t_i^{\beta })ln{t}_i-{(\beta ln{t}_i)}^2}{{(1+t_i^{\beta })}^2}]}\end{array}$$

(8)

$$\begin{array}{cc}\hfill A& ={(1+t_i^{\beta })}^{-2}{t}_i^{\beta }ln{t}_i-{(1+t_{i-1}^{\beta })}^{-2}{t}_{i-1}^{\beta }ln{t}_{i-1}\hfill \\ \hfill A^{\prime }& =\frac{{ln}^2{t}_i(t_i^{\beta }-t_i^{2\beta })}{{(1+t_i^{\beta })}^3}-\frac{{ln}^2{t}_{i-1}(t_{i-1}^{\beta }-t_{i-1}^{2\beta })}{{(1+t_{i-1}^{\beta })}^3}\hfill \\ \hfill B& ={(1+t_{i-1}^{\beta })}^{-1}-{(1+t_i^{\beta })}^{-1}\hfill \\ \hfill B^{\prime }& ={(1+t_i^{\beta })}^{-2}{t}_i^{\beta }ln{t}_i-{(1+t_{i-1}^{\beta })}^{-2}{t}_{i-1}^{\beta }ln{t}_{i-1}\hfill \\ \hfill C& =\frac{t_i^{\beta }ln{t}_i}{1+t_i^{\beta }}\hfill \\ \hfill C^{\prime }& =\frac{t_i^{\beta }{ln}^2{t}_i}{{(1+t_i^{\beta })}^2}\hfill \end{array}$$

(9)

From the initial data of size n putting life testing at time zero, the cdf of the log-logistic distribution, the following conclusions can be drawn:

$$X_i|X_{i-1},\dots ,X_1;R_{i-1},\dots ,R_1$$

$$\begin{array}{c}\hfill {\displaystyle \sim Binomial(n-\sum _{j=1}^{i-1}(X_j+R_j),\frac{F(t_i|\beta )-F(t_{i-1}|\beta )}{1-F(t_{i-1}|\beta )})}\end{array}$$

(10)

Let $q_i=\frac{F(t_i|\beta )-F(t_{i-1}|\beta )}{1-F(t_{i-1}|\beta )}=1-\frac{1+t_{i-1}^{\beta }}{1+t_i^{\beta }},i=1,\dots ,m$. From (10), we have:

$$\begin{array}{cc}\hfill j& =1n\stackrel{fail}{\to }n(1-q_1)\stackrel{censor}{\to }n(1-q_1)(1-p_1)=n_1\hfill \\ \hfill j& =2n_1\stackrel{fail}{\to }{n}_1(1-q_2)\stackrel{censor}{\to }{n}_1(1-q_2)(1-p_2)=n_2\hfill \\ \hfill j& =i-1n_{i-2}\stackrel{fail}{\to }{n}_{i-2}(1-q_{i-1})\stackrel{censor}{\to }n\prod _{j=1}^{i-1}(1-q_j)(1-p_j)\hfill \end{array}$$

$$\begin{array}{c}E\left(X_i\right)=EE(X_i|X_{i-1},\cdots ,X_1,R_{i-1},\cdots ,R_1)\\ =n{q}_i\prod _{j=1}^{i-1}(1-q_j)(1-p_j),i=1,\cdots ,m\end{array}$$

(11)

$$\begin{array}{c}\hfill E\left(R_i\right)=n[\prod _{j=1}^{i-1}(1-q_j)(1-p_j)](1-q_i)p_i\end{array}$$

(12)

The reduced Fisher information can be obtained from the above (8), (11) and (12):

$$\begin{array}{c}\hfill {\displaystyle I\left(\beta \right)=-E[\frac{d^{2}lnL\left(\beta \right)}{d{\beta }^2}]=-n\sum _{i=1}^m[q_i\frac{A^{\prime }B-A{B}^{\prime }}{B^2}-p_i(1-q_i)C^{\prime }]\prod _{j=1}^{i-1}(1-q_j)(1-p_j)}\end{array}$$

(13)

$A,A^{\prime },B,B^{\prime },C^{\prime }$ can be obtained from (9). Therefore, $\beta$ obeys the asymptotic normal distribution.

$$\sqrt{m}(\tilde{\beta }-\beta )\underset{m\to \infty }{\overset{d}{\to }}N(0,I^{-1}\left(\beta \right))$$

The observation of the sample under the progressive type-I censoring is performed within two consecutive specified times. Considering the special case that the interval duration is equal, letting $t_{i-1}=(i-1)t$, $t_i=it$, then the monitoring and deletion take place in cycles of t. (7) can be converted into:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{d\beta }lnL(\beta )=\sum _{i=1}^m[X_i\frac{{(1+{(it)}^{\beta })}^{-2}{(it)}^{\beta }lnit-{(1+{((i-1)t)}^{\beta })}^{-2}{((i-1)t)}^{\beta }ln((i-1)t)}{{(1+{((i-1)t)}^{\beta })}^{-1}-{(1+{(it)}^{\beta })}^{-1}}}\\ \hfill -R_i\frac{{(it)}^{\beta }lnit}{1+{(it)}^{\beta }}]=0\end{array}$$

(14)

We can get the MLE of $\beta$ as $\tilde{\beta }$ through the above equation. Because the above equation does not have a closed form of the maximum likelihood estimation solution, a Newton–Raphson method is proposed here, which is a method of iterative numerical search to obtain MLE.

Let $g\left(\beta \right)=\frac{d}{d\beta }lnL\left(\beta \right)$. The iteration is defined as ${\beta }_i={\beta }_{i-1}+\frac{g\left({\beta }_{i-1}\right)}{g^{\prime }\left({\beta }_{i-1}\right)}$, where ${\beta }_i$ is the estimated value of $\beta$ for the $i^{\mathrm{th}}$ iteration and ${\beta }_0$ is the initial estimate of $\beta$. When $|{\beta }_i-{\beta }_{i-1}|<{10}^{-4}$ holds, the iteration is over. On this basis, each time with the same percentage p of censored data, (13) can be converted into:

$$\begin{array}{c}\hfill {\displaystyle I(\beta )=-E[\frac{d^{2}lnL(\beta )}{d{\beta }^2}]=-n\sum _{i=1}^m[q_i\frac{A^{\prime }B-A{B}^{\prime }}{B^2}-p(1-q_i)C^{\prime }]\prod _{j=1}^{i-1}(1-q_j)(1-p_j)}\end{array}$$

(15)

Then, the asymptotic variance of $\tilde{\beta }$ can be given by $V(\tilde{\beta })=I^{-1}(\beta )$. According to the invariance of the maximum likelihood estimate, $\widetilde{H_f}$ is the likelihood estimate of $H_f$. Since we have that $\sqrt{m}(\tilde{\beta }-\beta )\underset{m\to \infty }{\overset{d}{\to }}N(0,I^{-1}(\beta ))$ obeys the asymptotic normal distribution:

$$\begin{array}{c}\hfill \widetilde{H_f}\underset{m\to \infty }{\overset{d}{\to }}N(H_f,V(\widetilde{H_f}))\end{array}$$

(16)

The MLE $\widetilde{H_f}=2-log\tilde{\beta }$ is an asymptotic and unbiased estimator of $H_f$. By using the delta method, the estimate of the asymptotic variance of $\widetilde{H_f}$ is proposed as:

$$\begin{array}{c}\hfill g^{\prime }\left(\beta \right)=\frac{d{H}_f}{d\beta }=-\frac{1}{\beta }\end{array}$$

(17)

$$\begin{array}{c}\hfill V(\widetilde{H_f})=I^{-1}\left(\beta \right){\left[g^{\prime }\left(\beta \right)\right]}^2=\frac{1}{{\beta }^2}{I}^{-1}\left(\beta \right)=\gamma \left(\beta \right)\end{array}$$

(18)

The explicit solution of the shape parameter $\beta$ cannot be obtained from the equation. If the approximate solution is obtained by numerical methods, it cannot be proven that such a solution is unique, so the maximum likelihood estimation of the shape parameter $\beta$ is not easy to obtain. We apply the Expectation Maximization Algorithm (EM algorithm) to determine the estimate of the parameter.

3.2. EM Algorithm

The EM algorithm is an iterative method mainly used to find the maximum likelihood estimation of the posterior distribution. Each iteration includes two steps: E step (seeking expectation) and M step (maximizing). The posterior density function of $\beta$ obtained from the observation data Y is represented by $f(\beta |Y)$, which is called the observation posterior density, and $f(\beta |Y,Z)$ represents the posterior density function about $\beta$ obtained after adding the data Z; called the addition of a posterior distribution. $f(Z|\beta ,Y)$ represents the conditional density function of the latent data Z for a given $\beta$ and observation data Y. The EM algorithm proceeds as follows. Let ${\beta }^{\left(i\right)}$ be the estimated value of the parameter $\beta$ at the beginning of the ${(i+1)}^{\mathrm{th}}$ iteration, then the two steps of the ${(i+1)}^{\mathrm{th}}$ iteration are:

• Step E: Find the conditional distribution of $f(\beta |Y,Z)$ or $lnf(\beta |Y,Z)$ with respect to Z, i.e.,

  $$Q(\beta |{\beta }^{\left(i\right)},Y)=E[lnf(\beta |Y,Z)|{\beta }^{\left(i\right)},Y]$$
• Step M: Maximize $Q(\beta |{\beta }^{\left(i\right)},Y)$, that is find a point ${\beta }^{(i+1)}$ to make $Q({\beta }^{(i+1)}|{\beta }^{\left(i\right)},Y)=maxQ(\beta |{\beta }^{\left(i\right)},Y)$.

This completes the iteration, ${\beta }^{\left(i\right)}\to {\beta }^{(i+1)}$. Iterate the above step E and step M until $|{\beta }^{(i+1)}-{\beta }^{\left(i\right)}|$ or $|Q({\beta }^{(i+1)}|{\beta }^{\left(i\right)},Y)-Q({\beta }^{\left(i\right)}|{\beta }^{\left(i\right)},Y)|$ is sufficiently small to stop. For the previous progressive type-I interval censorship test, record the observation results $Y=\{(X_j,R_j,t_j),(j=1,2,\cdots ,k)\}$, and $Z_j$ is the random variable falling into the interval $(t_{j-1},t_j]$. According to the conditional density formula, the conditional density function of $Z_j$ can be obtained as:

$$\begin{array}{c}\hfill f_j(z|{\beta }^{(i)},Y)=\frac{\frac{{\beta }^{(i)}{z}^{{\beta }^{(i)}-1}}{{(1+z^{{\beta }^{(i)}})}^2}}{{\int }_{t_{j-1}}^{t_j}\frac{{\beta }^{(i)}{z}^{{\beta }^{(i)}-1}}{{(1+z^{{\beta }^{(i)}})}^2}dz}=\frac{\frac{{\beta }^{(i)}{z}^{{\beta }^{(i)}-1}}{{(1+z^{{\beta }^{(i)}})}^2}}{{(1+t_{j-1}^{{\beta }^{(i)}})}^{-1}-{(1+t_j^{{\beta }^{(i)}})}^{-1}}\end{array}$$

(19)

• Step E: According to the concept of the likelihood function:

  $$\begin{array}{c}\hfill f(\beta |Y,Z)=\prod _{j=1}^k{\beta }^{X_j}{Z}_j^{(\beta -1)X_j}{(1+Z_j^{\beta })}^{-2X_j}{(1+t_j)}^{-R_j}\end{array}$$

  (20)

  $$\begin{array}{c}\hfill lnf(\beta |Y,Z)=\sum _{j=1}^k(X_{j}ln\beta +(\beta -1)X_{j}ln{Z}_j-2X_{j}ln(1+Z_j^{\beta })-R_{j}ln(1+t_j^{\beta }))\end{array}$$

  (21)

  $$\begin{array}{cc}\hfill Q(\beta |{\beta }^{(i)},Y)& \stackrel{△}{=}E[lnf(\beta |Y,Z)|{\beta }^{(i)},Y]\hfill \\ \hfill & =\sum _{j=1}^k(X_{j}ln\beta +(\beta -1)X_{j}E(ln{Z}_j)-2X_{j}E(ln(1+Z_j^{\beta }))-R_{j}ln(1+t_j^{\beta }))\hfill \end{array}$$

  (22)
• Step M: Deriving $Q(\beta |{\beta }^{(i)},Y)$ with respect to $\beta$ to find the maximum point ${\beta }^{(i+1)}$ of $Q(\beta |{\beta }^{(i)},Y)$:

  $$\begin{array}{ccc}\hfill \frac{\partial Q}{\partial \beta }& =& \sum _{j=1}^k[\frac{X_j}{\beta }+X_{j}E(ln{Z}_j)-R_j\frac{t_j^{\beta }ln{t}_j}{1+t_j^{\beta }}]\hfill \\ & =& \frac{1}{\beta }\sum _{j=1}^k{X}_j+\sum _{j=1}^k[X_{j}E(ln{Z}_j)-R_j\frac{t_j^{\beta }ln{t}_j}{1+t_j^{\beta }}]\hfill \end{array}$$

  (23)
  Let $\frac{\partial Q}{\partial \beta }=0$; $\beta$ can be calculated as:

  $$\begin{array}{c}\hfill \beta =-\frac{{\sum }_{j=1}^k{X}_j}{{\sum }_{j=1}^k[X_{j}E(ln{Z}_j)-R_j\frac{t_j^{\beta }ln{t}_j}{1+t_j^{\beta }}]}\end{array}$$

  (24)

  $$\begin{array}{c}\hfill E[ln{Z}_j]=[{(1+t_{j-1}^{{\beta }^{(i)}})}^{-1}-{(1+t_j^{\beta (i)})}^{-1}]{\int }_{t_{j-1}}^{t_j}\frac{{\beta }^{(i)}{z}^{{\beta }^{(i)}-1}lnz}{{(1+z^{{\beta }^{(i)}})}^2}dz\stackrel{△}{=}{A}_j\end{array}$$

  (25)
  Let $B_j=\frac{t_j^{\beta }ln{t}_j}{1+t_j^{\beta }}$, and replace $\beta$ with ${\beta }^{(i+1)}$, then ${\beta }^{(i+1)}$ can be defined as:

  $$\begin{array}{c}\hfill {\beta }^{(i+1)}=-\frac{{\sum }_{j=1}^k{X}_j}{{\sum }_{j=1}^k[X_j{A}_j-R_j{B}_j]}\end{array}$$

  (26)

An iterative process from ${\beta }^{(i)}\to {\beta }^{(i+1)}$ is completed by Equation (26), and the estimation of the parameter $\beta$ can be obtained by using Equation (26) repeatedly, which is denoted as $\tilde{\beta }$. The EM algorithm is an effective way to find the parameter estimates, the biggest advantage of which is the stability of the estimate, especially in the case of censored samples. The following two lemmas illustrate the convergence of the EM algorithm.

Lemma 1.

The EM algorithm increases the posterior density function value (observes) after each iteration, i.e., $f({\beta }^{(i+1)}|Y)\ge f({\beta }^{\left(i\right)}|Y)$.

Lemma 2.

1. If $f(\beta |Y)$ has an upper bound, then $L({\beta }^{\left(i\right)}|Y)$ converges to $L^{*}$.

2. If $Q(\beta |\phi )$ is continuous with respect to β and φ, the convergence value ${\beta }^{*}$ of the estimated sequence ${\beta }^{\left(i\right)}$ obtained by the EM algorithm is a stable point of L under a condition on L that is very general.

Proofs of Lemma 1 and 2 are found in [15].

4. Hypothesis Testing Algorithm

In recent years, interdisciplinary research on “information entropy” has developed rapidly and has penetrated into many disciplines such as computer science and technology, systems science and geography and has derived research topics from multiple interdisciplinary subjects, such as:

(i)

The estimation of the (conditional) entropy or mutual information can be applied to independent component analysis in order to measure the dependency among random variables (see [16]).

(ii)

A discretization algorithm for continuous features and attributes of a raw and rough set for selecting cut points can be illustrated on the basis of information entropy, which is defined for every candidate cut point and treated as a measurement of importance (see [17]).

(iii)

The information entropy can be applied in a multi-population genetic algorithm used to narrow the search space. By defining the probabilities that the best solution appears in each population, information-entropy is introduced into the evolution process, which will enhance the ability of searching optimization solution for the evolution algorithms (see [18]).

In summary, any activity process that decreases or increases the affirmation, organization, regularity or order of random event sets can be measured by the unified scale of the change of information entropy, so the research on information entropy has become especially important. From the perspective of information dissemination, information entropy can represent the value of information, that is give a standard for measuring the value of information.

In this section, we propose an information entropy hypothesis testing algorithm based on the log-logistic distribution, assuming that the data are progressive type-I censored data. Let h be the critical amount of information required to reduce the source input to a certain standard.

The physical meaning of entropy represents the average uncertainty of the source before the source is output. The hypothesis test of entropy is used to check whether the obtained source data meet the requirements. If it passes the test, no additional data are needed, and the input of the source can be reduced, further reducing the amount of human and material expenditure on data collection.

The null hypothesis and alternative hypothesis are given as:

$$H_0:H\left(f\right)\le hv.s.H_{\beta }:H\left(f\right)>h$$

Adopting to the MLE of $H\left(f\right)$ as the test statistic, then critical value $H_0$ of the right-tailed hypothesis test can be obtained as:

$$\begin{array}{cc}supP(\widetilde{H_f}>H_0)\le \alpha & \Rightarrow P(\frac{\widetilde{H_f}-H_f}{\sqrt{Var(\gamma (\tilde{\beta }))}}>\frac{H_0-H_f}{\sqrt{Var(\gamma (\tilde{\beta }))}}|H_f\le h)\le \alpha \hfill \\ & \Rightarrow P(\frac{\widetilde{H_f}-H_f}{\sqrt{Var(\gamma (\tilde{\beta }))}}>\frac{H_0-H_f}{\sqrt{Var(\gamma (\tilde{\beta }))}}|H_f=h)=\alpha \hfill \\ & \Rightarrow P(\frac{\widetilde{H_f}-h}{\sqrt{Var(\gamma (\tilde{\beta }))}}>\frac{H_0-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})=\alpha \hfill \\ & \Rightarrow P({(\frac{\widetilde{H_f}-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})}^2>{(\frac{H_0-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})}^2)=\alpha \hfill \\ & \Rightarrow P({(\frac{\widetilde{H_f}-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})}^2\le {(\frac{H_0-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})}^2)=1-\alpha \hfill \end{array}$$

(27)

where $\gamma (\tilde{\beta })=I^{-1}(\tilde{\beta })\ast {(g^{\prime }(\tilde{\beta }))}^2$ and under $H_f=h,{(\frac{\widetilde{H_f}-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})}^2\stackrel{D}{\to }{\chi (1)}^2$. From (27), by using the $CHIINV(1-\alpha )$ function, which stands for the lower $100{(1-\alpha )}^{\mathrm{th}}$ percentile of ${\chi (1)}^2$, then:

$$\begin{array}{c}\hfill {(\frac{H_0-h}{\sqrt{Var(\gamma (\tilde{\beta }))}})}^2=CHIINV(1-\alpha )\end{array}$$

(28)

can be obtained. Therefore, the critical value can be expressed as:

$$\begin{array}{c}\hfill H_0=h+\sqrt{Var(\gamma (\tilde{\beta }))}\ast \sqrt{CHIINV(1-\alpha )}\end{array}$$

(29)

where h and $\alpha$ represent the target value and the determined significance level. To determine whether the obtained source data meet the requirements, managers can perform a one-sided hypothesis test on information entropy. The test algorithm for $H_f$ is as follows. The power function $w\left(h_1\right)$ of the test of this point $H_f=h_1>h_0$ is:

$$\begin{array}{cc}w(h_1)& =P(\widetilde{H_f}>H_0|{\beta }_1=e^{2-h_1})\hfill \\ & =P(2-ln\tilde{\beta }>h_0+\sqrt{Var(\gamma (\widetilde{{\beta }_0}))CHIINV(1-\alpha )}|{\beta }_0=e^{2-h_0},{\beta }_1=e^{2-h_1})\hfill \\ & =P(\tilde{\beta }<e^{2-h_0-\sqrt{Var(\gamma (\widetilde{{\beta }_0}))CHIINV(1-\alpha )}}|{\beta }_0=e^{2-h_0},{\beta }_1=e^{2-h_1})\hfill \\ & =P(\frac{\tilde{\beta }-{\beta }_1}{\sqrt{I^{-1}({\beta }_1)}}<\frac{e^{2-h_0-\sqrt{Var(\gamma (\widetilde{{\beta }_0}))CHIINV(1-\alpha )}}-{\beta }_1}{\sqrt{I^{-1}({\beta }_1)}})\hfill \\ & =\Phi (\frac{e^{2-h_0-\sqrt{Var(\gamma (\widetilde{{\beta }_0}))CHIINV(1-\alpha )}}-{\beta }_1}{\sqrt{I^{-1}({\beta }_1)}})\hfill \end{array}$$

(30)

where $\Phi (·)$ is the cdf for the known standard normal distribution. The power function values of $w\left(h_1\right)$ for testing $H_0:H_f\le 0.8$ are summarized in

Table 1. The values of $w\left(h_1\right)$ at $\alpha =0.01$ for $h_1=0.65\left(0.15\right)2,n=60\left(20\right)100,m=5\left(1\right)8$ and $p=0.05\left(0.025\right)0.1$ under $T=0.5$ and $h_0=0.8$.

							${\mathit{h}}_1$
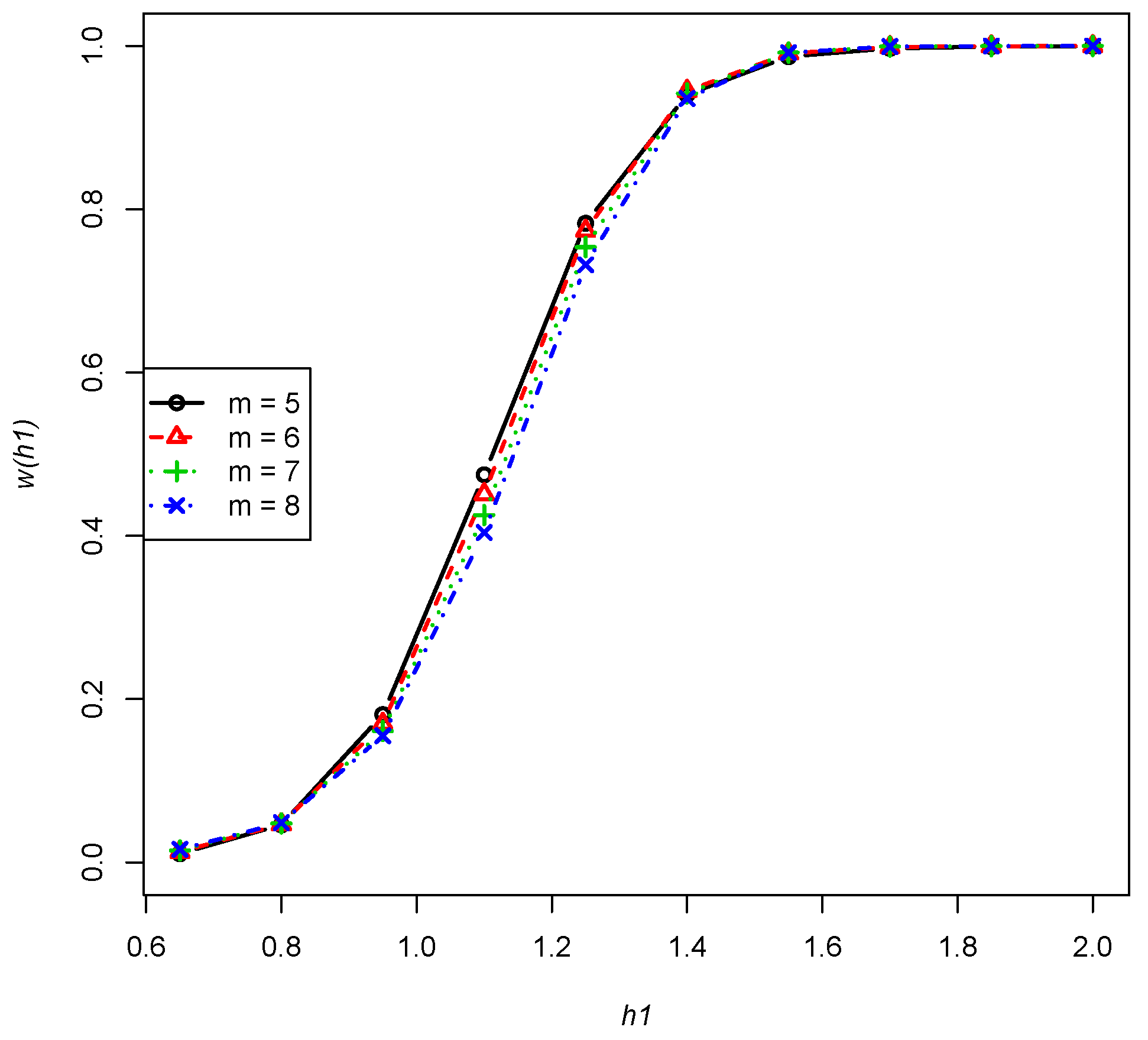
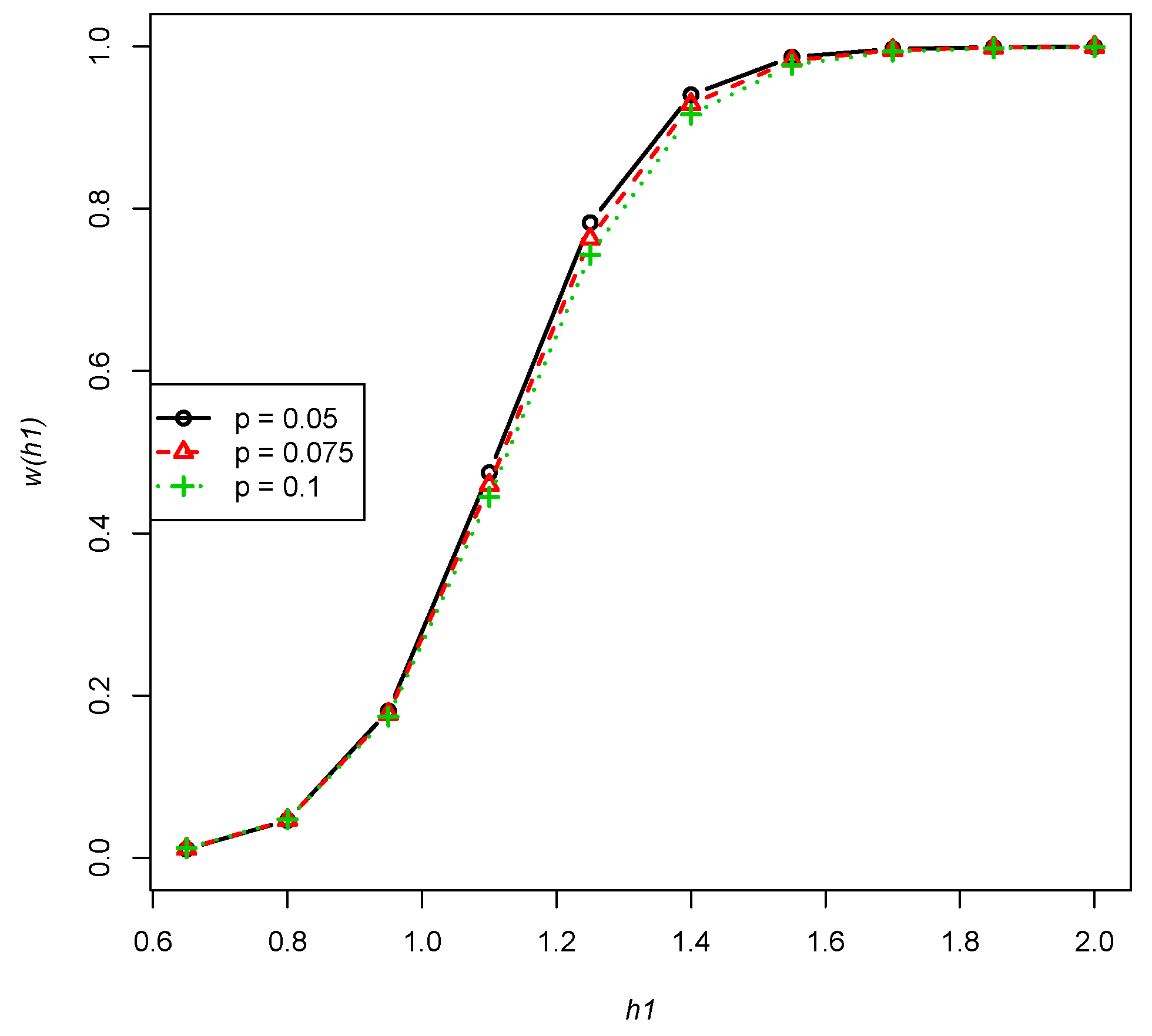
m	n	p	0.65	0.8	0.95	1.1	1.25	1.4	1.55	1.7	1.85	2
5	60	0.05	0.003800	0.017245	0.081148	0.276383	0.587226	0.836528	0.949660	0.985413	0.995253	0.998054
		0.075	0.004032	0.017650	0.079868	0.265915	0.564973	0.815618	0.937988	0.980286	0.993032	0.996955
		0.1	0.004284	0.018076	0.078677	0.255964	0.543147	0.793769	0.924717	0.973913	0.990040	0.995381
	80	0.05	0.002183	0.015033	0.095768	0.363243	0.729005	0.932958	0.988235	0.998036	0.999598	0.999882
		0.075	0.002336	0.015356	0.093514	0.347988	0.705013	0.918962	0.983776	0.996901	0.999286	0.999771
		0.1	0.002504	0.015695	0.091385	0.333371	0.680742	0.903316	0.978118	0.995260	0.998781	0.999575
	100	0.05	0.001342	0.013628	0.112273	0.451078	0.832886	0.975445	0.997651	0.999781	0.999972	0.999994
		0.075	0.001449	0.013899	0.108974	0.431713	0.811215	0.967936	0.996335	0.999592	0.999940	0.999986
		0.1	0.001566	0.014185	0.105847	0.412975	0.788483	0.958886	0.994453	0.999270	0.999876	0.999968
6	60	0.05	0.004883	0.017812	0.074107	0.250705	0.561279	0.833421	0.956602	0.990605	0.997878	0.999399
		0.075	0.005045	0.018186	0.073611	0.243013	0.540752	0.811918	0.945089	0.986392	0.996484	0.998884
		0.1	0.005230	0.018583	0.073132	0.235600	0.520662	0.789520	0.931792	0.980875	0.994414	0.998031
	80	0.05	0.002900	0.015485	0.087078	0.334081	0.710792	0.935323	0.991557	0.999122	0.999898	0.999983
		0.075	0.003011	0.015783	0.085822	0.321862	0.687350	0.921040	0.987709	0.998435	0.999778	0.999956
		0.1	0.003137	0.016098	0.084597	0.310052	0.663750	0.905018	0.982626	0.997337	0.999549	0.999896
	100	0.05	0.001839	0.014008	0.101885	0.420290	0.822110	0.978050	0.998653	0.999936	0.999996	1.000000
		0.075	0.001918	0.014258	0.099808	0.403906	0.800241	0.970707	0.997707	0.999857	0.999989	0.999999
		0.1	0.002010	0.014524	0.097781	0.387973	0.777431	0.961735	0.996257	0.999700	0.999971	0.999996
7	60	0.05	0.005761	0.018483	0.069396	0.227948	0.527358	0.817161	0.955804	0.992186	0.998704	0.999743
		0.075	0.005817	0.018796	0.069612	0.223634	0.511146	0.796710	0.944284	0.988356	0.997680	0.999455
		0.1	0.005910	0.019137	0.069752	0.219159	0.494940	0.775408	0.930965	0.983214	0.996057	0.998920
	80	0.05	0.003498	0.016019	0.080815	0.305489	0.680614	0.928605	0.992033	0.999417	0.999959	0.999996
		0.075	0.003538	0.016268	0.080510	0.297471	0.660316	0.914282	0.988308	0.998892	0.999897	0.999987
		0.1	0.003603	0.016539	0.080111	0.289328	0.639687	0.898304	0.983342	0.998005	0.999762	0.999963
	100	0.05	0.002264	0.014457	0.093988	0.387302	0.798857	0.975914	0.998856	0.999968	0.999999	1.000000
		0.075	0.002295	0.014667	0.093118	0.375615	0.778690	0.968368	0.998005	0.999920	0.999997	1.000000
		0.1	0.002343	0.014894	0.092138	0.363819	0.757631	0.959218	0.996669	0.999815	0.999989	0.999999
8	60	0.05	0.006372	0.019094	0.066647	0.211436	0.496750	0.797345	0.952000	0.992552	0.999033	0.999861
		0.075	0.006325	0.019329	0.067386	0.210105	0.485710	0.779344	0.940671	0.988891	0.998195	0.999674
		0.1	0.006334	0.019602	0.067964	0.208126	0.473880	0.760275	0.927569	0.983926	0.996808	0.999297
	80	0.05	0.003922	0.016505	0.076893	0.283451	0.650493	0.918498	0.991494	0.999511	0.999977	0.999999
		0.075	0.003890	0.016692	0.077317	0.279394	0.634761	0.904809	0.987749	0.999051	0.999937	0.999995
		0.1	0.003897	0.016909	0.077527	0.274567	0.618106	0.889515	0.982776	0.998255	0.999843	0.999983
	100	0.05	0.002571	0.014865	0.088823	0.360549	0.773440	0.971817	0.998821	0.999977	1.000000	1.000000
		0.075	0.002549	0.015023	0.088903	0.353590	0.756498	0.964200	0.997973	0.999940	0.999999	1.000000
		0.1	0.002556	0.015204	0.088720	0.345768	0.738370	0.955043	0.996647	0.999855	0.999994	1.000000

,

Table 2. The values of $w\left(h_1\right)$ at $\alpha =0.05$ for $h_1=0.65\left(0.15\right)2,n=60\left(20\right)100,m=5\left(1\right)8$ and $p=0.05\left(0.025\right)0.1$ under $T=0.5$ and $h_0=0.8$.

							${\mathit{h}}_1$
m	n	p	0.65	0.8	0.95	1.1	1.25	1.4	1.55	1.7	1.85	2
5	60	0.05	0.010636	0.046060	0.181003	0.474751	0.782816	0.940493	0.986955	0.997095	0.999202	0.999697
		0.075	0.011153	0.046622	0.177388	0.459489	0.763251	0.928988	0.982639	0.995690	0.998700	0.999472
		0.1	0.011703	0.047209	0.173927	0.444650	0.743263	0.916199	0.977317	0.993767	0.997949	0.999112
	80	0.05	0.006827	0.042893	0.212941	0.581850	0.884698	0.982370	0.997991	0.999758	0.999960	0.999989
		0.075	0.007220	0.043365	0.207659	0.563229	0.868646	0.977054	0.996940	0.999570	0.999918	0.999976
		0.1	0.007639	0.043859	0.202583	0.544881	0.851533	0.970624	0.995462	0.999264	0.999842	0.999949
	100	0.05	0.004598	0.040788	0.245816	0.674392	0.942291	0.995271	0.999729	0.999983	0.999998	1.000000
		0.075	0.004902	0.041201	0.238886	0.654207	0.931014	0.993245	0.999524	0.999963	0.999996	0.999999
		0.1	0.005228	0.041633	0.232212	0.634008	0.918416	0.990560	0.999193	0.999924	0.999990	0.999998
6	60	0.05	0.012925	0.046845	0.169828	0.451170	0.773750	0.945074	0.990947	0.998680	0.999777	0.999947
		0.075	0.013271	0.047359	0.167452	0.438091	0.754239	0.933478	0.987263	0.997804	0.999564	0.999881
		0.1	0.013660	0.047900	0.165119	0.425308	0.734376	0.920492	0.982529	0.996487	0.999194	0.999753
	80	0.05	0.008534	0.043553	0.199632	0.559181	0.881627	0.985367	0.998941	0.999933	0.999995	0.999999
		0.075	0.008808	0.043985	0.195841	0.542395	0.865285	0.980369	0.998228	0.999857	0.999985	0.999998
		0.1	0.009114	0.044439	0.192121	0.525822	0.847913	0.974197	0.997145	0.999713	0.999964	0.999993
	100	0.05	0.005900	0.041366	0.230547	0.654074	0.942088	0.996545	0.999896	0.999997	1.000000	1.000000
		0.075	0.006120	0.041743	0.225333	0.635237	0.930590	0.994819	0.999790	0.999992	1.000000	1.000000
		0.1	0.006367	0.042140	0.220219	0.616397	0.917752	0.992446	0.999597	0.999980	0.999999	1.000000
7	60	0.05	0.014708	0.047764	0.161024	0.425370	0.753648	0.941871	0.991909	0.999150	0.999907	0.999986
		0.075	0.014830	0.048189	0.159959	0.415859	0.736027	0.930271	0.988426	0.998486	0.999793	0.999962
		0.1	0.015025	0.048649	0.158767	0.406226	0.717977	0.917311	0.983883	0.997431	0.999569	0.999905
	80	0.05	0.009903	0.044324	0.188439	0.531179	0.868523	0.984874	0.999179	0.999969	0.999999	1.000000
		0.075	0.010008	0.044681	0.186311	0.518031	0.852898	0.979833	0.998572	0.999926	0.999996	1.000000
		0.1	0.010168	0.045067	0.184040	0.504721	0.836307	0.973619	0.997619	0.999834	0.999987	0.999999
	100	0.05	0.006973	0.042040	0.217055	0.626106	0.934584	0.996556	0.999932	0.999999	1.000000	1.000000
		0.075	0.007064	0.042352	0.213841	0.610595	0.923141	0.994839	0.999853	0.999997	1.000000	1.000000
		0.1	0.007198	0.042689	0.210472	0.594800	0.910443	0.992476	0.999702	0.999991	1.000000	1.000000
8	60	0.05	0.015915	0.048590	0.155104	0.404095	0.732049	0.935697	0.991801	0.999320	0.999949	0.999995
		0.075	0.015833	0.048906	0.155119	0.398271	0.717478	0.924473	0.988366	0.998752	0.999874	0.999984
		0.1	0.015859	0.049270	0.154831	0.391745	0.702122	0.911917	0.983877	0.997818	0.999716	0.999954
	80	0.05	0.010848	0.045018	0.180545	0.506603	0.852691	0.982997	0.999216	0.999980	1.000000	1.000000
		0.075	0.010793	0.045283	0.179838	0.497552	0.838775	0.977893	0.998636	0.999949	0.999998	1.000000
		0.1	0.010823	0.045588	0.178759	0.487726	0.823790	0.971646	0.997719	0.999878	0.999994	1.000000
	100	0.05	0.007728	0.042646	0.207223	0.600230	0.924505	0.996092	0.999940	1.000000	1.000000	1.000000
		0.075	0.007692	0.042878	0.205765	0.588809	0.913737	0.994305	0.999869	0.999998	1.000000	1.000000
		0.1	0.007722	0.043144	0.203870	0.576536	0.901746	0.991875	0.999730	0.999995	1.000000	1.000000

and

Table 3. The values of $w\left(h_1\right)$ at $\alpha =0.1$ for $h_1=0.65\left(0.15\right)2,m=5\left(1\right)8,n=60\left(20\right)100$ and $p=0.05\left(0.025\right)0.1$ under $T=0.5$ and $h_0=0.8$.

							${\mathit{h}}_1$
m	n	p	0.65	0.8	0.95	1.1	1.25	1.4	1.55	1.7	1.85	2
5	60	0.05	0.017792	0.073840	0.259702	0.590335	0.862265	0.969759	0.994548	0.998951	0.999736	0.999903
		0.075	0.018563	0.074431	0.254462	0.574080	0.846532	0.962638	0.992401	0.998355	0.999543	0.999821
		0.1	0.019376	0.075048	0.249400	0.558055	0.830049	0.954421	0.989623	0.997493	0.999237	0.999679
	80	0.05	0.012008	0.070473	0.302042	0.694889	0.935704	0.992577	0.999337	0.999933	0.999990	0.999997
		0.075	0.012631	0.070979	0.294897	0.676950	0.924651	0.989905	0.998930	0.999873	0.999978	0.999994
		0.1	0.013290	0.071506	0.287976	0.658967	0.912494	0.986519	0.998322	0.999767	0.999954	0.999986
	100	0.05	0.008430	0.068202	0.343607	0.777338	0.971524	0.998330	0.999928	0.999996	1.000000	1.000000
		0.075	0.008936	0.068650	0.334695	0.759552	0.964778	0.997486	0.999865	0.999991	0.999999	1.000000
		0.1	0.009476	0.069116	0.326041	0.741390	0.956959	0.996307	0.999755	0.999981	0.999998	0.999999
6	60	0.05	0.021057	0.074666	0.246967	0.571566	0.860041	0.974226	0.996759	0.999623	0.999946	0.999988
		0.075	0.021569	0.075205	0.243110	0.556817	0.844067	0.967343	0.995130	0.999318	0.999883	0.999971
		0.1	0.022139	0.075770	0.239312	0.542244	0.827367	0.959275	0.992894	0.998819	0.999763	0.999932
	80	0.05	0.014582	0.071180	0.287321	0.678744	0.936457	0.994488	0.999716	0.999986	0.999999	1.000000
		0.075	0.015014	0.071640	0.281772	0.661839	0.925225	0.992162	0.999483	0.999968	0.999997	1.000000
		0.1	0.015494	0.072123	0.276311	0.644898	0.912863	0.989116	0.999100	0.999928	0.999992	0.999999
	100	0.05	0.010486	0.068827	0.327209	0.764319	0.972851	0.998941	0.999979	1.000000	1.000000	1.000000
		0.075	0.010850	0.069235	0.320061	0.747123	0.966101	0.998296	0.999952	0.999999	1.000000	1.000000
		0.1	0.011255	0.069663	0.313024	0.729597	0.958241	0.997346	0.999900	0.999996	1.000000	1.000000
7	60	0.05	0.023565	0.075628	0.235989	0.547795	0.847890	0.973750	0.997383	0.999797	0.999983	0.999998
		0.075	0.023759	0.076072	0.233736	0.536112	0.832763	0.966862	0.995940	0.999597	0.999955	0.999993
		0.1	0.024051	0.076551	0.231339	0.524286	0.816928	0.958785	0.993905	0.999242	0.999895	0.999980
	80	0.05	0.016619	0.072002	0.273811	0.655201	0.929912	0.994622	0.999809	0.999995	1.000000	1.000000
		0.075	0.016797	0.072382	0.270223	0.641045	0.918816	0.992331	0.999631	0.999986	0.999999	1.000000
		0.1	0.017055	0.072790	0.266476	0.626623	0.906652	0.989320	0.999322	0.999965	0.999998	1.000000
	100	0.05	0.012156	0.069556	0.311419	0.742747	0.969715	0.999022	0.999988	1.000000	1.000000	1.000000
		0.075	0.012318	0.069892	0.306544	0.727752	0.962851	0.998409	0.999971	1.000000	1.000000	1.000000
		0.1	0.012545	0.070254	0.301497	0.712304	0.954917	0.997497	0.999935	0.999999	1.000000	1.000000
8	60	0.05	0.025253	0.076490	0.228102	0.526692	0.833155	0.971331	0.997504	0.999858	0.999992	0.999999
		0.075	0.025160	0.076819	0.227254	0.518499	0.819777	0.964485	0.996118	0.999701	0.999977	0.999998
		0.1	0.025216	0.077196	0.226038	0.509643	0.805548	0.956479	0.994149	0.999410	0.999940	0.999992
	80	0.05	0.018018	0.072738	0.263705	0.632941	0.920841	0.994091	0.999833	0.999997	1.000000	1.000000
		0.075	0.017960	0.073019	0.261895	0.622242	0.910430	0.991750	0.999672	0.999992	1.000000	1.000000
		0.1	0.018024	0.073342	0.259645	0.610807	0.898963	0.988696	0.999387	0.999977	0.999999	1.000000
	100	0.05	0.013326	0.070208	0.299260	0.721232	0.964803	0.998927	0.999991	1.000000	1.000000	1.000000
		0.075	0.013292	0.070457	0.296503	0.709320	0.958059	0.998292	0.999977	1.000000	1.000000	1.000000
		0.1	0.013359	0.070743	0.293244	0.696586	0.950294	0.997356	0.999945	0.999999	1.000000	1.000000

at $\alpha =0.01,0.05,0.1$, respectively, for $h_1=0.65\left(0.15\right)2,m=5\left(1\right)8,n=60\left(20\right)100$ and $p=0.05\left(0.025\right)0.1,T=0.5$. Figure 1, Figure 2, Figure 3 and Figure 4 shows the power of the proposed algorithm for some common situations. From Table 1, Table 2 and Table 3, we conclude:

• For $m=5$, $p=0.05$ and $\alpha =0.05$, the power function $w\left(h_1\right)$ presents a non-decreasing trend with respect to n, as performed in Figure 1 (any combinations of m, p and $\alpha$ will have the same trend).
• The power $w\left(h_1\right)$ is a fixed non-increasing function of m, $n=60$, $p=0.05$, $\alpha =0.05$, as performed in Figure 2 (any combinations of n, $\alpha$ and p will have a similar trend).
• The power function $w\left(h_1\right)$ presents a non-increasing trend of the fixed deleted percentage p of $n=60$, $\alpha =0.05$, $m=5$, as performed in Figure 3 (any combinations of n, m and $\alpha$ will have a similar trend).
• From Figure 1, Figure 2 and Figure 3, the power function $w\left(h_1\right)$ increases as the value of $h_1$ increases for any combination of n, m, p and $\alpha$.
• From Figure 4, for any combination of n, m and p, the power function $w\left(h_1\right)$ presents a non-decreasing trend with respect to $\alpha$.

Algorithm:

Step 1

Observe the progressive type-I interval censored data $X_1,\cdots ,X_m$ at the pre-scheduled times $t_1,\cdots ,t_m$ with censoring schemes of $R_1,\cdots ,R_m$ from the log-logistic distribution.

Step 2

In practical applications, h represents the critical amount of information required to reduce the source input to a certain standard. Then, the testing null hypothesis $H_0:H_f\le h$ and the alternative hypothesis $H_{\beta }:H_f>h$ are constructed.

Step 3

Calculate the maximum likelihood estimate of $\beta$ and the value of the test statistic $\widetilde{H_f}=2-log\tilde{\beta }$.

Step 4

The critical value can be calculated for the level of significance of $\alpha$ as:

$$\begin{array}{c}\hfill H_0=h+\sqrt{Var(\gamma (\tilde{\beta }))}\ast \sqrt{CHIINV(1-\alpha )}\end{array}$$

(31)

Step 5

Compare the size of $\widetilde{H_f}$ and $H_0$. Determine whether the obtained source data meet the requirements.

Based on the proposed algorithm, information entropy represents whether the amount of information contained in the data meets the requirements. Two numerical examples are given in the next section.

5. Monte Carlo Simulation

To demonstrate and illustrate the above test algorithm program, Monte Carlo simulation generates two datasets.

Monte Carlo simulation is a computational method that realistically simulates actual physical processes based on probabilistic and statistical theoretical methods. It is widely used in many fields, such as physical science, estimating micro economic models, engineering and data analysis (see, e.g., the recent works [19,20,21]).

Example 1.

The R software is used to generate $n=60$ sets of failure time values, which obey the log-logistic distribution under $\beta =4$. The log-logistic distribution is generated as follows: if M is a random number with uniform distribution (0,1), then $U={(\frac{M}{1-M})}^{\frac{1}{\beta }}$ follows a log-logistic distribution.

$$0.3118375,0.3715598,0.4876330,0.5205967,0.5424458,0.5445681,0.5819012$$

$$0.5882983,0.6189600,0.6723682,0.6790795,0.6936371,0.7221577,0.7227560$$

$$0.7424159,0.7487004,0.7490484,0.7517022,0.7750581,0.8431784,0.8434412$$

$$0.8686997,0.8835853,0.8855607,0.8898366,0.9227385,0.9633077,0.9638518$$

$$0.9643345,0.9701875,0.9810045,0.9890877,1.0151853,1.0301795,1.0597236$$

$$1.0836868,1.0853866,1.1076366,1.1599594,1.1661035,1.2076103,1.2394994$$

$$1.2654396,1.2813285,1.3142395,1.3628084,1.3895883,1.3966131,1.4486672$$

$$1.4501228,1.4574971,1.5251246,1.6315132,1.6351908,1.7744221,2.0102572$$

$$2.1783054,2.5374440,3.1885393,6.4965022$$

According to these data, we are able to obtain a progressive type-I censored sample. The number of checking times is $m=7$; the check interval is equal to $t=0.2$ (h); and the predetermined deleted percentage of the survival units is given by $(p_1,p_2,p_3,p_4,p_5,p_6,p_7,p_8)=(0.05,0.05,0.05,0.05,0.05,0.05,0.05,1)$. Now, we can start executing the test algorithm program about $H_f$.

Step 1

Observe the progressive type-I interval censored data $(0,2,6,11,13,8,8)$ at the pre-set times $(t_1,t_2,t_3,t_4,t_5,t_6,t_7)=(0.2,0.4,0.6,0.8,1.0,1.2,1.4)$ with the censoring schemes of

$(R_1,R_2,R_3,R_4,R_5,R_6,R_7)=(3,3,2,2,1,0,1)$.

Step 2

Let the critical amount of information required $h=0.6$, and then, propose the test null hypothesis $H_0:H_f\le 0.6$ and the alternative hypothesis $H_{\beta }:H_f>0.6$.

Step 3

Calculate the maximum likelihood estimate of parameter $\tilde{\beta }=4.725352$ and the value of the test statistic $\widetilde{H_f}=2-ln\tilde{\beta }=0.447058$.

Step 4

The critical value can be calculated for the level of significance of $\alpha =0.05$ as: $H_0=h+\sqrt{Var(\gamma (\beta ))}\ast \sqrt{CHIINV(1-\alpha )}=1.212735$.

Step 5

Since $\widetilde{H_f}=0.447058<H_0=1.212735$, we accept the null hypothesis $H_0:H_f\le 0.6$. Thus, the obtained source data do not meet the requirements.

Example 2.

The R software is used to generate $n=60$ sets of failure time values, which obey the log-logistic distribution under $\beta =6$.

$$0.2517733,0.5072381,0.5850387,0.6208714,0.6625793,0.6954254,0.7241406$$

$$0.7372249,0.7407151,0.7610365,0.7614509,0.7616830,0.7782394,0.8252179$$

$$0.8414707,0.8571038,0.8703908,0.8931475,0.9007681,0.9008163,0.9077517$$

$$0.9100598,0.9200725,0.9301961,0.9513207,0.9545003,0.9609950,0.9635523$$

$$0.9856276,0.9955788,1.0130551,1.0324070,1.0612042,1.0750621,1.0762970$$

$$1.0783691,1.1241678,1.1481179,1.1530923,1.1605018,1.1649218,1.1785074$$

$$1.1838348,1.1876701,1.2244942,1.2383936,1.2795402,1.2886820,1.3056510$$

$$1.3163001,1.3368304,1.3685482,1.4333597,1.4493346,1.4811992,1.8535557$$

$$1.9116135,2.1423352,2.2983347,2.4595617$$

According to these data, we are able to obtain a progressive type-I censored sample. The number of checking times is $m=8$; the check interval is equal to $t=0.2$ (h); and the predetermined deleted percentage of the survival units is given by $(p_1,p_2,p_3,p_4,p_5,p_6,p_7,p_8)=(0.02,0.02,0.02,0.02,0.02,0.02,0.02,1)$. Now, we can start executing the test algorithm program about $H_f$.

Step 1

Record the progressive type-I interval censored sample $(0,1,2,10,17,14,8,3)$ at the pre-set times $(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8)=(0.2,0.4,0.6,0.8,1.0,1.2,1.4,1.6)$ with the censoring scheme of $(R_1,R_2,\cdots ,R_8)=(1,1,1,1,1,0,0,0)$.

Step 2

If the critical amount of information required $h=0.1$, then, we can propose the test null hypothesis $H_0:H_f\le 0.1$ and the alternative hypothesis $H_{\beta }:H_f>0.1$.

Step 3

Calculate the maximum likelihood estimate of parameter $\tilde{\beta }=6.530128$ and the value of the test statistic $\widetilde{H_f}=2-ln\tilde{\beta }=0.123574$.

Step 4

The critical value can be calculated for the level of significance of $\alpha =0.05$ as: $H_0=h+\sqrt{Var\left(\gamma (\beta \right))}\ast \sqrt{CHIINV(1-\alpha )}=0.609365$.

Step 5

Since $\widetilde{H_f}=0.123574<H_0=0.609365$, we accept the null hypothesis $H_0:H_f\le 0.1$. Thus, the obtained source data do not meet the requirements.

6. Conclusions

In practice, due to some reasons such as time and cost, usually only incomplete data can be collected and observed. We consider that the data come from the progressive type-I censoring scheme and use the MLE method and EM algorithm to estimate the parameters and the information entropy. In combination with the hypothesis test, we establish the information entropy calculation algorithm, using information entropy to measure the amount of uncertainty in an object in information theory. Extensive simulations justify that the algorithm is feasible and effective. This information entropy algorithm based on censored data will be widely used in interdisciplinary fields such as system science, geography, computer science and technology in the future.