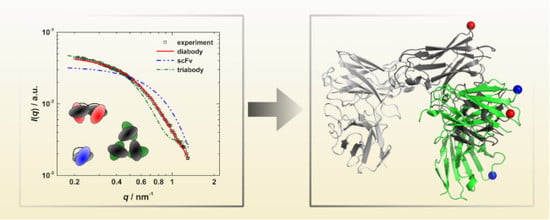
Distinguishing Between Monomeric scFv and Diabody in Solution Using Light and Small Angle X-ray Scattering
Abstract
1. Introduction
2. Materials and Methods
2.1. Protein Expression and Purification
2.2. Analytical Size Exclusion Chromatography
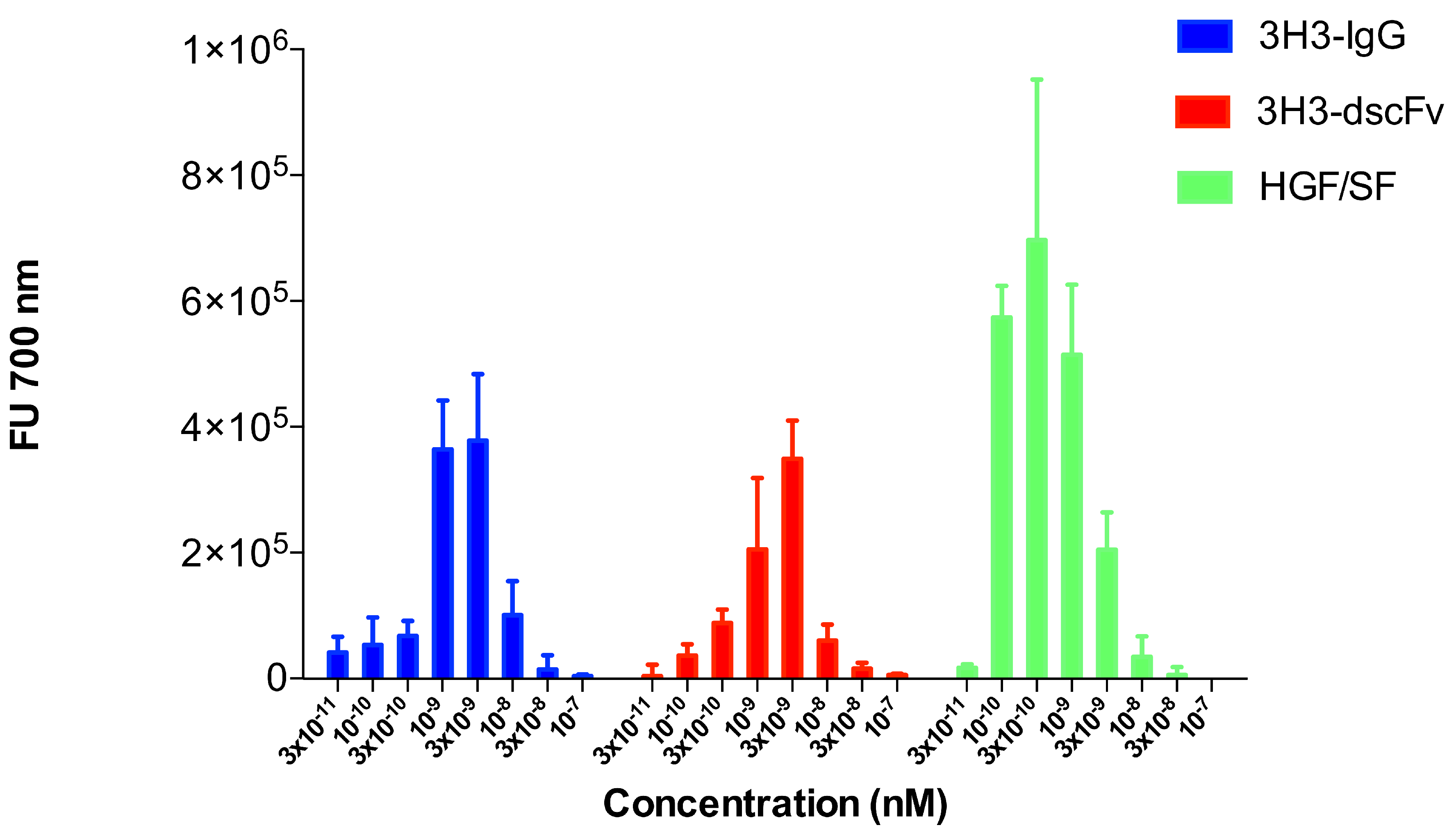
2.3. Cell Motility Assay
2.4. Small-Angle X-ray Scattering
2.5. Photon Correlation Spectroscopy
2.6. Static Light Scattering
2.7. Molecular Mass Determination with SLS—The Zimm-Plot
2.8. Density, Refractive Index and Refractive Index Increment Measurement
2.9. Molecular Mass Calculation from SAXS Data
2.10. Prediction and Evaluation of a Possible Structure Model
3. Results and Discussion
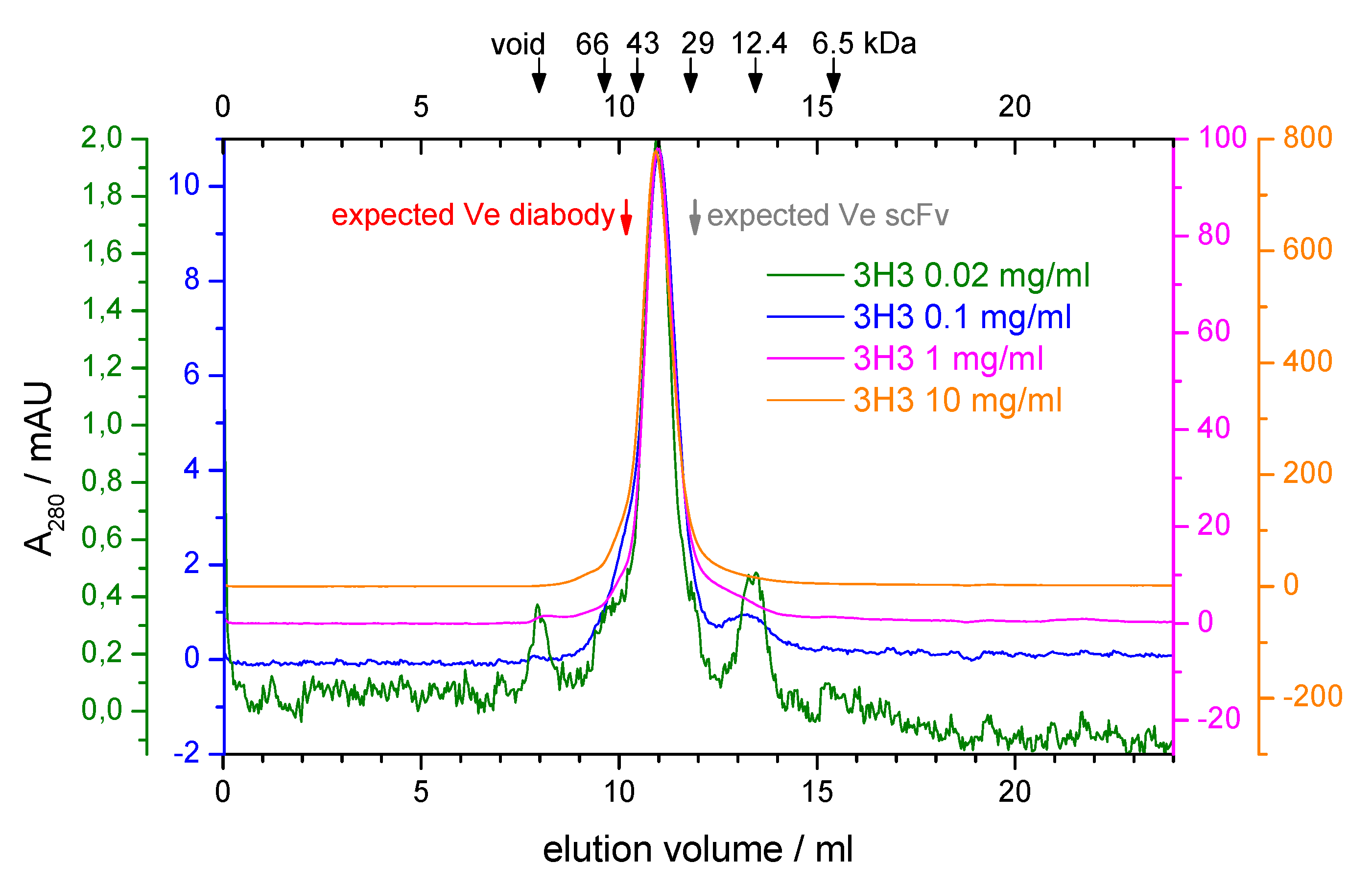
3.1. SEC Analysis
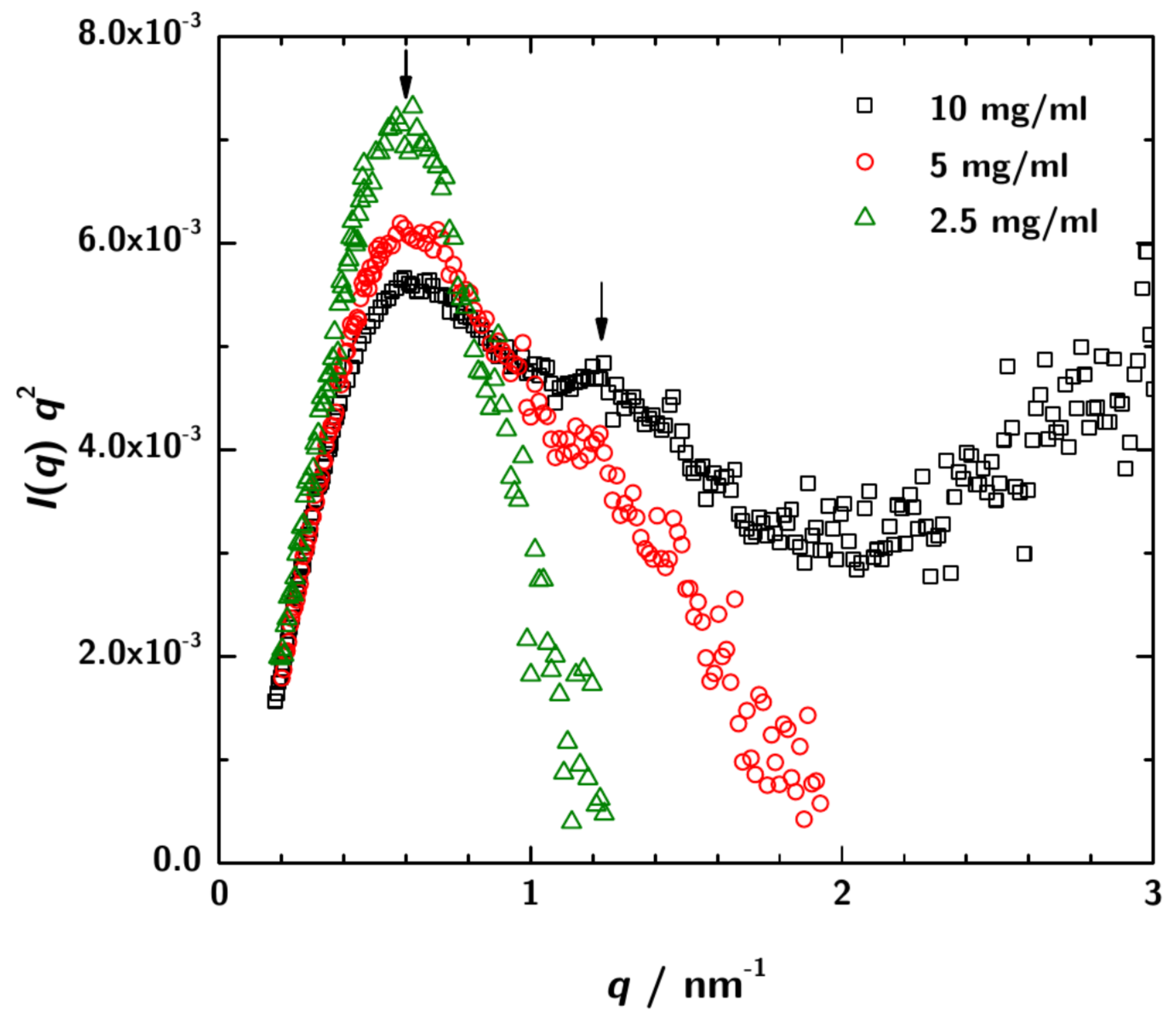
3.2. SAXS Data Analysis
3.3. Calculation of SAXS Data with CRYSOL
3.4. Photon Correlation Spectroscopy (PCS) Data
3.5. Calculation of Hydrodynamic Data with HYDROPRO
3.6. Zimm Analysis
3.7. Cell Motility Assay
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Elgert, K.D. Immunology: Understanding the Immune System; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Spiegelberg, H.L. Biological Role of Different Antibody Classes. Int. Arch. Allergy Immunol. 1989, 90, 22–27. [Google Scholar] [CrossRef] [PubMed]
- Beale, D.; Feinstein, A. Structure and function of the constant regions of immunoglobulins. Q. Rev. Biophys. 1976, 9, 135–180. [Google Scholar] [CrossRef] [PubMed]
- Padlan, E.A. Anatomy of the antibody molecule. Mol. Immunol. 1994, 31, 169–217. [Google Scholar] [CrossRef]
- Davidson, G.P.; Daniels, E.; Nunan, H.; Moore, A.G.; Whyte, P.B.; Franklin, K.; McCloud, P.I.; Moore, D.J. Passive immunisation of children with bovine colostrum containing antibodies to human rotavirus. Lancet 1989, 334, 709–712. [Google Scholar] [CrossRef]
- Schaffer, A.C.; Lee, J.C. Vaccination and passive immunisation against Staphylococcus aureus. Int. J. Antimicrob. Agents 2008, 32, S71–S78. [Google Scholar] [CrossRef] [PubMed]
- Weiner, H.L.; Hafler, D.A. Immunotherapy of multiple sclerosis. Ann. Neurol. 1988, 23, 211–222. [Google Scholar] [CrossRef] [PubMed]
- Meuth, S.G.; Bittner, S.; Wiendl, H. Immunotherapy of multiple sclerosis. Acta Neuropsychiatr. 2009, 21, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Molina, M.A.; Codony-Servat, J.; Albanell, J.; Rojo, F.; Arribas, J.; Baselga, J. Trastuzumab (herceptin), a humanized anti-Her2 receptor monoclonal antibody, inhibits basal and activated Her2 ectodomain cleavage in breast cancer cells. Cancer Res. 2001, 61, 4744–4749. [Google Scholar]
- Goldenberg, M.M. Trastuzumab, a recombinant DNA-derived humanized monoclonal antibody, a novel agent for the treatment of metastatic breast cancer. Clin. Ther. 1999, 21, 309–318. [Google Scholar] [CrossRef]
- Hortobagyi, G.N. Overview of treatment results with trastuzumab (Herceptin) in metastatic breast cancer. Semin. Oncol. 2001, 28, 43–47. [Google Scholar] [CrossRef]
- Rossin, R.; Versteegen, R.M.; Wu, J.; Khasanov, A.; Wessels, H.J.; Steenbergen, E.J.; ten Hoeve, W.; Janssen, H.M.; van Onzen, A.H.; Hudson, P.J.; et al. Chemically triggered drug release from an antibody-drug conjugate leads to potent antitumour activity in mice. Nat. Commun. 2018, 9, 1484. [Google Scholar] [CrossRef] [PubMed]
- Baum, R.P.; Lorenz, M.; Senekowitsch, R.; Albrecht, M.; Hör, G. Klinische Ergebnisse der Immunszintigraphie und Radioimmuntherapie. Nuklearmedizin 1987, 26, 68–78. [Google Scholar] [PubMed]
- Zettlitz, K.A.; Tavare, R.; Tsai, W.T.; Yamada, R.E.; Ha, N.S.; Collins, J.; van Dam, R.M.; Timmerman, J.M.; Wu, A.M. F-18-labeled anti-human CD20 cys-diabody for same-day immunoPET in a model of aggressive B cell lymphoma in human CD20 transgenic mice. Eur. J. Nuclear Med. Mol. Imaging 2019, 46, 489–500. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.J. Recombinant antibody fragments. Curr. Opin. Biotechnol. 1998, 9, 395–402. [Google Scholar] [CrossRef]
- Hudson, P.J. Recombinant antibody constructs in cancer therapy. Curr. Opin. Immunol. 1999, 11, 548–557. [Google Scholar] [CrossRef]
- Le Gall, F.; Kipriyanov, S.M.; Moldenhauer, G.; Little, M. Di-, tri- and tetrameric single chain Fv antibody fragments against human CD19: Effect of valency on cell binding. FEBS Lett. 1999, 453, 164–168. [Google Scholar] [CrossRef]
- Della Cristina, P.; Castagna, M.; Lombardi, A.; Barison, E.; Tagliabue, G.; Ceriotti, A.; Koutris, I.; Di Leandro, L.; Giansanti, F.; Vago, R.; et al. Systematic comparison of single-chain Fv antibody-fusion toxin constructs containing Pseudomonas Exotoxin A or saporin produced in different microbial expression systems. Microb. Cell Factories 2015, 14, 19. [Google Scholar] [CrossRef] [PubMed]
- Dall’Acqua, W.; Carter, P. Antibody engineering. Curr. Opin. Struct. Biol. 1998, 8, 443–450. [Google Scholar] [CrossRef]
- Plückthun, A.; Pack, P. New protein engineering approaches to multivalent and bispecific antibody fragments. Immunotechnology 1997, 3, 83–105. [Google Scholar] [CrossRef]
- Bird, R.E.; Hardman, K.D.; Jacobson, J.W.; Johnson, S.; Kaufman, B.M.; Lee, S.M.; Lee, T.; Pope, S.H.; Riordan, G.S.; Whitlow, M. Single-chain antigen-binding proteins. Science (80-) 1988, 242, 423–426. [Google Scholar] [CrossRef]
- Huston, J.S.; Levinson, D.; Mudgett-Hunter, M.; Tai, M.S.; Novotn, I.; Margolies, M.N.; Ridge, R.J.; Bruccoleri, R.E.; Haber, E.; Crea, R. Protein engineering of antibody binding sites: Recovery of specific activity in an anti-digoxin single-chain Fv analogue produced in Escherichia coli. Proc. Natl. Acad. Sci. USA 1988, 85, 5879–5883. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.J.; Kortt, A.A. High avidity scFv multimers; diabodies and triabodies. J. Immunol. Methods 1999, 231, 177–189. [Google Scholar] [CrossRef]
- Arndt, K.M.; Müller, K.M.; Plückthun, A. Factors influencing the dimer to monomer transition of an antibody single-chain Fv fragment. Biochemistry (Mosc.) 1998, 37, 12918–12926. [Google Scholar] [CrossRef] [PubMed]
- Kortt, A.A.; Lah, M.; Oddie, G.W.; Gruen, C.L.; Burns, J.E.; Pearce, L.A.; Atwell, J.L.; McCoy, A.J.; Howlett, G.J.; Metzger, D.W.; et al. Single-chain Fv fragments of anti-neuraminidase antibody NC10 containing five-and ten-residue linkers form dimers and with zero-residue linker a trimer. Protein Eng. 1997, 10, 423–433. [Google Scholar] [CrossRef] [PubMed]
- Atwell, J.L.; Breheney, K.A.; Lawrence, L.J.; McCoy, A.J.; Kortt, A.A.; Hudson, P.J. scFv multimers of the anti-neuraminidase antibody NC10: Length of the linker between VH and VL domains dictates precisely the transition between diabodies and triabodies. Protein Eng. 1999, 12, 597–604. [Google Scholar] [CrossRef]
- Perisic, O.; Webb, P.A.; Holliger, P.; Winter, G.; Williams, R.L. Crystal structure of a diabody, a bivalent antibody fragment. Structure 1994, 2, 1217–1226. [Google Scholar] [CrossRef]
- Atwell, J.L.; Pearce, L.A.; Lah, M.; Gruen, L.C.; Kortt, A.A.; Hudson, P.J. Design and expression of a stable bispecific scFv dimer with affinity for both glycophorin and N9 neuraminidase. Mol. Immunol. 1996, 33, 1301–1312. [Google Scholar] [CrossRef]
- Holliger, P.; Prospero, T.; Winter, G. Diabodies: Small bivalent and bispecific antibody fragments. Proc. Natl. Acad. Sci. USA 1993, 90, 6444–6448. [Google Scholar] [CrossRef]
- Kim, J.H.; Song, D.H.; Youn, S.J.; Kim, J.W.; Cho, G.; Kim, S.C.; Lee, H.; Jin, M.S.; Lee, J.O. Crystal structures of mono- and bi-specific diabodies and reduction of their structural flexibility by introduction of disulfide bridges at the Fv interface. Sci. Rep. 2016, 6, 34515. [Google Scholar] [CrossRef]
- Kwon, N.Y.; Kim, Y.; Lee, J.O. Structural diversity and flexibility of diabodies. Methods 2019, 154, 136–142. [Google Scholar] [CrossRef]
- Carmichael, J.A.; Power, B.E.; Garrett, T.P.J.; Yazaki, P.J.; Shively, J.E.; Raubischek, A.A.; Wu, A.M.; Hudson, P.J. The crystal structure of an anti-CEA scFv diabody assembled from T84. 66 scFvs in V L-to-V H orientation: Implications for diabody flexibility. J. Mol. Biol. 2003, 326, 341–351. [Google Scholar] [CrossRef]
- Moraga, I.; Wernig, G.; Wilmes, S.; Gryshkova, V.; Richter, C.P.; Hong, W.J.; Sinha, R.; Guo, F.; Fabionar, H.; Wehrman, T.S.; et al. Tuning Cytokine Receptor Signaling by Re-orienting Dimer Geometry with Surrogate Ligands. Cell 2015, 160, 1196–1208. [Google Scholar] [CrossRef] [PubMed]
- Banatao, D.R.; Cascio, D.; Crowley, C.S.; Fleissner, M.R.; Tienson, H.L.; Yeates, T.O. An approach to crystallizing proteins by synthetic symmetrization. Proc. Natl. Acad. Sci. USA 2006, 103, 16230–16235. [Google Scholar] [CrossRef] [PubMed]
- Birchmeier, C.; Birchmeier, W.; Gherardi, E.; Vande Woude, G.F. Met, metastasis, motility and more. Nat. Rev. Mol. Cell Biol. 2003, 4, 915–925. [Google Scholar] [CrossRef] [PubMed]
- Bukowska, M.A.; Grütter, M.G. New concepts and aids to facilitate crystallization. Curr. Opin. Struct. Biol. 2013, 23, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Niemann, H.H. Structural basis of MET receptor dimerization by the bacterial invasion protein InlB and the HGF/SF splice variant NK1. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2013, 1834, 2195–2204. [Google Scholar] [CrossRef] [PubMed]
- Vanhoudt, J.; Abgar, S.; Aerts, T.; Clauwaert, J. A small-angle X-ray solution scattering study of bovine α-crystallin. Eur. J. Biochem. 2000, 267, 3848–3858. [Google Scholar] [CrossRef] [PubMed]
- Hellweg, T.; Hinssen, H.; Eimer, W. The Ca (2+)-induced conformational change of gelsolin is located in the carboxyl-terminal half of the molecule. Biophys. J. 1993, 65, 799–805. [Google Scholar] [CrossRef]
- Hahn, K.; Hertle, Y.; Bloess, S.; Kottke, T.; Hellweg, T.; von Mollard, G.F. Activation of Recombinantly Expressed l-Amino Acid Oxidase from Rhizoctonia solani by Sodium Dodecyl Sulfate. Molecules 2017, 22, 2272. [Google Scholar] [CrossRef]
- Users Manual: Multi-Copy Pichia Expression Kit - Invitrogen. Available online: https://www.thermofisher.com/order/catalog/product/K175001?SID=srch-srp-K175001 (accessed on 23 September 2019).
- Kramer, N.; KrebsWalzl, A.; Unger, C.; Rosner, M.; Krupitza, G.; Hengstschläger, M.; Dolznig, H. In vitro cell migration and invasion assays. Mutat. Res. Rev. Mutat. Res. 2013, 752, 10–24. [Google Scholar] [CrossRef]
- Zhang, F.; Ilavsky, J.; Long, G.G.; Quintana, J.P.G.; Allen, A.J.; Jemian, P.R. Glassy carbon as an absolute intensity calibration standard for small-angle scattering. Metall. Mater. Trans. A 2010, 41, 1151–1158. [Google Scholar] [CrossRef]
- Zouni, A.; Kern, J.; Frank, J.; Hellweg, T.; Behlke, J.; Saenger, W.; Irrgang, K.D. Size Determination of Cyanobacterial and Higher Plant Photosystem II by Gel Permeation Chromatography, Light Scattering, and Ultracentrifugation. Biochemistry (Mosc.) 2005, 44, 4572–4581. [Google Scholar] [CrossRef] [PubMed]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Yadav, S.; Scherer, T.M.; Shire, S.J.; Kalonia, D.S. Use of dynamic light scattering to determine second virial coefficient in a semidilute concentration regime. Anal. Biochem. 2011, 411, 292–296. [Google Scholar] [CrossRef] [PubMed]
- Chu, B. Laser Light Scattering. In Quantum Electronics; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Rajagopalan, R.; Hiemenz, P.C. Principles of Colloid and Surface Chemistry, 3rd ed.; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Zimm, B.H. The Scattering of Light and the Radial Distribution Function of High Polymer Solutions. J. Chem. Phys. 1948, 16, 1093. [Google Scholar] [CrossRef]
- Jacques, D.A.; Guss, J.M.; Svergun, D.I.; Trewhella, J. Publication guidelines for structural modelling of small-angle scattering data from biomolecules in solution. Acta Cryst. D 2012, 68, 620–626. [Google Scholar] [CrossRef]
- Orthaber, D.; Bergmann, A.; Glatter, O. SAXS experiments on absolute scale with Kratky systems using water as a secondary standard. J. Appl. Crystallogr. 2000, 33, 218–225. [Google Scholar] [CrossRef]
- Mylonas, E.; Svergun, D.I. Accuracy of molecular mass determination of proteins in solution by small-angle X-ray scattering. J. Appl. Crystallogr. 2007, 40, 245–249. [Google Scholar] [CrossRef]
- Midelfort, K.S.; Hernandez, H.H.; Lippow, S.M.; Tidor, B.; Drennan, C.L.; Wittrup, K.D. Substantial Energetic Improvement with Minimal Structural Perturbation in a High Affinity Mutant Antibody. J. Mol. Biol. 2004, 343, 685–701. [Google Scholar] [CrossRef]
- Pei, X.Y.; Holliger, P.; Murzin, A.G.; Williams, R.L. The 2.0-Å resolution crystal structure of a trimeric antibody fragment with noncognate VH–VL domain pairs shows a rearrangement of VH CDR3. Proc. Natl. Acad. Sci. USA 1997, 94, 9637–9642. [Google Scholar] [CrossRef] [PubMed]
- Svergun, D.; Barberato, C.; Koch, M.H. CRYSOL-a program to evaluate X-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Crystallogr. 1995, 28, 768–773. [Google Scholar] [CrossRef]
- Ortega, A.; Amorós, D.; de La Torre, J.G. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic-and residue-level models. Biophys. J. 2011, 101, 892–898. [Google Scholar] [CrossRef] [PubMed]
- De La Torre, J.G.; Bloomfield, V.A. Hydrodynamics of macromolecular complexes. III. Bacterial viruses. Biopolymers 1977, 16, 1779–1793. [Google Scholar] [CrossRef] [PubMed]
- De La Torre, J.G.; Bloomfield, V.A. Hydrodynamic properties of complex, rigid, biological macromolecules: Theory and applications. Q. Rev. Biophys. 1981, 14, 81–139. [Google Scholar] [CrossRef]
- De La Torre, J.G.L.; Carrasco, B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 2000, 78, 719–730. [Google Scholar] [CrossRef]
- Czuryło, E.A.; Hellweg, T.; Eimer, W.; Dabrowska, R. The size and shape of caldesmon and its fragments in solution studied by dynamic light scattering and hydrodynamic model calculations. Biophys. J. 1997, 72, 835–842. [Google Scholar] [CrossRef]
- Hellweg, T.; Eimer, W.; Krahn, E.; Schneider, K.; Müller, A. Hydrodynamic properties of nitrogenase—The MoFe protein from Azotobacter vinelandii studied by dynamic light scattering and hydrodynamic modelling. Biochim. Biophys. Acta (BBA) Protein Struct. Mol. Enzymol. 1997, 1337, 311–318. [Google Scholar] [CrossRef]
- Lee, Y.C.; Boehm, K.M.; Chester, A.K.; Begent, H.J.R.; Perkins, J.S. Reversible Dimer Formation and Stability of the Anti-tumour Single-chain Fv Antibody MFE-23 by Neutron Scattering, Analytical Ultracentrifugation, and NMR and FT-IR Spectroscopy. J. Mol. Biol. 2002, 320, 107–127. [Google Scholar] [CrossRef]
- Tardieu, A.; Verge, A.L.; Malfois, M.; Bonnete, F.; Finet, S.; Ries-Kautt, M.; Belloni, L. Proteins in solution: From X-ray scattering intensities to interaction potentials. J. Cryst. Growth 1999, 196, 193–203. [Google Scholar] [CrossRef]
- Zhao, H.; Brown, P.; Schuck, P. On the Distribution of Protein Refractive Index Increments. Biophys. J. 2011, 100, 2309–2317. [Google Scholar] [CrossRef] [PubMed]

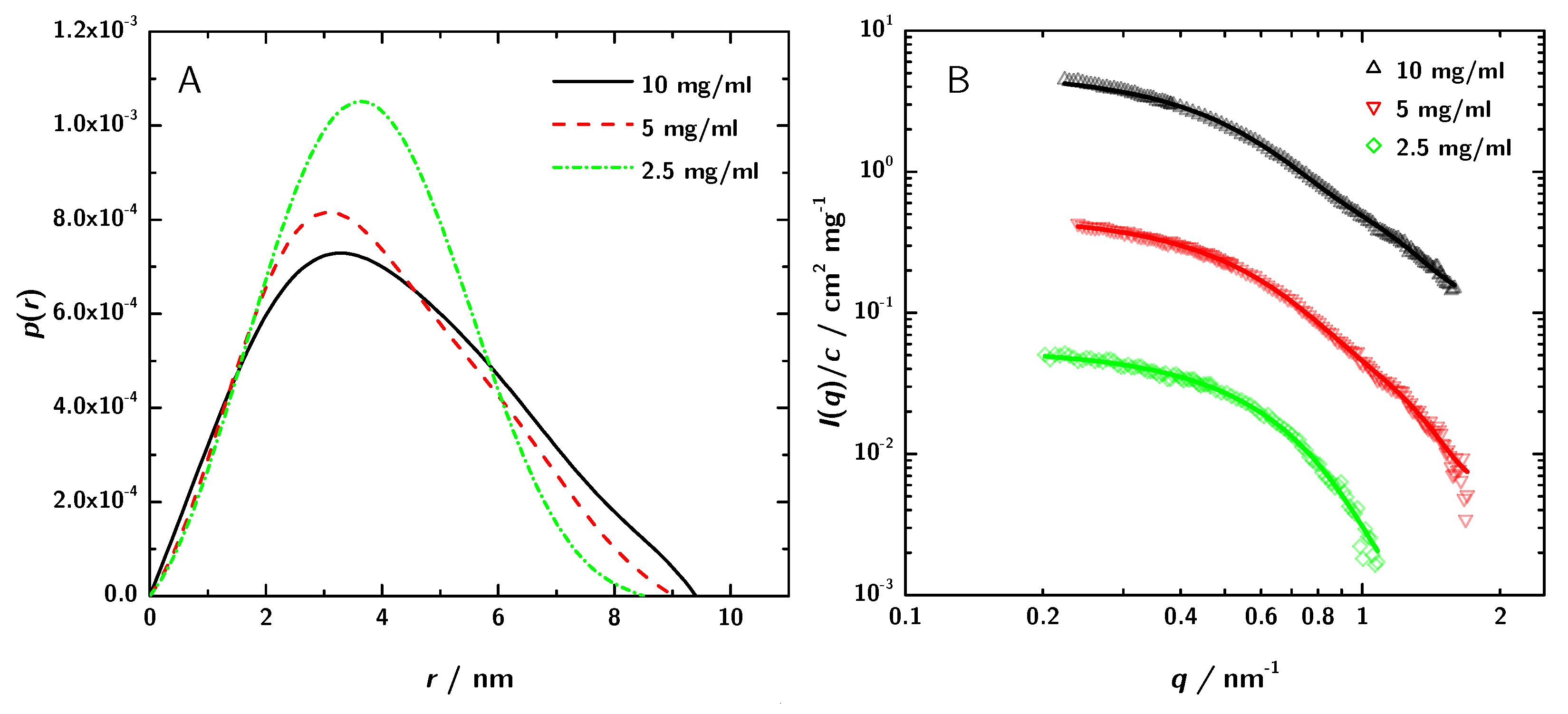
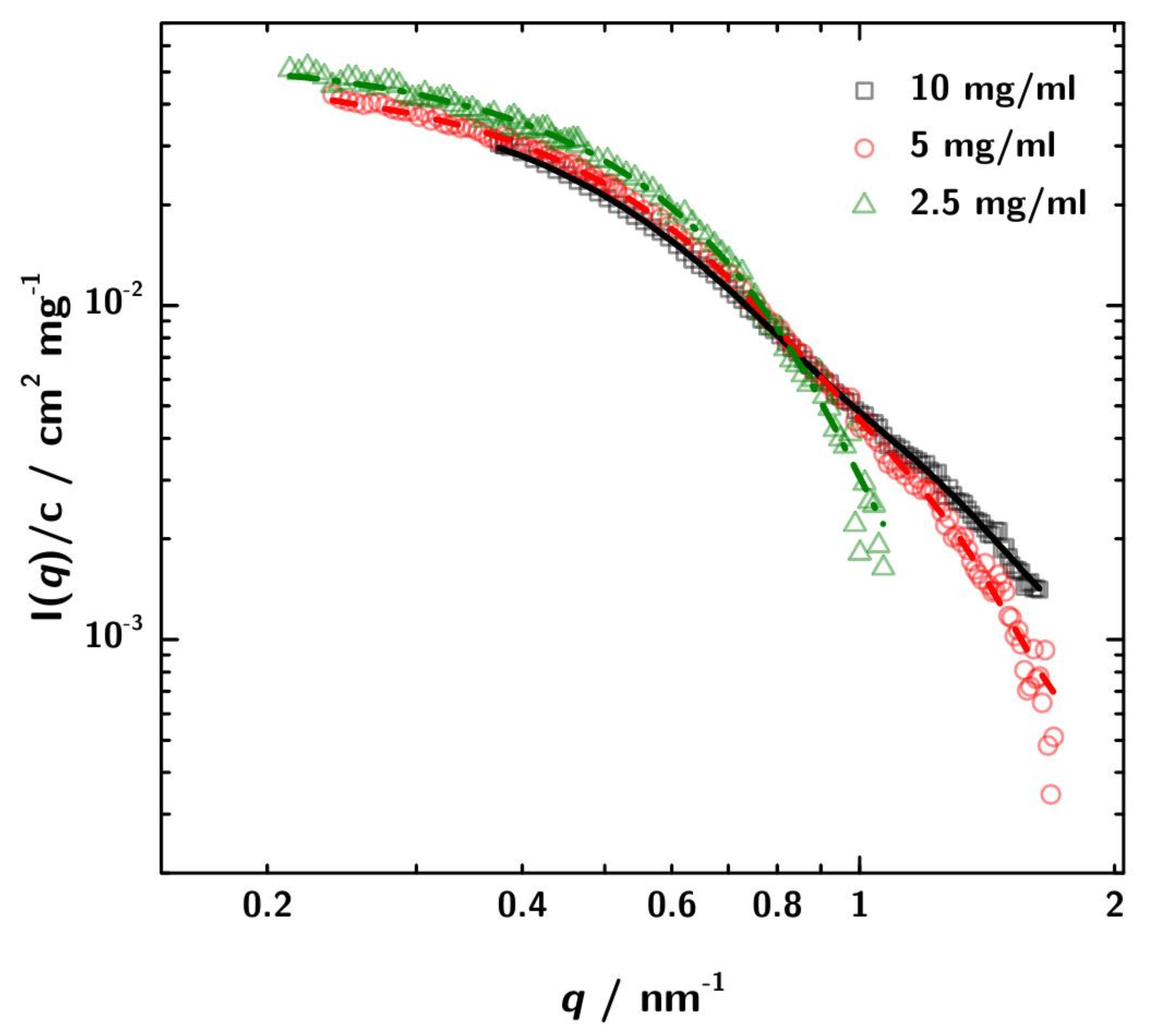
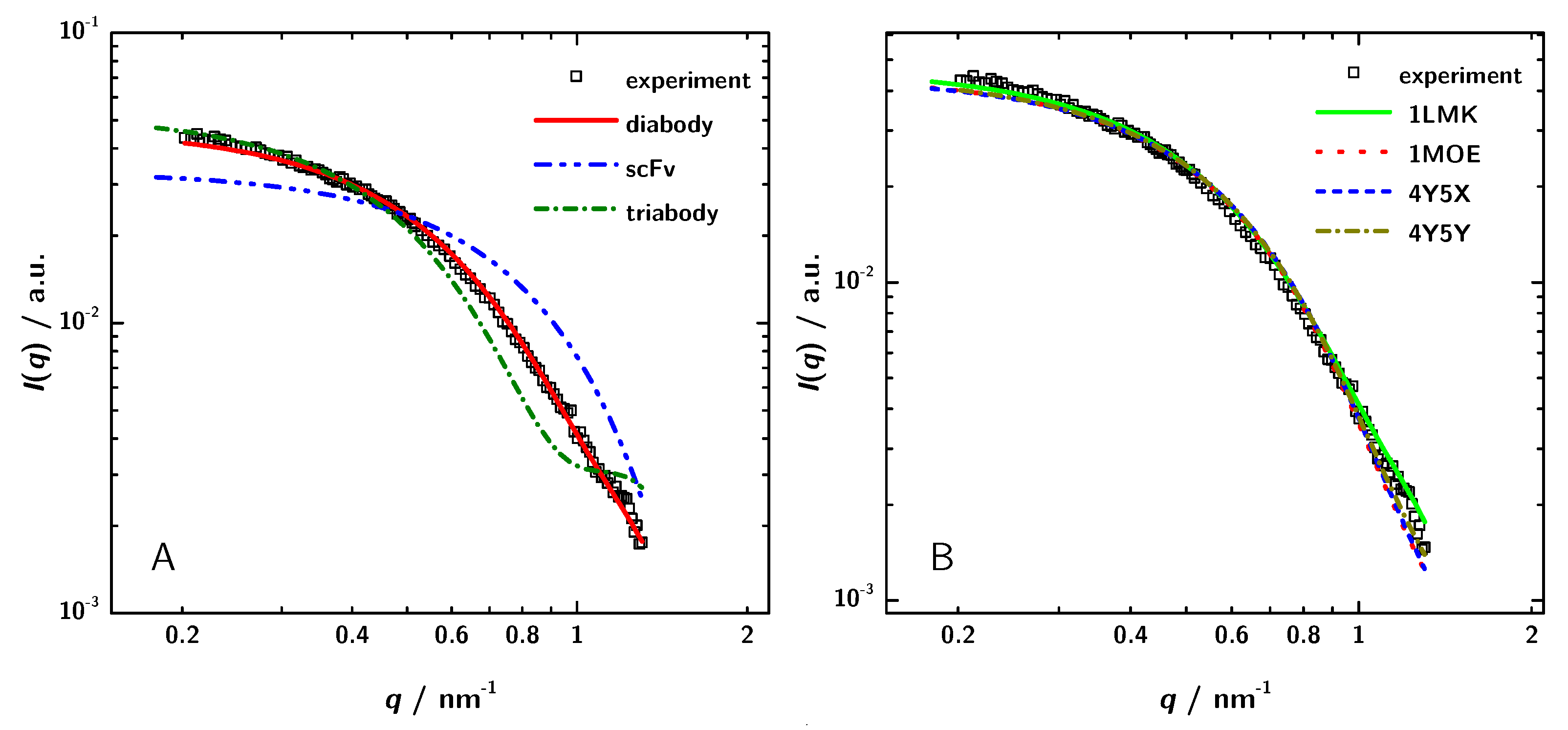


| Parameter | Experiment | 1LMK | ||
|---|---|---|---|---|
| 10 mg·mL−1 | 5 mg·mL−1 | 2.5 mg·mL−1 | ||
| (Guinier)/nm | 3.66 | 3.29 | 3.27 | 2.9 |
| (GNOM)/nm | 3.24 | 3.04 | 2.89 | |
| Dmax/nm | 9.4 | 9.02 | 8.50 | |
| M(lys)/kDa | 46.8 | 43.4 | 49.3 |
| Parameter | 2.5 mg·mL−1 | 10 mg·mL−1 |
|---|---|---|
| Dexp/nm2·s−1 | 5.95 × 107 | 5.06 × 107 |
| /nm | 3.60 | 4.24 |
| 1X9Q (scFv) | 1LMK (Diabody) | Experiment | |
|---|---|---|---|
| /Å | 5.9 | 5.9 | - |
| Type of calculation | 1 | 1 | - |
| T/°C | 20 | 20 | 20 |
| /mPa s | 101.6 | 101.6 | 101.6 |
| M/kDa | 29.447 | 53.911 | - |
| /cm3g−1 | 0.725 | 0.731 | - |
| /g cm−3 | 1.00677 | 1.00677 | - |
| /m2·s−1 | 7.74 × | 5.94 × | 6.295 × |
| / | 2.1 | 2.9 | - |
| / | 2.8 | 3.6 | 3.4 |
| 0.75 | 0.81 | - |
| Parameter | Value |
|---|---|
| c/ mgmL | 0.91, 2.58, 4.9, 7.71, 10.0 |
| /cm−1 | 13.43 × 10−6 |
| /cm3g−1 | 0.267 |
| 1.335 | |
| 1.496 | |
| k/ g | 10 |
| K/mol (m/g)2 | 5.55038 × 10−11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lüdel, F.; Bufe, S.; Bleymüller, W.M.; de Jonge, H.; Iamele, L.; Niemann, H.H.; Hellweg, T. Distinguishing Between Monomeric scFv and Diabody in Solution Using Light and Small Angle X-ray Scattering. Antibodies 2019, 8, 48. https://doi.org/10.3390/antib8040048
Lüdel F, Bufe S, Bleymüller WM, de Jonge H, Iamele L, Niemann HH, Hellweg T. Distinguishing Between Monomeric scFv and Diabody in Solution Using Light and Small Angle X-ray Scattering. Antibodies. 2019; 8(4):48. https://doi.org/10.3390/antib8040048
Chicago/Turabian StyleLüdel, Frank, Sandra Bufe, Willem M. Bleymüller, Hugo de Jonge, Luisa Iamele, Hartmut H. Niemann, and Thomas Hellweg. 2019. "Distinguishing Between Monomeric scFv and Diabody in Solution Using Light and Small Angle X-ray Scattering" Antibodies 8, no. 4: 48. https://doi.org/10.3390/antib8040048
APA StyleLüdel, F., Bufe, S., Bleymüller, W. M., de Jonge, H., Iamele, L., Niemann, H. H., & Hellweg, T. (2019). Distinguishing Between Monomeric scFv and Diabody in Solution Using Light and Small Angle X-ray Scattering. Antibodies, 8(4), 48. https://doi.org/10.3390/antib8040048