Thinking outside the Laboratory: Analyses of Antibody Structure and Dynamics within Different Solvent Environments in Molecular Dynamics (MD) Simulations
Abstract
1. Introduction
2. Materials and Methods
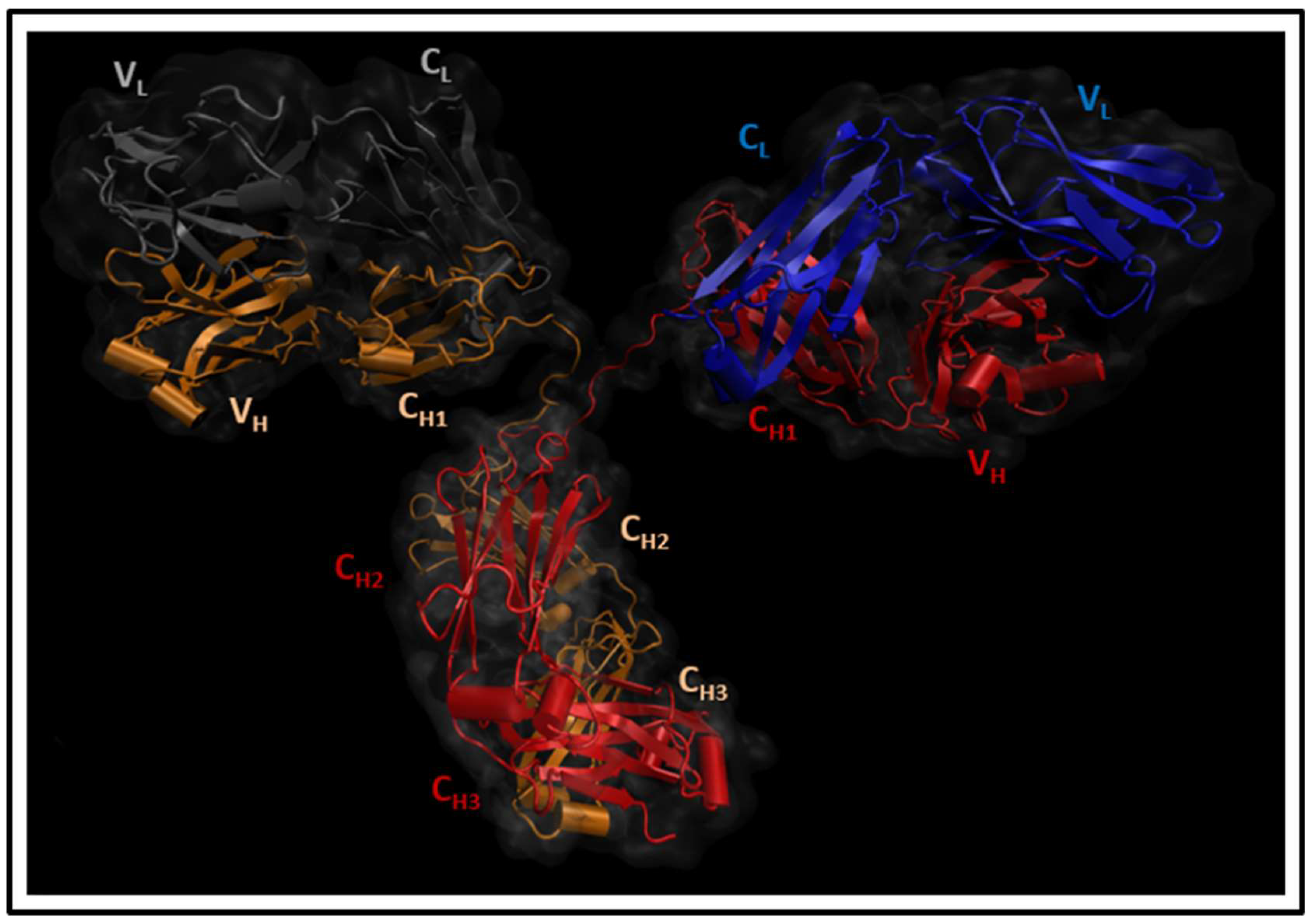
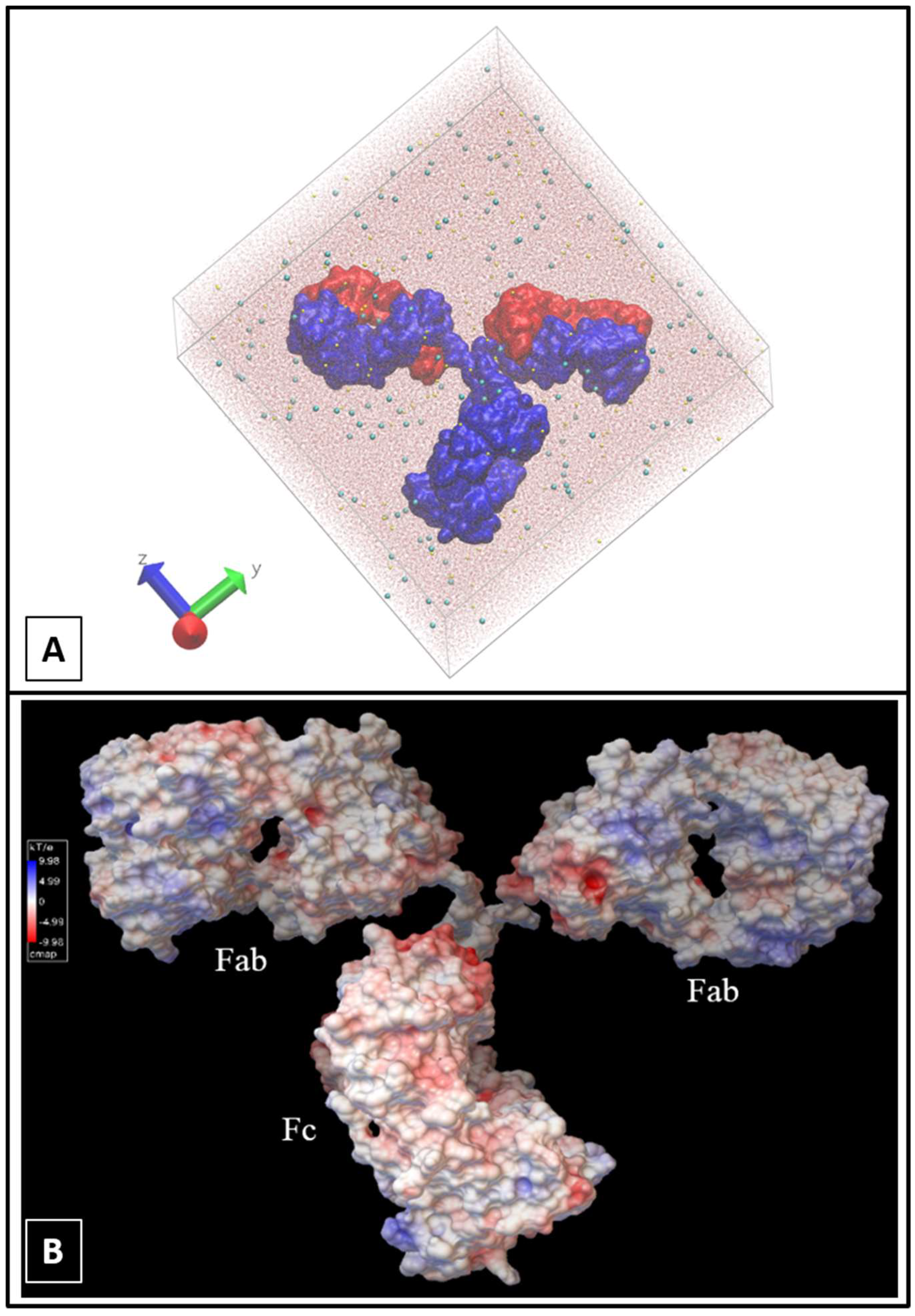
2.1. Molecular Dynamics Simulations
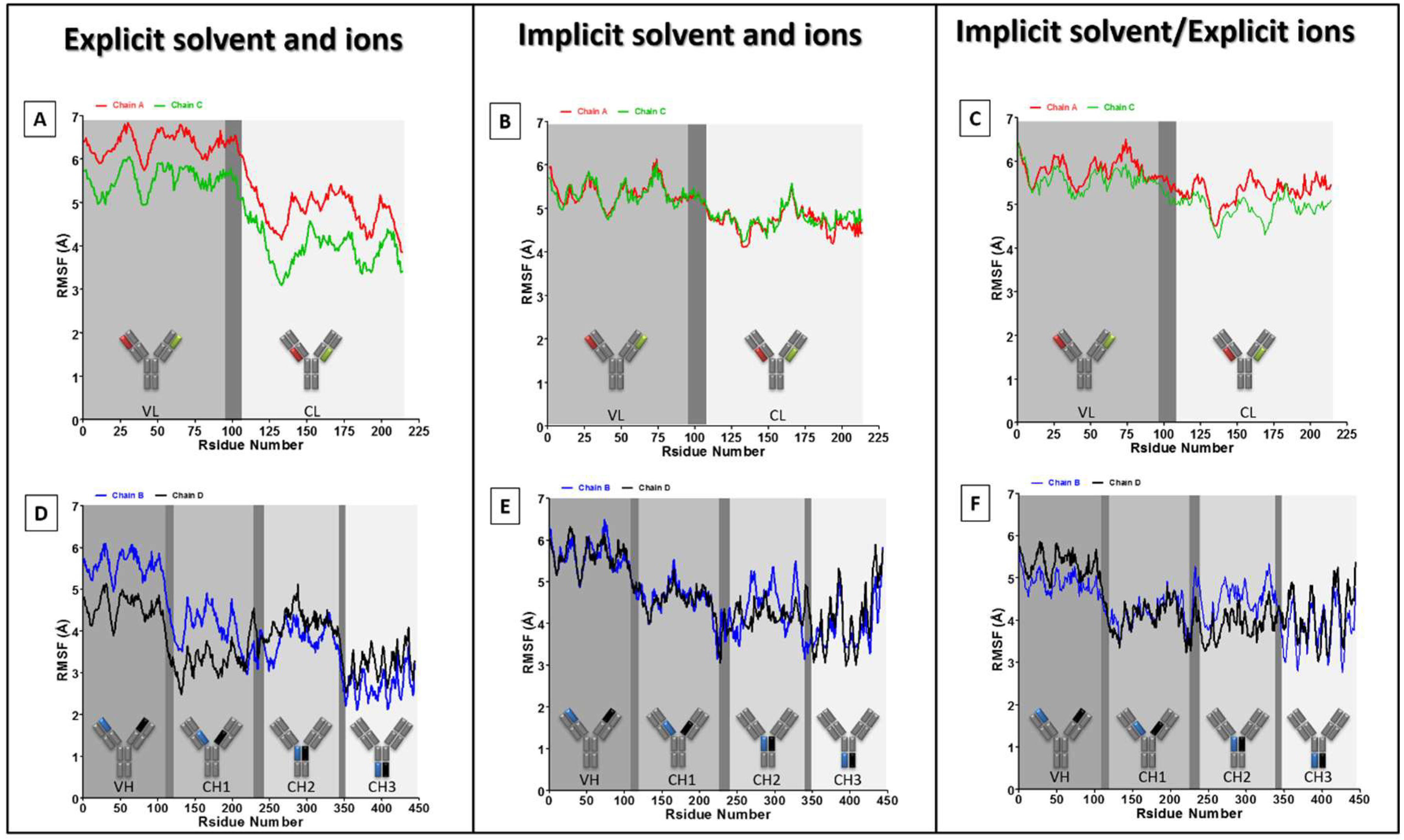
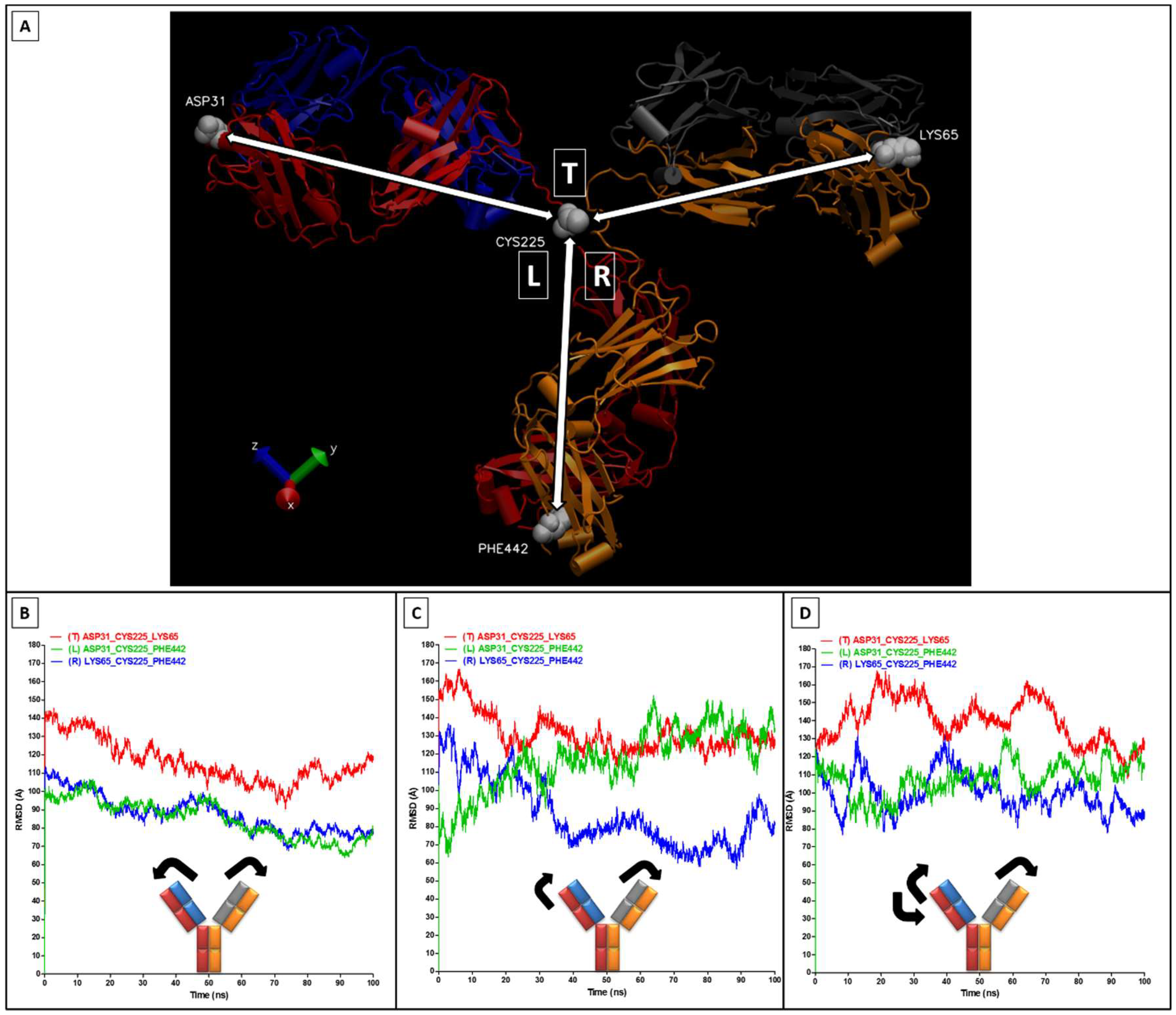
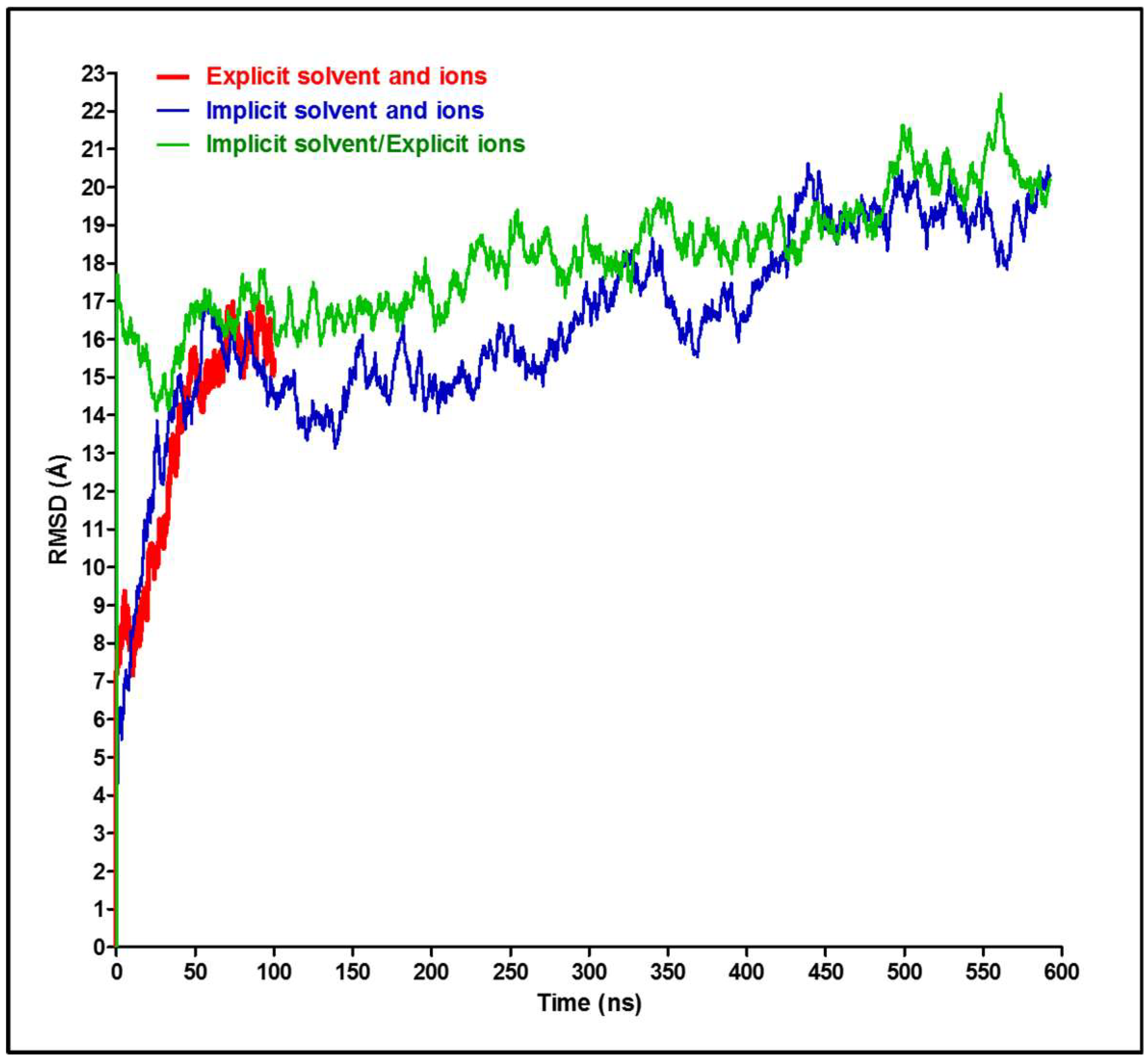
2.2. RMSD, RMSF, and Interchain Angles
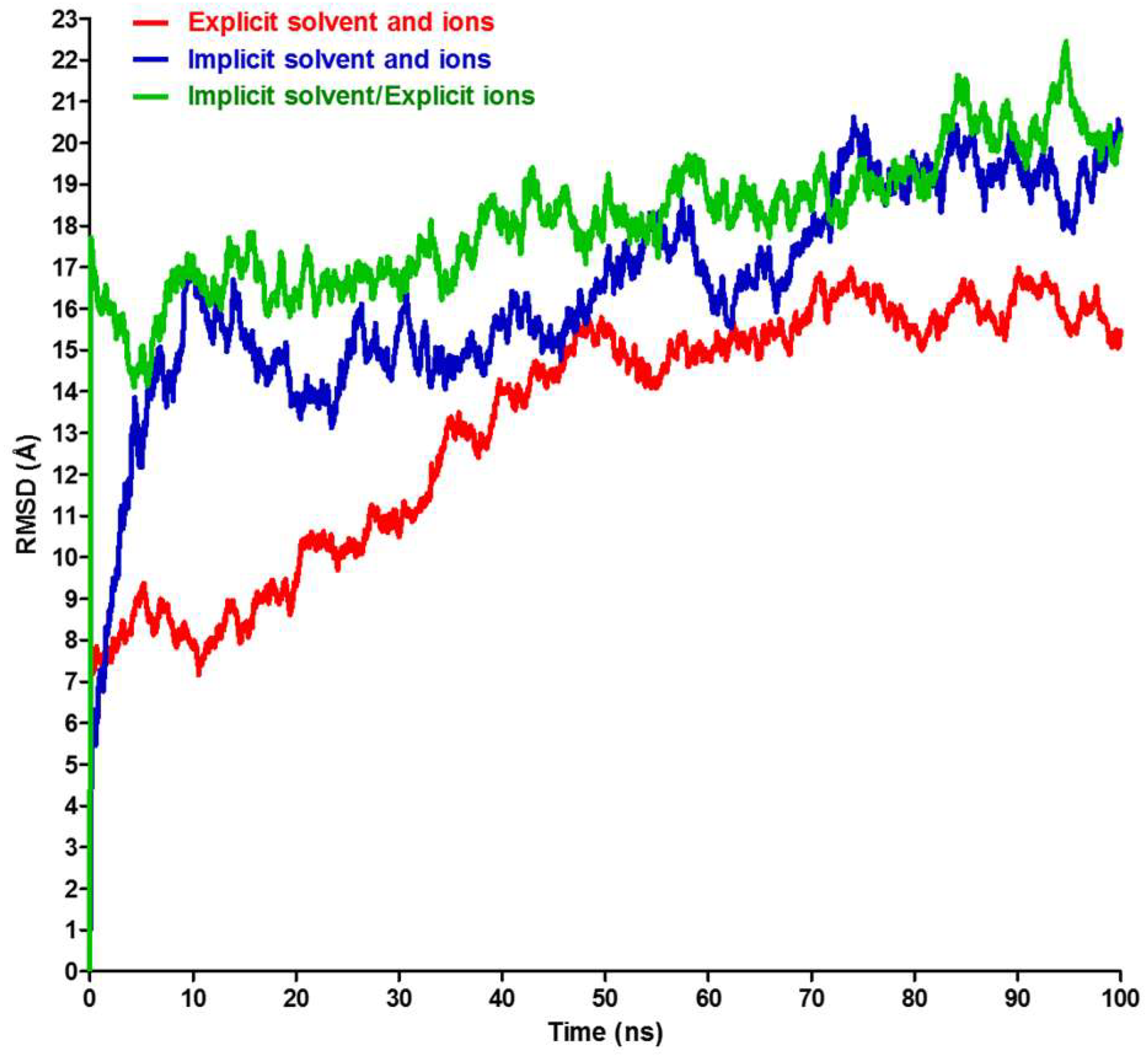
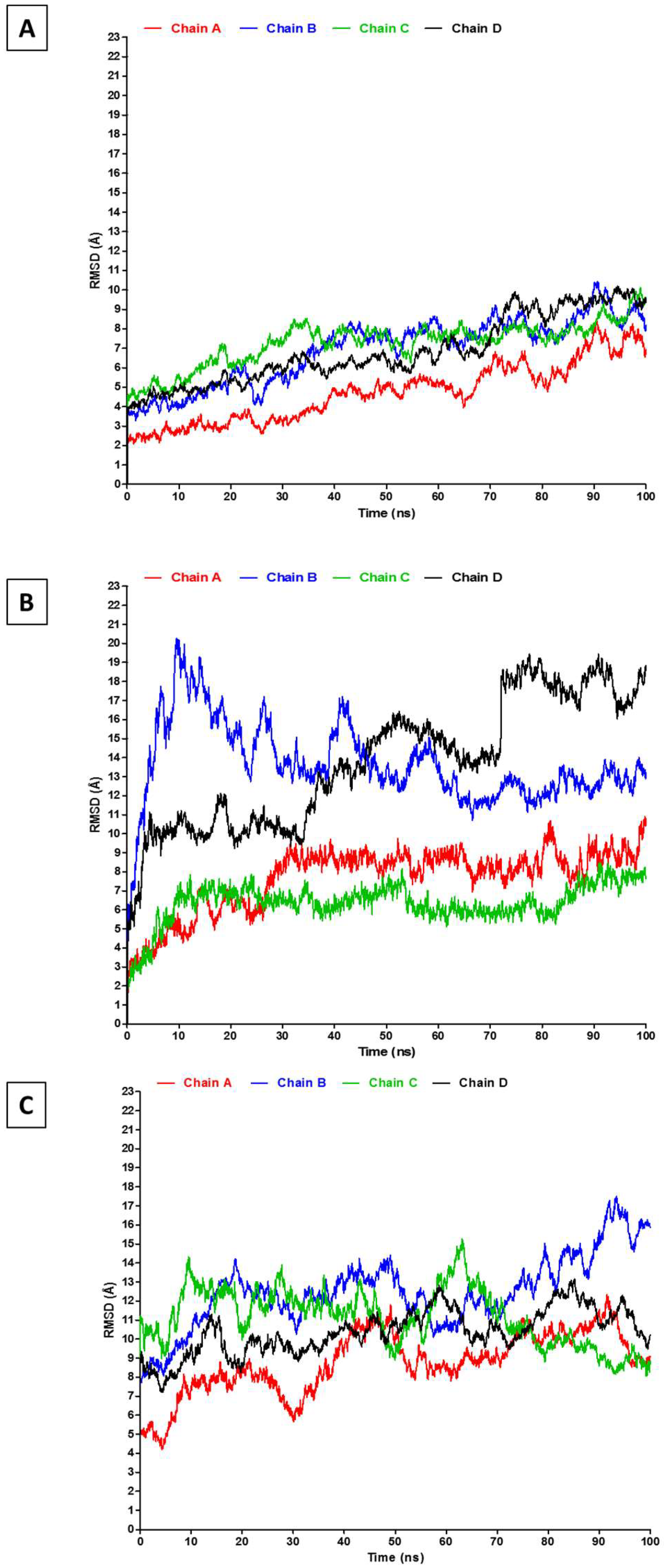
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Reichert, J.M. Antibodies to watch in 2016. mAbs 2016, 8, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Kaplon, H.; Reichert, J.M. Antibodies to watch in 2018. mAbs 2018, 10, 183–203. [Google Scholar] [CrossRef] [PubMed]
- Edelman, G.M. Dissociation of γ-globulin. J. Am. Chem. Soc. 1959, 81, 3155–3156. [Google Scholar] [CrossRef]
- Charles, A.; Janeway, J.; Travers, P.; Walport, M.; Shlomchik, M.J. The structure of a typical antibody molecule. In Immunobiology: The Immune System in Health and Disease, 5th ed.; Garland Science: New York, NY, USA, 2001. [Google Scholar]
- Maynard, J.; Georgiou, G. Antibody engineering. Annu. Rev. Biomed. Eng. 2000, 2, 339–376. [Google Scholar] [CrossRef] [PubMed]
- Irani, V.; Guy, A.J.; Andrew, D.; Beeson, J.G.; Ramsland, P.A.; Richards, J.S. Molecular properties of human IgG subclasses and their implications for designing therapeutic monoclonal antibodies against infectious diseases. Mol. Immunol. 2015, 67, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Marcon, E.; Jain, H.; Bhattacharya, A.; Guo, H.; Phanse, S.; Pu, S.; Byram, G.; Collins, B.C.; Dowdell, E.; Fenner, M.; et al. Assessment of a method to characterize antibody selectivity and specificity for use in immunoprecipitation. Nat. Methods 2015, 12, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Thiagarajan, G.; Semple, A.; James, J.K.; Cheung, J.K.; Shameem, M. A comparison of biophysical characterization techniques in predicting monoclonal antibody stability. mAbs 2016, 8, 1088–1097. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Karim, M.R.; Ahsan, M.Q.; Khalipha, A.B.R.; Chowdhury, M.R.; Saifuzzaman, M. Use of computer in drug design and drug discovery: A review. Int. J. Pharm. Life Sci. 2012, 1. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, W.; Chen, K.; Jiang, H. New technologies in computer-aided drug design: Toward target identification and new chemical entity discovery. Drug Discov. Today Technol. 2006, 3, 307–313. [Google Scholar] [CrossRef] [PubMed]
- Sliwoski, G.; Kothiwale, S.; Meiler, J.; Lowe, E.W. Computational Methods in Drug Discovery. Pharmacol. Rev. 2014, 66, 334–395. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chen, L.; Wang, Y.; Chen, S. Molecular dynamics simulations of the adsorption of DNA segments onto graphene oxide. J. Phys. Appl. Phys. 2014, 47, 505401. [Google Scholar] [CrossRef]
- Margreitter, C.; Mayrhofer, P.; Kunert, R.; Oostenbrink, C. Antibody humanization by molecular dynamics simulations—In-silico guided selection of critical backmutations. J. Mol. Recognit. 2016, 29, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Comer, J.; Chen, R.; Poblete, H.; Vergara-Jaque, A.; Riviere, J.E. Predicting Adsorption Affinities of Small Molecules on Carbon Nanotubes Using Molecular Dynamics Simulation. ACS Nano 2015, 9, 11761–11774. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Zhang, Q.; Chen, L.Y. Insights into scFv:drug binding using the molecular dynamics simulation and free energy calculation. J. Mol. Model. 2011, 17, 1919–1926. [Google Scholar] [CrossRef] [PubMed]
- Lai, B.; Hasenhindl, C.; Obinger, C.; Oostenbrink, C. Molecular Dynamics Simulation of the Crystallizable Fragment of IgG1—Insights for the Design of Fcabs. Int. J. Mol. Sci. 2014, 15, 438–455. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Kumar, S.; Buck, P.M.; Singh, S.K. Impact of deglycosylation and thermal stress on conformational stability of a full length murine IgG2a monoclonal antibody: Observations from molecular dynamics simulations. Proteins 2013, 81, 443–460. [Google Scholar] [CrossRef] [PubMed]
- Kortkhonjia, E.; Brandman, R.; Zhou, J.Z.; Voelz, V.A.; Chorny, I.; Kabakoff, B.; Patapoff, T.W.; Dill, K.A.; Swartz, T.E. Probing antibody internal dynamics with fluorescence anisotropy and molecular dynamics simulations. mAbs 2013, 5, 306–322. [Google Scholar] [CrossRef] [PubMed]
- Hua, D.P.; Huang, H.; Roy, A.; Post, C.B. Evaluating the dynamics and electrostatic interactions of folded proteins in implicit solvents. Protein Sci. Publ. Protein Soc. 2016, 25, 204–218. [Google Scholar] [CrossRef] [PubMed]
- Saunders, M.G.; Voth, G.A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Feig, M.; Brooks, C.L. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr. Opin. Struct. Biol. 2004, 14, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Anandakrishnan, R.; Drozdetski, A.; Walker, R.C.; Onufriev, A.V. Speed of Conformational Change: Comparing Explicit and Implicit Solvent Molecular Dynamics Simulations. Biophys. J. 2015, 108, 1153–1164. [Google Scholar] [CrossRef] [PubMed]
- Feig, M. Kinetics from Implicit Solvent Simulations of Biomolecules as a Function of Viscosity. J. Chem. Theory Comput. 2007, 3, 1734–1748. [Google Scholar] [CrossRef] [PubMed]
- Izadi, S.; Anandakrishnan, R.; Onufriev, A.V. Implicit Solvent Model for Million-Atom Atomistic Simulations: Insights into the Organization of 30-nm Chromatin Fiber. J. Chem. Theory Comput. 2016, 12, 5946–5959. [Google Scholar] [CrossRef] [PubMed]
- Beauchamp, K.A.; Lin, Y.-S.; Das, R.; Pande, V.S. Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements. J. Chem. Theory Comput. 2012, 8, 1409–1414. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R. Free energy landscape of protein folding in water: Explicit vs. implicit solvent. Proteins 2003, 53, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Kubiak-Ossowska, K.; Tokarczyk, K.; Jachimska, B.; Mulheran, P.A. Bovine Serum Albumin Adsorption at a Silica Surface Explored by Simulation and Experiment. J. Phys. Chem. B 2017, 121, 3975–3986. [Google Scholar] [CrossRef] [PubMed]
- Russell, B.A.; Jachimska, B.; Komorek, P.; Mulheran, P.A.; Chen, Y. Lysozyme encapsulated gold nanoclusters: Effects of cluster synthesis on natural protein characteristics. Phys. Chem. Chem. Phys. PCCP 2017, 19, 7228–7235. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Harris, L.J.; Larson, S.B.; Hasel, K.W.; McPherson, A. Refined structure of an intact IgG2a monoclonal antibody. Biochemistry (Mosc.) 1997, 36, 1581–1597. [Google Scholar] [CrossRef] [PubMed]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Sanner, M.F. Python: A programming language for software integration and development. J. Mol. Graph. Model. 1999, 17, 57–61. [Google Scholar] [PubMed]
- Carugo, O.; Pongor, S. A normalized root-mean-square distance for comparing protein three-dimensional structures. Protein Sci. Publ. Protein Soc. 2001, 10, 1470–1473. [Google Scholar] [CrossRef] [PubMed]
- Carugo, O. Statistical validation of the root-mean-square-distance, a measure of protein structural proximity. Protein Eng. Des. Sel. PEDS 2007, 20, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Brandt, J.P.; Patapoff, T.W.; Aragon, S.R. Construction, MD Simulation, and Hydrodynamic Validation of an All-Atom Model of a Monoclonal IgG Antibody. Biophys. J. 2010, 99, 905–913. [Google Scholar] [CrossRef] [PubMed]
- Matsui, H.; Hanaki, H.; Inoue, M.; Akama, H.; Nakae, T.; Sunakawa, K.; Omura, S. Development of an Immunochromatographic Strip for Simple Detection of Penicillin-Binding Protein 2′. Clin. Vaccine Immunol. 2011, 18, 248–253. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Qaraghuli, M.M.; Kubiak-Ossowska, K.; Mulheran, P.A. Thinking outside the Laboratory: Analyses of Antibody Structure and Dynamics within Different Solvent Environments in Molecular Dynamics (MD) Simulations. Antibodies 2018, 7, 21. https://doi.org/10.3390/antib7030021
Al Qaraghuli MM, Kubiak-Ossowska K, Mulheran PA. Thinking outside the Laboratory: Analyses of Antibody Structure and Dynamics within Different Solvent Environments in Molecular Dynamics (MD) Simulations. Antibodies. 2018; 7(3):21. https://doi.org/10.3390/antib7030021
Chicago/Turabian StyleAl Qaraghuli, Mohammed M., Karina Kubiak-Ossowska, and Paul A. Mulheran. 2018. "Thinking outside the Laboratory: Analyses of Antibody Structure and Dynamics within Different Solvent Environments in Molecular Dynamics (MD) Simulations" Antibodies 7, no. 3: 21. https://doi.org/10.3390/antib7030021
APA StyleAl Qaraghuli, M. M., Kubiak-Ossowska, K., & Mulheran, P. A. (2018). Thinking outside the Laboratory: Analyses of Antibody Structure and Dynamics within Different Solvent Environments in Molecular Dynamics (MD) Simulations. Antibodies, 7(3), 21. https://doi.org/10.3390/antib7030021





