The Moderate Operation Scales of Apples Based on Output, Profit, and Unit Production Costs in the Shaanxi Province of China
Abstract
1. Introduction
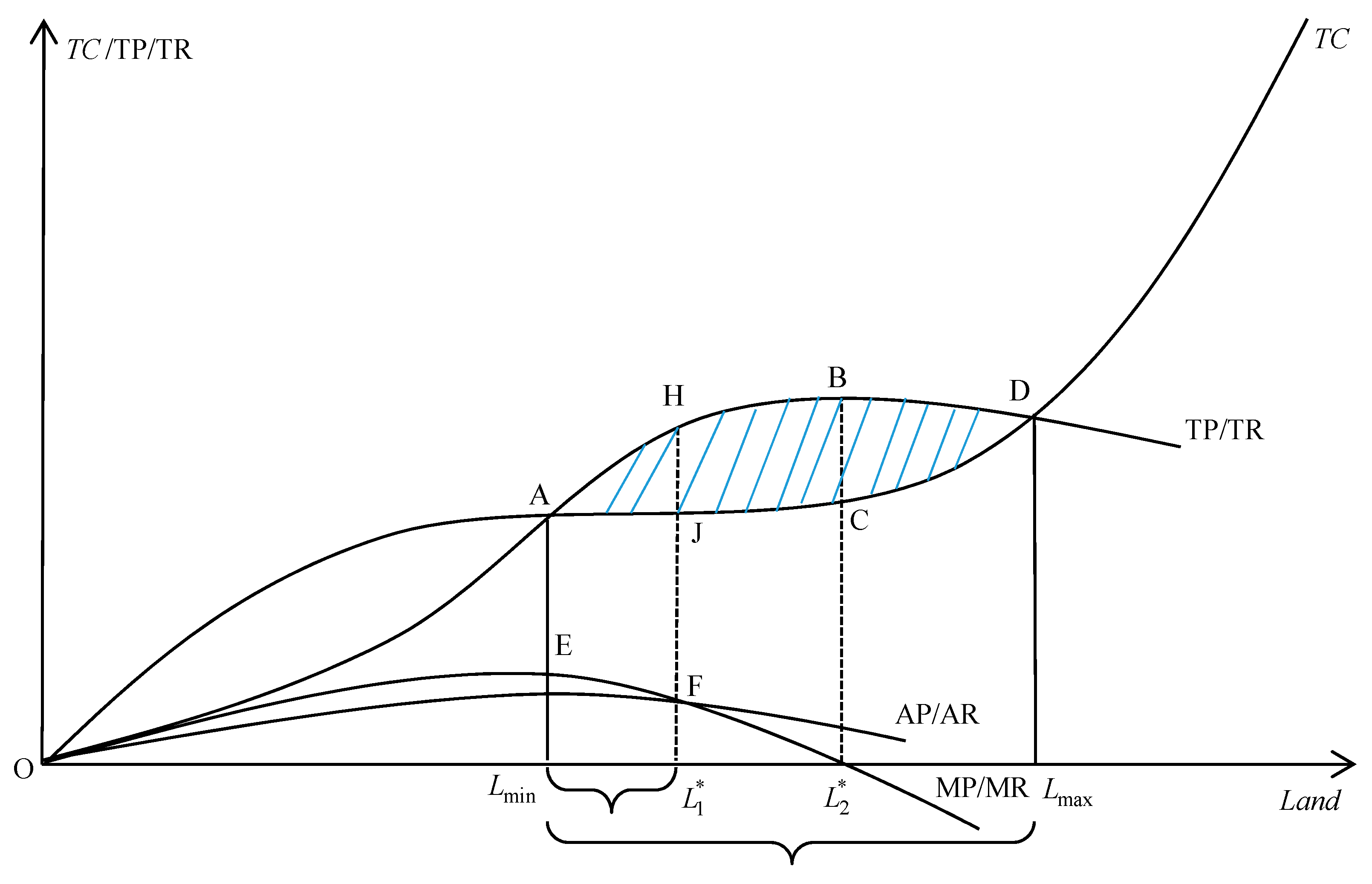
2. The Moderate Operation Scale in Theory
3. Study Area and Methods
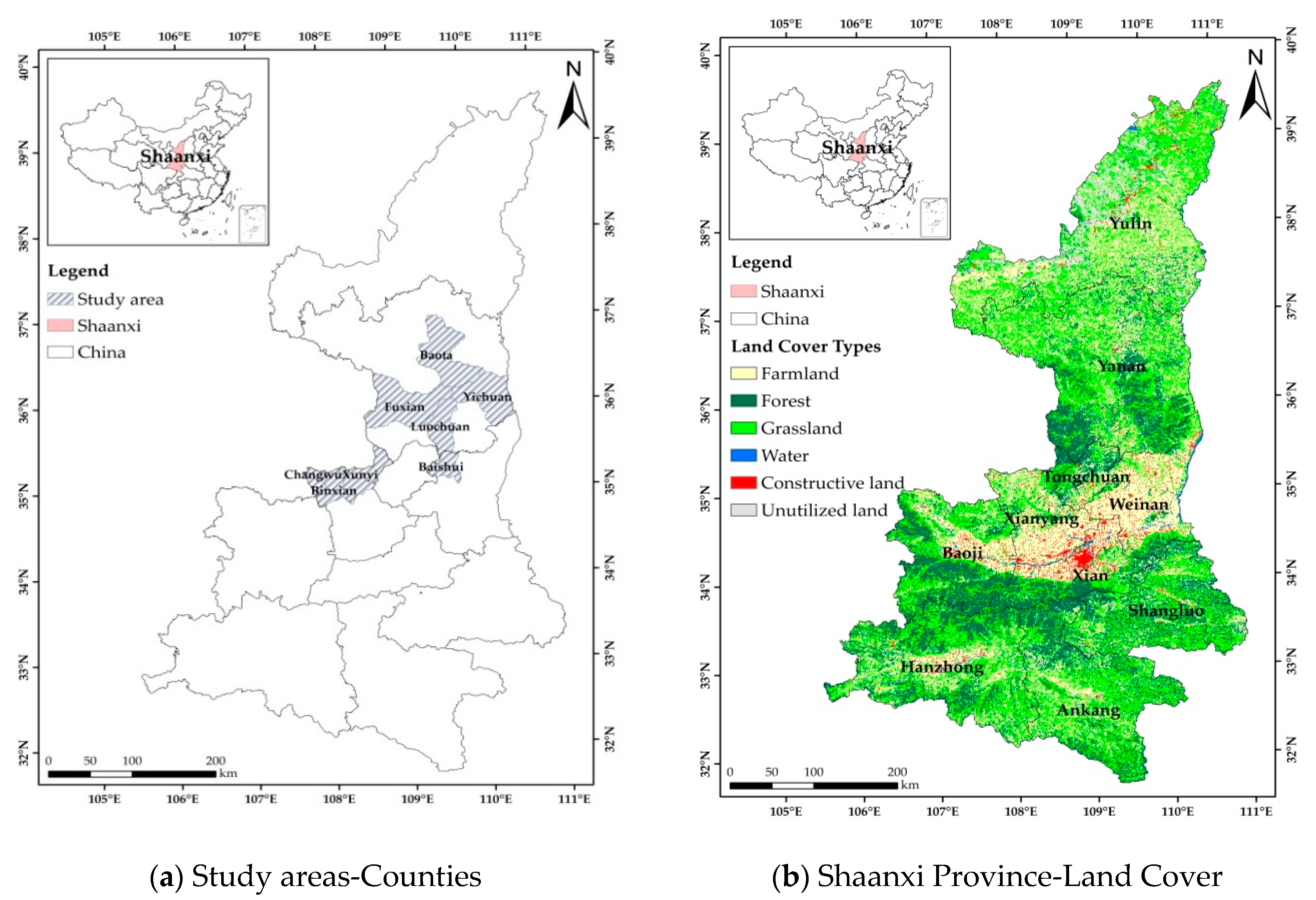
3.1. Description of Study Area
- Shaanxi is one of the most important apple planting regions in China, where the area and the quantity of apple production are the biggest.
- The diversity of agro-climatic in Shaanxi is the epitome of the distribution of agroclimatic zone in China.
- The continious expanding of apple planting area in Shaanxi province leading to a more obvious contradiction on how to develop moderate operation scale (The apple planting area was 601,518 ha in 2010 and increased to 695,159 ha in 2015).
- The author’s local knowledge.
3.2. Sampling Design, Data Collection, and Statistical Description
3.3. Methods of Data Analsis
3.3.1. Model
3.3.2. Model Selection and Estimation Method
4. Results
4.1. Results of the Input-Output Models
4.2. Results of the Net Profit Model
4.3. Results of Unit Production Cost Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Law of the People’s Republic of China on Land Contract in Rural Areas (Order of the President No.73) (Adopted on 29 August 2002), Gov.Cn Website (Chinese Government’s Official Web Portal). Available online: http://english.gov.cn/2005-10/09/content_179389 (accessed on 18 May 2007).
- Lin, J.Y. Rural Reforms and Agricultural Growth in China. Am. Econ. Rev. 1992, 82, 34–51. [Google Scholar]
- Cao, D.B. Moderate Scale: Towards a Steady Growth Agricultural Model. China Rural Obs. 2013, 2, 29–36. [Google Scholar]
- Chen, X.W. It is Urgent to Construct a New Agricultural Management System. Seek Truth 2013, 22, 38–41. [Google Scholar]
- Zhang, H.Y.; Wang, L.J.; Li, Y.B.; Li, W.Y. Several Issues Needing Attention in Deepening the Reform of Rural Land System. China Party Gov. Cadres Forum 2014, 6, 13–17. [Google Scholar]
- Chen, Y.F.; Sun, W.L.; Xue, G.X. Literature review and theoretical thinking on the appropriate scale of grain management. Land Sci. China 2015, 29, 8–15. [Google Scholar]
- Zhang, X.; Zhao, D.Y.; Zhao, S.H. Study on Moderate Operation Scale in Hebei Province. Bus. Age 2010, 7, 124–126. [Google Scholar]
- Ma, J.; Ma, Y. Discussion on the moderate operation scale mode of rural land in Shanghai suburbs. Reg. Res. Dev. 2010, 29, 119–123. [Google Scholar]
- Qian, K.M.; Peng, T.J. Economic analysis on the moderate operation scale of grain production in China. Agric. Econ. Issues 2014, 35, 4–7, 110. [Google Scholar]
- Zhang, C.Z. Study on the Determination of the Moderate Operation Scale: Taking Henan Province as an Example. Agric. Econ. Issues 2015, 36, 57–63, 111. [Google Scholar]
- Wan, G.H. A new method for measuring technological progress and scale effect. Agric. Technol. Econ. 1996, 2, 22–25, 53. [Google Scholar]
- Luo, B.L. Efficiency Decision of Agricultural Land Management Scale. China Rural Obs. 2000, 5, 18–24, 80. [Google Scholar]
- Gao, M.T.; Zhang, Y. Small farmers are more efficient? Empirical evidence from rural areas in eight provinces. Stat. Res. 2006, 8, 21–26. [Google Scholar]
- Li, G.C.; Feng, Z.K. China’s Agricultural Total Factor Productivity Growth: Technology Promotion or Efficiency Driven: A Comparative Study of Industries Based on Stochastic Frontier Production Function. Agric. Technol. Econ. 2010, 5, 4–14. [Google Scholar]
- Kimhi, A. Plot Size and Maize Productivity in Zambia: Is There an Inverse Relationship? Agric. Econ. 2006, 35, 1–9. [Google Scholar] [CrossRef]
- Assuncao, J.J.; Bradio, L.H. Testing Household-specific Explanations for the Inverse Productivity Relationship. Am. J. Agric. Econ. 2007, 89, 980–990. [Google Scholar] [CrossRef]
- Wang, J.J.; Chen, P.Y.; Chen, F.B. A comparative study on the management behavior and economic benefits of farmers of different land scales: Based on the survey data of rice farmers in the Yangtze River Basin. Surv. World 2012, 5, 34–37. [Google Scholar]
- Xu, Q.; Yin, R.L.; Zhang, H. Scale Economy, Scale Remuneration and Agricultural Moderate Scale Management: An Empirical Study Based on China’s Grain Production. Econ. Res. 2011, 46, 59–71, 94. [Google Scholar]
- Guo, J.P. Expanding the scale of land management and improving agricultural efficiency go hand in hand. Theor. Explor. 2003, 3, 11–12. [Google Scholar]
- Song, W.; Chen, B.M.; Chen, X.W. Study on the grain production function of farmers in economically developed areas along the southeast coast: A case study of Changshu City of Jiangsu Province. Resour. Sci. 2007, 6, 206–211. [Google Scholar]
- Fan, H.Z.; Zhou, Q.L. The relationship between farmer’s planting area and land productivity: Based on the survey data of farmers in seven counties (cities) in central and Western China. Popul. Resour. Environ. China 2014, 24, 38–45. [Google Scholar]
- Ni, G.H.; Cai, F. How large scale of farmland management do farmers need? Study on decision maps of farmland management scale. Econ. Res. 2015, 50, 159–171. [Google Scholar]
- Xin, L.J.; Li, X.B.; Zhu, H.Y.; Liu, X.J.; Tan, M.H.; Tian, Y.J. The relationship between land scale and productivity and the confirmation of their explanations: Case study of Jilin Province. Geogr. Res. 2009, 28, 1276–1284. [Google Scholar]
- Wang, Y.H.; Li, X.B.; Xin, L.J.; Tan, M.H.; Li, W. The impact of the scale of farmland management on agricultural labor productivity and its regional differences. J. Nat. Resour. 2017, 32, 539–552. [Google Scholar]
- Tan, S.; Heerink, N.; Kruseman, G.; Qu, F. Do Fragmented Landholdings Have Higher Production Costs? Evidence from Rice Farmers in Northeastern Jiangxi Province, P.R. China. China Econ. Rev. 2008, 19, 347–358. [Google Scholar] [CrossRef]
- Song, G.; Zou, C.H.; Chen, C.C. Study on Moderate Scale Management of Land in Northeast China’s Main Grain-producing Areas Based on Double Objectives. Land Sci. China 2016, 30, 38–46. [Google Scholar]
- Wang, M.M.; Liu, Y.; Chen, S. Moderate Scale Management of Agriculture from the Perspective of Scale Remuneration, Output Profit and Production Cost: Based on the Study of 354 Rice Growers in Jianghan Plain. Agric. Technol. Econ. 2017, 4, 83–94. [Google Scholar]
- Li, W.M.; Luo, D.; Chen, J.; Xie, J. Moderate Scale Management of Agriculture: Scale Benefit, Output Level and Production Cost: Based on the Survey Data of 1552 Rice Growers. Rural Econ. China 2015, 3, 4–17, 43. [Google Scholar]
- Zhang, X.H.; Zhou, Y.H.; Yan, B.J. Farmland Management Scale and Production Cost of Rice: A case study of Jiangsu case. Agric. Econ. Issues 2017, 38, 48–55. [Google Scholar]
- Zhang, H.L.; Wu, C.C. Agricultural Scale Management Conditions and Appropriate Scale Determination in Jiangsu and Zhejiang Provinces. Econ. Geogr. 1998, 1, 85–90. [Google Scholar]
- Zheng, S.F. Study on the Moderation of Land Scale Management. Agric. Econ. Issues 1998, 11, 9–13. [Google Scholar]
- Qi, C. Empirical Analysis of Rural Labor Transfer and Moderate Scale Management of Land: A case study of Xinyang City, Henan Province. Agric. Econ. Issues 2008, 4, 38–41. [Google Scholar]
- Zhou, C. On China’s urban state-owned land leasing system. Manag. World 1995, 1, 76–83. [Google Scholar]
- Wan, B.R. Meeting new opportunities and new challenges. Agric. Econ. Issues 2002, 1, 3–7. [Google Scholar]
- Qu, X.B. Analysis on the differences of production technology efficiency of different scale farmers and its influencing factors based on the random frontier production function and micro data of farmers. J. Nanjing Agric. Univ. (Soc. Sci. Ed.) 2009, 9, 27–35. [Google Scholar]
- Luo, D.; Li, W.M.; Chen, J. Moderate operation scale of grain production: A two-dimensional perspective of output and efficiency. Manag. World 2017, 1, 78–88. [Google Scholar]
- Guo, G.C.; Ding, C.X. Quantitative research on the impact of land fragmentation on the returns to grain production scale: Based on the empirical data of Yancheng and Xuzhou in Jiangsu Province. J. Nat. Resour. 2016, 31, 202–214. [Google Scholar]
- Bizimana, C.; Nieuwoudt, W.L.; Ferrer, S.R.D. Farm size, land fragmentation and economic efficiency in southern Rwanda. Agrekon 2004, 43, 244–262. [Google Scholar] [CrossRef]
- Wan, G.H.; Cheng, E. Effects of Land Fragmentation and Returns to Scale in the Chinese Farming Sector. Appl. Econ. 2001, 33, 183–194. [Google Scholar] [CrossRef]
- Qian, G.X.; Li, N.H. Benefit analysis of farmers with different grain production and operation scales. Agric. Technol. Econ. 2005, 4, 60–63. [Google Scholar]
- Lu, T.; Ji, Y.Q.; Yi, Z.Y. Land-scale economy in rice production: Based on the investigation and analysis of Jintan, Changzhou, Jiangsu. Agric. Technol. Econ. 2014, 2, 68–75. [Google Scholar]
- Latruffe, L.; Piet, L. Does land fragmentation affect farm performance? A case study from Brittany, France. Agric. Syst. 2014, 129, 68–80. [Google Scholar] [CrossRef]
| 1 | Individuals (or companies) have the right to use land under land-use contracts which do not entail actual ownership. In rural China, arable land owned by rural collectives was distributed amongst individual farmers through a system of land-use (not land ownership) contracts under the Household Responsibility System in the early 1980s. Source: https://www.refworld.org/pdfid/4b6fe1840.pdf. |
| 2 | Net profit is equal to total income minus total cost. In this paper, the costs of family labor and own land were excluded when calculating the net profit of apple production. |
| 3 | According to the National Compilation of Cost and Benefits of Agricultural Products Data, production costs can be divided into three categories: material and service costs, labor costs, and land costs. The material costs contain the cost of inputs such as fertilizers and pesticides. The service costs contain irrigation fees and machinery maintenance fees. The labor costs contain the costs of family labor and hired labor. The land costs contain land rent and the cost of owned land. |
| 4 | The constraints of Wald joint hypothesis test are as follows:; . |
| Major Variables | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|
| Output of apple production (kg per household) | 11,745.46 | 17,552.97 | 100.00 | 70,000.00 |
| Net profit of apple production (¥ per household) | 37,154.84 | 50,732.12 | −70,360.00 | 665,786.00 |
| Total cost of apple production (¥ per household) | 27,532.70 | 20,485.40 | 1,230.00 | 191,360.00 |
| Labor input (working days per household) | 226.74 | 244.19 | 26.50 | 5,442.00 |
| Capital input (¥ per household) | 27,532.74 | 20,500.95 | 1,230.00 | 191,360.00 |
| Operating scale (ha per household) | 0.48 | 4.77 | 0.03 | 2.33 |
| Land fragmentation (plots per household) | 2.75 | 1.63 | 1 | 16 |
| Gender of household head (dummy) | 0.98 | 0.13 | 0 | 1 |
| Age of household head (year) | 50.86 | 8.80 | 24 | 75 |
| Educational level of household head (year) | 7.92 | 3.04 | 0 | 15 |
| Number of family labors (people per household) | 2.13 | 0.68 | 1 | 7 |
| C-D Function or Translog Function | ||||
|---|---|---|---|---|
| Null Hypothesis H0: C-D Function (No High-Order Term) | ||||
| F-Value | DF | Adjoint Probability | ||
| 13.18 *** | (3; 654) | 0.0000 | ||
| Logarithmic or Linear Model; Neutral Effect of Land Fragmentation with F Test | ||||
| Efficiency Function | Adjusted R2 | Null Hypothesis H0: Neutral Effect of Land Fragmentation | ||
| F-Value | DF | Adjoint Probability | ||
| Logarithmic | 0.6258 | 12.99 *** | (3; 653) | 0.0000 |
| Variable | Model I | Model II | ||
|---|---|---|---|---|
| Coefficient | Robust Standard Error | Coefficient | Robust Standard Error | |
| Labor | 4.761 *** | 1.313 | 4.791 *** | 1.302 |
| Land | −3.022 ** | 1.455 | −2.931 ** | 1.433 |
| Capital | 1.420 | 1.666 | 1.400 | 1.655 |
| Labor Square | −0.141 *** | 0.043 | −0.142 *** | 0.043 |
| Land Square | −0.191 * | 0.103 | −0.202 ** | 0.093 |
| Capital Square | 0.019 | 0.116 | 0.021 | 0.116 |
| Labor × Capital | −0.336 ** | 0.149 | −0.338 ** | 0.148 |
| Labor × Land | 0.378 ** | 0.161 | 0.377 ** | 0.157 |
| Land × Capital | 0.187 | 0.180 | 0.186 | 0.178 |
| Land fragmentation | 0.357 | 1.059 | 0.323 | 1.044 |
| Land fragmentation × Labor | −0.130 | 0.131 | −0.126 | 0.128 |
| Land fragmentation × Land | −0.083 | 0.111 | −0.075 | 0.108 |
| Land fragmentation × Capital | 0.058 | 0.131 | 0.058 | 0.129 |
| Age | −0.023 | 0.020 | −0.024 | 0.020 |
| Age Square | 0.000 | 0.000 | 0.000 | 0.000 |
| Educational years | −0.009 | 0.006 | −0.008 | 0.006 |
| Planting years | 0.014 *** | 0.004 | 0.014 *** | 0.004 |
| Land transfer | −0.046 | 0.05 | −0.045 | 0.050 |
| 0.20–0.53 ha | 0.065 | 0.098 | — | — |
| 0.53–0.87 ha | 0.085 | 0.148 | — | — |
| 0.87–1.53 ha | 0.119 | 0.194 | — | — |
| Over 1.53 ha | 0.015 | 0.339 | — | — |
| Xianyang | −0.202 *** | 0.055 | −0.203 *** | 0.055 |
| Yan’an | −0.112 ** | 0.056 | −0.114 ** | 0.056 |
| Constant | −10.094 | 6.582 | −10.086 | 6.536 |
| Adjusted R2 | 0.6932 | 0.6927 | ||
| White Heteroscedasticity Test | 286.66 * | 233.63 *** | ||
| Samples | 661 | 661 | ||
| Apple Production | Output Elasticity of Factors | Scale Return Coefficients | H0: Constant Returns to Scale | |||
|---|---|---|---|---|---|---|
| Labor | Land | Capital | F-Value | Significance | ||
| Model I | 1.223 | 0.414 | 0.232 | 1.869 | 2.48 * | 0.0845 |
| Model II | 1.231 | 0.478 | 0.220 | 1.929 | 3.10 ** | 0.0457 |
| Variable | Net Profit Model I | Net Profit Model II | ||
|---|---|---|---|---|
| Coefficient | Robust Standard Error | Coefficient | Robust Standard Error | |
| Labor | 1.172 | 10.327 | −0.385 | 10.309 |
| Land | −45.198 *** | 11.020 | −48.336 *** | 10.848 |
| Capital | 58.071 *** | 14.038 | 59.806 *** | 13.986 |
| Labor Square | −0.685 | 0.517 | −0.659 | 0.514 |
| Land Square | −4.651 *** | 0.999 | −3.700 *** | 0.820 |
| Capital Square | −3.673 *** | 1.026 | −3.804 *** | 1.023 |
| Labor × Capital | 0.732 | 1.383 | 0.865 | 1.381 |
| Labor × Land | 2.233 | 1.43 | 2.361 * | 1.423 |
| Land × Capital | 4.820 *** | 1.504 | 4.856 *** | 1.503 |
| Land fragmentation | 1.708 | 8.347 | 2.340 | 8.326 |
| Land fragmentation × Labor | −1.889 | 1.327 | −2.12 | 1.316 |
| Land fragmentation × Land | 1.238 | 1.002 | 0.923 | 0.978 |
| Land fragmentation × Capital | 0.699 | 1.227 | 0.801 | 1.222 |
| Age | −0.288 | 0.223 | −0.289 | 0.222 |
| Age Square | 0.002 | 0.002 | 0.002 | 0.002 |
| Educational years | −0.095 | 0.079 | −0.101 | 0.079 |
| Planting years | 0.087 ** | 0.038 | 0.088 ** | 0.038 |
| Land transfer | −0.787 | 0.647 | −0.896 | 0.643 |
| 0.20–0.53 ha | −0.386 | 1.017 | — | — |
| 0.53–0.87 ha | 0.825 | 1.657 | — | — |
| 0.87–1.53 ha | 1.022 | 2.416 | — | — |
| Over 1.53 ha | 6.411 | 4.130 | — | — |
| Xianyang | −1.213 | 0.782 | −1.209 | 0.780 |
| Yan’an | −0.839 | 0.759 | −0.888 | 0.759 |
| Constant | −233.551 *** | 52.159 | −236.586 *** | 51.994 |
| Adjusted R2 | 0.1335 | 0.1321 | ||
| White Heteroscedasticity Test | 270.68 | 200.04 | ||
| Samples | 661 | 661 | ||
| Variable | Unit Total Cost | Unit Chemical Fertilizer Cost | Unit Organic Fertilizer Cost | Unit Pesticide Cost | Unit Fruit Bags Cost | Unit Agricultural Film Cost | Unit Labor Cost |
|---|---|---|---|---|---|---|---|
| Number of family labors | 0.087 ** (0.043) | 0.134 (0.112) | 0.025 (0.236) | −0.001 (0.047) | −0.080 (0.056) | −0.342 (0.239) | 0.121 *** (0.044) |
| Operation scale | −0.012 (0.014) | −0.140 ** (0.054) | 0.206 ** (0.083) | −0.045** (0.018) | 0.009 (0.027) | 0.185 * (0.095) | −0.022 (0.014) |
| Land fragmentation | −0.013 (0.025) | 0.105 ** (0.053) | 0.007 (0.096) | −0.063 *** (0.017) | 0.018 (0.026) | 0.051 (0.079) | 0.001 (0.018) |
| Age | 0.013 (0.025) | 0.009 (0.070) | 0.072 (0.144) | 0.007 (0.027v | 0.033 (0.035) | −0.024 (0.130) | 0.008 (0.027) |
| Age Square | −0.000 (0.000) | −0.000 (0.001) | −0.001 (0.001) | −0.000 (0.000) | −0.000 (0.000) | −0.000 (0.001) | −0.000 (0.000) |
| Educational years | 0.010 (0.006) | 0.023 (0.025) | 0.142** (0.055) | 0.012 (0.008) | 0.004 (0.012) | −0.005 (0.055) | 0.009 (0.007) |
| Planting years | −0.017 *** (0.004) | −0.020 * (0.012) | 0.009 (0.024) | −0.021 *** (0.005) | 0.004 (0.006) | 0.071 *** (0.027) | −0.014 *** (0.004) |
| Land transfer | −0.003 (0.051) | 0.178 (0.205) | 0.681 ** (0.281v | 0.006 (0.066) | −0.161 (0.102) | −0.232 (0.353) | −0.085 (0.053) |
| 0.20–0.53 ha | −0.095 (0.078) | 0.262 (0.257) | −0.565 (0.528) | −0.122 (0.095) | −0.071 (0.127) | −0.595 (0.555) | −0.135 * (0.080) |
| 0.53–0.87 ha | −0.091 (0.137) | 0.757 (0.473) | −0.981 (0.828) | 0.008 (0.172) | 0.058 (0.235) | −0.970 (0.882) | −0.129 (0.138) |
| 0.87–1.53 ha | −0.050 (0.202) | 1.757 ** (0.777) | −2.353 * (1.292) | 0.217 (0.265) | −0.004 (0.386) | −1.653 (1.321) | −0.061 (0.207) |
| Over 1.53 ha | 0.044 (0.373) | −2.418 (1.486) | −3.267 (2.110) | 0.533 (0.506) | −0.172 (0.738) | −4.848 * (2.492) | 0.170 (0.407) |
| Xianyang | 0.144 *** (0.055) | 0.381 (0.249) | 0.291 (0.438) | 0.071 (0.066) | 0.060 (0.123) | −1.575 *** (0.430) | 0.107 * (0.063) |
| Yan’an | 0.224 *** (0.056) | −0.206 (0.245) | −0.033 (0.428) | 0.214 *** (0.071) | −0.044 (0.121) | −0.231 (0.354) | 0.253 *** (0.064) |
| Constant | 1.278 ** (0.610) | −0.564 (1.782) | −5.936 * (3.564) | −0.986 (0.681) | −1.976 ** (0.885) | −3.970 (3.246) | 0.497 (0.645) |
| Adjusted R2 | 0.0912 | 0.1411 | 0.0466 | 0.1427 | 0.0038 | 0.0916 | 0.1066 |
| White Heteroscedasticity Test | 152.58 *** | 88.87 | 143.63 *** | 134.67 ** | 96.58 | 172.54 *** | 136.16 ** |
| Samples | 661 | 661 | 661 | 661 | 661 | 661 | 661 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Chang, Q.; Shao, L.; Huo, X. The Moderate Operation Scales of Apples Based on Output, Profit, and Unit Production Costs in the Shaanxi Province of China. Land 2020, 9, 25. https://doi.org/10.3390/land9010025
Zhang C, Chang Q, Shao L, Huo X. The Moderate Operation Scales of Apples Based on Output, Profit, and Unit Production Costs in the Shaanxi Province of China. Land. 2020; 9(1):25. https://doi.org/10.3390/land9010025
Chicago/Turabian StyleZhang, Congying, Qian Chang, Liqun Shao, and Xuexi Huo. 2020. "The Moderate Operation Scales of Apples Based on Output, Profit, and Unit Production Costs in the Shaanxi Province of China" Land 9, no. 1: 25. https://doi.org/10.3390/land9010025
APA StyleZhang, C., Chang, Q., Shao, L., & Huo, X. (2020). The Moderate Operation Scales of Apples Based on Output, Profit, and Unit Production Costs in the Shaanxi Province of China. Land, 9(1), 25. https://doi.org/10.3390/land9010025





