Analysis of High Temporal Resolution Land Use/Land Cover Trajectories
Abstract
:1. Introduction
2. Life Course Trajectories Analysis and Its Potential Application to LUCC Trajectories
- The distinct observed states present in a set of sequences,
- The within-sequence state distribution,
- The timing (the date at which each state occurs),
- The duration (the consecutive and total time spent in the different successive states) and,
- The sequencing (the order of the different successive states).
3. Study Area
4. Materials
5. Methods
5.1. Preprocessing
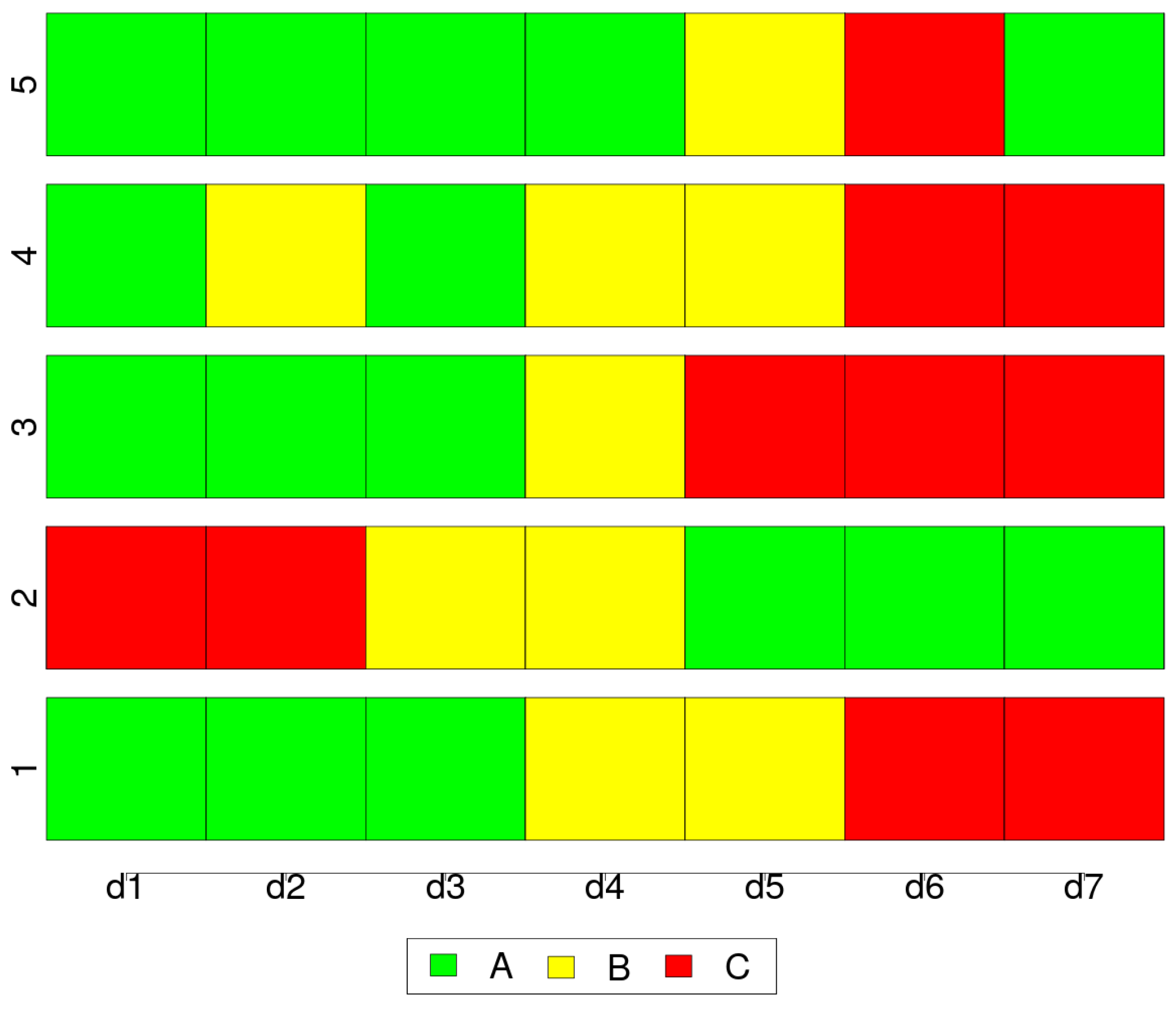
5.2. Land Use/Cover Sequence Analysis
5.3. Pairwise Dissimilarities between Sequences
- The first approach consists in determining the costs on a theoretical base to evaluate the similarity of two states. For example, in career trajectory, Senior Manager is closer to Manager than to Employee and in order to reflect this hierarchy, the cost of replacing Senior Manager with Employee can be set higher than the cost of substitution between Senior Manager and Manager [30]. In LUCC, a similar hierarchy between categories can be imagined, for instance based on vegetation succession processes.
- Another approach is based on state attributes on which closeness between states is evaluated. For instance, for career trajectories, the qualification required, level of responsibility or the degree of precariousness can be taken into account [30]. In LUCC a similar approach could be envisaged taking into account ecological value associated with each land category.
- A third strategy is to derive the cost from the data. For instance, a common way to obtain the substitution costs is assigning larger costs to substitution between states when the transitions rates are low, and inversely, assigning a smaller cost when frequent transitions are observed. Another approach considers that two states are close when they are frequently followed by a common state.
5.4. Assessment of the Effect of Covariates
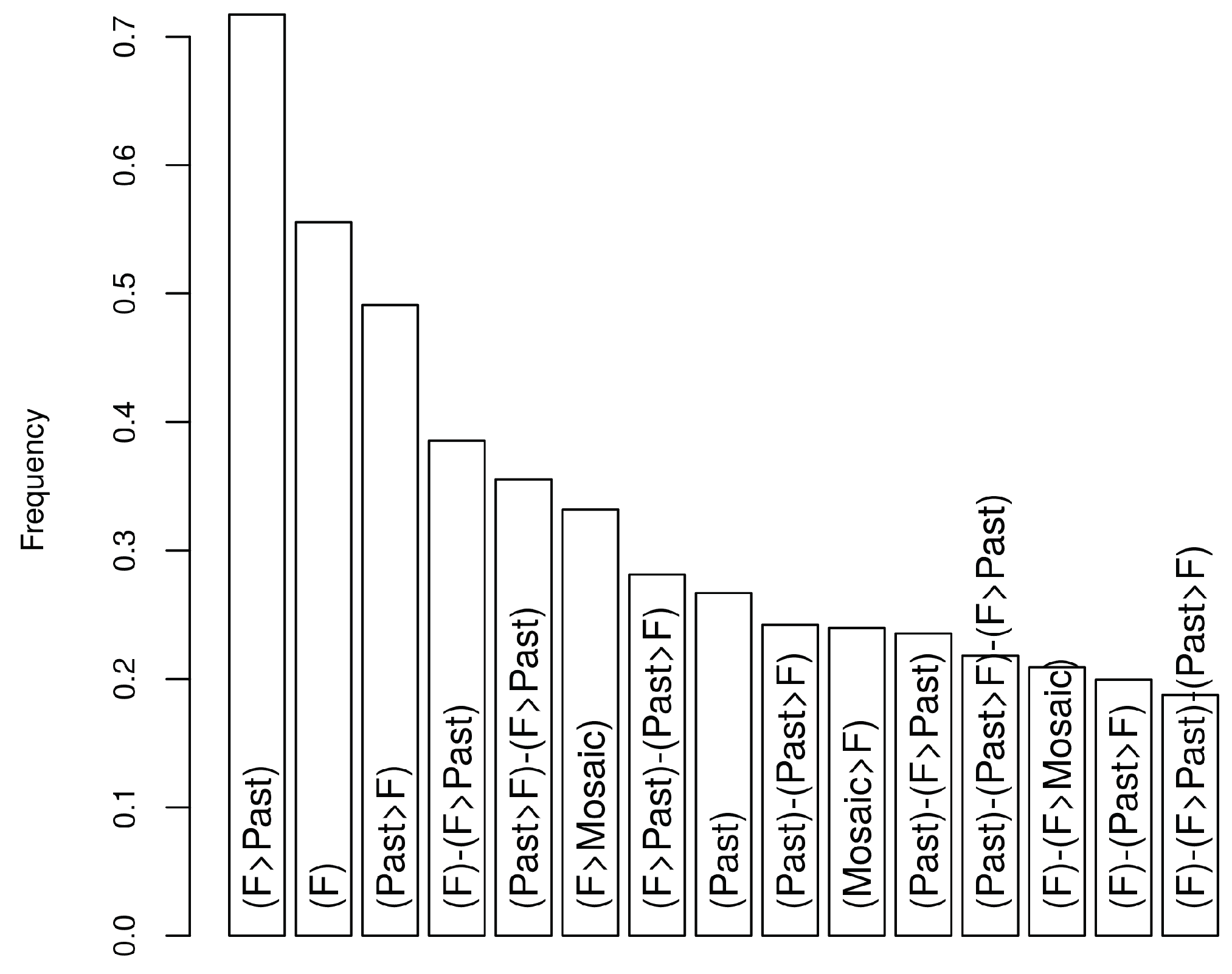
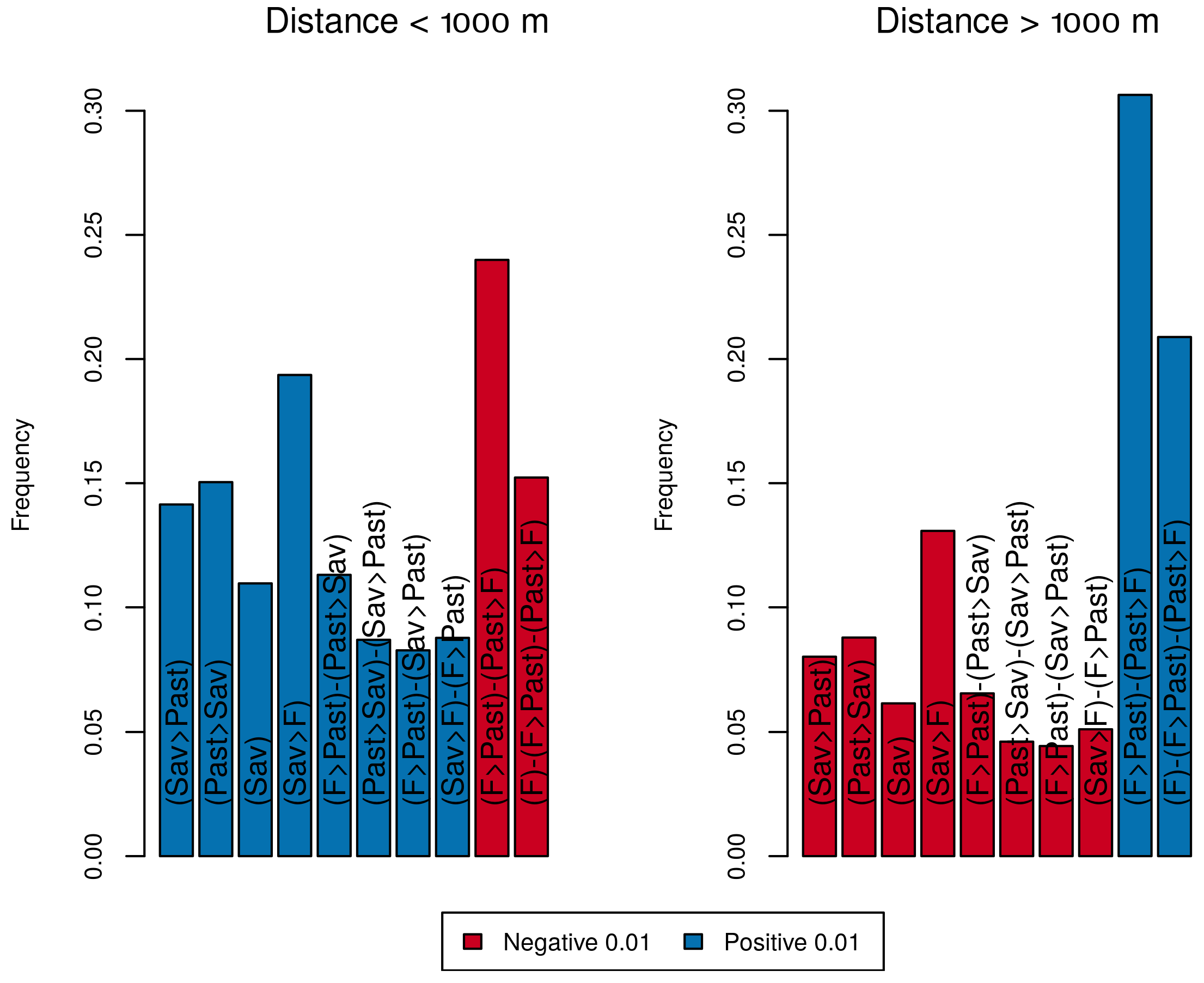
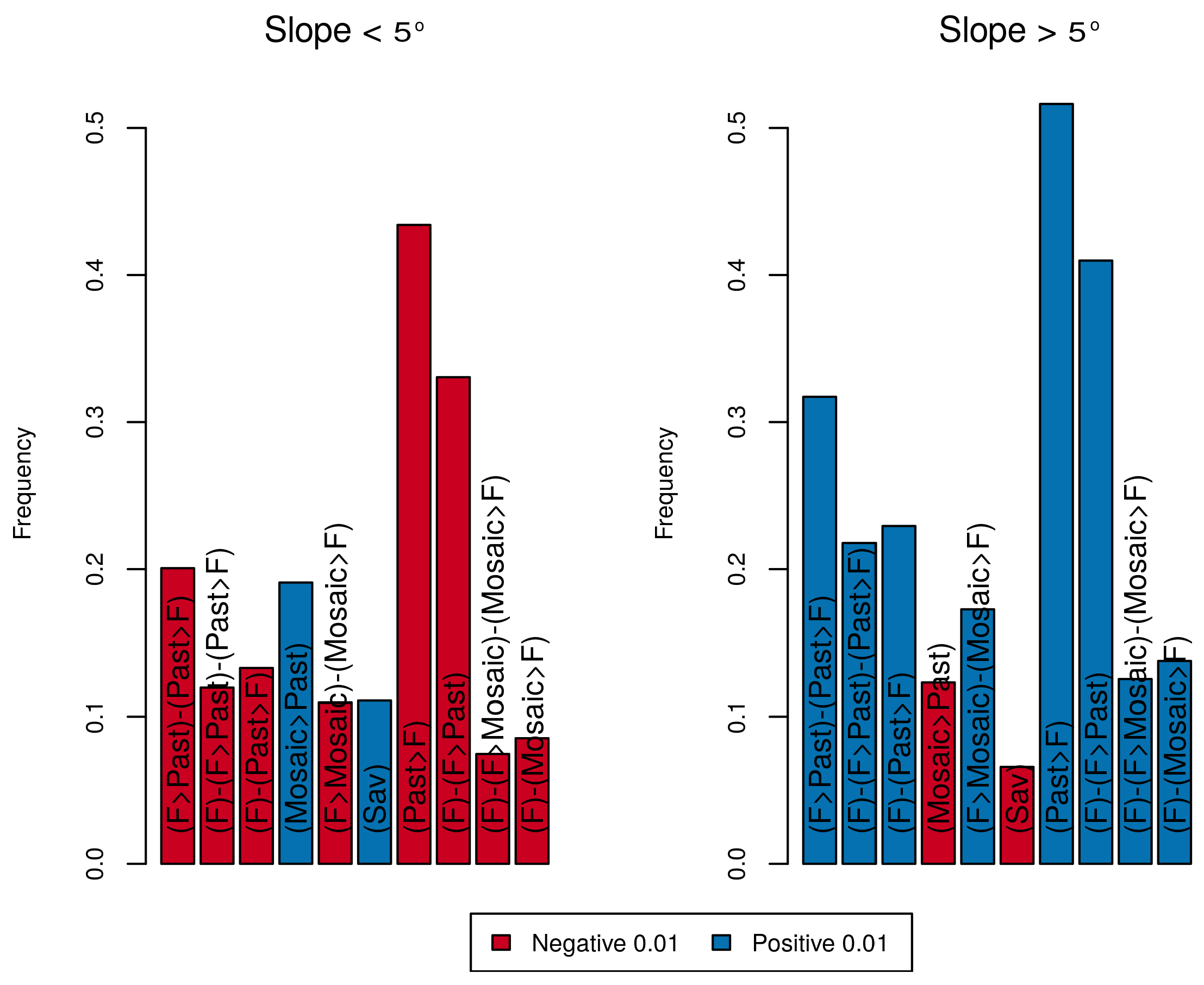
6. Results and Discussion
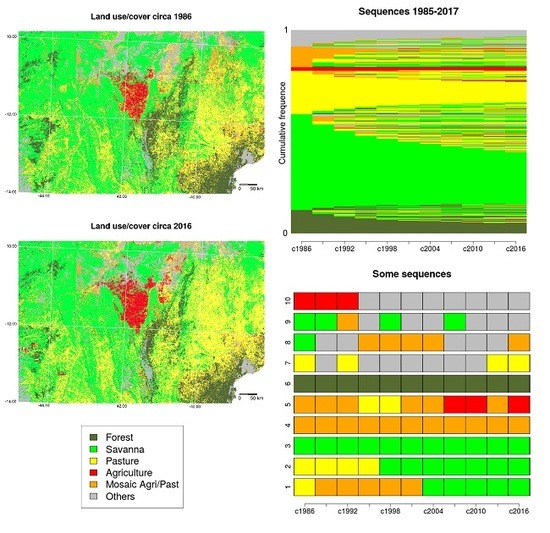
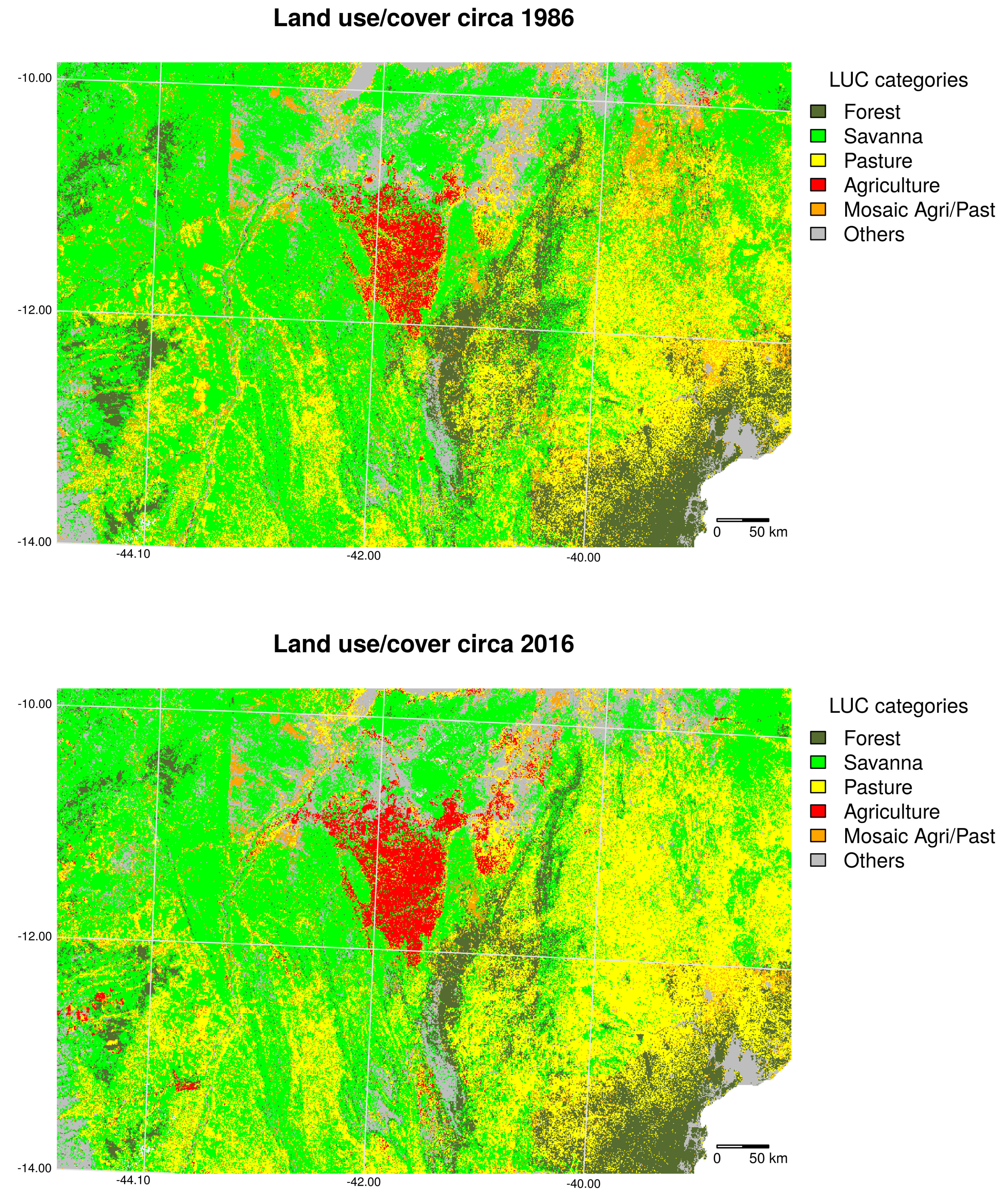
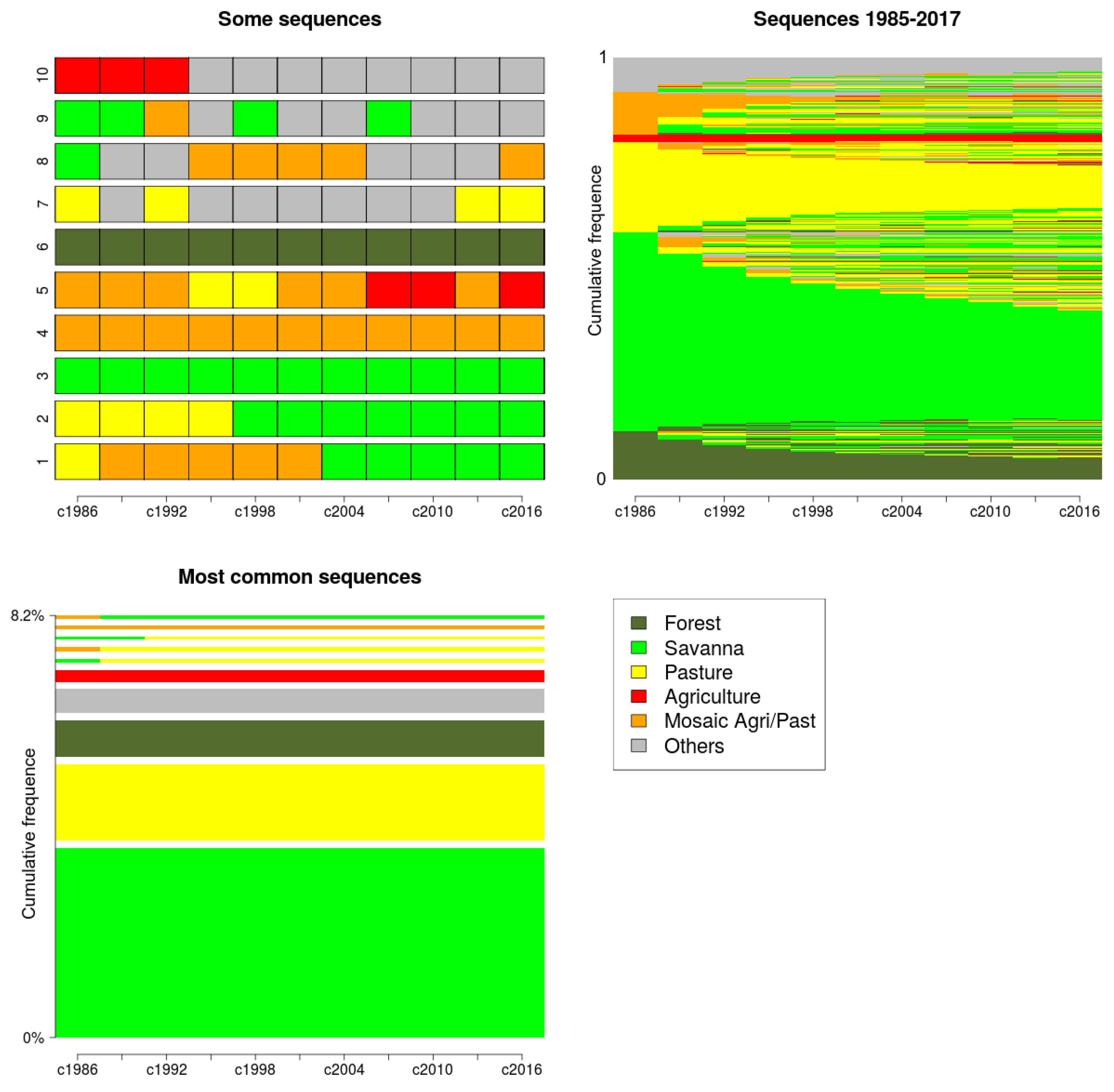
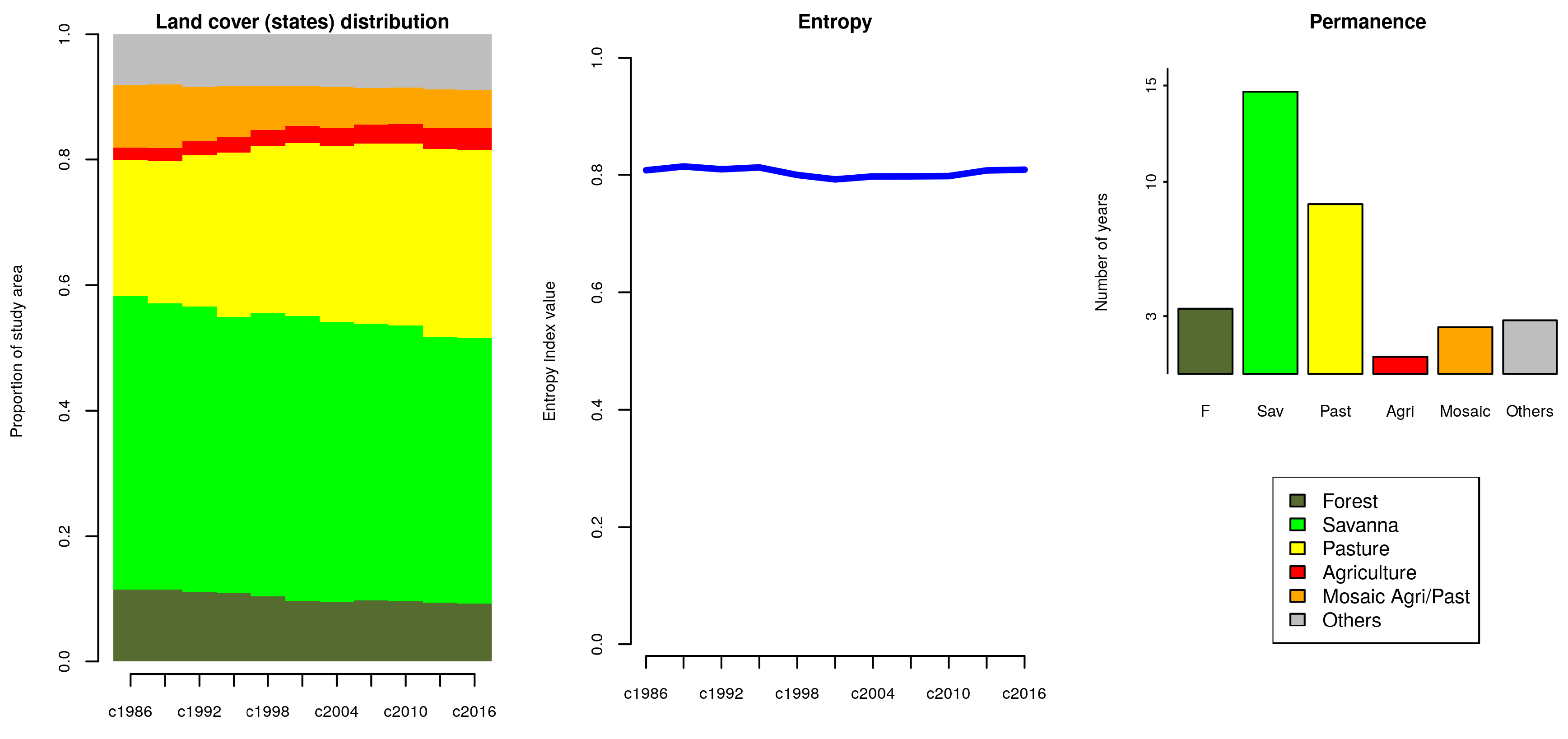
6.1. Preprocessing
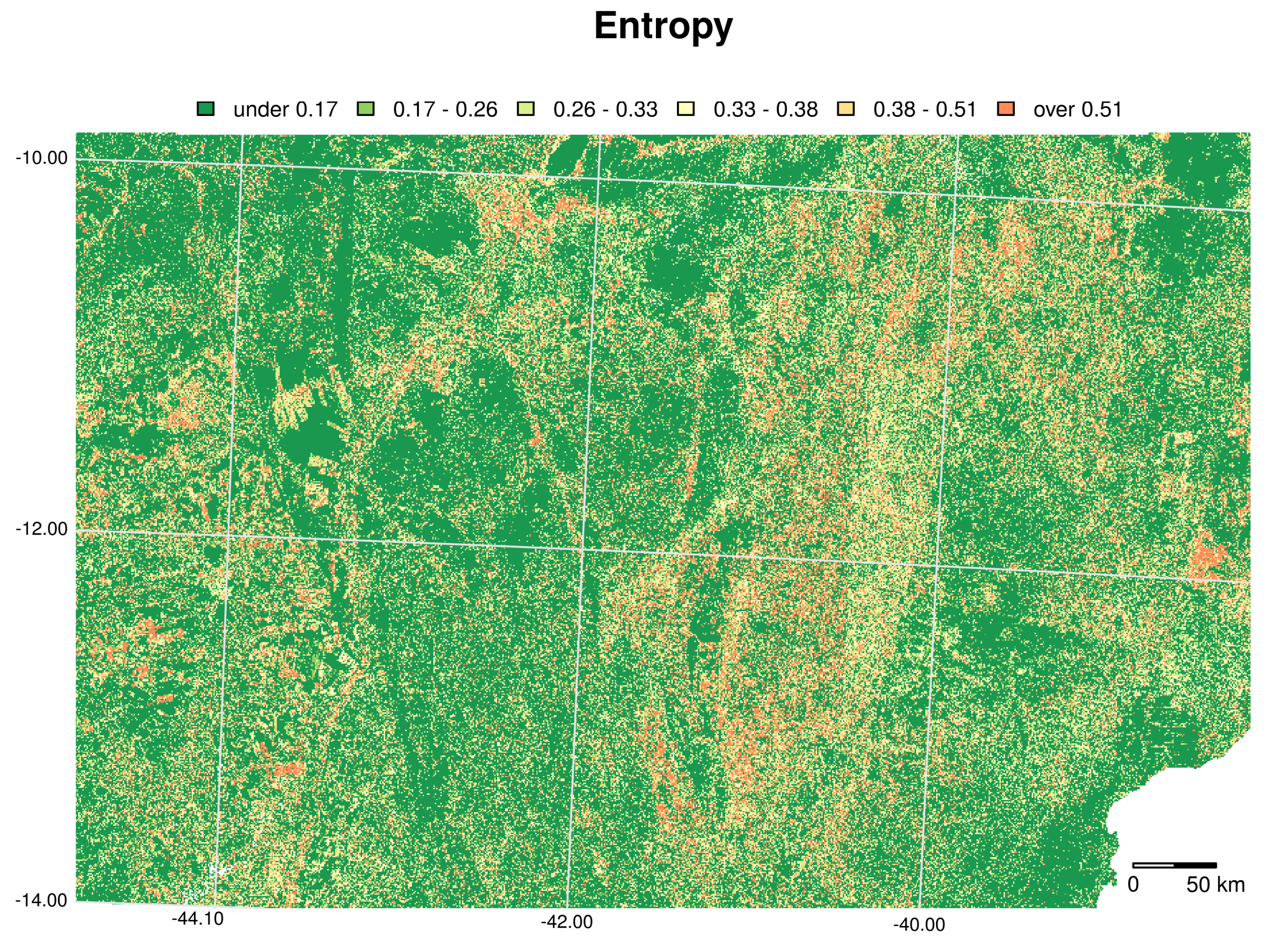
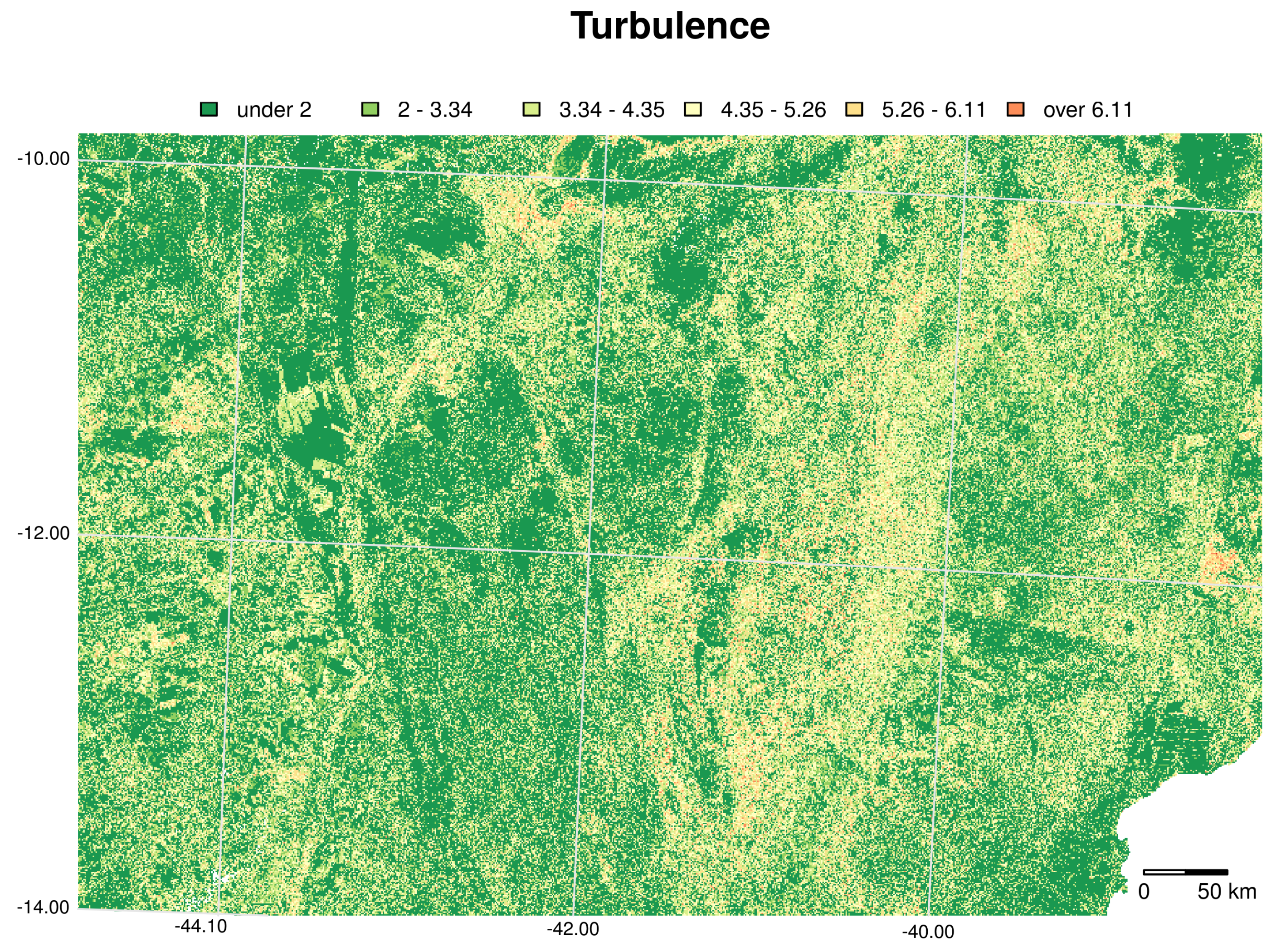
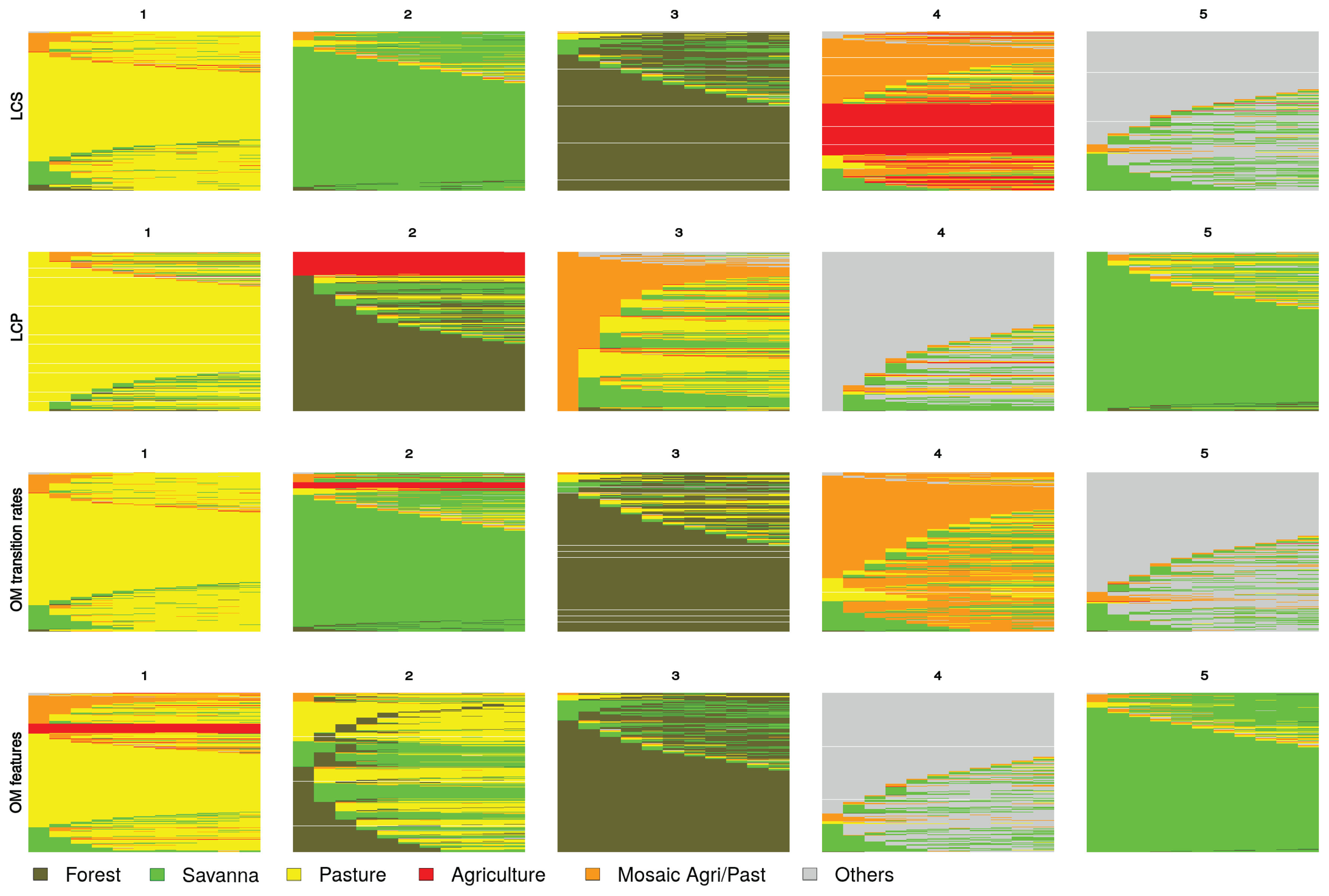
6.2. Land Use/Cover Sequence Analysis
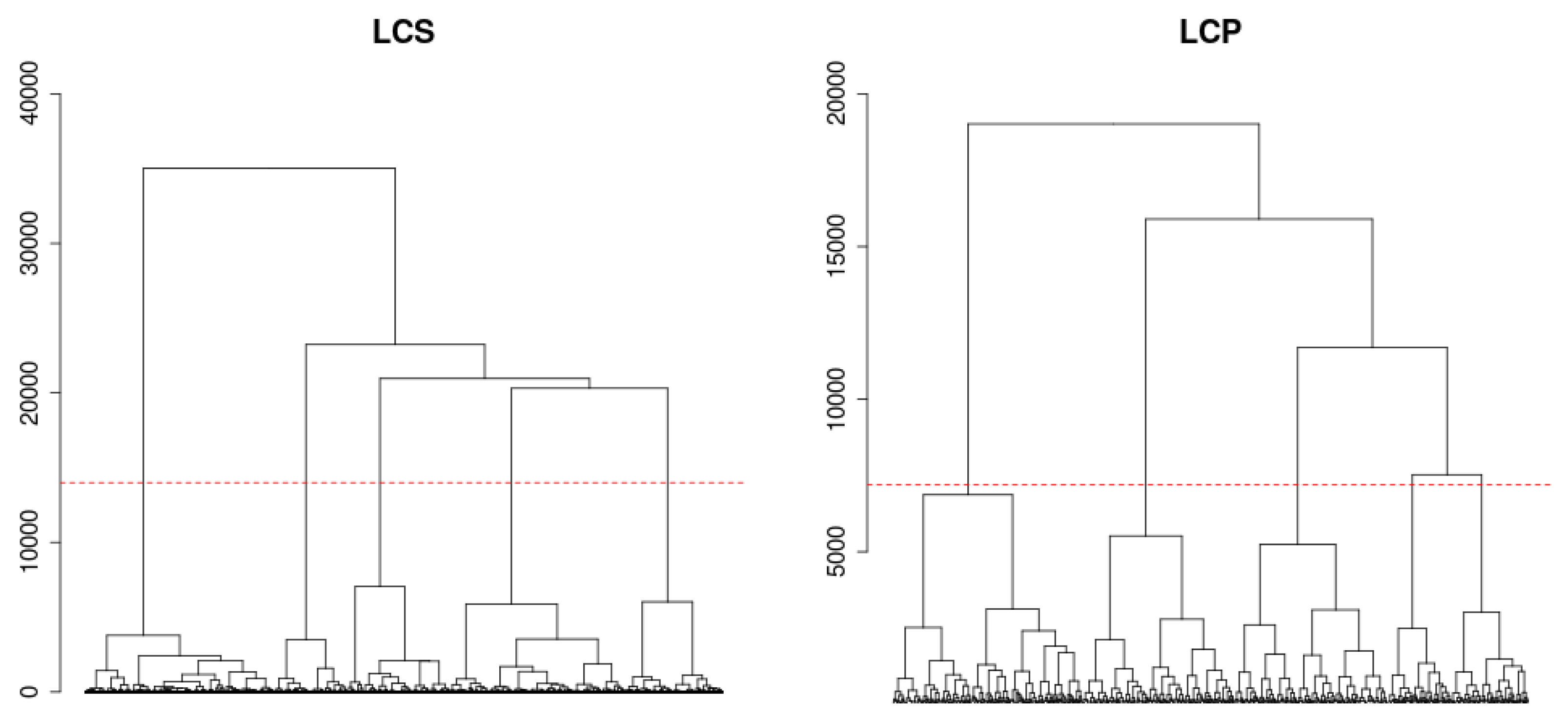
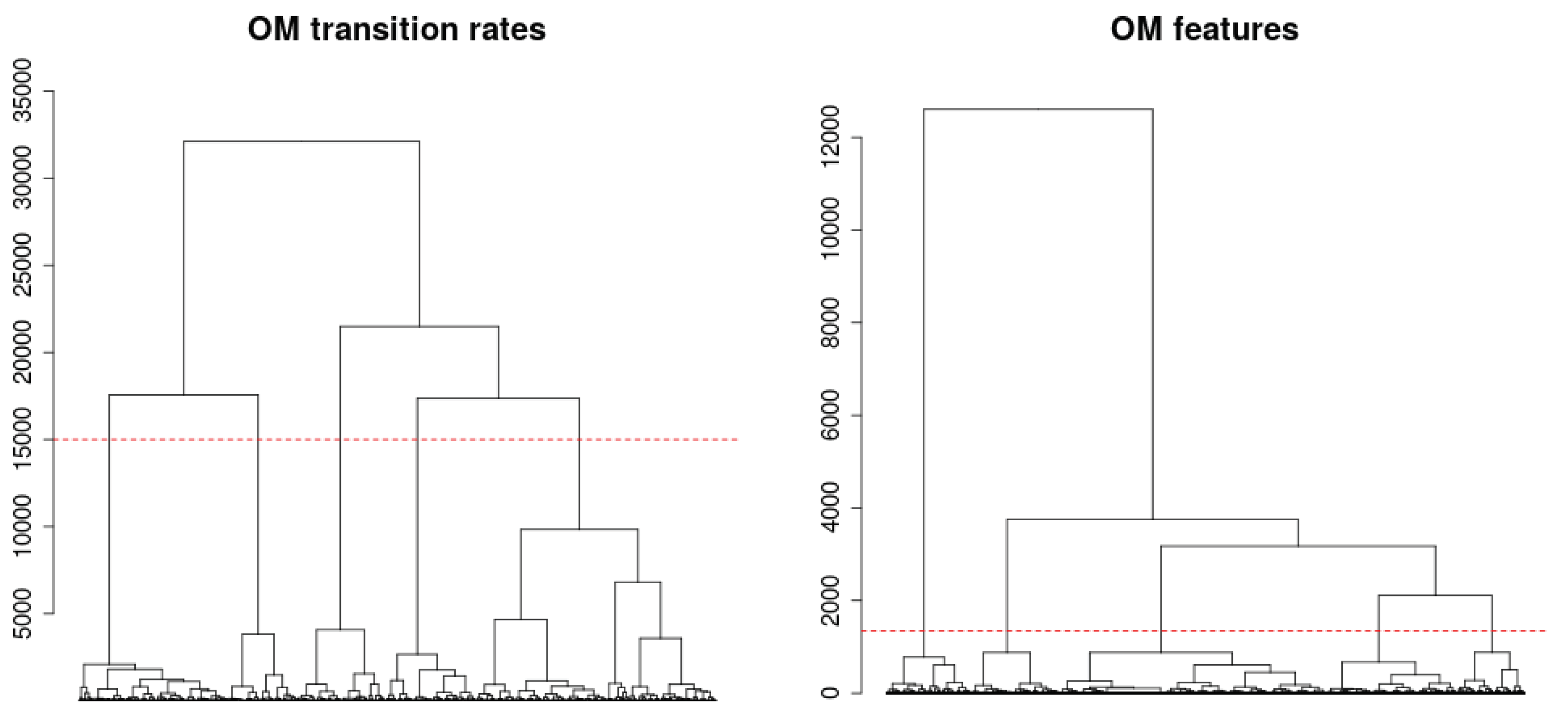
6.3. Pairwise Dissimilarities between Sequences
6.4. Assessment of the Effect of Covariates
6.5. Limitations and Potentials of Sequence Analysis in Land Change Studies
7. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Watson, S.J.; Luck, G.W.; Spooner, P.G.; Watson, D.M. Land-use change: Incorporating the frequency, sequence, time span, and magnitude of changes into ecological research. Front. Ecol. Environ. 2014, 12, 241–249. [Google Scholar] [CrossRef]
- Zaehringer, J.; Eckert, S.; Messerli, P. Revealing Regional Deforestation Dynamics in North-Eastern Madagascar—Insights from Multi-Temporal Land Cover Change Analysis. Land 2015, 4, 454–474. [Google Scholar] [CrossRef]
- Pontius, R.G.; Shusas, E.; McEachern, M. Detecting important categorical land changes while accounting for persistence. Agric. Ecosyst. Environ. 2004, 101, 251–268. [Google Scholar] [CrossRef]
- Baral, P.; Wen, Y.; Urriola, N. Forest Cover Changes and Trajectories in a Typical Middle Mountain Watershed of Western Nepal. Land 2018, 7, 72. [Google Scholar] [CrossRef]
- van der Laan, C.; Budiman, A.; Verstegen, J.; Dekker, S.; Effendy, W.; Faaij, A.; Kusuma, A.; Verweij, P. Analyses of Land Cover Change Trajectories Leading to Tropical Forest Loss: Illustrated for the West Kutai and Mahakam Ulu Districts, East Kalimantan, Indonesia. Land 2018, 7, 108. [Google Scholar] [CrossRef]
- Paegelow, M. LUCC Budget. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 437–440. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Q.; Feng, C.; Feng, Q.; Zhang, S. Understanding Land Use and Land Cover Dynamics from 1976 to 2014 in Yellow River Delta. Land 2017, 6, 20. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Colditz, R.R.; Llamas, R.M.; Ressl, R.A. Annual land cover monitoring using 250M MODIS data for Mexico. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec, QC, Canada, 13–18 July 2014; pp. 4664–4667. [Google Scholar] [CrossRef]
- He, Y.; Lee, E.; Warner, T.A. A time series of annual land use and land cover maps of China from 1982 to 2013 generated using AVHRR GIMMS NDVI3g data. Remote Sens. Environ. 2017, 199, 201–217. [Google Scholar] [CrossRef]
- Kiswanto; Tsuyuki, S.; Mardiany; Sumaryono. Completing yearly land cover maps for accurately describing annual changes of tropical landscapes. Glob. Ecol. Conserv. 2018, 13, e00384. [Google Scholar] [CrossRef]
- Zhong, C.; Wang, C.; Li, H.; Chen, W.; Hou, Y. Mapping Inter-Annual Land Cover Variations Automatically Based on a Novel Sample Transfer Method. Remote Sens. 2018, 10, 1457. [Google Scholar] [CrossRef]
- Zaehringer, J.G.; Llopis, J.C.; Latthachack, P.; Thein, T.T.; Heinimann, A. A novel participatory and remote-sensing-based approach to mapping annual land use change on forest frontiers in Laos, Myanmar, and Madagascar. J. Land Use Sci. 2018, 13, 16–31. [Google Scholar] [CrossRef]
- Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W. Disturbance-Informed Annual Land Cover Classification Maps of Canada’s Forested Ecosystems for a 29-Year Landsat Time Series. Can. J. Remote Sens. 2018, 44, 67–87. [Google Scholar] [CrossRef]
- Franklin, S.E.; Ahmed, O.S.; Wulder, M.A.; White, J.C.; Hermosilla, T.; Coops, N.C. Large Area Mapping of Annual Land Cover Dynamics Using Multitemporal Change Detection and Classification of Landsat Time Series Data. Can. J. Remote Sens. 2015, 41, 293–314. [Google Scholar] [CrossRef]
- Sheffield, K.; Morse-McNabb, E.; Clark, R.; Robson, S.; Lewis, H. Mapping dominant annual land cover from 2009 to 2013 across Victoria, Australia using satellite imagery. Sci. Data 2015, 2, 150069. [Google Scholar] [CrossRef]
- Karlin, S.; Cardon, L.R. Computational DNA sequence analysis. Annu. Rev. Microbiol. 1994, 48, 619–654. [Google Scholar] [CrossRef] [PubMed]
- Ababneh, F.; Jermiin, L.; Ma, C.; Robinson, J. Matched-pairs tests of homogeneity with applications to homologous nucleotide sequences. Bioinformatics 2006, 22, 1225–1231. [Google Scholar] [CrossRef] [PubMed]
- Silberer, G. Analyzing Sequences in Marketing Research. In Quantitative Marketing and Marketing Management: Marketing Models and Methods in Theory and Practice; Diamantopoulos, A., Fritz, W., Hildebrandt, L., Eds.; Gabler Verlag: Wiesbaden, Germany, 2012; pp. 209–224. [Google Scholar] [CrossRef]
- Jackson, C.H.; Sharples, L.D.; Thompson, S.G.; Duffy, S.W.; Couto, E. Multistate Markov models for disease progression with classification error. J. R. Stat. Soc. Ser. D 2003, 52, 193–209. [Google Scholar] [CrossRef]
- Jacob, C.M.; Baird, J.; Barker, M.; Cooper, C.; Hanson, M. The Importance of a Life-Course Approach to Health: Chronic Disease Risk from Preconception Through Adolescence and Adulthood; Technical Report; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Wang, Y.; Hou, W.; Wang, F. Mining co-occurrence and sequence patterns from cancer diagnoses in New York State. PLoS ONE 2018, 13, e0194407. [Google Scholar] [CrossRef]
- Elder, G.H.; Johnson, M.K.; Crosnoe, R. The Emergence and Development of Life Course Theory. In Handbook of the Life Course; Mortimer, J.T., Shanahan, M.J., Eds.; Springer: Boston, MA, USA, 2003; pp. 3–19. [Google Scholar] [CrossRef]
- Kok, J. Principles and Prospects of the Life Course Paradigm. Annales de Démographie Historique 2007, 113, 203–230. [Google Scholar] [CrossRef]
- López, S.; Solís, M.; Hernández, L.A. Estudio de tres regiones. In La Precariedad Laboral en México. Dimensiones, Dinámicas y Significados; Guadarrama, R., Hualde, S., López, A., Eds.; Universidad Autónoma Metropolitana: Mexico City, México, 2014; Chapter 4; pp. 189–220. [Google Scholar]
- MapBiomas. MapBiomas—Projeto de Mapeamento Anual da Cobertura e Uso do Solo no Brasil - Coleção 3 da Série Anual de Mapas de Cobertura e Uso de Solo do Brasil. Available online: http://mapbiomas.org/ (accessed on 5 Feburary 2019).
- Abbott, A. Sequences of Social Events: Concepts and Methods for the Analysis of Order in Social Processes. Hist. Methods J. Quant. Interdiscip. Hist. 1983, 16, 129–147. [Google Scholar] [CrossRef]
- Ritschard, G.; Bürgin, R.; Studer, M. Contemporary Issues in Exploratory Data Mining in Behavioral Sciences. In Contemporary Issues in Exploratory Data Mining in Behavioral Sciences; Ritschard, J., McArdle, G., Eds.; Routeledge: New York, NY, USA, 2013; pp. 221–253. [Google Scholar]
- Abbott, A.; Forrest, J. Optimal Matching Methods for Historical Sequences. J. Interdiscip. Hist. 1986, 16, 471–494. [Google Scholar] [CrossRef]
- Studer, M.; Ritschard, G. What matters in differences between life trajectories: A comparative review of sequence dissimilarity measures. J. R. Stat. Soc. Ser. A 2016, 179, 481–511. [Google Scholar] [CrossRef]
- Aassve, A.; Billari, F.C.; Piccarreta, R. Strings of Adulthood: A Sequence Analysis of Young British Women’s Work-Family Trajectories. Eur. J. Popul. 2007, 23, 369–388. [Google Scholar] [CrossRef]
- Abbott, A.; Hrycak, A. Measuring Resemblance in Sequence Data: An Optimal Matching Analysis of Musicians’ Careers. Am. J. Sociol. 1990, 96, 144–185. [Google Scholar] [CrossRef]
- Martin, P.; Schoon, I.; Ross, A. Beyond Transitions: Applying Optimal Matching Analysis to Life Course Research. Int. J. Soc. Res. Methodol. 2008, 11, 179–199. [Google Scholar] [CrossRef]
- Gabadinho, A.; Ritschard, G. Searching for Typical Life Trajectories Applied to Childbirth Histories. In Gendered Life Courses—Between Individualization and Standardization. A European Approach Applied to Switzerland; Levy, R., Widmer, E., Eds.; LIT: Vienna, Austria, 2013; Chapter 14; pp. 287–312. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Müllner, D. Fastcluster: Fast Hierarchical, Agglomerative Clustering Routines for R and Python. J. Stat. Softw. 2013, 53, 1–18. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. Available online: https://rdrr.io/cran/raster (accessed on 5 Feburary 2019).
- Gabadinho, A.; Ritschard, G.; Müller, N.; Studer, M. Analyzing and Visualizing State Sequences in R with TraMineR. J. Stat. Softw. 2011, 40, 1–37. [Google Scholar] [CrossRef]
- Elzinga, C. Sequence Analysis: Metric Representations of Categorical Time Series; Technical Report; Department of Social Science Research Methods Vrije Universiteit Amsterdam: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Stovel, K. Local Sequential Patterns: The Structure of Lynching in the Deep South, 1882–1930. Soc. Forces 2001, 79, 843–880. [Google Scholar] [CrossRef]
- Rindfuss, R.R.; Walsh, S.J.; Turner, B.L.; Fox, J.; Mishra, V. Developing a science of land change: Challenges and methodological issues. Proc. Natl. Acad. Sci. USA 2004, 101, 13976–13981. [Google Scholar] [CrossRef]
- Kolb, M.; Mas, J.F.; Galicia, L. Evaluating drivers of land-use change and transition potential models in a complex landscape in Southern Mexico. Int. J. Geogr. Inf. Sci. 2013, 27, 1804–1827. [Google Scholar] [CrossRef]
- Crews, K.; Young, K. Forefronting the Socio-Ecological in Savanna Landscapes through Their Spatial and Temporal Contingencies. Land 2013, 2, 452–471. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using stratified estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Mas, J.F.; Couturier, S.; Paneque-Gálvez, J.; Skutsch, M.; Pérez-Vega, A.; Castillo-Santiago, M.; Bocco, G. Comment on Gebhardt et al. MAD-MEX: Automatic wall-to-wall land cover monitoring for the Mexican REDD-MRV program using all landsat data. remote sens. 2014, 6, 3923-3943. Remote Sens. 2016, 8, 533. [Google Scholar] [CrossRef]
- Nagendra, H.; Reyers, B.; Lavorel, S. Impacts of land change on biodiversity: Making the link to ecosystem services. Curr. Opin. Environ. Sustain. 2013, 5, 503–508. [Google Scholar] [CrossRef]
- Ochoa-Gaona, S.; Hernández-Vázquez, F.; De Jong, B.H.J.; Gurri García, F.D. Pérdida de diversidad florística ante un gradiente de intensificación del sistema agrícola de roza-tumba-quema: Un estudio de caso en la Selva Lacandona, Chiapas, México. Boletín de la Sociedad Botánica de México 2007, 81, 65–80. [Google Scholar]
- Kuemmerle, T.; Erb, K.; Meyfroidt, P.; Müller, D.; Estel, S.; Haberl, H.; Hostert, P.; Jepsen, M.R.; Kastner, T.; Levers, C.; et al. Challenges and opportunities in mapping land use intensity globally. Curr. Opin. Environ. Sustain. 2013, 5, 484–493. [Google Scholar] [CrossRef] [PubMed]
- Mas, J.F.; Paegelow, M.; Camacho Olmedo, M.T. LUCC Modeling Approaches to Calibration. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 11–25. [Google Scholar] [CrossRef]
- Paegelow, M.; Camacho Olmedo, M.T.; Mas, J.F. Techniques for the Validation of LUCC Modeling Outputs. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 53–80. [Google Scholar] [CrossRef]
| Level 1 | Level 2 | Level 3 |
|---|---|---|
| 1. Forest | 1.1. Natural forest | 1.1.1. Forest formation |
| 1.1.2. Savanna formation | ||
| 1.1.3. Mangrove | ||
| 1.2. Forest plantation | ||
| 2. Non forest natural formation | 2.1. Wetland | |
| 2.2. Grassland formation | ||
| 2.3. Salt flat | ||
| 2.3. Other non forest natural formation | ||
| 3. Farming | 3.1. Pasture | 3.1.1. Natural Pasture |
| 3.1.2. Planted Pasture | ||
| 3.2. Agriculture | ||
| 3.3. Mosaic of agriculture and pasture | ||
| 4. Non vegetated area | 4.1. Beach and dune | |
| 4.2. Urban infrastructure | ||
| 4.3. Rocky outcrop | ||
| 4.4. Mining | ||
| 4.5. Other non vegetated area | ||
| 5. Water | 5.1. River, lake and ocean | |
| 5.2. Aquaculture | ||
| 6. Non observed |
| Forest | Savanna | Pasture | Agriculture | Mosaic | Others | |
|---|---|---|---|---|---|---|
| Forest | 0.832 | 0.091 | 0.049 | 0.001 | 0.020 | 0.007 |
| Savanna | 0.019 | 0.890 | 0.038 | 0.001 | 0.029 | 0.023 |
| Pasture | 0.016 | 0.046 | 0.884 | 0.007 | 0.040 | 0.007 |
| Agriculture | 0.002 | 0.009 | 0.037 | 0.936 | 0.010 | 0.007 |
| Mosaic | 0.027 | 0.187 | 0.176 | 0.008 | 0.540 | 0.063 |
| Others | 0.007 | 0.110 | 0.029 | 0.003 | 0.052 | 0.798 |
| Variable | PseudoF | Pseudo R2 | p Value |
|---|---|---|---|
| Elevation | 77.31 | 0.013 | 0.02 |
| Slope | 93.51 | 0.015 | 0.02 |
| Distance from roads | 40.25 | 0.007 | 0.02 |
| Annual precipitation | 213.51 | 0.035 | 0.02 |
| Precipitation of driest quarter | 256.69 | 0.042 | 0.02 |
| Total | 210.55 | 0.174 | 0.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mas, J.-F.; Nogueira de Vasconcelos, R.; Franca-Rocha, W. Analysis of High Temporal Resolution Land Use/Land Cover Trajectories. Land 2019, 8, 30. https://doi.org/10.3390/land8020030
Mas J-F, Nogueira de Vasconcelos R, Franca-Rocha W. Analysis of High Temporal Resolution Land Use/Land Cover Trajectories. Land. 2019; 8(2):30. https://doi.org/10.3390/land8020030
Chicago/Turabian StyleMas, Jean-François, Rodrigo Nogueira de Vasconcelos, and Washington Franca-Rocha. 2019. "Analysis of High Temporal Resolution Land Use/Land Cover Trajectories" Land 8, no. 2: 30. https://doi.org/10.3390/land8020030
APA StyleMas, J.-F., Nogueira de Vasconcelos, R., & Franca-Rocha, W. (2019). Analysis of High Temporal Resolution Land Use/Land Cover Trajectories. Land, 8(2), 30. https://doi.org/10.3390/land8020030