New 1 km Resolution Datasets of Global and Regional Risks of Tree Cover Loss
Abstract
1. Introduction
2. Materials and Methods
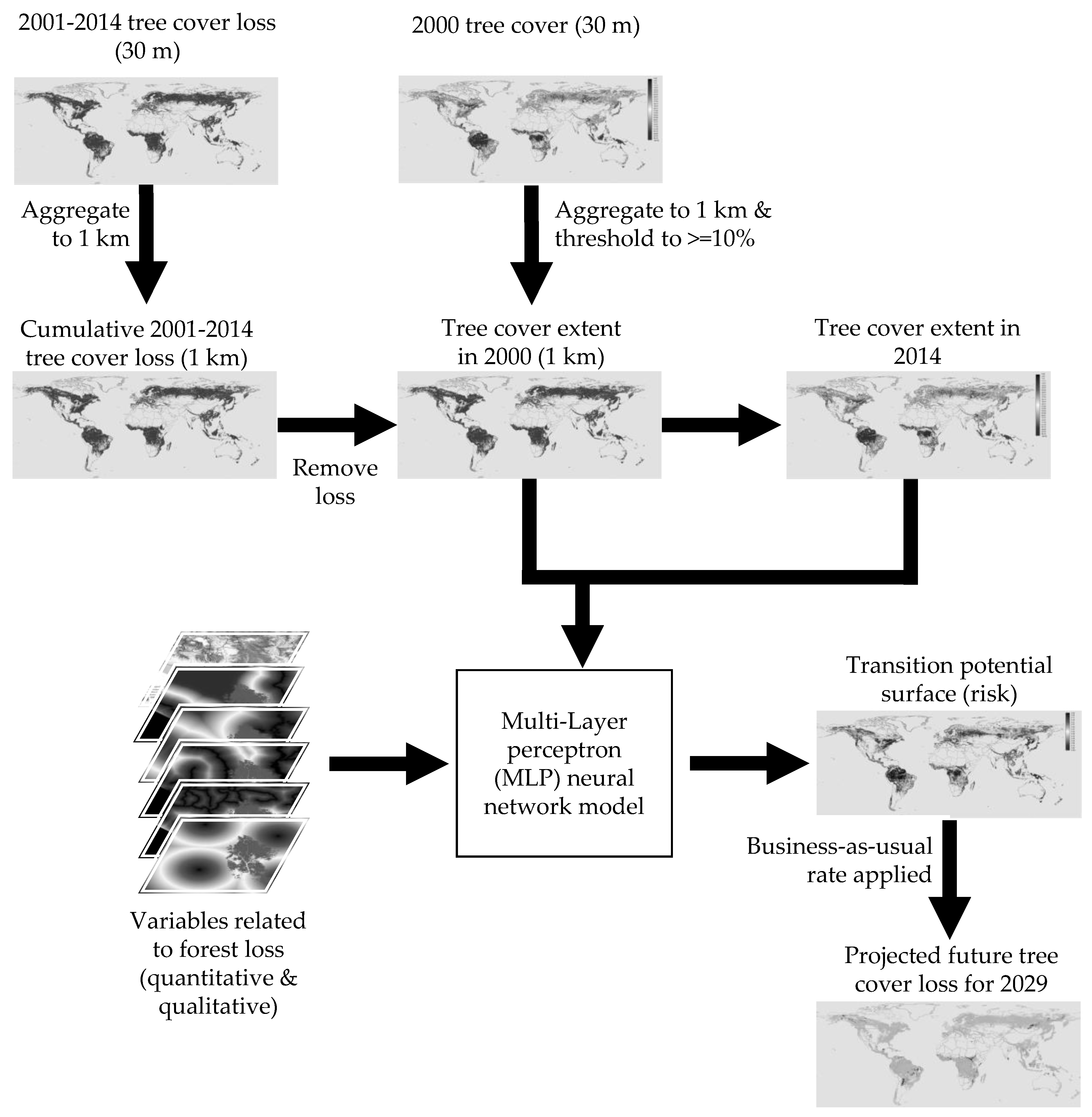
2.1. Tree Cover Extent and Tree Cover Loss Data
2.2. Variables Related to Forset Loss
2.3. Model Development and Projections
3. Results
3.1. Explanatory Variables
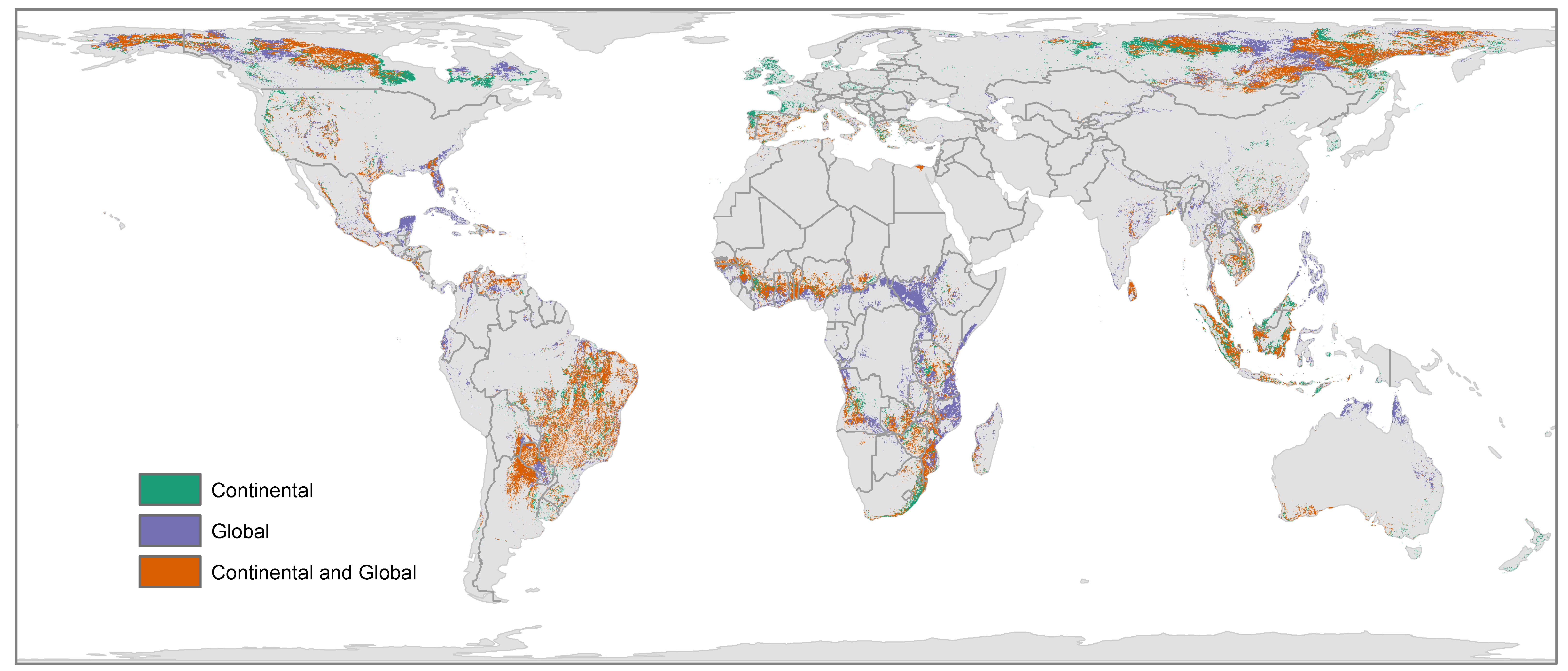
3.2. Transition Potential Surface
3.3. Tree Cover Loss Projection Images
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- E(A) = expected accuracy;
- T = the number of transitions in the submodel;
- P = the number of persistence classes = the number of “from” classes in the sub-model.
- S = model skill measure;
- A = measured accuracy;
- E(A) = expected accuracy.
References
- Giam, X. Global biodiversity loss from tropical deforestation. Proc. Natl. Acad. Sci. USA 2017, 114, 5775–5777. [Google Scholar] [CrossRef] [PubMed]
- Commission on Genetic Resources for food and Agriculture, FAO. State of the World’s Forest Genetic Resources. 2014. Available online: http://www.fao.org/3/a-i3825e.pdf (accessed on 19 October 2018).
- Restrepo, J.D.; Kettner, A.J.; Syvitski, J.P.M. Recent deforestation causes rapid increase in river sediment load in the Colombian Andes. Anthropocene 2015, 10, 13–28. [Google Scholar] [CrossRef]
- Van der Werf, G.R.; Morton, D.C.; DeFries, R.S.; Olivier, J.G.; Kasibhatla, P.S.; Jackson, R.B.; Collatz, G.J.; Randerson, J.T. CO2 Emissions from Forest Loss. Nat. Geosci. 2009, 11, 737–738. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Harris, N.L.; Brown, S.; Hagen, S.C.; Saatchi, S.S.; Petrova, S.; Salas, W.; Hansen, M.C.; Potapov, P.V.; Lotsch, A. Baseline Map of Carbon Emissions from Deforestation in Tropical Regions. Science 2012, 336, 1573–1576. [Google Scholar] [CrossRef] [PubMed]
- Keenan, R.J.; Reams, G.A.; Achard, F.; de Freitas, J.V.; Grainger, A.; Lindquist, E. Dynamics of global forest area: Results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 2015, 352, 9–20. [Google Scholar] [CrossRef]
- Tropical Forest Alliance 2020. Available online: https://www.tfa2020.org/en/ (accessed on 19 October 2018).
- Congo Basin Forest Fund-African Development Bank. Available online: https://www.afdb.org/en/topics-and-sectors/initiatives-partnerships/congo-basin-forest-fund/ (accessed on 19 October 2018).
- Amazon Fund. Available online: http://www.amazonfund.gov.br/en/home/ (accessed on 19 October 2018).
- Sandel, B.; Svenning, J.-C. Human impacts drive a global topographic signature in tree cover. Nat. Commun. 2013, 4, 2474. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Kim, D.-H.; Sexton, J.O.; Noojipady, P.; Huang, C.; Anand, A.; Channan, S.; Feng, M.; Townshend, J.R. Landsat-based forest-cover change from 1990 to 2000. Remote Sens. Environ. 2014, 155, 178–193. [Google Scholar] [CrossRef]
- Achard, F.; House, J.I. Reporting carbon losses from tropical deforestation with Pan-tropical biomass maps. Environ. Res. Lett. 2015, 10, 101002. [Google Scholar] [CrossRef]
- Song, X.-P.; Huang, C.; Saatchi, S.S.; Hansen, M.C.; Townshend, J.R. Annual Carbon Emissions from Deforestation in the Amazon Basin between 2000 and 2010. PLoS ONE 2015, 10, e0126754. [Google Scholar] [CrossRef] [PubMed]
- Southworth, J.; Marsik, M.; Qiu, Y.; Perz, S.; Cumming, G.; Stevens, F.; Rocha, K.; Duchelle, A.; Barnes, G. Roads as Drivers of Change: Trajectories across the Tri‑National Frontier in MAP, the Southwestern Amazon. Remote Sens. 2011, 3, 1047–1066. [Google Scholar] [CrossRef]
- Pérez-Vega, A.; Mas, J.-F.; Ligmann-Zielinska, A. Comparing two approaches to land use/cover change modeling and their implications for the assessment of biodiversity loss in a deciduous tropical forest. Environ. Model. Softw. 2012, 29, 11–23. [Google Scholar] [CrossRef]
- Fuller, D.O.; Hardiono, M.; Meijaard, E. Deforestation Projections for Carbon-Rich Peat Swamp Forests of Central Kalimantan, Indonesia. Environ. Manag. 2011, 48, 436–447. [Google Scholar] [CrossRef]
- Vieilledent, G.; Grinand, C.; Vaudry, R. Forecasting deforestation and carbon emissions in tropical developing countries facing demographic expansion: A case study in Madagascar. Ecol. Evol. 2013, 3, 1702–1716. [Google Scholar] [CrossRef] [PubMed]
- Cramer, W.; Bondeau, A.; Schaphoff, S.; Lucht, W.; Smith, B.; Sitch, S. Tropical forests and the global carbon cycle: Impacts of atmospheric carbon dioxide, climate change and rate of deforestation. Philos. Trans. R. Soc. B Biol. Sci. 2004, 359, 331–343. [Google Scholar] [CrossRef]
- Tracewski, Ł.; Butchart, S.H.M.; Donald, P.F.; Evans, M.; Fishpool, L.D.C.; Buchanan, G.M. Patterns of twenty-first century forest loss across a global network of important sites for biodiversity. Remote Sens. Ecol. Conserv. 2016, 2, 37–44. [Google Scholar] [CrossRef]
- Pahari, K.; Murai, S. Modelling for Prediction of Global Deforestation Based on the Growth of Human Population. Available online: http://paper/Modelling-for-prediction-of-global-deforestation-on-Pahari-Murai/0e29acd1426cd542f0a45de1211d303d8865ca09 (accessed on 19 October 2018).
- Yeh, A.G.-O.; Li, X. Urban simulation using neural networks and cellular automata for land use planning. In Advances in Spatial Data Handling; Richardson, D.D.E., van Oosterom, P.D.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 451–464. ISBN 978-3-642-62859-7. [Google Scholar]
- Pijanowski, B.C.; Brown, D.G.; Shellito, B.A.; Manik, G.A. Using neural networks and GIS to forecast land use changes: A Land Transformation Model. Comput. Environ. Urban Syst. 2002, 26, 553–575. [Google Scholar] [CrossRef]
- FAO. FRA 2015 Terms and Definitions. Forest Resources Assessment Working Paper 180. Available online: http://www.fao.org/docrep/017/ap862e/ap862e00.pdf (accessed on 15 March 2018).
- Sangermano, F.; Toledano, J.; Eastman, J.R. Land cover change in the Bolivian Amazon and its implications for REDD+ and endemic biodiversity. Landsc. Ecol. 2012, 27, 571–584. [Google Scholar] [CrossRef]
- Sudhakar Reddy, C.; Saranya, K.R.L. Earth observation data for assessment of nationwide land cover and long-term deforestation in Afghanistan. Glob. Planet. Chang. 2017, 155, 155–164. [Google Scholar] [CrossRef]
- Eastman, J.R.; Toledano, J. A short presentation of the Land Change Modeler (LCM). In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, T.M., Paegelow, M., Mas, J.-F., Escobar, F., Eds.; Lecture Notes in Geoinformation and Cartography; Springer: New York, NY, USA, 2018; pp. 499–505. ISBN 978-3-319-60801-3. [Google Scholar]
- Potts, J.M. Basic concepts. In Forecast Verification; Jolliffe, I.T., Stephenson, D.B., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2012; pp. 11–29. ISBN 978-1-119-96000-3. [Google Scholar]
- Saifullah, K.; Barus, B.; Rustiadi, E. Spatial modelling of land use/cover change (LUCC) in South Tangerang City, Banten. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 012018. [Google Scholar] [CrossRef]
- Tompkins, A.M.; Caporaso, L.; Biondi, R.; Bell, J.P. A Generalized Deforestation and Land-Use Change Scenario Generator for Use in Climate Modelling Studies. PLoS ONE 2015, 10, e0136154. [Google Scholar] [CrossRef] [PubMed]
- Mackey, B.; DellaSala, D.A.; Kormos, C.; Lindenmayer, D.; Kumpel, N.; Zimmerman, B.; Hugh, S.; Young, V.; Foley, S.; Arsenis, K.; et al. Policy Options for the World’s Primary Forests in Multilateral Environmental Agreements. Conserv. Lett. 2014, 8, 139–147. [Google Scholar] [CrossRef]
- Swamy, L.; Drazen, E.; Johnson, W.R.; Bukoski, J.J. The future of tropical forests under the United Nations Sustainable Development Goals. J. Sustain. For. 2017, 37, 221–256. [Google Scholar] [CrossRef]
- Sunderlin, W.D.; Angelsen, A.; Belcher, B.; Burgers, P.; Nasi, R.; Santoso, L.; Wunder, S.; Sunderlin, W.D.; Angelsen, A.; Belcher, B.; et al. Livelihoods, forests, and conservation in developing countries: An Overview. World Dev. 2005, 33, 1383–1402. [Google Scholar] [CrossRef]
- Musinsky, J.; Tabor, K.; Cano, C.A.; Ledezma, J.C.; Mendoza, E.; Rasolohery, A.; Sajudin, E.R. Conservation impacts of a near real-time forest monitoring and alert system for the tropics. Remote Sens. Ecol. Conserv. 2018. [Google Scholar] [CrossRef]
- Curtis, P.G.; Slay, C.M.; Harris, N.L.; Tyukavina, A.; Hansen, M.C. Classifying Drivers of Global Forest Loss. Science 2018, 361, 1108–1111. [Google Scholar] [CrossRef]
- Gauthier, S.; Bernier, P.; Kuuluvainen, T.; Shvidenko, A.Z.; Schepaschenko, D.G. Boreal forest health and global change. Science 2015, 349, 819–822. [Google Scholar] [CrossRef] [PubMed]
- Potapov, P.V.; Turubanova, S.A.; Tyukavina, A.; Krylov, A.M.; McCarty, J.L.; Radeloff, V.C.; Hansen, M.C. Eastern Europe’s Forest Cover Dynamics from 1985 to 2012 Quantified from the Full Landsat Archive. Remote Sens. Environ. 2015, 159, 28–43. [Google Scholar] [CrossRef]
- Li, Z.; Deng, X.; Shi, O.; Ke, X.; Liu, Y. Modeling the Impacts of Boreal Deforestation on the Near-Surface Temperature in European Russia. Adv. Meteorol. 2013, 1–9. [Google Scholar] [CrossRef]
- d’Annunzio, R.; Sandker, M.; Finegold, Y.; Min, Z. Projecting global forest area towards 2030. For. Ecol. Manag. 2015, 352, 124–133. [Google Scholar] [CrossRef]
- Global Forest Atlas|Roads & Forests. Available online: https://globalforestatlas.yale.edu/land-use/infrastructure/roads-forests (accessed on 19 October 2018).
- Hosonuma, N.; Herold, M.; De Sy, V.; De Fries, R.S.; Brockhaus, M.; Verchot, L.; Angelsen, A.; Romijn, E. An assessment of deforestation and forest degradation drivers in developing countries. Environ. Res. Lett. 2012, 7, 044009. [Google Scholar] [CrossRef]
- Kissinger, G.; Herold, M.; de Sy, V. Drivers of Deforestation and Forest Degradation: A Synthesis Report for REDD+ Policymakers; Lexeme Consulting: Vancouver, BC, Canada, 2012. [Google Scholar]
- Salvini, G.; Herold, M.; De Sy, V.; Kissinger, G.; Brockhaus, M.; Skutsch, M. How countries link REDD+ interventions to drivers in their readiness plans: Implications for monitoring systems. Environ. Res. Lett. 2014, 9, 074004. [Google Scholar] [CrossRef]
- Newbold, T.; Hudson, L.N.; Hill, S.L.L.; Contu, S.; Lysenko, I.; Senior, R.A.; Börger, L.; Bennett, D.J.; Choimes, A.; Collen, B.; et al. Global effects of land use on local terrestrial biodiversity. Nature 2015, 520, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Segan, D.B.; Murray, K.A.; Watson, J.E.M. A global assessment of current and future biodiversity vulnerability to habitat loss–climate change interactions. Glob. Ecol. Conserv. 2016, 5, 12–21. [Google Scholar] [CrossRef]
- Lawrence, D.; Vandecar, K. Effects of tropical deforestation on climate and agriculture. Nat. Clim. Chang. 2015, 5, 27–36. [Google Scholar] [CrossRef]
| Variable | Source | |
|---|---|---|
| 1 | Distance to railroads | VMap0 (Esri) |
| 2 | Distance to roads | VMap0 (Esri) |
| 3 | Distance to trails | VMap0 (Esri) |
| 4 | Distance to Airports | VMap0 (Esri) |
| 5 | Distance to urban areas | Nelson (2008). Estimated travel time to the nearest city of 50,000 or more people in year 2000 |
| 6 | Elevation | Danielson and Gesch (2011). Global Multi-resolution Terrain Elevation Data (GMTED2010) |
| 7 | Slope | Derived from Elevation |
| 8 | Aboveground Biomass | Avitabile et al. (2016). GEOCARBON global aboveground forest biomass map |
| 9 | Human Influence Index | Wildlife Conservation Society et al. (2005). Global Human Influence Index Dataset of the Last of the Wild Project generated at 1km for the period 1995–2004 by the World Conservation Society and the Columbia University Center for International Earth Science Information Network (CIESIN). |
| 10 | Crop suitability | Zabel et al. (2014). Global Assessment of Land Use Dynamics, Greenhouse Gas Emissions and Ecosystem Services (GLUES) data agricultural suitability data |
| 11 | Irrigation area | Siebert et al. (2013). FAO Irrigation Dataset |
| 12 | World Population 2000 | CIESIN (2016). World population in 2000 from NASA’s Socioeconomic Data and Application Center (SEDAC) |
| 13 | Global Opportunity Cost | Naidoo and Iwamura (2007). Global-scale mapping of economic benefits from agricultural lands: Implications for conservation priorities |
| 14 | Annual Precipitation | Hijmans et al. (2005). Average monthly precipitation in mm at a spatial resolution of 2.5 m from the WorldClim dataset |
| 15 | Annual Mean temperature | Hijmans et al. (2005). Average monthly mean temperature in in °C (×10) at a spatial resolution of 2.5 m from the WorldClim dataset |
| 16 | Protected Areas—Normalized Likelihoods | WDPA (2016). World Database on Protected Areas |
| 17 | Ecoregions—Normalized Likelihoods | WWF (2004). World Wildlife Fund—Global 200 (terrestrial) Ecoregions |
| 18 | Biomes—Normalized Likelihoods | WWF (2004). World Wildlife Fund—Global 200 (terrestrial) Ecoregions |
| 19 | Soil Depth—Normalized Likelihoods | HWSD (2014). Harmonized World Soil Database, version 1.2 |
| 20 | Soil Drainage—Normalized Likelihoods | HWSD (2014). Harmonized World Soil Database, version 1.2 |
| 21 | Soil Texture—Normalized Likelihoods | HWSD (2014). Harmonized World Soil Database, version 1.2 |
| 22 | Soil pH—Normalized Likelihoods | HWSD (2014). Harmonized World Soil Database, version 1.2 |
| 23 | Regions—Normalized Likelihoods | VMap0 (Esri) |
| 24 | Countries—Normalized Likelihoods | VMap0 (Esri) |
| 25 | States & Provinces—Normalized Likelihoods | VMap0 (Esri) |
| Variable | Relative Importance |
|---|---|
| Precipitation | 1 |
| Mean temperature | 2 |
| Crop suitability | 3 |
| Biomes (NL) | 4 |
| AGB | 5 |
| Elevation | 6 |
| Slope | 7 |
| Irrigation area | 8 |
| Distance to roads | 9 |
| Distance to railroads | 10 |
| Distance to trails | 11 |
| Human Influence Index | 12 |
| Distance to urban areas | 13 |
| Opportunity Cost | 14 |
| Protected areas (NL) | 15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hewson, J.; Crema, S.C.; González-Roglich, M.; Tabor, K.; Harvey, C.A. New 1 km Resolution Datasets of Global and Regional Risks of Tree Cover Loss. Land 2019, 8, 14. https://doi.org/10.3390/land8010014
Hewson J, Crema SC, González-Roglich M, Tabor K, Harvey CA. New 1 km Resolution Datasets of Global and Regional Risks of Tree Cover Loss. Land. 2019; 8(1):14. https://doi.org/10.3390/land8010014
Chicago/Turabian StyleHewson, Jennifer, Stefano C. Crema, Mariano González-Roglich, Karyn Tabor, and Celia A. Harvey. 2019. "New 1 km Resolution Datasets of Global and Regional Risks of Tree Cover Loss" Land 8, no. 1: 14. https://doi.org/10.3390/land8010014
APA StyleHewson, J., Crema, S. C., González-Roglich, M., Tabor, K., & Harvey, C. A. (2019). New 1 km Resolution Datasets of Global and Regional Risks of Tree Cover Loss. Land, 8(1), 14. https://doi.org/10.3390/land8010014





