Approximating Forest Resource Dynamics in Peninsular Malaysia Using Parametric and Nonparametric Models, and Its Implications for Establishing Forest Reference (Emission) Levels under REDD+
Abstract
1. Introduction
2. Materials and Methods
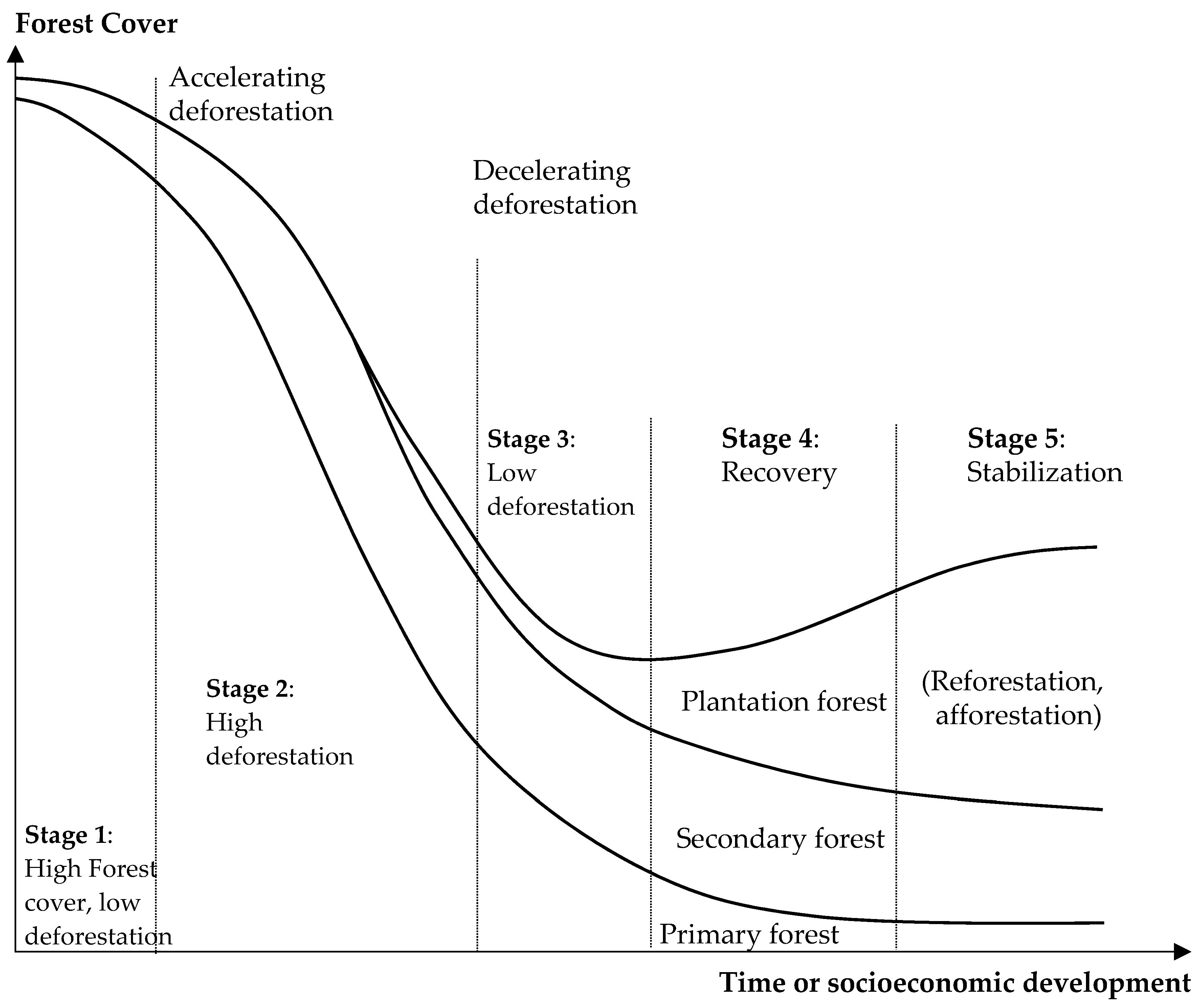
2.1. Stages of Forest Transition Curves
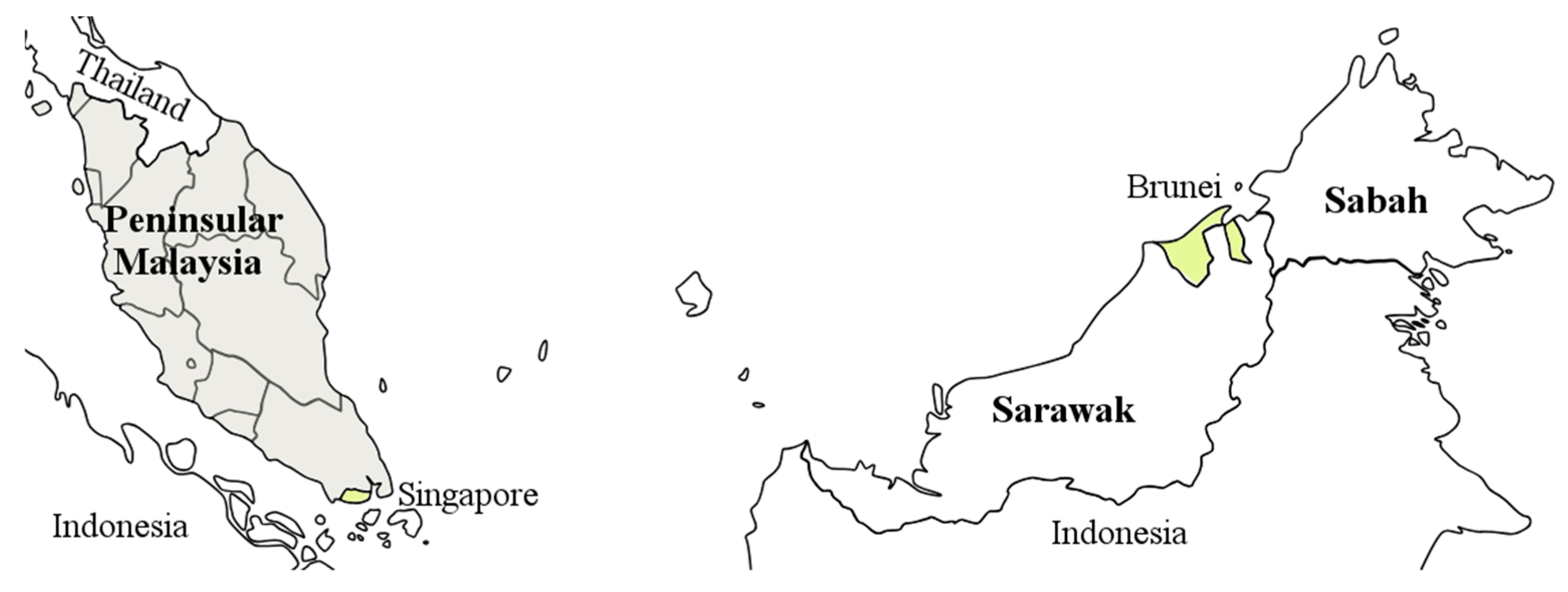
2.2. Study Site and Data
2.3. Methods
2.3.1. Parametric Models
2.3.2. Nonparametric Models
2.3.3. Model Comparations
3. Results
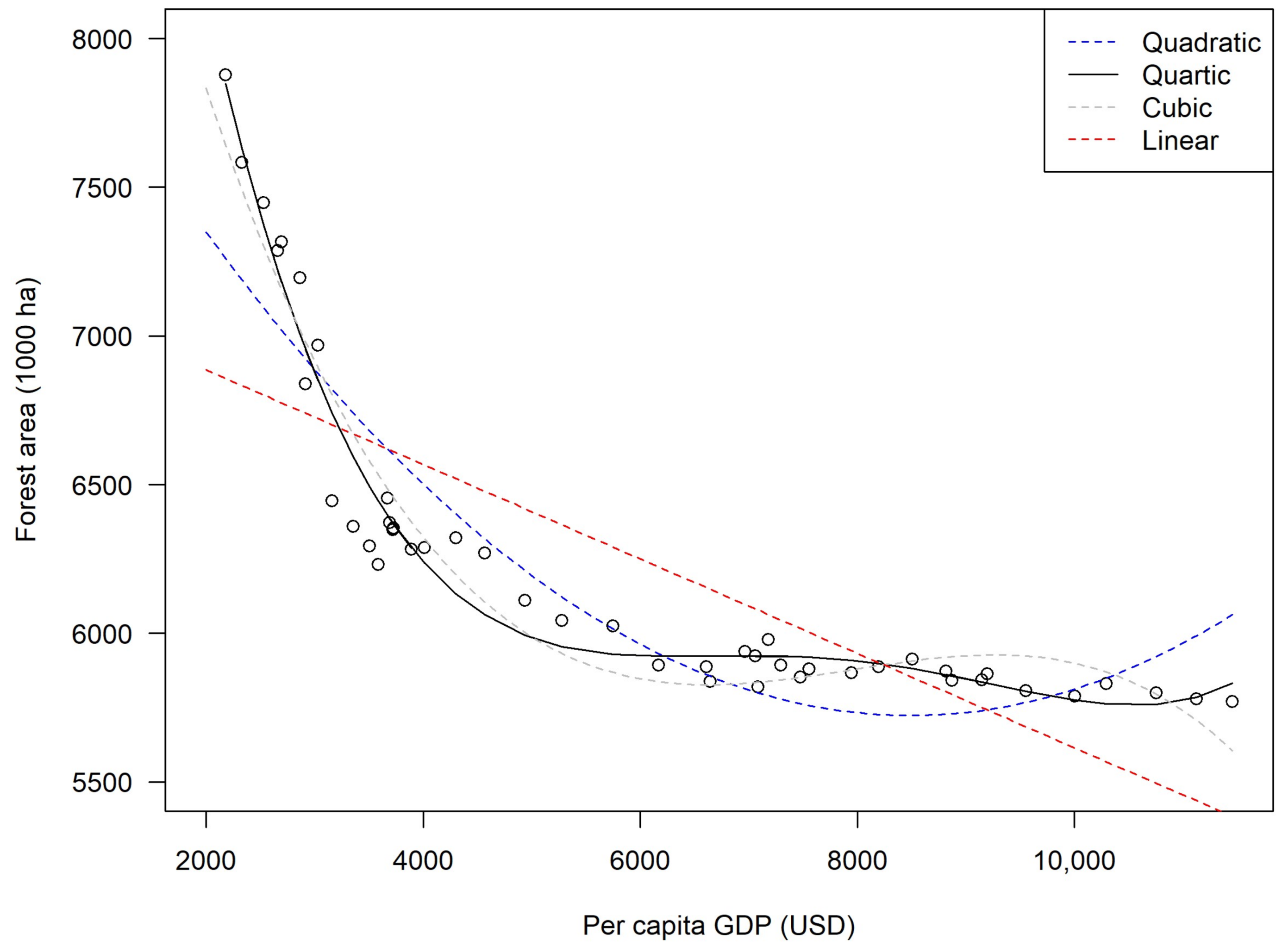
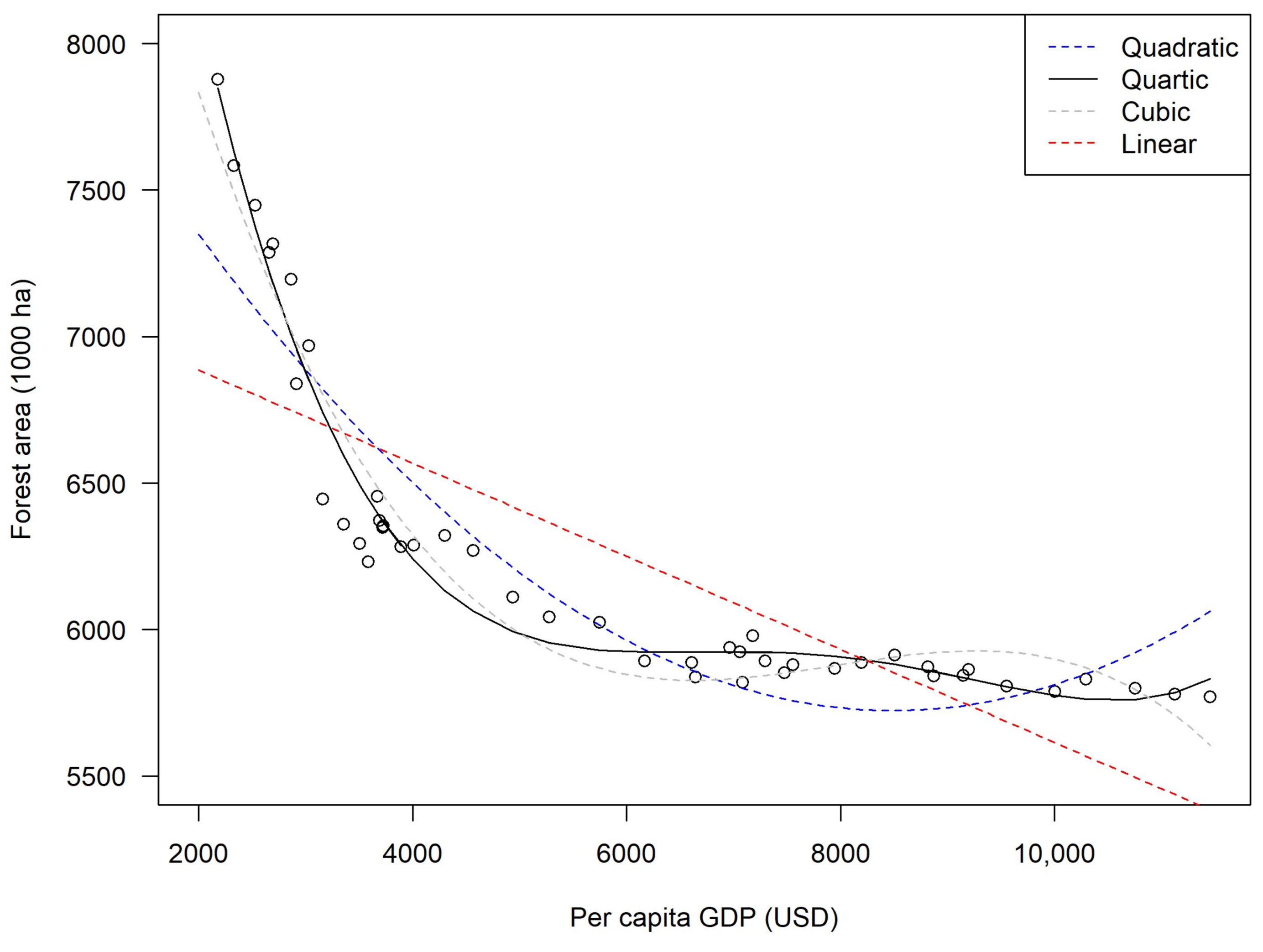
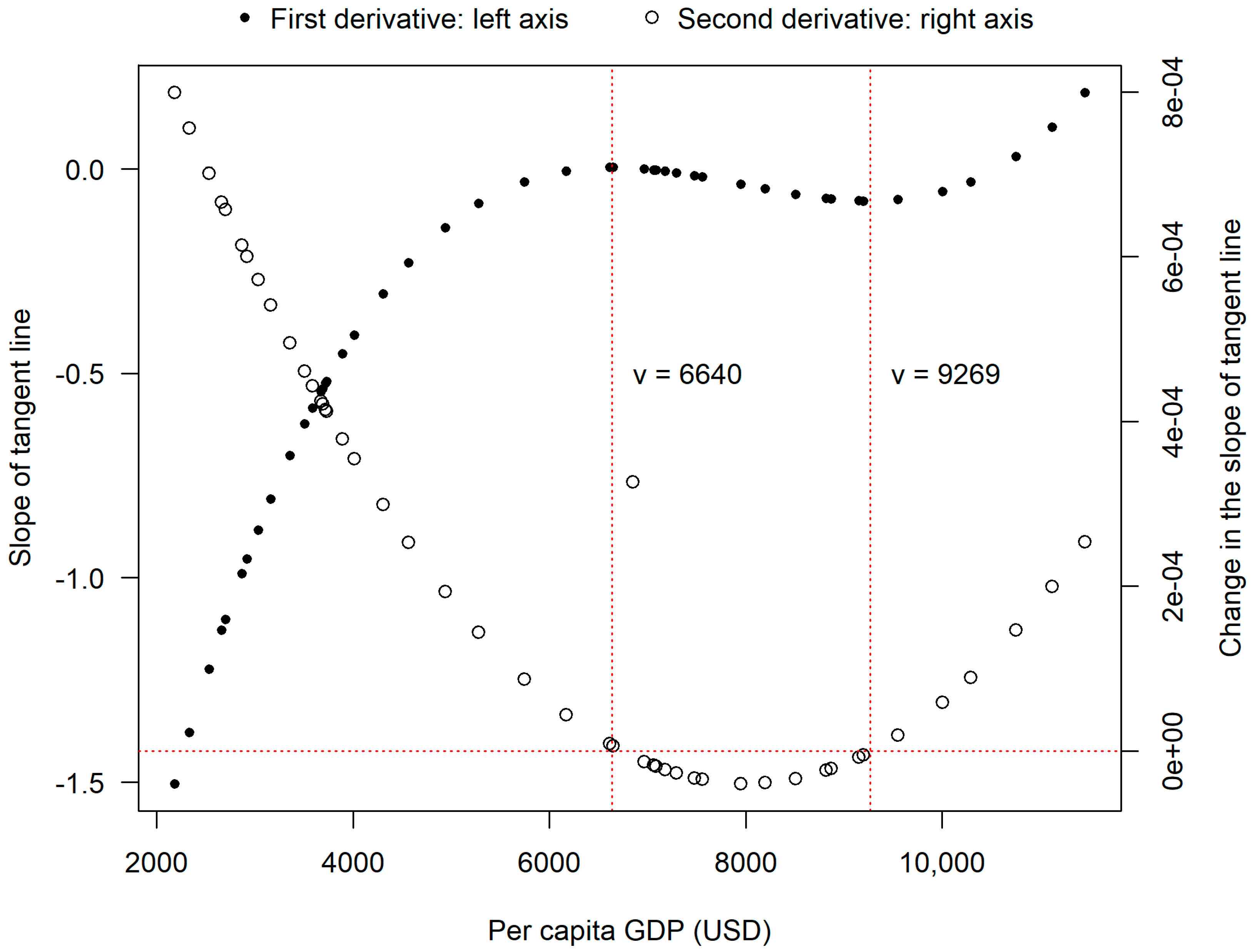
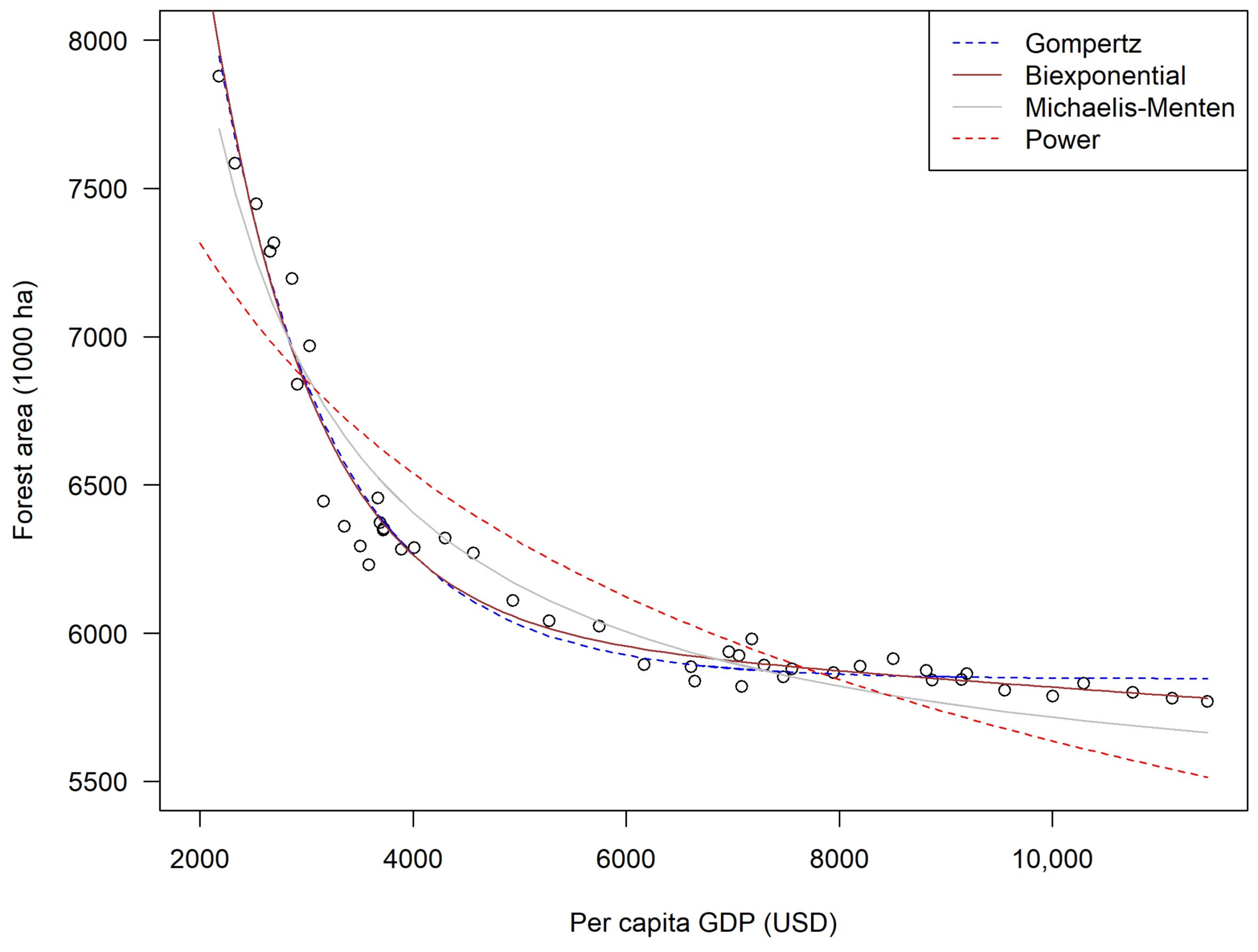
3.1. Parametric Models
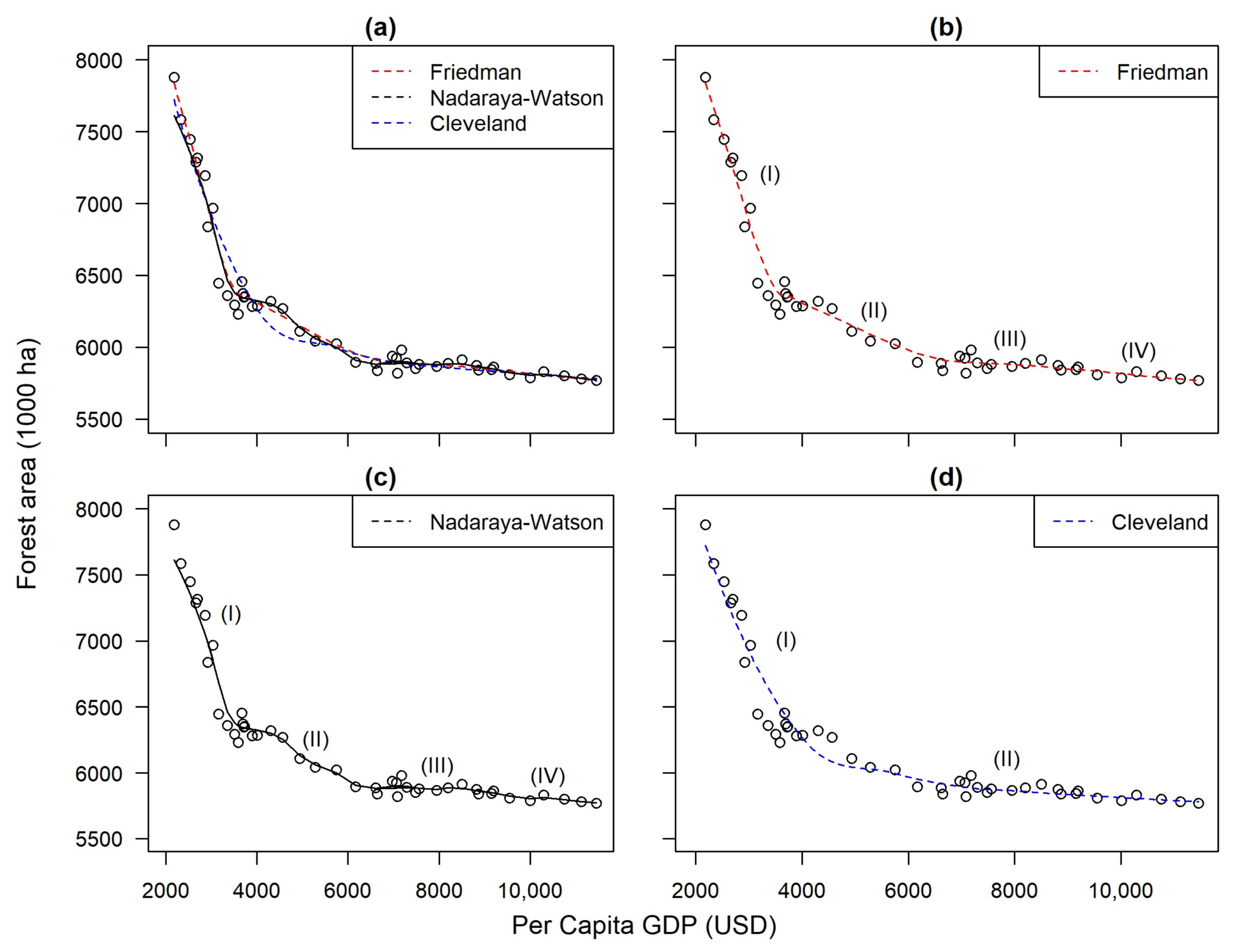
3.2. Nonparametric Models
3.3. Cross-Validation
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- UN-REDD Programme. Available online: http://www.un-redd.org/ (accessed on 10 March 2018).
- The UNFCCC REDD+ Web Platform. Available online: http://redd.unfccc.int/ (accessed on 10 March 2018).
- Neeff, T.; Maniatis, D.; Lee, D.; Mertens, E.; Jonckheere, I.; Perez, J.G.; DeValue, K.; Birigazzi, L.; Sandker, M.; Condor, R. From Reference Levels to Results Reporting: REDD+ under the UNFCCC; Forests and Climate Change Working Paper 15; Food and Agriculture Organization (FAO): Rome, Italy, 2017; p. 34. [Google Scholar]
- Mather, A.S. Global Forest Resources; Belhaven Press, a Division of Printer Publishers: London, UK, 1990; p. 342. ISBN 1-85293-055-1. [Google Scholar]
- Mather, A.S. The forest transition. Area 1992, 24, 367–379. [Google Scholar]
- Mather, A.S.; Needle, C.L. The forest transition: A theoretical basis. Area 1998, 30, 117–124. [Google Scholar] [CrossRef]
- Angelsen, A. Forest Cover Change in Space and Time: Combining the Von Thunen and Forest Transition Theories; World Bank Policy Research Working Paper No. 4117; World Bank Publications: Washington, DC, USA, 2007; p. 43. [Google Scholar]
- Angelsen, A. (Ed.) Moving Ahead with REDD: Issues, Options and Implications; CIFOR: Bogor, Indonesia, 2008; p. 156. [Google Scholar]
- Kothke, M.; Leischaner, B.; Elsasser, P. Uniform global deforestation patterns–an empirical analysis. For. Policy Econ. 2013, 28, 23–37. [Google Scholar] [CrossRef]
- Nagata, S.; Inoue, M.; Oka, Y. Testing u-shape hypothesis about forest resources. J. For. Econ. 1993, 123, 100–104. (In Japanese) [Google Scholar]
- Nagata, S.; Inoue, M.; Oka, H. The Utility and Regeneration of Forest Resources; Rural Culture Association: Tokyo, Japan, 1994; p. 234. (In Japanese) [Google Scholar]
- Shafik, N.; Bandyopadhyay, S. Economic Growth and Environmental Quality: Time Series and Cross-Country Evidence; Policy Research Working Paper Series 904; The World Bank: Washington, DC, USA, 1992; p. 55. [Google Scholar]
- Panayotou, T. Empirical Tests and Policy Analysis of Environmental Degradation at Different Stages of Economic Development; Working Paper WP238, Technology and Employment Programme; International Labour Organization (ILO): Geneva, Switzerland, 1993; p. 42. [Google Scholar]
- Stern, D.I.; Common, M.S.; Barbier, E.B. Economic growth and environmental degradation: The environmental Kuznets curve and sustainable development. World Dev. 1996, 24, 1151–1160. [Google Scholar] [CrossRef]
- Bhattarai, M.; Hammig, M. Institutions and the environmental Kuznets curve for deforestation: A crosscountry analysis for Latin America, Africa and Asia. World Dev. 2001, 29, 995–1010. [Google Scholar] [CrossRef]
- Stern, D.I. The rise and fall of the environmental Kuznets curve. World Dev. 2004, 32, 1419–1439. [Google Scholar] [CrossRef]
- Choumert, J.; Motel, P.C.; Dakpo, H.K. Is the Environmental Kuznets Curve for deforestation a threatened theory? A meta-analysis of the literature. Ecol. Econ. 2013, 90, 19–28. [Google Scholar] [CrossRef]
- Kaimowitz, D.; Angelsen, A. Economic Models of Tropical Deforestation: A Review; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 1998; p. 153. [Google Scholar]
- Huettner, M.; Leemans, R.; Kok, K.; Ebeling, J. A comparison of baseline methodologies for ‘reducing emissions from deforestation and degradation’. Carbon Balance Manag. 2009, 4. [Google Scholar] [CrossRef] [PubMed]
- Herold, M.; Angelsen, A.; Verchot, L.V.; Wijaya, A.; Ainembabazi, J.H. A stepwise framework for developing REDD+ reference levels. Chapter 16; In Analysing REDD+: Challenges and Choices; Angelsen, A., Brockhaus, M., Sunderlin, W.D., Verchot, L.V., Eds.; CIFOR: Bogor, Indonesia, 2012; pp. 279–299. [Google Scholar]
- Gutman, P.; Aguilar-Amuchastegui, N. Reference Levels and Payments for REDD+: Lessons from the Recent Guyana-Norway Agreement. World Wildlife Fund USA, 2012. Available online: http://assets.panda.org/downloads/rls_and_payments_for_redd__lessons.pdf (accessed on 24 May 2012).
- Southworth, F.; Dale, V.H.; O’Neill, R.V. Contrasting patterns of land use in Rondonia, Brazil: Simulating the effects on carbon release. Int. Soc. Sci. J. 1991, 130, 681–698. [Google Scholar]
- Angelsen, A. Shifting Cultivation Expansion and the Intensity of Production: The Open Economy Case; Working Paper #3. Chr.; Michelsen Institute: Bergen, Norway, 1994; p. 52. [Google Scholar]
- Angelsen, A. Deforestation: Population or Market Driven? Different Approaches in Modeling of Agricultural Expansion; Working Paper #9. Chr.; Michelsen Institute: Bergen, Norway, 1996; p. 42. [Google Scholar]
- Hyde, W.F.; Amacher, G.S.; Magrath, W. Deforestation and forest land use: Theory, evidence and policy implications. World Bank Res. Obs. 1996, 11, 223–248. [Google Scholar] [CrossRef]
- Michinaka, T.; Miyamoto, M. Forests and human development: Analysis pf the socio-economic factors affecting global forest area changes. J. For. Plan. 2013, 18, 141–150. [Google Scholar]
- Ashraf, J.; Pandey, R.; Jong, W. Assessment of bio-physical, social and economic drivers for forest transition in Asia-Pacific region. For. Policy Econ. 2017, 76, 35–44. [Google Scholar] [CrossRef]
- Angelsen, A.; Kaimowitz, D. Rethinking the causes of deforestation: Lessons from economic models. World Bank Res. Obs. 1999, 14, 73–98. [Google Scholar] [CrossRef] [PubMed]
- Bae, J.S.; Joo, R.W.; Kim, Y. Forest transition in South Korea: Reality, path and drivers. Land Use Policy 2012, 29, 198–207. [Google Scholar] [CrossRef]
- Barbier, E.B.; Delacote, P.; Wolfersberger, J. The economic analysis of the forest transition: A review. J. For. Econ. 2017, 27, 10–17. [Google Scholar] [CrossRef]
- Angelsen, A.; Brockhaus, M.; Kanninen, M.; Sills, E.; Sunderlin, W.D.; Wertz-Kanounnikoff, S. (Eds.) Realising REDD+: National Strategy and Policy Options; CIFOR: Bogor, Indonesia, 2009; p. 361. [Google Scholar]
- Oduro, K.A.; Mohren, G.M.J.; Pena-Claros, M.; Kyereh, B.; Arts, B. Tracing forest resource development in Ghana through forest transition pathways. Land Use Policy 2015, 48, 63–72. [Google Scholar] [CrossRef]
- Perz, S.G. Grand Theory and Context-Specificity in the Study of Forest Dynamics: Forest Transition Theory and Other Directions. Prof. Geogr. 2007, 59, 105–114. [Google Scholar] [CrossRef]
- Barbier, E.B.; Burgess, J.C.; Grainger, A. The forest transition: Towards a more comprehensive theoretical framework. Land Use Policy 2010, 27, 98–107. [Google Scholar] [CrossRef]
- Inoue, M. Basic forest conservation policy based on the distinctive feature of forest utilization patterns in the tropics. Rev. For. Culture 1992, 13, 27–32. (In Japanese) [Google Scholar]
- Forestry Department Peninsular Malaysia (FDPM). (1979 and Other Years) Forestry Statistics Peninsular Malaysiay; FDPM: Kuala Lumpur, Malaysia, 1979.
- Henson, I.E. An assessment of changes in biomass carbon stocks in tree crops and forests in Malaysia. J. Trop. For. Sci. 2005, 17, 279–296. [Google Scholar]
- Abdullah, S.A.; Nakagoshi, N. Changes in agricultural landscape pattern and its spatial relationship with forestland in the State of Selangor, peninsular Malaysia. Landsc. Urban Plan. 2008, 87, 147–155. [Google Scholar] [CrossRef]
- Miyamoto, M.; Parid, M.M.; Aini, Z.N.; Michinaka, T. Proximate and underlying causes of forest cover change in Peninsular Malaysia. For. Policy Econ. 2014, 44, 18–25. [Google Scholar] [CrossRef]
- Ministry of Plantation Industries and Commodities (MPIC). (Various years) Statistics on Commodities; MPIC: Putrajaya, Malaysia, 2014.
- Malaysian Administrative Modernisation and Management Planning Unit (MAMPU). Malaysia’s Open Data Portal; Data and Information Are Subject to the Malaysian Government Open Data Terms of Use 1.0. Available online: www.data.gov.my (accessed on 12 April 2018).
- Department of Statistics Malaysia. Table Publication GDP 2010–2016. p. 32. Available online: https://www.dosm.gov.my/v1/uploads/files/1_Articles_By_Themes/National%20Accounts/GDPbyState/Table%20Publication%20GDP%202010-2016.pdf (accessed on 5 December 2017).
- World Bank. World Development Indicators. Available online: https://data.worldbank.org/indicator/NY.GDP.DEFL.ZS?locations=MY (accessed on 30 October 2017).
- Bank Negara Malaysia (Central Bank of Malaysia). Exchange Rates. Available online: http://www.bnm.gov.my/index.php?ch=statistic&pg=stats_exchangerates&lang=en&StartMth=1&StartYr=2010&EndMth=12&EndYr=2010&sess_time=1200&pricetype=Mid&unit=rm (accessed on 24 November 2017).
- FAO (Forestry Department, Food and Agriculture Organization of the United Nations). Global Forest Resources Assessment 2010, Country Report, Malaysia. Rome, Italy, 2010. Available online: http://www.fao.org/docrep/013/al558E/al558e.pdf (accessed on 10 May 2018).
- Culas, R.J. REDD and Forest Transition: Tunnelling through the environmental Kuxnet curve. Ecol. Econ. 2012, 79, 44–51. [Google Scholar] [CrossRef]
- Shafik, N. Economic development and environmental quality: An econometric analysis. Oxf. Econ. Pap. 1994, 46, 757–773. [Google Scholar] [CrossRef]
- Michinaka, T.; Sokh, H.; Parid, M.M.; Abdullah, M.B.; Miyamoto, M. U-shape hypothesis of forest resources: In cases of Peninsular Malaysia and Cambodia. In Proceedings of the Abstracts of the 126th Annual Meeting of the Japanese Forest Society, Sapporo, Hokkaido, 27–29 March 2015; p. 97. [Google Scholar]
- Winsor, C.P. The Gompertz curve as a growth curve. Proc. Natl. Acad. Sci. USA 1932, 18, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Sweda, T.; Koide, T. Applicability of Growth Equations to the Growth of Trees in Stem Radius (I). J. Jpn. For. Soc. 1981, 63, 113–124. [Google Scholar]
- Minowa, M. A theoretical approach to forest growth modeling (I): The log-Mitscherlich theory. J. Jpn. For. Soc. 1982, 64, 461–467. [Google Scholar]
- Yoshimoto, A.; Kamo, K.; Yanagihara, H. Environmental Data Analysis by R; Asakura Syoten: Tokyo, Japan, 2012; p. 202. (In Japanese) [Google Scholar]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods, 3rd ed.; Wiley: Hoboken, NJ, USA, 2014; p. 819. ISBN 978-0-470-38737-5. [Google Scholar]
- Racine, J.; Li, Q. Nonparametric estimation of regression functions with both categorical and continuous data. J. Econom. 2004, 119, 99–130. [Google Scholar] [CrossRef]
- Fox, J.; Weisberg, S. Nonparametric Regression in R: An Appendix to An R Companion to Applied Regression, 2nd ed.; SAGE Publications: Thousand Oaks, CA, USA, 2010; p. 17. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 30 March 2018).
- Racine, J.S.; Hayfield, T. Nonparametric Kernel Smoothing Methods for Mixed Data Types. R Package, np. p. 218. Available online: https://cran.r-project.org/web/packages/np/np.pdf (accessed on 17 November 2017).
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; Kyoritsu Shuppan: Tokyo, Japan, 1983; p. 254. (In Japanese) [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002; p. 488. [Google Scholar]
- Sugiura, N. Further analysis of the data by Akaike’s information criterion and the finite corrections. Commun. Stat.-Theory Methods 1978, 7, 13–26. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Model selection for extended quasi-likelihood models in small samples. Biometrics 1995, 51, 1077–1084. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.R.; Link, W.A.; Johnson, D.H.; Burnham, K.P. Suggestions for Presenting the Results of Data Analysis. J. Wildl. Manag. 2001, 65, 373–378. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Farrell, S. AIC model selection using Akaike weights. Psychon. Bull. Rev. 2004, 11, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Angelsen, A. How do we set the reference levels for REDD payments. In Moving Ahead with REDD: Issues, Options and Implications; Angelsen, A., Ed.; CIFOR: Bogor, Indonesia, 2008; p. 156. [Google Scholar]
- Angelsen, A.; Ainembabazi, J.H. Using the forest transition to predict deforestation and set reference levels for REDD+. In Proceedings of the 5th World Congress of Environmental and Resource Economists, Istanbul, Turkey, 28 June–2 July 2014. [Google Scholar]
- Shukri, W.A.H.W.A.R. Comparison results of forest cover mapping of Peninsular Malaysia using geospatial technology. IOP Conf. Ser. Earth Environ. Sci. 2016, 37, 012027. [Google Scholar] [CrossRef]
- Shukri, W.A.H.W.A.R.; Shahrulnizam, K.; Basri, M.M. Forest Cover Mapping using Geospatial Technology in Peninsular Malaysia—Towards the Enhancement of Future Spatial-based Forestry Reporting. In Proceedings of the 17th Malaysian Forestry Conference: A Century of Forest Management: Lessons Learnt & the Way Forward, Sabah, Malaysia, 11–12 November 2014; pp. 96–115. [Google Scholar]
| No. | Models | Equations |
|---|---|---|
| 1 | Linear | |
| 2 | Quadratic | |
| 3 | Cubic | |
| 4 | Quartic | |
| 5 | Power | |
| 6 | Michaelis–Menten | |
| 7 | Biexponential | |
| 8 | Gompertz growth |
| No. | Models | RSS | Log (L) | No. Par | AICc | Δj | wj | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Biex. | 419,622 | −275.00 | 5 | 561.49 | 0.00 | 0.612 | 96 | 67 |
| 2 | Gom. | 452,497 | −276.73 | 4 | 562.44 | 0.95 | 0.382 | 99 | 74 |
| 3 | Quartic | 483,607 | −278.26 | 6 | 570.67 | 9.18 | 0.006 | 103 | 74 |
| 4 | Cubic | 833,612 | −290.78 | 5 | 593.07 | 31.58 | 0.000 | 135 | 107 |
| 5 | M-M | 902,040 | −292.60 | 3 | 591.77 | 30.28 | 0.000 | 140 | 114 |
| 6 | Qua. | 2,246,443 | −313.58 | 4 | 636.14 | 74.65 | 0.000 | 221 | 177 |
| 7 | Power | 2,698,227 | −317.80 | 3 | 642.17 | 80.68 | 0.000 | 242 | 201 |
| 8 | Linear | 5,017,771 | −332.07 | 3 | 670.70 | 109.21 | 0.000 | 330 | 271 |
| No. | Models | RSS | RMSE | MAE |
|---|---|---|---|---|
| 9 | Friedman | 200,926 | 66 | 46 |
| 10 | Nadaraya–Watson | 285,149 | 79 | 52 |
| 11 | Cleveland | 569,620 | 111 | 75 |
| No. | Models | RMSE | MAE |
|---|---|---|---|
| 1 | Biexponential | 25 | 22 |
| 2 | Nadaraya–Watson kernel smoothing | 25 | 23 |
| 3 | Gompertz growth | 76 | 73 |
| 4 | Michaelis–Menten | 132 | 131 |
| 5 | Power | 322 | 320 |
| 6 | linear | 533 | 525 |
| 7 | Quadratic | 789 | 749 |
| 8 | Cubic | 849 | 754 |
| 9 | Quartic | 895 | 758 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michinaka, T. Approximating Forest Resource Dynamics in Peninsular Malaysia Using Parametric and Nonparametric Models, and Its Implications for Establishing Forest Reference (Emission) Levels under REDD+. Land 2018, 7, 70. https://doi.org/10.3390/land7020070
Michinaka T. Approximating Forest Resource Dynamics in Peninsular Malaysia Using Parametric and Nonparametric Models, and Its Implications for Establishing Forest Reference (Emission) Levels under REDD+. Land. 2018; 7(2):70. https://doi.org/10.3390/land7020070
Chicago/Turabian StyleMichinaka, Tetsuya. 2018. "Approximating Forest Resource Dynamics in Peninsular Malaysia Using Parametric and Nonparametric Models, and Its Implications for Establishing Forest Reference (Emission) Levels under REDD+" Land 7, no. 2: 70. https://doi.org/10.3390/land7020070
APA StyleMichinaka, T. (2018). Approximating Forest Resource Dynamics in Peninsular Malaysia Using Parametric and Nonparametric Models, and Its Implications for Establishing Forest Reference (Emission) Levels under REDD+. Land, 7(2), 70. https://doi.org/10.3390/land7020070