Vegetation in Drylands: Effects on Wind Flow and Aeolian Sediment Transport
Abstract
1. Introduction: The Drylands Context
2. The Effect of Vegetation on Wind Flow
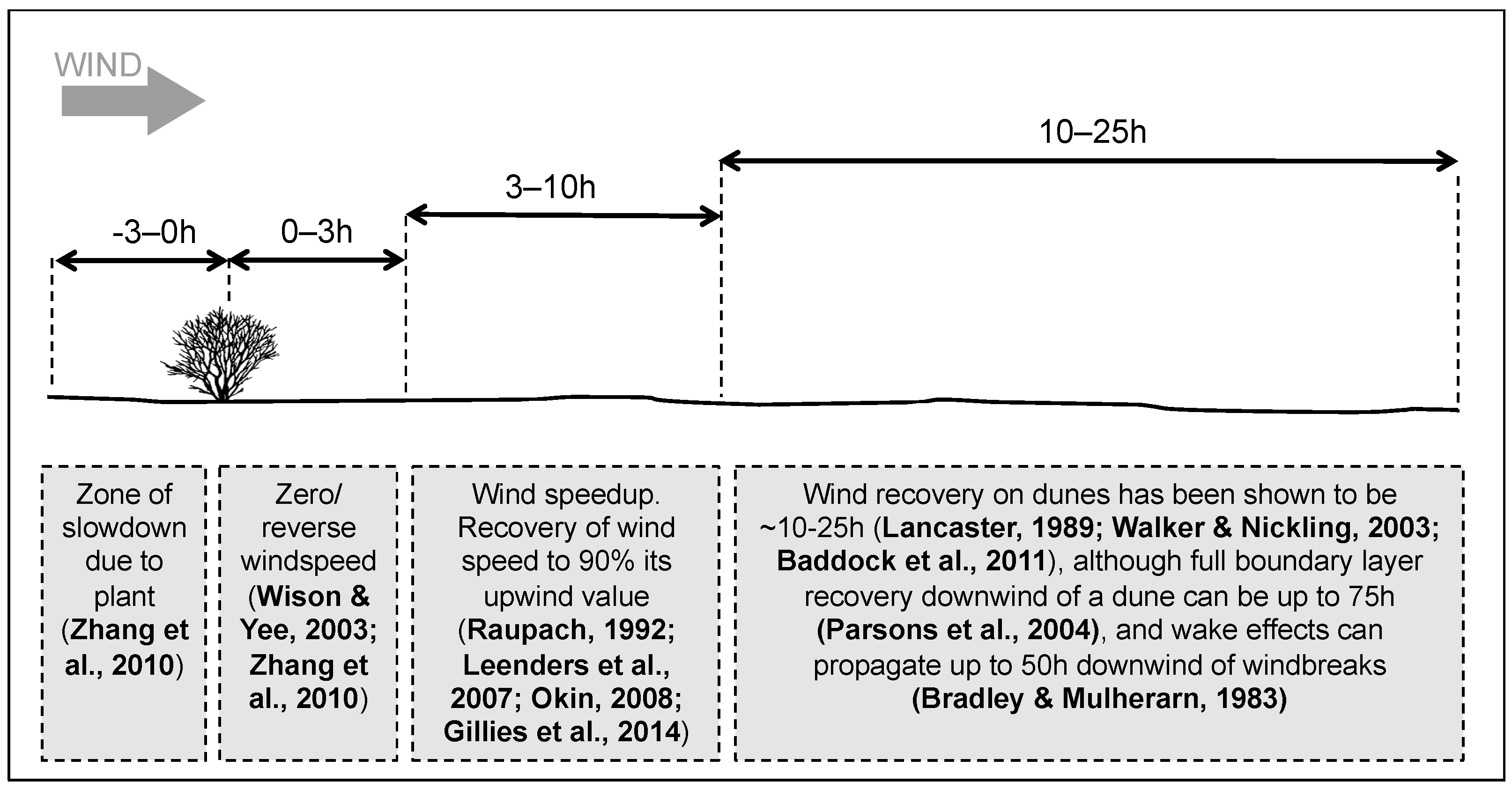
2.1. Effects on the Wind Velocity Profile
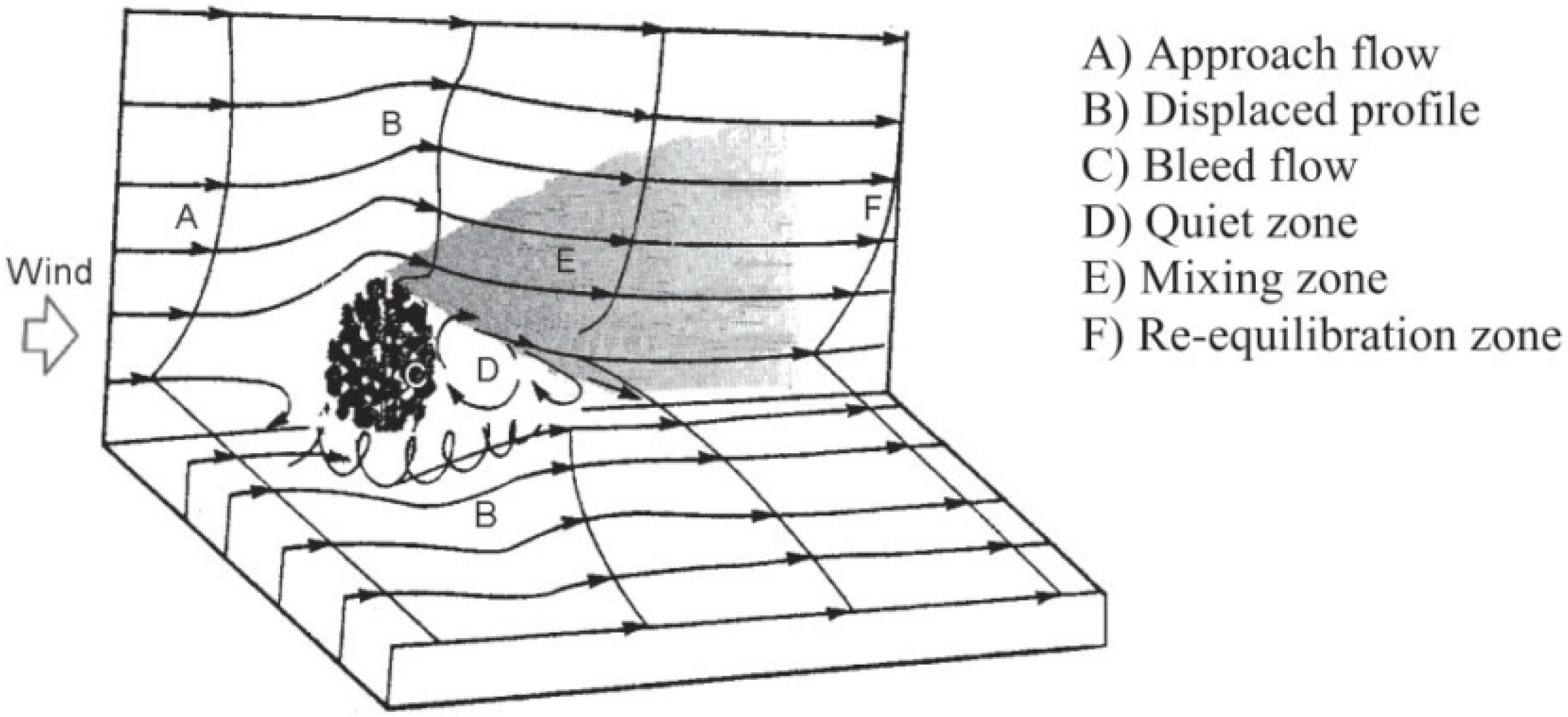
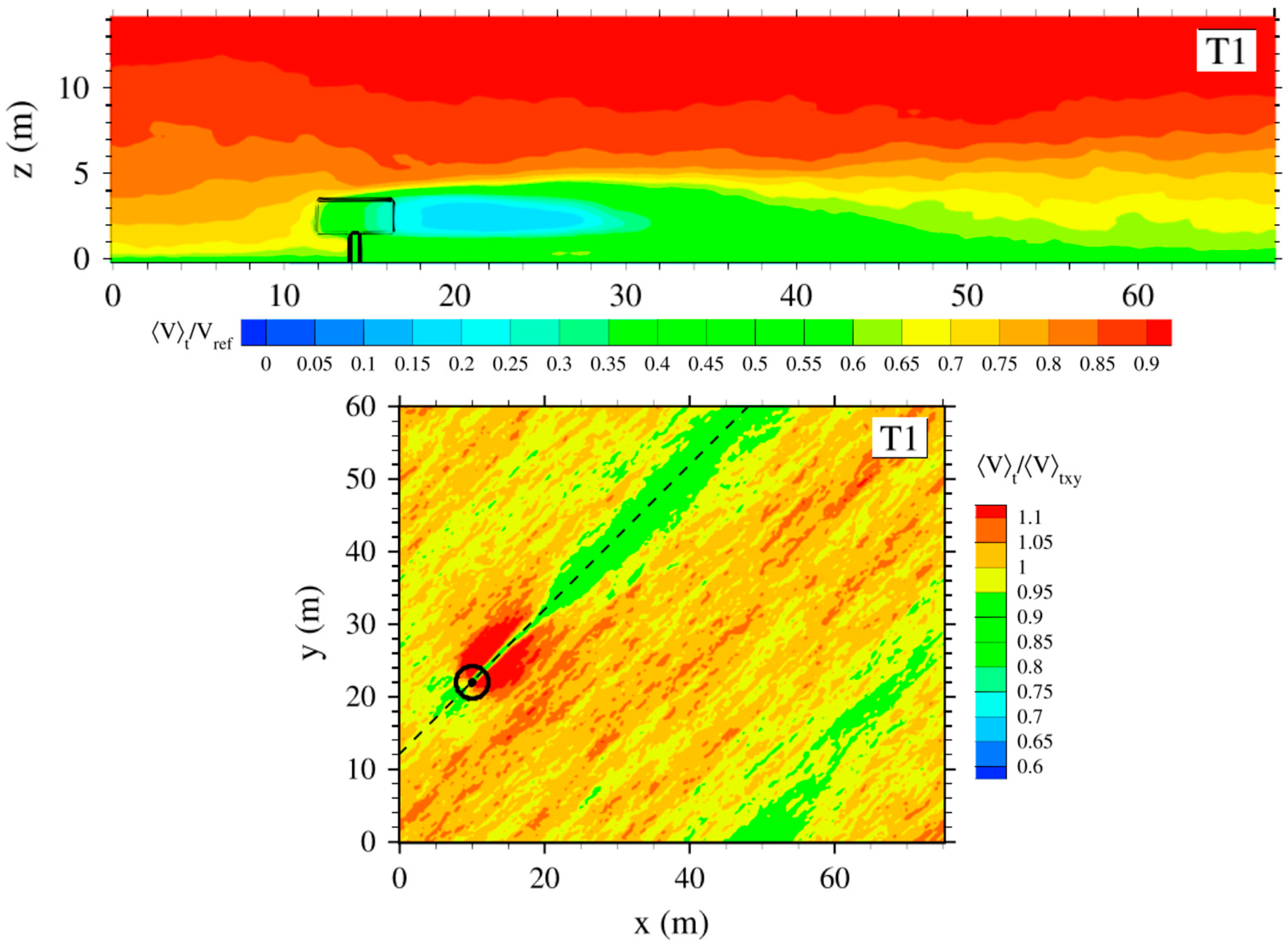
2.1.1. Plant Wake Dynamics
2.1.2. Vegetation as a Form of Roughness
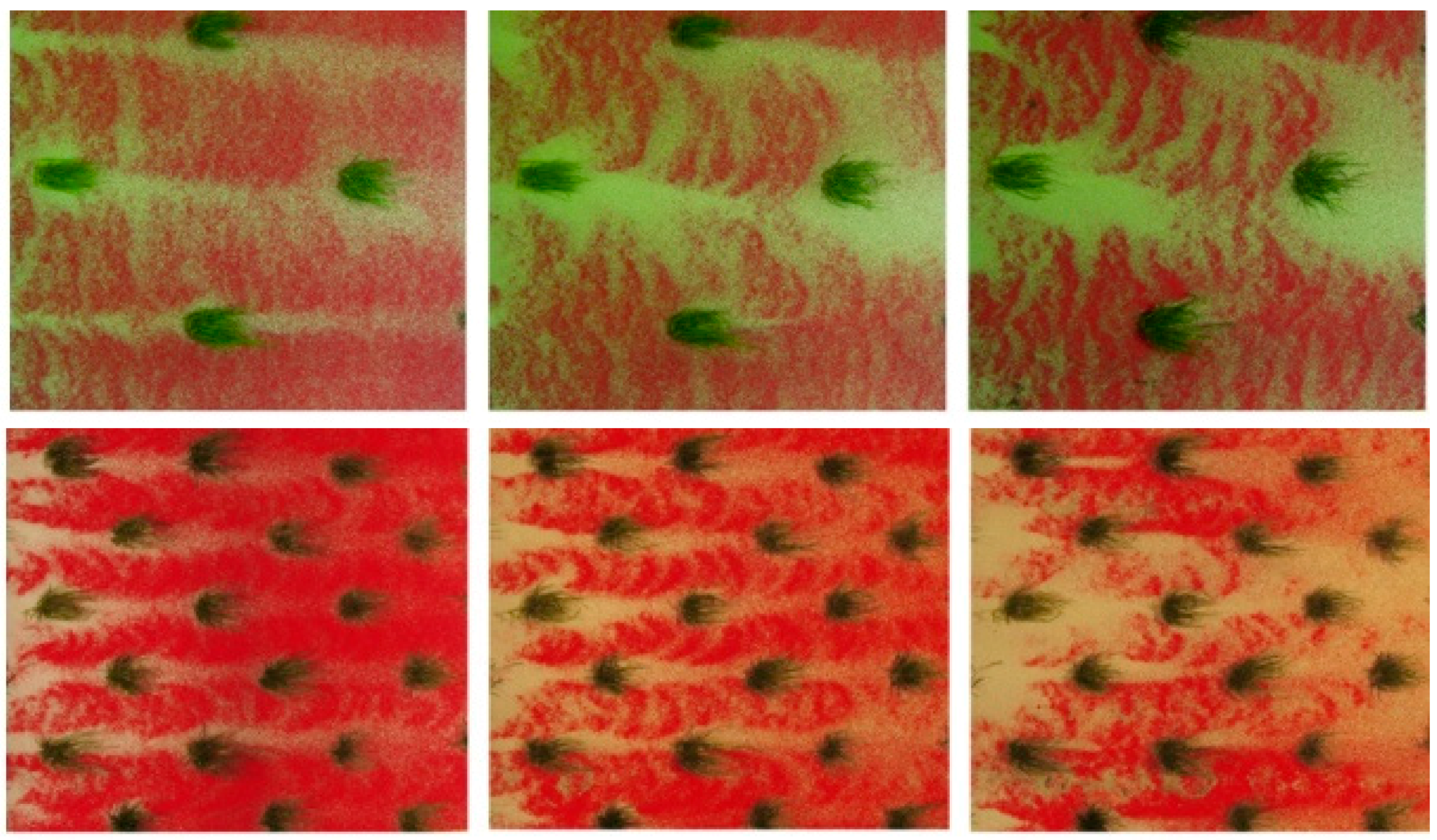
2.1.3. Trapping of Windborne Sediment
2.1.4. Effects of Plant Porosity, Pliability and Configuration
2.2. Effects on Drag
3. Sediment Transport on Vegetated Surfaces
3.1. Evidence from Wind Tunnel, Windbreak and Field Studies
3.2. Modelling Sediment Transport on Vegetated Surfaces
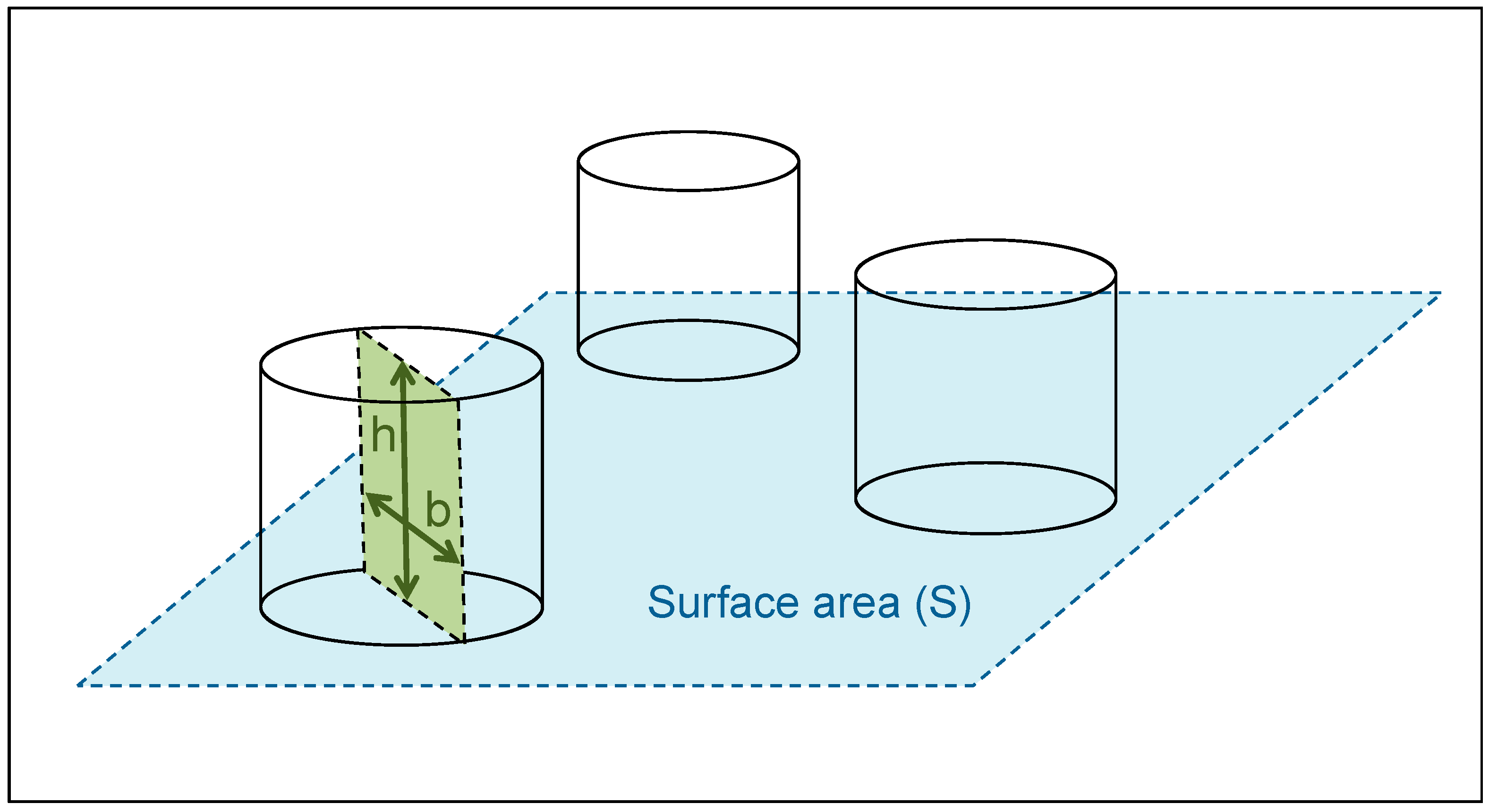
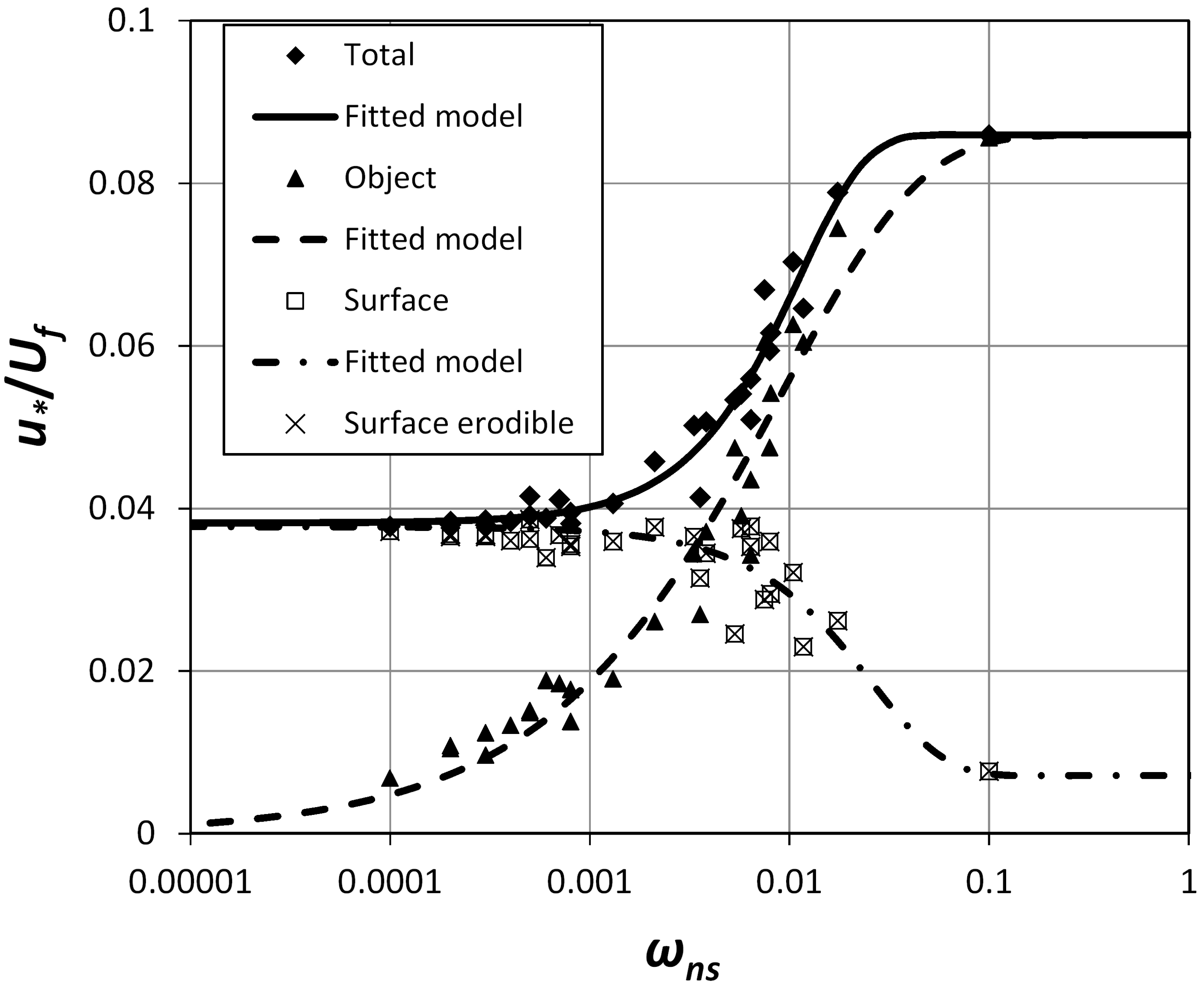
3.2.1. Drag Partition Schemes
3.2.2. Okin (2008) Model
3.2.3. Remote Sensing Approaches
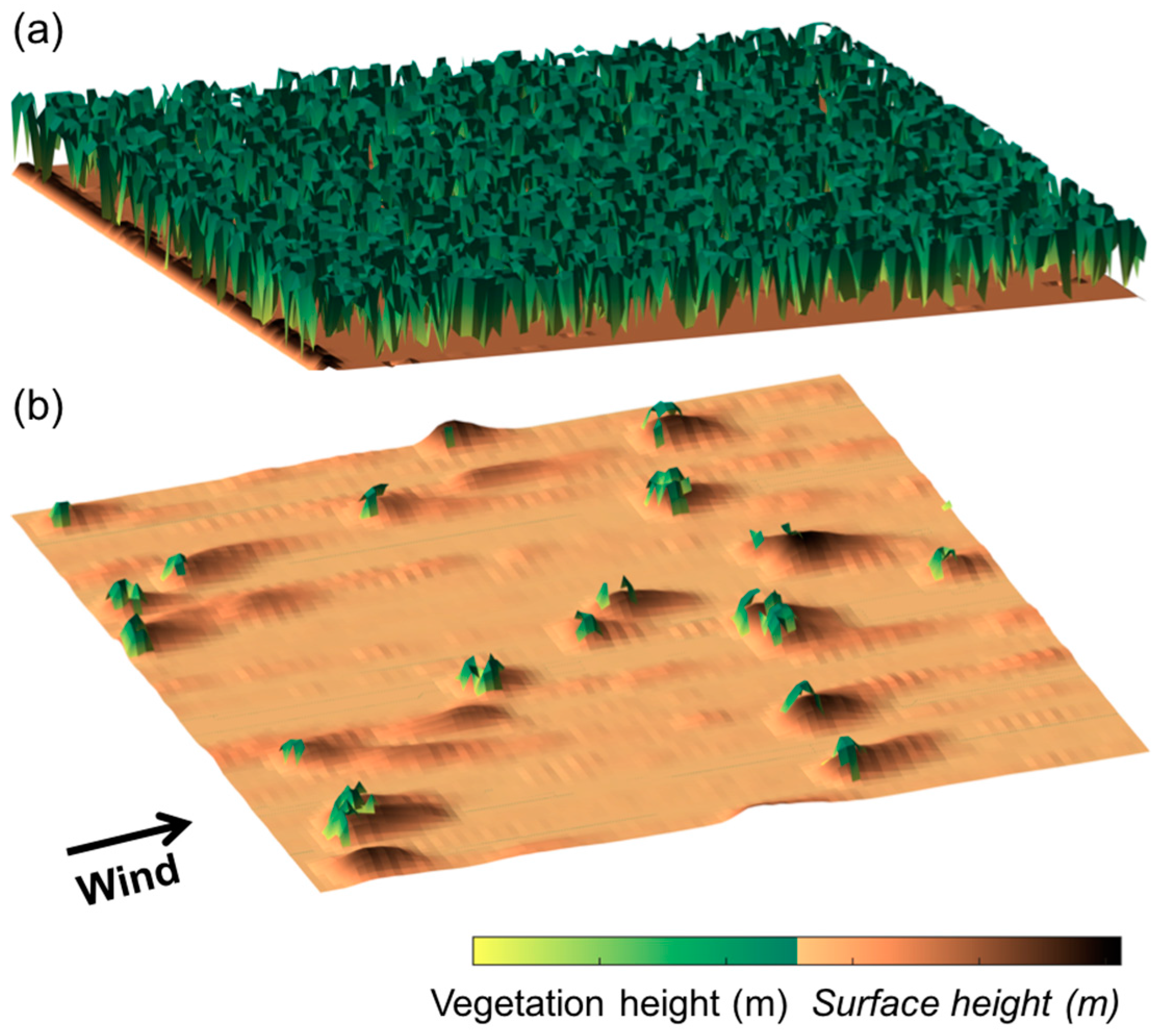
3.2.4. Computational Fluid Dynamics (CFD) Modelling
3.2.5. Cellular Automaton (CA) Modelling
4. Potential Future Avenues for Research
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- UNEP. World Atlas of Desertification, 2nd ed.; Edward Arnold: Sevenoaks, UK, 1998. [Google Scholar]
- Baas, A.C.W.; Nield, J.M. Modelling vegetated dune landscapes. Geophys. Res. Lett. 2007, 34, L06405. [Google Scholar] [CrossRef]
- Viles, H.A. Weathering systems. In Arid Zone Geomorphology: Process, Form and Change in Drylands, 3rd ed.; Thomas, D.S.G., Ed.; John Wiley & Sons Ltd.: Chichester, UK, 2011; pp. 85–101. [Google Scholar]
- Thomas, D.S.G.; Shaw, P.A. The Kalahari Environment; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Goudie, A.S. Great Warm Deserts of the World; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ravi, S.; Breshears, D.D.; Huxman, T.E.; D’Odorico, P. Land degradation in drylands: Interactions among hydrologic–aeolian erosion and vegetation dynamics. Geomorphology 2010, 116, 236–245. [Google Scholar] [CrossRef]
- Kéfi, S.; Rietkerk, M.; Alados, C.L.; Pueyo, Y.; Papanastasis, V.P.; Elaich, A.; de Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Thomas, D.S.G.; Knight, M.; Wiggs, G.F.S. Remobilization of southern African desert dune systems by twenty-first century global warming. Nature 2005, 435, 1218–1221. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, Y.; Dong, Z.; Zhang, C. Responses of dune activity and desertification in China to global warming in the twenty-first century. Glob. Planet. Chang. 2009, 67, 167–185. [Google Scholar] [CrossRef]
- Reynolds, R.; Belnap, J.; Reheis, M.; Lamothe, P.; Luiszer, F. Aeolian dust in Colorado Plateau soils: Nutrient inputs and recent change in source. Proc. Natl. Acad. Sci. USA 2001, 98, 7123–7127. [Google Scholar] [CrossRef] [PubMed]
- Ravi, S.; D’Odorico, P.; Breshears, D.D.; Field, J.P.; Goudie, A.S. Aeolian processes and the biosphere. Rev. Geophys. 2011, 49, 1–45. [Google Scholar] [CrossRef]
- Goudie, A.S.; Middleton, N.J. Desert Dust in the Global System; Springer: Berlin, Germany, 2006. [Google Scholar]
- Seager, R.; Ting, M.; Held, M.I.; Kushnir, Y.; Lu, J.; Vecchi, G.; Huang, H.-P.; Harnik, N.; Leetmaa, A.; Lau, N.-C.; et al. Model projections of an imminent transition to a more arid climate in southwestern North America. Science 2007, 316, 1181–1184. [Google Scholar] [CrossRef] [PubMed]
- Bogle, R.; Redsteer, M.H.; Vogel, J. Field measurement and analysis of climatic factors affecting dune mobility near Grand Falls on the Navajo Nation, southwestern United States. Geomorphology 2015, 228, 41–51. [Google Scholar] [CrossRef]
- Barbier, N.; Couteron, P.; Lejoly, J.; Deblauwe, V.; Lejeune, O. Self-organized vegetation patterning as a fingerprint of climate and human impact on semi-arid ecosystems. J. Ecol. 2006, 94, 537–547. [Google Scholar] [CrossRef]
- D’Odorico, P.; Bhattachan, A.; Davis, K.F.; Ravi, S.; Runyan, C.W. Global desertification: Drivers and feedbacks. Adv. Water Resour. 2013, 51, 326–344. [Google Scholar] [CrossRef]
- Middleton, N.J.; Sternberg, T. Climate hazards in drylands: A review. Earth Sci. Rev. 2013, 126, 48–57. [Google Scholar] [CrossRef]
- Griffin, D.W.; Garrison, V.H.; Herman, J.R.; Shinn, E.A. African desert dust in the Caribbean atmosphere: Microbiology and public health. Aerobiologia 2001, 17, 203–213. [Google Scholar] [CrossRef]
- Wiggs, G.F.S.; O’Hara, S.L.; Wegerdt, J.; Van Der Meer, J.; Small, I.; Hubbard, R. The dynamics and characteristics of aeolian dust in dryland Central Asia: Possible impacts on human exposure and respiratory health in the Aral Sea basin. Geogr. J. 2003, 169, 142–157. [Google Scholar] [CrossRef]
- Wasson, R.J.; Hyde, R. Factors determining desert dune type. Nature 1983, 304, 337–339. [Google Scholar] [CrossRef]
- Werner, B.T. Eolian dunes: Computer simulations and attractor interpretation. Geology 1995, 23, 1107–1110. [Google Scholar] [CrossRef]
- Momiji, H.; Carretero-Gonzalez, R.; Bishop, S.R.; Warren, A. Simulation of the effect of wind speedup in the formation of transverse dune fields. Earth Surf. Process. Landf. 2000, 25, 905–918. [Google Scholar] [CrossRef]
- Bishop, S.R.; Momiji, H.; Carretero-Gonzalez, R.; Warren, A. Modelling desert dune fields based on discrete dynamics. Discret. Dyn. Nat. Soc. 2002, 7, 7–17. [Google Scholar] [CrossRef]
- Hesp, P. Foredunes and blowouts: Initiation, geomorphology and dynamics. Geomorphology 2002, 48, 245–268. [Google Scholar] [CrossRef]
- Nield, J.M.; Baas, A.C.W. Investigating parabolic and nebkha dune formation using a cellular automaton modelling approach. Earth Surf. Process. Landf. 2008, 33, 724–740. [Google Scholar] [CrossRef]
- Mayaud, J.R.; Bailey, R.M.; Wiggs, G.F.S. A coupled vegetation/sediment-transport model for dryland environments. J. Geophys. Res. Earth Surf. 2017, 122, 875–900. [Google Scholar] [CrossRef]
- Okin, G.S.; Gillette, D.A.; Herrick, J.E. Multi-scale controls on and consequences of aeolian processes in landscape change in arid and semi-arid environments. J. Arid Environ. 2006, 65, 253–275. [Google Scholar] [CrossRef]
- Li, J.; Okin, G.S.; Herrick, J.E.; Belnap, J.; Miller, M.E.; Vest, K.; Draut, A.E. Evaluation of a new model of aeolian transport in the presence of vegetation. J. Geophys. Res. Earth Surf. 2013, 118, 288–306. [Google Scholar] [CrossRef]
- Huang, J.; Minnis, P.; Yan, H.; Yi, Y.; Chen, B.; Zhang, L.; Ayers, J. Dust aerosol effect on semi-arid climate over Northwest China detected from A-Train satellite measurements. Atmos. Chem. Phys. 2010, 10, 6863–6872. [Google Scholar] [CrossRef]
- UNDP. The Forgotten Billion: MDG Achievement in Drylands; UNDP: New York, NY, USA, 2011. [Google Scholar]
- Held, I.M.; Delworth, T.M.; Lu, J.; Findell, K.L.; Knutson, T.R. Simulation of Sahel Drought in the 20th and 21st centuries. Proc. Natl. Acad. Sci. USA 2005, 102, 17891–17896. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Mayaud, J.R.; Bailey, R.M.; Wiggs, G.F.S. Modelled responses of the Kalahari Desert to 21st century climate and land use change. Sci. Rep. 2017, 7, 3887. [Google Scholar] [CrossRef] [PubMed]
- Kinast, S.; Meron, E.; Yizhaq, H.; Ashkenazy, Y. Biogenic crust dynamics on sand dunes. Phys. Rev. E 2013, 87, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Bestelmeyer, B.T.; Okin, G.S.; Duniway, M.C.; Archer, S.R.; Sayre, N.F.; Williamson, J.C.; Herrick, J.E. Desertification, land use, and the transformation of global drylands. Front. Ecol. Environ. 2015, 13, 28–36. [Google Scholar] [CrossRef]
- Webb, N.P.; Marshall, N.A.; Stringer, L.C.; Reed, M.S.; Chappell, A.; Herrick, J.E. Land degradation and climate change: Building climate resilience in agriculture. Front. Ecol. Environ. 2017. [Google Scholar] [CrossRef]
- Meron, E.; Gilad, E.; von Hardenberg, J.; Shachak, M.; Zarmi, Y. Vegetation patterns along a rainfall gradient. Chaos Solitons Fractals 2004, 19, 367–376. [Google Scholar] [CrossRef]
- Borgogno, F.; D’Odorico, P.; Laio, F.; Ridolfi, L. Mathematical models of vegetation pattern formation in ecohydrology. Rev. Geophys. 2009, 47, RG1005. [Google Scholar] [CrossRef]
- Wainwright, J. Desert Ecogeomorphology. In Geomorphology of Desert Environments, 2nd ed.; Parsons, A.J., Abrahams, A.D., Eds.; Springer: Berlin, Germany, 2009; pp. 21–66. [Google Scholar]
- Bailey, R.M. Spatial and temporal signatures of fragility and threshold proximity in modelled semi-arid vegetation. Proc. R. Soc. B 2011, 278, 1064–1071. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.; Parsons, A.J.; Wainwright, J.; Okin, G.S.; Bestelmeyer, B.; Fredrickson, E.L.; Schlesinger, W.H. Modelling emergent patterns of dynamic desert ecosystems. Ecol. Monogr. 2014, 84, 373–410. [Google Scholar] [CrossRef]
- Getzin, S.; Wiegand, K.; Wiegand, T.; Yizhaq, H.; von Hardenberg, J.; Meron, E. Adopting a spatially explicit perspective to study the mysterious fairy circles of Namibia. Ecography 2014. [Google Scholar] [CrossRef]
- Wolfe, S.A.; Nickling, W.G. The protective role of sparse vegetation in wind erosion. Prog. Phys. Geogr. 1993, 17, 50–68. [Google Scholar] [CrossRef]
- Judd, M.J.; Raupach, M.R.; Finnigan, J.J. A wind tunnel study of turbulent flow around single and multiple windbreaks, part I: Velocity fields. Bound. Layer Meteorol. 1996, 80, 127–165. [Google Scholar] [CrossRef]
- Al-Awadhi, J.M.; Willetts, B.B. Sand transport and deposition within arrays of non-erodible cylindrical elements. Earth Surf. Process. Landf. 1999, 24, 423–435. [Google Scholar] [CrossRef]
- Leenders, J.K.; van Boxel, J.H.; Sterk, G. The effect of single vegetation elements on wind velocity and sediment transport in the Sahelian zone of Burkina Faso. Earth Surf. Process. Landf. 2007, 32, 1454–1474. [Google Scholar] [CrossRef]
- Wasson, R.J.; Nanninga, P.M. Estimating wind transport of sand on vegetated surfaces. Earth Surf. Process. Landf. 1986, 11, 505–514. [Google Scholar] [CrossRef]
- Gillette, D.A.; Stockton, P.A. The effects of non-erodible particles on wind erosion of erodible surfaces. J. Geophys. Res. 1989, 94, 12885–12893. [Google Scholar] [CrossRef]
- Gillies, J.A.; Nickling, W.G.; King, J. Drag coefficient and plant form-response to wind velocity in three plant species: Burning bush (Euonymus alatus), Colorado blue spruce (Picea pungens glauca.), and fountain grass (Pennisetum setaceum). J. Geophys. Res. 2002, 107, 4760. [Google Scholar] [CrossRef]
- Crawley, D.M.; Nickling, W.G. Drag partition for regularly-arrayed rough surfaces. Bound. Layer Meteorol. 2003, 107, 445–468. [Google Scholar] [CrossRef]
- Gillette, D.A.; Herrick, J.E.; Herbert, G.A. Wind characteristics of Mesquite Streets in the northern Chihuahuan Desert, New Mexico, USA. Environ. Fluid Mech. 2006, 6, 241–275. [Google Scholar] [CrossRef]
- Dupont, S.; Bergametti, G.; Simoëns, S. Modeling aeolian erosion in presence of vegetation. J. Geophys. Res. Earth Surf. 2014, 119, 168–187. [Google Scholar] [CrossRef]
- Gillies, J.A.; Lancaster, N.; Nickling, W.G.; Crawley, D. Field determination of drag forces and shear stress partitioning effects for a desert shrub (Sarcobatus vermiculatus, Greasewood). J. Geophys. Res. Atmos. 2000, 105, 24871–24880. [Google Scholar] [CrossRef]
- Gillies, J.A.; Nield, J.M.; Nickling, W.G. Wind velocity and sediment transport recovery in the lee of a vegetated and denuded nebkha within a nebkha dune field. Aeolian Res. 2014, 12, 135–141. [Google Scholar] [CrossRef]
- Davidson-Arnott, R.G.D.; Bauer, B.O.; Walker, I.J.; Hesp, P.A.; Ollerhead, J.; Chapman, C. High-frequency sediment transport responses on a vegetated foredune. Earth Surf. Process. Landf. 2012, 37, 1227–1241. [Google Scholar] [CrossRef]
- Van Gardingen, P.; Grace, J. Plants and wind. Adv. Bot. Res. 1991, 18, 189–253. [Google Scholar]
- Raupach, M.R. Drag and drag partition on rough surfaces. Bound. Layer Meteorol. 1992, 60, 375–395. [Google Scholar] [CrossRef]
- Okin, G.S. A new model of wind erosion in the presence of vegetation. J. Geophys. Res. 2008, 113, F02S10. [Google Scholar] [CrossRef]
- Sutton, S.L.F.; McKenna-Neuman, C. Sediment entrainment to the lee of roughness elements: Effects of vortical structures. J. Geophys. Res. 2008, 113, F02S09. [Google Scholar] [CrossRef]
- Suter-Burri, K.; Gromke, C.; Leonard, K.C.; Graf, F. Spatial patterns of aeolian sediment deposition in vegetation canopies: Observations from wind tunnel experiments using colored sand. Aeolian Res. 2013, 8, 65–73. [Google Scholar] [CrossRef]
- Lee, J.-P.; Lee, E.-J.; Lee, S.-J. Shelter effect of a fir tree with different porosities. J. Mech. Sci. Technol. 2014, 28, 565–572. [Google Scholar] [CrossRef]
- Wu, X.; Zou, X.; Zhou, N.; Zhang, C.; Shi, S. Deceleration efficiencies of shrub windbreaks in a wind tunnel. Aeolian Res. 2015, 16, 11–23. [Google Scholar] [CrossRef]
- Hesp, P.A.; Smyth, T.A.G. Nebkha flow dynamics and shadown dune formation. Geomorphology 2017, 282, 27–38. [Google Scholar] [CrossRef]
- Mayaud, J.R.; Wiggs, G.F.S.; Bailey, R.M. Characterizing turbulent wind flow around dryland vegetation. Earth Surf. Process. Landf. 2016, 41, 1421–1436. [Google Scholar] [CrossRef]
- Hagen, L.J.; Skidmore, E.L. Turbulent velocity fluctuations and vertical flow as affected by windbreak porosity. Trans. Am. Soc. Agric. Eng. 1971, 14, 634–637. [Google Scholar]
- Perera, M.D. Shelter behind two-dimensional solid and porous fences. J. Wind Eng. Ind. Aerodyn. 1981, 8, 93–104. [Google Scholar] [CrossRef]
- Gross, G. A numerical study of the air flow within and around a single tree. Bound. Layer Meteorol. 1987, 40, 311–327. [Google Scholar] [CrossRef]
- Kim, H.B.; Lee, S.-J. The structure of turbulent shear flow around a two-dimensional porous fence having a bottom gap. J. Fluids Struct. 2002, 16, 317–329. [Google Scholar] [CrossRef]
- Endalew, A.M.; Hertog, M.; Gebrehiwot, M.G.; Baelmans, M.; Ramon, H.; Nicolaï, B.M.; Verboven, P. Modelling airflow within model plant canopies using an integrated approach. Comput. Electron. Agric. 2009, 66, 9–24. [Google Scholar] [CrossRef]
- Lee, B.E.; Soliman, B.F. An investigation of the forces on three-dimensional bluff bodies in rough wall turbulent boundary layer. J. Fluids 1977, 99, 503–509. [Google Scholar] [CrossRef]
- King, J.; Nickling, W.G.; Gillies, J.A. Representation of vegetation and other non-erodible elements in aeolian shear stress partitioning models for predicting transport threshold. J. Geophys. Res. 2005, 110, F04015. [Google Scholar] [CrossRef]
- Liu, S.; Wul, H.; Lytton, R.L.; Sharpe, P.J. Aerodynamic sheltering effects of vegetative arrays on wind erosion: A numerical approach. J. Environ. Manag. 1990, 30, 281–294. [Google Scholar] [CrossRef]
- Ash, J.E.; Wasson, R.H. Vegetation and sand mobility in the Australian desert dunefield. Z. Geomorphol. 1983, 45, 7–25. [Google Scholar]
- Walter, B.; Gromke, C.; Leonard, K.C.; Manes, C.; Lehning, M. Spatio-temporal surface shear-stress variability in live plant canopies and cube arrays. Bound. Layer Meteorol. 2012, 143, 337–356. [Google Scholar] [CrossRef]
- Breshears, D.D.; Whicker, J.J.; Zou, C.B.; Field, J.P.; Allen, C.D. A conceptual framework for dryland aeolian sediment transport along the grassland–forest continuum: Effects of woody plant canopy cover and disturbance. Geomorphology 2009, 105, 28–38. [Google Scholar] [CrossRef]
- Wiggs, G.F.S.; Livingstone, I.; Thomas, D.S.G.; Bullard, J.E. Effect of vegetation removal on airflow patterns and dune dynamics in the southwest Kalahari Desert. Land Degrad. Rehabil. 1994, 5, 13–24. [Google Scholar] [CrossRef]
- Mayaud, J.R.; Wiggs, G.F.S.; Bailey, R.M. Dynamics of skimming flow in the wake of a vegetation patch. Aeolian Res. 2016, 22, 141–151. [Google Scholar] [CrossRef]
- Burri, K.; Gromke, C.; Lehning, M.; Graf, F. Aeolian sediment transport over vegetation canopies: A wind tunnel study with live plants. Aeolian Res. 2011, 3, 205–213. [Google Scholar] [CrossRef]
- Youssef, F.; Visser, S.M.; Karssenberg, D.; Erpul, G.; Cornelis, W.M.; Gabriels, D.; Poortinga, A. The effect of vegetation patterns on wind-blown mass transport at the regional scale: A wind tunnel experiment. Geomorphology 2012, 159–160, 178–188. [Google Scholar] [CrossRef]
- Gash, J.H.C. Observations of turbulence downwind of a forest-heath interface. Bound. Layer Meteorol. 1986, 36, 227–237. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Black, T.A.; Novak, M.D. E-ε modelling of turbulent air flow downwind of a model forest edge. Bound. Layer Meteorol. 1996, 77, 21–44. [Google Scholar] [CrossRef]
- Belcher, S.; Jerram, N.; Hunt, J. Adjustment of a turbulent boundary layer to a “canopy” of roughness elements. J. Fluid Mech. 2003, 488, 369–398. [Google Scholar] [CrossRef]
- Frank, C.; Ruck, B. Numerical study of the airflow over forest clearings. Forestry 2008, 81, 259–277. [Google Scholar] [CrossRef]
- Le, H.; Moin, P.; Kim, J. Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef]
- Wengle, H.; Huppertz, A.; Bärwolff, G.; Janke, G. Manipulated transitional backward-facing step flow: An experimental and direct numerical simulation investigation. Eur. J. Mech. 2001, 20, 25–46. [Google Scholar] [CrossRef]
- Gillies, J.A.; Nickling, W.G.; Nickolich, G.; Etyemezian, V. A wind tunnel study of the aerodynamic and sand trapping properties of porous mesh 3-dimensional roughness elements. Aeolian Res. 2017, 25, 23–35. [Google Scholar] [CrossRef]
- Raupach, M.R.; Lu, H. Representation of land-surface processes in aeolian transport models. Environ. Model. Softw. 2004, 19, 93–112. [Google Scholar] [CrossRef]
- Raupach, M.R.; Woods, N.; Dorr, G.; Leys, J.F.; Cleugh, H.A. The entrapment of particles by windbreaks. Atmos. Environ. 2001, 35, 3373–3383. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, Y. A new parameterization of particle dry deposition over rough surfaces. Atmos. Chem. Phys. 2014, 14, 12429–12440. [Google Scholar] [CrossRef]
- Minvielle, F.; Marticorena, B.; Gillette, D.A.; Lawson, R.E.; Thompson, R.; Bergametti, G. Relationship between the aerodynamic roughness length and the roughness density in cases of low roughness density. Environ. Fluid Mech. 2003, 3, 249–267. [Google Scholar] [CrossRef]
- Grant, P.F.; Nickling, W.G. Direct field measurement of wind drag on vegetation for application to windbreak design and modeling. Land Degrad. Dev. 1998, 9, 57–66. [Google Scholar] [CrossRef]
- Taylor, P.A. Turbulent wakes in the boundary layer. In Flow and Transport in the Natural Environment: Advances and Applications; Steffen, W.L., Denmead, O.T., Eds.; Springer: Berlin, Germany, 1988; pp. 270–292. [Google Scholar]
- Wang, H.; Takle, E.S. Momentum budget and shelter mechanism of bounda-layer flow near a shelterbelt. Bound. Layer Meteorol. 1996, 82, 417–435. [Google Scholar] [CrossRef]
- Vigiak, O.; Sterk, G.; Warren, A.; Hagen, L.J. Spatial modeling of wind speed around windbreaks. Catena 2003, 52, 273–288. [Google Scholar] [CrossRef]
- Cornelis, W.M.; Gabriels, D. Optimal windbreak design for wind-erosion control. J. Arid Environ. 2005, 61, 315–332. [Google Scholar] [CrossRef]
- Musick, H.B.; Trujillo, S.M.; Truman, C.R. Wind-tunnel modelling of the influence of vegetation structure on saltation threshold. Earth Surf. Process. Landf. 1996, 21, 589–605. [Google Scholar] [CrossRef]
- Lee, S.-J.; Park, K.C.; Park, C.W. Wind tunnel observations about the shelter effect of porous fences on the sand particle movements. Atmos. Environ. 2002, 36, 1453–1463. [Google Scholar] [CrossRef]
- Bradley, E.F.; Mulhearn, P.J. Development of velocity and shear-stress distributions in the wake of a porous shelter fence. J. Wind Eng. Ind. Aerodyn. 1983, 15, 145–156. [Google Scholar] [CrossRef]
- Gillies, J.A.; Etyemezian, V.; Nikolich, G.; Glick, R.; Rowland, P.; Pesce, T.; Skinner, M. Effectiveness of an array of porous fences to reduce sand flux: Oceano Dunes, Oceano CA. J. Wind Eng. Ind. Aerodyn. 2017, 168, 247–259. [Google Scholar] [CrossRef]
- Walter, B.; Gromke, C.; Leonard, K.; Clifton, A.; Lehning, M. Spatially resolved skin friction velocity measurements using Irwin sensors: A calibration and accuracy analysis. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 314–321. [Google Scholar] [CrossRef]
- Wilson, J.D.; Yee, E. Calculation of winds disturbed by an array of fences. Agric. For. Meteorol. 2003, 115, 31–50. [Google Scholar] [CrossRef]
- Hagen, L.J. WEPS: Wind Erosion Prediction System, Technical Documentation; Wind Erosion Research Unit: Manhattan, NY, USA, 1996. [Google Scholar]
- McKenna-Neuman, C.; Bédard, O. A wind tunnel study of flow structure adjustment on deformable sand beds containing a surface-mounted obstacle. J. Geophys. Res. Earth Surf. 2015, 120, 1824–1840. [Google Scholar] [CrossRef]
- Clifford, N.J.; French, J.R. Monitoring and modelling turbulent flows: Historical and contemporary perspectives. In Turbulence: Perspectives on Flow and Sediment Transport; Clifford, N.J., French, J.R., Hardisty, J., Eds.; John Wiley & Sons: New York, NY, USA, 1993; pp. 1–34. [Google Scholar]
- Butterfield, G.R. Grain transport rates in steady and unsteady turbulent airflows. Acta Mech. 1991, 1, 97–122. [Google Scholar]
- Sterk, G.; Jacobs, A.F.G.; van Boxel, J.H. The effect of turbulent flow structures on saltation sand transport in the atmospheric boundary layer. Earth Surf. Process. Landf. 1998, 23, 877–887. [Google Scholar] [CrossRef]
- Namikas, S.L.; Bauer, B.O.; Sherman, D.J. Influence of averaging interval on shear velocity estimates for aeolian transport modelling. Geomorphology 2003, 53, 235–246. [Google Scholar] [CrossRef]
- Schönfeldt, H.J.; von Löwis, S. Turbulence-driven saltation in the atmospheric surface layer. Meteorol. Z. 2003, 12, 257–268. [Google Scholar] [CrossRef]
- Baas, A.C.W.; Sherman, D.J. Formation and behaviour of aeolian streamers. J. Geophys. Res. 2005, 110, F03011. [Google Scholar] [CrossRef]
- Baas, A.C.W.; Sherman, D.J. Spatiotemporal variability of aeolian sand transport in a coastal dune environment. J. Coast. Res. 2005, 22, 1198–1205. [Google Scholar] [CrossRef]
- Leenders, J.K.; van Boxel, J.H.; Sterk, G. Wind forces and related saltation transport. Geomorphology 2005, 71, 357–372. [Google Scholar] [CrossRef]
- Weaver, C.M.; Wiggs, G.F.S. Field measurements of mean and turbulent airflow over a barchan sand dune. Geomorphology 2011, 128, 32–41. [Google Scholar] [CrossRef]
- Wiggs, G.F.S.; Weaver, C.M. Turbulent flow structures and aeolian sediment transport over a barchan sand dune. Geophys. Res. Lett. 2012, 39, 1–7. [Google Scholar] [CrossRef]
- Mayaud, J.R.; Bailey, R.M.; Wiggs, G.F.S. Modelling aeolian sand transport using a dynamic mass balancing approach. Geomorphology 2016, 280, 108–121. [Google Scholar] [CrossRef]
- Musick, H.B.; Gillette, D.A. Field evaluation of relationships between a vegetation structural parameter and sheltering against wind erosion. Land Degrad. Rehabil. 1990, 2, 87–94. [Google Scholar] [CrossRef]
- Schlichting, H. Experimentelle untersuchungen zum Rauhigkeitsproblem. Ing.-Arch. 1936, 7, 1–34. [Google Scholar] [CrossRef]
- Marshall, J.K. Drag measurements in roughness arrays of varying densities and distribution. Agric. Meteorol. 1971, 8, 269–292. [Google Scholar] [CrossRef]
- Marticorena, B.; Bergametti, G. Modeling the atmospheric dust cycle: 1. Design of a soil-derived dust emission scheme. J. Geophys. Res. 1995, 100, 16415. [Google Scholar] [CrossRef]
- Brown, S.; Nickling, W.G.; Gillies, J.A. A wind tunnel examination of shear stress partitioning for an assortment of surface roughness distributions. J. Geophys. Res. 2008, 113, F02S06. [Google Scholar] [CrossRef]
- Lyles, L.; Schrandt, R.L.; Schmeidler, N.F. How aerodynamic roughness elements control sand movement. Trans. ASAE 1974, 17, 134–139. [Google Scholar] [CrossRef]
- Raupach, M.R.; Gillette, D.A.; Leys, J.F. The effect of roughness elements on wind erosion threshold. J. Geophys. Res. 1993, 98, 3023–3029. [Google Scholar] [CrossRef]
- Shao, Y.; Yang, Y. A scheme for drag partition over rough surfaces. Atmos. Environ. 2005, 39, 7351–7361. [Google Scholar] [CrossRef]
- Shao, Y.; Yang, Y. A theory for drag partition over rough surfaces. J. Geophys. Res. 2008, 113, F02S05. [Google Scholar] [CrossRef]
- Lancaster, N. Development of linear dunes in the southwestern Kalahari, southern Africa. J. Arid Environ. 1988, 14, 233–244. [Google Scholar]
- Molina-Aiz, F.D.; Valera, D.L.; Álvarez, A.J.; Madueño, A. A wind tunnel study of airflow through horticultural crops: Determination of the drag coefficient. Biosyst. Eng. 2006, 93, 447–457. [Google Scholar] [CrossRef]
- Udo, K.; Takewaka, S. Experimental study of blown sand in a vegetated area. J. Coast. Res. 2007, 23, 1175–1182. [Google Scholar] [CrossRef]
- Wuyts, K.; Verheyen, K.; De Schrijver, A.; Cornelis, W.M.; Gabriels, D. The impact of forest edge structure on longitudinal patterns of deposition, wind speed, and turbulence. Atmos. Environ. 2008, 42, 8651–8660. [Google Scholar] [CrossRef]
- Sherman, D.; Farrell, E. Aerodynamic roughness lengths over movable beds: Comparison of wind tunnel and field data. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Li, B.; Neuman, M.C. Boundary-layer turbulence characteristics during aeolian saltation. Geophys. Res. Lett. 2012, 39, L11402. [Google Scholar] [CrossRef]
- Martin, R.L.; Kok, J.F. Linear scaling of wind-driven sand flux with shear stress. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Kang, J.-H.; Lee, S.-J. Wind tunnel observation on the effect of a porous wind fence on shelter of saltating sand particles. Geomorphology 2010, 120, 224–232. [Google Scholar] [CrossRef]
- Wiggs, G.F.S.; Thomas, D.S.G.; Bullard, J.E.; Livingstone, I. Dune mobility and vegetation cover in the southwest Kalahari Desert. Earth Surf. Process. Landf. 1995, 20, 515–529. [Google Scholar] [CrossRef]
- Lancaster, N.; Baas, A. Influence of vegetation cover on sand transport by wind: Field studies at Owens Lake, California. Earth Surf. Process. Landf. 1998, 23, 69–82. [Google Scholar] [CrossRef]
- Munson, S.M.; Belnap, J.; Okin, G.S. Responses of wind erosion to climate-induced vegetation changes on the Colorado Plateau. Proc. Natl. Acad. Sci. USA 2011, 108, 3854–3859. [Google Scholar] [CrossRef] [PubMed]
- Webb, N.P.; Herrick, J.E.; Duniway, M.C. Ecological site-based assessments of wind and water erosion: Informing accelerated soil erosion management in rangelands. Ecol. Appl. 2014, 24, 1405–1420. [Google Scholar] [CrossRef]
- Turpin, C.; Badr, T.; Harion, J.-L. Numerical modeling of aeolian erosion over rough surfaces. Earth Surf. Process. Landf. 2010, 35, 1418–1429. [Google Scholar] [CrossRef]
- Chepil, W.S. Utilization of crop residue for wind erosion control. Sci. Agric. 1944, 24, 307–319. [Google Scholar]
- Siddoway, F.H.; Chepil, W.S.; Armbrust, D.V. Effect of kind, and placement of residue on wind erosion control. Trans. ASAE 1965, 8, 327–331. [Google Scholar] [CrossRef]
- Lyles, L.; Allison, B.E. Wind erosion: The protective role of simulated standing stubble. Trans. ASAE 1976, 19, 61–64. [Google Scholar] [CrossRef]
- King, J.; Nickling, W.G.; Gillies, J.A. Aeolian shear stress ratio measurements within mesquite-dominated landscapes of the Chihuahuan Desert, New Mexico, USA. Geomorphology 2006, 82, 229–244. [Google Scholar] [CrossRef]
- Gillies, J.A.; Nickling, W.G.; King, J. Aeolian sediment transport through large patches of roughness in the atmospheric inertial sublayer. J. Geophys. Res. 2006, 111, F02006. [Google Scholar] [CrossRef]
- Gillies, J.A.; Nickling, W.G.; King, J. Shear stress partitioning in large patches of roughness in the atmospheric inertial sublayer. Bound. Layer Meteorol. 2007, 122, 367–396. [Google Scholar] [CrossRef]
- Gillies, J.A.; Nickling, W.G.; King, J.; Lancaster, N. Modeling aeolian sediment transport thresholds on physically rough Martian surfaces: A shear stress partitioning approach. Geomorphology 2010, 121, 15–21. [Google Scholar] [CrossRef]
- Okin, G.S.; Gillette, D.A. Distribution of vegetation in wind-dominated landscapes: Implications for wind erosion modeling and landscape processes. J. Geophys. Res. 2001, 106, 9673–9683. [Google Scholar] [CrossRef]
- Lancaster, N.; Nickling, W.G.; Gillies, J.A. Sand transport by wind on complex surfaces: Field studies in the McMurdo Dry Valleys, Antarctica. J. Geophys. Res. 2010, 115, F03027. [Google Scholar] [CrossRef]
- Webb, N.P.; Okin, G.S.; Brown, S. The effect of roughness elements on wind erosion: The importance of surface shear stress distribution. J. Geophys. Res. Atmos. 2014, 119, 6066–6084. [Google Scholar] [CrossRef]
- Gillies, J.A.; Green, H.L.; McCarley-Holder, G.; Grimm, S.; Howard, C.; Barbieri, N.; Ono, D.; Schade, T. Using solid element roughness to control sand movement: Keeler Dunes, Keeler, California. Aeolian Res. 2015, 18, 35–46. [Google Scholar] [CrossRef]
- Chappell, A.; Webb, N.P. Using albedo to reform wind erosion modelling, mapping and monitoring. Aeolian Res. 2016, 23, 63–78. [Google Scholar] [CrossRef]
- Chen, Q.; Jia, L.; Hutjes, R.; Menenti, M. Estimation of aerodynamic roughness length over oasis in the Heihe River Basin by utilizing remote sensing and ground data. Remote Sens. 2015, 7, 3690–3709. [Google Scholar] [CrossRef]
- Yu, M.; Wu, B.; Yan, N.; Xing, Q.; Zhu, W. A method for estimating the aerodynamic roughness length with NDVI and BRDF signatures using multi-temporal Proba-V data. Remote Sens. 2017, 9, 6. [Google Scholar] [CrossRef]
- Shao, Y.; Nickling, W.; Bergametti, G.; Butler, H.; Chappell, A.; Findlater, P.; Gillies, J.; Ishizuka, M.; Klose, M.; Kok, J.F.; et al. A tribute to Michael R. Raupach for contributions to aeolian fluid dynamics. Aeolian Res. 2015, 19, 37–54. [Google Scholar] [CrossRef]
- Sankey, J.B.; Law, D.J.; Breshears, D.D.; Munson, S.M.; Webb, R.H. Employing lidar to detail vegetation canopy architecture for prediction of aeolian transport. Geophys. Res. Lett. 2013, 40, 1724–1728. [Google Scholar] [CrossRef]
- Herrick, J.E.; Van Zee, J.W.; McCord, S.E.; Courtright, E.M.; Karl, J.W.; Burkett, L.M. Monitoring Manual for Grassland, Shrubland, and Savanna Ecosystems, Volume 1: Core Methods, 2nd ed.; USDA-ARS Jornada Experimental Range: Las Cruces, NM, USA, 2017; Available online: http://www.landscapetoolbox.org/manuals/monitoring-manual/ (accessed on 1 January 2017).
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called ‘Echidna’. Tree Physiol. 2008, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Karl, J.W.; Duniway, M.C.; Schrader, T.S. A technique for estimating rangeland canopy-gap size distributions from high-resolution digital imagery. Rangel. Ecol. Manag. 2011, 65, 196–207. [Google Scholar] [CrossRef]
- Shao, Y. Physics and Modelling of Wind Erosion; Kluwer Academic Publishers: London, UK, 2008. [Google Scholar]
- Ito, A.; Kok, J.F. Do dust emissions from sparsely vegetated regions dominate atmospheric iron supply to the Southern Ocean? J. Geophys. Res. Atmos. 2017, 122, 3987–4002. [Google Scholar] [CrossRef]
- Galloza, M.S.; Webb, N.P.; Bleiweiss, M.P.; Winters, C.; Herrick, J.E.; Ayers, E. Resolving dust emission responses to land cover change using an ecological land classification. Aeolian Res. 2017, in press. [Google Scholar]
- Greeley, R.; Gaddis, L.; Lancaster, N.; Dobrovolskies, A.; Iversen, J.; Rasmussen, K.; Saunders, S.; van Zyl, J.; Wall, S.; Zebker, H.; et al. Assessment of aerodynamic roughness via airborne radar observations. Acta Mech. 1991, 2, 77–88. [Google Scholar]
- Greeley, R.; Blumberg, D.G.; McHone, J.F.; Dobrovolskis, A.; Iversen, J.D.; Lancaster, N.; Rasmussen, K.R.; Wall, S.D.; White, B.R. Applications of spaceborne radar laboratory data to the study of aeolian processes. J. Geophys. Res. 1997, 102, 10971–10983. [Google Scholar] [CrossRef]
- Marticorena, B.; Chazette, P.; Bergametti, G.; Dulac, F.; Legrand, M. Mapping the aerodynamic roughness length of desert surfaces from the POLDER/ADEOS bidirectional reflectance product. Int. J. Remote Sens. 2004, 25, 603–626. [Google Scholar] [CrossRef]
- Marticorena, B.; Kardous, M.; Bergametti, G.; Callot, Y.; Chazette, P.; Khatteli, H.; Le Hegarat-Mascle, S.; Maille, M.; Rajot, J.-L.; Vidal-Madjar, D.; et al. Surface and aerodynamic roughness in arid and semiarid areas and their relation to radar backscatter coefficient. J. Geophys. Res. 2006, 111, F03017. [Google Scholar] [CrossRef]
- Chappell, A.; Heritage, G.L. Using illumination and shadow to model aerodynamic resistance and flow separation: An isotropic study. Atmos. Environ. 2007, 41, 5817–5830. [Google Scholar] [CrossRef]
- Chappell, A.; Van Pelt, S.; Zobeck, T.; Dong, Z. Estimating aerodynamic resistance of rough surfaces using angular reflectance. Remote Sens. Environ. 2010, 114, 1462–1470. [Google Scholar] [CrossRef]
- Dupont, S.; Bergametti, G.; Marticorena, B.; Simoëns, S. Modeling saltation intermittency. J. Geophys. Res. Atmos. 2013, 118, 1–20. [Google Scholar] [CrossRef]
- Maruyama, T. Large eddy simulation of turbulent flow around a windbreak. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1998–2006. [Google Scholar] [CrossRef]
- Schröttle, J.; Dörnbrack, A. Turbulence structure in a diabatically heated forest canopy composed of fractal Pythagoras trees. Theor. Comput. Fluid Dyn. 2012, 27, 337–359. [Google Scholar] [CrossRef]
- Schwämmle, V.; Herrmann, H.J. A model for barchan dunes including lateral shear stress. Eur. Phys. J. E 2005, 16, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Hermann, H.J.; Duran, O.; Parteli, E.J.R.; Schatz, V. Vegetation and induration as sand dunes stabilizators. J. Coast. Res. 2008, 24, 1357–1368. [Google Scholar] [CrossRef]
- Durán, O.; Hermann, H.J. Vegetation against dune mobility. Phys. Rev. Lett. 2006, 97, 188001. [Google Scholar] [CrossRef] [PubMed]
- Turnbull, L.; Hochstrasser, T.; Wieczorek, M.; Baas, A.; Wainwright, J.; Scarsoglio, S.; Tietjen, B.; Jeltsch, F.; Mueller, E.N. Approaches to modelling ecogeomorphic systems. In Patterns of Land Degradation in Drylands: Understanding Self-Organised Ecogeomorphic Systems; Mueller, E.N., Wainwright, J., Parsons, A.J., Turnbull, L., Eds.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Narteau, C.; Lajeunesse, E.; Métivier, F.; Rozier, O. Modelling of dune patterns by short range interactions. River Coast. Estuar. Morphodyn. 2006, 2, 1035–1046. [Google Scholar]
- Baas, A.C.W. Complex systems in aeolian geomorphology. Geomorphology 2007, 91, 311–331. [Google Scholar] [CrossRef]
- Nield, J.M.; Baas, A.C.W. The influence of different environmental and climatic conditions on vegetated aeolian dune landscape development and response. Glob. Planet. Chang. 2008, 64, 76–92. [Google Scholar] [CrossRef]
- Peters, D.P.C.; Bestelmeyer, B.T.; Herrick, J.E.; Monger, H.C.; Fredrickson, E.; Havstad, K.M. Disentangling complex landscapes: New insights to forecasting arid and semiarid system dynamics. BioScience 2006, 56, 491–501. [Google Scholar] [CrossRef]
- Okin, G.S.; Parsons, A.J.; Wainwright, J.; Herrick, J.E.; Bestelmeyer, B.T.; Peters, D.C.; Fredrickson, E.L. Do changes in connectivity explain desertification? Bioscience 2009, 59, 237–244. [Google Scholar] [CrossRef]
- Turnbull, L.; Wainwright, J.; Brazier, R.E. A conceptual framework for understanding semi-arid land degradation: Ecohydrological interactions across multiple-space and time scales. Ecohydrology 2008, 1, 23–34. [Google Scholar] [CrossRef]
- Turnbull, L.; Wilcox, B.; Belnap, J. Understanding the role of ecohydrological feedbacks in ecosystem state change in drylands. Ecohydrology 2012, 183, 174–183. [Google Scholar] [CrossRef]
- Yan, N.; Baas, A.C.W. Environmental controls, morphodynamic processes, and ecogeomorphic interactions of barchan to parabolic dune transformations. Geomorphology 2017, 278, 209–237. [Google Scholar] [CrossRef]
- Omasa, K.; Hosoi, F.; Konishi, A. 3D lidar imaging for detecting and understanding plant responses and canopy structure. J. Exp. Bot. 2007, 58, 881–898. [Google Scholar] [CrossRef] [PubMed]
- Cruzan, M.B.; Weinstein, B.G.; Grasty, M.R.; Kohrn, B.F.; Hendrickson, E.C.; Arredondo, T.M.; Thompson, P.G. Small unmanned aerial vehicles (micro-UAVs, drones) in plant ecology. Appl. Plant Sci. 2016, 4. [Google Scholar] [CrossRef] [PubMed]
- Fonstad, M.A.; Marcus, W.A. High resolution, basin extent observations and implications for understanding river form and process. Earth Surf. Process. Landf. 2010, 35, 680–698. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res. Earth Surf. 2012, 117, F03017. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Nield, J.M.; King, J.; Wiggs, G.F.S.; Leyland, J.; Bryant, R.G. Estimating aerodynamic roughness over complex surface terrain. J. Geophys. Res. Atmos. 2013, 118, 12948–12961. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayaud, J.R.; Webb, N.P. Vegetation in Drylands: Effects on Wind Flow and Aeolian Sediment Transport. Land 2017, 6, 64. https://doi.org/10.3390/land6030064
Mayaud JR, Webb NP. Vegetation in Drylands: Effects on Wind Flow and Aeolian Sediment Transport. Land. 2017; 6(3):64. https://doi.org/10.3390/land6030064
Chicago/Turabian StyleMayaud, Jerome R., and Nicholas P. Webb. 2017. "Vegetation in Drylands: Effects on Wind Flow and Aeolian Sediment Transport" Land 6, no. 3: 64. https://doi.org/10.3390/land6030064
APA StyleMayaud, J. R., & Webb, N. P. (2017). Vegetation in Drylands: Effects on Wind Flow and Aeolian Sediment Transport. Land, 6(3), 64. https://doi.org/10.3390/land6030064




