Predicting Heavy Metal and Nutrient Availability in Agricultural Soils Under Climatic Variability Using Regression and Mixed-Effects Models
Abstract
1. Introduction
2. Materials and Methods
2.1. The Study Area
2.2. Soil Chemical and Physical Analysis
2.3. Statistical Procedures and Modeling Libraries
2.4. Linear and Quadratic Regression Analysis
2.5. Robust Quadratic Regression (RQR) and Huber Approximation
2.6. Linear Mixed-Effects Models (LMMs)
2.7. Quadratic Mixed-Effects Models (QMMs)
3. Results and Discussion
3.1. Physicochemical Parameters of Soil Samples
3.2. Levels of Metal Concentrations
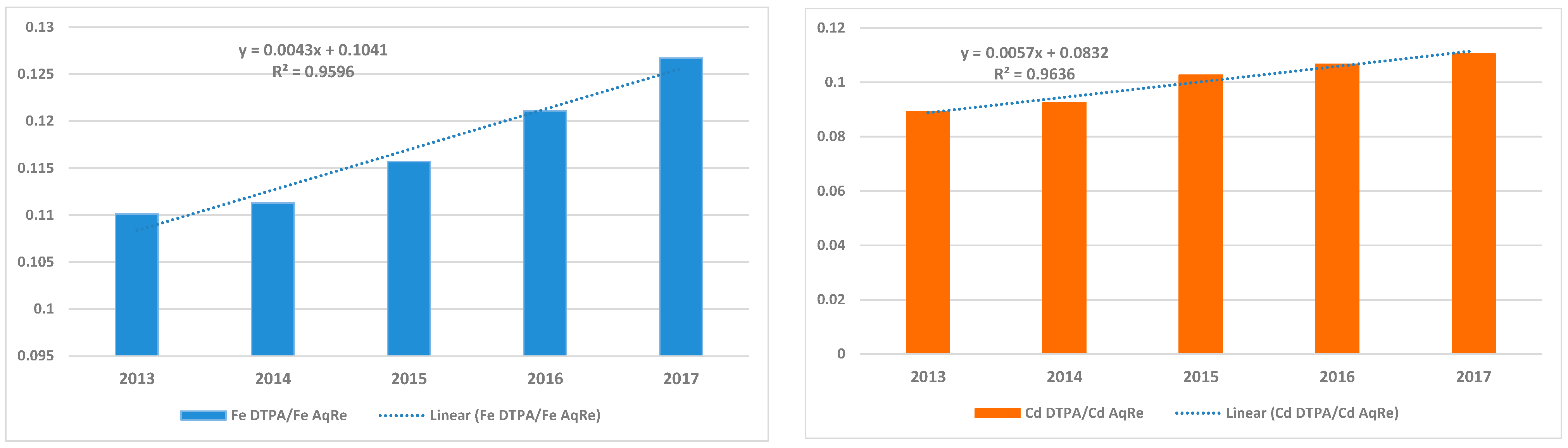
3.3. Available to Total Fe/Cd Concentrations
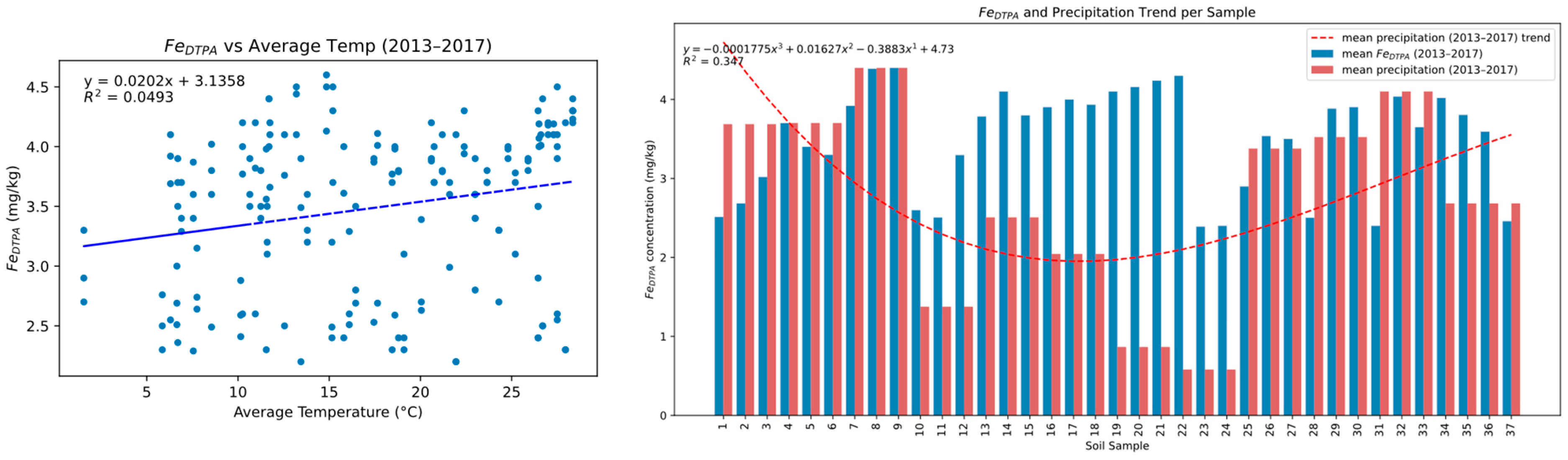
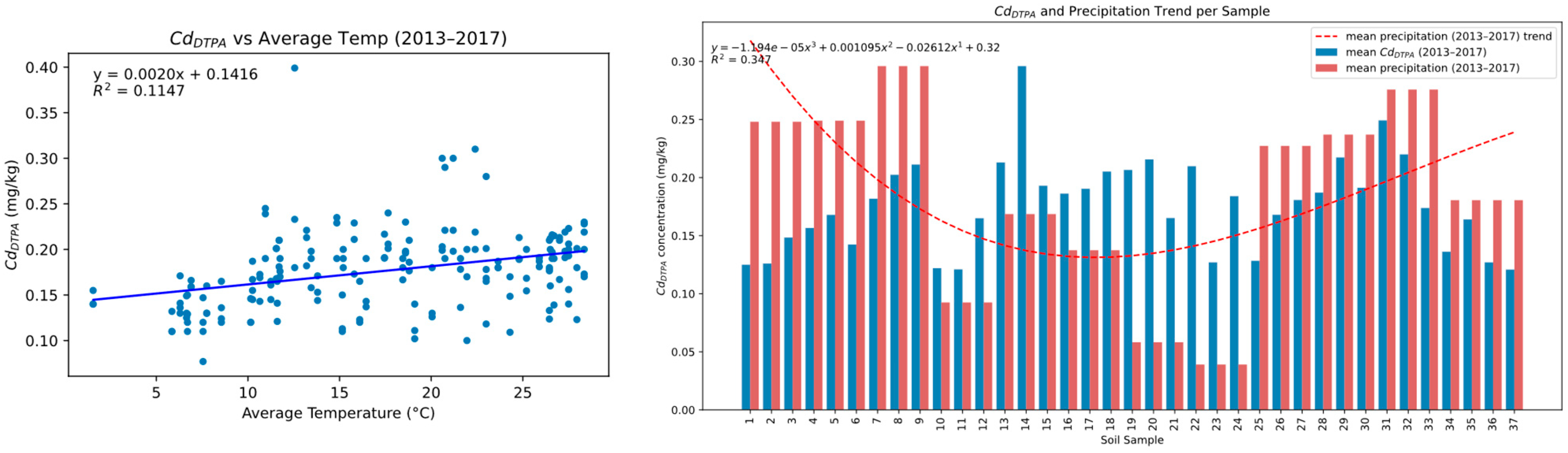
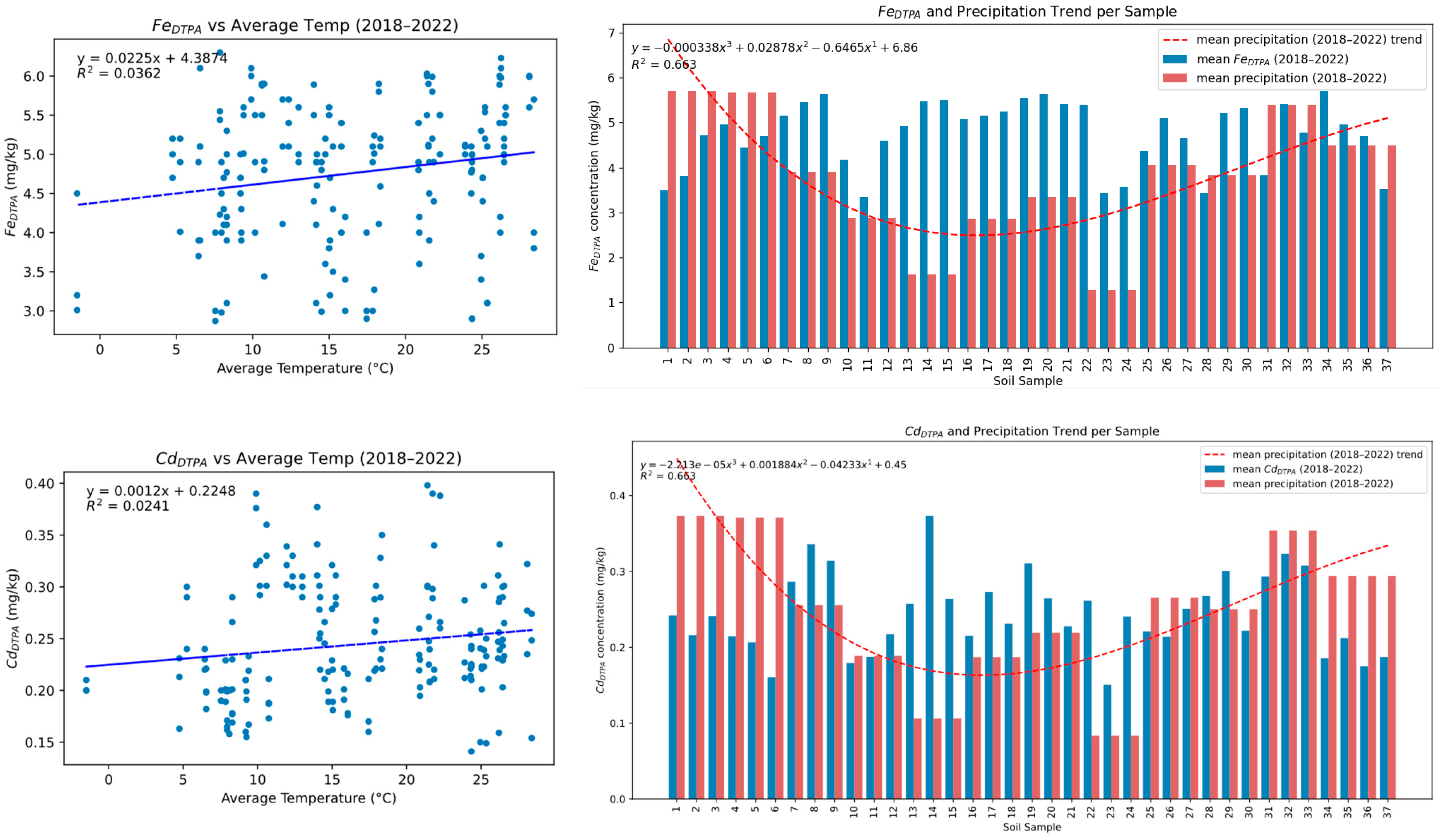
3.4. Climatic Influence on Fe and Cd Availability
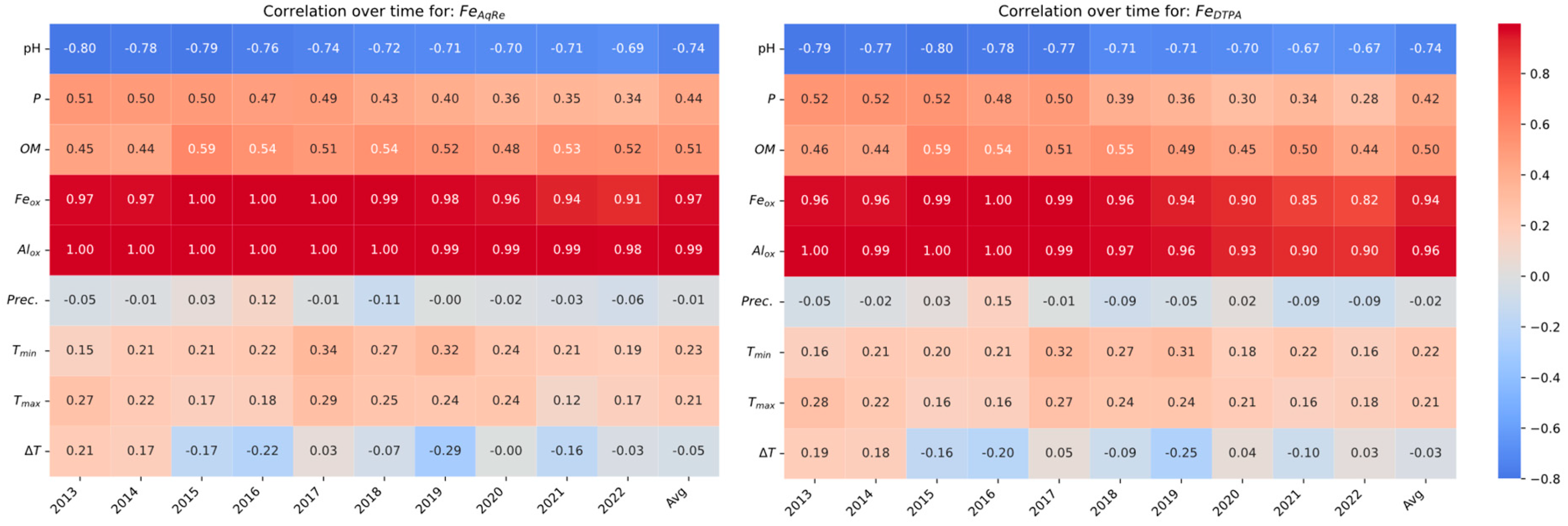
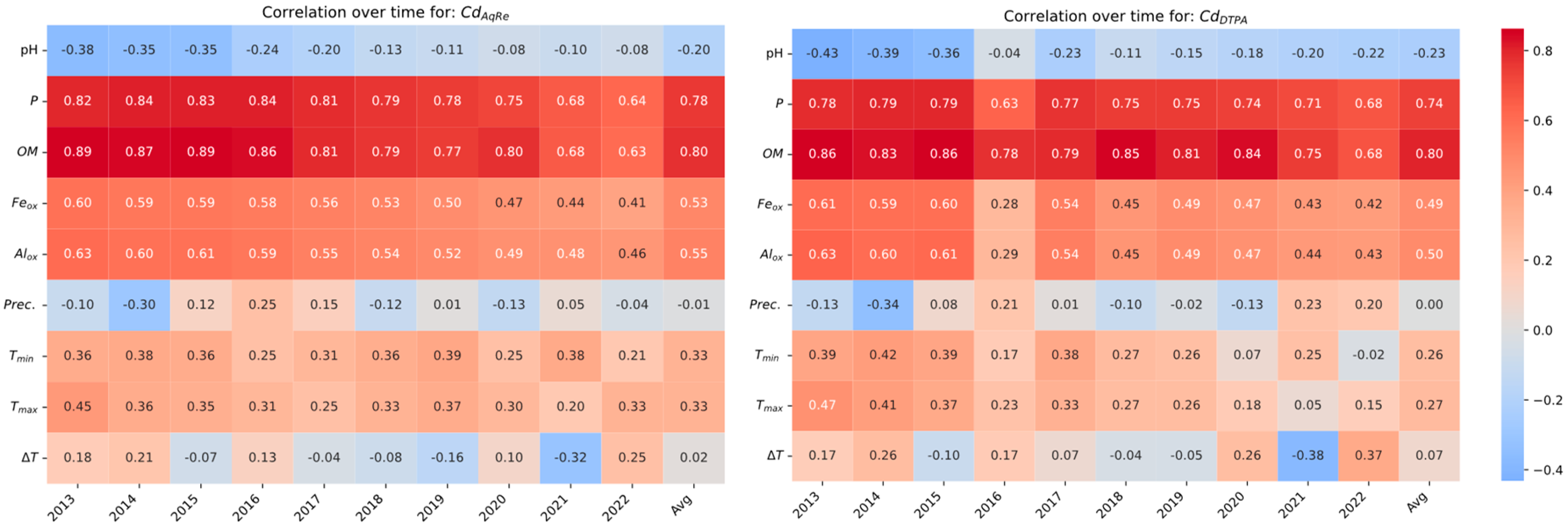
3.5. Spatial Correlation Trends over Time for Fe/Cd
3.6. Robust Quadratic Regression (RQR) Prediction of Metal Concentration
3.7. Linear Mixed-Effects Model (LMM) Prediction Formulae
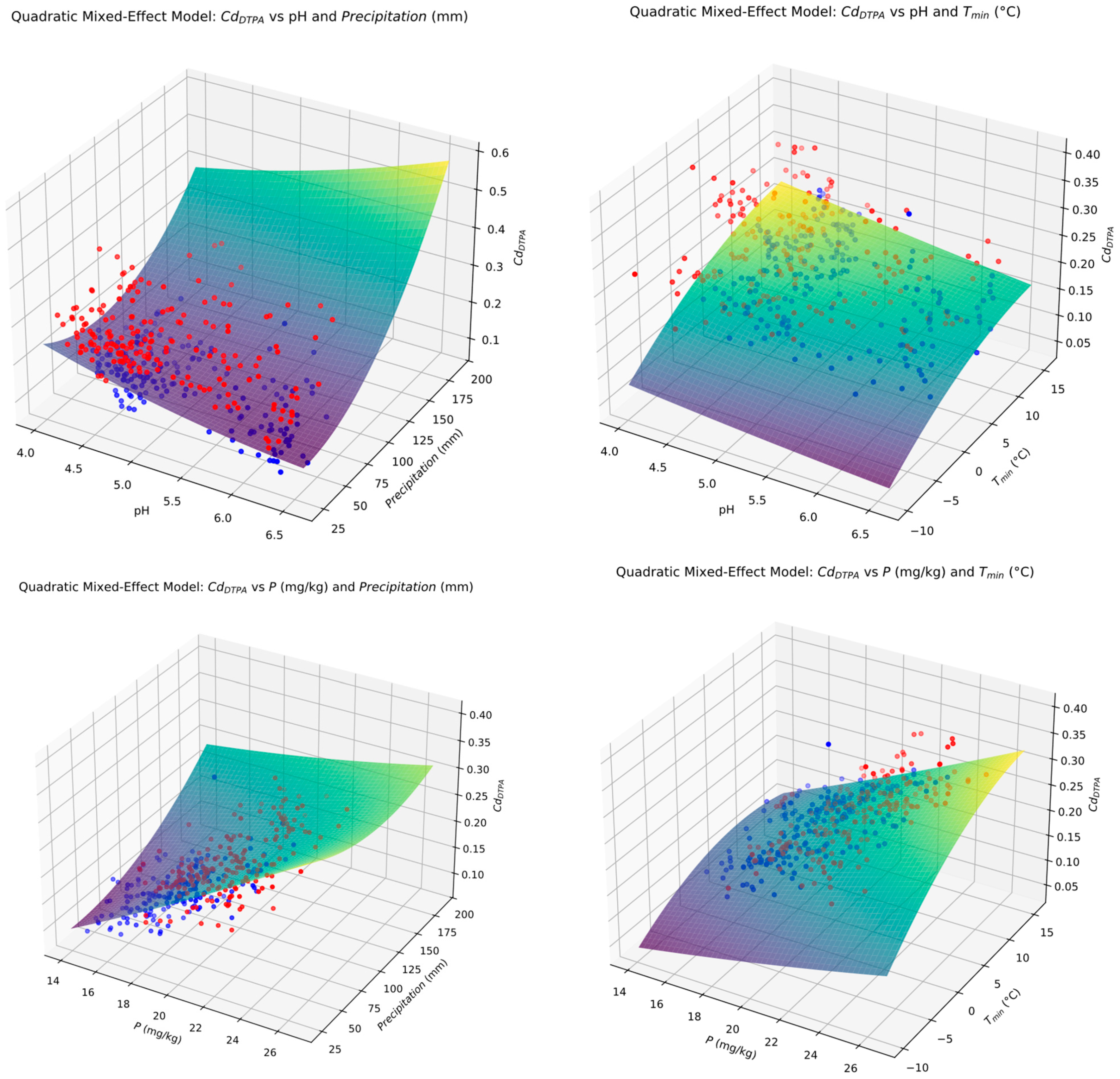
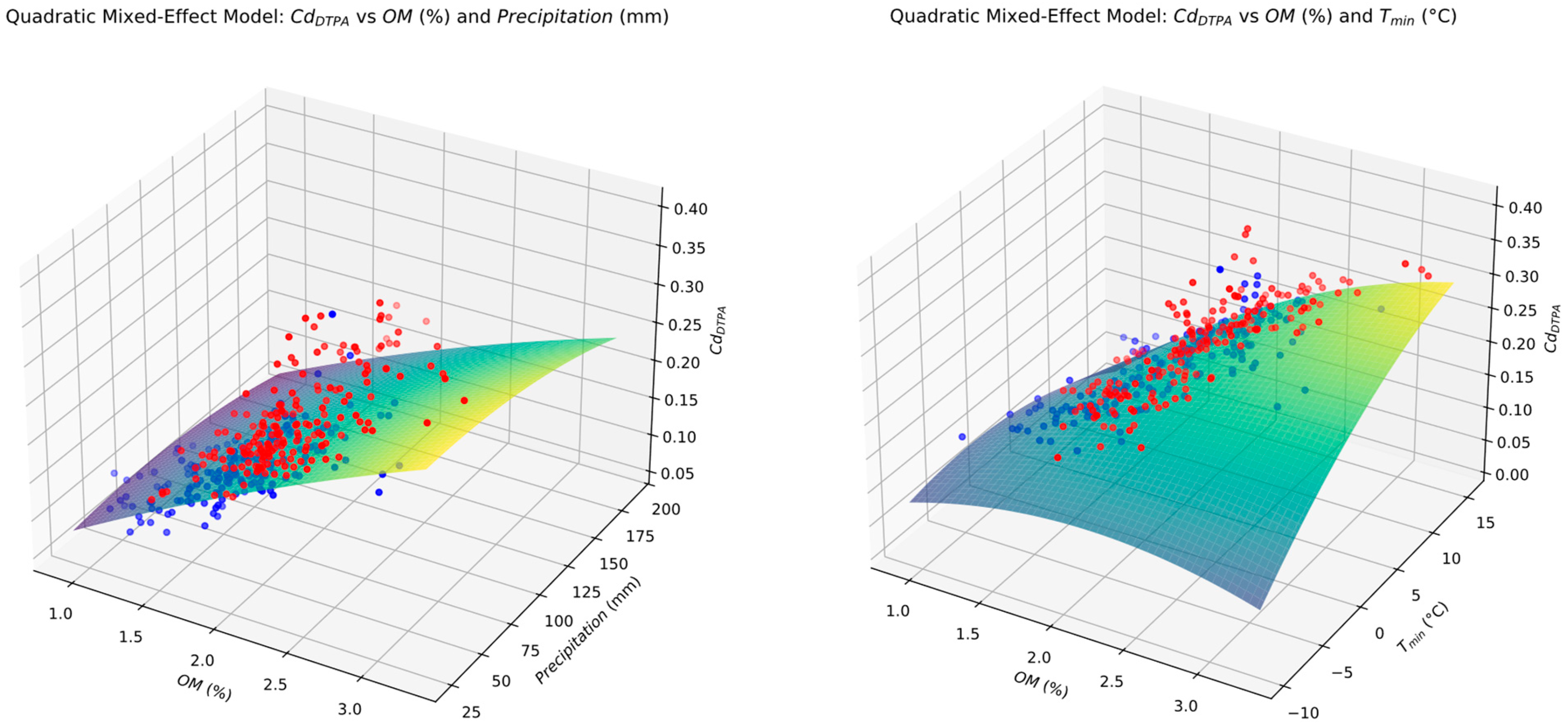
3.8. Quadratic Mixed Model (QMM) Prediction Formulae
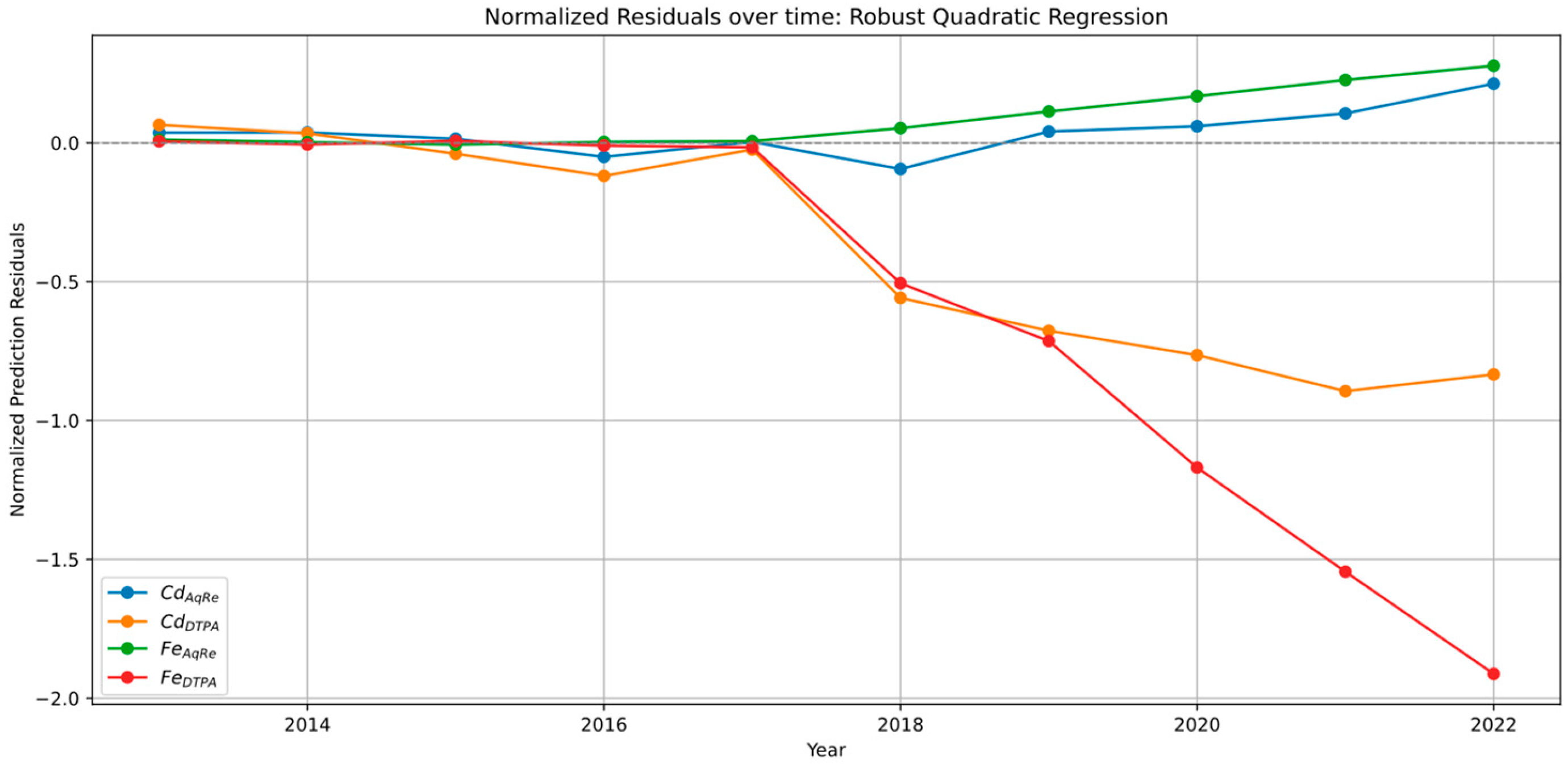
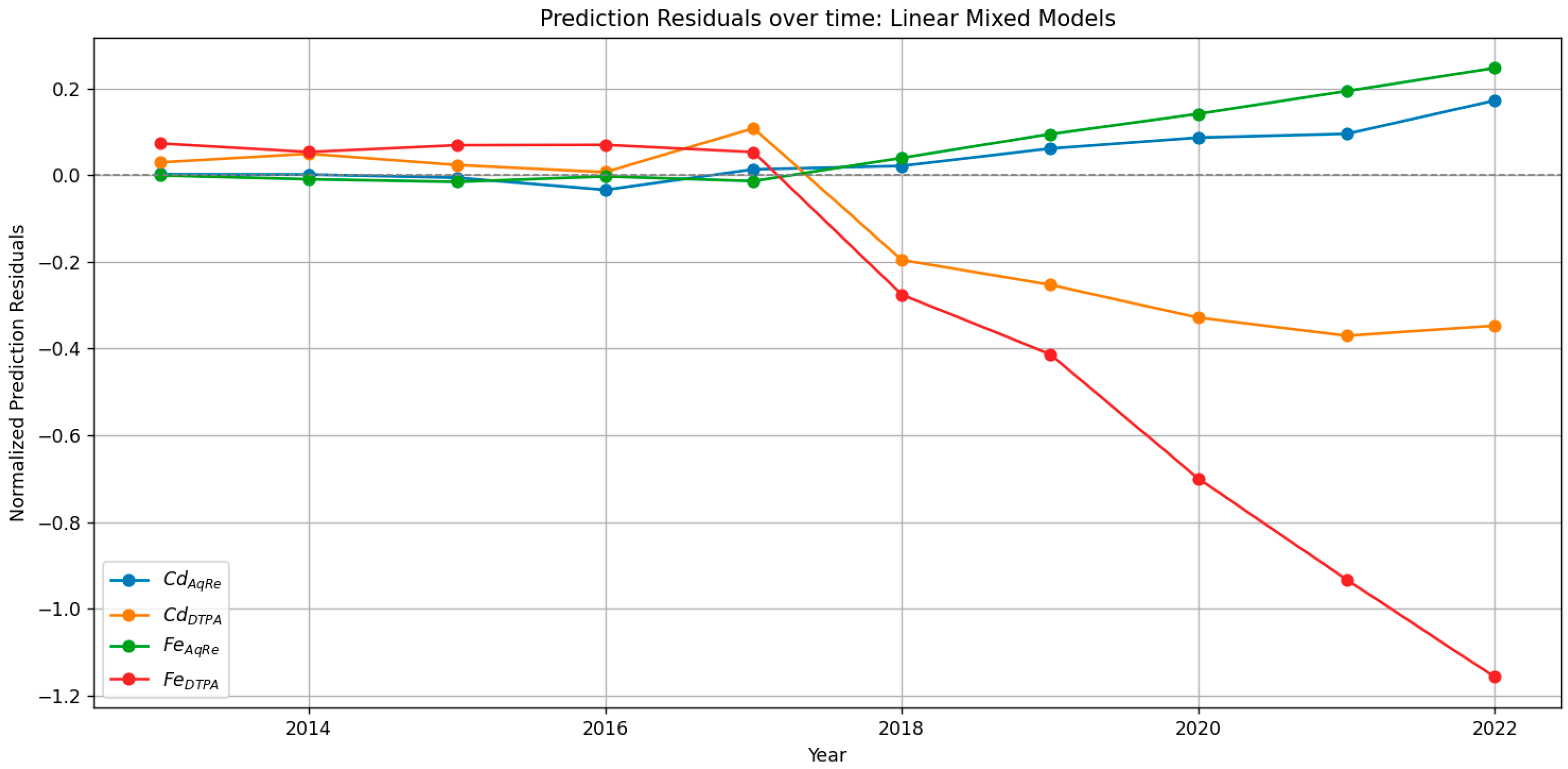
3.9. LMM and QMM Residuals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arafin, S.A.K.; Fazlul Hoque, A.K.M.; Abedin, M.J.; El-Taher, A. Heavy Metal Detection in Soil and Related Health Aspect at Aila Inundated Sundarban Region, Bangladesh. Int. J. Sci. Technol. Res. 2019, 8, 2702–2708. [Google Scholar]
- Luo, N. Methods for Controlling Heavy Metals in Environmental Soils Based on Artificial Neural Networks. Sci. Rep. 2024, 14, 2563. [Google Scholar] [CrossRef] [PubMed]
- Sodango, T.H.; Li, X.; Sha, J.; Bao, Z. Review of the Spatial Distribution, Source and Extent of Heavy Metal Pollution of Soil in China: Impacts and Mitigation Approaches. J. Health Pollut. 2018, 8, 53–70. [Google Scholar] [CrossRef] [PubMed]
- Golia, E.E.; Emmanouil, C.; Charizani, A.; Koropouli, A.; Kungolos, A. Assessment of Cu and Zn Contamination and Associated Human Health Risks in Urban Soils from Public Green Spaces in the City of Thessaloniki, Northern Greece. Euro-Mediterr. J. Environ. Integr. 2023, 8, 517–525. [Google Scholar] [CrossRef]
- Schwanen, C.A.; Stauch, G.; Schulte, P.; Schwarzbauer, J. Reconstruction of the Pollution History of the Urft Reservoir: An Organic-Geochemical Investigation. Environ. Sci. Eur. 2024, 36, 103. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Y.; Lan, X.; Yang, Y.; Wu, X.; Du, L. Comprehensive Assessment of Harmful Heavy Metals in Contaminated Soil in Order to Score Pollution Level. Sci. Rep. 2022, 12, 3552. [Google Scholar] [CrossRef]
- Qi, D.; Chen, H.; Hu, L.; Sun, J. Multimethod Analysis of Heavy Metal Pollution and Source Apportionment in a Southeastern Chinese Region. Appl. Sci. 2024, 14, 10559. [Google Scholar] [CrossRef]
- Golia, E.E.; Bethanis, J.; Xagoraris, C.; Tziourrou, P. Potentially Toxic Elements in Urban and Peri-Urban Soils—A Critical Meta-Analysis of Their Sources, Availability, Interactions, and Spatial Distribution. J. Ecol. Eng. 2024, 25, 335–350. [Google Scholar] [CrossRef]
- Chen, F.; Chen, X.; Zhu, F.; Sun, Q. Study on the Factors Affecting the Spatial Distribution of Heavy Metal Elements. IOP Conf. Ser. Earth Environ. Sci. 2019, 330, 042013. [Google Scholar] [CrossRef]
- Onwuka, B. Effects of Soil Temperature on Some Soil Properties and Plant Growth. Adv. Plants Agric. Res. 2018, 8, 34–37. [Google Scholar] [CrossRef]
- Xu, H.; Huang, L.; Chen, J.; Zhou, H.; Wan, Y.; Qu, Q.; Wang, M.; Xue, S. Changes in Soil Microbial Activity and Their Linkages with Soil Carbon under Global Warming. Catena 2023, 232, 107419. [Google Scholar] [CrossRef]
- Sun, W.; Li, S.; Zhang, G.; Fu, G.; Qi, H.; Li, T. Effects of Climate Change and Anthropogenic Activities on Soil PH in Grassland Regions on the Tibetan Plateau. Glob. Ecol. Conserv. 2023, 45, e02532. [Google Scholar] [CrossRef]
- Sebola Tshisikhawe, C.; Ngole-Jeme, V.M. Temperature Induced Changes on Heavy Metal Geochemical Partitioning and Mobility in Contaminated and Uncontaminated Soils. Environ. Pollut. Bioavailab. 2024, 36, 2317747. [Google Scholar] [CrossRef]
- Biswas, B.; Qi, F.; Biswas, J.K.; Wijayawardena, A.; Khan, M.A.I.; Naidu, R. The Fate of Chemical Pollutants with Soil Properties and Processes in the Climate Change Paradigm—A Review. Soil Syst. 2018, 2, 51. [Google Scholar] [CrossRef]
- Cornu, J.-Y.; Denaix, L.; Lacoste, J.; Sappin-Didier, V.; Nguyen, C.; Schneider, A. Impact of Temperature on the Dynamics of Organic Matter and on the Soil-to-Plant Transfer of Cd, Zn and Pb in a Contaminated Agricultural Soil. Environ. Sci. Pollut. Res. 2016, 23, 2997–3007. [Google Scholar] [CrossRef]
- Papadimou, S.G.; Golia, E.E.; Barbayiannis, N.; Tsiropoulos, N.G. Dual Role of the Hyperaccumulator Silybum Marianum (L.) Gaertn. in Circular Economy: Production of Silymarin, a Valuable Secondary Metabolite, and Remediation of Heavy Metal Contaminated Soils. Sustain. Chem. Pharm. 2024, 38, 101454. [Google Scholar] [CrossRef]
- Elferjani, R.; Soolanayakanahally, R. Canola Responses to Drought, Heat, and Combined Stress: Shared and Specific Effects on Carbon Assimilation, Seed Yield, and Oil Composition. Front. Plant Sci. 2018, 9, 1224. [Google Scholar] [CrossRef]
- Bayraklı, B.; Dengiz, O.; Özyazıcı, M.A.; Koç, Y.; Kesim, E.; Türkmen, F. Assessment of Heavy Metal Concentrations and Behavior in Cultivated Soils under Humid-Subhumid Environmental Condition of the Black Sea Region. Geoderma Reg. 2023, 32, e00593. [Google Scholar] [CrossRef]
- Peng, L.; Liu, P.; Feng, X.; Wang, Z.; Cheng, T.; Liang, Y.; Lin, Z.; Shi, Z. Kinetics of Heavy Metal Adsorption and Desorption in Soil: Developing a Unified Model Based on Chemical Speciation. Geochim. Cosmochim. Acta 2018, 224, 282–300. [Google Scholar] [CrossRef]
- Wijngaard, R.R.; van der Perk, M.; van der Grift, B.; de Nijs, T.C.M.; Bierkens, M.F.P. The Impact of Climate Change on Metal Transport in a Lowland Catchment. Water Air Soil Pollut. 2017, 228, 107. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Zeraatpisheh, M.; Valavi, R.; Davatgar, N.; Heung, B.; Johnson, M.S.; Mosavi, A. Modelling the spatial–temporal variation of multiple heavy metals in the soil of a large catchment using a random forest model. Remote Sens. 2021, 13, 1698. [Google Scholar] [CrossRef]
- Keçeci, M.; Gökmen, F.; Usul, M.; Koca, C.; Uygur, V. Prediction of Cadmium Content Using Machine Learning Methods. Environ. Earth Sci. 2024, 82, 12. [Google Scholar] [CrossRef]
- Golia, E.E.; Diakoloukas, V. Soil Parameters Affecting the Levels of Potentially Harmful Metals in Thessaly Area, Greece: A Robust Quadratic Regression Approach of Soil Pollution Prediction. Environ. Sci. Pollut. Res. 2022, 29, 29544–29561. [Google Scholar] [CrossRef] [PubMed]
- Page, A.L. Methods of Soil Analysis-Part 2: Chemical and Microbiological Properties, 2nd ed.; American Society of Agronomy, Inc.: Madison, MI, USA, 1982; Volume 9, pp. 421–422. [Google Scholar]
- Lindsay, W.; Norvell, W.A. Development of a DTPA Soil Test for Zinc, Iron, Manganese, and Copper. Soil Sci. Soc. Am. J. 1978, 42, 421–428. [Google Scholar] [CrossRef]
- ISO/DIS 11466.(1994); Environment Soil Quality. ISO Standards Compendium: Geneva, Switzerland, 1994.
- Arkes, J. Regression Analysis; Routledge: London, UK, 2019; ISBN 9781351011099. [Google Scholar]
- Kuchibhotla, A.K.; Brown, L.D.; Buja, A.; Cai, J. All of Linear Regression. arXiv 2019, arXiv:1910.06386. [Google Scholar]
- Yu, C.; Yao, W. Robust Linear Regression: A Review and Comparison. Commun. Stat. Simul. Comput. 2017, 46, 6261–6282. [Google Scholar] [CrossRef]
- Green, P.J. Iteratively Reweighted Least Squares for Maximum Likelihood Estimation, and Some Robust and Resistant Alternatives. J. R. Stat. Soc. Ser. B Stat. Methodol. 1984, 46, 149–170. [Google Scholar] [CrossRef]
- Wang, Y.-G.; Lin, X.; Zhu, M.; Bai, Z. Robust Estimation Using the Huber Function with a Data-Dependent Tuning Constant. J. Comput. Graph. Stat. 2007, 16, 468–481. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, Q. A Statistical Learning Assessment of Huber Regression. J. Approx. Theory 2022, 273, 105660. [Google Scholar] [CrossRef]
- West, B.T.; Welch, K.B.; Galecki, A.T. Linear Mixed Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006; ISBN 9780429186554. [Google Scholar]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Linear Mixed Models. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Switzerland, 2022; pp. 141–170. [Google Scholar]
- Bolker, B.M.; Brooks, M.E.; Clark, C.J.; Geange, S.W.; Poulsen, J.R.; Stevens, M.H.H.; White, J.-S.S. Generalized Linear Mixed Models: A Practical Guide for Ecology and Evolution. Trends Ecol. Evol. 2009, 24, 127–135. [Google Scholar] [CrossRef]
- Ojo, A.O.; Nwosu, N.J.; Oshunsanya, S.O.; Ayantayo-Ojo, V.I.; Aladele, S.E. Impacts of Soil Conservation Techniques on Soil Erodibility on an Alfisol. Heliyon 2023, 9, e13768. [Google Scholar] [CrossRef]
- Debnath, J.; Sow, P.; Kundu, M.C. Variation of PH Dependent Acidity and Total Potential Acidity as Influenced by Land Uses and Soil Depths in Lateritic Belt of West Bengal. Int. J. Curr. Microbiol. Appl. Sci. 2021, 10, 1289–1298. [Google Scholar] [CrossRef]
- Gök, G.; Tulun, Ş.; Çelebi, H. Mapping of Heavy Metal Pollution Density and Source Distribution of Campus Soil Using Geographical Information System. Sci. Rep. 2024, 14, 29918. [Google Scholar] [CrossRef]
- Bouslihim, Y.; John, K.; Miftah, A.; Azmi, R.; Aboutayeb, R.; Bouasria, A.; Razouk, R.; Hssaini, L. The Effect of Covariates on Soil Organic Matter and PH Variability: A Digital Soil Mapping Approach Using Random Forest Model. Ann. GIS 2024, 30, 215–232. [Google Scholar] [CrossRef]
- Badagliacca, G.; Lo Presti, E.; Gelsomino, A.; Monti, M. Repeated Solid Digestate Amendment Increases Denitrifying Enzyme Activity in an Acid Clayey Soil. Soil Syst. 2024, 8, 14. [Google Scholar] [CrossRef]
- Rajabi Hamedani, S.; Cardarelli, M.; Rouphael, Y.; Bonini, P.; Colantoni, A.; Colla, G. Comparative Environmental Assessment of the Iron Fertilisers’ Production: Fe-Biochelate versus Fe-EDDHA. Sustainability 2023, 15, 7488. [Google Scholar] [CrossRef]
- Li, E.; Li, K.; Li, J.; Wu, Y.; Ma, Y. A New Approach to Differentiate the Causes of Excessive Cadmium in Rice: Soil Cadmium Extractability or Rice Variety. Agronomy 2024, 14, 2519. [Google Scholar] [CrossRef]
- Wu, Y.; Li, H.; Liang, X.; Jiang, M.; He, S.; He, Y. Mechanisms Behind the Soil Organic Carbon Response to Temperature Elevations. Agriculture 2025, 15, 1118. [Google Scholar] [CrossRef]
- Reis, A.R.; Roboredo, M.; Pinto, J.P.R.M.; Vieira, B.; Varandas, S.G.P.; Fernandes, L.F.S.; Pacheco, F.A.L. Distribution and Potential Availability of As, Metals and P in Sediments from a Riverine Reservoir in a Rural Mountainous Catchment (NE Portugal). Int. J. Environ. Res. Public Health 2021, 18, 5616. [Google Scholar] [CrossRef]
- Shang, E.; Long, A.; Yang, J.; Ma, Y.; Yao, W.; Zhang, S. Dynamics of Cadmium Pollution Risk in Agricultural Land Soil of Tropical Islands in China from 2000 to 2024: A Case Study of Hainan Island. Appl. Sci. 2025, 15, 3817. [Google Scholar] [CrossRef]
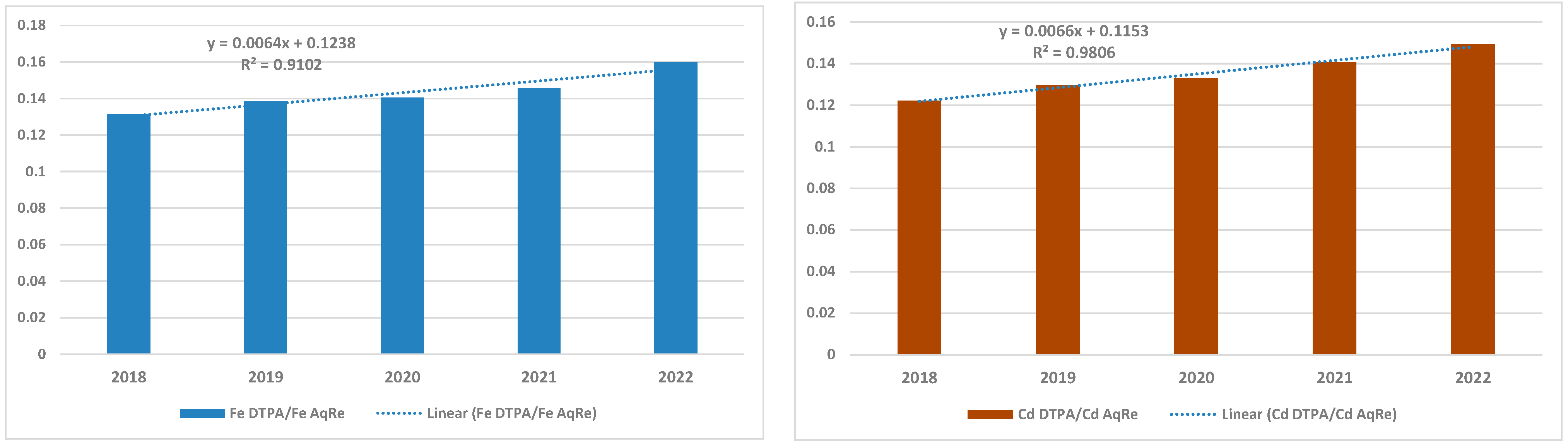


| pH | EC (mS cm−1) | OM (%) | Clay (%) | CEC (cmolc kg−1) | |
|---|---|---|---|---|---|
| Min | 4.9 | 1.1 | 0.9 | 17 | 17.2 |
| Max | 5.9 | 1.9 | 2.2 | 22 | 23.1 |
| Mean | 5.3 | 1.4 | 1.7 | 20 | 20.1 |
| RSD (%) | 9.7 | 6.8 | 5.9 | 8.3 | 9.2 |
| FeAqRe | CdAqRe | FeDTPA | CdDTPA | |
|---|---|---|---|---|
| (mg kg−1) | ||||
| Min | 22.9 | 0.45 | 2.09 | 0.05 |
| Max | 48.1 | 1.88 | 5.8 | 0.19 |
| Mean | 38.6 | 0.77 | 4.1 | 0.09 |
| RSD (%) | 10.5 | 11.8 | 11.4 | 12.6 |
| Min | Max | Mean | STDEV | |
|---|---|---|---|---|
| FeDTPA (2013–2017) | 4.01 | 20.2 | 11.0 | 4.8 |
| FeDTPA (2018–2022) | 2.30 | 30.1 | 15.1 | 9.1 |
| CdDTPA (2013–2017) | 0.12 | 0.29 | 0.18 | 0.3 |
| CdDTPA (2018–2022) | 0.19 | 0.48 | 0.30 | 0.6 |
| Min soil temperature (2013–2017) | −5.16 | 16.5 | 6.19 | 6.8 |
| Min soil temperature (2018–2022) | −7.48 | 16.02 | 4.59 | 7.5 |
| Max soil temperature (2013–2017) | 17.34 | 38.6 | 28.3 | 7.2 |
| Max soil temperature (2018–2022) | 17.9 | 37.6 | 28.9 | 6.9 |
| Mean soil temperature (2013–2017) | 6.39 | 27.54 | 17.4 | 7.29 |
| Mean soil temperature (2018–2022) | 5.21 | 26.8 | 16.8 | 7.3 |
| Mean annual precipitation (2013–2017) | 10.84 | 82.2 | 57.7 | 22.9 |
| Mean annual precipitation (2018–2022) | 20.64 | 92.3 | 59.8 | 22.6 |
| Real Mean Annual Values | Predicted Mean Annual Values | |||||||
|---|---|---|---|---|---|---|---|---|
| FeAqRe | FeDTPA | CdAqRe | Cd DTPA | FeAqRe | FeDTPA | CdAqRe | Cd DTPA | |
| 2013 | 33.25 | 3.29 | 1.61 | 0.158 | 34.47 | 3.30 | 1.628 | 0.16 |
| 2014 | 33.11 | 3.39 | 1.71 | 0.168 | 34.92 | 3.38 | 1.722 | 0.168 |
| 2015 | 35.19 | 3.49 | 1.789 | 0.177 | 35.27 | 3.49 | 1.793 | 0.175 |
| 2016 | 35.98 | 3.59 | 1.878 | 0.186 | 35.61 | 3.58 | 1.87 | 0.182 |
| 2017 | 36.82 | 3.68 | 1.95 | 0.191 | 35.39 | 3.65 | 1.965 | 0.192 |
| 2018 | 37.26 | 4.14 | 2.013 | 0.218 | 36.01 | 3.74 | 2.05 | 0.20 |
| 2019 | 37.66 | 4.41 | 2.065 | 0.231 | 36.12 | 3.81 | 2.136 | 0.209 |
| 2020 | 38.09 | 4.76 | 2.108 | 0.244 | 36.4 | 3.89 | 2.20 | 0.215 |
| 2021 | 38.54 | 5.09 | 2.162 | 0.258 | 36.58 | 3.96 | 2.298 | 0.226 |
| 2022 | 38.93 | 5.38 | 2.21 | 0.269 | 36.63 | 4.03 | 2.40 | 0.237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diakoloukas, V.; Koutopoulis, G.; Papadimou, S.G.; Spiliotopoulos, M.-E.; Golia, E.E. Predicting Heavy Metal and Nutrient Availability in Agricultural Soils Under Climatic Variability Using Regression and Mixed-Effects Models. Land 2025, 14, 1743. https://doi.org/10.3390/land14091743
Diakoloukas V, Koutopoulis G, Papadimou SG, Spiliotopoulos M-E, Golia EE. Predicting Heavy Metal and Nutrient Availability in Agricultural Soils Under Climatic Variability Using Regression and Mixed-Effects Models. Land. 2025; 14(9):1743. https://doi.org/10.3390/land14091743
Chicago/Turabian StyleDiakoloukas, Vassilios, Georgios Koutopoulis, Sotiria G. Papadimou, Marios-Efstathios Spiliotopoulos, and Evangelia E. Golia. 2025. "Predicting Heavy Metal and Nutrient Availability in Agricultural Soils Under Climatic Variability Using Regression and Mixed-Effects Models" Land 14, no. 9: 1743. https://doi.org/10.3390/land14091743
APA StyleDiakoloukas, V., Koutopoulis, G., Papadimou, S. G., Spiliotopoulos, M.-E., & Golia, E. E. (2025). Predicting Heavy Metal and Nutrient Availability in Agricultural Soils Under Climatic Variability Using Regression and Mixed-Effects Models. Land, 14(9), 1743. https://doi.org/10.3390/land14091743










