An Enhanced Interval Type-2 Fuzzy C-Means Algorithm for Fuzzy Time Series Forecasting of Vegetation Dynamics: A Case Study from the Aksu Region, Xinjiang, China
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Satellite Data
2.3. Satellite Data Sources
2.4. Land Use Data
3. Methods
3.1. Sequential Stages in Fuzzy Time Series Implementation
- (1)
- Partitioning the universe based on the sample data.
- (2)
- Constructing fuzzy sets and applying fuzzification to the time series.
- (3)
- Extracting fuzzy relationships from the fuzzified sequence and establishing the fuzzy relationship matrix.
- (4)
- Predicting future values based on the fuzzy relationship matrix obtained in Step (3) and defuzzifying the prediction results.
3.2. Modeling NDVI Time Series Using the IT2-FCM-FTS Approach
3.2.1. Universe Partitioning of NDVI Data Based on IT2-FCM
- (1)
- Parameter setting: Define two fuzzy parameters, and assign the maximum and minimum values of m, respectively. is the number of clusters, and the objective threshold of the objective function is ε. The number of iterations is .
- (2)
- Initialize the clustering center .
- (3)
- Calculate or update the fuzzy interval upper , lower interval matrices according to Equations (2) and (3).
- (4)
- When , or reaches the preset value, the iteration stops; otherwise, go back to Step (3) with t = t + 1.
- (5)
- To derive the final clustering assignments, the IT2 fuzzy partition matrix is first reduced to a type-1 fuzzy set through an averaging operation between its lower and upper membership matrices, i.e., . The clustering results are subsequently determined by applying the maximum defuzzification criterion.
3.2.2. Construction of Interval Type-2 Fuzzy Sets for NDVI Representation
3.2.3. Relationship Modeling
3.2.4. Defuzzification and Prediction of Future NDVI Values
3.3. IT2-FCM-FTS Model Parameter Settings
3.4. Evaluation Indices for Prediction Accuracy
4. Results
4.1. Model Evaluation
4.2. NDVI Trend Analysis in the Aksu Region
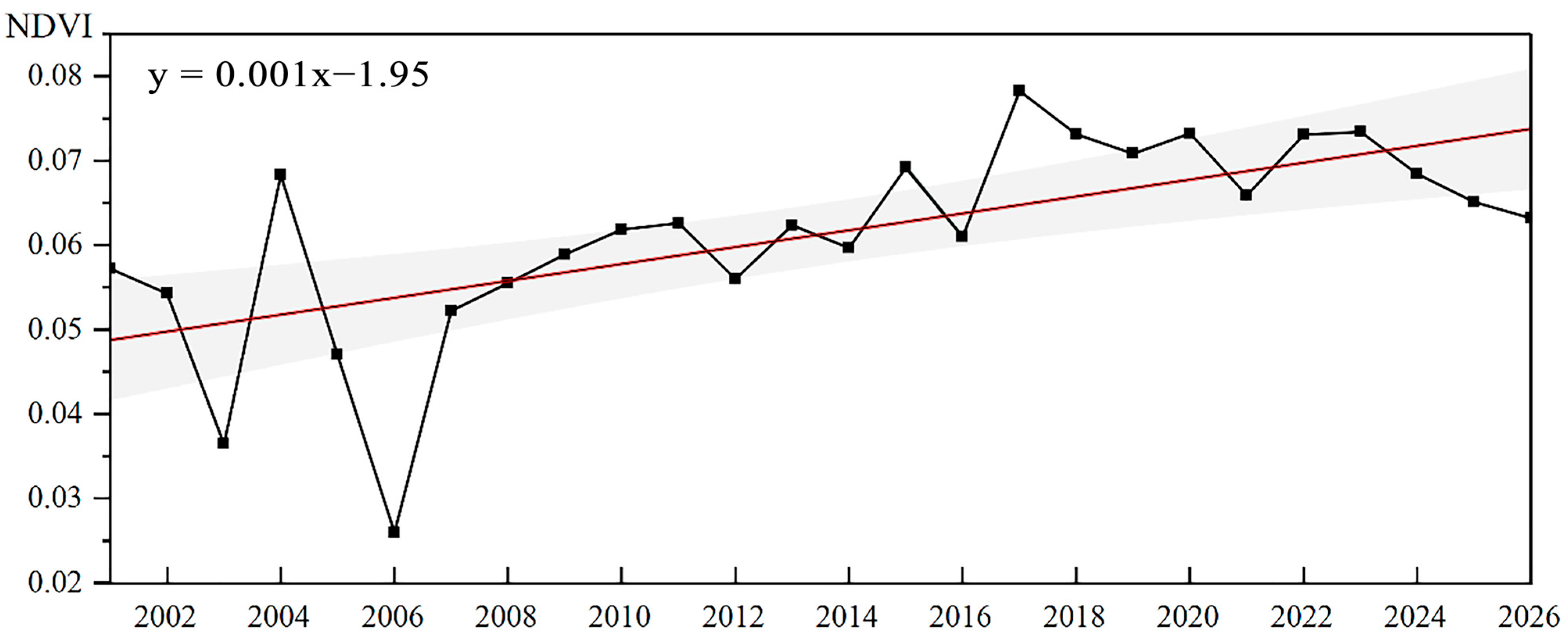
4.2.1. Interannual NDVI Dynamics at the Regional Scale
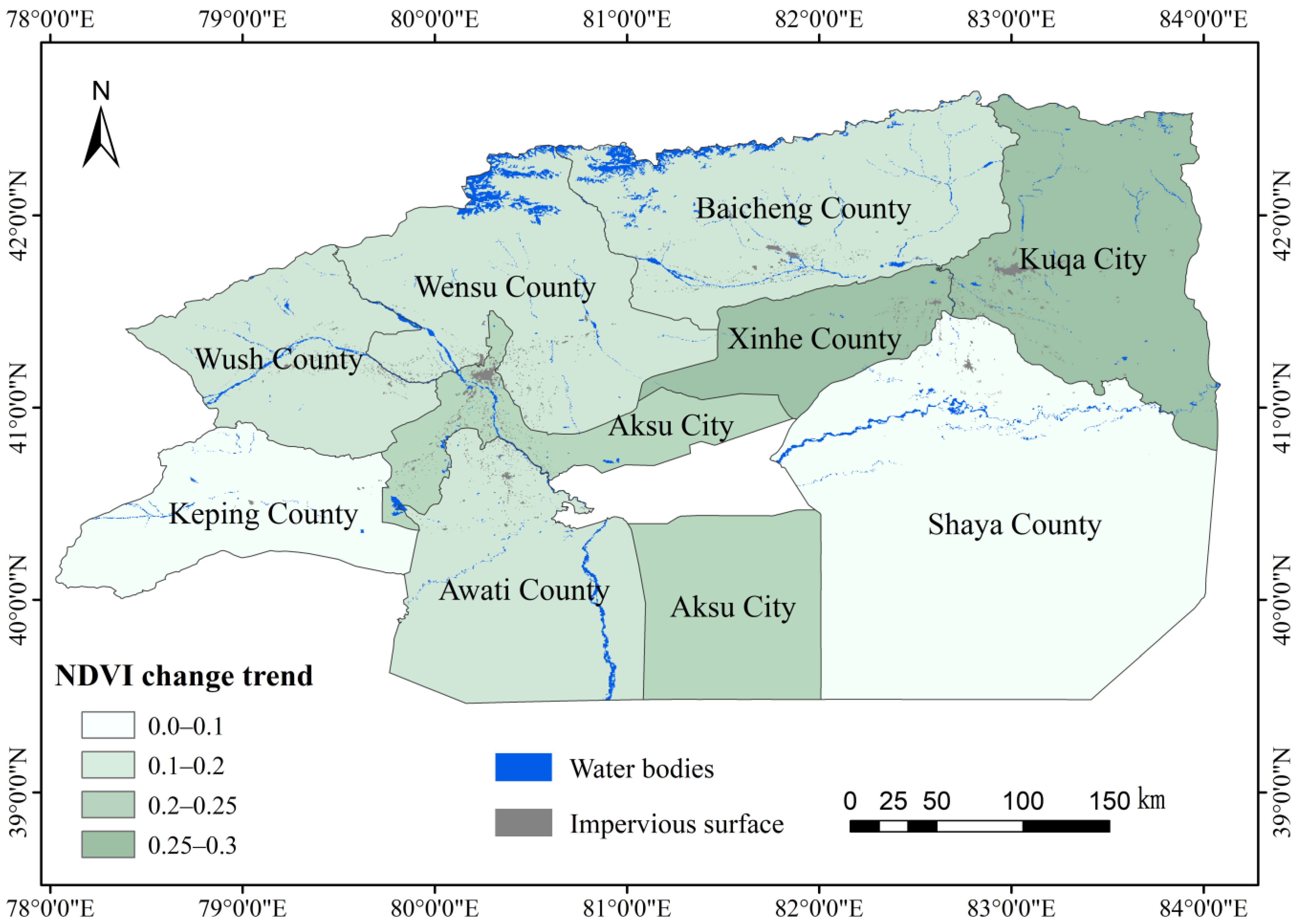
4.2.2. Temporal and Spatial Characteristics of Vegetation Dynamics at the Pixel Scale
5. Discussion
5.1. Model Performance and Limitations
5.2. Implications for Sustainable Land Management
6. Conclusions
- (1)
- The improved IT2-FCM-FTS algorithm showed better performance in short-term NDVI prediction than ARIMA and FCM-FTS models, achieving the lowest RMSE (0.0624), MAE (0.0437), and SEM (0.000209) in 2021.
- (2)
- From 2001 to 2026, the NDVI in the Aksu region exhibited a general increasing trend. Notably, areas with a continuous increase accounted for 61.12% of the total area, primarily located in Aksu City, Xinhe County, southern Baicheng County, central Kuqa City, and northern Keping County. Areas with a continuous decrease constituted 2.6% of the total area, mainly along the borders of Kuqa City, Shaya County, Xinhe County, Aksu City, Wensu County, and Wush County.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NDVI | Normalized Difference Vegetation Index |
| IT2 | Interval type-2 |
| FCM | Fuzzy C-means |
| FTS | Fuzzy time-series |
| ARIMA | Autoregressive Integrated Moving Average |
| RNN | Recurrent neural networks |
| GEE | Google Earth Engine |
| LSTM | Long short-term memory |
| EVI | Enhanced Vegetation Index |
| QA | Quality Assessment |
| MVC | Maximum Value Composite |
| RMSE | Root Mean Square Error |
| SEM | Standard Error of the Mean |
| MAE | Mean Absolute Error |
| SG | Savitzky–Golay |
Appendix A
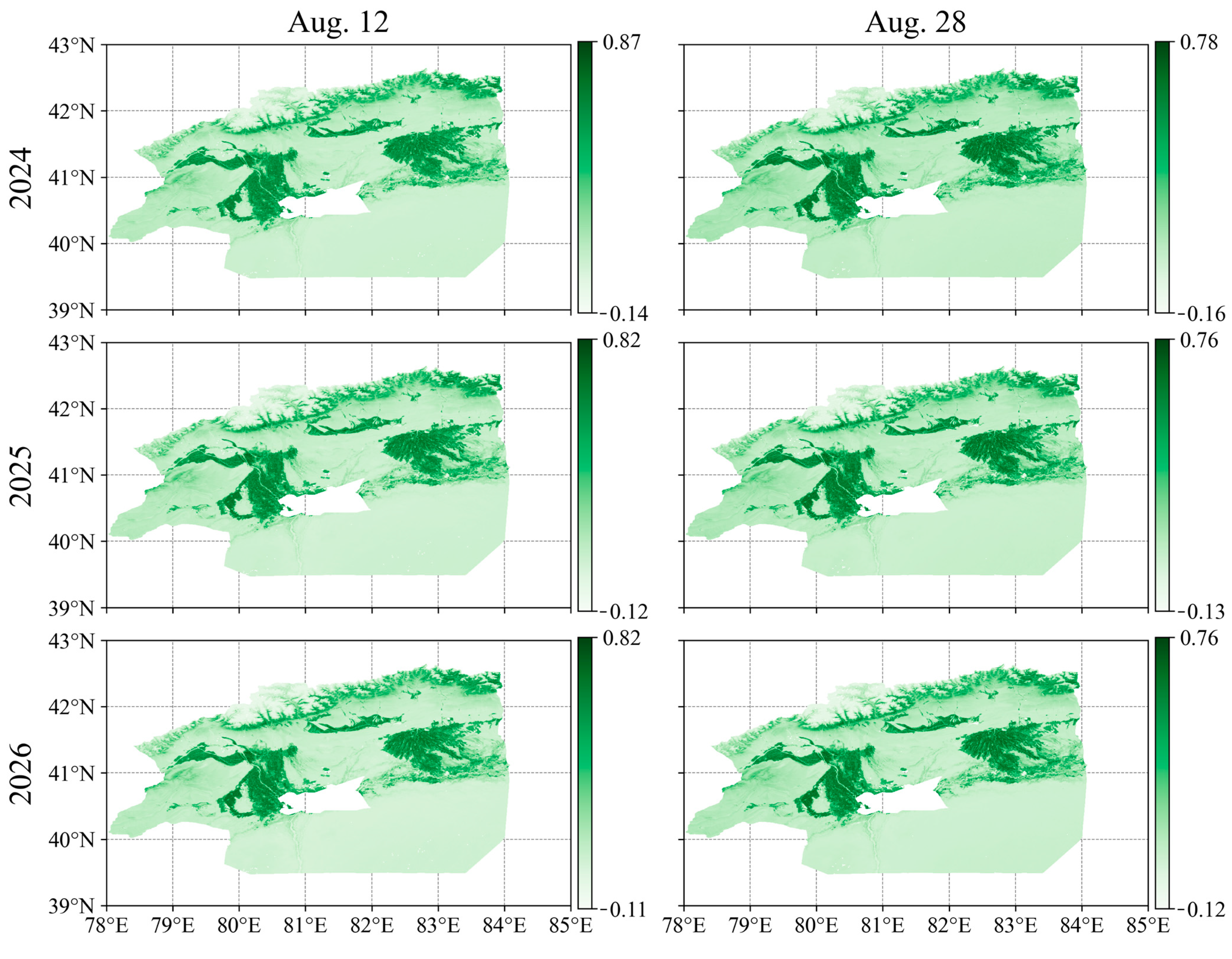
References
- Liu, Y.; Li, L.; Chen, X.; Zhang, R.; Yang, J. Temporal-spatial variations and influencing factors of vegetation cover in Xinjiang from 1982 to 2013 based on GIMMS-NDVI3g. Glob. Planet. Chang. 2018, 169, 145–155. [Google Scholar] [CrossRef]
- Alexander, L.; Allen, S.; Bindoff, N.; Breon, F.-M.; Church, J.; Cubasch, U.; Emori, S.; Forster, P.; Friedlingstein, P.; Gillett, N.; et al. Climate Change 2013: The Physical Science Basis.Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Zhang, Y.; Ye, A.J.G.; Sensing, R. Quantitatively distinguishing the impact of climate change and human activities on vegetation in mainland China with the improved residual method. GISci. Remote. Sens. 2021, 58, 235–260. [Google Scholar] [CrossRef]
- Kang, L.; Di, L.; Deng, M.; Shao, Y.; Yu, G.; Shrestha, R. Use of geographically weighted regression model for exploring spatial patterns and local factors behind NDVI-precipitation correlation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4530–4538. [Google Scholar] [CrossRef]
- Yang, X.; Liu, S.; Yang, T.; Xu, X.; Kang, C.; Tang, J.; Wei, H.; Ghebrezgabher, M.G.; Li, Z. Spatial-temporal dynamics of desert vegetation and its responses to climatic variations over the last three decades: A case study of Hexi region in Northwest China. J. Arid. Land 2016, 8, 556–568. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Jaber, S.M. On the relationship between normalized difference vegetation index and land surface temperature: MODIS-based analysis in a semi-arid to arid environment. Geocarto Int. 2021, 36, 1117–1135. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Ciais, P.; Zhu, B.; Wang, T.; Liu, J. Changes in satellite-derived vegetation growth trend in temperate and boreal Eurasia from 1982 to 2006. Glob. Change Biol. 2011, 17, 3228–3239. [Google Scholar] [CrossRef]
- Zheng, K.; Wei, J.-Z.; Pei, J.-Y.; Cheng, H.; Zhang, X.-L.; Huang, F.-Q.; Li, F.-M.; Ye, J.-S. Impacts of climate change and human activities on grassland vegetation variation in the Chinese Loess Plateau. Sci. Total. Environ. 2019, 660, 236–244. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, H.; Krause, C.M.; Cobb, N.S. Climate change and human activities: A case study in Xinjiang, China. Clim. Chang. 2010, 99, 457–472. [Google Scholar] [CrossRef]
- Xu, C.; Li, J.; Zhao, J.; Gao, S.; Chen, Y. Climate variations in northern Xinjiang of China over the past 50 years under global warming. Quat. Int. 2015, 358, 83–92. [Google Scholar] [CrossRef]
- Farbo, A.; Sarvia, F.; De Petris, S.; Basile, V.; Borgogno-Mondino, E. Forecasting corn NDVI through AI-based approaches using sentinel 2 image time series. ISPRS J. Photogramm. Remote. Sens. 2024, 211, 244–261. [Google Scholar] [CrossRef]
- Stepchenko, A. NDVI index forecasting using a layer recurrent neural network coupled with stepwise regression and the PCA. In Proceedings of the 5th International Virtual Scientific Conference on Informatics and Management Sciences, Shanghai, China, 5–7 November 2016; pp. 130–135. [Google Scholar]
- Reddy, D.S.; Prasad, P.R.C. Prediction of vegetation dynamics using NDVI time series data and LSTM. Model. Earth Syst. Environ. 2018, 4, 409–419. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, L.; He, Y.; Cao, S.; Li, H.; Ran, L.; Ding, Y.; Filonchyk, M. LSTM time series NDVI prediction method incorporating climate elements: A case study of Yellow River Basin, China. J. Hydrol. 2024, 629, 130518. [Google Scholar] [CrossRef]
- Cui, L.; Zhao, Y.; Liu, J.; Wang, H.; Han, L.; Li, J.; Sun, Z. Vegetation coverage prediction for the Qinling mountains using the CA–Markov model. ISPRS Int. J. Geo-Inf. 2021, 10, 679. [Google Scholar] [CrossRef]
- Darvishi, S.; Solaimani, K. Monitoring and prediction spatiotemporal vegetation changes using NDVI index and CA-Markov model (case study: Kermanshah city). Environ. Sci. 2020, 18, 161–182. [Google Scholar]
- Alhamad, M.; Stuth, J.; Vannucci, M. Biophysical modelling and NDVI time series to project near-term forage supply: Spectral analysis aided by wavelet denoising and ARIMA modelling. Int. J. Remote Sens. 2007, 28, 2513–2548. [Google Scholar] [CrossRef]
- Fernández-Manso, A.; Quintano, C.; Fernández-Manso, O. Forecast of NDVI in coniferous areas using temporal ARIMA analysis and climatic data at a regional scale. Int. J. Remote Sens. 2011, 32, 1595–1617. [Google Scholar] [CrossRef]
- Rhif, M.; Ben Abbes, A.; Martinez, B.; Farah, I.R. A deep learning approach for forecasting non-stationary big remote sensing time series. Arab. J. Geosci. 2020, 13, 1174. [Google Scholar] [CrossRef]
- Ruspini, E.H. A new approach to clustering. Inf. Control 1969, 15, 22–32. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series—Part I. Fuzzy Sets Syst. 1993, 54, 1–9. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series—Part II. Fuzzy Sets Syst. 1994, 62, 1–8. [Google Scholar] [CrossRef]
- Belyakova, P.; Gartsman, B. Possibilities of flood forecasting in the West Caucasian rivers based on FCM model. Water Resour. 2018, 45, 50–58. [Google Scholar] [CrossRef]
- Zhu, L.; Chung, F.-L.; Wang, S. Generalized fuzzy c-means clustering algorithm with improved fuzzy partitions. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 578–591. [Google Scholar]
- Rustam, Z.; Vibranti, D.; Widya, D. Predicting the direction of Indonesian stock price movement using support vector machines and fuzzy Kernel C-Means. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2018. [Google Scholar]
- Salmeron, J.L.; Ruiz-Celma, A.; Mena, A. Learning FCMs with multi-local and balanced memetic algorithms for forecasting industrial drying processes. Neurocomputing 2017, 232, 52–57. [Google Scholar] [CrossRef]
- Rhee, F.C.H.; Cheul, H. A type-2 fuzzy C-means clustering algorithm. In Proceedings of the Proceedings Joint 9th IFSA World Congress and 20th NAFIPS International Conference (Cat. No. 01TH8569), Vancouver, BC, Canada, 25–28 July 2001; Volume 1924, pp. 1926–1929. [Google Scholar]
- Linda, O.; Manic, M. General Type-2 Fuzzy C-Means Algorithm for Uncertain Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2012, 20, 883–897. [Google Scholar] [CrossRef]
- Sotudian, S.; Zarandi, M.H.F. Interval type-2 enhanced possibilistic fuzzy c-means clustering for gene expression data analysis. arXiv 2021, arXiv:2101.00304. [Google Scholar]
- Yin, Y.; Sheng, Y.; Qin, J. Interval type-2 fuzzy C-means forecasting model for fuzzy time series. Appl. Soft Comput. 2022, 129, 109574. [Google Scholar] [CrossRef]
- Kamel, D.; Munoz, A.; Ramon, S.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); University of Arizona, Vegetation Index and Phenology Lab: Tucson, AZ, USA, 2015. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Yuan, F.; Zhan, Y.; Wang, Y. Interval Type-2 Fuzzy c-Means Clustering Method for Interval Data. 2013. Engineering, I. 2013, 34, 1–5. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Shen, L.; Sun, Y.; Yu, Z.; Ding, L.; Tian, X.; Tao, D. On efficient training of large-scale deep learning models: A literature review. arXiv 2023, arXiv:2304.03589. [Google Scholar]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
| Assessment | Model | RMSE | SEM | MAE |
|---|---|---|---|---|
| Year 2021 | ARIMA | 0.0654 | 0.000227 | 0.0446 |
| FCM-FTS | 0.0788 | 0.000253 | 0.0545 | |
| IT2-FCM-FTS | 0.0624 | 0.000209 | 0.0437 | |
| ARIMA | 0.0704 | 0.000235 | 0.0489 | |
| Year 2022 | FCM-FTS | 0.0777 | 0.000248 | 0.0553 |
| IT2-FCM-FTS | 0.0683 | 0.000220 | 0.0489 | |
| Year 2023 | ARIMA | 0.0741 | 0.000258 | 0.0513 |
| FCM-FTS | 0.0792 | 0.000265 | 0.0556 | |
| IT2-FCM-FTS | 0.0724 | 0.000242 | 0.0513 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, L.; Cao, J.; Wang, K.; Li, S.; Yin, Y. An Enhanced Interval Type-2 Fuzzy C-Means Algorithm for Fuzzy Time Series Forecasting of Vegetation Dynamics: A Case Study from the Aksu Region, Xinjiang, China. Land 2025, 14, 1242. https://doi.org/10.3390/land14061242
Chen Y, Liu L, Cao J, Wang K, Li S, Yin Y. An Enhanced Interval Type-2 Fuzzy C-Means Algorithm for Fuzzy Time Series Forecasting of Vegetation Dynamics: A Case Study from the Aksu Region, Xinjiang, China. Land. 2025; 14(6):1242. https://doi.org/10.3390/land14061242
Chicago/Turabian StyleChen, Yongqi, Li Liu, Jinhua Cao, Kexin Wang, Shengyang Li, and Yue Yin. 2025. "An Enhanced Interval Type-2 Fuzzy C-Means Algorithm for Fuzzy Time Series Forecasting of Vegetation Dynamics: A Case Study from the Aksu Region, Xinjiang, China" Land 14, no. 6: 1242. https://doi.org/10.3390/land14061242
APA StyleChen, Y., Liu, L., Cao, J., Wang, K., Li, S., & Yin, Y. (2025). An Enhanced Interval Type-2 Fuzzy C-Means Algorithm for Fuzzy Time Series Forecasting of Vegetation Dynamics: A Case Study from the Aksu Region, Xinjiang, China. Land, 14(6), 1242. https://doi.org/10.3390/land14061242






