A Novel Framework for Improving Soil Organic Carbon Mapping Accuracy by Mining Temporal Features of Time-Series Sentinel-1 Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil Sample Collection and Preparation
2.3. Data Collection and Analysis
2.3.1. Topographic Covariates
2.3.2. S-1 Images
| Variable Category | Predictor | Acronyms | Formula | Reference |
|---|---|---|---|---|
| Topographic variable | Elevation | DEM | [7] | |
| Aspect | AS | |||
| Topographic Wetness Index | TWI | |||
| Slope | S | |||
| Topographic Roughness Index | TRI | [34] | ||
| Remote sensing variable | Vertically polarized backscatter | VV | [35] | |
| Horizontally polarized backscatter | VH | |||
| VV-VH Cross-Polarization Ratio | VVVHR | |||
| VH-VV Cross-Polarization Ratio | VHVVR | |||
| Normalized Difference VV-VH Ratio | NDIVV | |||
| SAR Sum Vegetation Index | SSVI | [36] | ||
| GLCM Angular Second Moment from VV | VV_ASM | [29] | ||
| GLCM Angular Second Moment from VH | VH_ASM | |||
| GLCM Contrast from VV | VV_Contrast | |||
| GLCM Contrast from VH | VH_Contrast | |||
| GLCM Dissimilarity from VV | VV_Dissimilarity | |||
| GLCM Dissimilarity from VH | VH_Dissimilarity | |||
| GLCM Entropy from VV | VV_Entropy | |||
| GLCM Entropy from VH | VH_Entropy | |||
| GLCM Correlation from VV | VV_Correlation | |||
| GLCM Correlation from VH | VH_Correlation | |||
| GLCM Variance from VV | VV_Variance | |||
| GLCM Variance from VH | VH_Variance | |||
| Annual Maximum VV Cumulative Index | VV-Max | this study | ||
| Annual Maximum VH Cumulative Index | VH-Max | |||
| Annual Minimum VV Cumulative Index | VV-Min | |||
| Annual Minimum VH Cumulative Index | VH-Min | |||
| Annual Mean VV Cumulative Index | VV-Mean | |||
| Annual Mean VH Cumulative Index | VH-Mean |
2.4. Feature Selection Algorithm
2.5. Construction of SOC Prediction Models
2.6. Model Assessment and Uncertainty
3. Results
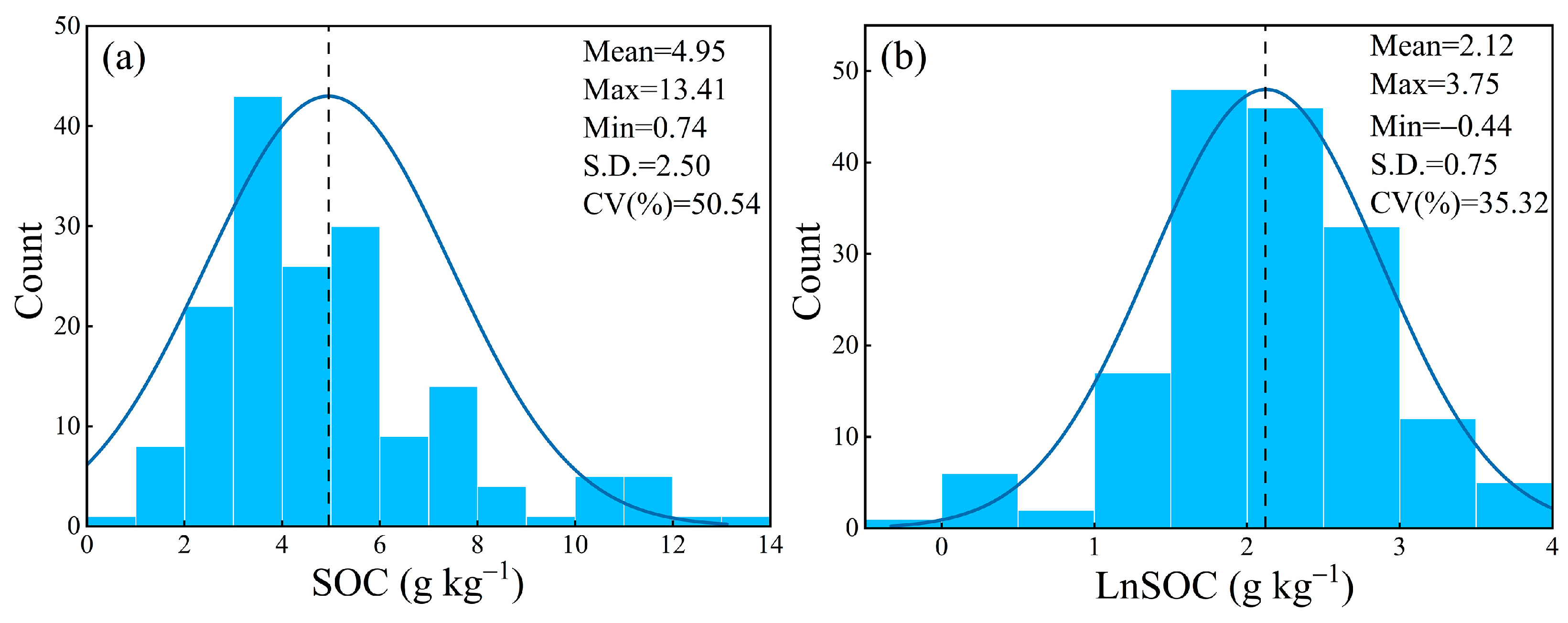
3.1. Summary Statistics of SOC
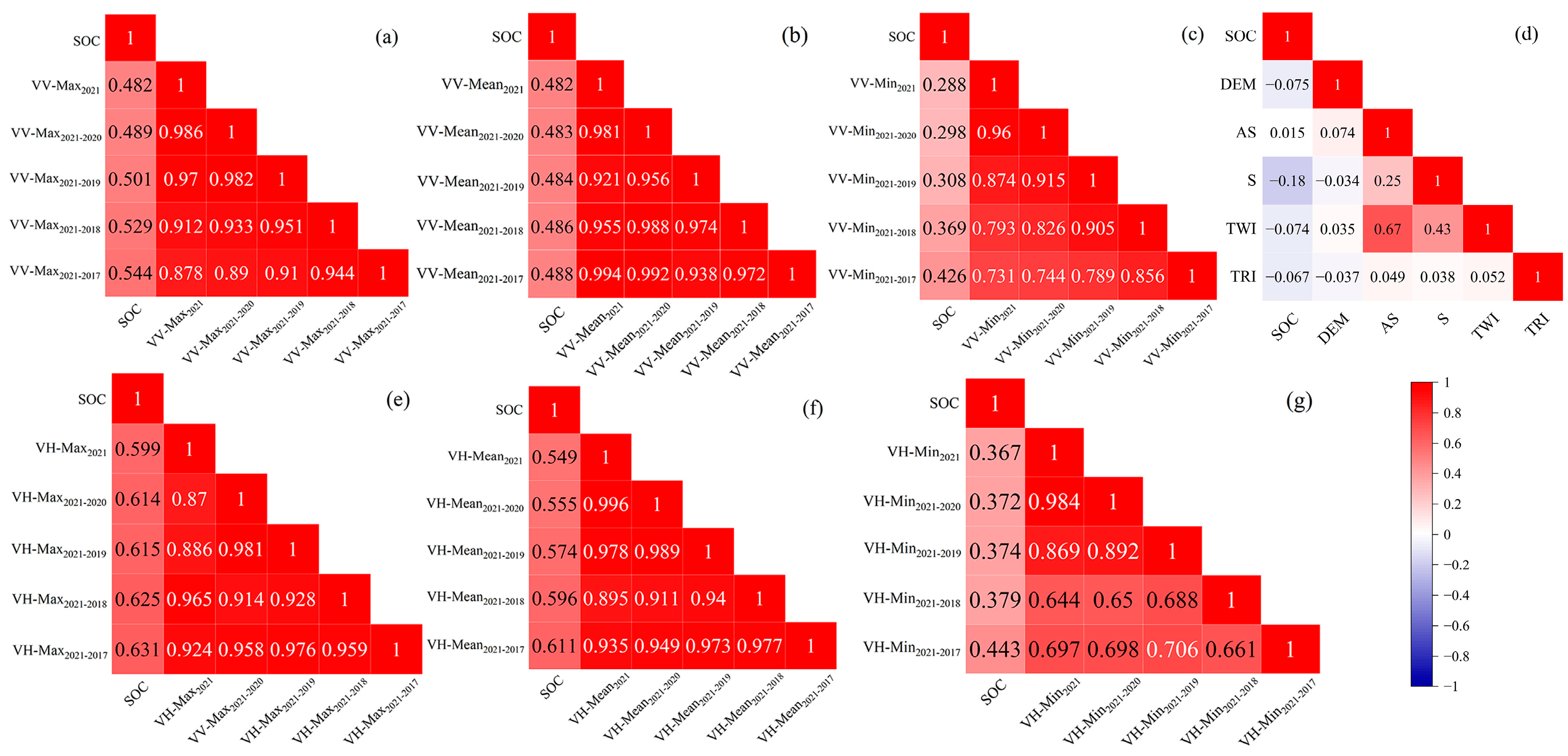
3.2. Correlation Analysis of Covariates with SOC
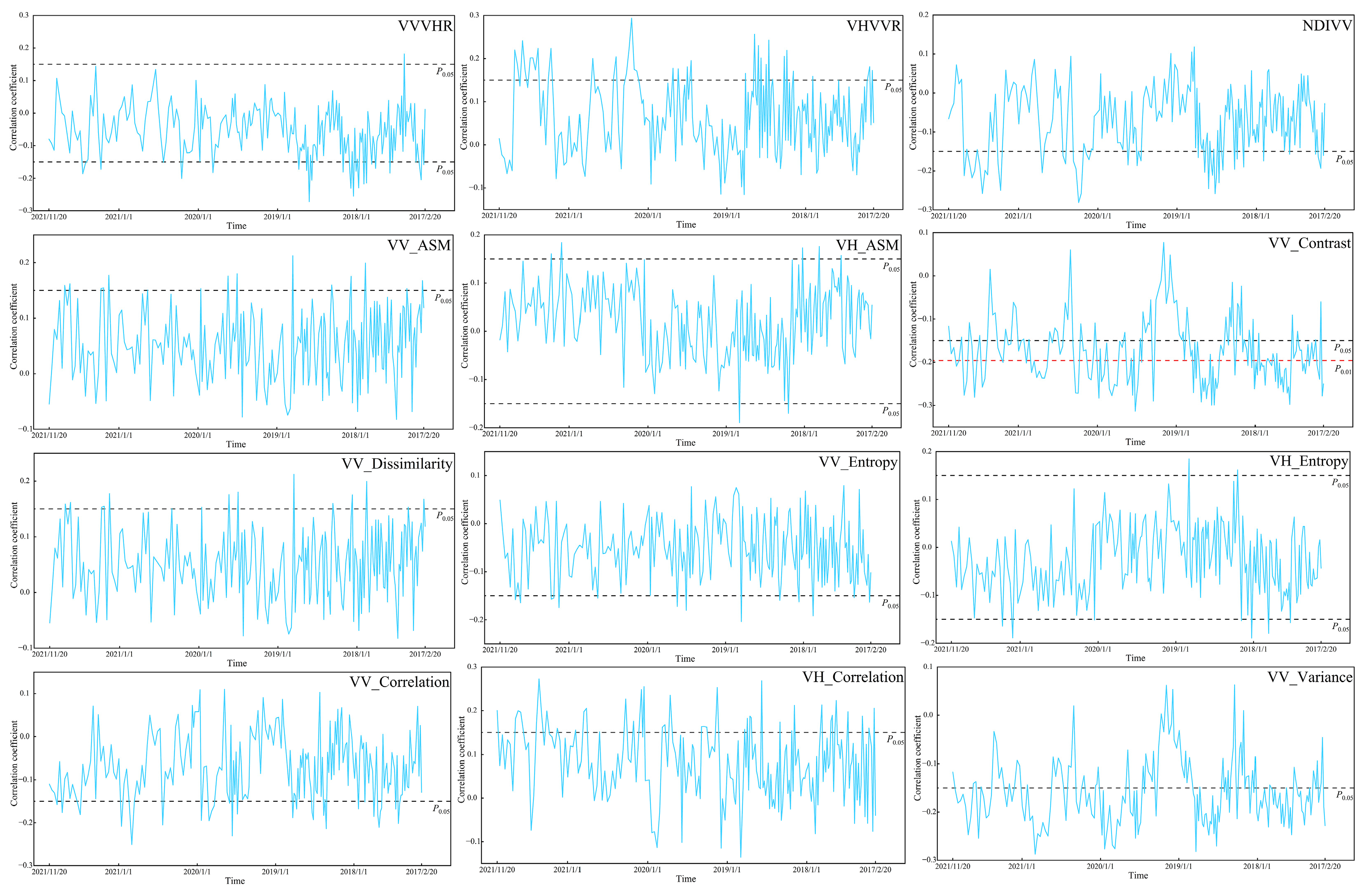
3.2.1. The Temporal Correlation Patterns Between SOC and Time-Series S-1 Data
3.2.2. Correlation Analysis of SAR Annual Cumulative Indices and Topographic Covariates with SOC
3.3. Evaluation and Comparison of Three Predictive Models
3.4. The Relative Variable Importance
3.5. Spatial Distribution of SOC and Its Uncertainty
4. Discussion
4.1. Potential of Time-Series S-1 Data for Mapping SOC
4.2. Optimal Monitoring Period for SOC Using S-1 Data
4.3. Prediction Performance of Different Models for SOC
4.4. Uncertainty Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hu, B.; Xie, M.; Shi, Z.; Li, H.; Chen, S.; Wang, Z.; Zhou, Y.; Ni, H.; Geng, Y.; Zhu, Q.; et al. Fine-Resolution Mapping of Cropland Topsoil PH of Southern China and Its Environmental Application. Geoderma 2024, 442, 116798. [Google Scholar] [CrossRef]
- Odebiri, O.; Mutanga, O.; Odindi, J.; Naicker, R. Modelling Soil Organic Carbon Stock Distribution across Different Land-Uses in South Africa: A Remote Sensing and Deep Learning Approach. ISPRS J. Photogramm. Remote Sens. 2022, 188, 351–362. [Google Scholar] [CrossRef]
- Chen, Z.; Xue, J.; Wang, Z.; Zhou, Y.; Deng, X.; Liu, F.; Song, X.; Zhang, G.; Su, Y.; Zhu, P.; et al. Ensemble Modelling-Based Pedotransfer Functions for Predicting Soil Bulk Density in China. Geoderma 2024, 448, 116969. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Liu, M.; Haase, D.; Lausch, A. Mapping Soil Organic Carbon Content Using Multi-Source Remote Sensing Variables in the Heihe River Basin in China. Ecol. Indic. 2020, 114, 106288. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, J.; Zhao, W.; Qu, Y.; Gou, Z.; Chen, H.; Tian, Y.; Wu, F. Digital Mapping of Soil Organic Carbon Density in China Using an Ensemble Model. Environ. Res. 2023, 231, 116131. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Martínez, P.; Maestre, F.T.; Moreno-Jiménez, E.; Delgado-Baquerizo, M.; Eldridge, D.J.; Saiz, H.; Gross, N.; Le Bagousse-Pinguet, Y.; Gozalo, B.; Ochoa, V.; et al. Vulnerability of Mineral-Associated Soil Organic Carbon to Climate across Global Drylands. Nat. Clim. Change 2024, 14, 976–982. [Google Scholar] [CrossRef]
- Peng, J.; Biswas, A.; Jiang, Q.; Zhao, R.; Hu, J.; Hu, B.; Shi, Z. Estimating Soil Salinity from Remote Sensing and Terrain Data in Southern Xinjiang Province, China. Geoderma 2019, 337, 1309–1319. [Google Scholar] [CrossRef]
- Ren, Z.; Li, C.; Fu, B.; Wang, S.; Stringer, L.C. Effects of Aridification on Soil Total Carbon Pools in China’s Drylands. Glob. Change Biol. 2023, 30, e17091. [Google Scholar] [CrossRef]
- Zhao, M.; Cao, G.; Zhao, Q.; Ma, Y.; Zhang, F.; Li, H.; He, Q.; Qiu, X. Distribution Patterns and Influencing Factors Controlling Soil Carbon in the Heihe River Source Basin, Northeast Qinghai–Tibet Plateau. Land 2025, 14, 409. [Google Scholar] [CrossRef]
- De Benedetto, D.; Barca, E.; Castellini, M.; Popolizio, S.; Lacolla, G.; Stellacci, A.M. Prediction of Soil Organic Carbon at Field Scale by Regression Kriging and Multivariate Adaptive Regression Splines Using Geophysical Covariates. Land 2022, 11, 381. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Z.; Zhang, X.; Luo, Z.; Schillaci, C.; Arrouays, D.; Richer-De-Forges, A.C.; Shi, Z. European Topsoil Bulk Density and Organic Carbon Stock Database (0-20 Cm) Using Machine-Learning-Based Pedotransfer Functions. Earth Syst. Sci. Data 2024, 16, 2367–2383. [Google Scholar] [CrossRef]
- Salgado, L.; González, L.M.; Gallego, J.L.R.; López-Sánchez, C.A.; Colina, A.; Forján, R. Mapping Soil Organic Carbon in Degraded Ecosystems Through Upscaled Multispectral Unmanned Aerial Vehicle–Satellite Imagery. Land 2025, 14, 377. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Leatitia Mulder, V.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital Mapping of GlobalSoilMap Soil Properties at a Broad Scale: A Review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Zolfaghari Nia, M.; Moradi, M.; Moradi, G.; Taghizadeh-Mehrjardi, R. Machine Learning Models for Prediction of Soil Properties in the Riparian Forests. Land 2023, 12, 32. [Google Scholar] [CrossRef]
- Lamichhane, S.; Kumar, L.; Wilson, B. Digital Soil Mapping Algorithms and Covariates for Soil Organic Carbon Mapping and Their Implications: A Review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
- Odebiri, O.; Mutanga, O.; Odindi, J. Deep Learning-Based National Scale Soil Organic Carbon Mapping with Sentinel-3 Data. Geoderma 2022, 411, 115695. [Google Scholar] [CrossRef]
- Pouladi, N.; Gholizadeh, A.; Khosravi, V.; Borůvka, L. Digital Mapping of Soil Organic Carbon Using Remote Sensing Data: A Systematic Review. Catena 2023, 232, 107409. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, Y.; Huang, H.; Li, A.; Yang, L.; Zhou, C. A CNN-LSTM Model for Soil Organic Carbon Content Prediction with Long Time Series of MODIS-Based Phenological Variables. Remote Sens. 2022, 14, 4441. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Peng, X.; Hu, B.; Song, X. Synergetic Use of DEM Derivatives, Sentinel-1 and Sentinel-2 Data for Mapping Soil Properties of a Sloped Cropland Based on a Two-Step Ensemble Learning Method. Sci. Total Environ. 2023, 866, 161421. [Google Scholar] [CrossRef]
- Wang, J.; Feng, C.; Hu, B.; Chen, S.; Hong, Y.; Arrouays, D.; Peng, J.; Shi, Z. A Novel Framework for Improving Soil Organic Matter Prediction Accuracy in Cropland by Integrating Soil, Vegetation and Human Activity Information. Sci. Total Environ. 2023, 903, 166112. [Google Scholar] [CrossRef]
- Zhou, T.; Lv, W.; Geng, Y.; Xiao, S.; Chen, J.; Xu, X.; Pan, J.; Si, B.; Lausch, A. National-Scale Spatial Prediction of Soil Organic Carbon and Total Nitrogen Using Long-Term Optical and Microwave Satellite Observations in Google Earth Engine. Comput. Electron. Agric. 2023, 210, 107928. [Google Scholar] [CrossRef]
- Yang, R.M.; Guo, W.W. Modelling of Soil Organic Carbon and Bulk Density in Invaded Coastal Wetlands Using Sentinel-1 Imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101906. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, W.; Zhang, X.; Liu, H. Mapping the Soil Organic Matter Content in a Typical Black-Soil Area Using Optical Data, Radar Data and Environmental Covariates. Soil Tillage Res. 2024, 235, 105912. [Google Scholar] [CrossRef]
- Kunkel, V.R.; Wells, T.; Hancock, G.R. Modelling Soil Organic Carbon Using Vegetation Indices across Large Catchments in Eastern Australia. Sci. Total Environ. 2022, 817, 152690. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, A.; Tiwari, R.K. Utilisation of Spaceborne C-Band Dual Pol Sentinel-1 SAR Data for Simplified Regression-Based Soil Organic Carbon Estimation in Rupnagar, Punjab, India. Adv. Space Res. 2022, 69, 1786–1798. [Google Scholar] [CrossRef]
- Ali, M.; Budillon, A.; Afzal, Z.; Schirinzi, G.; Hussain, S. PSInSAR-Based Time-Series Coastal Deformation Estimation Using Sentinel-1 Data. Land 2025, 14, 536. [Google Scholar] [CrossRef]
- dos Santos, E.P.; Moreira, M.C.; Fernandes-Filho, E.I.; Demattê, J.A.M.; Dionizio, E.A.; Silva, D.D.d.; Cruz, R.R.P.; Moura-Bueno, J.M.; Santos, U.J.d.; Costa, M.H. Sentinel-1 Imagery Used for Estimation of Soil Organic Carbon by Dual-Polarization SAR Vegetation Indices. Remote Sens. 2023, 15, 5464. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Wu, W.; Liu, H. Prediction of Soil Organic Carbon under Different Land Use Types Using Sentinel-1/-2 Data in a Small Watershed. Remote Sens. 2021, 13, 1229. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pham, T.D.; Nguyen, C.T.; Delfos, J.; Archibald, R.; Dang, K.B.; Hoang, N.B.; Guo, W.; Ngo, H.H. A Novel Intelligence Approach Based Active and Ensemble Learning for Agricultural Soil Organic Carbon Prediction Using Multispectral and SAR Data Fusion. Sci. Total Environ. 2022, 804, 150187. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Lv, W.; Xiao, S.; Zhang, P.; Xu, X.; Chen, J.; Wu, Z.; Pan, J.; Si, B.; et al. Effects of Optical and Radar Satellite Observations within Google Earth Engine on Soil Organic Carbon Prediction Models in Spain. J. Environ. Manag. 2023, 338, 117810. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, J.; Chen, S.; Zhuo, Z.; Wang, Z.; Chen, X.; Xiao, Y.; Shi, Z. Improving Model Performance in Mapping Cropland Soil Organic Matter Using Time-Series Remote Sensing Data. J. Integr. Agric. 2024, 23, 2820–2841. [Google Scholar] [CrossRef]
- Hu, B.; Ni, H.; Xie, M.; Li, H.; Wen, Y.; Chen, S.; Zhou, Y.; Teng, H.; Bourennane, H.; Shi, Z. Mapping Soil Organic Matter and Identifying Potential Controls in the Farmland of Southern China: Integration of Multi-Source Data, Machine Learning and Geostatistics. Land Degrad. Dev. 2023, 34, 5468–5485. [Google Scholar] [CrossRef]
- Mullissa, A.; Vollrath, A.; Odongo-Braun, C.; Slagter, B.; Balling, J.; Gou, Y.; Gorelick, N.; Reiche, J. Sentinel-1 SAR Backscatter Analysis Ready Data Preparation in Google Earth Engine. Remote Sens. 2021, 13, 1954. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valavi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sens. 2020, 12, 1095. [Google Scholar] [CrossRef]
- Schulz, C.; Förster, M.; Vulova, S.V.; Rocha, A.D.; Kleinschmit, B. Spectral-Temporal Traits in Sentinel-1 C-Band SAR and Sentinel-2 Multispectral Remote Sensing Time Series for 61 Tree Species in Central Europe. Remote Sens. Environ. 2024, 307, 114162. [Google Scholar] [CrossRef]
- Mastro, P.; De Peppo, M.; Crema, A.; Boschetti, M.; Pepe, A. Statistical Characterization and Exploitation of Synthetic Aperture Radar Vegetation Indexes for the Generation of Leaf Area Index Time Series. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103498. [Google Scholar] [CrossRef]
- Zhang, T.T.; Qi, J.G.; Gao, Y.; Ouyang, Z.T.; Zeng, S.L.; Zhao, B. Detecting Soil Salinity with MODIS Time Series VI Data. Ecol. Indic. 2015, 52, 480–489. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Wang, Y.; Men, Z.; Liu, H. Regional Soil Organic Matter Mapping Models Based on the Optimal Time Window, Feature Selection Algorithm and Google Earth Engine. Soil Tillage Res. 2022, 219, 105325. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Starzec, G.; Starzec, M.; Rutkowski, L.; Kisiel-Dorohinicki, M.; Byrski, A. Ant Colony Optimization Using Two-Dimensional Pheromone for Single-Objective Transport Problems. J. Comput. Sci. 2024, 79, 102308. [Google Scholar] [CrossRef]
- Hu, B.; Xie, M.; Zhou, Y.; Chen, S.; Zhou, Y.; Ni, H.; Peng, J.; Ji, W.; Hong, Y.; Li, H.; et al. A High-Resolution Map of Soil Organic Carbon in Cropland of Southern China. Catena 2024, 237, 107813. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, S.; Hu, B.; Ji, W.; Li, S.; Hong, Y.; Xu, H.; Wang, N.; Xue, J.; Zhang, X.; et al. Global Soil Salinity Prediction by Open Soil Vis-NIR Spectral Library. Remote Sens. 2022, 14, 5627. [Google Scholar] [CrossRef]
- Shi, P.; Six, J.; Sila, A.; Vanlauwe, B.; Van Oost, K. Towards Spatially Continuous Mapping of Soil Organic Carbon in Croplands Using Multitemporal Sentinel-2 Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2022, 193, 187–199. [Google Scholar] [CrossRef]
- Yang, R.M.; Guo, W.W.; Zheng, J.B. Soil Prediction for Coastal Wetlands Following Spartina Alterniflora Invasion Using Sentinel-1 Imagery and Structural Equation Modeling. Catena 2019, 173, 465–470. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Minaei, F.; Talebi-khiyavi, H.; Xu, T.; Homaee, M. Synergetic Use of Multi-Temporal Sentinel-1, Sentinel-2, NDVI, and Topographic Factors for Estimating Soil Organic Carbon. Catena 2022, 212, 106077. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, W.; Zhang, X.; Liu, H. Mapping of Soil Organic Matter in a Typical Black Soil Area Using Landsat-8 Synthetic Images at Different Time Periods. Catena 2023, 231, 107336. [Google Scholar] [CrossRef]
- Yang, C.; Yang, L.; Zhang, L.; Zhou, C. Soil Organic Matter Mapping Using INLA-SPDE with Remote Sensing Based Soil Moisture Indices and Fourier Transforms Decomposed Variables. Geoderma 2023, 437, 116571. [Google Scholar] [CrossRef]
- Castaldi, F.; Halil Koparan, M.; Wetterlind, J.; Žydelis, R.; Vinci, I.; Özge Savaş, A.; Kıvrak, C.; Tunçay, T.; Volungevičius, J.; Obber, S.; et al. Assessing the Capability of Sentinel-2 Time-Series to Estimate Soil Organic Carbon and Clay Content at Local Scale in Croplands. ISPRS J. Photogramm. Remote Sens. 2023, 199, 40–60. [Google Scholar] [CrossRef]
- Odebiri, O.; Mutanga, O.; Odindi, J.; Slotow, R.; Mafongoya, P.; Lottering, R.; Naicker, R.; Matongera, T.N.; Mngadi, M. Mapping Sub-Surface Distribution of Soil Organic Carbon Stocks in South Africa’s Arid and Semi-Arid Landscapes: Implications for Land Management and Climate Change Mitigation. Geoderma Reg. 2024, 37, e00817. [Google Scholar] [CrossRef]
- Zhang, M.W.; Wang, X.Q.; Ding, X.G.; Yang, H.L.; Guo, Q.; Zeng, L.T.; Cui, Y.P.; Sun, X.L. Monitoring Regional Soil Organic Matter Content Using a Spatiotemporal Model with Time-Series Synthetic Landsat Images. Geoderma Reg. 2023, 34, e00702. [Google Scholar] [CrossRef]
- Nieto, L.; Houborg, R.; Tivet, F.; Olson, B.J.S.C.; Prasad, P.V.V.; Ciampitti, I.A. Limitations and Future Perspectives for Satellite-Based Soil Carbon Monitoring. Environ. Chall. 2024, 14, 100839. [Google Scholar] [CrossRef]
- Dai, W.; Huang, Y. Relation of Soil Organic Matter Concentration to Climate and Altitude in Zonal Soils of China. Catena 2006, 65, 87–94. [Google Scholar] [CrossRef]





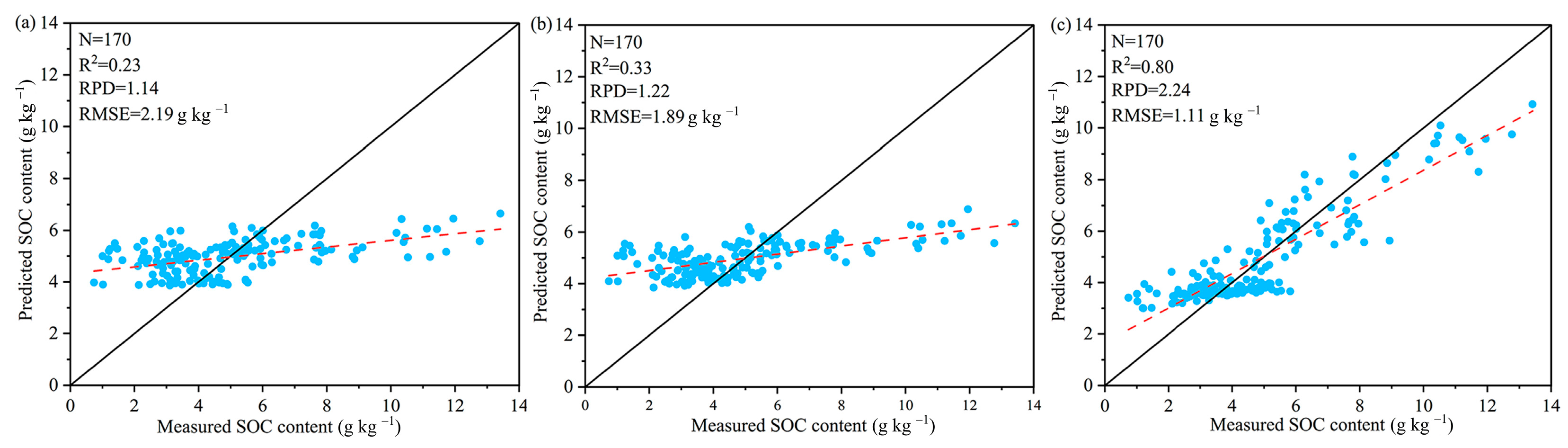
| Model | Dataset | Training | Testing | ||||
|---|---|---|---|---|---|---|---|
| R2 | RPD | RMSE | R2 | RPD | RMSE | ||
| PLSR | All | 0.41 | 1.30 | 2.06 | 0.28 | 1.18 | 2.10 |
| ACO | 0.43 | 1.33 | 1.37 | 0.36 | 1.25 | 2.00 | |
| RFE | 0.44 | 1.34 | 1.89 | 0.38 | 1.27 | 1.76 | |
| Boruta | 0.46 | 1.36 | 1.88 | 0.39 | 1.28 | 1.92 | |
| RF | All | 0.52 | 1.46 | 1.53 | 0.43 | 1.32 | 1.65 |
| ACO | 0.70 | 1.83 | 1.37 | 0.56 | 1.51 | 1.64 | |
| RFE | 0.75 | 2.02 | 1.24 | 0.69 | 1.78 | 1.39 | |
| Boruta | 0.79 | 2.19 | 1.14 | 0.72 | 1.88 | 1.32 | |
| CNN-LSTM | All | 0.59 | 1.57 | 1.50 | 0.51 | 1.43 | 1.52 |
| ACO | 0.78 | 2.14 | 1.20 | 0.67 | 1.75 | 1.25 | |
| RFE | 0.81 | 2.28 | 1.10 | 0.73 | 1.93 | 1.33 | |
| Boruta | 0.85 | 2.54 | 0.99 | 0.80 | 2.24 | 1.11 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Hu, B.; Chen, S.; Wang, N.; Luo, D.; Peng, J. A Novel Framework for Improving Soil Organic Carbon Mapping Accuracy by Mining Temporal Features of Time-Series Sentinel-1 Data. Land 2025, 14, 677. https://doi.org/10.3390/land14040677
Cui Z, Hu B, Chen S, Wang N, Luo D, Peng J. A Novel Framework for Improving Soil Organic Carbon Mapping Accuracy by Mining Temporal Features of Time-Series Sentinel-1 Data. Land. 2025; 14(4):677. https://doi.org/10.3390/land14040677
Chicago/Turabian StyleCui, Zhibo, Bifeng Hu, Songchao Chen, Nan Wang, Defang Luo, and Jie Peng. 2025. "A Novel Framework for Improving Soil Organic Carbon Mapping Accuracy by Mining Temporal Features of Time-Series Sentinel-1 Data" Land 14, no. 4: 677. https://doi.org/10.3390/land14040677
APA StyleCui, Z., Hu, B., Chen, S., Wang, N., Luo, D., & Peng, J. (2025). A Novel Framework for Improving Soil Organic Carbon Mapping Accuracy by Mining Temporal Features of Time-Series Sentinel-1 Data. Land, 14(4), 677. https://doi.org/10.3390/land14040677









