Unequal Impact of Road Expansion on Regional Ecological Quality
Abstract
1. Introduction
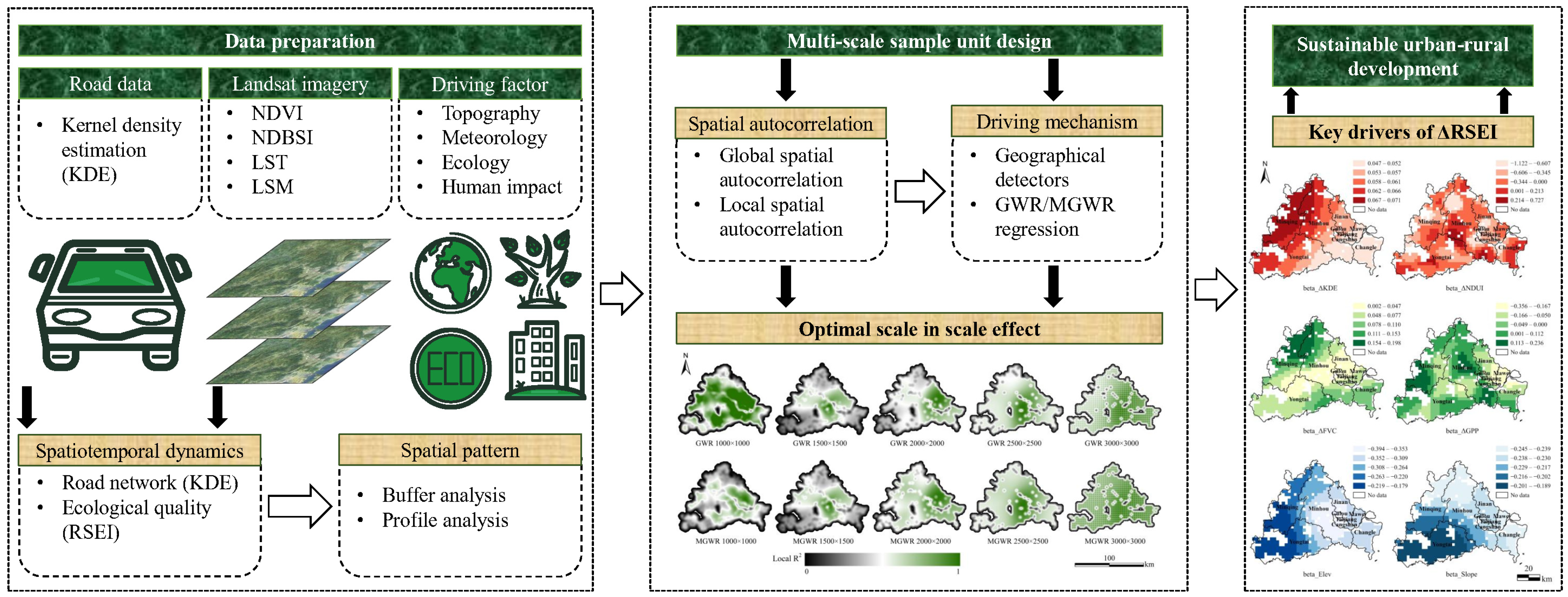
2. Materials and Methods
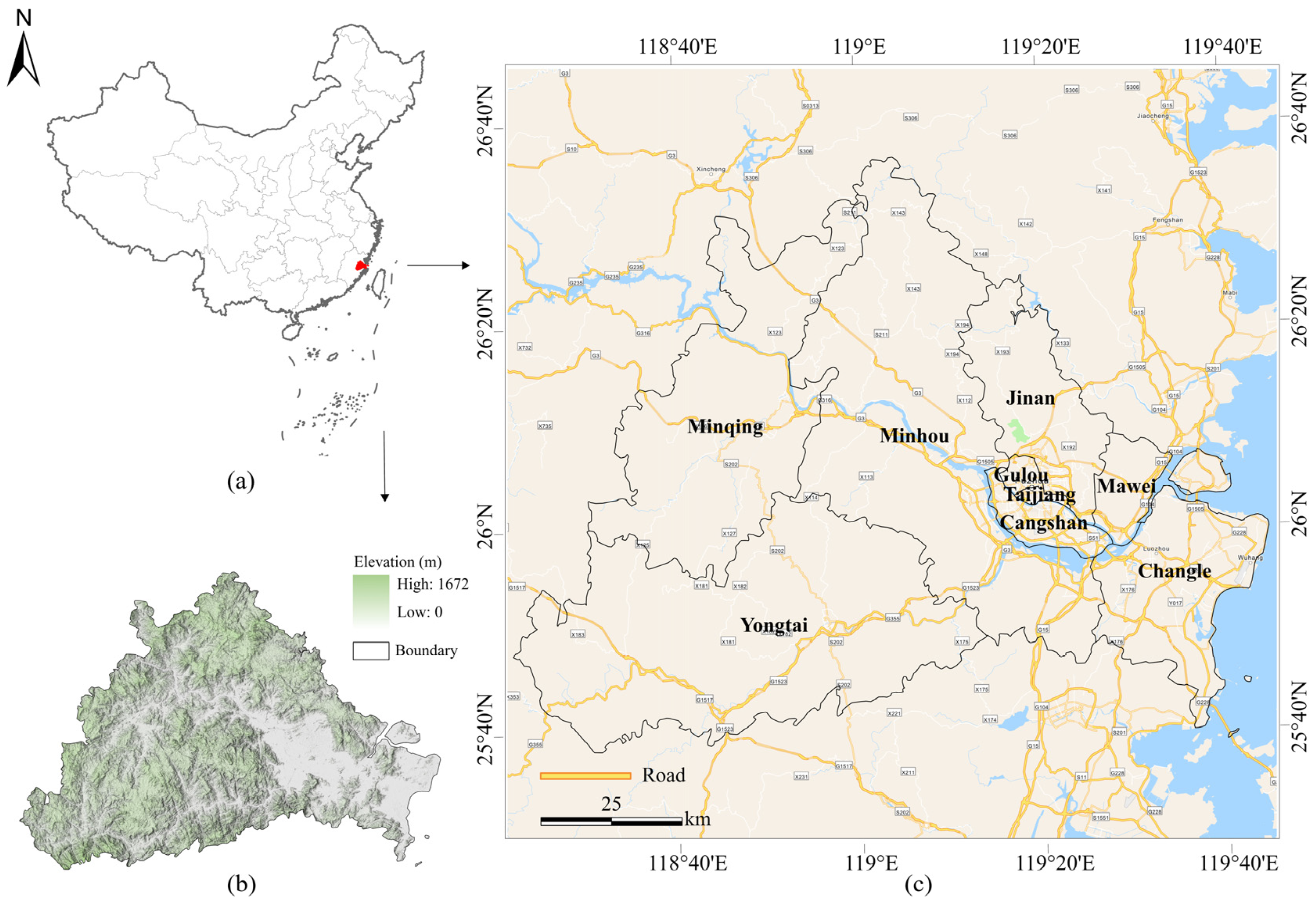
2.1. Study Area
2.2. Data Sources and Preprocessing
2.3. Calculation of RSEI
2.4. Kernel Density Estimation
2.5. Buffer Analysis
2.6. Profile Analysis
2.7. Sample Unit Design
2.8. Spatial Autocorrelation Analysis
2.9. Geographical Detectors
2.10. Global and Local Regression Models
3. Results
3.1. Urban–Rural Gradient Patterns in Road Networks and Ecological Quality
3.2. Univariate Global Spatial Autocorrelation Analysis of Road Networks and Ecological Quality at Multi-Scale
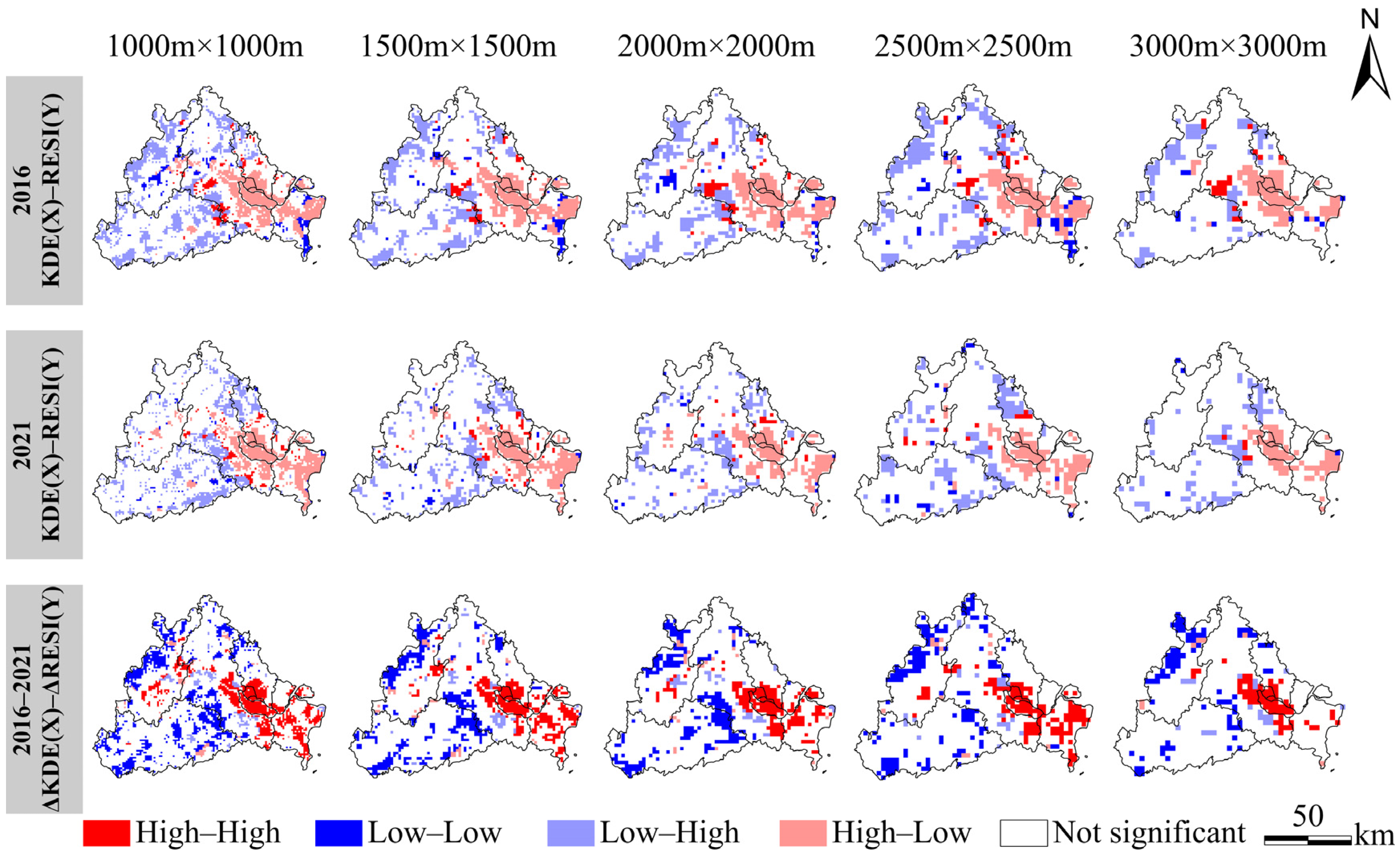
3.3. Spatiotemporal Coupling Relationships of Road Networks and Ecological Quality at Multi-Scale
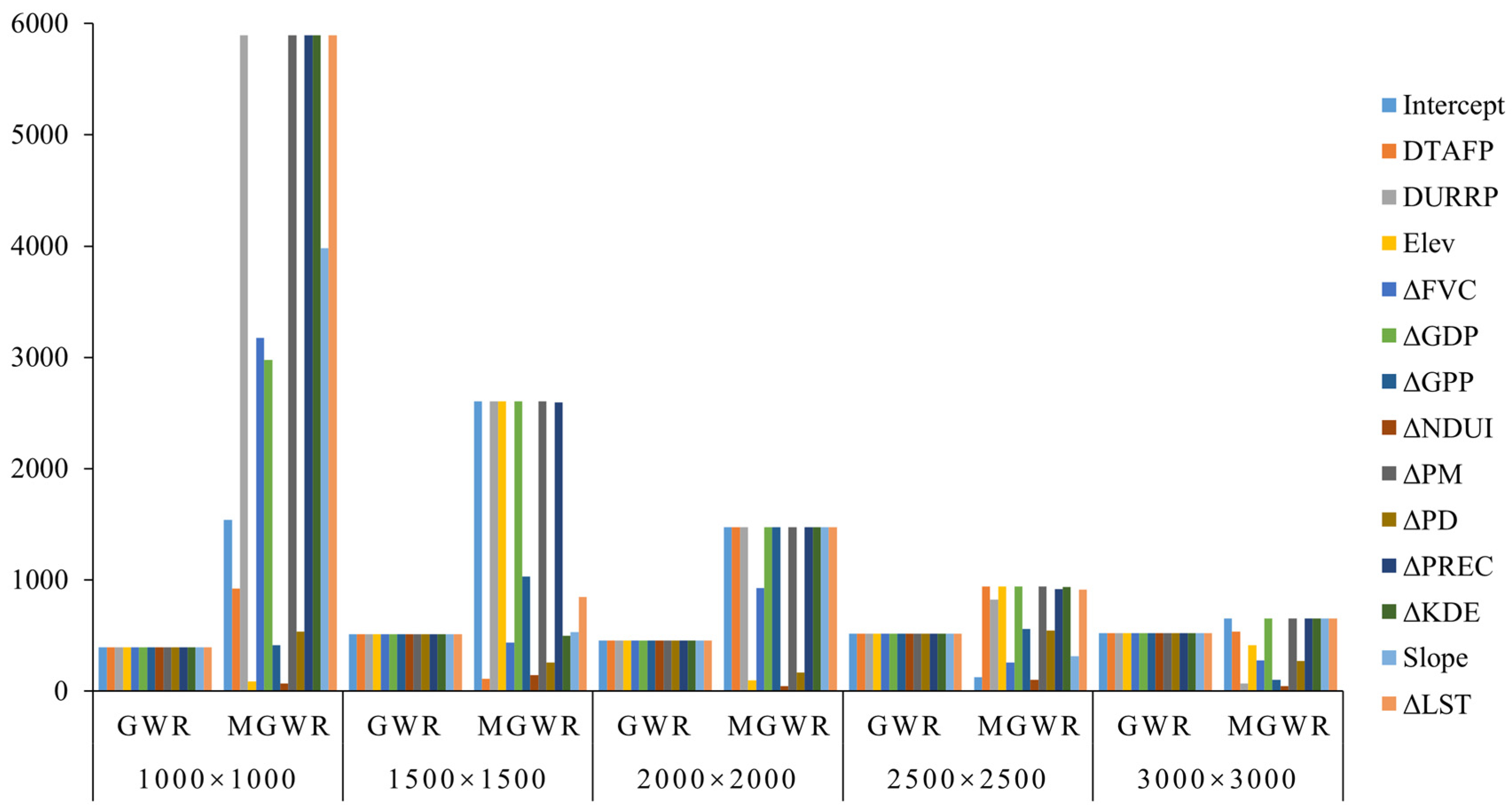
3.4. Driving Patterns of Road Network on Ecological Quality
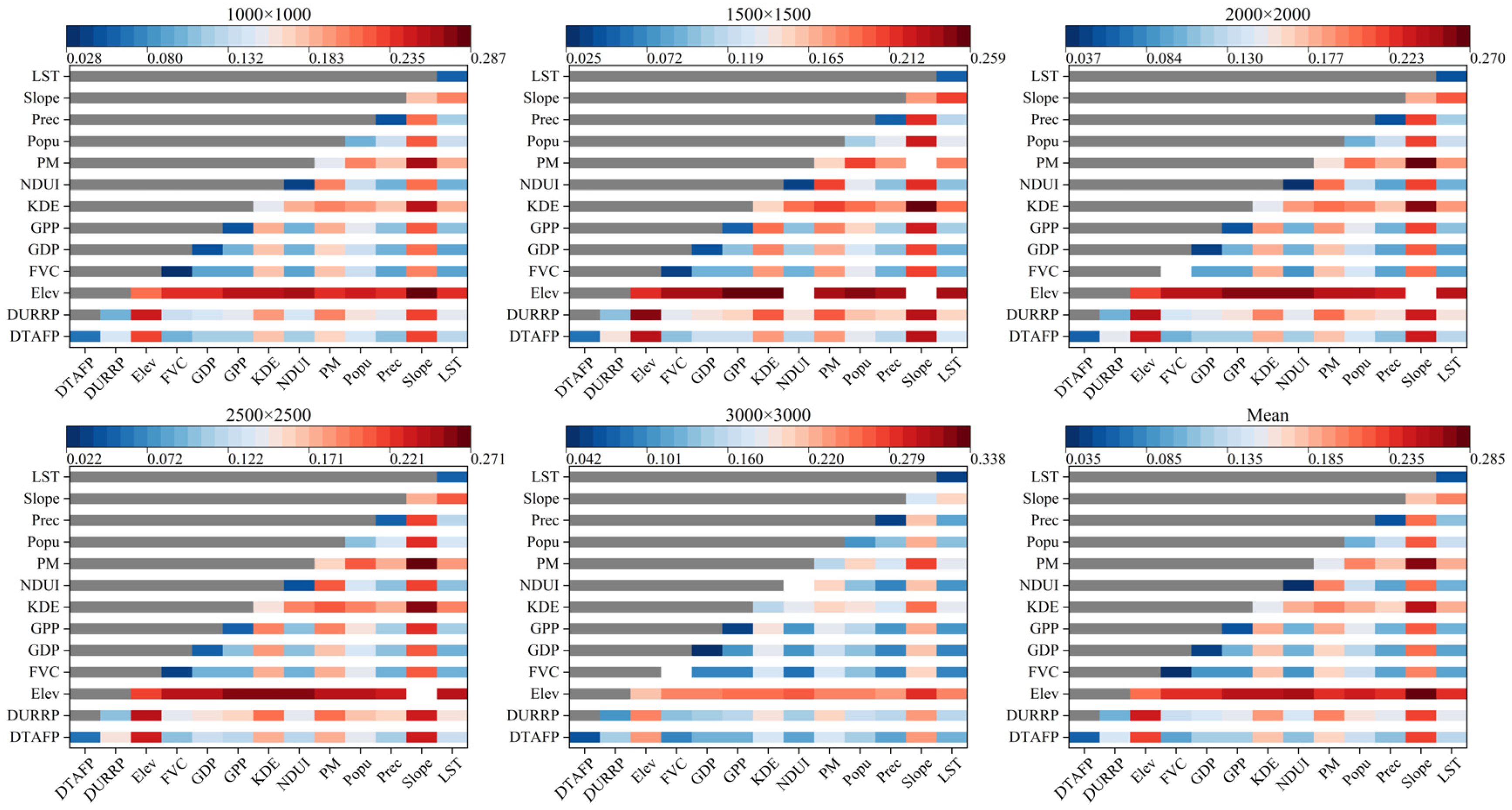
3.4.1. Individual and Interactive Effects of Road Network on Ecological Quality
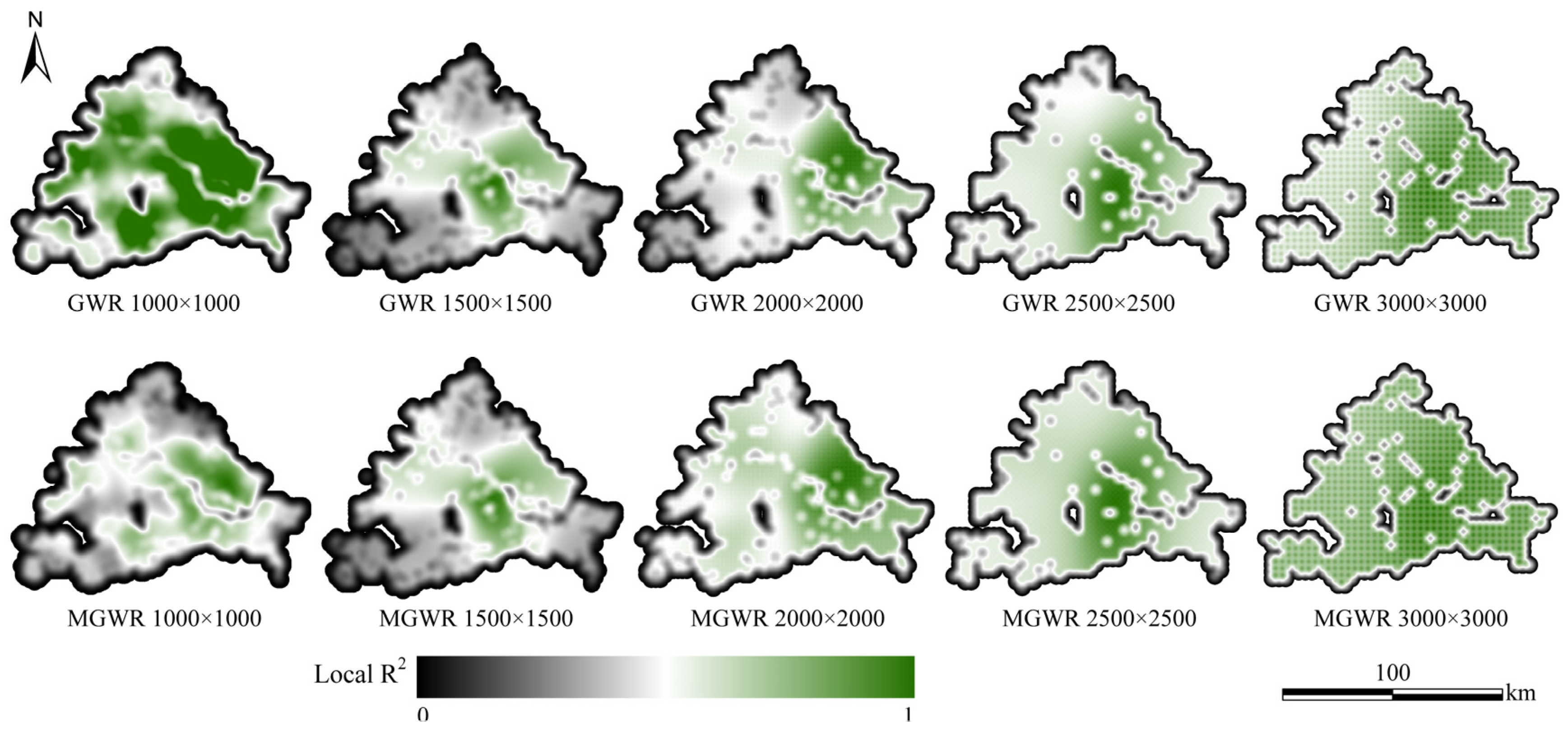
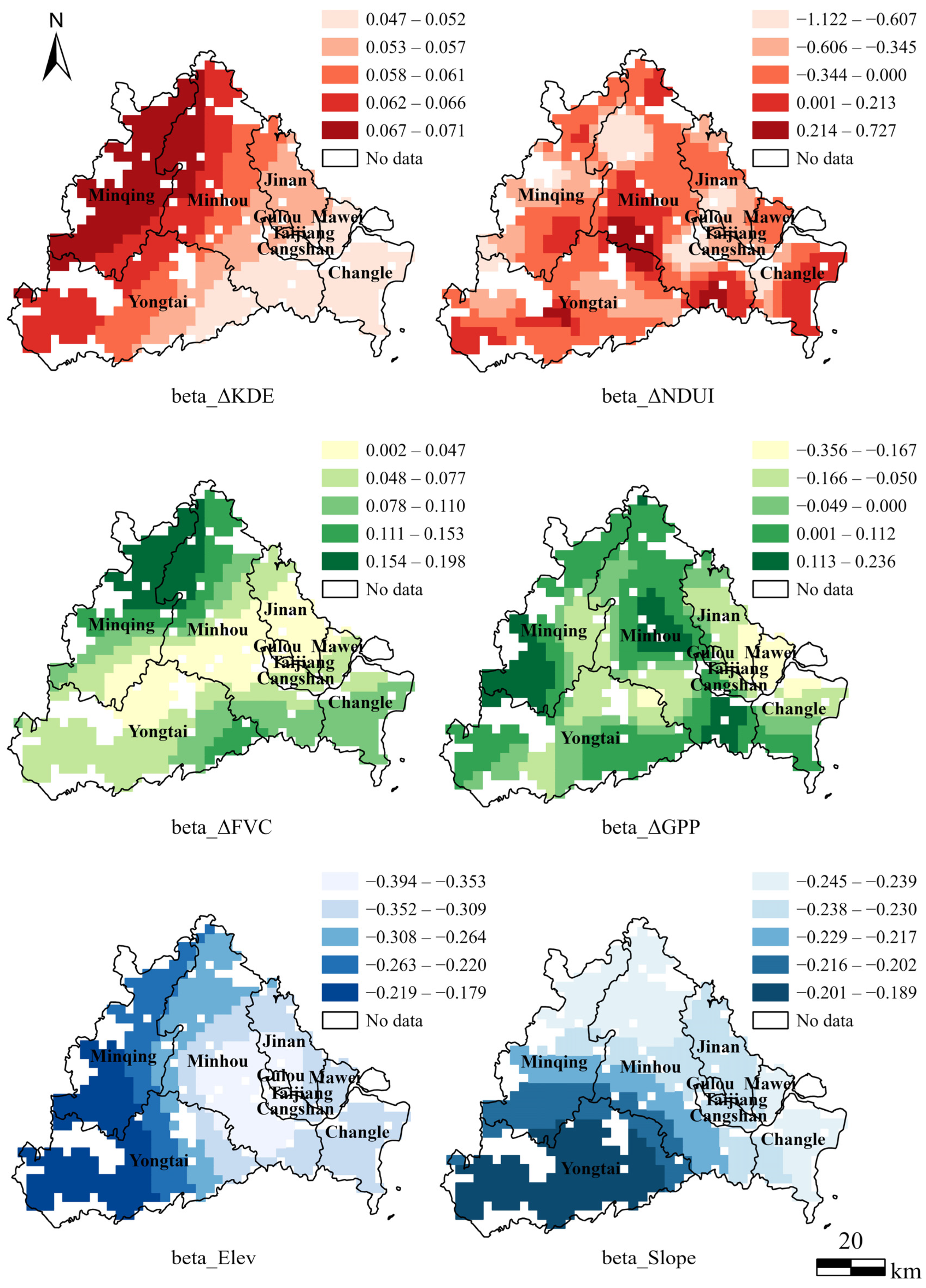
3.4.2. Spatial Variations in the Driving Patterns of Road Network on Ecological Quality
4. Discussion
4.1. Changing Relationships Between Road Networks and Ecological Quality
4.2. GD, GWR, and MGWR: Differences in Exploring Spatial Heterogeneity
4.3. Ecological Mitigation for Road Network Development
4.4. Limitations and Expectations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Forman, R.T.T. Road Ecology: Science and Solutions; Island Press: Washington, DC, USA, 2003; ISBN 978-1-55963-932-3. [Google Scholar]
- Dulac, J. Global Land Transport Infrastructure Requirements: Estimating Road and Railway Infrastructure Capacity and Costs to 2050; International Energy Agency: Paris, France, 2013. [Google Scholar]
- Laurance, W.F.; Peletier-Jellema, A.; Geenen, B.; Koster, H.; Verweij, P.; Van Dijck, P.; Lovejoy, T.E.; Schleicher, J.; Van Kuijk, M. Reducing the Global Environmental Impacts of Rapid Infrastructure Expansion. Curr. Biol. 2015, 25, R259–R262. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Ma, L.; Broyd, T.; Li, J.; Jia, J.; Luo, H. Systematic Framework for Sustainable Urban Road Alignment Planning. Transp. Res. Part D Transp. Environ. 2023, 120, 103796. [Google Scholar] [CrossRef]
- Laurance, W.F.; Clements, G.R.; Sloan, S.; O’Connell, C.S.; Mueller, N.D.; Goosem, M.; Venter, O.; Edwards, D.P.; Phalan, B.; Balmford, A.; et al. A Global Strategy for Road Building. Nature 2014, 513, 229–232. [Google Scholar] [CrossRef]
- da Silva, C.F.A.; de Andrade, M.O.; dos Santos, A.M.; de Melo, S.N. Road Network and Deforestation of Indigenous Lands in the Brazilian Amazon. Transp. Res. Part D Transp. Environ. 2023, 119, 103735. [Google Scholar] [CrossRef]
- St-Pierre, F.; Drapeau, P.; St-Laurent, M.-H. Stairway to Heaven or Highway to Hell? How Characteristics of Forest Roads Shape Their Use by Large Mammals in the Boreal Forest. For. Ecol. Manag. 2022, 510, 120108. [Google Scholar] [CrossRef]
- Balmford, A.; Chen, H.; Phalan, B.; Wang, M.; O’Connell, C.; Tayleur, C.; Xu, J. Getting Road Expansion on the Right Track: A Framework for Smart Infrastructure Planning in the Mekong. PLoS Biol. 2016, 14, e2000266. [Google Scholar] [CrossRef]
- Jaarsma, C.F. Approaches for the Planning of Rural Road Networks According to Sustainable Land Use Planning. Landsc. Urban Plan. 1997, 39, 47–54. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, W.; Luo, Y.; Li, J. Road Construction and Air Quality: Empirical Study of Cities in China. J. Clean. Prod. 2021, 319, 128649. [Google Scholar] [CrossRef]
- Flanagan, E.; Malmqvist, E.; Oudin, A.; Sunde Persson, K.; Alkan Ohlsson, J.; Mattisson, K. Health Impact Assessment of Road Traffic Noise Exposure Based on Different Densification Scenarios in Malmö, Sweden. Environ. Int. 2023, 174, 107867. [Google Scholar] [CrossRef]
- Adugbila, E.J.; Martinez, J.A.; Pfeffer, K. Road Infrastructure Expansion and Socio-Spatial Fragmentation in the Peri-Urban Zone in Accra, Ghana. Cities 2023, 133, 104154. [Google Scholar] [CrossRef]
- Ministry of Transport of China. China’s Total Road Mileage Has Increased by 1.12 Million Km in the Past Ten Years. Available online: https://www.gov.cn/yaowen/liebiao/202311/content_6916796.htm (accessed on 11 May 2024).
- Ministry of Transport of China. What Will China’s Comprehensive Three-Dimensional Transportation Network Look like in 2035? Available online: https://www.gov.cn/xinwen/2021-03/02/content_5589594.htm (accessed on 3 May 2024).
- State Council of China. The Central Committee of the Communist Party of China and the State Council Have Issued the “National Comprehensive Three-Dimensional Transportation Network Planning Outline”, as Published in the 8th Issue of the State Council Gazette in 2021. Available online: https://www.gov.cn/gongbao/content/2021/content_5593440.htm (accessed on 29 April 2024).
- van der Ree, R.; Smith, D.J.; Grilo, C. The Ecological Effects of Linear Infrastructure and Traffic. In Handbook of Road Ecology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 1–9. ISBN 978-1-118-56817-0. [Google Scholar]
- Qin, X.; Wang, Y.; Cui, S.; Liu, S.; Liu, S.; Wangari, V.W. Post-Assessment of the Eco-Environmental Impact of Highway Construction—A Case Study of Changbai Mountain Ring Road. Environ. Impact Assess. Rev. 2023, 98, 106963. [Google Scholar] [CrossRef]
- Cai, X.; Wu, Z.; Cheng, J. Using Kernel Density Estimation to Assess the Spatial Pattern of Road Density and Its Impact on Landscape Fragmentation. Int. J. Geogr. Inf. Sci. 2013, 27, 222–230. [Google Scholar] [CrossRef]
- Anderson, T.K. Kernel Density Estimation and K-Means Clustering to Profile Road Accident Hotspots. Accid. Anal. Prev. 2009, 41, 359–364. [Google Scholar] [CrossRef]
- Vu, V.-H.; Le, X.-Q.; Pham, N.-H.; Hens, L. Application of GIS and Modelling in Health Risk Assessment for Urban Road Mobility. Environ. Sci. Pollut. Res. 2013, 20, 5138–5149. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Hu, X.; Zheng, X.; Hou, X.; Zhang, Z.; Zhou, X.; Qiu, R.; Lin, J. Spatial Variations in the Relationships between Road Network and Landscape Ecological Risks in the Highest Forest Coverage Region of China. Ecol. Indic. 2019, 96, 392–403. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, L.; Ye, L.; Lin, Y.; Qiu, R. Locating Spatial Variation in the Association between Road Network and Forest Biomass Carbon Accumulation. Ecol. Indic. 2017, 73, 214–223. [Google Scholar] [CrossRef]
- Kamran, M.; Yamamoto, K. Evolution and Use of Remote Sensing in Ecological Vulnerability Assessment: A Review. Ecol. Indic. 2023, 148, 110099. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H. A New Remote Sensing Index for Assessing the Spatial Heterogeneity in Urban Ecological Quality: A Case from Fuzhou City, China. Ecol. Indic. 2018, 89, 11–21. [Google Scholar] [CrossRef]
- Li, W.; Kang, J.; Wang, Y. Spatiotemporal Changes and Driving Forces of Ecological Security in the Chengdu-Chongqing Urban Agglomeration, China: Quantification Using Health-Services-Risk Framework. J. Clean. Prod. 2023, 389, 136135. [Google Scholar] [CrossRef]
- Song, W.; Gu, H.-H.; Song, W.; Li, F.-P.; Cheng, S.-P.; Zhang, Y.-X.; Ai, Y.-J. Environmental Assessments in Dense Mining Areas Using Remote Sensing Information over Qian’an and Qianxi Regions China. Ecol. Indic. 2023, 146, 109814. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Qian, C. Analysis of the Implementation Effects of Ecological Restoration Projects Based on Carbon Storage and Eco-Environmental Quality: A Case Study of the Yellow River Delta, China. J. Environ. Manag. 2023, 340, 117929. [Google Scholar] [CrossRef]
- Zhang, L.; Fang, C.; Zhao, R.; Zhu, C.; Guan, J. Spatial–Temporal Evolution and Driving Force Analysis of Eco-Quality in Urban Agglomerations in China. Sci. Total Environ. 2023, 866, 161465. [Google Scholar] [CrossRef]
- Ibisch, P.L.; Hoffmann, M.T.; Kreft, S.; Pe’er, G.; Kati, V.; Biber-Freudenberger, L.; DellaSala, D.A.; Vale, M.M.; Hobson, P.R.; Selva, N. A Global Map of Roadless Areas and Their Conservation Status. Science 2016, 354, 1423–1427. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, X.; Zhang, C.; Fu, Z.-P.; Yang, H.-Z. Novel Method for Ecosystem Services Assessment and Analysis of Road-Effect Zones. Transp. Res. Part D Transp. Environ. 2024, 127, 104057. [Google Scholar] [CrossRef]
- Shi, G.; Shan, J.; Ding, L.; Ye, P.; Li, Y.; Jiang, N. Urban Road Network Expansion and Its Driving Variables: A Case Study of Nanjing City. Int. J. Environ. Res. Public Health 2019, 16, 2318. [Google Scholar] [CrossRef]
- Zheng, X.; Zou, Z.; Xu, C.; Lin, S.; Wu, Z.; Qiu, R.; Hu, X.; Li, J. A New Remote Sensing Index for Assessing Spatial Heterogeneity in Urban Ecoenvironmental-Quality-Associated Road Networks. Land 2022, 11, 46. [Google Scholar] [CrossRef]
- Goodchild, M.F. The Openshaw Effect. Int. J. Geogr. Inf. Sci. 2022, 36, 1697–1698. [Google Scholar] [CrossRef]
- Ma, J.; Li, J.; Wu, W.; Liu, J. Global Forest Fragmentation Change from 2000 to 2020. Nat. Commun. 2023, 14, 3752. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Kao, C.-L.; Yu, H.; Bardin, S.; Oshan, T.; Li, Z.; Sachdeva, M.; Luo, W. Exploring Spatial Context: A Comprehensive Bibliography of GWR and MGWR. Available online: https://arxiv.org/abs/2404.16209v1 (accessed on 5 May 2024).
- Hu, X.; Xu, H. Spatial Variability of Urban Climate in Response to Quantitative Trait of Land Cover Based on GWR Model. Environ. Monit. Assess. 2019, 191, 194. [Google Scholar] [CrossRef]
- Fuzhou Transportation Bureau Transportation Overview of Fuzhou City. Available online: https://fzjt.fuzhou.gov.cn/zwgk/ztzl/jtjs/jtgk/201708/t20170821_1621082.htm (accessed on 15 May 2024).
- Lin, Z.; Xu, H.; Yao, X.; Yang, C.; Yang, L. Exploring the Relationship between Thermal Environmental Factors and Land Surface Temperature of a “Furnace City” Based on Local Climate Zones. Build. Environ. 2023, 243, 110732. [Google Scholar] [CrossRef]
- Geng, J.; Yu, K.; Xie, Z.; Zhao, G.; Ai, J.; Yang, L.; Yang, H.; Liu, J. Analysis of Spatiotemporal Variation and Drivers of Ecological Quality in Fuzhou Based on RSEI. Remote Sens. 2022, 14, 4900. [Google Scholar] [CrossRef]
- Kilic, A.; Allen, R.; Trezza, R.; Ratcliffe, I.; Kamble, B.; Robison, C.; Ozturk, D. Sensitivity of Evapotranspiration Retrievals from the METRIC Processing Algorithm to Improved Radiometric Resolution of Landsat 8 Thermal Data and to Calibration Bias in Landsat 7 and 8 Surface Temperature. Remote Sens. Environ. 2016, 185, 198–209. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Koks, E.E.; Rozenberg, J.; Zorn, C.; Tariverdi, M.; Vousdoukas, M.; Fraser, S.A.; Hall, J.W.; Hallegatte, S. A Global Multi-Hazard Risk Analysis of Road and Railway Infrastructure Assets. Nat. Commun. 2019, 10, 2677. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Q.; Wang, M.; Koks, E.E. Global Transportation Infrastructure Exposure to the Change of Precipitation in a Warmer World. Nat. Commun. 2023, 14, 2541. [Google Scholar] [CrossRef]
- Barrington-Leigh, C.; Millard-Ball, A. Global Trends toward Urban Street-Network Sprawl. Proc. Natl. Acad. Sci. USA 2020, 117, 1941–1950. [Google Scholar] [CrossRef]
- Chen, J.; Xu, C.; Lin, S.; Wu, Z.; Qiu, R.; Hu, X. Is There Spatial Dependence or Spatial Heterogeneity in the Distribution of Vegetation Greening and Browning in Southeastern China? Forests 2022, 13, 840. [Google Scholar] [CrossRef]
- Xue, C.; Chen, X.; Xue, L.; Zhang, H.; Chen, J.; Li, D. Modeling the Spatially Heterogeneous Relationships between Tradeoffs and Synergies among Ecosystem Services and Potential Drivers Considering Geographic Scale in Bairin Left Banner, China. Sci Total Environ. 2023, 855, 158834. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Z.; Xiao, Z.; Jiang, S.; He, Z.; Zhang, M. Spatiotemporal Characteristics and Driving Factors of CO2 Emissions from Road Freight Transportation. Transp. Res. Part D Transp. Environ. 2023, 125, 103983. [Google Scholar] [CrossRef]
- Lv, Y.; Xiu, L.; Yao, X.; Yu, Z.; Huang, X. Spatiotemporal Evolution and Driving Factors Analysis of the Eco-Quality in the Lanxi Urban Agglomeration. Ecol. Indic. 2023, 156, 111114. [Google Scholar] [CrossRef]
- Zhou, S.; Lin, R. Spatial-Temporal Heterogeneity of Air Pollution: The Relationship between Built Environment and on-Road PM2.5 at Micro Scale. Transp. Res. Part D Transp. Environ. 2019, 76, 305–322. [Google Scholar] [CrossRef]
- Spellerberg, I. Ecological Effects of Roads and Traffic: A Literature Review. Glob. Ecol. Biogeogr. Lett. 1998, 7, 317–333. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Liu, M.; Lv, X.; Dong, Z.; Yan, X. Urban Ecological Environment Evaluation and Influencing Factors Analysis at the Residential Quarter-Level in Xi’an, China. Ecol. Indic. 2024, 158, 111348. [Google Scholar] [CrossRef]
- Yang, M.; Xue, L.; Liu, Y.; Liu, S.; Han, Q.; Yang, L.; Chi, Y. Asymmetric Response of Vegetation GPP to Impervious Surface Expansion: Case Studies in the Yellow and Yangtze River Basins. Environ. Res. 2024, 243, 117813. [Google Scholar] [CrossRef]
- Frantz, D.; Schug, F.; Wiedenhofer, D.; Baumgart, A.; Virág, D.; Cooper, S.; Gómez-Medina, C.; Lehmann, F.; Udelhoven, T.; van der Linden, S.; et al. Unveiling Patterns in Human Dominated Landscapes through Mapping the Mass of US Built Structures. Nat. Commun. 2023, 14, 8014. [Google Scholar] [CrossRef]
- Brodie, J.F.; Mohd-Azlan, J.; Chen, C.; Wearn, O.R.; Deith, M.C.M.; Ball, J.G.C.; Slade, E.M.; Burslem, D.F.R.P.; Teoh, S.W.; Williams, P.J.; et al. Landscape-Scale Benefits of Protected Areas for Tropical Biodiversity. Nature 2023, 620, 807–812. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, Q. 30 M-Scale Annual Global Normalized Difference Urban Index Datasets from 2000 to 2021. V2. Sci. Data Bank 2023. [Google Scholar] [CrossRef]
- Xu, H.; Wang, M.; Shi, T.; Guan, H.; Fang, C.; Lin, Z. Prediction of Ecological Effects of Potential Population and Impervious Surface Increases Using a Remote Sensing Based Ecological Index (RSEI). Ecol. Indic. 2018, 93, 730–740. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, X.; Lin, M.; Qiu, R.; Lin, J.; Li, B. Spatial Paradigms in Road Networks and Their Delimitation of Urban Boundaries Based on KDE. ISPRS Int. J. Geo-Inf. 2020, 9, 204. [Google Scholar] [CrossRef]
- Gatrell, A.C.; Bailey, T.C.; Diggle, P.J.; Rowlingson, B.S. Spatial Point Pattern Analysis and Its Application in Geographical Epidemiology. Trans. Inst. Br. Geogr. 1996, 21, 256. [Google Scholar] [CrossRef]
- Salgado-Ugarte, I.H.; Pérez-Hernández, M.A. Exploring the Use of Variable Bandwidth Kernel Density Estimators. Stata J. Promot. Commun. Stat. Stata 2003, 3, 133–147. [Google Scholar] [CrossRef]
- Feng, S.; Liu, S.; Jing, L.; Zhu, Y.; Yan, W.; Jiang, B.; Liu, M.; Lu, W.; Ning, Y.; Wang, Z.; et al. Quantification of the Environmental Impacts of Highway Construction Using Remote Sensing Approach. Remote Sens. 2021, 13, 1340. [Google Scholar] [CrossRef]
- Wei, W.; Bao, Y.; Wang, Z.; Chen, X.; Luo, Q.; Mo, Y. Response of Habitat Quality to Urban Spatial Morphological Structure in Multi-Mountainous City. Ecol. Indic. 2023, 146, 109877. [Google Scholar] [CrossRef]
- Ahmed, M.F.; Ali, M.Z.; Rogers, J.D.; Khan, M.S. A Study of Knickpoint Surveys and Their Likely Association with Landslides along the Hunza River Longitudinal Profile. Environ. Earth Sci. 2019, 78, 176. [Google Scholar] [CrossRef]
- Quattrochi, D.A.; Goodchild, M.F. Scale in Remote Sensing and GIS; CRC Press: Boca Raton, FL, USA, 2023; ISBN 978-1-56670-104-4. [Google Scholar]
- Openshaw, S. The Modifiable Areal Unit Problem; Geobooks: Norwich, UK, 1984; ISBN 0-86094-134-5. [Google Scholar]
- Jelinski, D.E.; Wu, J. The Modifiable Areal Unit Problem and Implications for Landscape Ecology. Landsc. Ecol. 1996, 11, 129–140. [Google Scholar] [CrossRef]
- Ju, H.; Zhang, Z.; Zuo, L.; Wang, J.; Zhang, S.; Wang, X.; Zhao, X. Driving Forces and Their Interactions of Built-up Land Expansion Based on the Geographical Detector—A Case Study of Beijing, China. Int. J. Geogr. Inf. Sci. 2016, 30, 2188–2207. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Anselin, L.; Li, X.; Koschinsky, J. GeoDa, From the Desktop to an Ecosystem for Exploring Spatial Data. Geogr. Anal. 2022, 54, 439–466. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical Detectors-Based Health Risk Assessment and Its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D (Stat.) 2002, 47, 431–443. [Google Scholar] [CrossRef]
- Tran, D.X.; Pearson, D.; Palmer, A.; Lowry, J.; Gray, D.; Dominati, E.J. Quantifying Spatial Non-Stationarity in the Relationship between Landscape Structure and the Provision of Ecosystem Services: An Example in the New Zealand Hill Country. Sci. Total Environ. 2022, 808, 152126. [Google Scholar] [CrossRef]
- Oshan, T.; Li, Z.; Kang, W.; Wolf, L.; Fotheringham, A. Mgwr: A Python Implementation of Multiscale Geographically Weighted Regression for Investigating Process Spatial Heterogeneity and Scale. ISPRS Int. J. Geo-Inf. 2019, 8, 269. [Google Scholar] [CrossRef]
- Forman, R.T.T. Town Ecology: For the Land of Towns and Villages. Landsc. Ecol. 2019, 34, 2209–2211. [Google Scholar] [CrossRef]
- Freitas, S.R.; Constantino, E.; Alexandrino, M.M. Computational Geometry Applied to Develop New Metrics of Road and Edge Effects and Their Performance to Understand the Distribution of Small Mammals in an Atlantic Forest Landscape. Ecol. Model. 2018, 388, 24–30. [Google Scholar] [CrossRef]
- Karlson, M.; Mörtberg, U. A Spatial Ecological Assessment of Fragmentation and Disturbance Effects of the Swedish Road Network. Landsc. Urban Plan. 2015, 134, 53–65. [Google Scholar] [CrossRef]
- Laforge, A.; Barbaro, L.; Bas, Y.; Calatayud, F.; Ladet, S.; Sirami, C.; Archaux, F. Road Density and Forest Fragmentation Shape Bat Communities in Temperate Mosaic Landscapes. Landsc. Urban Plan. 2022, 221, 104353. [Google Scholar] [CrossRef]
- Laurance, W.F.; Goosem, M.; Laurance, S.G.W. Impacts of Roads and Linear Clearings on Tropical Forests. Trends Ecol. Evol. 2009, 24, 659–669. [Google Scholar] [CrossRef]
- Liu, S.; Dong, Y.; Deng, L.; Liu, Q.; Zhao, H.; Dong, S. Forest Fragmentation and Landscape Connectivity Change Associated with Road Network Extension and City Expansion: A Case Study in the Lancang River Valley. Ecol. Indic. 2014, 36, 160–168. [Google Scholar] [CrossRef]
- Ji, J.; Tang, Z.; Zhang, W.; Liu, W.; Jin, B.; Xi, X.; Wang, F.; Zhang, R.; Guo, B.; Xu, Z.; et al. Spatiotemporal and Multiscale Analysis of the Coupling Coordination Degree between Economic Development Equality and Eco-Environmental Quality in China from 2001 to 2020. Remote Sens. 2022, 14, 737. [Google Scholar] [CrossRef]
- Leng, S.; Sun, R.; Yang, X.; Jin, M.; Chen, L. Diverse Types of Coupling Trends in Urban Tree and Nontree Vegetation Associated with Urbanization Levels. NPJ Urban Sustain. 2023, 3, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.; Zohner, C.M.; Crowther, T.W.; Li, M.; Shen, F.; Guo, M.; Qin, J.; Yao, L.; Zhou, C. Direct and Indirect Impacts of Urbanization on Vegetation Growth across the World’s Cities. Sci. Adv. 2022, 8, eabo0095. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yu, W.; Qian, Y.; Han, L.; Pickett, S.T.A.; Wang, J.; Li, W.; Ouyang, Z. Beyond City Expansion: Multi-Scale Environmental Impacts of Urban Megaregion Formation in China. Natl. Sci. Rev. 2022, 9, nwab107. [Google Scholar] [CrossRef]
- Altman, N.; Krzywinski, M. Association, Correlation and Causation. Nat. Methods 2015, 12, 899–900. [Google Scholar] [CrossRef]
- Wu, J. Landscape Sustainability Science (II): Core Questions and Key Approaches. Landsc. Ecol. 2021, 36, 2453–2485. [Google Scholar] [CrossRef]
- Laurance, W.F.; Balmford, A. A Global Map for Road Building. Nature 2013, 495, 308–309. [Google Scholar] [CrossRef]
- Urban, M.C.; Strauss, S.Y.; Pelletier, F.; Palkovacs, E.P.; Leibold, M.A.; Hendry, A.P.; De Meester, L.; Carlson, S.M.; Angert, A.L.; Giery, S.T. Evolutionary Origins for Ecological Patterns in Space. Proc. Natl. Acad. Sci. USA 2020, 117, 17482–17490. [Google Scholar] [CrossRef]
- Goodchild, M.F. The Validity and Usefulness of Laws in Geographic Information Science and Geography. Ann. Assoc. Am. Geogr. 2004, 94, 300–303. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Turner, M. How Is the Third Law of Geography Different? Ann. GIS 2022, 28, 57–67. [Google Scholar] [CrossRef]
- Wu, J. Effects of Changing Scale on Landscape Pattern Analysis: Scaling Relations. Landsc. Ecol. 2004, 19, 125–138. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yue, H.; Li, Z. Examining the Influences of Air Quality in China’s Cities Using Multi-Scale Geographically Weighted Regression. Trans. GIS 2019, 23, 1444–1464. [Google Scholar] [CrossRef]
- Chien, Y.-M.C.; Carver, S.; Comber, A. Using Geographically Weighted Models to Explore How Crowdsourced Landscape Perceptions Relate to Landscape Physical Characteristics. Landsc. Urban Plan. 2020, 203, 103904. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yu, H.; Wolf, L.J.; Oshan, T.M.; Li, Z. On the Notion of ‘Bandwidth’ in Geographically Weighted Regression Models of Spatially Varying Processes. Int. J. Geogr. Inf. Sci. 2022, 36, 1485–1502. [Google Scholar] [CrossRef]
- Fuzhou Transportation Bureau Interpretation of “Fuzhou City’s ‘14th Five-Year Plan’ Comprehensive Transportation Development Special Plan”_Interpretation of This City’s Policies_Fuzhou Municipal People’s Government Portal. Available online: http://www.fuzhou.gov.cn/zcjd/bs/202203/t20220311_4324178.htm (accessed on 27 April 2024).
- Fuzhou Municipal People’s Government Government Work Report. 2021. Available online: https://www.fuzhou.gov.cn/zwgk/zfgzbg/202101/t20210126_3989941.htm (accessed on 14 February 2025).

| Categories | Data | Data Sources and Preprocessing | Resolution | Definition | Abbreviation |
|---|---|---|---|---|---|
| Topographical factors | Digital elevation model (DEM) | National Aeronautics and Space Administration (https://earthdata.nasa.gov/, accessed on 20 March 2023); Slope computed by GIS | 30 m/2019 | Static elevation | Elev |
| Static slope | Slope | ||||
| Meteorological factors | Monthly precipitation | National Earth System Science Data Center, National Science & Technology Infrastructure of China (http://www.geodata.cn, accessed on 20 March 2023); Annual average computed by GIS | 1 km/ 2016–2021 | Dynamics of annual average precipitation | ΔPREC |
| Monthly average land surface temperature | Dynamics of annual average land surface temperature | ΔLST | |||
| Particulate matter 2.5 (PM2.5) | Yangtze River Delta Science Data Center, National Earth System Science Data Center, National Science & Technology Infrastructure of China (http://geodata.nnu.edu.cn/, accessed on 20 March 2023) | Dynamics of annual PM2.5 concentration | ΔPM | ||
| Ecological factors | Monthly average Fractional vegetation cover | National Qinghai-Tibet Plateau Scientific Data Center (https://data.tpdc.ac.cn/, accessed on 22 March 2023); Annual average computed by GIS | 250 m/ 2016–2021 | Dynamics of annual average fractional vegetation cover | ΔFVC |
| Gross primary productivity | The USGS Earth Resources Observation and Science Center (https://lpdaac.usgs.gov/, accessed on 22 March 2023) | 500 m/ 2016–2021 | Dynamics of annual gross primary productivity | ΔGPP | |
| Anthropogenic factors | Population density | Oak Ridge National Laboratory (https://landscan.ornl.gov/, accessed on 27 March 2023); | 1 km/ 2016–2021 | Dynamics of annual population density | ΔPD |
| Normalized difference urban index | Science Data Bank (https://www.scidb.cn/en, accessed on 27 March 2023) | 30 m/ 2016–2021 | Dynamics of annual normalized difference urban index | ΔNDUI | |
| Gross domestic product | Statistical Yearbook of Fujian Province and Statistical Yearbook of Fuzhou City, accessed on 27 March 2023; Inverse distance weight generated by GIS | Panel/ 2016–2021 | Dynamics of annual gross domestic product | ΔGDP | |
| Urban and rural residential points | National Basic Geographic Information Center (https://www.webmap.cn/, accessed on 27 March 2023); Euclidean distance computed by GIS | Vector/2019 | Static distance to urban and rural residential points | DURRP | |
| Traffic ancillary facilities points | Static distance to traffic ancillary facilities points | DTAFP |
| Research Scale | 2016-KDE-RSEI | 2021-KDE-RSEI | 2016–2021-ΔKDE-ΔRESI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Moran’s I | z-Score | p-Value | Moran’s I | z-Score | p-Value | Moran’s I | z-Score | p-Value | |
| 1000 m × 1000 m | −0.439 | −90.665 | 0.001 | −0.404 | −81.875 | 0.001 | 0.393 | 86.166 | 0.001 |
| 1500 m × 1500 m | −0.442 | −58.085 | 0.001 | −0.403 | −55.016 | 0.001 | 0.385 | 52.586 | 0.001 |
| 2000 m × 2000 m | −0.442 | −43.283 | 0.001 | −0.364 | −38.476 | 0.001 | 0.385 | 38.444 | 0.001 |
| 2500 m × 2500 m | −0.383 | −31.252 | 0.001 | −0.357 | −28.497 | 0.001 | 0.335 | 27.991 | 0.001 |
| 3000 m × 3000 m | −0.372 | −24.448 | 0.001 | −0.324 | −22.139 | 0.001 | 0.265 | 17.909 | 0.001 |
| Index | 1000 × 1000 | 1500 × 1500 | 2000 × 2000 | 2500 × 2500 | 3000 × 3000 | Mean |
|---|---|---|---|---|---|---|
| Elev | 0.219 *** | 0.183 *** | 0.209 *** | 0.209 *** | 0.266 *** | 0.217 *** |
| Slope | 0.179 *** | 0.176 *** | 0.152 *** | 0.166 *** | 0.223 *** | 0.179 *** |
| ΔPM | 0.152 *** | 0.138 *** | 0.143 *** | 0.152 *** | 0.194 *** | 0.156 *** |
| ΔKDE | 0.158 *** | 0.126 *** | 0.139 *** | 0.137 *** | 0.207 *** | 0.153 *** |
| ΔPD | 0.104 *** | 0.111 *** | 0.108 *** | 0.101 ** | 0.099 | 0.105 * |
| DURRP | 0.108 *** | 0.093 *** | 0.102 *** | 0.102 *** | 0.109 *** | 0.103 *** |
| DTAFP | 0.061 *** | 0.055 *** | 0.062 *** | 0.066 *** | 0.071 *** | 0.063 *** |
| ΔLST | 0.05 *** | 0.052 *** | 0.080 *** | 0.048 *** | 0.043 *** | 0.055 *** |
| ΔGPP | 0.052 *** | 0.059 *** | 0.055 *** | 0.057 *** | 0.044 *** | 0.053 *** |
| ΔPREC | 0.045 *** | 0.049 *** | 0.057 *** | 0.065 *** | 0.051 *** | 0.053 *** |
| ΔGDP | 0.035 *** | 0.037 *** | 0.044 *** | 0.054 *** | 0.067 *** | 0.047 *** |
| ΔNDUI | 0.037 *** | 0.026 ** | 0.047 *** | 0.022 | 0.066 * | 0.040 |
| ΔFVC | 0.028 *** | 0.027 *** | 0.037 *** | 0.031 ** | 0.056 *** | 0.036 ** |
| Total | 1.228 | 1.132 | 1.235 | 1.210 | 1.496 | 1.260 |
| Model | Scale/m | R-Squared | Adjusted R-Squared | AICc | Residual Sum of Squares | Residual Moran’s I | Effective Number of Parameters |
|---|---|---|---|---|---|---|---|
| MGWR | 1000 × 1000 | 0.519 | 0.481 | 13,344.884 | 2838.477 | −0.017 | 426.359 |
| 1500 × 1500 | 0.483 | 0.447 | 6034.114 | 1348.042 | −0.016 | 166.236 | |
| 2000 × 2000 | 0.526 | 0.474 | 3416.028 | 700.429 | −0.039 | 145.877 | |
| 2500 × 2500 | 0.469 | 0.425 | 2240.709 | 501.132 | −0.018 | 72.479 | |
| 3000 × 3000 | 0.590 | 0.521 | 1499.084 | 268.651 | −0.026 | 94.508 | |
| GWR | 1000 × 1000 | 0.501 | 0.459 | 13,614.535 | 2945.024 | 0.016 | 448.781 |
| 1500 × 1500 | 0.461 | 0.427 | 6111.995 | 1403.622 | 0.027 | 154.199 | |
| 2000 × 2000 | 0.446 | 0.407 | 3531.646 | 818.506 | 0.013 | 97.816 | |
| 2500 × 2500 | 0.417 | 0.382 | 2285.036 | 550.137 | 0.027 | 53.496 | |
| 3000 × 3000 | 0.426 | 0.394 | 1571.115 | 375.935 | 0.016 | 34.850 | |
| OLS | 1000 × 1000 | 0.364 | 0.363 | 14,094.614 | 3749.410 | 0.080 | 5897 |
| 1500 × 1500 | 0.347 | 0.344 | 6311.110 | 1700.052 | 0.066 | 2605 | |
| 2000 × 2000 | 0.355 | 0.350 | 3571.023 | 952.117 | 0.078 | 1477 | |
| 2500 × 2500 | 0.347 | 0.338 | 2307.646 | 616.749 | 0.071 | 944 | |
| 3000 × 3000 | 0.386 | 0.373 | 1570.506 | 402.433 | 0.044 | 655 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, W.; Jia, D.; Guo, R.; Zhang, L.; Wang, Z.; Hu, X. Unequal Impact of Road Expansion on Regional Ecological Quality. Land 2025, 14, 523. https://doi.org/10.3390/land14030523
Qiu W, Jia D, Guo R, Zhang L, Wang Z, Hu X. Unequal Impact of Road Expansion on Regional Ecological Quality. Land. 2025; 14(3):523. https://doi.org/10.3390/land14030523
Chicago/Turabian StyleQiu, Weiguo, Dingyi Jia, Rongpeng Guo, Lanyi Zhang, Zhanyong Wang, and Xisheng Hu. 2025. "Unequal Impact of Road Expansion on Regional Ecological Quality" Land 14, no. 3: 523. https://doi.org/10.3390/land14030523
APA StyleQiu, W., Jia, D., Guo, R., Zhang, L., Wang, Z., & Hu, X. (2025). Unequal Impact of Road Expansion on Regional Ecological Quality. Land, 14(3), 523. https://doi.org/10.3390/land14030523






