Urban Sprawl in the Yangtze River Delta: Spatio-Temporal Characteristics and Impacts on PM2.5
Abstract
1. Introduction
2. Research Data and Methods
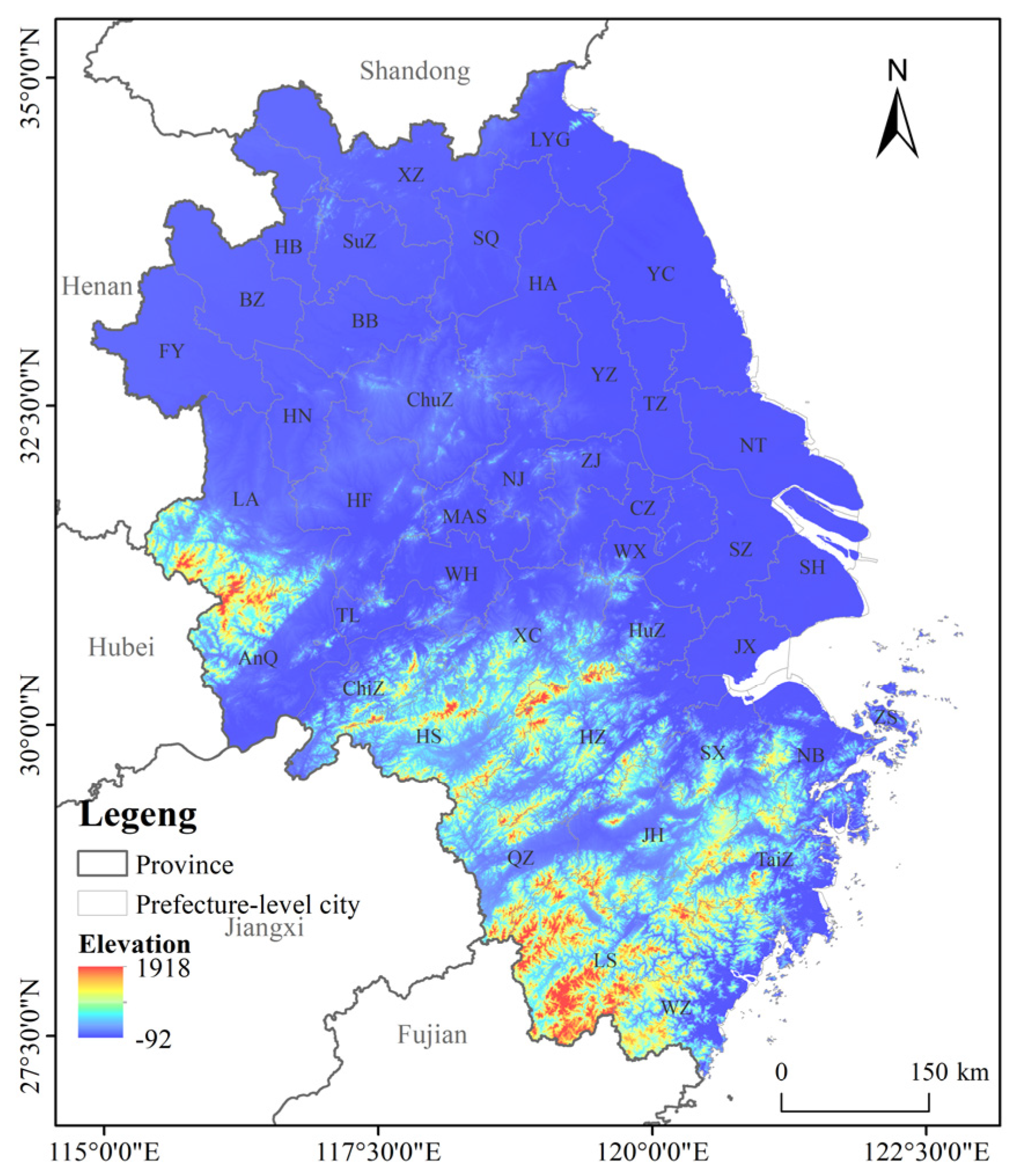
2.1. Study Area
2.2. Data Sources
- (1)
- Night-time light data. This data is sourced from the annual DMSP/OLS stable nighttime light data obtained from the study Annual-scale DMSP/OLS stable night-time light data (Defense Meteorological Satellite Program’s Operational Linescan System, DMSP/OLS) acquired for the period 2000–2013, featuring pixel grey values of 0–63, annual temporal resolution, and 1 km × 1 km spatial resolution. Annual-scale NPP/VIIRS night-time light data (Suomi National Polar-Orbiting Partnership satellite with the Visible Infrared Imaging Radiometer Suite, NPP/VIIRS) acquired for the period 2012–2020, featuring a spatial resolution of 0.5 km × 0.5 km. Using NPP/VIIRS night-time light data as the benchmark, the two night-time light imagery sets underwent mutual calibration, continuity correction, saturation correction, projection transformation, and resampling. This process established a spatio-temporal raster dataset of night-time lights for 2000–2020 [25,26].
- (2)
- PM2.5 concentration data: The 2000–2020 PM2.5-1 km high-resolution monthly average mass concentration spatiotemporal distribution raster data used herein originate from the China Atmospheric Composition Near-Real-Time Tracking (TAP) Data Resource Network (http://tapdata.org.cn/, accessed on 16 July 2025). This dataset is jointly created and maintained by Tsinghua University in collaboration with Nanjing University, Peking University, Fudan University, the Chinese Academy of Meteorological Sciences, and numerous other academic institutions. Its purpose is to integrate diverse data sources—including satellite remote sensing information, ground-based observational data, model simulation results, and emission inventories—to construct a multidimensional, near-real-time dataset covering atmospheric pollutant concentrations and atmospheric aerosol concentration information across China. By providing foundational data, TAP supports scientific research into the health impacts of air pollution, environmental management, and the evaluation of policies aimed at reducing atmospheric pollution [27,28].
- (3)
- Other Variable Data: Variables such as GDP, population, built-up area, and green coverage rate were sourced from China’s national and provincial statistical yearbooks. Vector data delineating provincial and municipal boundaries were obtained from the National Geographic (https://www.webmap.cn, accessed on 20 July 2025).
2.3. Research Methodology
2.3.1. Urban Sprawl Index Measurement Coefficients
2.3.2. Urban Sprawl Accuracy Verification Model
2.3.3. Slope Method
2.3.4. Spatial Autocorrelation Analysis
2.3.5. Local Indicators of Spatial Association (LISA) Time Path
2.3.6. Local Indicators of Spatial Association (LISA) Spatiotemporal Transitions
2.3.7. Multiple Regression Model
2.3.8. Spatial Econometric Model
2.3.9. Methodological Reflections and Limitation
3. Results and Discussion
3.1. Accuracy Assessment of Urban Sprawl Index Based on Nighttime Light Measurements
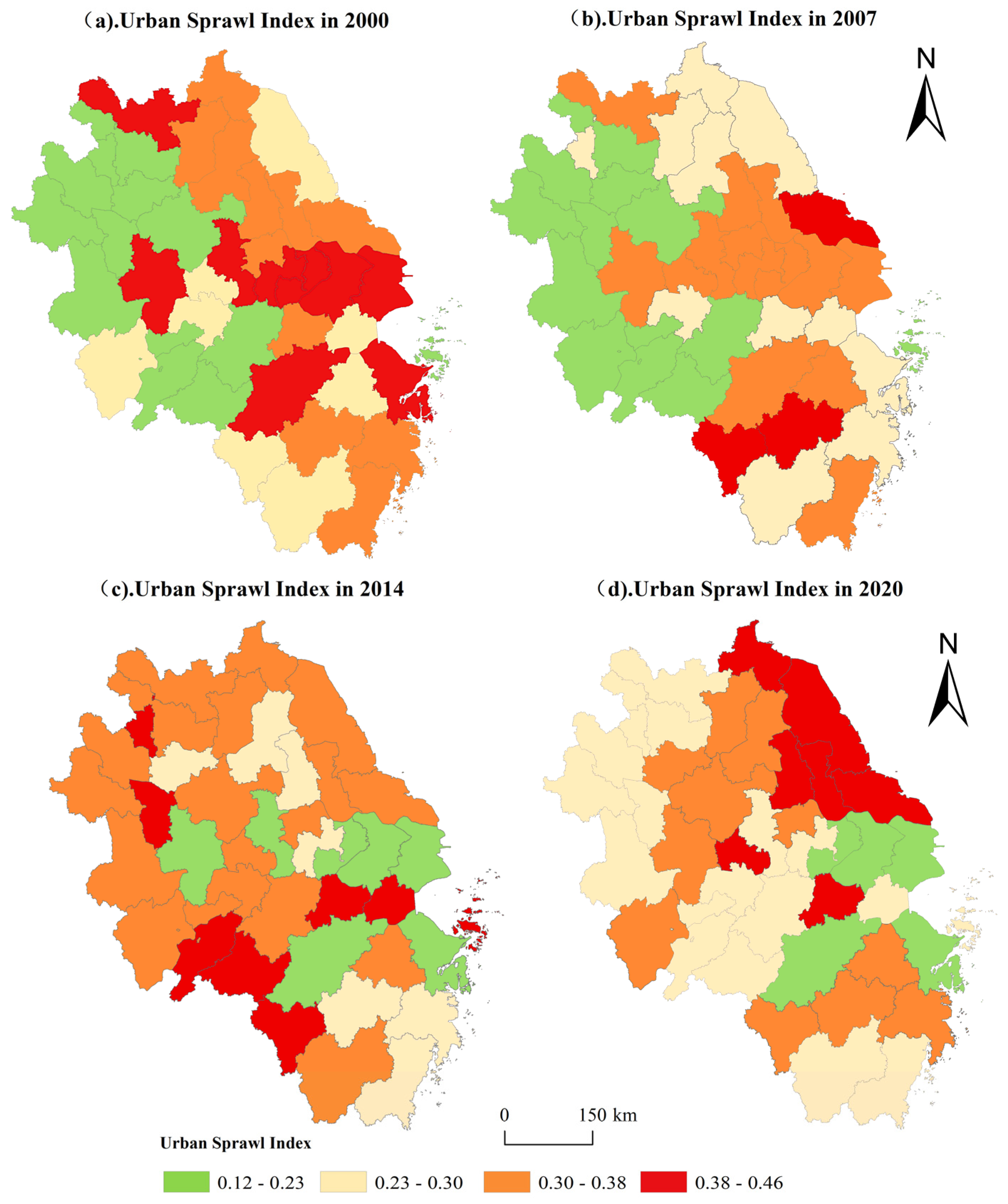
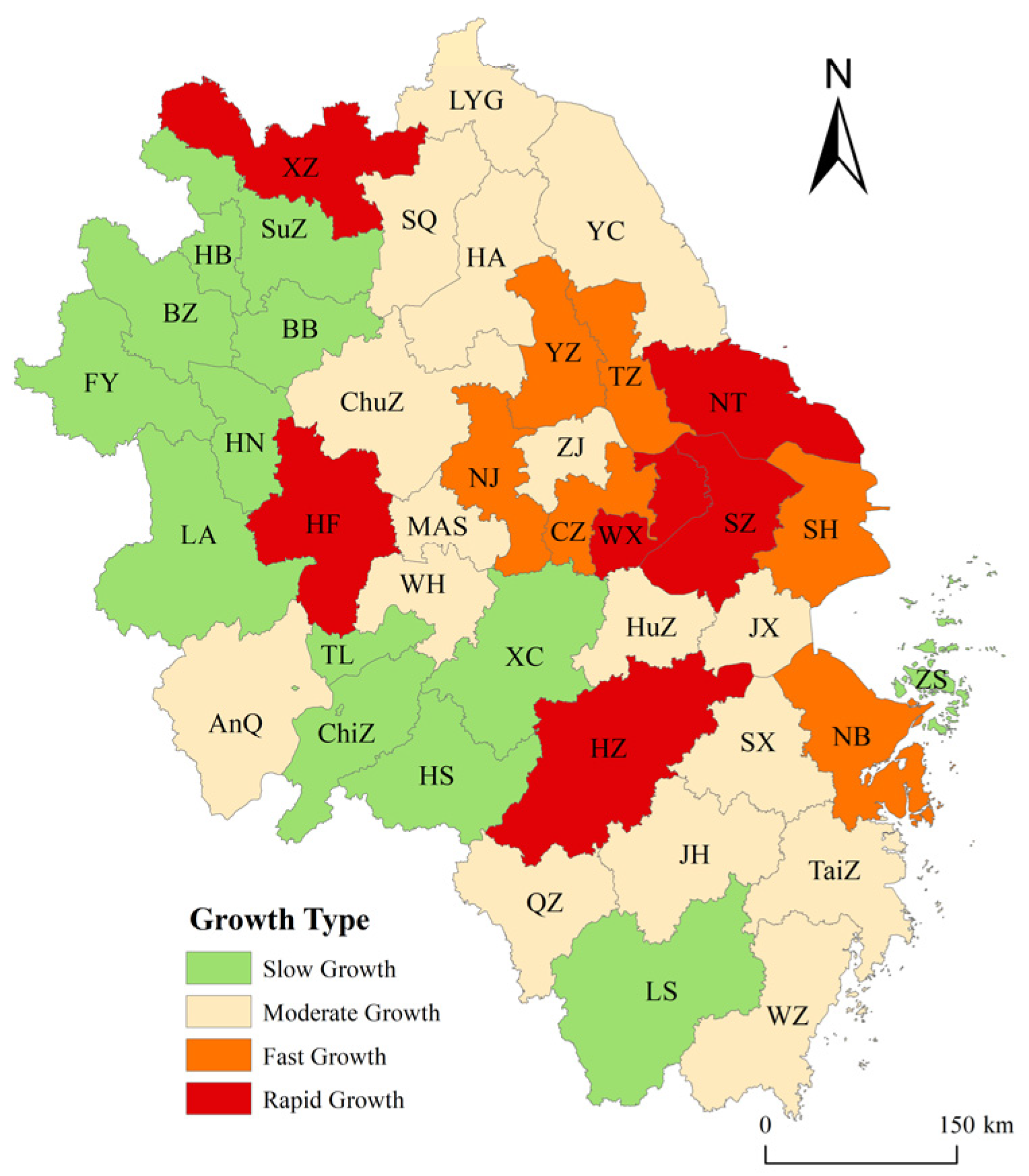
3.2. Spatial Patterns and Evolutionary Trends of Urban Sprawl in the Yangtze River Delta
3.2.1. Spatial Distribution Characteristics of Urban Sprawl in the Yangtze River Delta
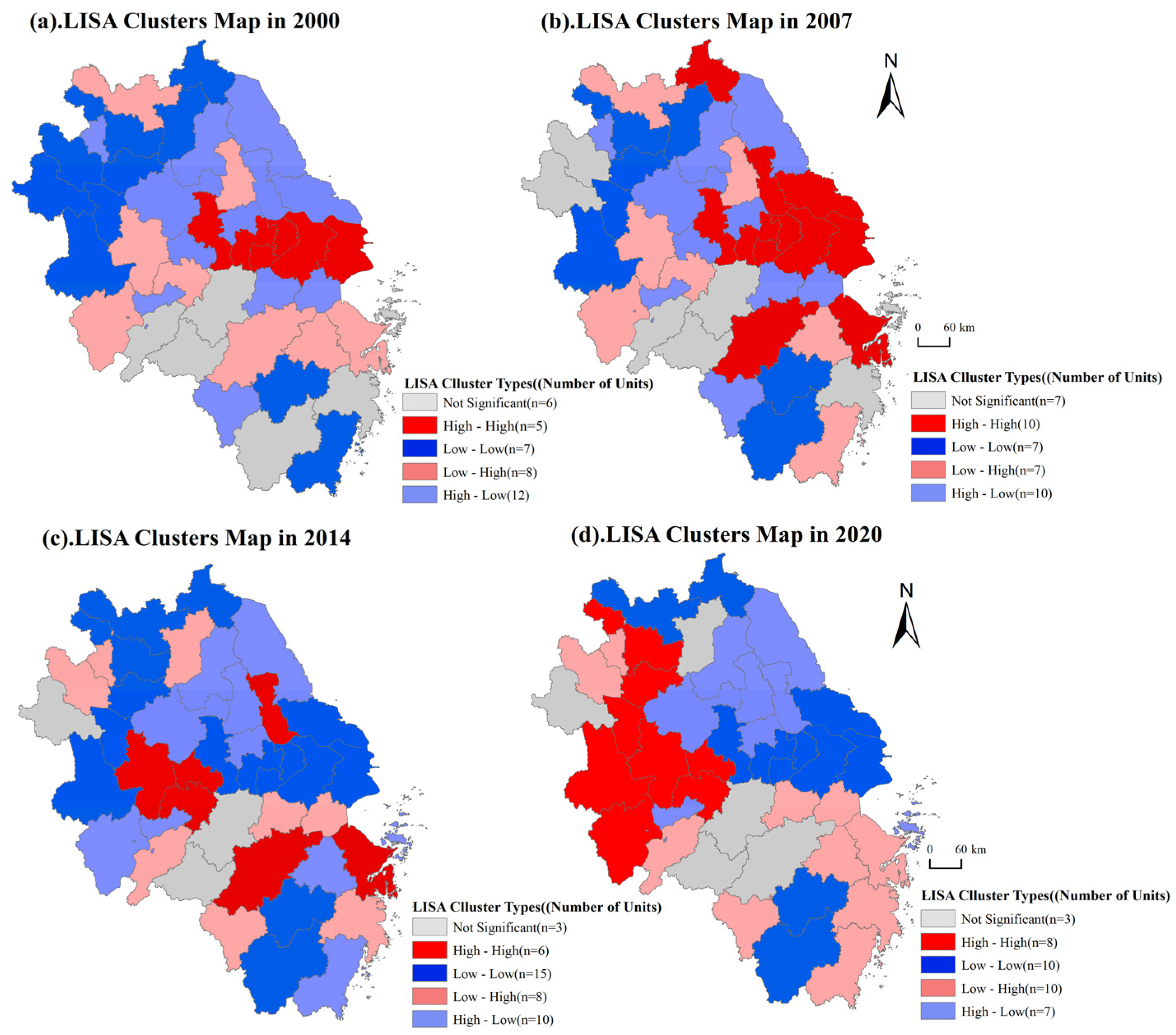
3.2.2. Spatial Correlation Characteristics of Urban Sprawl
3.2.3. Spatio-Temporal Interaction Characteristics of Urban Sprawl in the Yangtze River Delta
- (1)
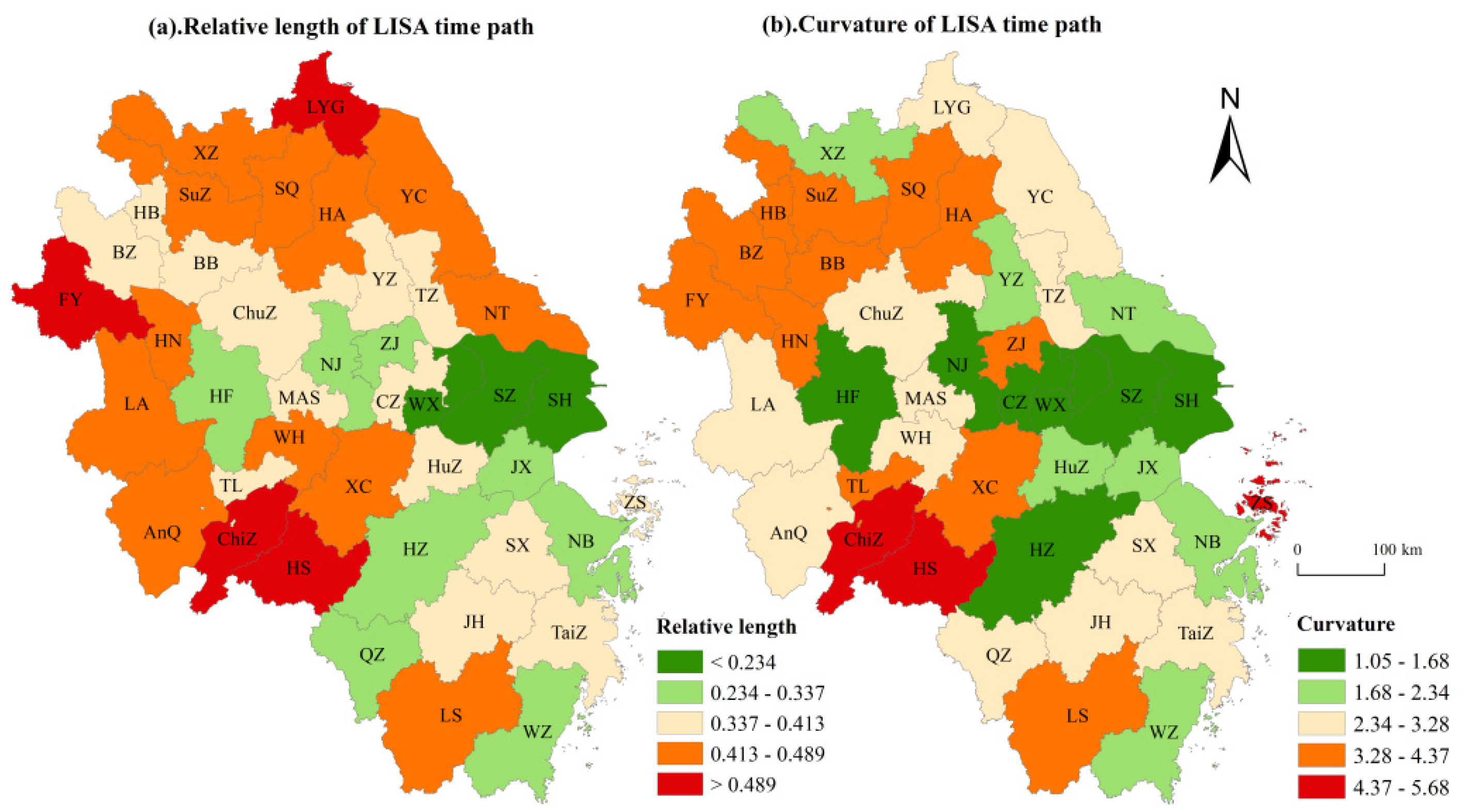
- Geometric Analysis of LISA Spatio-Temporal Pathways
- (2)
- Analysis of LISA spatio-temporal path movement directions
- (3)
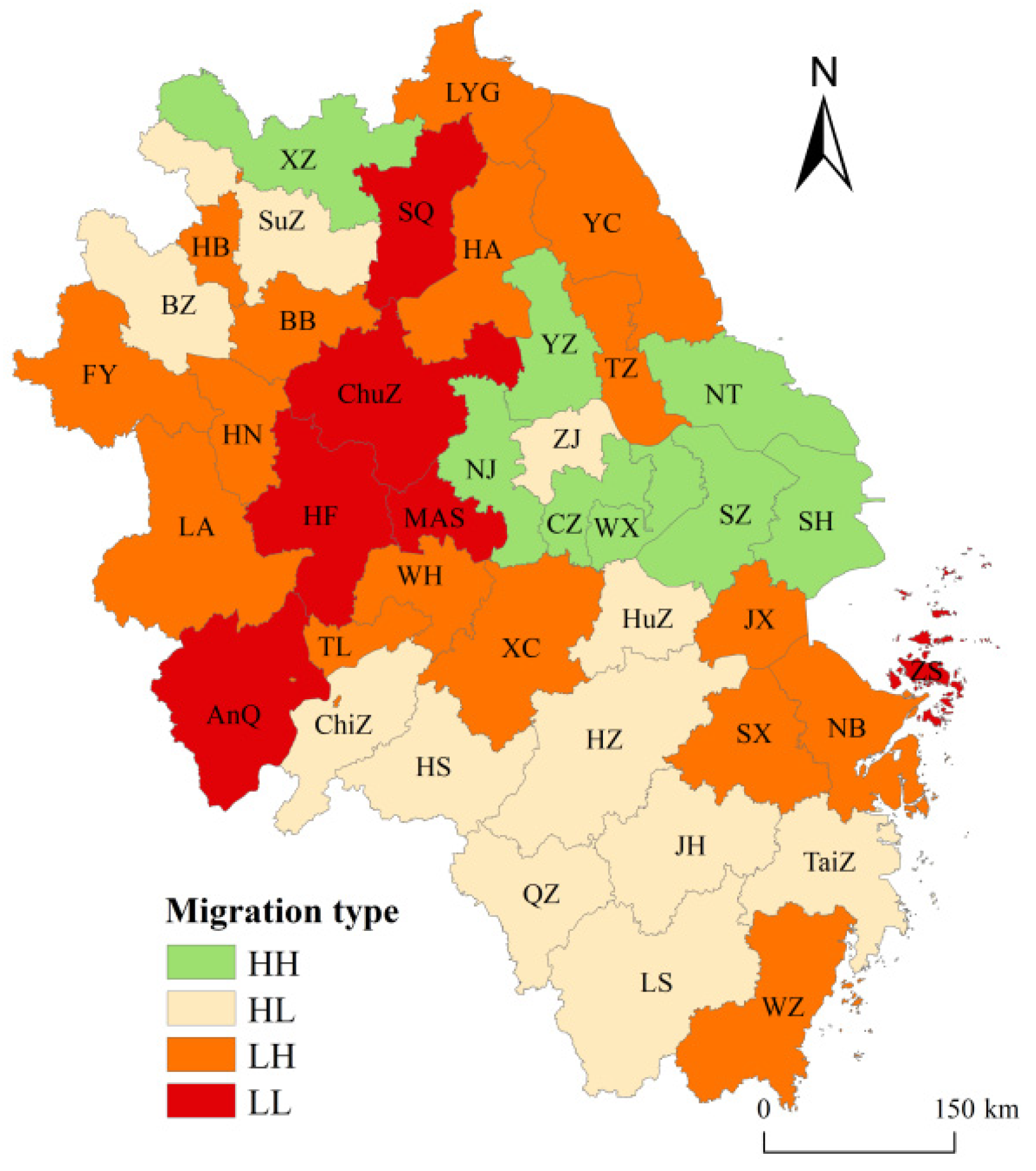
- LISA Spatio-Temporal Transition Analysis
3.3. Empirical Analysis of the Impact of Urban Sprawl in the Yangtze River Delta on PM2.5 Pollution
3.3.1. Multiple Linear Regression Results
3.3.2. Robustness Testing
3.3.3. Spatial Durbin Model Results
| 2000–2012 (N = 12) | 2013–2020 (N = 7) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Individual Fixed SDM | Fixed Time SDM | Double Fixed SDM | Individual Fixed SDM | Fixed Time SDM | Double Fixed SDM | ||||||
| Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | |
| SI | 2.428 * | 1.968 | 5.337 *** | 1.954 | 3.237 | 1.952 | −3.428 * | 1.948 | −5.217 *** | 1.924 | −4.517 | 1.923 |
| PSGDP | 24.467 ** | 9.754 | 11.323 | 11.228 | 20.963 * | 11.054 | 25.487 ** | 10.784 | 11.257 | 11.204 | 21.323 * | 10.747 |
| INDUS | 0.427 *** | 0.078 | 0.498 *** | 0.088 | 0.518 *** | 0.091 | 0.487 *** | 0.083 | 0.498 *** | 0.087 | 0.523 *** | 0.087 |
| SFDI | 0.077 | 0.061 | 0.0514 | 0.009 | 0.081 | 0.059 | 0.087 | 0.054 | 0.0514 | 0.014 | 0.074 | 0.055 |
| POP | 0.021 *** | 0.005 | 0.024 *** | 0.006 | 0.023 *** | 0.006 | 0.018 *** | 0.006 | 0.024 *** | 0.007 | 0.023 *** | 0.006 |
| W*SI | 0.663 | 2.436 | 2.147 | 2.658 | 6.989 *** | 2.498 | −0.654 | 2.436 | −2.147 | 2.874 | −7.484 *** | 2.547 |
| W *PSGDP | 40.216 | 16.475 | 12.547 | 17.668 | 33.634 * | 15.887 | 38.406 | 16.475 | 12.547 | 17.408 | 32.547 * | 16.243 |
| W*INDUS | −0.106 | 0.114 | 0.041 | 0.187 | 0.02 | 0.126 | −0.134 | 0.114 | 0.041 | 0.128 | 0.02 | 0.147 |
| W*SFDI | 0.059 | 0.095 | −0.154 * | 0.087 | −0.039 | 0.098 | 0.059 | 0.089 | −0.147 * | 0.087 | −0.039 | 0.089 |
| W*POP | −0.002 | 0.012 | −0.008 | 0.006 | 0.002 | 0.007 | −0.001 | 0.008 | −0.008 | 0.008 | 0.002 | 0.008 |
| pro | 0.424 *** | 0.028 | 0.324 *** | 0.0298 | 0.264 *** | 0.029 | 0.415 *** | 0.031 | 0.324 *** | 0.0341 | 0.274 *** | 0.031 |
| logliksfe | −4128.387 | −4257.696 | −4156.854 | −4226.457 | −4357.846 | −4183.764 | ||||||
| R-squared | 0.546 | 0.368 | 0.447 | 0.547 | 0.367 | 0.437 | ||||||
| Nobs | 492 | 492 | 492 | 328 | 328 | 328 | ||||||
| LR(lag) | 14.683 ** | 16.794 ** | 19.881 ** | 16.047 ** | 17.308 ** | 19.623 ** | ||||||
| LR(error) | 24.784 *** | 26.567 *** | 33.787 *** | 24.639 *** | 26.321 *** | 32.847 *** | ||||||
| Hausman | 942.127 *** | 942.127 *** | 942.127 *** | 928.567 *** | 928.567 *** | 928.567 *** | ||||||
| 2000–2012 (N = 12) | 2013–2020 (N = 7) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Direct Effect | Indirect Effect | Total Effect | Direct Effect | Indirect Effect | Total Effect | ||||||
| Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | Coef. | Std. Err. | |
| SI | 5.486 *** | 2.314 | 11.965 *** | 4.362 | 17.451 *** | 3.587 | −5.576 *** | 2.031 | −12.074 *** | 3.564 | −17.650 *** | 4.321 |
| PSGDP | 25.886 ** | 10.287 | 48.747 ** | 25.867 | 74.633 *** | 29.186 | 26.879 ** | 10.364 | 48.660 ** | 26.354 | 75.539 *** | 27.036 |
| INDUS | 0.559 *** | 0.078 | 0.375 | 0.141 | 0.934 *** | 0.187 | 0.560 *** | 0.074 | 0.237 | 0.132 | 0.797 *** | 0.197 |
| SFDI | 0.075 | 0.038 | 0.027 | 0.11 | 0.102 | 0.134 | 0.085 | 0.036 | 0.025 | 0.11 | 0.11 | 0.123 |
| POP | 0.021 *** | 0.006 | 0.005 | 0.009 | 0.026 ** | 0.014 | 0.021 *** | 0.005 | 0.005 | 0.01 | 0.026 ** | 0.013 |
3.3.4. Identification of Heterogeneous Mechanisms in Policy Interventions
4. Discussion
4.1. Spatial Insights and Model-Based Findings
4.2. Policy Recommendations
4.3. Limitations and Future Prospects
5. Conclusions
- (1)
- From a regional perspective, urban sprawl in the Yangtze River Delta exhibited a sustained growth trend between 2000 and 2020. The number of cities with low-level sprawl gradually increased, while the centre of sprawl shifted slightly northwestward. The predominant growth pattern was characterised by relatively rapid expansion, exhibiting significant spatial correlation. Adjacent cities influenced each other’s sprawl trajectories, demonstrating pronounced regional diffusion effects.
- (2)
- Most cities within the study area exhibited relatively short LISA time-path lengths, indicating overall spatial stability, particularly in developed cities such as Shanghai and Suzhou and their surrounding regions. In contrast, cities like Fuyang and Lianyungang demonstrated relatively dynamic local spatial structures. Additionally, Chizhou, Huangshan, and Zhoushan—cities influenced by tourism—exhibited stronger local spatial dependencies. Between 2000 and 2020, the curvature of LISA time paths for most cities in the study area was below average, indicating that the overall influence of local spatial patterns on urban sprawl was relatively weak. Most cities did not experience significant spatio-temporal jumps, demonstrating strong inertia in the transition of urban units and a high degree of stability in the associative patterns of urban sprawl.
- (3)
- Analyses using multiple linear and spatial regression models reveal a nonlinear relationship between urban sprawl and PM2.5 levels. Between 2000 and 2012, the disorderly expansion of urban sprawl in the Yangtze River Delta exacerbated PM2.5 pollution. This was primarily due to the lack of systematic planning in urban land development, which resulted in increased population density, traffic congestion, and industrial emissions. Conversely, from 2013 to 2020, the implementation of air pollution control policies significantly reduced PM2.5 pollution. Concurrently, a compact and orderly urban spatial structure, along with its spatial spillover effects, further contributed to the improvement in PM2.5 pollution levels. In addition, existing research suggests that foreign direct investment, industrial restructuring, urban scale, and economic development all contribute to the exacerbation of PM2.5 pollution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | City | Abbreviation | City |
|---|---|---|---|
| SH | Shanghai | QZ | Quzhou |
| NJ | Nanjing | ZS | Zhoushan |
| WX | Wuxi | TaiZ | Taizhou (Zhejiang Province) |
| XZ | Xuzhou | LS | Lishui |
| CZ | Changzhou | HF | Hefei |
| SZ | Suzhou (Jiangsu Province) | WH | Wuhu |
| NT | Nantong | BB | Bangbu |
| LYG | Lianyugang | HN | Huainan |
| HA | Huaian | MAS | Ma’anshan |
| YC | Yancheng | HB | Huaibei |
| YZ | Yangzhou | TL | Tongling |
| ZJ | Zhenjiang | AnQ | Anqing |
| TZ | Taizhou (Jiangsu Province) | HS | Huangshan |
| SQ | Suqian | ChuZ | Chuzhou |
| HZ | Hangzhou | FY | Fuyang |
| NB | Ningbo | SuZ | Suzhou (Anhui Province) |
| WZ | Wenzhou | LA | Lu’an |
| JX | Jiaxing | BZ | Bozhou |
| HuZ | Huzhou | ChiZ | Chizhou |
| SX | Shaoxing | XC | Xuancheng |
| JH | Jinhua |
References
- Hou, Y.; Huang, Q.; Ren, Q.; Gu, T.; Zhou, Y.; Wu, P.; Fan, Y.; Zhu, G. Spatiotemporal dynamics of urban sprawl in China from 2000 to 2020. GISci. Remote Sens. 2024, 61, 2351262. [Google Scholar] [CrossRef]
- Jiang, G.; Zhang, R.; Ma, W.; Zhou, D.; Wang, X.; He, X. Cultivated land productivity potential improvement in land consolidation schemes in Shenyang, China: Assessment and policy implications. Land Use Policy 2017, 68, 80–88. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Yue, H.; Dong, Z. Spatiotemporal pattern of urban sprawl based on the weighted urban proliferation model: A case study of the Bohai Rim region in China. Land 2024, 13, 55. [Google Scholar] [CrossRef]
- Kang, T.; Zhao, J.; Zeng, L.; Han, Q.; Ding, F. Unraveling PM2.5 Pollution Drivers through Digitalization-Climate-Urban Form Interactions in Chinese Cities. Environ. Technol. Innov. 2025, 40, 104515. [Google Scholar] [CrossRef]
- Fallah, B.N.; Partridge, M.D.; Olfert, M.R. Urban Sprawl and Productivity: Evidence from US Metropolitan Areas. Pap. Reg. Sci. 2011, 90, 451–472. [Google Scholar] [CrossRef]
- Krofcheck, D.J.; Litvak, M.E.; Lippitt, C.D.; Neuenschwander, A.; Ouyang, Z. Woody Biomass Estimation in a Southwestern U.S. Juniper Savanna Using LiDAR-Derived Clumped Tree Segmentation and Existing Allometries. Remote Sens. 2016, 8, 453. [Google Scholar] [CrossRef]
- Travisi, C.M.; Camagni, R.; Nijkamp, P. Impacts of Urban Sprawl and Commuting: A Modelling Study for Italy. J. Transp. Geogr. 2010, 18, 382–392. [Google Scholar] [CrossRef]
- Li, D.; Tang, J.; Hu, Q.; Dong, M.; Chithpanya, S. Spatiotemporal Urban Evolution Along the China–Laos Railway in Laos Determined Using Multiple Sources of Remote-Sensed Landscape Indicators and Interpretable Machine Learning. Land 2024, 13, 2094. [Google Scholar] [CrossRef]
- Seto, K.C.; Shepherd, J.M. Global urban land-use trends and climate change. J. Curr. Opin. Environ. Sustain. 2009, 1, 89–95. [Google Scholar] [CrossRef]
- Hao, L.; Li, X. Impact of urban sprawl on regional productivity improvement: Based on the perspective of dynamic industrial agglomeration. J. Cent. South Univ. Soc. Sci. Ed. 2020, 26, 21–23. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y. The spread of cities and the upgrading of the Yangtze Economic Belt Industry. J. Chongqing Univ. Soc. Sci. Ed. 2021, 27, 39–49. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; Vaz, E.D.N. Spatiotemporal Simulation of Urban Growth Patterns Using Agent-Based Modeling: The Case of Tehran. Cities 2013, 35, 27–37. [Google Scholar] [CrossRef]
- Plantinga, A.J.; Bernell, S. The Association Between Urban Sprawl and Obesity: Is It a Two-Way Street? J. Reg. Sci. 2010, 50, 651–671. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Cao, S.; Liu, X.; Jin, J.; Zhao, Y. Improved Anthropogenic Mercury Emission Inventories for China from 1980 to 2020: Toward More Accurate Effectiveness Evaluation for the Minamata Convention. Environ. Sci. Technol. 2023, 57, 8660–8670. [Google Scholar] [CrossRef]
- Irwin, E.G.; Bockstael, N.E. The Evolution of Urban Sprawl: Evidence of Spatial Heterogeneity and Increasing Land Fragmentation. Proc. Natl. Acad. Sci. USA 2007, 104, 20672–20677. [Google Scholar] [CrossRef]
- Yu, B.B.; Zhou, X.R. Land Finance and Urban Sprawl: Evidence from Prefecture-Level Cities in China. Habitat Int. 2024, 130, 103074. [Google Scholar] [CrossRef]
- Wen, H.; Yu, H.; Nghiem, X.H. Impact of Urban Sprawl on Carbon Emission Efficiency: Evidence from China. Urban Clim. 2024, 55, 101986. [Google Scholar] [CrossRef]
- Sarigiannis, D.A.; Karakitsios, S.P.; Gotti, A.; Papagiannakis, A. Benefits on public health from transport-related greenhouse gas mitigation policies in Southeastern European cities. Sci. Total Environ. 2017, 579, 1427–1438. [Google Scholar] [CrossRef]
- Tao, L.; Jian, G.; Zheng, W. Research on emergency reserves and layout of refined oil in the Yangtze River Delta. Resour. Sci. 2018, 40, 1450–1458. [Google Scholar] [CrossRef]
- Wu, J.; Weng, W.; Shen, L.; Fu, M. Transient and continuous effects of indoor human movement on nanoparticle concentrations in a sitting person’s breathing zone. Sci. Total Environ. 2022, 805, 149970. [Google Scholar] [CrossRef] [PubMed]
- Morán Uriel, J.; Camerin, F.; Córdoba Hernández, R. Urban Horizons in China: Challenges and Opportunities for Community Intervention in a Country Marked by the Heihe-Tengchong Line; Springer Nature: Singapore, 2024; pp. 105–125. [Google Scholar] [CrossRef]
- Wang, W. Breaking down the barriers to clean air: The Effects of China’s Zero-Waste City Policy on PM2.5 Concentration and Urban Sprawl. Chin. J. Popul. Resour. Environ. 2025, 23, 75–84. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Zhou, Z.; Zhong, S. Does the New-Type Urbanization Policy Help Reduce PM2.5 Pollution? Evidence from Chinese Counties. Sustainability 2025, 17, 7585. [Google Scholar] [CrossRef]
- Chang, Q.; Sha, Y.; Chen, Y. The Coupling Coordination and Influencing Factors of Urbanization and Ecological Resilience in the Yangtze River Delta Urban Agglomeration, China. Land 2024, 13, 111. [Google Scholar] [CrossRef]
- Zheng, Y.; Fan, M.; Cai, Y.; Fu, M.; Yang, K.; Wei, C. Spatio-Temporal Pattern Evolution of Carbon Emissions at the City-County-Town Scale in Fujian Province Based on DMSP/OLS and NPP/VIIRS Nighttime Light Data. J. Clean. Prod. 2024, 442, 140958. [Google Scholar] [CrossRef]
- Sarif, N.; Roy, A.K. Measuring Urban Shrinkage in India Using Night-Light Data from DMSP-OLS and VIIRS-NPP Satellite Sensors. Cities 2024, 152, 105176. [Google Scholar] [CrossRef]
- Zou, J.; Chen, Y.; Ding, G.; Xuan, W. A Clustered Threshold Method for Extracting Urban Built-up Area Using the DMSP/OLS Nighttime Light Images. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 196–201. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Yang, C.; Zhou, Y.; Qian, X.; Wang, C.; Wu, B.; Wu, J. An Extended Time Series (2000–2018) of Global NPP-VIIRS-like Nighttime Light Data from a Cross-Sensor Calibration. Earth Syst. Sci. 2021, 13, 889–906. [Google Scholar] [CrossRef]
- Qin, M.; Liu, X.; Tong, Y. Does Urban Sprawl Exacerbate Haze Pollution? Empirical Evidence from PM2.5 Data in China. Econ. Manag. Sci. 2016, 11, 146–160. [Google Scholar] [CrossRef]
- Chen, X.; Qin, M. Urban Sprawl, Population and Production Efficiency: Evidence from Chinese Enterprises Data. J. Chongqing Univ. Soc. Sci. Ed. 2019, 4, 38–52. [Google Scholar] [CrossRef]
- Wu, Y.; Shi, K.; Yu, B.; Li, C. Analysis of the Impact of Urban Sprawl on Haze Pollution Based on the NPP-VIIRS Nighttime Light Remote Sensing Data. J. Wuhan Univ. Geosci. 2021, 46, 777–789. [Google Scholar] [CrossRef]
- Cheng, K.; Xu, Y. The Impact of Urban Sprawl on Electricity Intensity: An Analysis Based on Panel Data of Prefecture-level and Above Cities in China. Urban Issues 2019, 7, 37–42+49. (In Chinese) [Google Scholar]
- Liao, B.; Luo, X.; Tian, C. Spatial threshold characteristics and radiation range of regional synergy development impact on urban sprawl. Syst. Eng. Theory Pract. 2025, 45, 371–390. (In Chinese) [Google Scholar] [CrossRef]
- Siddique, T.; Pradhan, S.P.; Vishal, V.; Singh, T.N. Applicability of Q-slope Method in the Himalayan Road Cut Rock Slopes and Its Comparison with CSMR. Rock Mech. Rock Eng. 2020, 53, 4509–4522. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Gedamu, W.T.; Plank-Wiedenbeck, U.; Wodajo, B.T. A Spatial Autocorrelation Analysis of Road Traffic Crash by Severity Using Moran’s I Spatial Statistics: A Comparative Study of Addis Ababa and Berlin Cities. Accid. Anal. Prev. 2024, 200, 107535. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Chen, Y.; Thill, J.-C. A Space-Time Flow LISA Approach for Panel Flow Data. Soc. Sci. Comput. Rev. 2023, 106, 102042. [Google Scholar] [CrossRef]
- Chen, Y. Reconstruction and Normalization of LISA for Spatial Analysis. PLoS ONE 2023, 18, e0303456. [Google Scholar] [CrossRef] [PubMed]
- Hesamian, G.; Akbari, M.G. A Robust Varying Coefficient Approach to Fuzzy Multiple Regression Model. J. Comput. Appl. Math. 2020, 371, 112704. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Marjan, S.; Wahid, A.; Syam, M.S.; Huang, M.; Tang, H.; Hasnain, A. The Effects of Socioeconomic Factors on Particulate Matter Concentration in China: New Evidence from Spatial Econometric Model. J. Clean. Prod. 2023, 393, 137969. [Google Scholar] [CrossRef]
- Zhang, Q.; Schaaf, C.; Seto, K.C. The vegetation adjusted nighttime light urban index: A new approach to reduce saturation and increase variation in nighttime luminosity. Remote Sens. Environ. 2016, 129, 232–245. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, Y.; Zhou, C.; Haynie, S.; Pei, T.; Xu, T. Night-time light derived estimation of spatio-temporal characteristics of urbanization dynamics using DMSP/OLS satellite data. Remote Sens. Environ. 2015, 158, 453–464. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, L. Urban Sprawl and Regional Economic High-Quality Development: A Study Based on DMSP/OLS Nighttime Light Data. Finance Econ. Sci. 2019, 6, 106–114. (In Chinese) [Google Scholar]
- Bai, Y.; Fan, J.; Lai, Y. Whole-Domain Spatial Dynamic Transition and Local Spatial Driving Differences of Ozone Pollution in the Yangtze River Economic Zone. J. China Univ. Geosci. Econ. Manag. 2024, 2, 100–113. (In Chinese) [Google Scholar] [CrossRef]
- Ali, M.A.; Huang, Z.W.; Bilal, M.; Assiri, M.E.; Mhawish, A.; Nichol, J.E.; de Leeuw, G.; Almazroui, M.; Wang, Y.; Alsubhi, Y. Long-term PM2.5 pollution over China: Identification of PM2.5 pollution hotspots and source contributions. Sci. Total Environ. 2023, 893, 164871. [Google Scholar] [CrossRef]
- Wen, X.; Lu, R.; Song, T.; Wang, Y.; Wu, J.; Gong, L. The Causal Effect of Land-Use Transformation on Urban Vitality in the Context of Urban Regeneration: A Case Study of Chengdu. Land 2025, 14, 2020. [Google Scholar] [CrossRef]
- Xu, X.; Chen, Z.; Ding, X. Measurements of Urban Sprawl of Regional Central Cities and Control Strategies: A Case Study in Linyi City of Shandong Province, China. China Land Sci. 2019, 33, 85–92. (In Chinese) [Google Scholar] [CrossRef]
- Hernández-Lamas, P.; Cabau-Anchuelo, B.; de Castro-Cuartero, Ó.; Bernabéu-Larena, J. Mobile Applications, Geolocation and Information Technologies for the Study and Communication of the Heritage Value of Public Works. Sustainability 2021, 13, 2083. [Google Scholar] [CrossRef]
- Banerjee, A.K.; Liang, X.; Harms, N.E.; Tan, F.; Lin, Y.; Feng, H.; Wang, J.; Li, Q.; Jia, Y.; Lu, X.; et al. Spatio-temporal pattern of cross-continental invasion: Evidence of climatic niche shift and predicted range expansion provide management insights for smooth cordgrass. Ecol. Indic. 2022, 140, 109052. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J.; Sun, C.; Zhang, X.; Kahn, M.E. Air pollution lowers Chinese urbanites’ expressed happiness on social media. Nat. Human Behav. 2019, 3, 237–243. [Google Scholar] [CrossRef]
- Seikkula-Leino, J.; Salomaa, M. Entrepreneurial Competencies and Organisational Change—Assessing Entrepreneurial Staff Competencies within Higher Education Institutions. Sustainability 2020, 12, 7323. [Google Scholar] [CrossRef]
| 2000–2012 (N = 12) | 2013–2020 (N = 7) | ||||
|---|---|---|---|---|---|
| Variable | Sample Size (N) | Mean | Standard Deviation | Mean | Standard Deviation |
| InP | 820 | 3.967 | 2.543 | 3.450 | 2.123 |
| InS | 820 | −0.398 | 0.428 | −0.703 | 0.323 |
| InINDUS | 820 | 0.043 | 0.233 | 0.086 | 0.201 |
| InSFDI | 820 | 3.596 | 1.958 | 3.748 | 1.902 |
| InPSGDP | 820 | 2.977 | 3.549 | 4.480 | 3.008 |
| InPOP | 820 | 4.912 | 5.404 | 5.238 | 3.088 |
| Variable | Random Effect Model | Fixed Effect Model | Dynamic SYS-GMM Model | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| L. lnssp | 0.934 *** (0.000) | 0.921 *** (0.000) | ||
| lnsp | 0.083 ** (0.024) | 0.213 *** (0.000) | 0.021 ** (0.048) | 0.131 *** (0.000) |
| Control variables | Yes | Yes | No | Yes |
| Constant | 3.561 *** (0.000) | 3.667 *** (0.000) | −0.028 *** (0.000) | 0.017 (0.632) |
| Hausman test | 113.57 *** | |||
| R2 | 0.883 | 0.883 | ||
| AR (1) | 0.001 | 0.001 | ||
| AR (2) | 0.349 | 0.363 | ||
| Hansen test | 0.852 | 0.848 | ||
| Observations | 920 | 920 | 906 | 906 |
| Year | Moran′s I | Z-Value |
|---|---|---|
| 2000 | 0.258 | 7.574 *** |
| 2001 | 0.287 | 8.321 *** |
| 2002 | 0.243 | 8.421 *** |
| 2003 | 0.288 | 8.314 *** |
| 2004 | 0.274 | 8.412 *** |
| 2005 | 0.314 | 8.238 *** |
| 2006 | 0.428 | 8.916 *** |
| 2007 | 0.267 | 8.788 *** |
| 2008 | 0.349 | 8.488 *** |
| 2009 | 0.283 | 11.524 *** |
| 2010 | 0.312 | 11.960 *** |
| 2011 | 0.247 | 12.348 *** |
| 2012 | 0.214 | 12.347 *** |
| 2013 | 0.363 | 12.157 *** |
| 2014 | 0.218 | 13.247 *** |
| 2015 | 0.314 | 12.238 *** |
| 2016 | 0.288 | 12.916 *** |
| 2017 | 0.267 | 12.788 *** |
| 2018 | 0.249 | 12.488 *** |
| 2019 | 0.268 | 11.875 *** |
| 2020 | 0.288 | 12.467 *** |
| Type | Description | Transition Pathways | Representative Cities |
|---|---|---|---|
| Type I (Stable Type) | Stable in both self and neighbors | HH→HHt+1, LH→LHt+1 LL→LHt+1, HL→HLt+1 | Shanghai, Suzhou, etc. (9 cities) |
| Type II (Self-transition- Stable Neighbor) | Self transitions, neighbors stable | HH→LHt+1, LH→HHt+1 LL→HLt+1, HL→LLt+1 | Suzhou, Lishui, etc. (11 cities) |
| Type III (Stable Self -Neighbor Transition) | Self stable, neighbors transition | HH→HLt+1, LH→LLt+1 LL→LHt+1, HL→HHt+1 | Wenzhou, Ningbo, etc. (16 cities) |
| Type IV (Transition Type) | Both self and neighbors transition | HH→LLt+1, LH→HLt+1 LL→HHt+1, HL→LHt+1 | Anqing, Hefei, etc. (5 cities) |
| t/t + 1 | HH | HL | LL | LH |
|---|---|---|---|---|
| HH | Type I (2.87%) | Type III (32.45%) | Type IV (2.37%) | Type II (2.36%) |
| HL | Type III (33.28%) | Type I (2.58%) | Type II (3.24%) | Type IV (0.23%) |
| LL | Type IV (3.27%) | Type II (3.12%) | Type I (4.23%) | Type III (2.15%) |
| LH | Type II (2.48%) | Type IV (1.24%) | Type III (2.18%) | Type I (3.12%) |
| 2000–2012 (N = 12) | 2013–2020 (N = 7) | |||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coefficient | Std. Error | T-Value | p-Value | Coefficient | Std. Error | T-Value | p-Value |
| Constant | 54.321 | 3.212 | 16.907 | <0.001 | 32.456 | 2.968 | 15.639 | <0.001 |
| SI | 0.621 | 0.110 | −8.372 | <0.001 | −0.921 | 0.132 | −7.656 | <0.001 |
| PSGDP | 0.435 | 0.217 | −2.004 | 0.058 | 0.386 | 0.247 | −3.021 | 0.039 |
| INDUS | −0.231 | 0.089 | −2.596 | 0.027 | −0.433 | 0.068 | −4.672 | 0.021 |
| SFDI | 0.001 | 0.002 | 5.003 | <0.001 | 0.001 | 0.001 | 3.985 | <0.001 |
| POP | 0.291 | 0.102 | 2.853 | 0.015 | 0.378 | 0.099 | 1.956 | 0.018 |
| Variable | Tolerance | VIF | Eigenvalue | Condition Index |
|---|---|---|---|---|
| PSGDP | 0.308 | 3.247 | 0.334 | 4.04 |
| INDUS | 0.254 | 3.937 | 0.122 | 6.671 |
| SFDI | 0.323 | 3.096 | 0.083 | 8.093 |
| POP | 0.158 | 6.329 | 0.013 | 8.527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, N.; Xu, J.; He, H. Urban Sprawl in the Yangtze River Delta: Spatio-Temporal Characteristics and Impacts on PM2.5. Land 2025, 14, 2078. https://doi.org/10.3390/land14102078
Ruan N, Xu J, He H. Urban Sprawl in the Yangtze River Delta: Spatio-Temporal Characteristics and Impacts on PM2.5. Land. 2025; 14(10):2078. https://doi.org/10.3390/land14102078
Chicago/Turabian StyleRuan, Ning, Jianhui Xu, and Huarong He. 2025. "Urban Sprawl in the Yangtze River Delta: Spatio-Temporal Characteristics and Impacts on PM2.5" Land 14, no. 10: 2078. https://doi.org/10.3390/land14102078
APA StyleRuan, N., Xu, J., & He, H. (2025). Urban Sprawl in the Yangtze River Delta: Spatio-Temporal Characteristics and Impacts on PM2.5. Land, 14(10), 2078. https://doi.org/10.3390/land14102078






