Accurate Identification of High-Potential Reserved Cultivated Land Resources: A Convolutional Neural Network-Based Intelligent Selection Framework Verified in Qinghai Province on the Qinghai–Tibet Plateau, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
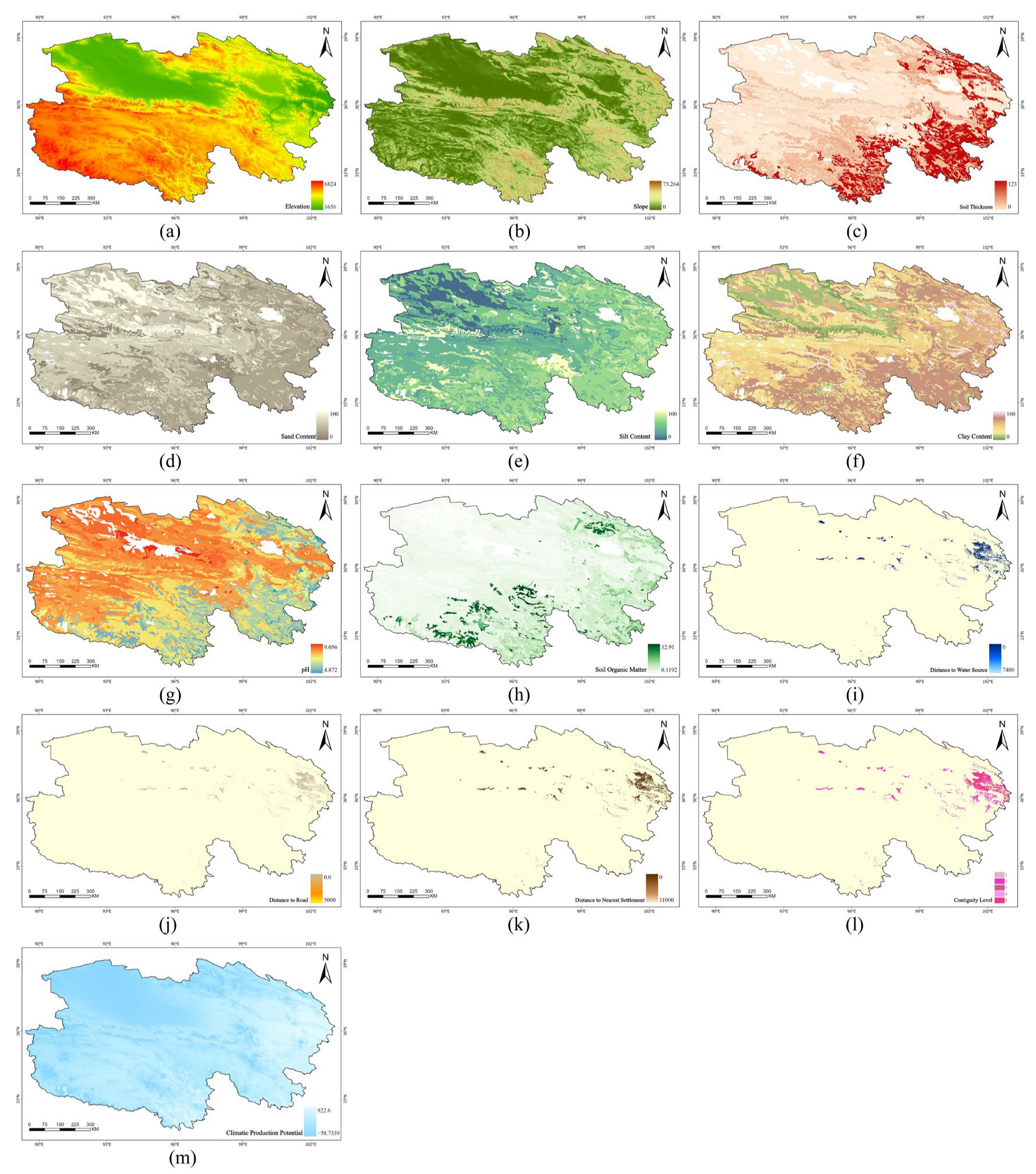
2.2. Data Sources
2.3. Methods
2.3.1. Indicator Construction
- (1)
- Elevation: vertical height above sea level. Higher elevations correspond to lower temperatures, larger diurnal ranges, and shorter growing seasons, which hinder crop growth. Scoring rules: <2500 m = 10; 2500–3200 m = 6; 3200–3800 m = 4; ≥3800 m = 2.
- (2)
- Slope: terrain inclination. Slope is closely related to soil erosion [45], and values above certain thresholds increase the difficulty and risk of mechanized farming. Scoring rules: 0–2° = 10; 2–6° = 8; 6–15° = 6; 15–25° = 4.
- (3)
- Effective Soil-Layer Thickness: depth available for root growth and water storage. Thicker soil layers favor root development and moisture retention. Scoring rules: ≥50 cm = 10; 30–50 cm = 6; <30 cm = 4.
- (4)
- Soil Texture: relative proportions of sand, silt, and clay. Loam provides an optimal balance for crop growth. Scoring rules: loam, light loam = 10; sandy loam, heavy loam = 6; sand, clay = 4.
- (5)
- Soil pH: soil acidity/alkalinity. Neutral to mildly acidic soils promote nutrient availability and microbial activity. Scoring rules: pH 5.5–7.5 = 10; 7.5–8.5 = 6; >8.5 = 4.
- (6)
- Soil Organic-Matter Content: proportion of decomposed residues and microbial biomass. Higher levels improve fertility, soil structure, aeration, and water retention. Scoring rules: ≥8% = 10; <8% = 6.
- (7)
- Irrigation Conditions: distance from a field patch to the nearest water source, calculated in ArcGIS. Shorter distances enable more reliable irrigation. As no unified national criterion is available, classification was conducted using the natural breaks method. Scoring rules: <600 m = 10; 600–1200 m = 8; ≥1200 m = 6.
- (1)
- Transportation Accessibility: distance from a field patch to major transport networks (e.g., township or county roads). Closer proximity and better road conditions reduce transport costs and losses. Distance to the nearest road was calculated in ArcGIS. Scoring rules: <100 m = 10; 100–300 m = 8; 300–500 m = 6; ≥500 m = 4.
- (2)
- Cultivation Accessibility: distance from a field patch to the nearest settlement, reflecting labor and management convenience. Distance to the nearest settlement was calculated in ArcGIS. Scoring rules: <100 m = 10; 100–700 m = 8; 700–1300 m = 6; ≥1300 m = 4.
- (3)
- Contiguity: degree of spatial aggregation of adjacent patches. Higher contiguity supports large-scale farming, facilitates unified management and mechanization, and reduces costs. Contiguity was calculated in ArcGIS by aggregating patches, computing their area, and applying corrections. Plains: ≥900 m2 = 10; 600–900 m2 = 8; 400–600 m2 = 6; 150–400 m2 = 4; <150 m2 = 2. Mountainous/Hilly areas: ≥400 m2 = 10; 250–400 m2 = 8; 150–250 m2 = 6; 80–150 m2 = 4; <80 m2 = 2.
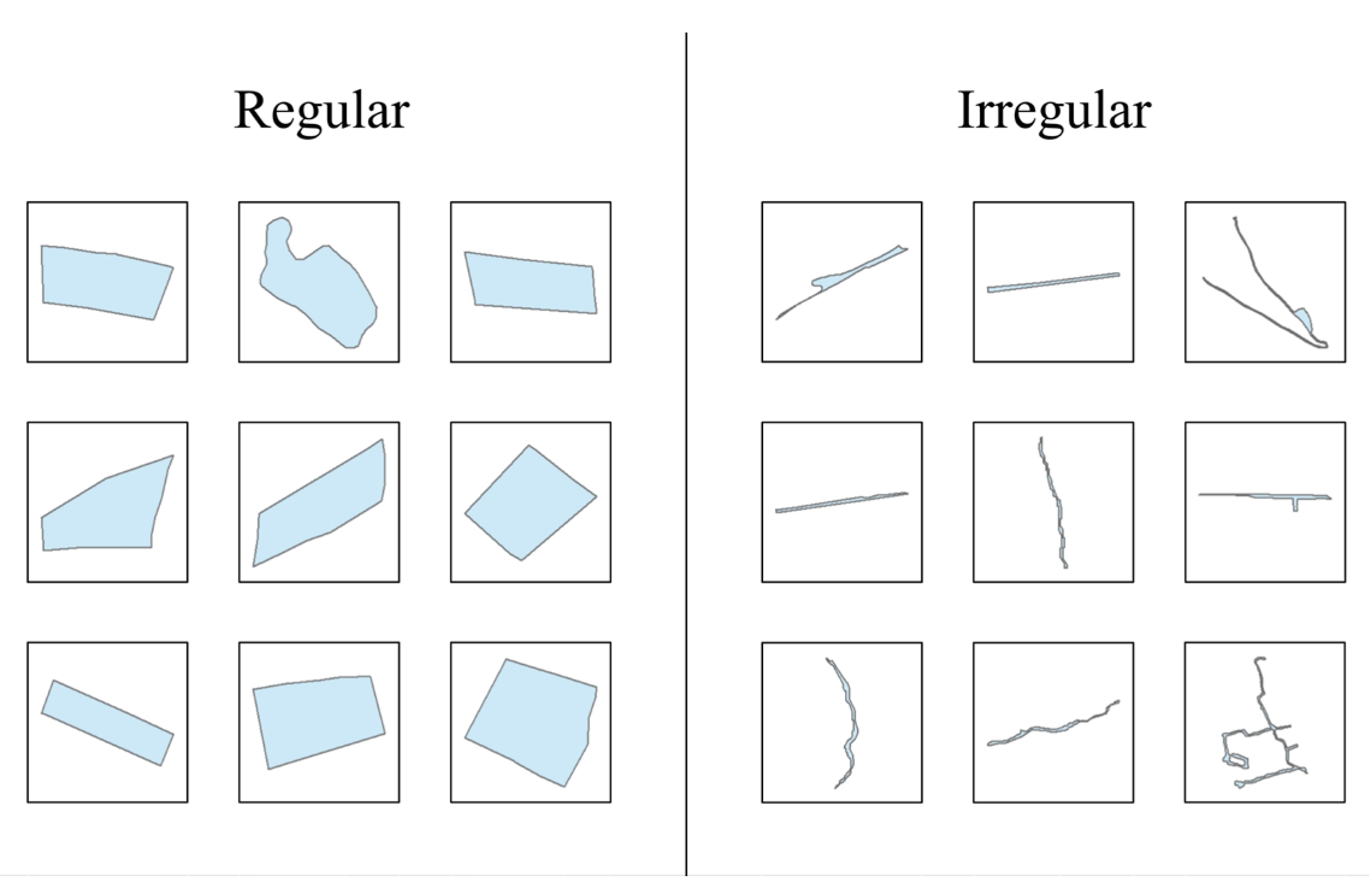
2.3.2. Sample-Set Preparation
2.3.3. Data Normalization
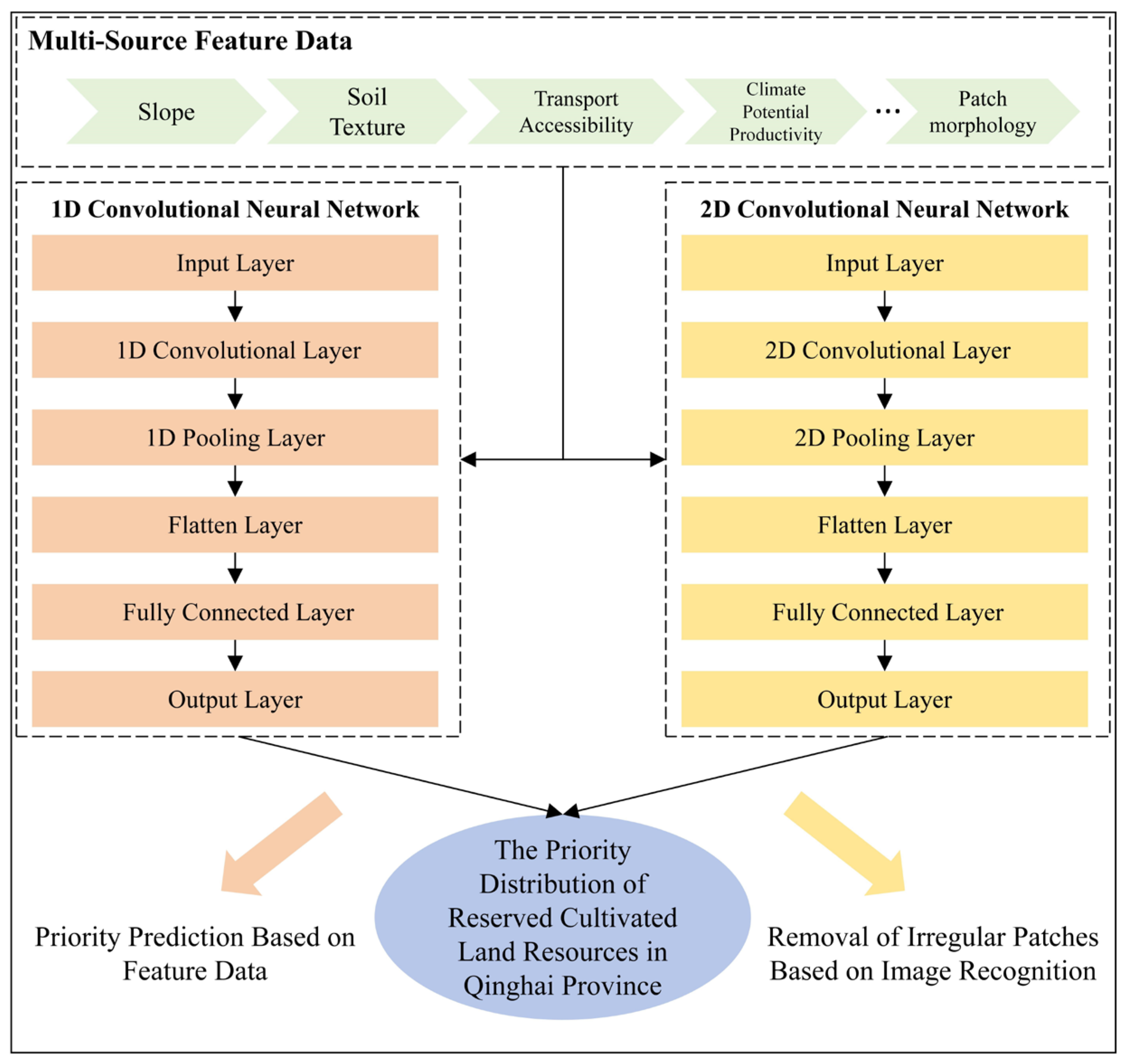
2.3.4. CNN Construction
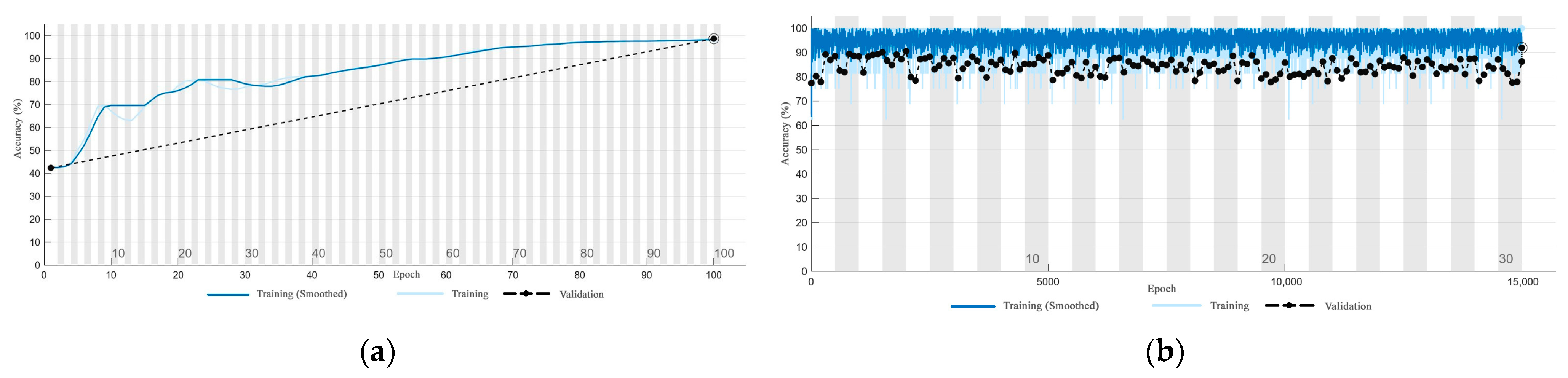
2.3.5. CNN Model Accuracy Validation
2.3.6. CNN Model Outputs
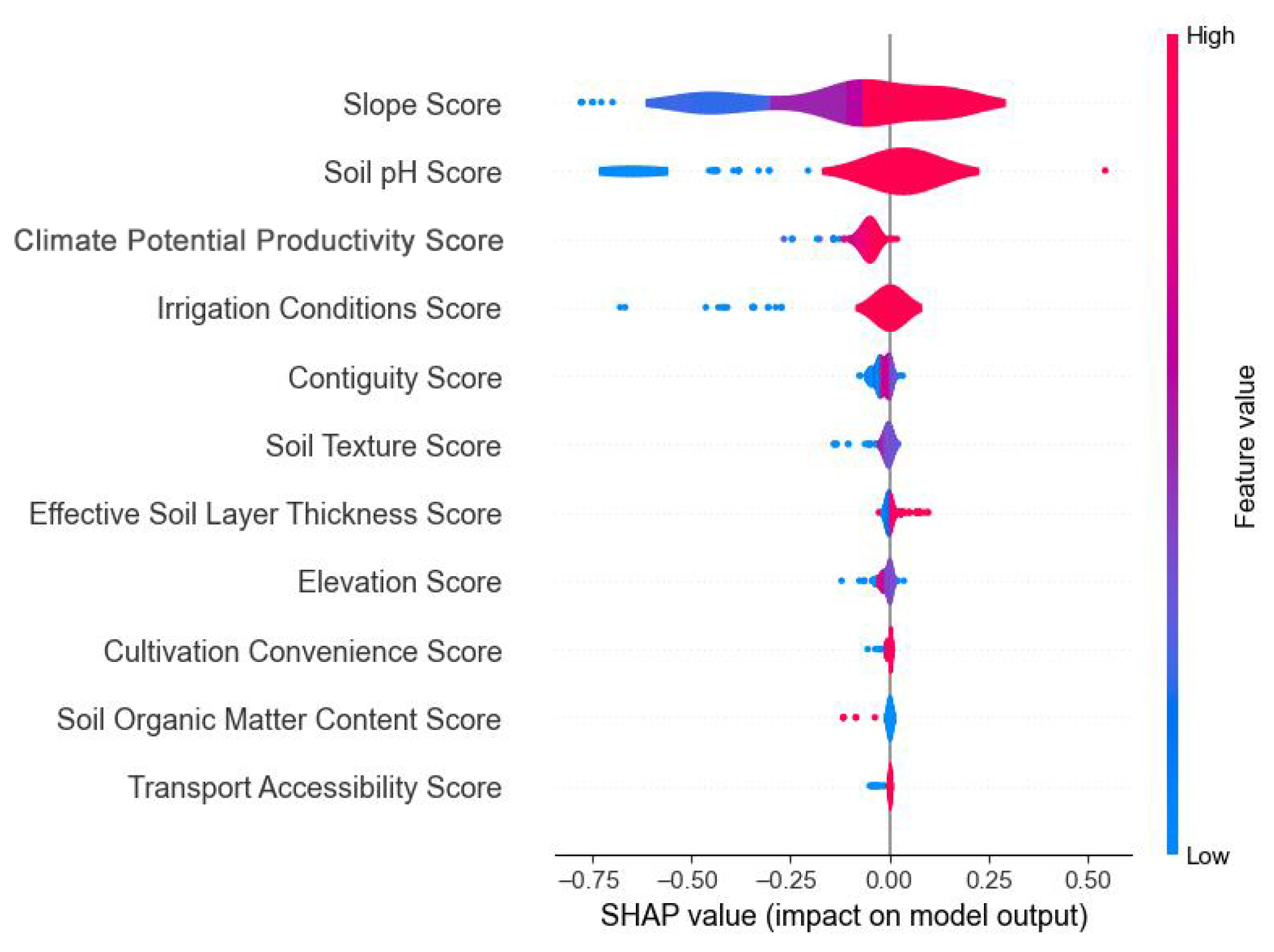
2.3.7. SHAP Analysis
2.3.8. Ablation Study
2.3.9. Baseline Method: AHP
3. Results
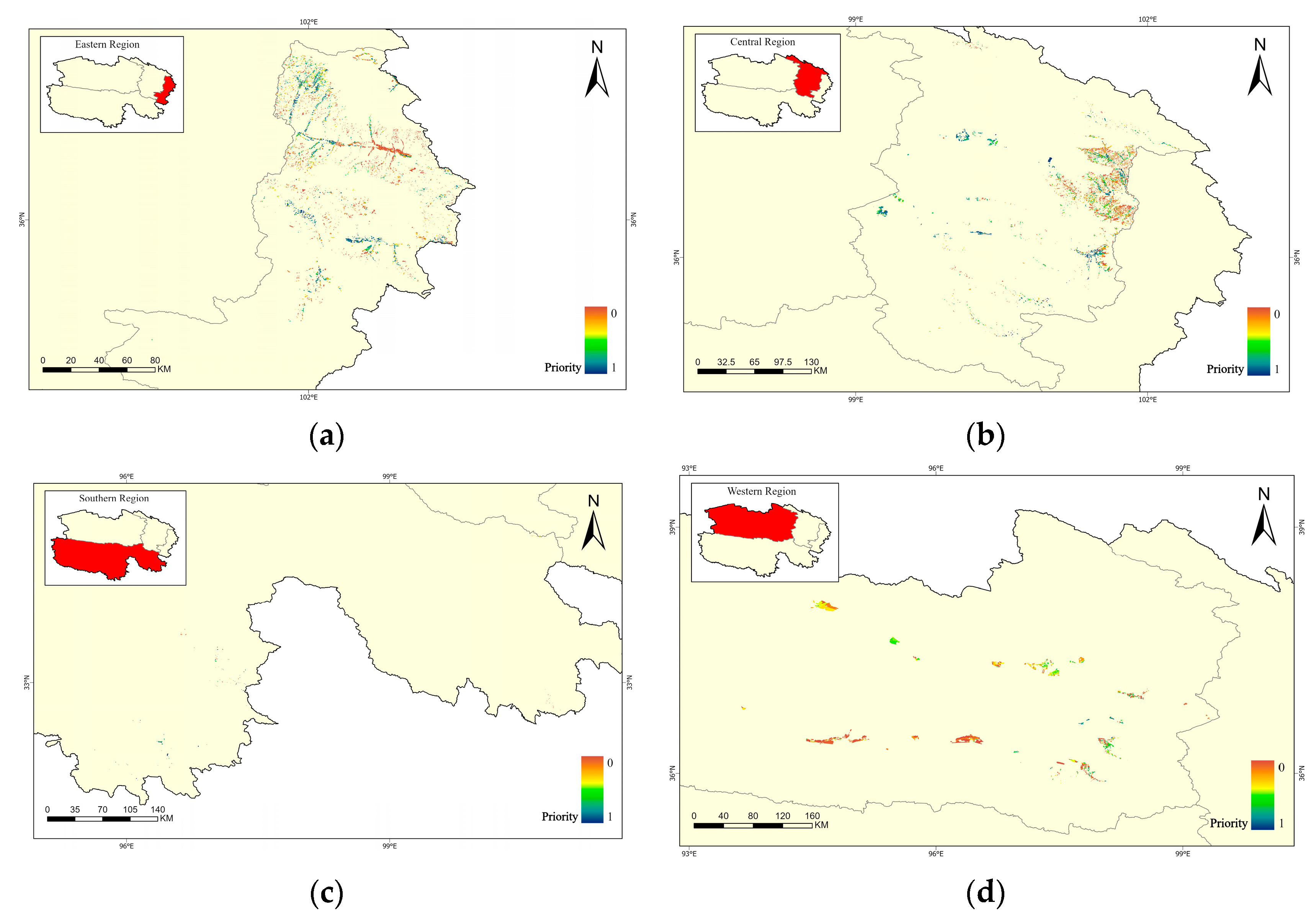
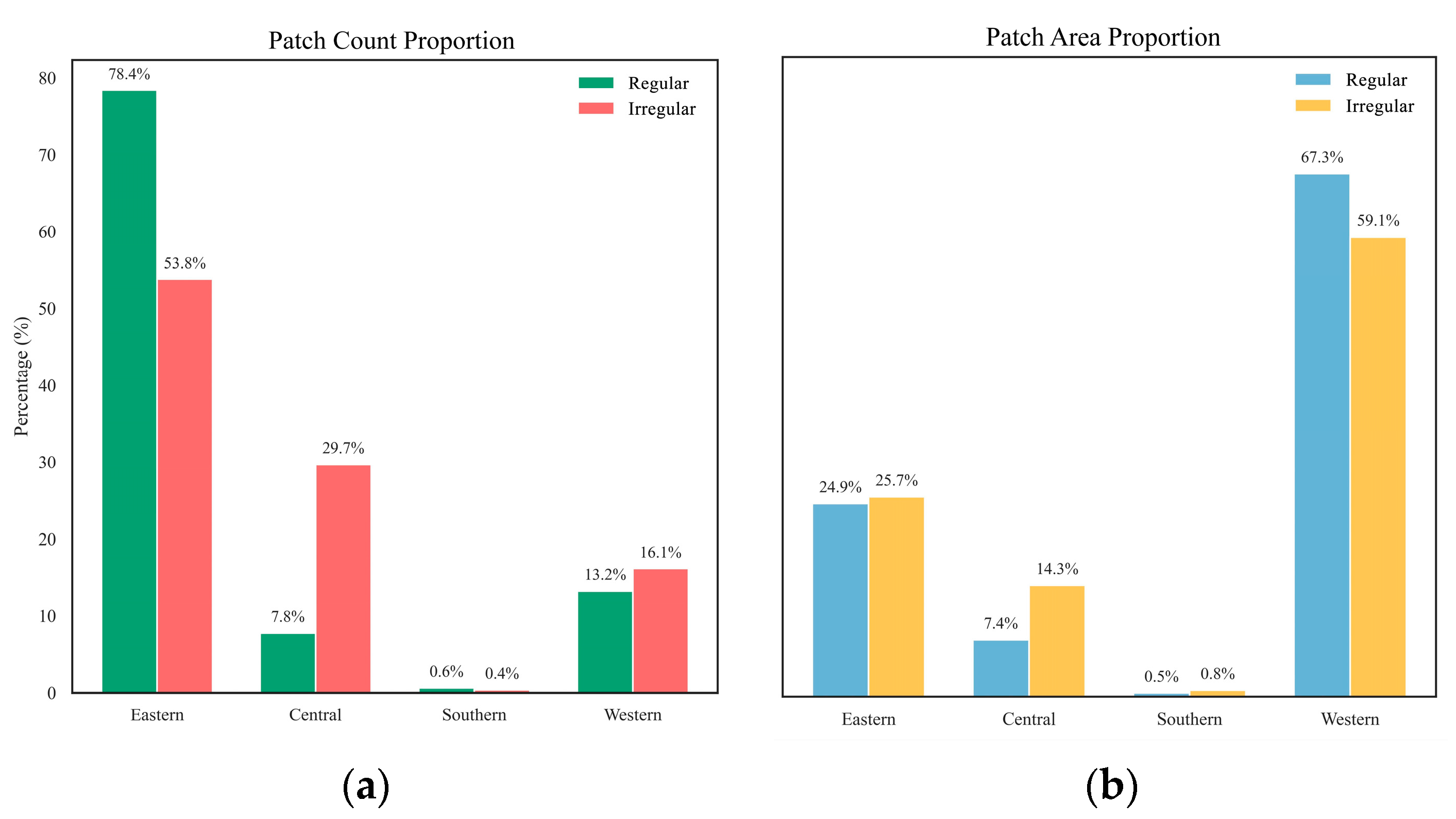
3.1. Priority-Ranking Results for Reserved Cultivated Land Resources in Qinghai Province
3.2. Performance of the CNN Models in the Evaluation
4. Discussion
4.1. Significance of the Priority Level of Reserved Cultivated Land Resources
4.2. Advantages of the Dual-Screening Model Framework
4.3. Limitations and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | convolutional neural networks |
| 1D-CNN | one-dimensional convolutional neural network |
| 2D-CNN | two-dimensional convolutional neural network |
| SHAP | shapley additive explanations |
| AHP | analytic hierarchy process |
| ANP | analytic network process |
| OWA | ordered weighted averaging |
| CPP | climate potential productivity |
| TP | true positive |
| TPR | true positive rate |
| FP | false positive |
| FPR | false positive rate |
| FN | false negative |
| TN | true negative |
| ROC | receiver operating characteristic |
| PR | precision-recall |
| AUC | area under the ROC curve |
| AP | average precision |
References
- Wu, Y.; Shan, L.; Guo, Z.; Peng, Y. Cultivated Land Protection Policies in China Facing 2030: Dynamic Balance System versus Basic Farmland Zoning. Habitat Int. 2017, 69, 126–138. [Google Scholar] [CrossRef]
- Yuan, X.; Shao, Y.; Li, Y.; Liu, Y.; Wang, Y.; Wei, X.; Wang, X.; Zhao, Y. Cultivated Land Quality Improvement to Promote Revitalization of Sandy Rural Areas along the Great Wall in Northern Shaanxi Province, China. J. Rural Stud. 2022, 93, 367–374. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Liu, Y. Cultivated Land Protection and Rational Use in China. Land Use Policy 2021, 106, 105454. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, T.; Feng, Z.; Wu, K. Identifying the Contradiction between the Cultivated Land Fragmentation and the Construction Land Expansion from the Perspective of Urban-Rural Differences. Ecol. Inform. 2022, 71, 101826. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhong, Z.; Cheng, G. Cultivated Land Loss and Construction Land Expansion in China: Evidence from National Land Surveys in 1996, 2009 and 2019. Land Use Policy 2023, 125, 106496. [Google Scholar] [CrossRef]
- Ariken, M.; Zhang, F.; Chan, N.w.; Kung, H.-t. Coupling Coordination Analysis and Spatio-Temporal Heterogeneity between Urbanization and Eco-Environment along the Silk Road Economic Belt in China. Ecol. Indic. 2021, 121, 107014. [Google Scholar] [CrossRef]
- Chai, C.; Zhang, B.; Li, Y.; Niu, W.; Zheng, W.; Kong, X.; Yu, Q.; Zhao, M.; Xia, X. A New Multi-Dimensional Framework Considering Environmental Impacts to Assess Green Development Level of Cultivated Land during 1990 to 2018 in China. Environ. Impact Assess. Rev. 2023, 98, 106927. [Google Scholar] [CrossRef]
- Feng, X.; Lin, X.; Li, Y.; Yang, J.; Yu, E.; He, C.; Lei, K.; Gao, W. Impact of Urban Land Development on Carbon Emission Performance Based on a Multidimensional Framework. Environ. Impact Assess. Rev. 2024, 105, 107429. [Google Scholar] [CrossRef]
- Huang, Z.; Du, X.; Castillo, C.S.Z. How Does Urbanization Affect Farmland Protection? Evidence from China. Resour. Conserv. Recycl. 2019, 145, 139–147. [Google Scholar] [CrossRef]
- Chen, L.; Song, G.; Meadows, M.E.; Zou, C. Spatio-Temporal Evolution of the Early-Warning Status of Cultivated Land and Its Driving Factors: A Case Study of Heilongjiang Province, China. Land Use Policy 2018, 72, 280–292. [Google Scholar] [CrossRef]
- Wang, X.; Feng, Q.; Li, B.; Fan, Y.; Fan, H.; Yang, N.; Quan, Y.; Ding, H.; Zhang, Y. Trends and Factors Influencing the Evolution of Spatial Patterns of Cropland toward Large-Scale Agricultural Production in China. Land 2024, 13, 607. [Google Scholar] [CrossRef]
- AbdelRahman, M.A.E.; Shalaby, A.; Essa, E.F. Quantitative Land Evaluation Based on Fuzzy-Multi-Criteria Spatial Model for Sustainable Land-Use Planning. Model. Earth Syst. Environ. 2018, 4, 1341–1353. [Google Scholar] [CrossRef]
- Kuang, B.; Han, J.; Lu, X.; Zhang, X.; Fan, X. Quantitative Evaluation of China’s Cultivated Land Protection Policies Based on the PMC-Index Model. Land Use Policy 2020, 99, 105062. [Google Scholar] [CrossRef]
- Chaudhary, S.; Kumar, A.; Pramanik, M.; Negi, M.S. Land Evaluation and Sustainable Development of Ecotourism in the Garhwal Himalayan Region Using Geospatial Technology and Analytical Hierarchy Process. Environ. Dev. Sustain. 2022, 24, 2225–2266. [Google Scholar] [CrossRef]
- Douglas, I. Climate Change, Flooding and Food Security in South Asia. Food Secur. 2009, 1, 127–136. [Google Scholar] [CrossRef]
- Chou, J.; Dong, W.; Wang, S.; Fu, Y. Quantitative Analysis of Agricultural Land Use Change in China. Phys. Chem. Earth 2015, 87–88, 3–9. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Zhou, C. Quantifying Embodied Cultivated Land-Use Change and Its Socioeconomic Driving Forces in China. Appl. Geogr. 2021, 137, 102601. [Google Scholar] [CrossRef]
- Akinci, H.; Özalp, A.Y.; Turgut, B. Agricultural Land Use Suitability Analysis Using GIS and AHP Technique. Comput. Electron. Agric. 2013, 97, 71–82. [Google Scholar] [CrossRef]
- Chivasaa, W.; Mutanga, O.; Biradarc, C. Mapping Land Suitability for Maize (Zea mays L.) Production Using GIS and AHP Technique in Zimbabwe. S. Afr. J. Geomat. 2022, 8, 265–281. [Google Scholar] [CrossRef]
- Mishra, A.K.; Deep, S.; Choudhary, A. Identification of Suitable Sites for Organic Farming Using AHP & GIS. Egypt. J. Remote Sens. Space Sci. 2015, 18, 181–193. [Google Scholar] [CrossRef]
- Wang, X.; Chai, L.; Zeng, S.; Su, J.; Ye, B.; Lü, H.; Chen, C.; Gong, J.; Liu, M.; Wang, X.; et al. Evaluating Cultivated Reserved Land Resources in a Highly Urbanized Region of China: A Case Study in Haishu District, Ningbo City. Land 2024, 13, 1444. [Google Scholar] [CrossRef]
- Zabihi, H.; Ahmad, A.; Vogeler, I.; Said, M.N.; Golmohammadi, M.; Golein, B.; Nilashi, M. Land Suitability Procedure for Sustainable Citrus Planning Using the Application of the Analytical Network Process Approach and GIS. Comput. Electron. Agric. 2015, 117, 114–126. [Google Scholar] [CrossRef]
- Malczewski, J.; Chapman, T.; Flegel, C.; Walters, D.; Shrubsole, D.; Healy, M.A. GIS Multicriteria Evaluation with Ordered Weighted Averaging (OWA): Case Study of Developing Watershed Management Strategies. Environ. Plan. A 2003, 35, 1769–1784. [Google Scholar] [CrossRef]
- Montgomery, B.; Dragićević, S.; Dujmović, J.; Schmidt, M. A GIS-Based Logic Scoring of Preference Method for Evaluation of Land Capability and Suitability for Agriculture. Comput. Electron. Agric. 2016, 124, 340–353. [Google Scholar] [CrossRef]
- Braimoh, A.K.; Vlek, P.L.G.; Stein, A. Land Evaluation for Maize Based on Fuzzy Set and Interpolation. Environ. Manag. 2004, 33, 226–238. [Google Scholar] [CrossRef]
- Liu, Y.; Jiao, L.; Liu, Y.; He, J. A Self-Adapting Fuzzy Inference System for the Evaluation of Agricultural Land. Environ. Model. Softw. 2013, 40, 226–234. [Google Scholar] [CrossRef]
- Reshmidevi, T.V.; Eldho, T.I.; Jana, R. A GIS-Integrated Fuzzy Rule-Based Inference System for Land Suitability Evaluation in Agricultural Watersheds. Agric. Syst. 2009, 101, 101–109. [Google Scholar] [CrossRef]
- Jamil, M.; Sahana, M.; Sajjad, H. Crop Suitability Analysis in the Bijnor District, UP, Using Geospatial Tools and Fuzzy Analytical Hierarchy Process. Agric. Res. 2018, 7, 506–522. [Google Scholar] [CrossRef]
- Tashayo, B.; Honarbakhsh, A.; Azma, A.; Akbari, M. Combined Fuzzy AHP–GIS for Agricultural Land Suitability Modeling for a Watershed in Southern Iran. Environ. Manag. 2020, 66, 364–376. [Google Scholar] [CrossRef]
- LI, B.; ZHANG, F.; ZHANG, L.-W.; HUANG, J.-F.; JIN, Z.-F.; GUPTA, D.K. Comprehensive Suitability Evaluation of Tea Crops Using GIS and a Modified Land Ecological Suitability Evaluation Model. Pedosphere 2012, 22, 122–130. [Google Scholar] [CrossRef]
- Feng, Y.; Li, H.; Tong, X.; Li, P.; Wang, R.; Chen, S.; Xi, M.; Sun, J.; Wang, Y.; He, H.; et al. Optimized Landing Site Selection at the Lunar South Pole: A Convolutional Neural Network Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10998–11015. [Google Scholar] [CrossRef]
- Tanoori, G.; Soltani, A.; Modiri, A. Predicting Urban Land Use and Mitigating Land Surface Temperature: Exploring the Role of Urban Configuration with Convolutional Neural Networks. J. Urban Plan. Dev. 2024, 150, 04024029. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Yang, W.; Chen, J.; Zhu, M. Analysis and Prediction of Land Use in Beijing-Tianjin-Hebei Region: A Study Based on the Improved Convolutional Neural Network Model. Sustainability 2020, 12, 3002. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Rasoli, L.; Kerry, R.; Scholten, T. Land Suitability Assessment and Agricultural Production Sustainability Using Machine Learning Models. Agronomy 2020, 10, 573. [Google Scholar] [CrossRef]
- Zhu, X.; Xiao, G.; Wang, S. Suitability Evaluation of Potential Arable Land in the Mediterranean Region. J. Environ. Manag. 2022, 313, 115011. [Google Scholar] [CrossRef]
- Zhu, X.; Li, N.; Pan, Y. Optimization Performance Comparison of Three Different Group Intelligence Algorithms on a SVM for Hyperspectral Imagery Classification. Remote Sens. 2019, 11, 734. [Google Scholar] [CrossRef]
- Dang, K.B.; Burkhard, B.; Windhorst, W.; Müller, F. Application of a Hybrid Neural-Fuzzy Inference System for Mapping Crop Suitability Areas and Predicting Rice Yields. Environ. Model. Softw. 2019, 114, 166–180. [Google Scholar] [CrossRef]
- Shastri, S.; Kumar, S.; Mansotra, V.; Salgotra, R. Advancing Crop Recommendation System with Supervised Machine Learning and Explainable Artificial Intelligence. Sci. Rep. 2025, 15, 25498. [Google Scholar] [CrossRef]
- Zhong, L.; Guo, X.; Ding, M.; Ye, Y.; Jiang, Y.; Zhu, Q.; Li, J. SHAP Values Accurately Explain the Difference in Modeling Accuracy of Convolution Neural Network between Soil Full-Spectrum and Feature-Spectrum. Comput. Electron. Agric. 2024, 217, 108627. [Google Scholar] [CrossRef]
- Hussein, E.E.; Zerouali, B.; Bailek, N.; Derdour, A.; Ghoneim, S.S.M.; Santos, C.A.G.; Hashim, M.A. Harnessing Explainable AI for Sustainable Agriculture: SHAP-Based Feature Selection in Multi-Model Evaluation of Irrigation Water Quality Indices. Water 2025, 17, 59. [Google Scholar] [CrossRef]
- Pham, T.H.; Acharya, P.; Bachina, S.; Osterloh, K.; Nguyen, K.D. Deep-Learning Framework for Optimal Selection of Soil Sampling Sites. Comput. Electron. Agric. 2024, 217, 108650. [Google Scholar] [CrossRef]
- Ganati, B.A.; Sitote, T.M. Predicting Land Suitability for Wheat and Barley Crops Using Machine Learning Techniques. Sci. Rep. 2025, 15, 15879. [Google Scholar] [CrossRef]
- Reese, M.; Dasgupta, A.; Waske, B. Farmland Quality Assessment Using Deep Learning and UAVs. Remote Sens. Appl. Soc. Environ. 2024, 35, 101235. [Google Scholar] [CrossRef]
- Mohan, R.N.V.J.; Rayanoothala, P.S.; Sree, R.P. Next-Gen Agriculture: Integrating AI and XAI for Precision Crop Yield Predictions. Front. Plant Sci. 2024, 15, 1451607. [Google Scholar] [CrossRef]
- Koulouri, M.; Giourga, C. Land Abandonment and Slope Gradient as Key Factors of Soil Erosion in Mediterranean Terraced Lands. Catena 2007, 69, 274–281. [Google Scholar] [CrossRef]
- Li, S.; Zhang, C.; Chen, C.; Yang, C.; Zhao, L.; Bai, X. Optimization Simulation and Comprehensive Evaluation Coupled with CNN-LSTM and PLUS for Multi-Scenario Land Use in Cultivated Land Reserve Resource Area. Remote Sens. 2025, 17, 1619. [Google Scholar] [CrossRef]
- Li, S.; Zhang, C.; Luo, C.; Li, S.; Yun, W.; Gao, B. Analysis of Comprehensive Land Consolidation in Cultivated Land Reserve Resource Areas Based on Two-Level Geographical Unit Division. Land 2024, 13, 470. [Google Scholar] [CrossRef]
- Liu, J.; Wang, T.; Skidmore, A.; Sun, Y.; Jia, P.; Zhang, K. Integrated 1D, 2D, and 3D CNNs Enable Robust and Efficient Land Cover Classification from Hyperspectral Imagery. Remote Sens. 2023, 15, 4797. [Google Scholar] [CrossRef]
- Chen, H.; He, G.; Peng, X.; Wang, G.; Yin, R. A Multi-Scale Feature Fusion Deep Learning Network for the Extraction of Cropland Based on Landsat Data. Remote Sens. 2024, 16, 4071. [Google Scholar] [CrossRef]
- António, V.; Kimani, G.; Umohoza, E.; Busogi, M. Cross-Regional Transferability of AI Crop-Type Mapping: Insights and Challenges. In Proceedings of the 2024 International Conference on Information Technology for Social Good, Bremen, Germany, 4–6 September 2024; ACM: New York, NY, USA, 2024; pp. 453–461. [Google Scholar]
- Karakullukcu, E. Leveraging Convolutional Neural Networks for Image-Based Classification of Feature Matrix Data. Expert Syst. Appl. 2025, 281, 127625. [Google Scholar] [CrossRef]
- Zhao, Q.; Bai, J.; Huang, L.; Gu, B.; Lu, Q.; Gao, Z. A Review of Methodologies and Success Indicators for Coastal Wetland Restoration. Ecol. Indic. 2016, 60, 442–452. [Google Scholar] [CrossRef]
- Lin, N.; Wang, X.; Zhang, Y.; Hu, X.; Ruan, J. Fertigation Management for Sustainable Precision Agriculture Based on Internet of Things. J. Clean. Prod. 2020, 277, 124119. [Google Scholar] [CrossRef]
- Wu, B.; Bao, Y.; Wang, Z.; Chen, X.; Wei, W. Multi-Temporal Evaluation and Optimization of Ecological Network in Multi-Mountainous City. Ecol. Indic. 2023, 146, 109794. [Google Scholar] [CrossRef]






| Indicator | Weight |
|---|---|
| Elevation | 0.0577 |
| Slope | 0.1346 |
| Soil thickness | 0.0962 |
| Soil texture | 0.0577 |
| Soil pH | 0.0385 |
| Organic matter | 0.0577 |
| Irrigation conditions | 0.1346 |
| Cultivation accessibility | 0.0962 |
| Transport accessibility | 0.0769 |
| Contiguity | 0.1154 |
| CPP | 0.1346 |
| Setting | Mean Accuracy | Mean AUC | Mean AP | ∆Accuracy | ∆AUC | ∆AP |
|---|---|---|---|---|---|---|
| Baseline (all) | 0.9996 | 0.9999 | 0.9965 | – | – | – |
| Drop Elevation | 0.9997 | 1.0000 | 0.9979 | +0.0001 | +0.0000 | +0.0014 |
| Drop Slope | 0.8668 | 0.8930 | 0.8842 | −0.1328 | −0.1070 | −0.1124 |
| Drop Soil pH | 0.8641 | 0.9466 | 0.9563 | −0.1355 | −0.0534 | −0.0402 |
| Drop Soil thickness | 0.9998 | 1.0000 | 0.9963 | +0.0002 | +0.0000 | −0.0002 |
| Drop Soil texture | 0.9997 | 0.9998 | 0.9965 | +0.0001 | −0.0002 | +0.0000 |
| Drop Organic matter | 0.9998 | 0.9998 | 0.9975 | +0.0002 | −0.0002 | +0.0010 |
| Drop Irrigation conditions | 0.9669 | 0.9758 | 0.9726 | −0.0327 | −0.0242 | −0.0239 |
| Drop Cultivation accessibility | 0.9992 | 1.0000 | 0.9982 | −0.0004 | −0.0000 | +0.0017 |
| Drop Transport accessibility | 0.9994 | 1.0000 | 0.9969 | −0.0002 | −0.0002 | +0.0003 |
| Drop Contiguity | 0.9998 | 1.0000 | 0.9986 | +0.0002 | +0.0000 | +0.0021 |
| Drop CPP | 0.9998 | 1.0000 | 0.9972 | +0.0002 | +0.0000 | +0.0007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, B.; Zhou, Y.; Zhu, J. Accurate Identification of High-Potential Reserved Cultivated Land Resources: A Convolutional Neural Network-Based Intelligent Selection Framework Verified in Qinghai Province on the Qinghai–Tibet Plateau, China. Land 2025, 14, 1931. https://doi.org/10.3390/land14101931
Miao B, Zhou Y, Zhu J. Accurate Identification of High-Potential Reserved Cultivated Land Resources: A Convolutional Neural Network-Based Intelligent Selection Framework Verified in Qinghai Province on the Qinghai–Tibet Plateau, China. Land. 2025; 14(10):1931. https://doi.org/10.3390/land14101931
Chicago/Turabian StyleMiao, Bohao, Yan Zhou, and Jianghong Zhu. 2025. "Accurate Identification of High-Potential Reserved Cultivated Land Resources: A Convolutional Neural Network-Based Intelligent Selection Framework Verified in Qinghai Province on the Qinghai–Tibet Plateau, China" Land 14, no. 10: 1931. https://doi.org/10.3390/land14101931
APA StyleMiao, B., Zhou, Y., & Zhu, J. (2025). Accurate Identification of High-Potential Reserved Cultivated Land Resources: A Convolutional Neural Network-Based Intelligent Selection Framework Verified in Qinghai Province on the Qinghai–Tibet Plateau, China. Land, 14(10), 1931. https://doi.org/10.3390/land14101931






