Testing the Applicability and Transferability of Data-Driven Geospatial Models for Predicting Soil Erosion in Vineyards
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Environmental Covariates
- (i)
- multitemporal Sentinel-2 satellite imagery data in the form of spectral bands and spectral indices,
- (ii)
- a digital elevation model derived from UAV flights performed in previous work [34], this time aggregated to the resolution of the above-mentioned satellite data and the morphometric parameters generated from it,
- (iii)
- digital primary soil property maps (soil fractions, CaCO3, Soil Organic Matter (SOM), rootable depth).
2.2.1. Spectral Data
2.2.2. Topographic Information
2.2.3. Digital Soil Property Maps
2.3. Training Data
2.4. Erosion Mapping Using Machine Learning
2.4.1. Applied Machine Learning Algorithms
Ranger
xgbLinear—Extreme Gradient Boosting
svmLinear—Regularized Support Vector Machine with Linear Kernel
2.4.2. Modelling Process
2.4.3. Workflow of Testing Model Transferability
2.4.4. Evaluation of Model Accuracy
2.4.5. Evaluation of Model Transferability
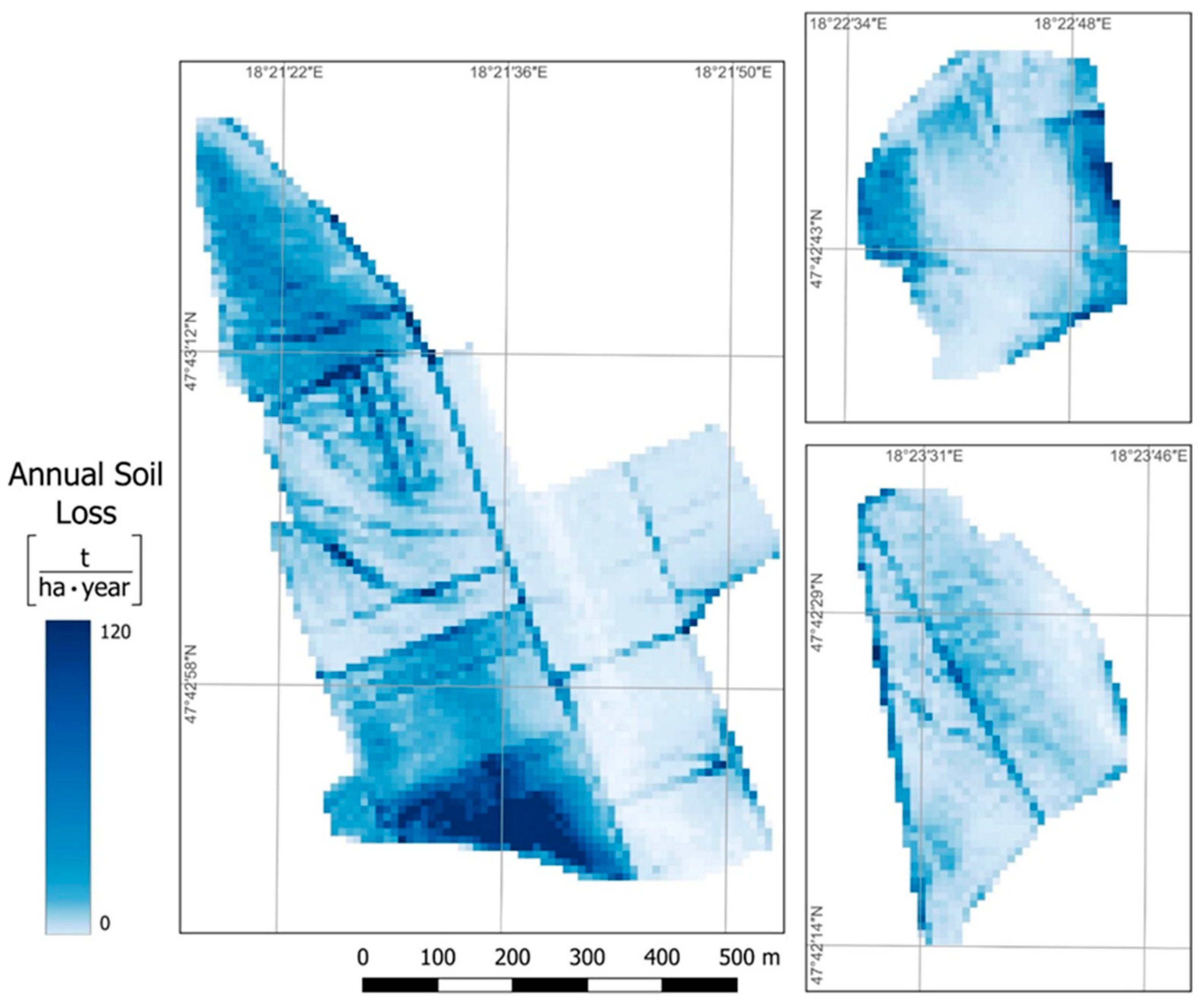
3. Results and Discussion
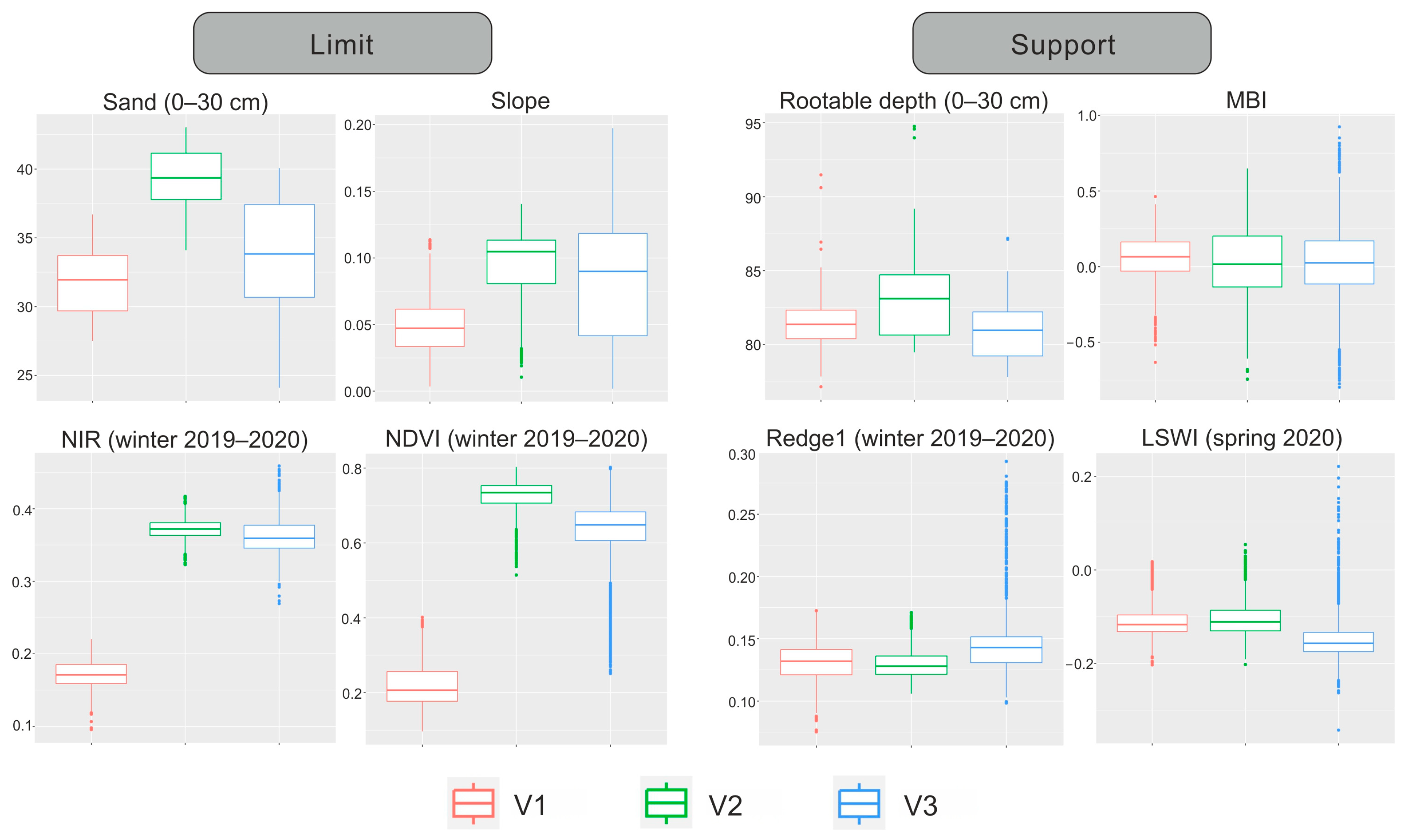
3.1. Predictor-Based Comparison of the Three Vineyards
3.2. Evaluation of the Trained Models
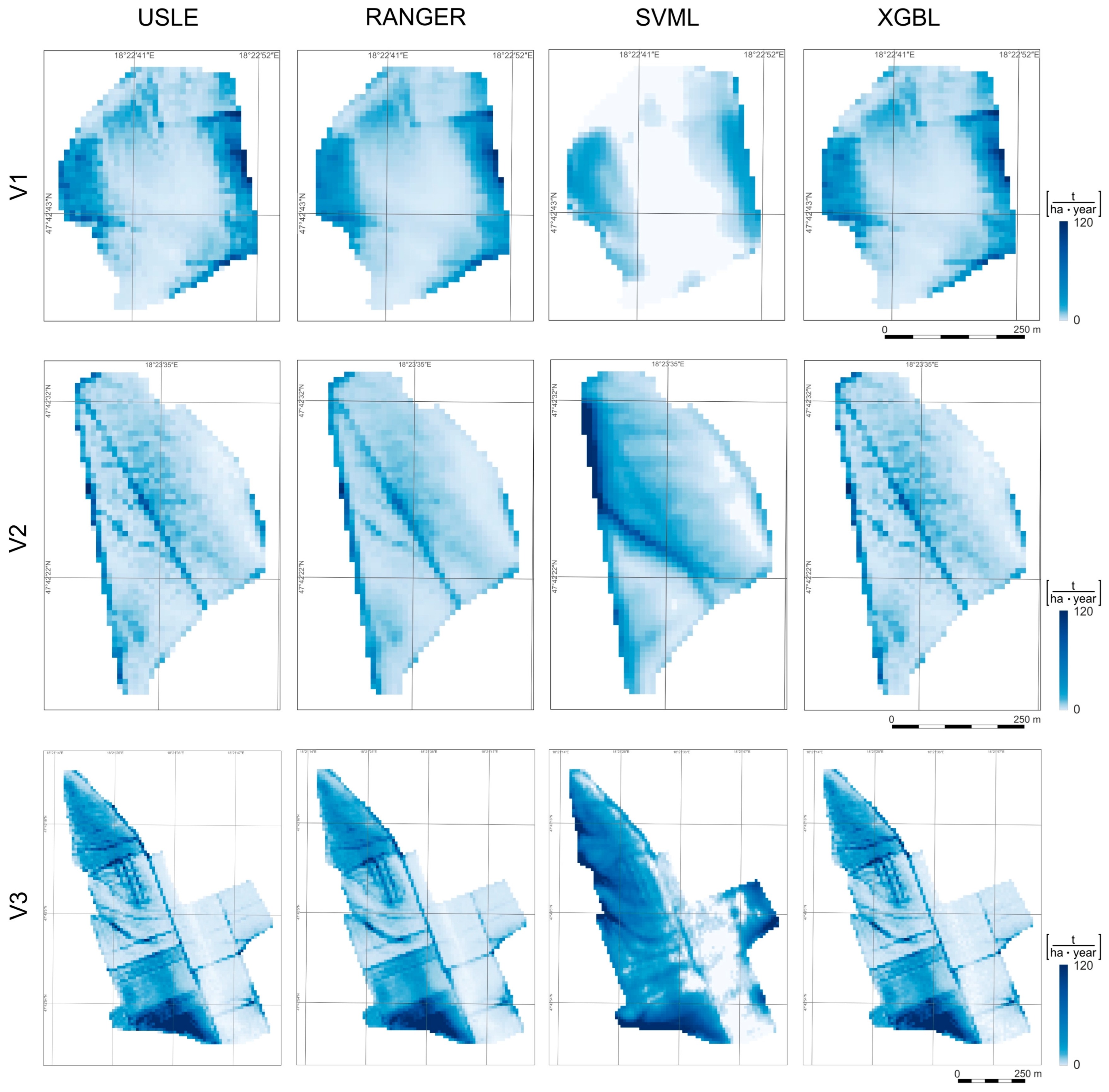
3.3. Machine Learning-Based Soil Erosion Maps
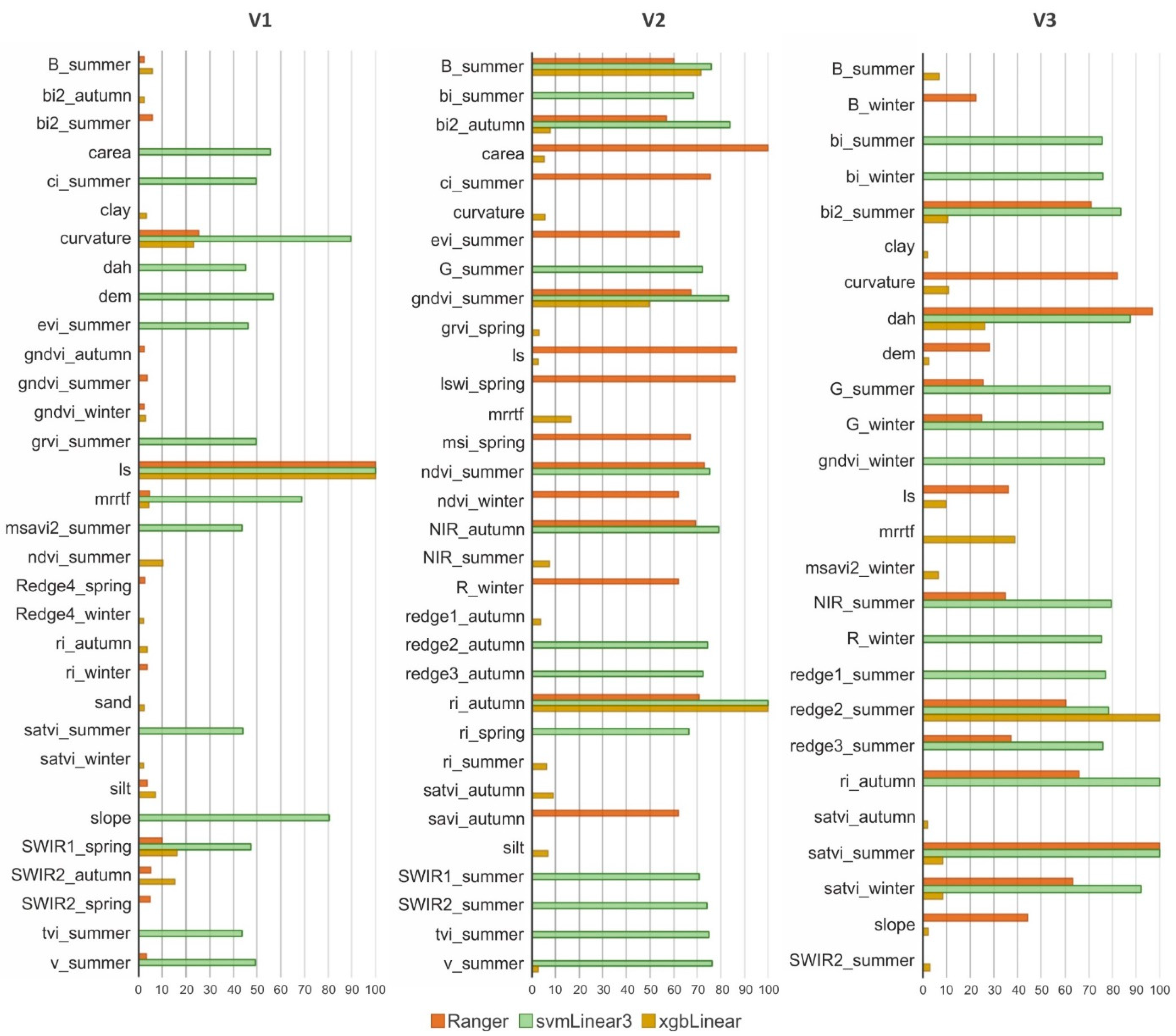
3.4. Variable Importance
3.5. Evaluation of the Model Transferability
3.6. Soil Loss Maps Produced by Model Transferability
4. Conclusions
- The applicability of data-driven geospatial models proved to be successful in predicting soil erosion in three studied vineyards using non-observation-based reference datasets for the calibration derived from previously elaborated spatial soil loss predictions.
- Similarity analysis is important for model transferability, which is reflected in the results. The ensemble predictions gave more accurate results for the two similar areas. Despite the fact that the ML-generated soil erosion maps estimated a higher rate of degradation than the USLE-based maps, they reproduce the more significant erosion patterns, so areas more exposed to erosion can be delineated.
- Observing the inner accuracy of the constructed model, the accuracy metrics values strongly depend on the study site and the applied ML method. The best results were obtained for the most homogeneous and the most diverse area, with the better ML methods (Ranger, xgbLinear) achieving R2 values as high as 0.85. On the other hand, the SVM method performed the worst in none of the areas, reaching R2 = 0.4.
- Concerning the importance of environmental ancillary variables, for the area with bare soil, the topographic variables are more significant, while for the other two areas with vegetation (in our case, vines and grass between the rows of vines), the spectral indices and bands are more informative. Information on soil properties is rarely among the most important auxiliary variables, which may be due to the lower spatial resolution of the applied soil data.
- In the case of transferred models (between the study sites), lower values were obtained in the accuracy metrics. Only in a few cases was R2 = 0.3 reached, but even cases with R2 < 0.01 occurred.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kertész, Á. The global problem of land degradation and desertification. Hung. Geogr. Bull. 2009, 58, 19–31. [Google Scholar]
- Gobin, A.; Govers, G.; Jones, R.; Kirkby, M.; Kosmas, C.; Gentile, A.R. Assessment and reporting on soil erosion. Eur. Environ. Agency Tech. Rep. 2003, 94, 103. [Google Scholar]
- Rodrigo-Comino, J.; Keesstra, S.; Cerdà, A.A. Soil erosion as an environmental concern in vineyards: The case study of Celler del Roure, Eastern Spain, by means of rainfall simulation experiments. Beverages 2018, 4, 31. [Google Scholar] [CrossRef]
- FAO. Provisional Methodology for Soil Degradation Assessment; FAO-UNEP-UNESCO: Rome, Italy, 1979. [Google Scholar]
- Pool, R.; Dunst, R.; Lakso, A. Comparison of sod, mulch, cultivation, and herbicide floor management practices for grape production in nonirrigated vineyards. J. Am. Soc. Hortic. Sci. 1990, 115, 872–877. [Google Scholar] [CrossRef]
- Biddoccu, M.; Ferraris, S.; Pitacco, A.; Cavallo, E. Temporal variability of soil management effects on soil hydrological properties, runoff and erosion at the field scale in a hillslope vineyard, North-West Italy. Soil Tillage Res. 2017, 165, 46–58. [Google Scholar] [CrossRef]
- Batista PV, G.; Davies, J.; Silva ML, N.; Quinton, J.N. On the evaluation of soil erosion models: Are we doing enough? Earth-Sci. Rev. 2019, 197, 102898. [Google Scholar] [CrossRef]
- Wischmeier, W.; Smith, D. Predicting Rainfall Erosion Losses. In USDA Agricultural Research Services Handbook 537; USDA: Washington, DC, USA, 1978. [Google Scholar]
- Renard, K.; Foster, G.; Weesies, G.; Porter, J. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Christine, A.; Pasquale, B.; Katrin, M.; Panagos, P. Using the USLE: Chances, challenges and limitations of soil erosion modelling. Int. Soil Water Conserv. Res. 2019, 7, 203–225. [Google Scholar] [CrossRef]
- Pijl, A.; Reuter, L.E.; Quarella, E.; Teun, V.A.; Tarolli, P. GIS-based soil erosion modelling under various steep-slope vineyard practices. Catena 2020, 193, 104604. [Google Scholar] [CrossRef]
- Peter, K.D.; d’Oleire-Oltmanns, S.; Ries, J.B.; Marzolff, I.; Hssaine, A.A. Soil erosion in gully catchments affected by land-levelling measures in the Souss Basin, Morocco, analysed by rainfall simulation and UAV remote sensing data. Catena 2014, 113, 24–40. [Google Scholar] [CrossRef]
- Fernández, T.; Pérez-García, J.L.; Gómez-López, J.M.; Cardenal, J.; Calero, J.; Sánchez-Gómez, M.; Tovar-Pescador, J. Multitemporal Analysis of Gully Erosion in Olive Groves by Means of Digital Elevation Models Obtained with Aerial Photogrammetric and LiDAR Data. ISPRS Int. J. Geo-Inf. 2020, 9, 260. [Google Scholar] [CrossRef]
- Meinen, B.U.; Robinson, D.T. Agricultural erosion modelling: Evaluating USLE and WEPP field-scale erosion estimates using UAV time-series data. Environ. Model. Softw. 2021, 137, 104962. [Google Scholar] [CrossRef]
- Kirkby, M.; Jones, R.; Irvine, B.; Gobin, A.; Govers, G.; Cerdan, O.; Huting, J. Pan-European Soil Erosion Risk Assessment for Europe: The PESERA Map, Version 1 October 2003; Explanation of Special Publication Ispra 2004 No. 73 (SPI 04.73); Office for Official Publications of the European Communities: Luxembourg, 2004; No. 16, 21176. [Google Scholar]
- Lubos, M.; Mitasova, H. Distributed soil erosion simulation for effective erosion prevention. Water Resour. Res. 1998, 34, 505–516. [Google Scholar] [CrossRef]
- Pásztor, L.; Waltner, I.; Centeri, C.; Belényesi, M.; Takács, K. Soil erosion of Hungary assessed by spatially explicit modelling. J. Maps 2016, 12 (Suppl. 1), 407–414. [Google Scholar] [CrossRef]
- Waltner, I.; Pásztor, L.; Centeri, C.; Takács, K.; Pirkó, B.; Koós, S.; László, P. Evaluating the new soil erosion map of Hungary—A semiquantitative approach. Land Degrad. Dev. 2018, 29, 1295–1302. [Google Scholar] [CrossRef]
- Waltner, I.; Saeidi, S.; Grósz, J.; Centeri, C.; Laborczi, A.; Pásztor, L. Spatial assessment of the effects of land cover change on soil erosion in Hungary from 1990 to 2018. ISPRS Int. J. Geo-Inf. 2020, 9, 667. [Google Scholar] [CrossRef]
- Benavidez, R.; Jackson, B.; Maxwell, D.; Norton, K. A review of the (Revised) Universal Soil Loss Equation ((R) USLE): With a view to increasing its global applicability and improving soil loss estimates. Hydrol. Earth Syst. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef]
- Koldasbayeva, D.; Tregubova, P.; Gasanov, M.; Zaytsev, A.; Petrovskaia, A.; Burnaev, E. Challenges in data-driven geospatial modeling for environmental research and practice. Nat. Commun. 2024, 15, 10700. [Google Scholar] [CrossRef]
- McBratney, A.; Santos, M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A. Machine learning and soil sciences: A review aided by machine learning tools. Soil 2020, 6, 35–52. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, J.; Duan, X.; Tang, B.; Zou, L.; Wang, X.; Guo, Q. Spatial Quantification of Cropland Soil Erosion Dynamics in the Yunnan Plateau Based on Sampling Survey and Multi-Source LUCC Data. Remote Sens. 2024, 16, 977. [Google Scholar] [CrossRef]
- Avand, M.; Mohammadi, M.; Mirchooli, F.; Kavian, A.; Tiefenbacher, J.P. A New Approach for Smart Soil Erosion Modeling: Integration of Empirical and Machine-Learning Models. Environ. Model. Assess. 2023, 28, 145–160. [Google Scholar] [CrossRef]
- Sahour, H.; Gholami, V.; Vazifedan, M.; Saeedi, S. Machine learning applications for water-induced soil erosion modeling and mapping. Soil Tillage Res. 2021, 211, 105032. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Chen, W. DEM-and GIS-Based Analysis of Soil Erosion Depth Using Machine Learning. ISPRS Int. J. Geo-Inf. 2021, 10, 452. [Google Scholar] [CrossRef]
- Bag, R.; Mondal, I.; Dehbozorgi, M.; Bank, S.; Das, D.; Bandyopadhyay, J.; Nguyen, X. Modelling and mapping of soil erosion susceptibility using machine learning in a tropical hot sub-humid environment. J. Clean. Prod. 2022, 364, 132428. [Google Scholar] [CrossRef]
- Mokarram, M.; Zarei, A. Soil erosion prediction using Markov and CA-Markov chains methods and remote sensing drought indicators. Ecol. Inform. 2023, 78, 102386. [Google Scholar] [CrossRef]
- Nguyen, K.; Chen, W.; Lin, B.-S.; Seeboonruang, U. Using Machine Learning-Based Algorithms to Analyze Erosion Rates of a Watershed in Northern Taiwan. Sustainability 2022, 12, 2022. [Google Scholar] [CrossRef]
- Senanayake, S.; Pradhan, B.; Alamri, A.; Park, H. A new application of deep neural network (LSTM) and RUSLE models in soil erosion prediction. Sci. Total Environ. 2022, 845, 157220. [Google Scholar] [CrossRef]
- Fernández, D.; Adermann, E.; Pizzolato, M.; Pechenkin, R.; Rodríguez, C.; Taravat, A. Comparative Analysis of Machine Learning Algorithms for Soil Erosion Modelling Based on Remotely Sensed Data. Remote Sens. 2023, 15, 482. [Google Scholar] [CrossRef]
- Folharini, S.; Vieira, A.; Bento-Gonçalves, A.; Silva, S.; Marques, T.; Novais, J. Soil erosion quantification using Machine Learning in sub-watersheds of Northern Portugal. Hydrology 2023, 10, 7. [Google Scholar] [CrossRef]
- Takáts, T.; Mészáros, J.; Albert, G. Spatial Modelling of Vineyard Erosion in the Neszmély Wine Region, Hungary Using Proximal Sensing. Remote Sens. 2022, 14, 3463. [Google Scholar] [CrossRef]
- Mohebzadeh, H.; Biswas, A.; DeVries, B.; Rudra, R.; Daggupati, P. Transferability of predictive models to map susceptibility of ephemeral gullies at large scale. Nat. Hazards 2024, 120, 4527–4561. [Google Scholar] [CrossRef]
- Bihari, Z.; Babolcsai, G.; Bartholy, J.; Ferenczi, Z.; Kerényi, J.; Haszpra, L.; Homoki-Ujváry, K.; Kovács, T.; Lakatos, M.; Németh, Á.; et al. Climate in National Atlas of Hungary: Natural Environment; Kocsis, K., Ed.; MTA CSFK Geographical Institute: Budapest, Hungary, 2018; pp. 58–68. [Google Scholar]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; Update 2015; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
- Pásztor, L.; Dobos, E.; Michéli, E.; Várallyay, G. Soils. In National Atlas of Hungary: Natural Environment; Kocsis, K., Ed.; MTA CSFK Geographical Institute: Budapest, Hungary, 2018; pp. 82–92. [Google Scholar]
- Pásztor, L.; Laborczi, A.; Takács, K.; Illés, G.; Szabó, J.; Szatmári, G. Progress in the elaboration of GSM conform DSM products and their functional utilization in Hungary. Geoderma Reg. 2020, 21, e00269. [Google Scholar] [CrossRef]
- Takáts, T. Talajerózió és Üledékfelhalmozódás Térképezése Távérzékelési Adatok Alapján. BSc Thesis, Eötvös Loránd University, Budapest, Hungary, 2018. [Google Scholar]
- Gerzsenyi, D.; Albert, G. Landslide inventory validation and susceptibility mapping in the Gerecse Hills, Hungary. Geo-Spat. Inf. Sci. 2021, 24, 498–508. [Google Scholar] [CrossRef]
- Demattê; JA, M.; Fongaro, C.T.; Rizzo, R.; Safanelli, J.L. Geospatial Soil Sensing System (GEOS3): A powerful data mining procedure to retrieve soil spectral reflectance from satellite images. Remote Sens. Environ. 2018, 212, 161–175. [Google Scholar] [CrossRef]
- Escadafal, R. Remote sensing of arid soil surface color with Landsat thematic mapper. Adv. Space Res. 1989, 9, 159–163. [Google Scholar] [CrossRef]
- Parenteau, M.; Bannari, A.; El-Harti, A.; Bachaoui, M.; EL-Ghmari, A. Characterization of the State of Soil Degradation by Erosion Using the Hue and Coloration Indices. IGARSS 2003. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; IEEE Cat. No. 03CH37477. IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. 2284–2286. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; MODIS Science Team Members; Leeuwen, W. MODIS vegetation index (MOD13). Algorithm Theor. Basis Doc. 1999, 3, 295–309. [Google Scholar]
- Buschmann, C.; Nagel, E. In vivo spectroscopy and internal optics of leaves as basis for remote sensing of vegetation. Int. J. Remote Sens. 1993, 14, 711–722. [Google Scholar] [CrossRef]
- Tucker, C. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.; Kerr, Y.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of changes in leaf water content using Near- and Middle-Infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G.; Major, D.J. Crop biomass evaluation using radiometric measurements. Photogrammetria 1989, 43, 241–256. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Marsett, R.C.; Qi, J.; Heilman, P.; Biedenbender, S.H.; Watson, M.C.; Amer, S.; Marsett, R. Remote Sensing for Grassland Management in the Arid Southwest. Rangel. Ecol. Manag. 2006, 59, 530–540. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Rouse, J., Jr.; Haas, R.; Schell, J.; Deering, D.; Harlan, J. Monitoring the Vernal ADVANCEMENT and Retrogradation (Green Wave EFFECT) of Natural Vegetation (No. E75-10354); Texas A&M University, Remotes Sensing Center: College Station, TX, USA, 1974. [Google Scholar]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Brenning, A.; Bangs, D. Introduction to Terrain Analysis with RSAGA: Landslide Susceptibility Modeling. 2022. Available online: https://cran.r-project.org/web/packages/RSAGA/vignettes/RSAGA.html (accessed on 10 January 2025).
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Freeman, G.T. Calculating catchment area with divergent flow based on a regular grid. Comput. Geosci. 1991, 17, 413–422. [Google Scholar] [CrossRef]
- Boehner, J.; Koethe, R.; Conrad, O.; Gross, J.; Ringeler, A.; Selige, T. Soil Regionalisation by Means of Terrain Analysis and Process Parameterisation. In Soil Classification 2001; Micheli, E.N., Ed.; Research Report No. 7, EUR 20398 EN; European Soil Bureau: Luxembourg, 2002; pp. 2013–2222. [Google Scholar]
- Boehner, J.; Antonic, O. Land-surface parameters specific to topo-climatology. Dev. Soil Sci. 2009, 33, 195–226. [Google Scholar] [CrossRef]
- Moore, I.D.; Turner, K.K.; Wilson, J.P.; Jenson, S.K.; Band, L.E. GIS and land-surface-subsurface process modeling. Environ. Model. GIS 1993, 20, 196–230. [Google Scholar]
- Moeller, M.; Volk, M.; Friedrich, K.; Lymburner, L. Placing soil-genesis and transport processes into a landscape context: A multiscale terrain-analysis approach. J. Plant Nutr. Soil Sci. 2008, 171, 419–430. [Google Scholar] [CrossRef]
- Gallant, J.C.; Dowling, T.I. A multiresolution index of valley bottom flatness for mapping depositional areas. Water Resour. Res. 2003, 39, 2002WR001426. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Malone, B.P.; McBratney, A.B.; Minasny, B.; Wheeler, I. A general method for downscaling earth resource information. Comput. Geosci. 2012, 41, 119–125. [Google Scholar] [CrossRef]
- Odgers, N.P.; Sun, W.; McBratney, A.B.; Minasny, B.; Clifford, D. Disaggregating and harmonising soil map units through resampled classification trees. Geoderma 2014, 214, 91–100. [Google Scholar] [CrossRef]
- Pásztor, L.; Laborczi, A.; Takács, K.; Szatmári, G.; Dobos, E.; Bakacsi, Z.; Szabó, J. Compilation of novel and renewed, goal oriented digital soil maps using geostatistical and data mining tools. Hung. Geogr. Bull. 2015, 64, 49–64. [Google Scholar] [CrossRef]
- Roudier, P.; Malone, B.P.; Hedley, C.B.; Minasny, B.; McBratney, A.B. Comparison of regression methods for spatial downscaling of soil organic carbon stocks maps. Comput. Electron. Agric. 2017, 142, 91–100. [Google Scholar] [CrossRef]
- Gagkas, Z.; Lilly, A. Downscaling soil hydrological mapping used to predict catchment hydrological response with random forests. Geoderma 2019, 341, 216–235. [Google Scholar] [CrossRef]
- Møller, A.B.; Koganti, T.; Beucher, A.; Iversen, B.V.; Greve, M.H. Downscaling digital soil maps using electromagnetic induction and aerial imagery. Geoderma 2021, 385, 114852. [Google Scholar] [CrossRef]
- Team R Core. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org (accessed on 10 January 2025).
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Kuhn, M. The Caret Package. 2019. Available online: https://topepo.github.io/caret/ (accessed on 1 December 2024).
- Moon, J.; Park, S.; Rho, A.; Hwang, E. Robust building energy consumption forecasting using an online learning approach with R ranger. J. Build. Eng. 2022, 47, 103851. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support Vector Machines in R. J. Stat. Softw. 2006, 15, 1–28. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Su, J.; Yi, D.; Su, B.; Mi, Z.; Liu, C.; Hu, X.; Chen, W.-H. Aerial visual perception in smart farming: Field study of wheat yellow rust monitoring. IEEE Trans. Ind. Inform. 2020, 17, 2242–2249. [Google Scholar] [CrossRef]
- Saha, A.; Pal, S.; Chowdhuri, I.; Islam, A.; Roy, P.; Chakrabortty, R. Land degradation risk dynamics assessment in red and lateritic zones of eastern plateau, India: A combine approach of K-fold CV, data mining and field validation. Ecol. Inform. 2022, 69, 101653. [Google Scholar] [CrossRef]
- Kucuker, D.; Giraldo, D. Assesment of soil erosion risk using an integrated approach of GIS and Analytic Hierarchy Process (AHP) in Erzurum, Turkiye. Ecol. Inform. 2022, 71, 101788. [Google Scholar] [CrossRef]




| The Used Algorithm | Article |
|---|---|
| Adaptive Neuro-Fuzzy Inference System | Nguyen et al., 2022 [27] |
| Artificial Neural Network | Nguyen et al., 2022 [27], Avand et al., 2023 [25] |
| Boosted Regression Tree | Sahour et al., 2021 [26], Bag et al., 2022 [28] |
| Cellular Automata Marcov chain | Mokarram and Zarei, 2023 [29] |
| Classification and Regression Tree | Bag et al., 2022 [28] |
| Classification-Tree Analysis | Avand et al., 2023 [25] |
| Deep Learning | Sahour et al., 2021 [26] |
| Gradient Boosting Model | Nguyen and Chen, 2021 [30] |
| Generalized Linear Model | Avand et al., 2023 [25] |
| Long Short-Term Memory Neural Network Model | Senanayake et al., 2022 [31] |
| Markov | Mokarram and Zarei, 2023 [29] |
| Multilayer Perceptron | Fernández et al., 2023 [32] |
| Multiple Linear Regression | Sahour et al., 2021 [26] |
| Random Forest | Nguyen and Chen, 2021 [30], Avand et al., 2023 [25], Bag et al., 2022 [28], Fernández et al., 2023 [32], Folharini, S. et al., 2023 [33] |
| Support Vector Machine | Nguyen et al., 2022 [27], Bag et al., 2022 [28], Fernández et al., 2023 [32], Folharini S., et al., 2023 [33] |
| Band | Central Wavelength | Resolution |
|---|---|---|
| Blue (B2) | 496.6 nm | 10 m |
| Green (B3) | 560 nm | 10 m |
| Near Infrared (B8) | 835.1 nm | 10 m |
| Red (B4) | 664.5 nm | 10 m |
| Red Edge 1 (B5) | 703.9 nm | 20 m |
| Red Edge 2 (B6) | 740.2 nm | 20 m |
| Red Edge 3 (B7) | 782.5 nm | 20 m |
| Red Edge 4 (B8A) | 864.8 nm | 20 m |
| Short-Wave Infrared (B11) | 1613.7 nm | 20 m |
| Short-Wave Infrared (B12) | 2202.4 nm | 20 m |
| Index | Abbreviation | Index Description | Formula | References |
|---|---|---|---|---|
| Brightness Index | BI | It is sensitive to soil brightness, which is an indicator of the soil humidity and the presence of salt in the soil. | Escadafal, 1989 [43] | |
| Brightness Index 2 | BI2 | Escadafal, 1989 [43] | ||
| Coloration Index CI | CI | Soil reflectance curves are mainly affected by the absorption of iron oxides. Its general slope refers to the concept of saturation and expresses the colors’ vivacity. CI can be an implicit indicator of soil degradation. | Parenteau et al., 2003 [44] | |
| Enhanced Vegetation Index | EVI | It is sensitive to high biomass regions and improved vegetation monitoring through a decoupling of the canopy background signal and a reduction in atmosphere influences. | Huete et al., 1999 [45] | |
| Green Normalized Difference Vegetation Index | GNDVI | GNDVI is a vegetation index for estimating photo synthetic activity. | Buschmann and Nagel, 1993 [46] | |
| Green-Red Vegetation Index | GRVI | It is a valuable phenological indicator. | Tucker, 1979 [47] | |
| Land Surface Water Index | LSWI | It helps monitor vegetation growth by being sensitive to the total amount of liquid water and soil moisture. | Xiao et al., 2004 [48] | |
| Modified Soil Adjusted Vegetation Index | MSAVI2 | A vegetation index increases the dynamic range of the vegetation signal while minimizing the effects of bare soil. | Qi et al., 1994 [49] | |
| Moisture Stress Index | MSI | MSI is a reflectance measurement that is sensitive to increases in leaf water content. | Hunt Jr and Rock, 1989 [50] | |
| Normalized Difference Vegetation Index | NDVI | It is a widely used vegetation index for quantifying vegetation greenness and is useful for determining the amount and health of vegetation. | Baret et al., 1989 [51] | |
| Redness Index | RI | It is a correction factor for soil color effect on vegetation indices. | Bannari et al., 1995 [52] | |
| Soil Adjusted Total Vegetation Index | SATVI | It is a modification of several vegetation indices (NDVI, SAVI) that correlates the amount of green and senescent vegetation present on the ground. | Marsett et al., 2006 [53] | |
| Soil Adjusted Vegetation Index | SAVI | It is used for correct NDVI to minimize the influence of soil brightness. | Huete, 1988 [54] | |
| Transformed Vegetation Index | TVI | It is a modified NDVI index to avoid negative values. | Rouse et al., 1974 [55] | |
| Vegetation | V | It is a commonly used simple vegetation index based on the ratio of two spectral bands. | Jordan, 1969 [56] |
| Index | Abbreviation | Data Description | Reference |
|---|---|---|---|
| Aspect | Slope orientation | Zevenbergen and Thorne, 1987 [58] | |
| Catchment Area | Carea | Top–down processing of cells for calculation of flow accumulation and related parameters | Freeman, 1991 [59] |
| Modified Catchment Area | Carea_mod | Catchment area based on slope angle and neighboring specific catchment areas | Boehner et al., 2002 [60] |
| Curvature | Curvature of the surface defines the change in slope | Zevenbergen and Thorne, 1987 [58] | |
| Diurnal Anisotropic Heating | DAH | Continuous measurement of exposure-dependent energy | Boehner and Antonic, 2009 [61] |
| LS factor | LS | Combined effects of slope length and slope gradient | Moore et al., 1993 [62] |
| Mass Balance Index | MBI | Balance between soil mass deposited and eroded | Moeller et al., 2008 [63] |
| Multiresolution Index of the Ridge Top Flatness | MRRTF | Indicator of ridge tops based on elevation with respect to the surrounding areas | Gallant and Dowling, 2003 [64] |
| Multiresolution Index of Valley Bottom Flatness | MRVBF | Indicator of valley bottoms based on flat, low-lying areas | Gallant and Dowling, 2003 [64] |
| Topographic Wetness Index | TWI | Indicator of spatial distribution and extent of zones of water saturation | Beven and Kirkby, 1979 [65] |
| Slope | Steepness of the slopes | Zevenbergen and Thorne, 1987 [58] |
| Training Area | Ranger | svmLinear3 | xgbLinear | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| V1 | 0.849 | 6.815 | 3.183 | 0.326 | 17.179 | 10.123 | 0.860 | 7.014 | 3.114 |
| V2 | 0.551 | 7.750 | 3.747 | 0.092 | 26.118 | 10.257 | 0.567 | 8.316 | 3.495 |
| V3 | 0.875 | 12.146 | 5.916 | 0.189 | 42.225 | 24.173 | 0.844 | 13.651 | 6.613 |
| Predicted for V1 | ||||||
| Ranger | svmLinear3 | xgbLinear | ||||
| Training Area | R2 | RMSE | R2 | RMSE | R2 | RMSE |
| V2 | 0.019 | 27.888 | 0.026 | 33.542 | 0.005 | 62.234 |
| V3 | 0.259 | 67.473 | 0.238 | 55.005 | 0.345 | 82.161 |
| Predicted for V2. | ||||||
| Ranger | svmLinear3 | xgbLinear | ||||
| Training area | R2 | RMSE | R2 | RMSE | R2 | RMSE |
| V1 | 0.105 | 27.299 | 0.025 | 20.456 | 0.055 | 24.846 |
| V3 | 0.068 | 27.535 | 0.101 | 60.555 | 0.019 | 31.537 |
| Predicted for V3. | ||||||
| Ranger | svmLinear3 | xgbLinear | ||||
| Training area | R2 | RMSE | R2 | RMSE | R2 | RMSE |
| V1 | 0.338 | 30.123 | 0.173 | 37.280 | 0.332 | 29.484 |
| V2 | 0.327 | 31.788 | 0.060 | 35.838 | 0.131 | 48.650 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takáts, T.; Pásztor, L.; Árvai, M.; Albert, G.; Mészáros, J. Testing the Applicability and Transferability of Data-Driven Geospatial Models for Predicting Soil Erosion in Vineyards. Land 2025, 14, 163. https://doi.org/10.3390/land14010163
Takáts T, Pásztor L, Árvai M, Albert G, Mészáros J. Testing the Applicability and Transferability of Data-Driven Geospatial Models for Predicting Soil Erosion in Vineyards. Land. 2025; 14(1):163. https://doi.org/10.3390/land14010163
Chicago/Turabian StyleTakáts, Tünde, László Pásztor, Mátyás Árvai, Gáspár Albert, and János Mészáros. 2025. "Testing the Applicability and Transferability of Data-Driven Geospatial Models for Predicting Soil Erosion in Vineyards" Land 14, no. 1: 163. https://doi.org/10.3390/land14010163
APA StyleTakáts, T., Pásztor, L., Árvai, M., Albert, G., & Mészáros, J. (2025). Testing the Applicability and Transferability of Data-Driven Geospatial Models for Predicting Soil Erosion in Vineyards. Land, 14(1), 163. https://doi.org/10.3390/land14010163







