2. Literature Review
The issue of growth lies at the core of economic research. Classical economics considered labor and capital as the primary sources of growth, with corresponding measures mainly involving single-factor productivity, i.e., the output obtained per unit of input, such as labor productivity and capital productivity. Although such measures are straightforward and clear, they only reflect isolated and local production efficiency. For a more comprehensive measurement of social production efficiency, a comprehensive indicator needs to be constructed to measure the output efficiency of all factor inputs, i.e., the total factor productivity (TFP). Solow, R. M. (1957) [
2] proposed a Hicks-neutral and constant-return-to-scale Cobb–Douglas production function in his representative paper, characterizing the total output as the result of the combined effect of capital, labor input, and the “Solow Residual” and established a growth-accounting equation that can separate the contribution of technological progress to economic growth. The “Solow Residual” can be understood as a generalized TFP.
The advantage of the Solow Residual method is its clarity and simplicity, which have led to its widespread adoption [
3,
4,
5,
6]. However, its underlying assumption of “no production inefficiency” is too stringent. To remedy this, Aigner, D. J. and Chu, S. F. (1968) [
7] proposed the frontier analysis, which decomposes the source of TFP growth into the upward movement of the technological frontier, i.e., technical progress, and the closeness of the actual production face to the technological frontier, i.e., improvements in technical efficiency. The concept of technical efficiency can be traced back to Koopmans, T. C. (1951) [
8]. Koopmans proposed that an input–output vector is considered technically efficient if it is technically impossible to increase any output without increasing other inputs. Building on Koopmans’ research, different scholars have defined the connotation of technical efficiency. Farell, P. (1957) [
9] believed that “technical efficiency refers to the ratio of the minimum cost required to produce a certain quantity of products to the actual cost, given a certain factor input ratio, with unchanged output scale and market prices”. Uri, N. D. (2003) [
10] suggested that “technical efficiency refers to the proportion of actual input saved relative to the optimal production frontier at the same output level”. Wu, Y. and Zhang, L. (2004) [
11] posited that “technical efficiency refers to the extent to which a producer’s production activities approach the production frontier under the existing technology level”. By integrating these scholars’ views, it is not difficult to see that although there are differences in expression, the core idea of technical efficiency is the ratio of the actual economic output to the maximum possible output.
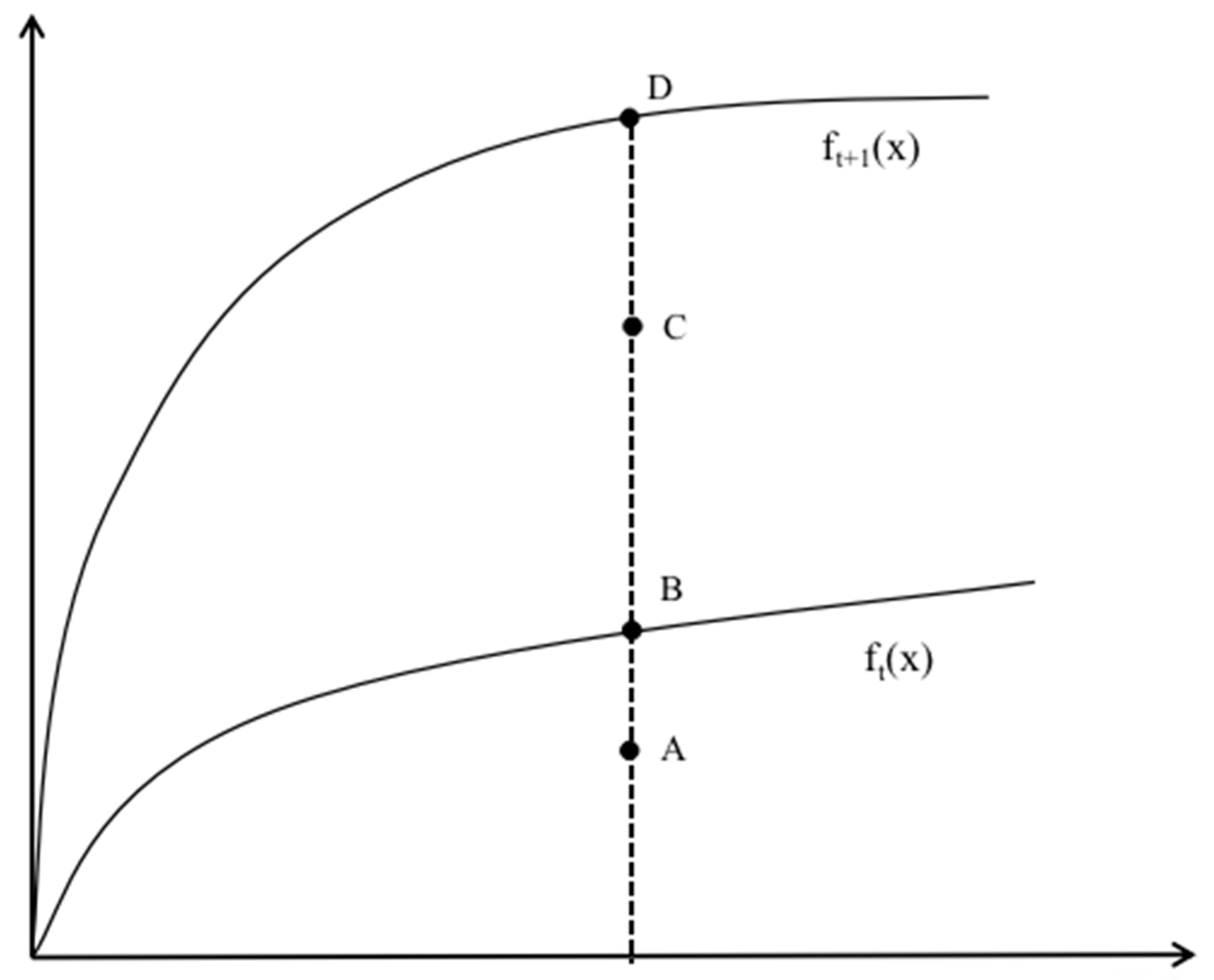
As shown in
Figure 1,
and
represent the production frontier at times
t + 1 and
t, i.e., the maximum possible output. Due to the influence of various controllable or uncontrollable factors, production on the production frontier is often an overly ideal situation (points D or B). Most of the time, activities occur off the production frontier (for example, points A and C). Therefore, given the level of technology, closeness to the production frontier implies an improvement in technical efficiency (movement from point A to B or from point C to D). Empirical research has found that most developing countries produce at positions off the production frontier, far from achieving possible technical efficiency [
12].
Given this, Aigner, D. et al. (1977) [
13] and Meeusen, W. and Van Den Broeck, J. (1977) [
14] pioneered the path of using the frontier production function method for the calculation of growth. A frontier analysis, depending on the setting of the frontier surface, can be divided into deterministic frontier and stochastic frontier methods. The deterministic frontier analysis implies that each production unit shares a fixed production frontier surface, and all factors influencing the output are included as reflections of technical inefficiency. Its advantage lies in simple calculations, but the main disadvantage is the absence of random factors, and it is thus unable to further separate inefficiency values from the error term.
A stochastic frontier analysis (SFA), on the other hand, assumes a random setting for the frontier production function. Each production unit does not need to share a frontier surface, allowing the inefficient term in the error term to be distinguished from the random error term, thus providing a more accurate calculation of the level of technical efficiency [
15]. Several studies have used the SFA method for the calculation of China’s economic growth [
16,
17,
18,
19,
20]. These studies focused on the decomposition of the sources of China’s economic growth efficiency and the measurement of efficiency losses and not specifically on the role of the financial sector.
In a research study performed from the financial perspective, Nourzad, F. (2002) [
21] argued that financial development could promote economic growth by reducing technical inefficiency. He, F. et al. (2003) [
22], based on the Cobb–Douglas production function setting, concluded that financial development had promoted the improvement of technical efficiency. Gu, N. (2010) [
23], based on city panel data, analyzed and measured the channels and effects of the productive service industry on industrial spillover effects from a micro-perspective. Sheng, W. (2017) [
1] used provincial panel data to study the relationship between financial development and China’s technical efficiency of production, focusing on the role of the scale and structure of the credit sector on the technical efficiency of production.
Additionally, many scholars have used non-parametric methods for calculating growth, the most typical of which is the Manquist index method, which is based on a data envelopment analysis (DEA). This method began with Sten Malmquist and became widely used after being optimized by Fare, R. et al. (1994) [
24], with representative studies including those by Xiaogang, C. et al. (2005), Guillaumont Jeanneney, S. et al. (2006), Bian, Y. and Yang, F. (2010), Shuai, S. and Fan, Z. (2021), and Chang, K. et al. (2023) [
25,
26,
27,
28,
29]. The DEA method does not require the specification of the production function’s form nor distribution assumption, thus avoiding potential setting errors. However, due to the lack of a production function setting, any deviation from the production boundary is measured as an inefficient component, which makes its decomposition and analytical capabilities inferior to the SFA method. Fu, X. and Wu, L. (2007) [
30] compared the applicability of the DEA and SFA in the calculation of the TFP in China. They found that the DEA’s estimation results are very sensitive to outliers, while the SFA’s results have good robustness and are thus more suitable for China.
Upon conducting a review of the aforementioned literature, the current research reveals several shortcomings.
First, from a research perspective, most of the literature on developmental economics focuses on the decomposition of the sources of economic growth efficiency and the measurement of efficiency loss rather than the role of the financial sector. Financial economics often starts with financial development, lacking a geographical perspective in terms of density. Therefore, this paper attempts to integrate the perspectives of developmental economics on growth and economic geography on space, focusing on the impact of financial density on technological efficiency.
Second, in terms of the research subject, most previous studies were limited to the national or provincial dimensions, with a dearth of quantitative research based on the city level.
Third, in terms of research methodology, most past studies used the setting of an inefficiency function to measure the overall impact of finance on economic development, without the ability to discuss the differential effects of finance in different cities. This paper attempts to address these shortcomings in the existing literature.
3. Theoretical Analysis
Theoretically, equilibrium production in a perfectly competitive market should be on an optimal production curve. However, due to “market defects” under the neoclassical framework, such as market failures, public goods, externalities, asymmetric information, transaction costs, price rigidity, irrational behavior, etc., actual production often deviates from the optimal production curve. The progress of technical efficiency manifests as an approach to the optimal production curve. Therefore, the promotional effect of finance on technical efficiency should theoretically originate from overcoming “market defects”. Referring to the analyses of financial functions by Merton, R. C. and Bodie, Z. (1995) and Allen, F and Gale, D. (2001) [
31,
32], this article argues that the improvement of financial density can correct “market defects” in terms of information failure and transaction costs by exerting its functions of resource allocation and information transmission.
From the perspective of information failure, information economics summarizes the issue of information failure as incomplete information [
33]. In terms of manifestation, incomplete information can be divided into two types: information distortion and information asymmetry. Information distortion refers to the fact that due to human cognitive limitations and the costs of obtaining information, the information grasped by each market participant is incomplete and insufficient. Information asymmetry refers to the disparity in the information possessed by different market participants, with some having more information and some less. The problem caused by information distortion is making the premise of a complete market untenable, thus hindering the achievement of an optimal equilibrium. The main problem with information asymmetry is that it causes adverse selection and moral hazard issues. The information transmission function of finance can effectively alleviate the problem of incomplete information [
34,
35].
From the perspective of transaction costs, transaction costs broadly refer to the costs that need to be expended to achieve a transaction. Common forms include search costs, information costs, bargaining costs, decision-making costs, and supervision costs. Their specific forms will change with the specific transaction. The main mechanism through which financial development reduces transaction costs is by pooling scattered individual transactions and small transactions, leveraging economies of scale and scope to spread transaction inputs such as venue rent, machinery and equipment, and labor costs, thereby significantly reducing the costs of individual transactions [
36].
In addition, the improvement of financial density will directly affect the technical efficiencies of cities through external economies of scale. The idea of external economies of scale originated from Marshall, A. (2009) [
37]. He once pointed out that larger professional labor markets, the sharing of intermediate inputs, and knowledge spillovers are the sources of external economies of scale, as well as the reasons for agglomeration and high density. And Duranton, G and Puga, D. (2004) [
38] further refined it into three micro-mechanisms of “sharing”, “matching”, and “learning”. Subsequent studies have demonstrated that the impact of density is greatest among knowledge-based industries in which the sharing of ideas is central to the production process [
39]. In reality, there is indeed a significant spatial agglomeration phenomenon in the financial industry which is specifically reflected in the widespread existence of financial center cities and financial functional areas. As the financial sector is an important economic component of a city, an increase in financial density means that the degree of agglomeration has increased. On one hand, this will lead to the improvement of the efficiency of the financial sector (through sharing, matching, and learning mechanisms), which will directly affect the improvement of the city’s technical efficiency; on the other hand, it will also indirectly affect the technical efficiency of other sectors due to the improvement of the efficiency of the financial sector and the enhancement of financial function.
In general, an increase in financial density will bring externalities and promote the improvement of the technical efficiency of the local financial sector through sharing, matching, and learning mechanisms. Moreover, it will also enhance financial functions, thus optimizing issues of information failure and transaction costs, and provide support for the actual production curve to approach the production possible curve, promoting the improvement of technical efficiency.
4. Measurement of Financial Density and the Rate of Change in Urban Technical Efficiency
This section focuses on the measurement of urban financial density and changes in technical efficiency.
4.1. Setting beyond the Logarithmic Production Function
Referring to the approach of Aigner, D. et al. (1977) [
13], the basic setting form for the frontier production function in this section is as follows:
Here,
represents the city, and
represents time;
is the actual output level;
is the combination of production factor inputs, and
is its coefficient. The error term consists of two parts: the random error term
and the technical inefficiency term
. The two are independent of each other.
follows a standard normal distribution with a mean of 0 and a variance of
, and
follows a truncated normal distribution with a mean of 0 and a variance of
. By restricting the value of
to be non-negative, the mean of the technical inefficiency can be represented as a linear combination of a set of variables, as follows:
where
is a combination of
M factors causing technical inefficiency. On this basis, Kumbhakar, S.C. (1991) [
40] proposed using a one-stage maximum likelihood estimation method to simultaneously estimate Equations (1) and (2), a method known as the “one-step estimation method”. Battese, G.E. and Coelli, T.J. (1995) [
41] further extended this method to use panel data and defined technical efficiency (TE) as the ratio of the actual output to the potential maximized output. The calculation formula is as follows:
According to the specification, the TE value should range between 0 and 1, with values closer to 1 indicating proximity to the optimal production frontier, while values closer to 0 indicate a deviation from the optimal production frontier. Following the approach of Kumbhakar, S. C. and Wang, H-J. (2005) [
42] in the specification of the production function, we transform the production function in Equation (1) into a transcendental logarithmic (trans-log) function form. The trans-log function was introduced by Christensen, L.R. et al. (1973) [
43] as a flexible production function that relaxes the assumption of constant substitution elasticities among multiple inputs in the traditional C-D function. It allows for the study of output elasticities, substitution elasticities, interaction effects, and technological differences within the production function. The effectiveness of using this function was demonstrated in previous research [
44]. The linearized form of the transcendental logarithmic production function can be expressed as follows:
In the above, represents the city, and represents time, denotes the actual output level, and represents the coefficient of production factors, in which represents labor, represents capital, and represents the time trend variable. Considering the non-monotonic transformation of technology, the function also introduces quadratic terms. Additionally, considering the non-neutral aspect of technological progress, interaction terms between the time trend and input factors are included.
4.2. Setting the Technological Inefficiency Function
Referring to the existing literature [
1,
6], we select financial density, infrastructure, government expenditure, scientific research patents, and business environment as explanatory variables for the inefficiency function. Therefore, the estimation equation for technological inefficiency is as follows:
4.3. Data Source and Statistical Description
Firstly, we introduce the sources and processing methods of the output, labor, and fixed capital stock data used for the estimation of the production function. In terms of output, many researchers use the GDP to measure output levels [
16,
45]. This article continues with this approach, using the actual gross domestic product of each city at constant prices from 2005 as the measure of output level. For the calculation of labor, considering the impact of education level on the quality of labor, we refer to Han, F. and Yang, L. (2020) [
46] and measure the effective labor quantity obtained by multiplying the average years of education by the actual number of employed personnel.
For data regarding the fixed capital stock, this article refers to the processing method of Zhang, Z. (2019) [
45] and uses the following formula:
in which
represents the fixed capital stock of a city
in the
-th year,
is the depreciation rate, and
represents the actual newly added fixed asset investment of the city
in the
-th year. During the calculation, due to the lack of base period capital stock data, we need to estimate a base period stock. Referring to Liu, C. et al. (2017) and Yu, Y. et al. (2019) and [
47,
48], taking 1991 as the base year, the base year capital stock is determined as
, in which
is the base year investment amount,
is the annual average growth rate of a real investment during the sample period, and
δ is the depreciation rate (which is 9.6%, referring to [
49]).
In the inefficiency equation, the variables include financial density, infrastructure, government expenditure, research patents, and business environment. Financial density is represented in this study by the average scale of financial activity per square kilometer (in billions of CNY/km2). The choice of this measure is due to the inclusion of the “density” concept, making it more appropriate for reflecting the supply of financial services. Financial activities can be divided into direct and indirect finance.
In terms of direct finance, this study, referencing existing research [
50], categorizes it into equity financing and debt financing. Equity financing includes IPOs, rights issues, additional issues, and preferred shares. For debt financing, this study primarily measures the scale of funds entering the real economy, hence selecting eight types of debts: corporate bonds, company bonds, medium-term notes, short-term financing bonds, targeted tools, asset-backed securities, convertible bonds, and exchangeable bonds. The data come from the Wind database.
Indirect finance is measured using the end-of-year balances of various loans of financial institutions in the urban district, with data sourced from the China Urban Statistical Yearbook. After obtaining data for the scales of the direct and indirect financial activities for the year, the sum of these two gives the scale of the city’s financial activity for that year. Dividing this by the area of the district gives the financial density (FD) variable.
Variables such as government expenditure, infrastructure, and research patents are calculated, respectively, as the logarithm of the current year’s fiscal expenditure as a percentage of the GDP, the logarithm of the actual road area at year end, and the logarithm of the number of new patents in the city each year. The data are sourced, respectively, from the China Economic Database (CEIC), the
Urban Statistical Yearbook of China, referring to versions published in various years, and the China Research Data Services Platform. The city business environment variable
1 is derived by collating data from the annual
China Provincial Marketization Index Report to obtain provincial-level data, which are then assigned to cities under the province’s jurisdiction and extended to the entire research period using the trend extrapolation method. Finally, this forms a panel data set covering 272 cities at the prefecture level and above, spanning from the year 2005 to 2018. A description of the data is provided in
Table 1.
4.4. Estimation Results
Before estimating the model parameters, it is necessary to test the validity of the specified frontier production function model. To do this, we need to construct the test statistic , where and represent the log-likelihood function values under the null hypothesis and the alternative hypothesis, respectively. The alternative hypothesis corresponds to the original model. If holds, the test statistic follows an asymptotic distribution with degrees of freedom equal to the number of constrained variables. The first test is to examine the presence of inefficiency. The null hypothesis, in this case, is that there is no inefficiency, which means the model can be reduced to ordinary least squares (OLSs), implying that the coefficients of all variables in the inefficiency function, as well as , are zero, i.e., =…=. The second test aims to determine if the Cobb–Douglas production function is superior to the transcendental logarithmic production function. The null hypothesis here is that all quadratic term coefficients in the production function are zero, while the first-order terms of capital, labor, and the technological progress term are retained. The third test investigates the existence of technological progress. The null hypothesis in this case is there is no technological progress but there exists interaction, meaning that all parameter coefficients associated with T are zero. The fourth test examines whether technological progress is Hick-neutral. The null hypothesis states that . The fifth test assesses if technological efficiency is a fixed effect. If technological efficiency is a fixed effect, a non-time-varying model should be selected; otherwise, a time-varying model is appropriate.
The test results, as shown in
Table 2, indicate that at a significance level of 1%, we should reject the five null hypotheses mentioned above. This suggests that the specified transcendental logarithmic production model and the maximum likelihood estimation method employed in this study are reasonable, and the model does not exhibit any degeneracy. Subsequently, utilizing the compiled data from 272 cities at or above the prefecture level for the years 2005–2018, the transcendental logarithmic production function and production inefficiency function were estimated using the Frontier 4.1 software through maximum likelihood estimation. The estimation results are presented in
Table 3.
From the estimation results in
Table 3, the γ of the model is 0.892, and it is significant at the 1% level. This indicates that the model effectively captures the factors that cause production inefficiency. Approximately 89.2% of the inefficiency can be explained by the model variables, while the impact of random error terms is minimal. Secondly, based on the results of the inefficiency production function, the regression coefficient of the financial density is negative, suggesting that an increase in the local financial density helps alleviate technical inefficiency and positively contributes to improving technical efficiency. On the other hand, government expenditure has a significant negative effect, indicating that government intervention often exhibits inefficiency, which is consistent with the conclusions of Wang, Z. et al. (2006) [
16] and Li, Q. et al. (2013) [
51]. Furthermore, it is observed that scientific patents, business environment, and infrastructure play significant roles in improving the state of production inefficiency, which aligns with empirical expectations.
6. Measurement of the Contribution of Financial Agglomeration to Urban Production Technical Efficiency
To grasp the relationship between urban productivity and financial density more precisely, this paper continues to calculate the impact of financial density on the technical efficiencies of different cities. Coelli, T. et al. (1999) [
53] and Henry, M. et al. (2009) [
54] have, respectively, proposed methods to measure the contributions of influencing factors to technical efficiency in the context of a stochastic frontier model, based on the “forward-looking” and “backward-looking” principles. Firstly, based on Battese, G.E., Coelli, T.J. (1995) [
41], and Coelli, T. et al. (1999) [
53], technical efficiency (TE) can be calculated through the following formula:
In Equation (6), represents the cumulative distribution function of standard, normal-distribution variables; in Equation (7), is a combination of factors that affect technical inefficiency. According to the “forward-looking” method, to judge the contribution rate of a certain influencing factor , it can be assumed that the situation of this influencing factor is completely the same for all individuals and is at the optimal level, that is, when in Equation (7) takes the minimum value , the calculated technical efficiency () is the potential technical efficiency under optimal conditions. The higher the ratio of the potential technical efficiency to the actual technical efficiency (-1) after conversion, the greater the contribution of this factor to the technical efficiency. The drawback of this method is that because the assumption of the optimal level of this influencing factor is based on the optimal situation of the existing observed individuals, it may underestimate the potential optimal level, resulting in an underestimation of the contribution rate.
The basic logic of the “backward-looking” calculation method can be described as judging the contribution rate of a certain influencing factor by excluding the effects of all other influencing factors; the obtained technical efficiency () and the actual technical efficiency are compared, and the difference () after conversion is the contribution rate of the influencing factor . For example, assuming that n = 1, i.e., when the promotion effect of other factors on technical efficiency is maximized, i.e., when in Equation (7) takes max(), the contribution of the influencing factor is the smallest; on the contrary, when the promotion effect of the other factors on the technical efficiency is the smallest, i.e., when it takes min(), the contribution of is the largest. The average of the minimum and maximum contributions is the average contribution rate of . The drawback of this method is that the combination of influencing factors in Equation (7) may not cover all the determinant variables of technical efficiency, which may result in overestimating the contribution rate.
In response to this, Wang, M. and Wong, M.S. (2012) [
55] comprehensively used the “forward-looking” and “backward-looking” methods to analyze the evolutionary trend of international R&D activities and their contribution to a country’s technical efficiency. The results show that the contribution rates calculated by the “forward-looking” and “backward-looking” methods have some differences, but the differences are systematic, and their results have consistency in time and regional dimensions and the fitting effect with the actual situation is good; overall, the robustness is strong. Therefore, this paper also comprehensively uses the “forward-looking” and “backward-looking” methods to calculate the contribution of financial agglomeration to the technical efficiency of Chinese cities.
6.1. Results and Comparison Based on “Forward-Looking” and “Backward-Looking” Calculations
The “forward-looking” and “backward-looking” methods have been used to measure the impact of financial density on technical efficiency, and the results are summarized in
Figure 6.
Firstly, overall, financial density has a positive promoting effect on improving technical efficiency. The calculation results based on the “forward-looking” method show that the contribution rate of financial density is relatively small, and the fluctuation is gentle. The highest value is 28.15% for 2006, and the lowest value is 19.79% for 2018, mainly showing a slow downward trend during the sample period. The results calculated based on the “backward-looking” method are systematically higher than those of the “forward-looking” method, but its upper limit, lower limit, and average maintain a synchronized change trend. For example, the average contribution rate reached its highest at 154.18% in 2009 and its lowest at 129.65% in 2011, showing a fluctuating downward trend during the sample period.
In addition, based on their calculation logic, the results of the “forward-looking” and “backward-looking” methods may be affected by extreme values; under the “forward-looking” method, because it is assumed that the financial density (FD) is completely the same for all entities and is at the optimal level, the result is affected by the extreme values of the financial density (FD); similarly, the “backward-looking” method is affected by the extreme values of other factors. Therefore, to test the robustness of the results, this paper conducted a robustness test after a basic calculation. The specific approach for the “forward-looking” method is to take the smallest 10, 20, 30, 40, and 50 values and take the average, replacing extreme values with the average; for the “backward-looking” method, the approach is to take the maximum and minimum of 10, 20, 30, 40, 50 values of other influencing factors and take the average, replacing extreme values with the average.
Table 6 compares the calculated results with the original results after updating the statistics.
As can be seen from
Table 6, within the research range of this study, the results calculated by the “backward-looking” method show better robustness (the average is relatively stable), while the results calculated by the “forward-looking” method are greatly influenced by extreme values. Therefore, the analysis in this article will mainly be based on the results calculated using the “backward-looking” method.
6.2. Results Based on the “Backward-Looking” Method
Overall, the contribution of financial density to technical efficiency had already shown a declining trend before the 2008 financial crisis (
Figure 7). After 2008, due to the 4 trillion stimulus plan, the financial density in 2009 increased dramatically, which also led to a surge in its contribution to technical efficiency. However, excessive financial density caused distortion in the factor structure, so the contribution of financial density to technical efficiency rapidly declined after 2010 and gradually recovered after 2013. But by 2018, it only returned to its approximate level before the crisis.
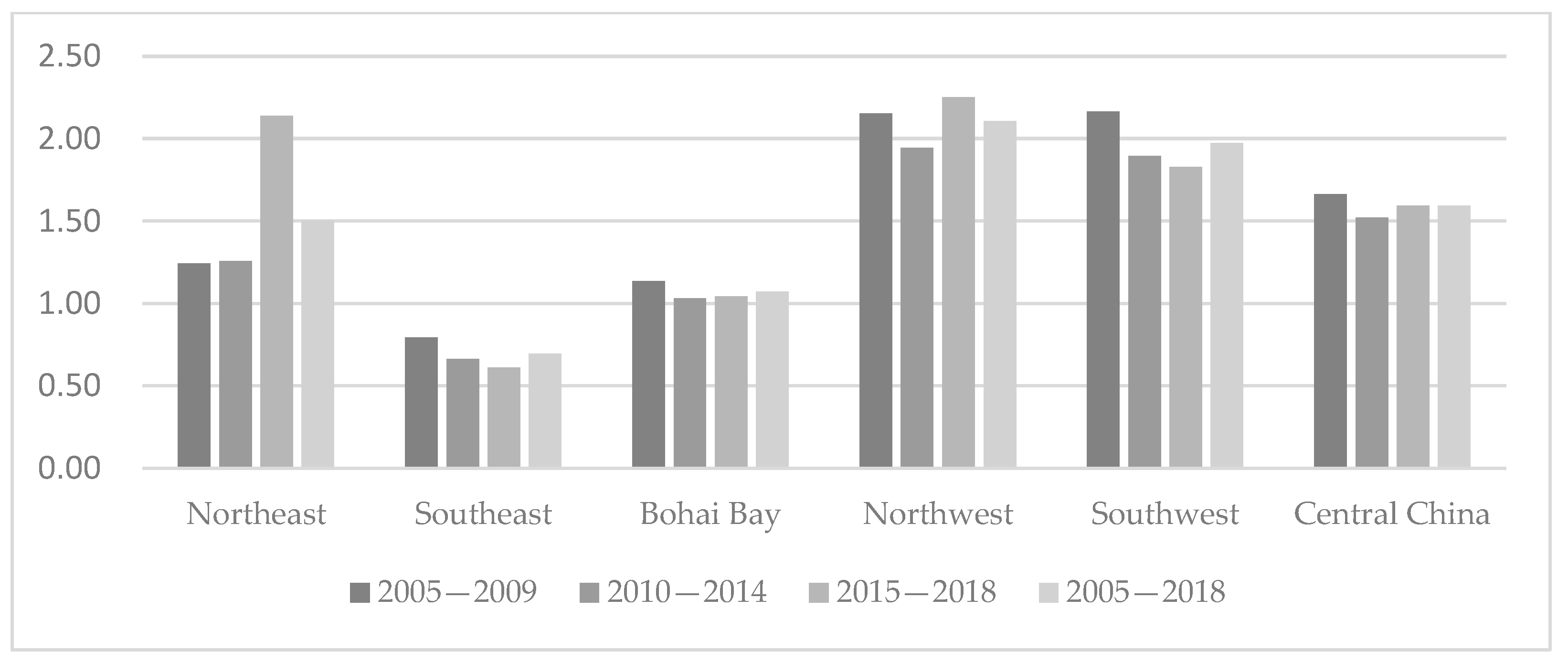
6.3. Regional Dimension
From the regional perspective, the efficiency contribution of financial density in each region generally follows the rule that it is higher in less-developed areas and lower in developed areas, which is consistent with the results of Sheng, W. (2017) [
1], which were calculated based on provincial data (
Figure 8). Looking at the average annual contribution rate during the research period, it is higher in the northwest and southwest regions, followed by the central and northeast regions, with the Bohai Bay and Southeast regions being the lowest. In terms of changes, after experiencing shocks, most regions show a trend of declining and then rebounding with respect to the contribution rate of financial density; the decline in the northeast in the second stage is not obvious, which may mainly stem from the fact that the impact of the financial crisis and the four trillion stimuli mainly affected foreign trade, industry, real estate, local finance, and employment but had a smaller impact on fixed asset investment and consumer loans [
56].
6.4. Provincial Dimension
As can be seen from
Table 7, during the research period, the annual average contribution rate of financial density to urban production technical efficiency is lower in developed provinces such as Zhejiang, Tianjin, Jiangsu, and Beijing and higher in developing provinces like Gansu, Ningxia, Chongqing, Sichuan, Guangxi, and Guizhou. Over time, the positive role of financial density generally decreases, but the positive role is expanding in certain developing regions (Gansu, Heilongjiang, Hebei, Shanxi, Liaoning, etc.).
6.5. City Dimension
Summarizing the annual average contribution rate of financial density to technical efficiency by period and selecting the 10 cities with the highest and lowest contribution rates in each period, as can be seen from
Table 8, it can be seen that cities in which the role of financial density in technical efficiency is relatively low can be divided into two categories. The first category is represented by resource-based cities such as Ordos, Dongying, Baotou, Daqing, and Panjin. Through research on resource-based cities in China, Sun, W. and Dong, G. (2010) [
57] found that due to the slow progress of technology, the technical efficiency of resource-based cities in China is generally low and shows a downward trend. Combined with the findings of this article, the financial density in resource-based cities not only fails to contribute to the improvement of technical efficiency but may also distort resource allocation through distorted price signals, thereby affecting technical efficiency. The other category is represented by advanced cities such as Shenzhen, Zhuhai, Suzhou, Wuxi, Foshan, and Changzhou; a possible explanation for this categorization is that the financial resources and activities in these cities are relatively abundant, so the contribution rate is not particularly prominent. In contrast, the cities in which the role of financial density in technical efficiency is relatively high are represented by Longnan, Bazhong, Dingxi, Fuyang, Bozhou, Pingliang, Tianshui, Guyuan, and others, and the common feature of these cities is that they are at a medium level of development and are often characterized by abundant human resources, convenient transportation, and a certain industrial foundation. In these cities, financial activity is relatively scarce. Therefore, the increase in financial density can generate greater value in coordination with other resources, which manifests as a greater role for financial density in promoting the improvement of technical efficiency.
8. Conclusions and Implications
The enhancement of financial density can exert resource allocation and information transmission functions, optimize information asymmetry and transaction cost issues, and thus provide support to help the actual production curve approach the maximum possibility curve, promoting the improvement of technical efficiency. The research in this article finds that the technical efficiency of Chinese cities shows a fluctuating trend from 2005 to 2018, with two troughs appearing in 2009 and 2016, respectively. Cities with higher levels of technical efficiency are distributed on two horizontal and two vertical axes and often appear in clusters, exhibiting obvious aggregation characteristics. The Southeast region and the Bohai Bay area lead the country in technical efficiency, and the leading advantage of the Southeast region is constantly expanding. On the city level, first-tier and strong second-tier cities always rank at the forefront of national technical efficiency; in terms of changes, the cities with rapidly improved technical efficiency are mostly regional centers, cities within city clusters, or those that have undergone important changes in recent years, while cities with declining levels of technical efficiency are mostly resource-based cities facing challenging transformations.
As for the role of financial density, in general, before the 2008 financial crisis, the contribution of financial density to technical efficiency had already shown a downward trend. After 2008, due to the distortion of factor structure caused by the 4 trillion stimulus plan, a surge in 2009 and a rapid drop after 2010 occurred, gradually recovering only after 2013. From the regional and provincial perspectives, the efficiency contribution of financial density in various regions generally conforms to a pattern of being higher in backward areas and lower in developed areas. In the city dimension, the contribution of financial density to resource-based cities with slow technological progress or advanced cities with abundant financial density is not very prominent and may even have a negative effect. However, for cities at a medium level of development with abundant human resources, convenient transportation, and a certain industrial base, it can significantly promote the improvement of technical efficiency. Therefore, it may be possible to optimize the marginal contribution of urban financial density to the technical efficiency of Chinese cities by encouraging the flow of financial resources and activities from cities with small marginal effects to those with large marginal effects.