Abstract
This study describes a new methodology for estimating gully widths based on their digitized borders. The procedure adapts a previous method developed to determine the mean displacement between two 3D linestrings, considering them continuously, which represents an advance over conventional approaches. In addition to the calculation of the average horizontal distance, it also considers the calculation of widths by sections of a given length in order to analyze differences in their behavior compared to the results for the entire gully. The method is also adapted to multi-temporal studies to analyze the evolution of the gully by comparing width values from several dates. Application was carried out with a large number of linestrings representing gullies of a wide area of olive groves, which were digitized from orthoimages with 0.5 m resolution of two dates. The results demonstrate the feasibility of the proposed method for characterizing gullies and analyzing their evolution between several dates both completely and by sections, allowing the detection of critical areas of gully development. Therefore, these results can be used as input data to improve gully erosion susceptibility maps and to define zones for preventive or corrective actions.
1. Introduction
Soil erosion by gullying is considered one of the main soil degradation processes worldwide [1], affecting key ecosystem services in cropland such as water cycles [2] and CO2 regulation [3]. This process is very active in semiarid climates with rainfall variability, and many studies have reported on it in the Mediterranean basin (Morocco, Spain, Tunisia, Portugal), where it might affect over the 10% of the surface [4], and the Loess Plateau in China, one of the most intensively eroded regions worldwide due to the characteristic lithology and the changes in land use [5]. Nevertheless, several other areas with wet tropical climates and huge, concentrated rainfall, such as northeast Australia [6], Brazil [7], and Southern Nigeria [8], are also concerned by gullying. Gully networks are systems with heterogeneous spatial and temporal growth mechanisms. A gully increases its length downstream, through incision, and upstream, through gully headcut retreat, both being processes conditioned mainly by flow hydrodynamics: velocity, turbulence, and flow shear stress [9]. However, a third mechanism, channel widening, involves complex interaction between hydrodynamic and gravitational processes (i.e., gully wall collapse), and it is probably the most disturbing and difficult to address from the point of view of gully restoration [10]. That is why an accurate determination of gully morphology is essential to understanding gully erosion dynamics and, most importantly, implementing effective control measures [1].
Width is considered one of the main morphological characteristics for modelling gully erosion processes, in addition to length, depth, volume, etc. [9]. The measurements for obtaining top or bottom width values in gullies have undergone a great evolution thanks to the development of geomatic techniques. From the use of simple measurements, such as those based on a simple measuring tape, to the current implementation of remote sensing, based on aerial or satellite images [11,12], LiDAR, and photogrammetry [13], the use of geomatic techniques in modelling gully evolution has shown a great improvement during recent years. In addition to the application of modern instrumentation and new techniques, we must also highlight the development of platforms such as remotely piloted aircraft systems, RPASs [14,15], which ease the elevation of sensors, and the improvement of hardware and those algorithms included in applications, which allow the use of these techniques even by non-professional users specialized in surveying [16,17]. As examples, more detailed descriptions of these techniques applied to this purpose are shown by several authors [15,18]. Obviously, the application of geomatic techniques must be adapted to the availability of instruments, methodologies, and requirements of the study. Therefore, we have to note the importance of accuracy related to the scale of the study as an important aspect to be considered when selecting the geomatic technique to be applied. Thus, some examples of using GNSS, total stations, or profilometers to obtain accurate measures have been described in the literature [19,20].
In recent years, several authors have described some examples of width determination [18,19,20,21,22,23]. Thus, Castillo et al. [18] compared the results obtained by applying several geomatic techniques (LiDAR, photo-reconstruction, laser profilometer, total station, and pole) using cross-section profiles. Giménez et al. [19] used photogrammetry and a profilometer to obtain cross-sections of several gullies. Danácová et al. [20] used Global Navigation Satellite Systems to obtain cross-section profiles. Fiorucci et al. [21] determined top widths from satellite stereo images by directly measuring some segments that are transversal to the channel that configures each segment of the gully. Momm et al. [22] described several laboratory experiments that replicated field conditions using a tilting hydraulic flume and two cameras to capture images. To determine widths, they used several cross-sections spaced two centimeters apart applied to polygons extracted from images. The experiment considers a determined time interval to analyze the evolution of the synthetic gully. Caraballo-Arias et al. [23] also used cross-sections measured using a total station to study a gully and several tributaries. Hayas et al. [10] selected 10 measures of distance between the borders obtained by digitizing from aerial orthophotos. These distances were obtained perpendicular to the flow direction over a short distance along gully segments to obtain an averaged gully width. However, width measures from discrete profiles are subjected to relative errors as high as 30% when the distances between cross-sections are greater than 5 m [18], intervals that are difficult to reduce in field studies under a reasonable cost/benefit ratio.
The olive grove is one of most important woody crops, with the Province of Jaén (Southern Spain) being the main producer of olive oil in the world [24]. With more than 6600 km2, olive groves there occupy 49% of the total surface [25], so soil degradation processes affecting olive groves have a significant role in the environmental, social and economic sustainability of the zone. Although the next statement is based on specific studies, it is possible that erosion by gullies is one of the main, if not the main, degradation processes of the Jaén olive groves [13].
As described above, the determination of widths is mainly based on measures obtained from discrete profiles (cross-sections) distributed with a determined separation along the gully. In this study, we describe a new approach for determining widths continuously from the linestrings that represent borders of gullies developed in olive groves. In addition, we also propose a procedure for sectioning gullies by length (with a specific distance) in order to analyze their local behavior and better understand the temporal evolution of gullies in olive groves, in order to plan better mitigating and/or restorative measures in response to this important degradation process.
2. Methodology
In this study, we propose a new methodology for determining widths between gully borders in order to model erosion processes between several dates. This methodology considers all gully borders continuously in order to obtain a mean value of width for each date, but it can also be applied to specific sections, defined by the user, to analyze local behaviors. Thus, the purpose is related to the achievement of two main objectives: firstly, the analysis of the evolution of the average width of a complete gully system; and secondly, the determination of the evolution of the widths related to sections defined by the user following a specific criterion. In our approach, we propose the implementation of a new metric that allows us to obtain mean width values directly, considering complete gully borders or whatever section is extracted from them. This supposes an improvement compared to those methodologies applied until this moment based on profiles (cross-sections), which provide width values at specific points or mean values based on several profiles with a certain separation. Therefore, widths will be not estimated by approximation of discrete values such as those from cross-section profiles; in contrast, we consider information on the complete geometry of gully borders.
The overall methodology is shown in Figure 1, and some specific aspects of width calculation and sectioning are shown in Figure 2 and Figure 3.
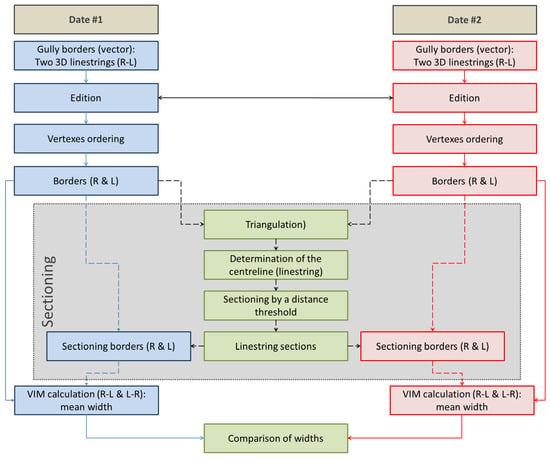
Figure 1.
Workflow of the proposed methodology adapting the Vertex influence method, VIM [26].
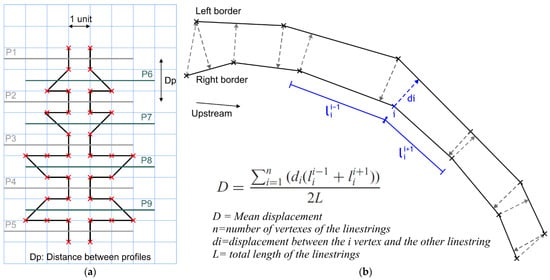
Figure 2.
Determination of the average width: (a) Example of issues using crossing profiles (P1–P9) method on two synthetic linestrings; (b) example of adaptation of the VIM [26].
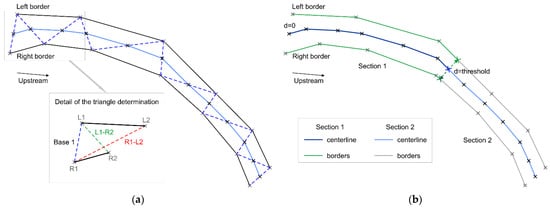
Figure 3.
Sectioning procedure: (a) triangulation and determination of the centerline; (b) sectioning of borders based on a distance threshold applied to the centerline.
The methodology is divided into two parts related to both purposes: the determination of the average width of gully borders completely or by sections, and the procedure for obtaining these sections. The workflow (Figure 1) starts with the obtaining of two datasets (from two different dates) containing gully borders in vector format (e.g., shapefile). Each gully border is defined by two linestrings, which are related to its right and left limits by considering the progress direction of the gully. In this study, we assume that linestrings that define gully borders are obtained using accurate geomatic techniques, such as GNSS surveys, photogrammetry, and remote sensing. The linestrings are composed of 3D vertexes with a specific order and a density adequate to represent gully borders, considering the scale of the study to be carried out. Obviously, the two linestrings cannot intersect and may have been digitized independently.
Therefore, there are some tasks to be performed prior to the calculation of width in order to guarantee data consistency but also to facilitate the application of algorithms for displacement calculation. Therefore, we suggest the implementation of an edition stage in order to obtain two linestrings ready to be compared. This involves several aspects concerning the linestrings of each border, such as the encoding of linestrings (e.g., an attribute can be used to ease the encoding of each linestring using shapefile format), the correspondence of linestrings (one linestring of the right border must correspond to one linestring of the left border), and the coherence of the starting points of both linestrings (considering that both points are spatially related) and, consequently, of the ending points. Obviously, the order of the vertexes of each linestring must be the same. Therefore, we have included an independent stage in this ordering to guarantee data consistency for subsequent tasks in the case of multi-temporal studies. In this context, all vertexes must be ordered with the same criteria. We suggest following an ascending order upstream from the mouth to the source of the gully. This criterion is selected considering the usual behavior of gully erosion, where the initiation point is more indeterminate than in the case of the mouth. In multi-temporal studies, the correspondence of mouth positions of both dates is very important if we consider them as starting points to compare the geometric behavior of the linestrings. The results of this edition and vertex ordering are the linestrings of each gully border (R and L), prepared for the next stages: on the one hand, the general gully width calculation, and, on the other hand, the width calculation by sections, after sectioning process of the whole gullies.
2.1. General Width
The calculation of the average width of a complete gully or by sections is based on the adaptation of a metric that determines the mean displacement between linestrings. In this case, we have adapted the “vertex influence method” (VIM) [26], which was originally developed to assess the positional uncertainty between linestrings. The selection of a metric based on mean displacements allows us to avoid approximations such as those implemented using profiles (Figure 2a), where a mean value of width will be obtained from discrete values of displacement (between both borders) implemented at a certain distance (Dp in Figure 2a). In the example shown in Figure 2a, the average width between 2 linestrings obtained using 5 profiles (P1 to P5) is 1 unit. However, these profiles are not sensitive to the behavior of both linestrings, because if we calculate the mean displacement, the result is 1.8 units (area divided by the length of the centerline, following the measure described by Mc Master [27] and Skidmore and Turner [28]). This case shows an underestimation of about 80% of the width value when profiles P1 to P5 are used. On the other hand, if we use profiles P6 to P9 (Figure 2a), the average width is 3 units, overestimating the true value by about 166%. Only the inclusion of all profiles (P1–P9 in Figure 2a) in the calculation allows us to obtain a correct value of average width. This synthetic example shows that the use of profiles is quite sensitive to their number and location, and therefore, it supposes an approximation to the average width. As a consequence, the use of a metric that considers the complete borders (linestrings) continuously will suppose an important improvement compared to those methods applied until this moment. In this context, a metric based on the determination of the area enclosed by both linestrings could be a solution. Considering this measure, this area is divided by the length of the linestring (linestring to be controlled in the case described by Skidmore and Turner [28]) to provide a mean value of displacement between them.
However, in this case, considering the behavior of the gully borders, which length value should be used? There are several options, such as the length obtained from the right or from the left border, the average value of both data, or a value obtained from an average axis calculated from both borders (centerline). It is not clear which is the most suitable option, as both borders may show large differences in length due to the different effects of the erosion processes on them. In this context, there is an alternative metric for obtaining a mean displacement between linestrings by avoiding the use of the length of the linestring in the calculation. In our approach, we suggest the use of the VIM method [26] adapted to the 3D context by Mozas-Calvache and Ariza-López [29], as it is shown in Figure 2b. It consists of the calculation of the displacement from each vertex of one linestring to the other linestring (di in Figure 2b) and weighting this value by the length of the segments adjacent to the vertex implicated (i in Figure 2b). The mean displacement is calculated by weighting all values of displacement from all vertexes of one linestring to the other and vice versa (D in Figure 2b), so the total length (L) is the length of the two linestrings. The adaptation of this method to the case of gully borders is easy if we consider some important aspects: the necessity of a density of vertexes that guarantees the complete representation of the gully at the scale demanded in the study, the correspondence between the end points of both linestrings, and the independent representation of the gully with respect to others at the selected level of scale (avoiding the inclusion of multiple gullies). Once this metric has been calculated using the linestrings that represent borders at each date, the mean displacement (width) obtained can be compared to study the erosion processes that occurred between both dates. The use of the VIM method includes another advantage related to the calculation of displacements in 3D. Therefore, our approach can be applied both in 2D and 3D applications. The final stage includes the analysis and comparison of results from several dates.
2.2. Sectioning
In these types of studies, it is sometimes necessary to analyze the behavior of the gully by sections in order to contrast differential effects of the erosion processes by zones, especially in gully systems of greater length [11]. Furthermore, an effective design of structural control measures, such as check dams, requires a careful analysis of the gully width sections along the whole profile in order to select the optimal placement [30]. Obviously, these sections can be defined by operators when digitizing both borders of the gully or dividing them manually, but in this study, we suggest an automatic procedure to divide the gully into several sections considering a selected length. Taking into account the geometrical behavior of gullies, which are usually represented by irregular borders, we suggest determining these sections using a cumulative distance calculated on a previously obtained centerline between both borders (Figure 3). Therefore, this centerline is used as a reference line to implement those sections. In multi-temporal studies, this reference line should be determined using those linestrings of the last date, considering that gully erosion will be increased from an earlier date (Figure 1). Once this sectioning has been implemented on the centerline (Figure 3a), we apply each section to the borders, considering the closest point of the linestring to the end points of the centerline determined after sectioning (Figure 3b).
The determination of the centerline can be carried out using several procedures, such as transverse segments and triangulation. In this case, we suggest the use of a basic triangulation between both linestrings. This triangulation is based on the selection of the point located at the shortest distance from a previously defined reference base to the next two possible points (one from each border). The triangulation starts with the selection of the reference base of the first triangle using the two homologous end points of the two borders (Base 1 in Figure 3a). After that, the first triangle is completed using one vertex selected from the two possibilities (next vertex of each border: R2 or L2 in Figure 3a). The selection of this vertex is based on the shortest distance from the point of the base included in the other border (L1–R2 in Figure 3a). Once the triangle is defined, the new base will be this last side of the triangle obtained (L1–R2 in Figure 3a). After that, the process continues until all vertexes of both borders are included in the triangulation. As a requirement, we must consider that the triangle must be inside both borders. Therefore, all internal segments must not intersect any border. Once the triangulation has been completed, the centerline is obtained by selecting the midpoints of the sequence of internal segments (Figure 3a).
After the determination of the centerline, this linestring is sectioned using a threshold of accumulated distance (Figure 3b) defined by the user carrying out the study. This sectioning is also applied to the linestrings of the borders of the gully, considering the closest point of the borders with respect to the end points of the centerlines. The process continues with the calculation of the mean displacement between both linestrings of the borders, considering each section in the same way that is applied to the complete gully.
3. Application
In order to apply the proposed methodology, a set of active permanent bottom-valley gullies in olive groves developed in the Municipality of Torredelcampo (Province of Jaén, Southeast Spain) was carefully digitized from data pertaining to two dates using QGIS software. More specifically, we used a set of linestrings defining both borders of several gullies, which were digitized using as reference a set of official orthoimages (PNOA, published by the Instituto Geográfico Nacional of Spain) with a resolution of 0.5 m, with the help of DTMs and 2,5 D views. This procedure was repeated twice, for two dates, using orthoimages from 2009 and 2011 (Figure 4). These dates were selected taking into account that 2009 to 2011 was a period of high activity in the gullies of the region, due to the intense rainfalls that occurred there [13,31].
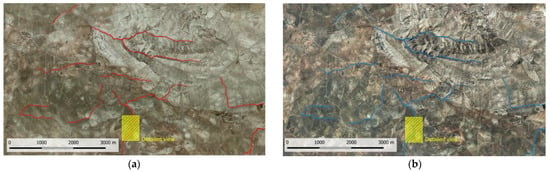
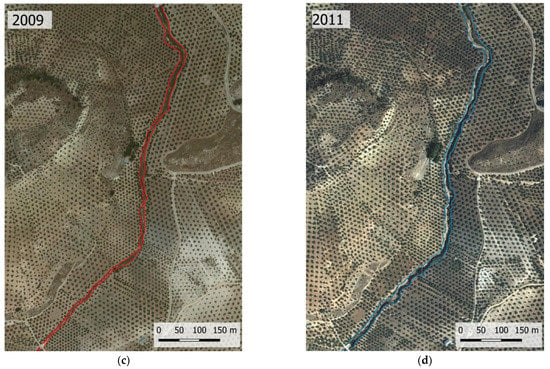
Figure 4.
Gully borders digitized at both dates: (a) gullies from 2009; (b) gullies from 2011; (c) detailed view of a gully from 2009; (d) detailed view of a gully from 2011.
Before the application to the whole area, we tested the methodology in a section of about 700 m of the analyzed gully system (Figure 4c,d), in which DSMs and edited DTMs of the two considered dates (2009 and 2011) were elaborated with a 2.5 m resolution in order to estimate the gully incision and the volumes of erosion and deposition involved [13]. From the edited DTM, cross-section profiles of the thalweg separated by 5 m were obtained in QGIS, and then the gully widths were estimated manually (Figure 5), in a manner similar to previous works [18,19,20]. The average and maximum widths for different distances between profiles were calculated and compared to the values obtained with the methodology developed in this study.
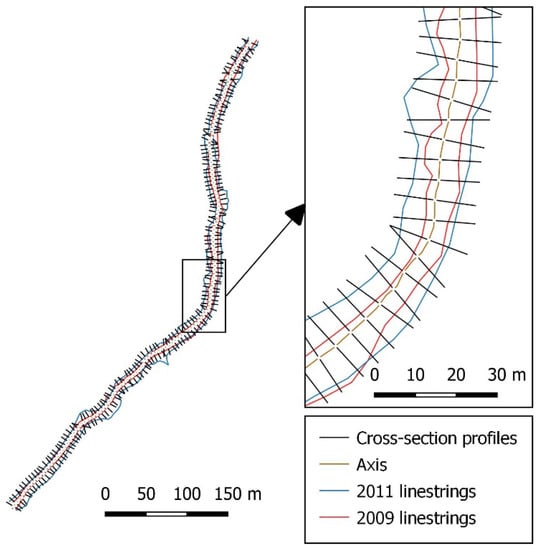
Figure 5.
Cross-section profiles separated by 5 m.
However, the aim was to contrast the proposed methodology by considering a large set of linestrings. Therefore, the dataset was composed of 30 gullies with a total length of about 24.3 and 24.5 km (2009 and 2011 respectively) (Figure 4), which implies a linear density of 0.68 km/km2, a remarkable density for permanent gullies. These data were obtained after the edition stage (Figure 1), and they are summarized in Table 1. The determination of the distance between both borders of each gully, which was based on the adaptation of the VIM method [26], was implemented using a specific application developed in Java for this purpose in this study. In addition, following the proposed methodology, a sectioning process considering a threshold of 50 m in length was applied to each gully in order to analyze their behavior locally. This threshold has been selected for this study according the orthoimage resolution (0.5 m) and the reference scale (1:5000–10,000), which produces a sectioning of 0.5–1 cm in the map, and the average length of the gullies (800 m) yields a significant average number of 16 sections per gully. Anyway, this threshold would vary in other studies according to the scale and the gully lengths. After sectioning, we obtained 505 sections of gullies related to each date. This procedure was also implemented in the previously indicated application. Finally, we obtained the results of the width values at each date for the complete gully or by sections, which were then compared and analyzed. The processing time consumed by the application to calculate the gully widths in an area such as the example used in this work (30 gullies/500 sections) was a few seconds.

Table 1.
Main characteristics of both datasets.
4. Results and Discussion
Before the presentation and discussion of the results of the widths of the whole gully system and by sections, we are showing the results in the test section of 700 m, comparing the widths obtained for different distances between cross-section profiles of the thalweg (Figure 5), which has been the method commonly used for determining gully widths [18,19,20,21,22,23], to those obtained with our methodology (Figure 4c,d). These widths for cross-section profiles separated by 5 m are 7.52 m in 2009 and 13.24 m in 2011, while with our methodology, they are 7.19 m and 13.17 m, respectively, which produces relative differences of 4.55% and 0.56%, respectively (a little overestimation with the profiles methodology). Therefore, both results allow the validation of the new methodology by means of a different approach, which is the manual estimation of the width in cross-section profiles obtained from DTMs. The widths are practically identical in 2011 but not so much in 2009, probably due to the greater development of the gully in 2011 that allows a better interpretation of profiles and the width measurement in cross-section methodology, as well as the delineation of linestrings from the orthoimage in our methodology. Moreover, the longer the distance between thalweg profiles, the larger the difference between the widths obtained with respect to those estimated with our own methodology, as shown in Figure 6. Thus, the average differences for profiles separated by 50 m are higher than 0.4 m in absolute value (5.7% in relative terms for 2009), but the maximum differences reach values near 0.9 m (12.3%). Furthermore, for profiles separated by 100 m, the average differences are 0.5–0.6 m (8.1% for 2009), while the maximum differences are around 1.5 m (19.8% for 2009).
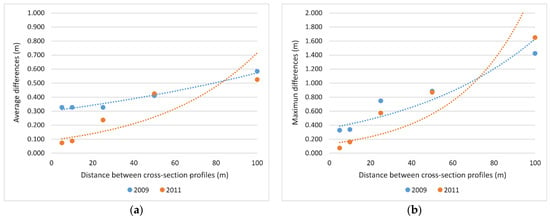
Figure 6.
Differences between the widths obtained from the cross-section profiles depending on the distance and those calculated with our methodology: (a) Average values; (b) Maximum values.
For the whole study area, the results obtained considering each gully completely show a mean value of width of about 5.83 m for the 2009 dataset and 7.84 m for the 2011 dataset. This supposes an increase in width of about 34% between the two dates and indicates a very significant growth with a widening rate of 1.01 m yr-1, which is in accordance with the high activity found in the gully systems of this area when comparing digital elevation models obtained with photogrammetric techniques [13]. Moreover, it is two or three times higher than those values reported by Hayas et al. [10] in an olive grove in the neighboring Cordoba Province, probably related to the high susceptibility of the Cretaceous–Paleogene clays of our study area compared to the calcareous sandstones of the latter.
Indeed, these widening rates seem to be surprisingly high. However, the weather conditions in this period were also exceptional. Thus, Fernandez et al. [13] carried out a detailed analysis of rainfall events during 2009–2010 and 2010–2011 in the study area, revealing the close relationship between the periods of maximum erosion rate and maximum accumulated daily, weekly, and monthly precipitations. They found the highest peak for monthly rainfall in December 2010 for the period 1980–2017. Moreover, the study of [32] revealed that the mean annual rainfall in 2010 (1069 mm) doubled the historical mean annual precipitation range for the period 1970–2000 (500–600 mm).
In any case, beyond physical factors such as weather or parent material, such widening ratios of gullies in Southern Spain olive groves are closely related with the conventional management of the crop, characterized by bare soils with low organic matter content, high bulk density, and low saturated hydraulic conductivity [33,34].
In the case of the 2009 dataset, the minimum average width of a gully is 0 (in a specific gully, the width was not significant at the orthoimage resolution) and the maximum value is 14.95 m. On the other hand, the 2011 dataset shows minimum and maximum values of average width of about 3.11 and 13.81 m, respectively. The possibility of evaluating by remote sensing and GIS techniques, quickly and automatically, the temporal evolution of gully widths can support gully erosion modelling at large scales, given the feasibility of developing robust empirical relationships between top-width and cross-sectional areas [35].
The results obtained by sectioning gullies every 50 m show width values for each section related to each date. Table 2 shows the main results obtained after applying the proposed methodology to the sections generated. More specifically, Table 2 includes the results of the mean, maximum, minimum, and deviation of widths related to sections in 2009 and 2011, and it considers the difference between both width values for each section. Obviously, the mean results are similar to those obtained without sectioning, but maximum, minimum, and deviation values show more information about the behavior of the gullies.

Table 2.
Results obtained for sections.
However, the main purpose of sectioning is the analysis of specific gullies locally. With this in mind, two examples (a and b) are shown in Figure 7 and Figure 8, where width values, widths differences, and ratios between both dates are displayed. In these cases, there are examples of sections that have clearly increased in width between 2009 and 2011 (e.g., Figure 8a) and another few cases where the width of the gully in a specific section has been slightly reduced (e.g., Figure 8b).

Figure 7.
Examples of two gullies (a,b) analyzed in this study.
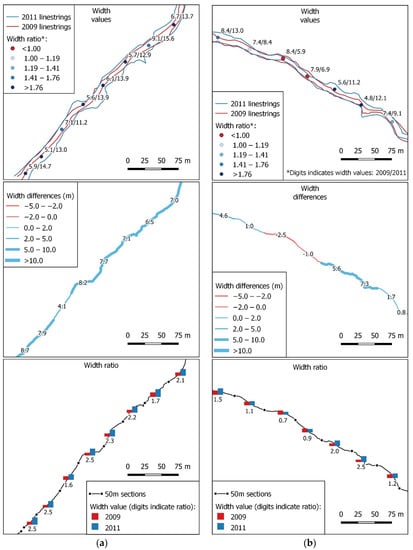
Figure 8.
Examples of the results obtained in two gullies (a,b) after sectioning: width values for each section in 2009 and 2011, width differences between both dates (2011 and 2009), and width ratio between both dates.
The advantage of this method that considers the gully border in a continuous way compared to the conventional ones, based on the estimation of distances or displacements in cross-section profiles [18,19,20,21,22,23] separated a certain distance, has been already explained theoretically in Section 2.1 and Figure 2a and also tested in a section of 700 m, with the results shown previously (Figure 6). Gully widths can be under or overestimated, especially when partial results by sections are considered and the distance between cross-section profiles of the thalweg increases, which is reasonable in large areas such as this one. Thus, the developed approach, which is additionally scalable, provides a much more accurate and reliable width estimation.
Regarding the overall accuracy, it depends on the method to obtain the gully borders. When images are used, as in this case, the accuracy is conditioned by the image based on which the operator digitizes the gully borders and on the digitizing process itself. Thus, the orthoimages corresponding to the flights of 2009 and 2011 of the Spanish National Plan of Orthophotography (PNOA) have a resolution of 0.5 m and a horizontal accuracy (XY) of 1 m, which coincides with that calculated in a study near to the study area from the original PNOA photographs [13]. If images of higher resolution were employed, such as those obtained from RPAS, the horizontal accuracy could be on the order of centimeters [15]. The digitizing error is more related in this case with photointerpretation than with tracking the lines with the cursor when digitizing.
Meanwhile, this methodology focuses on the determination of the gully width that is usually analyzed horizontally, although this approach allows us to analyze 3D displacements between gully borders. Moreover, the procedure is easily adaptable to contrast the behavior of the gully depth from a digitized 3D linestring representing the thalweg with the 3D centerline obtained from both borders (obtained in this study). Therefore, the displacement along the Z-axis obtained using VIM method [26] between these two linestrings would show the average depth of a complete gully or a gully section. Nevertheless, the approaches for a true 3D analysis, with involved volume estimations (erosion and deposition materials, etc.), should be based on digital elevation models [13,15], voxel modelling, and so on.
In any case, the simple method for gully width estimation developed in this work, especially when partial results are obtained for sections in a continuous way, is very interesting from the point of view of gully management, because the automatic procedure can reveal the critical zones of gully development (i.e., slope thresholds, soft soils, etc.) where rehabilitation actions (i.e., check dams, slope stabilization, revegetation, etc.) should be a priority [30,36]. In this sense, a rather interesting case is that of the gully showed in Figure 7a, whose temporal evolution has previously been characterized at the volumetric level by means of LiDAR by Fernández et al. [13]. The presence of a paved ford crossing a country road (bottom left of the image in Figure 7a) has caused a maximum widening ratio of 2.5 (from 5.9 m to 14.7 m, 4.35 m yr-1, as Figure 8a shows) related to the acceleration of the flow caused by the pavement, an effect described numerous times in gullies associated with roadways [37,38,39]. Implementation of mitigation measures, such as energy dissipators [40], seems to be urgent to address this kind of anthropogenic factors in gully development. Another critical point is the confluence of two gullies in the eastern part of Figure 7b that present a width ratio of 2.5 (from 4.8 to 12.1 m), as Figure 8b reveals; in this case, probably, this critical point is related to the increase in flow rate due to the addition of catchment areas of both gullies.
In summary, sectioning and the overall method have allowed us to determine different behaviors in each gully sector. The method can be applied to wide areas in an automatic way once the gully borders are obtained, which cannot be addressed with conventional methods such as cross-section profiles.
5. Conclusions
- In this study, a new methodology based on the automatic estimation of gully widths has been proposed, with the development of the corresponding application. The methodology could be of great interest in agricultural and geomorphological research for several reasons:
- First, it allows the determination of gully widths considering both borders in a continuous way, avoiding problems derived from discrete values (e.g., cross-section profiles), especially when applying automatic procedures. This algorithm yields more accurate results than conventional methods based on cross-section profiles obtained from DEMs, mainly when the distances between profiles increase, saving on time and resources.
- Second, because the resolution of the analysis depends on the starting dataset (satellite images, aerial photographs or those acquired from RPAS), this methodology can be easily adapted to the study scale of interest (the methodology is scalable), which in the case of gullies varies from the plot to the basin.
- Third, the analysis can be carried out in 2D or 3D, if the lines of gully borders are available in 3D (for example, by acquiring the Z coordinate of the vertexes of the linestrings from a DTM), so it is easily adaptable for checking depth changes in gullies that include a linestring depicting the thalweg.
- Fourth, as in the case studied, multi-temporal and evolution analysis can be addressed if gully borders of different dates are available.
This methodology has been applied to a real scenario in olive groves from the south of Spain, an environment severely affected by erosion processes. Obtained results reveal changes in gully widths, both positive (growth of the gullies, mainly due to gravitational processes) and negative (decrease in the gullies for other reasons, such as human actions), along a complex system of about 25 km length. The increase in width of the gully system studied exceeded values found in areas with similar processes. Moreover, it has permitted the detection of critical points of gully development, which can be analyzed in order to develop preventive or corrective actions or to use them as input data to improve gully erosion susceptibility maps (GESM). This tool can definitely help in the fight against degradation in the olive grove agroecosystem.
Author Contributions
Conceptualization, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; methodology, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; software, A.T.M.-C.; validation, A.T.M.-C.; formal analysis, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; investigation, A.T.M.-C., J.A.C.G., T.G.D., and T.M.F.d.C.; resources, J.A.C.G. and T.G.D.; data curation, A.T.M.-C. and T.G.D.; writing—original draft preparation, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; writing—review and editing, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; visualization, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; supervision, A.T.M.-C., J.A.C.G., and T.M.F.d.C.; project administration, J.A.C.G. and T.M.F.d.C.; funding acquisition, J.A.C.G. and T.M.F.d.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been financed with the funds of the research project SUSTAINOLIVE (PRIMA projects of the UE, grant nº 1811); the Convene “Risks associated to the Road Network of the Jaén Province” of the Deputy of Jaén and the University of Jaén; and the project “Monitoring of gully erosion in the province of Jaén using geomatic techniques” of the “Instituto de Estudios Giennenses”.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge the help of the Center for Advanced Studies on Earth Sciences, Energies and Environment of the University of Jaén and the groups TEP213 and RNM127 of PAIDI.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Castillo, C.; Gomez, J.A. A century of gully erosion research: Urgency, complexity and study approaches. Earth Sci. Rev. 2016, 160, 300–319. [Google Scholar] [CrossRef]
- Romero-Díaz, A.; Díaz-Pereira, E.; De Vente, J. Ecosystem services provision by gully control: A review. Cuad. Investig. Geogr. 2019, 45, 333–366. [Google Scholar] [CrossRef]
- Lal, R. Accelerated soil erosion as a source of atmospheric CO2. Soil Till. Res. 2019, 188, 35–40. [Google Scholar] [CrossRef]
- Martins, B.; Nunes, A.; Meira-Castro, A.; Lourenço, L.; Hermenegildo, C. Local Factors Controlling Gully Development in a Mediterranean Environment. Land 2022, 11, 204. [Google Scholar] [CrossRef]
- Wen, X.; Deng, X. Current soil erosion assessment in the Loess Plateau of China: A mini-review. J. Clean. Prod. 2020, 276, 123091. [Google Scholar] [CrossRef]
- Shellberg, J.C.; Brooks, A.P.; Rose, C.W. Sediment production and yield from alluvial gully in Northern Queensland, Australia. Earth Surf. Process. Landf. 2013, 38, 1765–1778. [Google Scholar] [CrossRef]
- Guerra, A.J.T.; Bezerra, J.F.R.; Fullen, M.A.; Mendoca, J.K.S.; Jorge, M.C.O. The effects of biological geotextile on gully stabilization in Sao Luis, Brazil. Nat. Hazards 2015, 75, 2625–2636. [Google Scholar] [CrossRef]
- Imwanga, F.M.; Vandecasteele, I.; Trefois, P.; Ozer, P.; Moeyersons, J. The origin and control of mega-gullies in Kinshasa (DR Congo). Catena 2015, 125, 38–49. [Google Scholar] [CrossRef]
- Poesen, J.; Natchtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Hayas, A.; Peña, A.; Vanwalleghem, T. Predicting gully width and widening rates from upstream contribution area and rainfall: A case study in SW Spain. Geomorphology 2019, 341, 130–139. [Google Scholar] [CrossRef]
- Frankl, A.; Poesen, J.; Mitiku Haile, M.; Deckers, J.; Nyssen, J. Quantifying long-term changes in gully networks and volumes in dryland. Geomorphology 2013, 201, 254–263. [Google Scholar] [CrossRef]
- Xu, Q.; Kou, P.; Wang, C. Evaluation of gully head retreat and fill rates based on high-resolution satellite images in the loess region of China. Environ. Earth Sci. 2019, 78, 465–480. [Google Scholar] [CrossRef]
- Fernández, T.; Pérez-García, J.L.; Gómez-López, J.M.; Cardenal, J.; Calero, J.; Sánchez-Gómez, M.; Delgado, J.; Tovar-Pescador, J. Multitemporal analysis of gully erosion in olive groves by means of digital elevation models obtained with aerial photogrammetric and LiDAR data. ISPRS Int. J. Geo-Inf. 2020, 9, 260. [Google Scholar] [CrossRef]
- Koci, J.; Jarihani, B.; Leon, J.X.; Sidle, R.C.; Wilkinson, S.N.; Bartley, R. Assessment of UAV and Ground-Based SfM with Multi-View Stereo Photogrammetry in a Gullied Savanna Catchment. ISPRS Int. J. Geo-Inf. 2017, 6, 328. [Google Scholar] [CrossRef]
- Fernández, T.; Gómez-López, J.M.; Pérez-García, J.L.; Cardenal, J.; Delgado, J.; Mata, E.; Sánchez-Gómez, M.; Calero, J.; Tovar-Pescador, J.; Moya, F. Analysis of gully erosion in a catchment area in olive groves using UAS photogrammetry techniques. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, 43, 1057–1064. [Google Scholar] [CrossRef]
- López-Vicente, M.; Álvarez, S. Influence of DEM resolution on modeling hydrological connectivity in a complex agricultural catchment with woody crops. Earth Surf. Process. Landf. 2018, 43, 1403–1415. [Google Scholar] [CrossRef]
- Yang, S.; Guan, Y.; Zhao, C.; Zhang, C.; Bai, J.; Chen, K. Determining the influence of catchment area on intensity of gully erosion using high-resolution aerial imagery: A 40-year case study from the Loess Plateau, northern China. Geoderma 2019, 347, 90–102. [Google Scholar] [CrossRef]
- Castillo, C.; Pérez, R.; James, M.; Quinton, J.; Taguas, E.V.; Gómez, J.A. Comparing the accuracy of several field methods for measuring gully erosion. Soil Sci. Soc. Am. J. 2012, 76, 1319–1332. [Google Scholar] [CrossRef]
- Giménez, R.; Marzolff, I.; Campo, M.A.; Seeger, M.; Ries, J.B.; Casalí, J.; Alvarez-Mozos, J. Accuracy of high-resolution photogrammetric measurements of gullies with contrasting morphology. Earth Surf. Process. Landf. 2009, 34, 1915–1926. [Google Scholar] [CrossRef]
- Danácová, M.; Aleksic, M.; Tomascik, M.; Liová, A.; Vyleta, R. Detection of gully erosion using Global Navigation Satellite Systems in Myjava—Turá Lúka. VTEI 2022, 64, 10–15. [Google Scholar] [CrossRef]
- Fiorucci, F.; Ardizzone, F.; Rossi, M.; Torri, D. The use of stereoscopic satellite images to map rills and ephemeral gullies. Remote Sens. 2015, 7, 14151–14178. [Google Scholar] [CrossRef]
- Momm, H.G.; Wells, R.R.; Bingner, R.L. GIS technology for spatiotemporal measurements of gully channel width evolution. Nat. Hazards 2015, 79, 97–112. [Google Scholar] [CrossRef]
- Caraballo-Arias, N.A.; Conoscenti, C.; Di Stefano, C.; Ferro, V.; Gómez-Gutiérrez, A. Morphometric and hydraulic geometry assessment of a gully in SW Spain. Geomorphology 2016, 274, 143–151. [Google Scholar] [CrossRef]
- International Olive Oil Council, IOC, 2019. Áreas de Actividad—Economía. Available online: http://www.internationaloliveoil.org/estaticos/view/131-world-olive-oil-figures%3Flang=es_ES (accessed on 25 September 2019).
- MAGRAMA. Encuesta Sobre Superficies y Rendimientos de Los Cultivos; Ministerio de Agricultura, Alimentación y Medio Ambiente: Madrid, Spain, 2015.
- Mozas, A.T.; Ariza, F.J. New method for positional quality control in cartography based on lines. A comparative study of methodologies. Int. J. Geogr. Inf. Sci. 2011, 25, 1681–1695. [Google Scholar] [CrossRef]
- McMaster, R.B. A statistical analysis of mathematical measures for linear simplification. Am. Cartogr. 1986, 13, 103–116. [Google Scholar] [CrossRef]
- Skidmore, A.; Turner, B. Map accuracy assessment using line intersect sampling. Photogramm. Eng. Remote Sens. 1992, 58, 1453–1457. [Google Scholar]
- Mozas-Calvache, A.T.; Ariza-López, F.J. Adapting 2D positional control methodologies based on linear elements to 3D. Surv. Rev. 2015, 47, 195–201. [Google Scholar] [CrossRef]
- Castillo, V.M.; Mosch, W.M.; Conesa-García, C.; Barberá, G.G.; Navarro-Cano, J.A.; López-Bermúdez, F. Effectiveness and Geomorphological impacts of check dams for soil erosion control in a semiarid Mediterranean catchment: El Cárcavo (Murcia, Spain). Catena 2007, 70, 416–427. [Google Scholar] [CrossRef]
- Hayas, A.; Vanwalleghen, T.; Laguna, A.; Peña, A.; Giráldez, J.V. Reconstruction long-term gully dynamics in Mediterranean agricultural areas. Hydrol. Earth Syst. Sci. 2017, 21, 235–249. [Google Scholar] [CrossRef]
- Carpena, R.; Tovar-Pescador, J.; Sánchez-Gómez, M.; Calero, J.; Mellado, I.; Moya, F.; Fernández, T. Rainfall-Induced Landslides and Erosion Processes in the Road Network of the Jaén Province (Southern Spain). Hydrology 2021, 8, 0830100. [Google Scholar] [CrossRef]
- Aranda, V.; Plaza, I.; Calero, J.; Ontiveros-Ortega, A. Long-term effects of olive mill pomace co-compost on wettability and soil quality in olive groves. Geoderma 2016, 267, 185–195. [Google Scholar] [CrossRef]
- Gómez, J.A.; Infante-Amate, J.; González de Molina, M.; Vanwallenghem, T.; Taguas, E.; Lorite, I. Olive Cultivation, its Impact on Soil Erosion and its Progression into Yield Impacts in Southern Spain in the Past a Key to Future of Increasing Climate Uncertainty. Agriculture 2014, 4, 170–198. [Google Scholar] [CrossRef]
- Vanmaercke, M.; Panagos, P.; Vanwalleghem, T.; Hayas, A.; Foersters, S.; Borrelli, P.; Rossi, M.; Torri, D.; Casali, J.; Borselli, L.; et al. Measuring, modelling and managing gully erosion at large scales: A state of the art. Earth Sci. Rev. 2021, 218, 103637. [Google Scholar] [CrossRef]
- Moeyersons, J. The topographic thresholds of hillslope incisions in Southwestern Rwanda. Catena 2003, 50, 381–400. [Google Scholar] [CrossRef]
- Jungerius, P.D.; Matundura, J.; Van de Ancker, J.A.M. Road construction and gully erosion in West Pokot, Kenya. Earth Surf. Process. Landf. 2002, 27, 1237–1247. [Google Scholar] [CrossRef]
- Croke, J.; Mockler, S. Gully initiation and Road-to-Strem linkage in forested catchment, Southeaster Australia. Earth Surf. Process. Landf. 2001, 26, 205–217. [Google Scholar] [CrossRef]
- Katz, H.A.; Daniels, J.M.; Ryans, S. Slope-area thresholds of road-induced gully erosion and consequent hillslope-channel interactions. Earth Surf. Process. Landf. 2014, 39, 285–295. [Google Scholar] [CrossRef]
- Thompson, P.L.; Kilgore, R.T. Hydraulic Design of Energy Dissipators for Culverts and Channels: Hydraulic Engineering Circular Number 14, 3rd ed.; Federal Highway Administration: Washington, DC, USA, 2006.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).