Spatial Prediction of Landslides Using Hybrid Multi-Criteria Decision-Making Methods: A Case Study of the Saqqez-Marivan Mountain Road in Iran
Abstract
1. Introduction
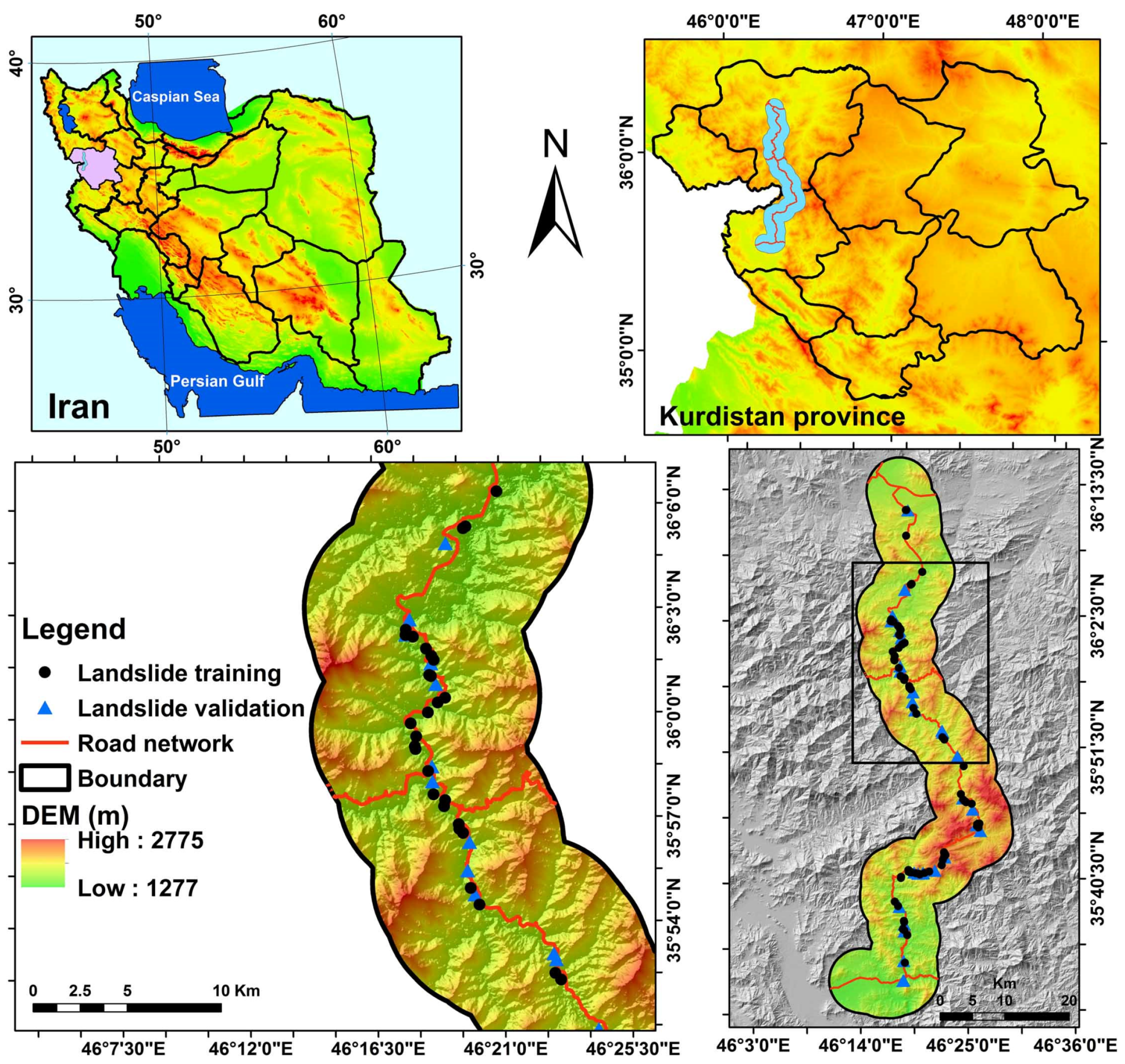
2. Data Acquisition and Preparation
Study Area
3. Materials and Methods
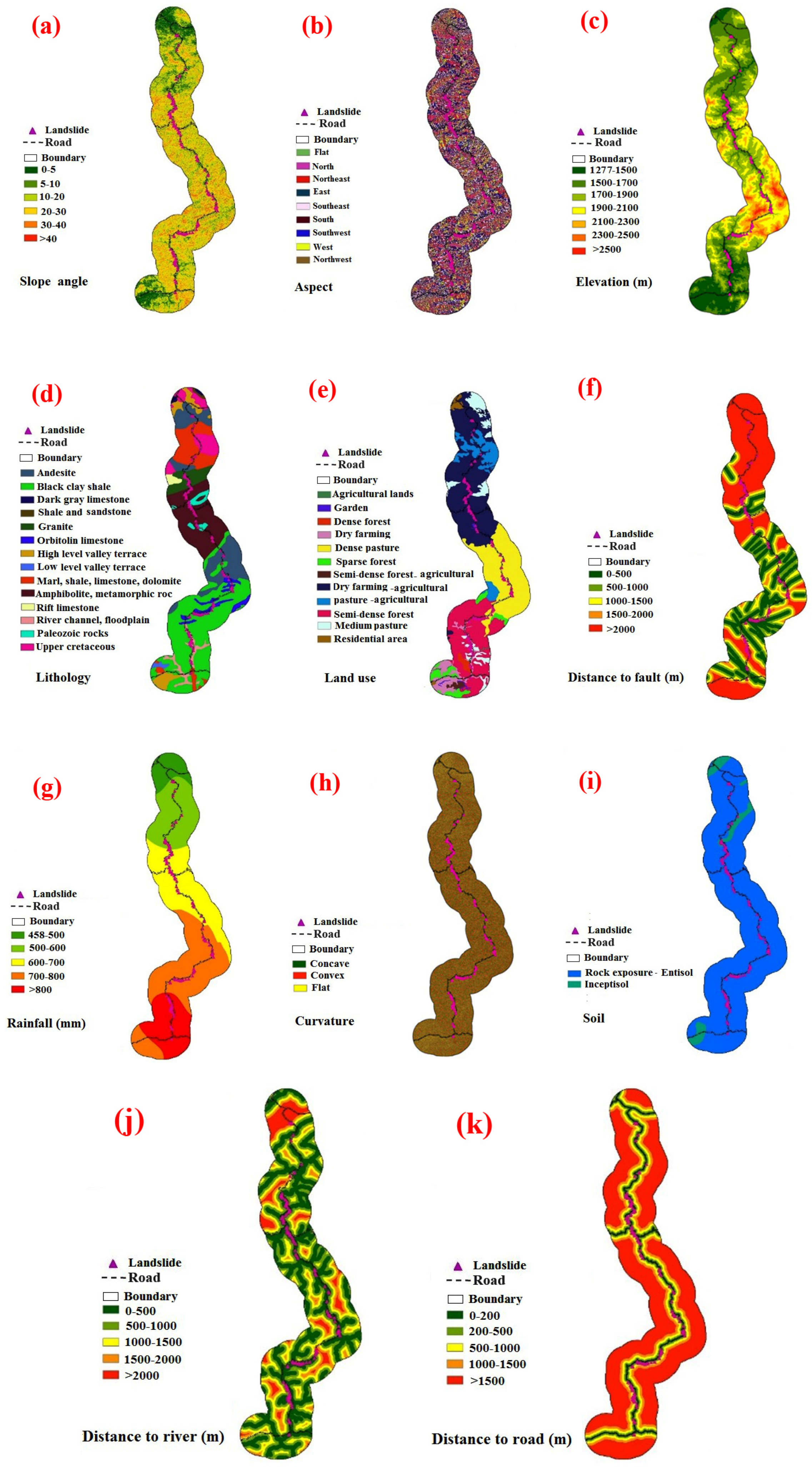
3.1. Landslide Conditioning Factors (LCFs)
3.2. Landslide Inventory Map (LIM)
3.3. Multi-Criteria Decision-Making Methods in LSM
3.3.1. Fuzzy TOPSIS Algorithm
3.3.2. Fuzzy Analytical Network Process Model (Fuzzy ANP)
- Step A: Building ANP Models and Structuring Problems
- Step B: Pairwise comparisons
- Step C: Calculating the Super Matrix

- Step D: Selection
3.4. Validation of the Methods
4. Results and Analysis
4.1. Model Building and Comparison
4.2. Developing Landslide Susceptibility Mapping
5. Discussion
6. Conclusions
- The three most significant factors influencing landslide occurrence were distance to the road, rainfall, and soil type.
- Our methodology concluded that the FLTOPSIS method (AUC = 0.983) outperformed the FLANP (AUC = 0.938) for predicting landslides in the study area. We conclude that FLTOPSIS is better at solving uncertainty and ambiguity in judgement operations than FLANP.
- FLTOPSIS, thus far an infrequently used method in landslide susceptibility assessment, constitutes a promising and innovative technique for creating susceptibility maps in other landslide-prone areas, although further testing is warranted.
- Local government agencies can implement the findings of this research to manage and plan land development in susceptible landslide areas strategically.
- In the future, we recommend combining fuzzy logic with other MCDM methods, such as ELECTRE, VI-KORE, and ELECTRE III, and comparing the results to determine which combination achieves the most reliable landslide susceptibility map.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Mukherjee, M.; Abhinay, K.; Rahman, M.M.; Yangdhen, S.; Sen, S.; Adhikari, B.R.; Nianthi, R.; Sachdev, S.; Shaw, R. Extent and evaluation of critical infrastructure, the status of resilience and its future dimensions in South Asia. Prog. Disaster Sci. 2023, 17, 100275. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Alamgir, M.; Campbell, M.J.; Sloan, S.; Goosem, M.; Clements, G.R.; Mahmoud, M.I.; Laurance, W.F. Economic, socio-political and environmental risks of road development in the tropics. Curr. Biol. 2017, 27, R1130–R1140. [Google Scholar] [CrossRef] [PubMed]
- Kanwar, N.; Kuniyal, J.C. Vulnerability assessment of forest ecosystems focusing on climate change, hazards and anthropogenic pressures in the cold desert of Kinnaur district, northwestern Indian Himalaya. J. Earth Syst. Sci. 2022, 131, 51. [Google Scholar] [CrossRef]
- Gecchele, G.; Ceccato, R.; Gastaldi, M. Road network vulnerability analysis: Case study considering travel demand and accessibility changes. J. Transp. Eng. Part A Syst. 2019, 145, 05019004. [Google Scholar] [CrossRef]
- Lacroix, P.; Handwerger, A.L.; Bièvre, G. Life and death of slow-moving landslides. Nat. Rev. Earth Environ. 2020, 1, 404–419. [Google Scholar] [CrossRef]
- Fang, K.; Tang, H.; Li, C.; Su, X.; An, P.; Sun, S. Centrifuge modelling of landslides and landslide hazard mitigation: A review. Geosci. Front. 2022, 14, 101493. [Google Scholar] [CrossRef]
- Ado, M.; Amitab, K.; Maji, A.K.; Jasińska, E.; Gono, R.; Leonowicz, Z.; Jasiński, M. Landslide susceptibility mapping using machine learning: A literature survey. Remote Sens. 2022, 14, 3029. [Google Scholar] [CrossRef]
- Xu, Y.; George, D.L.; Kim, J.; Lu, Z.; Riley, M.; Griffin, T.; de la Fuente, J. Landslide monitoring and runout hazard assessment by integrating multi-source remote sensing and numerical models: An application to the Gold Basin landslide complex, northern Washington. Landslides 2021, 18, 1131–1141. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, A.; Huang, D.; Huang, Z.; Zhang, B.; Xu, X. Total probabilistic measure for the potential risk of regional roads exposed to landslides. Reliab. Eng. Syst. Saf. 2022, 228, 108822. [Google Scholar] [CrossRef]
- Pantelidis, L. A critical review of highway slope instability risk assessment systems. Bull. Eng. Geol. Environ. 2011, 70, 395–400. [Google Scholar] [CrossRef]
- Pierson, L.A.; Van Vickle, R. Rockfall Hazard Rating System: Participant’s Manual; Federal Highway Administration: Washington, DC, USA, 1993. [Google Scholar]
- Budetta, P. Assessment of rockfall risk along roads. Nat. Hazards Earth Syst. Sci. 2004, 4, 71–81. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J.; Ibarbia, I.; Alonso, N.; Jugo, I.; Ruiz, J.; Luzuriaga, S.; Navarro, J.A. Integrated risk assessment due to slope instabilities in the roadway network of Gipuzkoa, Basque Country. Nat. Hazards Earth Syst. Sci. 2019, 19, 399–419. [Google Scholar] [CrossRef]
- Pregnolato, M.; Ford, A.; Wilkinson, S.M.; Dawson, R.J. The impact of flooding on road transport: A depth-disruption function. Transp. Res. Part D Transp. Environ. 2017, 55, 67–81. [Google Scholar] [CrossRef]
- Chamorro, A.; Echaveguren, T.; Allen, E.; Contreras, M.; Cartes, P.; Contreras, M.; Jimenez, G.; Pattillo, C.; De Solminihac, H.; Vargas, J. Risk Management System for Road Networks Exposed to Natural Hazards. In Lifelines 2022; ASCE American Society of Civil Engineers: Reston, VA, USA, 2022; pp. 166–177. [Google Scholar]
- Mattsson, L.-G.; Jenelius, E. Vulnerability and resilience of transport systems–A discussion of recent research. Transp. Res. Part A Policy Pract. 2015, 81, 16–34. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Gholamnia, K.; Ghamisi, P. The application of ResU-net and OBIA for landslide detection from multi-temporal sentinel-2 images. Big Earth Data 2022. [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef]
- Park, C.-J.; Kim, S.-Y.; Nguyen, M.V. Fuzzy TOPSIS application to rank determinants of employee retention in construction companies: South Korean case. Sustainability 2021, 13, 5787. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Elhag, T.M. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006, 31, 309–319. [Google Scholar] [CrossRef]
- Olson, D.L. Comparison of weights in TOPSIS models. Math. Comput. Model. 2004, 40, 721–727. [Google Scholar] [CrossRef]
- Abo-Sinna, M.A.; Amer, A.H. Extensions of TOPSIS for multi-objective large-scale nonlinear programming problems. Appl. Math. Comput. 2005, 162, 243–256. [Google Scholar] [CrossRef]
- Cheng, S.; Chan, C.W.; Huang, G.H. An integrated multi-criteria decision analysis and inexact mixed integer linear programming approach for solid waste management. Eng. Appl. Artif. Intell. 2003, 16, 543–554. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Pham, Q.B.; Achour, Y.; Ali, S.A.; Parvin, F.; Vojtek, M.; Vojteková, J.; Al-Ansari, N.; Achu, A.; Costache, R.; Khedher, K.M. A comparison among fuzzy multi-criteria decision making, bivariate, multivariate and machine learning models in landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2021, 12, 1741–1777. [Google Scholar] [CrossRef]
- Dano, U.L.; Balogun, A.-L.; Matori, A.-N.; Wan Yusouf, K.; Abubakar, I.R.; Said Mohamed, M.A.; Aina, Y.A.; Pradhan, B. Flood susceptibility mapping using GIS-based analytic network process: A case study of Perlis, Malaysia. Water 2019, 11, 615. [Google Scholar] [CrossRef]
- Abedi Gheshlaghi, H.; Feizizadeh, B.; Blaschke, T. GIS-based forest fire risk mapping using the analytical network process and fuzzy logic. J. Environ. Plan. Manag. 2020, 63, 481–499. [Google Scholar] [CrossRef]
- Zeraatkar, Z.; Siuki, A.K.; Shahidi, A. Delineation of the Areas with Potential Land Subsidence Using the Analytic Network Process (Case Study: Birjand Aquifer, Iran). Geogr. Nat. Resour. 2021, 42, 290–295. [Google Scholar] [CrossRef]
- Alizadeh, M.; Ngah, I.; Hashim, M.; Pradhan, B.; Pour, A.B. A hybrid analytic network process and artificial neural network (ANP-ANN) model for urban earthquake vulnerability assessment. Remote Sens. 2018, 10, 975. [Google Scholar] [CrossRef]
- Swetha, T.; Gopinath, G. Landslides susceptibility assessment by analytical network process: A case study for Kuttiyadi river basin (Western Ghats, Southern India). SN Appl. Sci. 2020, 2, 1776. [Google Scholar] [CrossRef]
- Neaupane, K.M.; Piantanakulchai, M. Analytic network process model for landslide hazard zonation. Eng. Geol. 2006, 85, 281–294. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Kutlug Sahin, E.; Colkesen, I. An assessment of multivariate and bivariate approaches in landslide susceptibility mapping: A case study of Duzkoy district. Nat. Hazards 2015, 76, 471–496. [Google Scholar] [CrossRef]
- El-Rashidy, R.A.; Grant-Muller, S.M. An assessment method for highway network vulnerability. J. Transp. Geogr. 2014, 34, 34–43. [Google Scholar] [CrossRef]
- Shano, L.; Raghuvanshi, T.K.; Meten, M. Landslide susceptibility evaluation and hazard zonation techniques—A review. Geoenvironmental Disasters 2020, 7, 18. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. CATENA 2012, 96, 28–40. [Google Scholar]
- Pradhan, B.; Mansor, S.; Pirasteh, S.; Buchroithner, M.F. Landslide hazard and risk analyses at a landslide prone catchment area using statistical based geospatial model. Int. J. Remote Sens. 2011, 32, 4075–4087. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y. Landslide spatial modelling using novel bivariate statistical based Naïve Bayes, RBF Classifier, and RBF Network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. CATENA 2020, 186, 104249. [Google Scholar] [CrossRef]
- Saleem, N.; Huq, M.E.; Twumasi, N.Y.D.; Javed, A.; Sajjad, A. Parameters derived from and/or used with digital elevation models (DEMs) for landslide susceptibility mapping and landslide risk assessment: A review. ISPRS Int. J. Geo Inf. 2019, 8, 545. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Han, L.; Chen, L.; Wang, L. Slope stability prediction using ensemble learning techniques: A case study in Yunyang County, Chongqing, China. J. Rock Mech. Geotech. Eng. 2022, 14, 1089–1099. [Google Scholar] [CrossRef]
- Cordeira, J.M.; Stock, J.; Dettinger, M.D.; Young, A.M.; Kalansky, J.F.; Ralph, F.M. A 142-year climatology of northern California landslides and atmospheric rivers. Bull. Am. Meteorol. Soc. 2019, 100, 1499–1509. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J. Vulnerability of simple reinforced concrete buildings to damage by rockfalls. Landslides 2010, 7, 169–180. [Google Scholar] [CrossRef]
- Antwi-Agyakwa, K.T.; Afenyo, M.K.; Angnuureng, D.B. Know to Predict, Forecast to Warn: A Review of Flood Risk Prediction Tools. Water 2023, 15, 427. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Devara, M.; Tiwari, A.; Dwivedi, R. Landslide susceptibility mapping using MT-InSAR and AHP enabled GIS-based multi-criteria decision analysis. Geomat. Nat. Hazards Risk 2021, 12, 675–693. [Google Scholar] [CrossRef]
- Asadi, M.; Goli Mokhtari, L.; Shirzadi, A.; Shahabi, H.; Bahrami, S. A comparison study on the quantitative statistical methods for spatial prediction of shallow landslides (case study: Yozidar-Degaga Route in Kurdistan Province, Iran). Environ. Earth Sci. 2022, 81, 51. [Google Scholar] [CrossRef]
- Shen, H.; Huang, F.; Fan, X.; Shahabi, H.; Shirzadi, A.; Wang, D.; Peng, C.; Zhao, X.; Chen, W. Improving the performance of artificial intelligence models using the rotation forest technique for landslide susceptibility mapping. Int. J. Environ. Sci. Technol. 2022, 1–16. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Kilicoglu, C. Investigation of the effects of approaches used in the production of training and validation data sets on the accuracy of landslide susceptibility mapping models: Samsun (Turkey) example. Arab. J. Geosci. 2021, 14, 2106. [Google Scholar] [CrossRef]
- Akinci, H.; Kilicoglu, C.; Dogan, S. Random forest-based landslide susceptibility mapping in coastal regions of Artvin, Turkey. ISPRS Int. J. Geo Inf. 2020, 9, 553. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Dholakia, M.; Prakash, I.; Pham, H.V. A comparative study of least square support vector machines and multiclass alternating decision trees for spatial prediction of rainfall-induced landslides in a tropical cyclones area. Geotech. Geol. Eng. 2016, 34, 1807–1824. [Google Scholar] [CrossRef]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Saha, S.; Roy, J.; Pradhan, B.; Hembram, T.K. Hybrid ensemble machine learning approaches for landslide susceptibility mapping using different sampling ratios at East Sikkim Himalayan, India. Adv. Space Res. 2021, 68, 2819–2840. [Google Scholar] [CrossRef]
- Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. CATENA 2019, 178, 172–188. [Google Scholar] [CrossRef]
- Kornejady, A.; Ownegh, M.; Rahmati, O.; Bahremand, A. Landslide susceptibility assessment using three bivariate models considering the new topo-hydrological factor: HAND. Geocarto Int. 2018, 33, 1155–1185. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Gautam, P.; Kubota, T.; Sapkota, L.M.; Shinohara, Y. Landslide susceptibility mapping with GIS in high mountain area of Nepal: A comparison of four methods. Environ. Earth Sci. 2021, 80, 359. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, J.; Zhao, S.; Wang, L.; Liu, J.; Guo, J. Comparative assessment of three nonlinear approaches for landslide susceptibility mapping in a coal mine area. ISPRS Int. J. Geo Inf. 2017, 6, 228. [Google Scholar] [CrossRef]
- Moosavi, V.; Niazi, Y. Development of hybrid wavelet packet-statistical models (WP-SM) for landslide susceptibility mapping. Landslides 2016, 13, 97–114. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhao, D.; Ding, Y.; Liu, Y.; Xu, Q.; Qiu, Y.; Liu, C.; Liu, Z.; Zha, Z.; Li, R. Performance evaluation for four GIS-based models purposed to predict and map landslide susceptibility: A case study at a World Heritage site in Southwest China. CATENA 2019, 183, 104221. [Google Scholar] [CrossRef]
- Kim, J.-C.; Lee, S.; Jung, H.-S.; Lee, S. Landslide susceptibility mapping using random forest and boosted tree models in Pyeong-Chang, Korea. Geocarto Int. 2018, 33, 1000–1015. [Google Scholar] [CrossRef]
- Park, I.; Lee, S. Spatial prediction of landslide susceptibility using a decision tree approach: A case study of the Pyeongchang area, Korea. Int. J. Remote Sens. 2014, 35, 6089–6112. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K.; Hwang, C.-L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications A State-of-The-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Gupta, S.; Soni, U.; Kumar, G. Green supplier selection using multi-criterion decision making under fuzzy environment: A case study in automotive industry. Comput. Ind. Eng. 2019, 136, 663–680. [Google Scholar] [CrossRef]
- Taherdoost, H.; Brard, A. Analyzing the process of supplier selection criteria and methods. Procedia Manuf. 2019, 32, 1024–1034. [Google Scholar] [CrossRef]
- Yu, C.; Shao, Y.; Wang, K.; Zhang, L. A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Expert Syst. Appl. 2019, 121, 1–17. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Xin, X.L.; Siddique, I.; Asghar Khan, W.; Yousif, M.A. TOPSIS method based on correlation coefficient under pythagorean fuzzy soft environment and its application towards green supply chain management. Sustainability 2021, 13, 1642. [Google Scholar] [CrossRef]
- Sahin, B.; Yip, T.L.; Tseng, P.-H.; Kabak, M.; Soylu, A. An application of a fuzzy TOPSIS multi-criteria decision analysis algorithm for dry bulk carrier selection. Information 2020, 11, 251. [Google Scholar] [CrossRef]
- Haddad, A.N.; da Costa, B.B.; de Andrade, L.S.; Hammad, A.; Soares, C.A. Application of fuzzy-TOPSIS method in supporting supplier selection with focus on HSE criteria: A case study in the oil and gas industry. Infrastructures 2021, 6, 105. [Google Scholar] [CrossRef]
- Chen, C.-T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Wei, G.-W. GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting. Knowl. Based Syst. 2010, 23, 243–247. [Google Scholar] [CrossRef]
- Saaty, T.L. Decisions with the analytic network process (ANP). In Proceedings of the ISAHP 1996, Vancouver, BC, Canada, 12–15 July 1996; Volume 96. [Google Scholar]
- Leung, L.C.; Lam, K.C.; Cao, D. Implementing the balanced scorecard using the analytic hierarchy process & the analytic network process. J. Oper. Res. Soc. 2006, 57, 682–691. [Google Scholar]
- Yalcin, A.; Reis, S.; Aydinoglu, A.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. CATENA 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Sefry, S.A. Flash flood susceptibility assessment in Jeddah city (Kingdom of Saudi Arabia) using bivariate and multivariate statistical models. Environ. Earth Sci. 2016, 75, 12. [Google Scholar] [CrossRef]
- Cheng, E.W.; Li, H. Application of ANP in process models: An example of strategic partnering. Build. Environ. 2007, 42, 278–287. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Jankowski, P.; Blaschke, T. A GIS based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis. Comput. Geosci. 2014, 64, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Soeters, R.; Van Westen, C. Slope instability recognition, analysis and zonation. Landslides Investig. Mitig. 1996, 247, 129–177. [Google Scholar]
- Lucchese, L.V.; de Oliveira, G.G.; Pedrollo, O.C. Mamdani fuzzy inference systems and artificial neural networks for landslide susceptibility mapping. Nat. Hazards 2021, 106, 2381–2405. [Google Scholar] [CrossRef]
- Goetz, J.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Tsakiris, G. Practical application of risk and hazard concepts in proactive planning. Eur. Water 2007, 19, 47–56. [Google Scholar]
- Cao, Y.; Yin, K.; Alexander, D.E.; Zhou, C. Using an extreme learning machine to predict the displacement of step-like landslides in relation to controlling factors. Landslides 2016, 13, 725–736. [Google Scholar] [CrossRef]
- Ahmed, B. Landslide susceptibility mapping using multi-criteria evaluation techniques in Chittagong Metropolitan Area, Bangladesh. Landslides 2015, 12, 1077–1095. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Saha, A.; Chakrabortty, R.; Roy, P. Mapping of earthquake hotspot and coldspot zones for identifying potential landslide hotspot areas in the Himalayan region. Bull. Eng. Geol. Environ. 2022, 81, 257. [Google Scholar] [CrossRef]
- Huang, W.; Ding, M.; Li, Z.; Yu, J.; Ge, D.; Liu, Q.; Yang, J. Landslide susceptibility mapping and dynamic response along the Sichuan-Tibet transportation corridor using deep learning algorithms. CATENA 2023, 222, 106866. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Jirandeh, A.G.; Pradhan, B.; Xu, C.; Gokceoglu, C. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran. J. Earth Syst. Sci. 2013, 122, 349–369. [Google Scholar] [CrossRef]
- Asmare, D. Application and validation of AHP and FR methods for landslide susceptibility mapping around choke mountain, northwestern ethiopia. Sci. Afr. 2023, 19, e01470. [Google Scholar] [CrossRef]
- Vittori Antisari, L.; Trenti, W.; Buscaroli, A.; Falsone, G.; Vianello, G.; De Feudis, M. Pedodiversity and Organic Matter Stock of Soils Developed on Sandstone Formations in the Northern Apennines (Italy). Land 2023, 12, 79. [Google Scholar] [CrossRef]
- Rosly, M.H.; Mohamad, H.M.; Bolong, N.; Harith, N.S.H. An Overview: Relationship of Geological Condition and Rainfall with Landslide Events at East Malaysia. Trends Sci. 2022, 19, 3464. [Google Scholar] [CrossRef]
- Ekmekçioğlu, M.; Kaya, T.; Kahraman, C. Fuzzy multicriteria disposal method and site selection for municipal solid waste. Waste Manag. 2010, 30, 1729–1736. [Google Scholar] [CrossRef] [PubMed]
- Chu, T.-C. Selecting plant location via a fuzzy TOPSIS approach. Int. J. Adv. Manuf. Technol. 2002, 20, 859–864. [Google Scholar] [CrossRef]
- Salih, M.M.; Zaidan, B.; Zaidan, A.; Ahmed, M.A. Survey on fuzzy TOPSIS state-of-the-art between 2007 and 2017. Comput. Oper. Res. 2019, 104, 207–227. [Google Scholar] [CrossRef]
- Kaur, P.; Mahanti, N. A fuzzy ANP-based approach for selecting ERP vendors. Int. J. Soft Comput. 2008, 3, 24–32. [Google Scholar]
- Balogun, A.-L.; Sheng, T.Y.; Sallehuddin, M.H.; Aina, Y.A.; Dano, U.L.; Pradhan, B.; Yekeen, S.; Tella, A. Assessment of data mining, multi-criteria decision making and fuzzy-computing techniques for spatial flood susceptibility mapping: A comparative study. Geocarto Int. 2022, 37, 12989–13015. [Google Scholar] [CrossRef]
- Alilou, H.; Rahmati, O.; Singh, V.P.; Choubin, B.; Pradhan, B.; Keesstra, S.; Ghiasi, S.S.; Sadeghi, S.H. Evaluation of watershed health using Fuzzy-ANP approach considering geo-environmental and topo-hydrological criteria. J. Environ. Manag. 2019, 232, 22–36. [Google Scholar] [CrossRef]



| Ratio (Percentage) | References |
|---|---|
| 70:30 | [52,53,54,55,56,57] |
| 80:20 | [58,59,60] |
| 75:25 | [61,62] |
| 50:50 | [63,64] |
| Model | Fuzzy ANP | Fuzzy TOPSIS | ||||
|---|---|---|---|---|---|---|
| Criteria | The Weight Final | Rank | Distance to Positive Ideal | Distance to Negative Ideal | Relative Proximity to the Ideal Solution | Rank |
| Distance to river | 0.095 | 5 | 0.232 | 0.108 | 0.317 | 8 |
| Distance to road | 0.141 | 1 | 0.108 | 0.235 | 0.675 | 1 |
| Land use | 0.080 | 9 | 0.343 | 0.105 | 0.295 | 10 |
| Lithology | 0.028 | 11 | 0.355 | 0.111 | 0.283 | 11 |
| Rainfall | 0.108 | 3 | 0.117 | 0.185 | 0.598 | 2 |
| Slope | 0.089 | 7 | 0.201 | 0.108 | 0.343 | 6 |
| Soil | 0.112 | 2 | 0.151 | 0.110 | 0.423 | 4 |
| curvature | 0.060 | 10 | 0.343 | 0.111 | 0.303 | 9 |
| Aspect | 0.095 | 6 | 0.189 | 0.091 | 0.337 | 7 |
| Distance to fault | 0.104 | 4 | 0.145 | 0.149 | 0.502 | 3 |
| Elevation | 0.088 | 8 | 0.168 | 0.112 | 0.385 | 5 |
| Landslide Classes | Fuzzy ANP | Fuzzy TOPSIS | ||
|---|---|---|---|---|
| Class Area (%Pixels) | Landslide (%Pixels) | Class Area (%Pixels) | Landslide (%Pixels) | |
| Very low susceptibility | 30.65 | 0.00 | 24.75 | 0.00 |
| Low susceptibility | 24.70 | 3.33 | 23.98 | 0.00 |
| Moderate susceptibility | 21.39 | 6.67 | 26.37 | 10.00 |
| High susceptibility | 14.74 | 3.33 | 15.53 | 6.67 |
| Very high susceptibility | 8.52 | 86.67 | 9.37 | 83.33 |
| Row | Models | Validating Dataset |
|---|---|---|
| 1 | Fuzzy TOPSIS | 0.983 |
| 2 | Fuzzy ANP | 0.938 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavakolifar, R.; Shahabi, H.; Alizadeh, M.; Bateni, S.M.; Hashim, M.; Shirzadi, A.; Ariffin, E.H.; Wolf, I.D.; Shojae Chaeikar, S. Spatial Prediction of Landslides Using Hybrid Multi-Criteria Decision-Making Methods: A Case Study of the Saqqez-Marivan Mountain Road in Iran. Land 2023, 12, 1151. https://doi.org/10.3390/land12061151
Tavakolifar R, Shahabi H, Alizadeh M, Bateni SM, Hashim M, Shirzadi A, Ariffin EH, Wolf ID, Shojae Chaeikar S. Spatial Prediction of Landslides Using Hybrid Multi-Criteria Decision-Making Methods: A Case Study of the Saqqez-Marivan Mountain Road in Iran. Land. 2023; 12(6):1151. https://doi.org/10.3390/land12061151
Chicago/Turabian StyleTavakolifar, Rahim, Himan Shahabi, Mohsen Alizadeh, Sayed M. Bateni, Mazlan Hashim, Ataollah Shirzadi, Effi Helmy Ariffin, Isabelle D. Wolf, and Saman Shojae Chaeikar. 2023. "Spatial Prediction of Landslides Using Hybrid Multi-Criteria Decision-Making Methods: A Case Study of the Saqqez-Marivan Mountain Road in Iran" Land 12, no. 6: 1151. https://doi.org/10.3390/land12061151
APA StyleTavakolifar, R., Shahabi, H., Alizadeh, M., Bateni, S. M., Hashim, M., Shirzadi, A., Ariffin, E. H., Wolf, I. D., & Shojae Chaeikar, S. (2023). Spatial Prediction of Landslides Using Hybrid Multi-Criteria Decision-Making Methods: A Case Study of the Saqqez-Marivan Mountain Road in Iran. Land, 12(6), 1151. https://doi.org/10.3390/land12061151













