The Use of Machine Learning in Real Estate Research

Abstract

This research seeks to demonstrate how machine learning, a branch of artificial intelligence, is able to deliver more accurate pricing predictions, using the real estate market as an example. Utilizing 24,936 housing transaction records, this paper employs Extra Trees (ET), k–Nearest Neighbors (KNN), and Random Forest (RF) to predict property prices and then compares their results with those of a hedonic price model. In particular, this paper uses a feature (property age x square footage) instead of property age in order to isolate the effect of land depreciation on property prices. Our results suggest that these three algorithms markedly outperform the traditional statistical techniques in terms of explanatory power and error minimization. Machine learning is expected to play an increasing role in shaping our future. However, it may raise questions about the privacy, fairness, and job displacement issues. It is therefore important to pay close attention to the ethical implications of machine learning and ensure that the technology is used responsibly and ethically. Researchers, legislators, and industry players must work together to create appropriate standards and legislation to govern the use of machine learning.

1. Introduction

When a new technology matures, it is typically adopted in business operations by firms in order to differentiate themselves from their competitors. There is a growing trend among private companies to advertise and sell their products and services via internet-based technologies. To compete, most large real estate-related firms have created and maintained their own websites to provide value-added and comprehensive services that assist customers in completing property transactions at a lower cost. Real estate marketing and brokerage, real estate appraisal, auctions, tenders, and mortgage brokerage are all available online. The goal of [1] is to propose the use of transaction data, hedonic models, and internet-based technologies by real estate-related firms to provide potential home buyers and sellers with instant and online property appraisal services. The hedonic price model is used to calculate the price index of many housing estates individually. Because the values of the attribute coefficients may change in response to changes in the environment, it may be required to make a professional decision on time intervals to re-run the hedonic price models, if necessary. Authenticated users can connect to the system via SSL after the algorithms have been updated. They can browse and search the valuation reports by entering search criteria for properties into the system, which instantly filters the results based on the users’ requests, and a detailed asset valuation report will be displayed in the browser.

A new wave of technology innovation, namely artificial intelligence (AI), has nowadays been being put to practical use in various business fields, especially in recent years, due to improvements in hardware performance and increases in the collection and use of big data [2]. Machine learning (a subset of AI) is a very powerful tool to collect, analyze, and interpret big data for predicting outcomes. It has been extensively deployed in many industries, including the real estate market. Using machine learning in the real estate market can help improve decision–making, reduce risk, and increase efficiency in property valuation, management, and investment. First, machine learning algorithms can analyze historical sales data and other relevant factors such as demographics, location, size, and amenities to accurately predict the value of a property [3]. They also automatically categorize properties, ranking search results and suggesting comparable properties. Machine learning can make real estate transactions simpler. This can also aid in the decision-making process for both buyers and sellers. Second, machine learning algorithms can locate properties that are anticipated to appreciate in value or yield a high rental income by using historical data and recent market patterns. They can be used to analyze market trends, property data, and economic indicators to assess the risk associated with investing in a particular property or market. Third, analysis of data on occupancy rates, rental rates, and tenant behavior can be used to optimize property management operations, such as lease renewal, rent collection, and maintenance scheduling. Fourth, machine learning algorithms can analyze data to detect potential fraud, such as mortgage fraud. Fifth, it can analyze energy consumption data from buildings and identify patterns to optimize energy use and reduce costs. Sixth, real estate websites and apps can utilize machine learning algorithms to recommend properties to consumers based on their interests, search histories, and activity [4].

Using the real estate market as an example, this paper attempts to illustrate how machine learning can provide more accurate price predictions than the traditional statistical technique. This paper is organized as follows. Section 2 presents the literature review of three machine learning algorithms, namely Extra Trees, k–Nearest Neighbors, and Random Forest, and explain why they are chosen for this study. Section 3 describes these methodologies and examines the algorithms, optimization, and hyperparameters. Section 4 describes the data, their definitions, and sources. Section 5 presents our empirical results based on these three algorithms and ordinary least squares (OLS), and then compares their results. The last section concludes the paper.

2. Literature Review

Residential properties are a source of wealth accumulation in an economy. In 2019, the median value of a primary residence (USD 225,000) was worth approximately ten times the median value of financial assets (USD 25,700) held by US families. Among the homeowners, the latter amounted to merely USD 63,400 [5]. On the one hand, buying a home is the most expensive consumption and investment for most people in their whole life. On the other hand, the development of the real estate market does not only boost economic progress but also other businesses, including real estate agents, decoration, furniture, home appliances, and property management, as well as building maintenance [6]. The combined contribution of housing (residential investment and housing services) to GDP averaged 15–18% in the US during the period between 1981 and 2022. Residential investment (typically 3–5% of GDP) includes new single-family and multifamily construction, residential remodeling, manufactured home production, and broker’s fees. Moreover, consumption spending on housing services (averaging approximately 12–13% of GDP) includes renters’ gross rents and utilities as well as owners’ imputed rents and utility payments [7].

There are many factors that can exert an influence on property prices, including demographic changes, real interest rates, speculation, tax incentives [8], construction costs, the presence of green spaces [9], and government regulations and policies. A change in property prices does not only affect a household’s affordability [10], but also necessitates a change in housing policies in order to dampen property speculation [11] or revitalize the real estate market. In many Western countries, there is a special type of housing called “non-profit” third-housing sector (THS) to help less economic affluent residents to alleviate their housing burdens. In particular, a study by [12] argues that an expansion of THS will crowd out residential investment in the private sector, which raises real estate prices in return (see also [13]).

In Hong Kong, the SAR Government has implemented new actions from time to time to depress property prices. Our government has imposed a Special Stamp Duty to curb short-term speculation in residential properties since November 2010, and imposed Buyer’s Stamp Duty to suppress the investment demand from non-Hong Kong permanent residents since October 2012. It has also raised the rate of ad valorem Stamp Duty to depress the investment sentiment of the buyers of multiple residential properties. Other measures also include a decrease in loan-to-value and debt-servicing ratios, and tighter credit control and household leverage.

Because changes in property prices can impact various stakeholders in an economy in a variety of ways, it is critical to obtain accurate property price signals in order to make informed decisions. The use of AI, particularly machine learning, in conducting real estate research has various advantages. Machine learning algorithms help handle and analyze an enormous volume of data by offering more flexible and powerful estimation procedures. However, huge data sets can occasionally contain exceedingly complicated correlations between variables, which means that linear model estimations in conventional estimation approaches are unable to identify them. Many sophisticated machine learning algorithms, such as Random Forest and Gradient Boosting Machine (GBM), enable researchers to model highly complex relationships between dependent variable and features (explanatory variables). Researchers can employ machine learning to analyze data in a variety of ways, which include analyzing texts, photos, remote sensing images, and numerical data, applying the results to generate predictions [3]. Moreover, researchers can now employ Optuna or other newly established optimization methods, such as BayesOpt, Hyperopt, and Ray, in order to tune hyperparameter values. The procedure of these new optimization methods can now be quickly completed with the high-speed processing capacity of modern computing devices.

This section focuses on the three selected machine learning algorithms only. First, a brand new tree-based ensemble method has been put forth by [14] for supervised classification and regression issues. Extra Trees (or Extremely Randomized Trees) involves dividing a tree node while extremely randomizing the choice of attribute and the cut-point. It creates completely random trees in the extreme case, whose architectures are independent of the learning sample’s output values. By selecting the right parameter, the power of the randomization can be adjusted to the particulars of the problem. This paper assesses the robustness of the default selection for this parameter and offer guidance on how to change it in specific circumstances. The algorithm’s biggest advantage, aside from accuracy, is computational speed. Additionally, a geometrical and kernel characterization of the induced models as well as a bias/variance analysis of the Extra-Trees approach are provided.

The effect of the COVID-19 epidemic on property prices in a Spanish city was measured by [15], identifying the best machine learning methods to predict house values. Their methodology covers the steps of model selection and evaluation, feature engineering, hyperparameter training and optimization, and model interpretation. In this study, ensemble learning algorithms based on bagging (Random Forest and Extra Trees regressors) and boosting (Gradient Boosting Regressor, Extreme Gradient Boosting, and Light Gradient Boosting Machine) are employed in comparison to a linear regression model.

Second, the k–Nearest Neighbors method of classification is straightforward but efficient. The two main disadvantages of KNN are its low efficiency, which makes it unsuitable for many applications such as dynamic web mining for large repositories, and its reliance on the choice of an optimum value for k. In order to address these issues, A unique classification approach utilizing the KNN type is presented by [16]. The data are replaced with a KNN model created by the new technique, which then serves as the foundation for categorization. Their model automatically determines different optimum values for k for different data sets to achieve classification accuracy The model’s design lessens the reliance on k and speeds up classification. KNN is also feasible for performing regression tasks [17].

Using the Adana Province of Turkey’s real estate data, hedonic regression, k–Nearest Neighbors, and artificial neural network (ANN) approaches are used to predict property prices [18]. Hedonic regression techniques have traditionally been used to forecast housing prices. Other approaches are required because the interactions between the variables that affect home prices are typically nonlinear. Artificial neural networks and k–Nearest Neighbors regression both offer flexible and nonlinear fits. A mixed-type data set is used to examine the root mean squared error, the coefficient of determination (R squared), the coefficient of determination, and mean absolute error associated with the hedonic price model and its nonlinear variants. The optimum hyperparameters associated with ANN and KNN are obtained using the cross-validation method (see also [19]).

Employing the data from the Salamanca district of Madrid (Spain), [3] have explored the application of different machine learning algorithms with the objective of identifying real estate opportunities for investment. In particular, Extra Trees, k–Nearest Neighbors, Support Vector Machines, and Multi–layer Perceptrons are employed to predict property prices. A cross-validation procedure has been used in order to minimize biases resulting from the split in training and test subsets. Their study revealed that Extra Trees outperforms other algorithms in terms of mean absolute error.

The Random Forest strategy (by combining classification and regression trees) was originally put forth by [20,21] and bootstrap aggregation [22]. To improve prediction performance, it is an ensemble classifier or regressor that uses several models of T decision trees. Using a bootstrap technique, this method generates several trees and trains each one using the original sample set of training data. To obtain a split at each node, it looks for a random subset of features. The randomly chosen features partitioned at each node and the bootstrap technique for each regression tree development lessen the correlations between the produced regression trees. In order to lower the variance of the model mistakes, Random Forest thus averages the prediction answers [22].

A research by [23] made an effort to determine the house values in the city of Krasnoyarsk using 1970 property transaction records. According to their research, housing characteristics include number of rooms, overall area, floor, parking, type of repair, number of balconies, type of bathroom, number of elevators, garbage disposal, year of construction, and accident rate. To forecast real estate values, they used Random Forest, ridge regression, and linear regression. According to their analysis, Random Forest outperforms the other two algorithms in terms of mean absolute error (see also [24,25,26]).

In order to estimate real estate prices, three machine learning algorithms, Support Vector Machine (SVM), Random Forest (RF), and gradient boosting machine (GBM), were employed by [27]. The authors then examined the results associated with these three algorithms while applying these techniques to a data sample of roughly 40,000 housing transactions over the course of more than 18 years in Hong Kong. When compared to SVM, RF and GBM demonstrated superior performance in terms of predictive power, while RF and GBM performed equally well. In terms of three performance criteria (MSE, RMSE, and MAPE), GBM surpasses SVM while doing marginally better than RF in terms of error minimization. As a result, this paper shows that RF and GBM are very effective methods for making precise predictions of real estate prices because their results are comparable.

3. Model Specification

In this paper, we attempt to compare the results obtained from estimating Extra Trees, k–Nearest Neighbors, Random Forest, and ordinary least squares, respectively. These three algorithms were chosen because they are easy to compute while generating very accurate predictions. First, ET, KNN, and RF can be used for both regression and classification tasks, handling high-dimensional data while maintaining the model’s accuracy. Second, these algorithms can handle both categorical and numerical data simultaneously, which makes them useful for data sets that have a mixture of data types. Third, they can be used with noisy data, as they can handle outliers and missing values well. Fourth, these algorithms can be a good choice for time-critical applications because they can generate predictions quickly, especially when using multiple CPU cores. Lastly, ET and RF can be used to determine feature importance in a data set, which can be useful in feature selection or understanding the underlying data structure. In our current research, we intend to use the RF results as a benchmark to assess the usefulness of ET and KNN.

The price, $P_i^t$, of a residential property, i, during time period t is hypothesized as a function of a fixed K, housing features measured by quantities, $x_{ik}^t.$ Mathematically, a hedonic price model is specified as Equation (1):

$$P_i^t={\alpha }_0+\sum _{k=1}^K{\beta }_k{x}_{ik}^t+{\epsilon }_i^t$$

(1)

where ${\alpha }_0$ represents the constant term, ${\beta }_k$ represents the estimated coefficients associated with the set of housing features, and ${\epsilon }_i^t$ represent the stochastic error term. Practically, Equation (1) is estimated by regressing property prices on physical, environmental, and accessibility characteristics. Based on the implicit price of each housing features, researchers can estimate the property prices.

More recent research has recommended removing the land component from estimates of property prices so that only the building structure and age of the property interact multiplicatively [28,29]. Property age should not be able to affect the size of individual parcels of land for two reasons. Firstly, land pieces do not depreciate. Second, a more expensive building structure inside a residential building suggests that it has a greater overall square footage. When compared to a similar residential property with a smaller footage area, larger residential homes will incur a higher rate of depreciation, which will result in higher maintenance costs. To isolate the effect of land on property prices, our estimated equation takes the specific form:

$$P_i^t={\alpha }_0+\sum _{k=1}^K{\beta }_k{z}_{ik}^t+\gamma S_i^t+\theta A_i^t{S}_i^t+{\epsilon }_i^t$$

(2)

where $z_{ik}^t$ represents a list of housing characteristics, excluding building structure and property age, $S_i^t$ represents the building structure, $A_i^t$ represents the age of a residential property, $\gamma$ represents the coefficient for the building structure, and $\theta$ represents the coefficient for the multiplication of age and building structure.

In this paper, Extra Trees, k–Nearest Neighbors, and Random Forest are employed to predict the property prices of a residential district of Hong Kong. First, Extra Trees are also known as extremely randomized trees. It is a type of ensemble learning technique for both classification regression tasks. Despite some significant changes in how the individual decision trees are trained and integrated, it is similar to Random Forest. In Extra Trees, a number of decision trees are trained on various subsets of the training data, and a random subset of characteristics is chosen for consideration at each split in each tree. Extra Trees, in contrast to Random Forest, does not attempt to locate the ideal split point at each node. Instead, it chooses one out of several potential split points at random based on how much variance it reduces. Each node in each tree goes through the same random splitting and optimal split point selection process once more, creating a collection of “extra randomized” trees.

The results of all the trees are averaged to obtain a final prediction in order to make a prediction for a new data point. With Extra Trees, the splits are supposed to be randomly chosen, which lowers the variance of each tree and makes it less likely for it to overfit the training set. Averaging several trees also lessens the effect of outliers and noise in the data, resulting in predictions that are more reliable. Unlike Random Forest, which creates each decision tree from a random sample with a replacement, additional trees fit each decision tree to the full training set. Additionally, it randomly selects a split point while sampling each feature at each split point in a decision tree.

Three key hyperparameters are used to fine-tune this technique. They comprise the number of estimators (M), the number of features (k), and the minimal number of samples needed in a node to establish a new split (n_min). We do not utilize bootstrap, but choose the criterion (MSE); set a range of values for max depth (2, 3, …, 20), max features (2, 3, …, 14), min samples leaf (2, 3, …, 10), min samples split (2, 3, …, 10), and number of estimators (10, 20, …, 200); and then select the best ones using Optuna.

Second, KNN is a nonparametric algorithm that can be used for both classification and regression tasks. Finding the k points that are physically nearest to the given point, $x_0$, is required, and classification is to performed via a majority vote among the k neighbors. We must determine the separation between these two places in order to determine a neighbor. The Minkowski distance can be defined as follows:

$$d={\left(\sum _{i=1}^n{|x_i-y_i|}^p\right)}^{1/p}$$

(3)

To vary the definitions of distance, we can select the value of p (a positive number). To optimize hyperparameters, we utilize Optuna to find the optimum hyperparameters by selecting one of the methods (ball_tree, kd_tree, brute, and auto), the number of leaf sizes (1, 2, ..., 31), the number of neighbors (1, 2, ..., 31), p (1, 2), and weights (uniform weights).

Third, RF is a supervised learning algorithm that employs ensemble learning methods to perform classification and regression tasks [30]. Instead of making predictions based on a single tree, many decision trees are built and merged into a single model to make more accurate and robust prediction [20,22]. Bagging (random sampling with replacement) reduces variance but slightly increases bias. Given a training set, bagging iteratively selects random samples of the training set for $\beta$ amount of times $\left(b=1,2,...,\beta \right)$ and fits a tree to those samples [22].

By using the training set and bagging, we can gather a sequence of instances to construct a tree. Every sequence of instances correlates to a random vector, ${\varnothing }_k$, that shapes a specific tree. Because each sequence varies somewhat from the others, no two decision trees are created exactly alike. Equation (4) can be employed to describe the prediction of the K–th tree for an input X [31]:

$$h_k\left(X\right)=h\left(X,{\varnothing }_k\right),\forall k\in \left\{\mathrm{1,2},\dots ,K\right\}$$

(4)

where K represents the number of decision trees. To eliminate feature correlations, a tree makes decisions by splitting nodes into sub-nodes, each of which randomly selects features. By selecting a threshold, c, that minimizes the variation in the sum of squared errors, a node, S, can be divided into two subsets, S₁ and S₂ [20]. Each subtree can be projected as the mean or median output of instances by applying the same decision procedures. The final forecast can then be derived by casting a class-specific majority vote among the ensemble’s trees.

$$SSE=\left(\sum _{i\in S_i}{\left(v_i-\frac{1}{\left|S_1\right|}\sum _{i\in S_1}{v}_i\right)}^2+\sum _{i:i\in S_2}{\left(v_i-\frac{1}{\left|S_2\right|}\sum _{i\in S_2}{v}_i\right)}^2\right)$$

(5)

For hyperparameter optimization, we employ bootstrapping, select the criterion of choice (mean square error), and set a range of values for maximum depth (1, 2, ..., 20), maximum features (1, 2, ..., 14), minimum samples leaf (1, 2, ..., 10), minimum samples split (1, 2, ..., 10), and number of estimators (10, 20, ..., 200) to tune. Then, we use Optuna to choose their best values.

When estimating each machine learning algorithm; our data set is partitioned into k = 5 equal folds, each of which will occasionally be used as a test set. The model is tested on the initial subset (k = 1), and the remaining subsets are utilized to train the model. The second fold (k = 2) is used as the test data in the second iteration, while the remaining folds are used as the training data. Once each fold has been used as test data, the process will be repeated. We may compute the mean value of each iteration’s $R^2$ score in order to assess the overall performance of our model.

Cross-validation, also known as resampling, is a technique used to evaluate machine learning models on a subsample, or training set in machine learning (for example, 80% of the entire sample). In this method, the training data set is used to estimate how well the model predicts in general, and the test data set (the remaining 20% of the entire sample) is used to actually make predictions. In order to reduce problems such as overfitting (the model performs well on the training set but badly on the test set) and underfitting (the model performs poorly in both training and test sets), it aims to determine the number of observations that should be utilized to test the model during the training phase. Data scientists can then gain some understanding into how well the model can work with different subsamples. We develop k distinct models using k–fold cross validation so that all our data may be used for both training and testing while assessing our methods on unobserved data.

Once we have computed the predicted values for our training data set with Python, we obtain ${\theta =\left(X^{T}X\right)}^{-1}\left(X^{T}y\right)$, which minimizes the cost value for the training set. In order to determine whether our estimates are still accurate for the test data, we then incorporate the coefficients (or weights) into our models using the test data. We assess this by looking at the mean square error (MSE), root mean square error (RMSE), mean absolute percentage error (MAPE), and coefficient of determination $R^2$. These three performance metrics (Equations (6)–(8)) have a range from 0 to ∞, and when they are computed to be 0, they all say that the fit is perfect.

$$MSE=\frac{1}{m}\sum _{i=1}^m{\left(h\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2$$

(6)

$$RMSE=\sqrt{\frac{1}{m}\sum _{i=1}^m{\left(h\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2}$$

(7)

$$MAPE=\frac{100\mathrm{\%}}{m}\sum _{i=1}^m\left|\frac{\left(h\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}{y^{\left(i\right)}}\right|$$

(8)

where $h\left(x^{\left(i\right)}\right)$ represents the predicted value of the property, $y^{\left(i\right)}$ represents the actual value of the property, and m represents the number of observations in the test data.

4. Data Definitions and Sources

In this study, we selected four private housing estates (Grand Promenade, Kornhill Garden, Les Saisons, Taikoo Shing) in the Quarry Bay district of Hong Kong, categorized as the “selected popular residential developments” by the Rating and Valuation Department, Hong Kong SAR Government. Our data series are computed from January 1997 through May 2021, yielding a total of 24,317 pooled cross-sectional data observations. Disaggregated information regarding building names, locations, dates of transactions and occupation permits, sums paid, square footage, and other details (such as whether a property is sold with a parking space) is kept by the government and collated by a commercial company named “EPRC”. Property prices are deflated into real terms by dividing the popular housing estate price index [32] compiled by the Rating and Valuation Department. Unfortunately, some of these records were excluded from our data set because they contained inaccurate or insufficient information (missing transaction dates or footage areas, for example). Property transactions with no consideration are considered as gifts (often from parents to their children) and are therefore excluded from our sample. Our data definitions are summarized in

Table 1. Data Definitions.

Variable	Definition
$P_i^t$	Represents the total consideration of residential property i during time period t, measured in HK dollars, inflation adjusted.
${GFA}_i^t$	Represents the gross floor area of residential property i, including the area of penthouse, bay windows, and balconies if any.
${AGE}_i^t$	Represents the age of residential property i in years, which is calculated using the time elapsed between when the occupation permit was issued and when the homes were sold.
${ZZ}_i^t$	Represents the multiplication of building structure and property age of residential property i.
${FL}_i^t$	Represents the floor level of residential property i.
${FR}_i^t$	Dummy variable that is set to be 1 if property i has a flat roof, 0 otherwise.
$ROO{F}_i^t$	Dummy variable that is set to be 1 if property i has a roof top, 0 otherwise.
${CP}_i^t$	Represents the number of carpark(s) transacted with residential property i.
${MTR}_i^t$	Dummy variable that is set to be 1 if it takes no more than ten minutes to walk from property i to the nearest mass transit railway station, 0 otherwise.
$$\begin{gathered} E_i^t,S_i^t,W_i^t \\ {N}_i^t,{NE}_i^t,{SE}_i^t \\ {SW}_i^t\&{NW}_i^t \end{gathered}$$	Represent eight possible directions in which property i could be facing. If a property is facing a specific direction, they are set to be 1; 0 otherwise. Northwest has been left out of the analysis so that these coefficients can be evaluated in relation to this category.

.

Each variable is shown as a histogram in Figure 1, which roughly estimates its probability distribution by showing the frequency of observations within a particular range of values. A correlation matrix showing the linear relationship between each variable is shown in Figure 2. An unanimously high correlation has been found between footage area and residential property prices (0.8), floor level (0.4), age (−0.3), and mass transport railway (0.3). Figure 3 illustrates a data visualization of Figure 2, which illustrates the relationship between each explanatory variable and residential property prices. Finally,

Table 2. Descriptive Statistics.

	P	GFA	AGE	ZZ	FL	FR	ROOF	CP	MTR	E	S	W	N	NE	SE	SW	NW
Count	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936	24,936
Mean	4.063	784.773	21.295	16390.458	18.299	0.003	0.020	0.002	0.714	0.169	0.155	0.174	0.197	0.063	0.090	0.083	0.069
Std	1.854	179.593	9.749	8015.426	13.813	0.054	0.140	0.056	0.452	0.375	0.362	0.379	0.397	0.244	0.286	0.276	0.253
Min	0.4400	413	0.003	1.756	1	0	0	0	0	0	0	0	0	0	0	0	0
25%	2.997	675	15.129	11,320.293	8	0	0	0	0	0	0	0	0	0	0	0	0
50%	3.594	751	22.030	16,470.828	16	0	0	0	1	0	0	0	0	0	0	0	0
75%	4.576	858	28.215	21,429.866	24	0	0	0	1	0	0	0	0	0	0	0	0
Max	46.463	3155	44.449	53,920.613	73	1	1	3	1	1	1	1	1	1	1	1	1
Skew	3.854	1.694	–0.255	0.162	1.591	18.402	6.848	30.573	–0.948	1.765	1.903	1.719	1.528	3.584	2.873	3.029	3.401

presents a summary of the descriptive statistics for the variables used in this inquiry. Descriptive statistics offer brief descriptions of a particular data set, which may represent the full population or a sample of the population.

5. Results

Table 3. Estimated results based on Random Forest and Ordinary Least Squares.

	${\mathit{R}}^2$	MSE	RMSE	MAPE
ET (Training Set)	0.95800	0.14405	0.37953	6.49588%
ET (Test Set)	0.91164	0.30561	0.55282	9.04653%
KNN (Training Set)	0.93007	0.23986	0.48976	8.49793%
KNN (Test Set)	0.89530	0.36211	0.60176	10.39521%
Random Forest (Training Set)	0.96165	0.13155	0.36270	6.22301%
Random Forest (Test Set)	0.91928	0.27918	0.52837	8.88930%
Ordinary Least Squares	0.81400	0.63890	0.79931	14.54268%

presents our results associated with Extra Trees, k–Nearest Neighbors, Random Forest, and OLS. In machine learning, we normally do not use $R^2$ as a principal performance metric to evaluate the accuracy of a model, but its value still conveys some useful information. In ET, the $R^2$ is as high as 0.96 in the training set and 0.91 in the test set. The negligible difference indicates no evidence of overfitting or underfitting. The results are then evaluated by the MSE, RMSE, and MAPE criteria. These three performance metrics are estimated to be 0.14405, 0.37953, and 6.49588%, demonstrating that ET fits our training data set very well. For our test set, MSE, RMSE, and MAPE are estimated to be 0.30561, 0.55282, and 9.04653%, respectively, demonstrating that ET also fits our test data set very well.

In k–Nearest Neighbors, the $R^2$ is as high as 0.93 in the training set and 0.90 in the test set. The negligible difference indicates no evidence of overfitting or underfitting. The results are then evaluated by the MSE, RMSE, and MAPE criteria. These three performance metrics are estimated to be 0.23986, 0.48976, and 8.49793%, demonstrating that KNN fits our training data set very well. For our test set, MSE, RMSE, and MAPE are estimated to be 0.36211, 0.60176, and 10.39521%, respectively, demonstrating that KNN also fits our test data set very well.

In Random Forest, the $R^2$ is as high as 0.96 in the training set and 0.92 in the test set. The negligible difference indicates no evidence of overfitting or underfitting. The results are then evaluated by the MSE, RMSE, and MAPE criteria. These three performance metrics are estimated to be 0.13155, 0.36270, and 6.22301%, respectively, demonstrating that RF fits our training data set very well. For our test set, MSE, RMSE, and MAPE are estimated to be 0.27918, 0.52837, and 8.88930%, respectively, demonstrating that RF also fits our test data set very well.

However, although $R^2$ is estimated to be reasonably good at 0.814 in our OLS model, this value is less than $R^2$ of the test set associated with three algorithms by 6.62~12.90%. Such a difference is remarkable by any standard. Moreover, its three performance metrics are also worse than those of the test set associated with the three algorithms. In terms of MSE, its value for OLS is higher than those of these three algorithms by 76.44~128.85%. In terms of RMSE, its value for OLS is higher than those of these three algorithms by 32.83~51.28%. For MAPE, its value for OLS is higher than those of these three algorithms by 39.90~63.60%. Hence, we can surely confirm that Extra Trees, k–Nearest Neighbors, and Random Forest outperforms OLS in terms of prediction and error minimization.

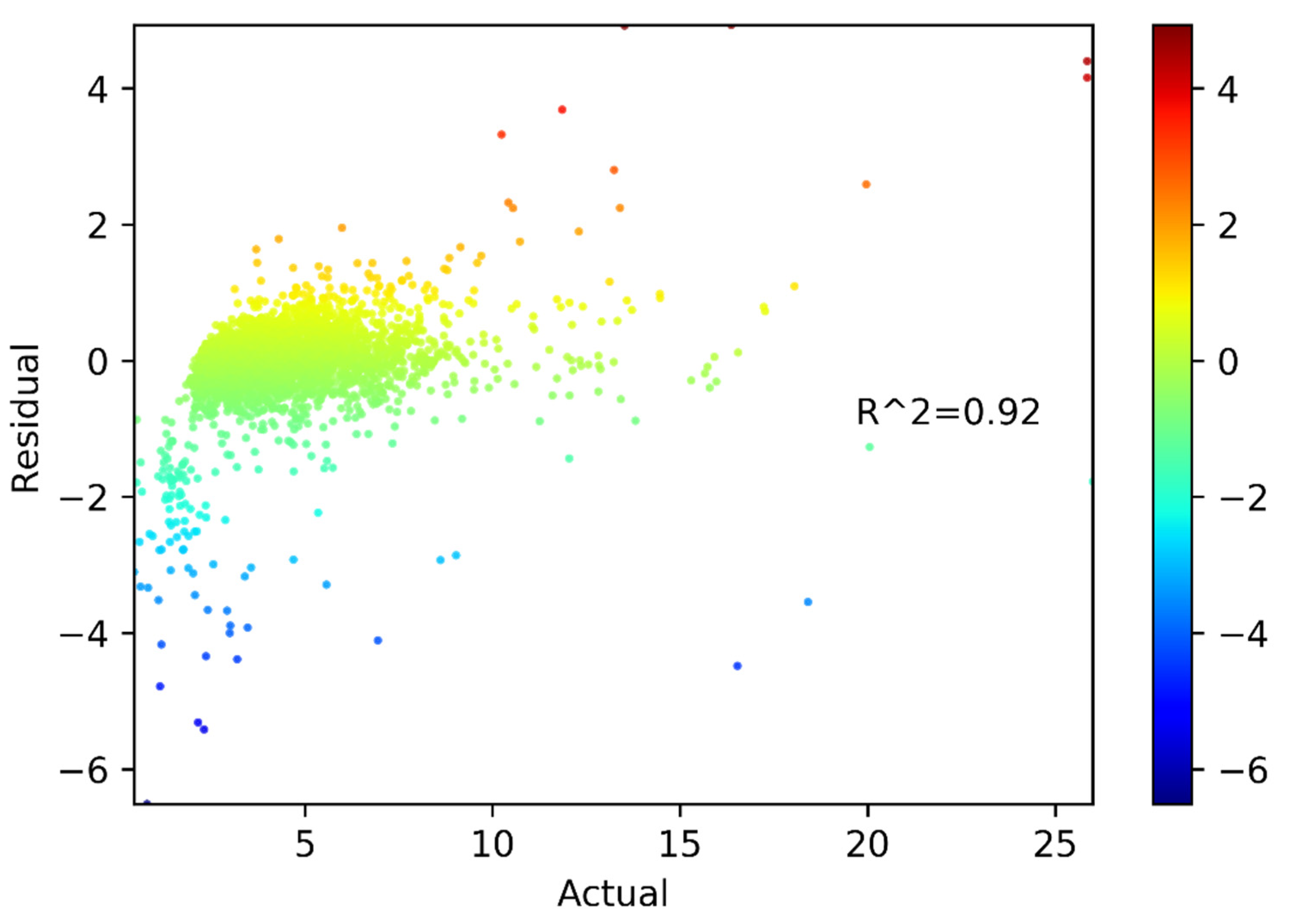
Based on the results of our RF estimation, the scatterplot of real estate prices and the residuals for the training set are shown in Figure 4. It demonstrates that RF typically matches the data quite well. The relationship between actual prices and their expected values is further illustrated in Figure 5. It is noticeable that one dot (whose property price is larger than 40 million) is lying far away from the clustering. With such an exception, almost all our predicted values closely follow the red line, showing that our model adequately fits our training data.

Figure 6 displays the scatterplot of real estate prices and the residuals for the test set based on the findings of our RF estimation. It proves that RF usually closely matches the data. Figure 7 also shows the relationship between actual prices and their expected values. Because almost all our predicted values closely follow the red line, with the exception of a few outliers, our model fits the test data set very well.

6. Conclusions

This paper attempted to illustrate how machine learning can provide more accurate price predictions than traditional statistical technique, using the real estate market as an example. Extra Trees, k-Nearest Neighbors, and Random Forest have been found to outperform the hedonic price model in terms of explanatory power and cost minimization. The increase in R square ranges between 6.62% and 12.9%. Accurate price signals in the property market predicted by machine learning algorithms play an important role in promoting sustainable production and consumption patterns. The government can incentivize homeowners to choose sustainable options and encourage developers to invest in sustainable practices by identifying where energy-efficiency improvements are needed. These contribute to the development of a more sustainable real estate market that benefits both the environment and society. With more accurate price information, buyers can identify properties that are overpriced and not worth the investment. This can help to reduce waste from unnecessary property development.

In conclusion, machine learning is expected to play a growing role in shaping our future. It has already been utilized in a variety of industries, ranging from healthcare to finance, and is having a significant impact on how we live and work. Although machine learning has the ability to significantly advance civilization, it also raises certain ethical issues that need to be resolved. For machine learning algorithms to work properly, a significant amount of data is needed. This may give rise to questions regarding the privacy of the people whose data is being exploited. In addition, there is a chance that private information will accidently leak or be misused. Machine learning algorithms can significantly affect people’s life by influencing things such as loan or employment approval rates. It is crucial that these decisions are made equitably, openly, and without unduly disadvantaging any particular age group, gender, or race. Furthermore, employment displacement occurs when tasks that were previously carried out by humans are automated via machine learning. It is crucial to take into account how machine learning will affect the workforce and to make sure that employees have access to the training and assistance they need to adjust to these changes. Therefore, it is critical to pay close attention to the ethical implications of machine learning and to make sure that technology is applied responsibly and ethically. To create proper standards and laws to control the use of machine learning, it is necessary for researchers, legislators, and industry stakeholders to work together.