Examining Relationships between Regional Ecological Risk and Land Use Using the Granger Causality Test Applied to a Mining City, Daye, China
Abstract
:1. Introduction
2. Materials and Methods
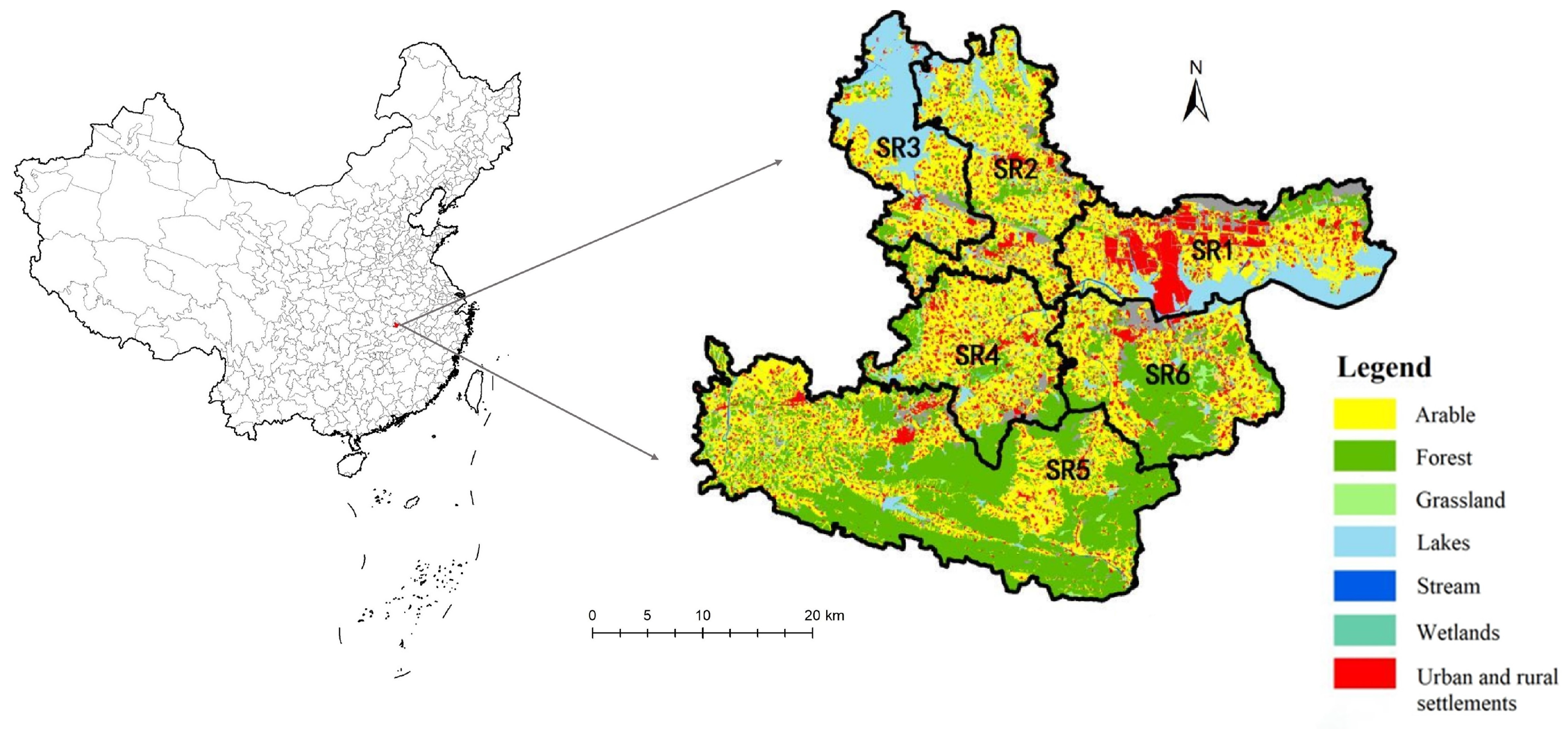
2.1. Study Area
2.2. Calculation of Land Use Degree
2.3. Comprehensive Risk Assessment Model
2.3.1. Risk Calculation
2.3.2. Analysis of the Ecological Risk in Study Area
- (1)
- Indicator system for regional ecological risk
| System Layer | Variable Layer | Factor Layer | Index Layer | Observational Variable |
|---|---|---|---|---|
| Indicator system for regional ecological risks assessment | Probability of composite risk source | Probability of single risk | Refer to Table 3 for details | |
| Ecological vulnerability indicator (vulnerability) | Ecological quality index | Refer to Table 4 for details | ||
| Vulnerability index | ||||
| Risk Source Type | Weight, % | Type | Weight, % | Ecological Risk Source | Weight, % |
|---|---|---|---|---|---|
| Natural disaster | 0.2 | Meteorological disaster | 0.5 | Storm flood | 0.385 |
| Extreme weather | 0.155 | ||||
| Acid rain | 0.46 | ||||
| Geological disaster | 0.5 | Geological disaster | 1 | ||
| Human activity | 0.8 | Urban industrialization | 0.559 | Population aggregation | 0.223 |
| The area ratio of industrial land | 0.601 | ||||
| Fixed investments (mining) | 0.427 | ||||
| Agricultural land reclamation | 0.106 | ||||
| Pollutant discharges | 0.266 | Point source | 0.45 | ||
| Accumulation | Areal source | 0.55 | |||
| Resource consumption and occupation | 0.175 | Agricultural irrigation | 0.512 | ||
| Forest harvesting | 0.38 | ||||
| Grazing | 0.108 |
| Object Layer | Factor Layer | Weight | Index Layer | Weight | Observational Variable | Weight |
|---|---|---|---|---|---|---|
| Ecological vulnerability degree | Ecological quality index | 0.8 | Natural biotope index (topography, geomorphology and climate) | 0.135 | Ground elevation | 0.325 |
| Ratio of slope > 20 degrees to total area% | 0.438 | |||||
| Multi-year average precipitation | 0.237 | |||||
| Biotope index | 0.259 | Vegetation coverage | 0.512 | |||
| Water network density | 0.284 | |||||
| Abundance of biological resources | 0.204 | |||||
| Vitality index | 0.185 | Ecological resilience value | 0.415 | |||
| Primary productivity NPP | 0.585 | |||||
| Interreference index | 0.192 | Landscape fragmentation | 0.632 | |||
| Shannon diversity index | 0.368 | |||||
| Environmental quality index | 0.229 | Water environment index | 0.363 | |||
| Soil quality index | 0.486 | |||||
| Atmospheric index (fallout) | 0.151 | |||||
| Vulnerability index | 0.2 | Socioeconomic pressure index | 1 | Consumer price index (CPI) | 0.381 | |
| Fiscal income (GDP) | 0.452 |
- (2)
- Indicator system for hazardous degree assessment of the risk source
- (3)
- Indicator system for ecological vulnerability
2.4. Cointegration Analysis
2.4.1. Unit Root Test
2.4.2. Cointegration Test
- Regression Model Estimation
- 2.
- Residual Sequence Unit Root Test
2.5. Granger Causality Test and Impulse Response Function
2.5.1. Granger Causality Test
2.5.2. Impulse Response Function
3. Results
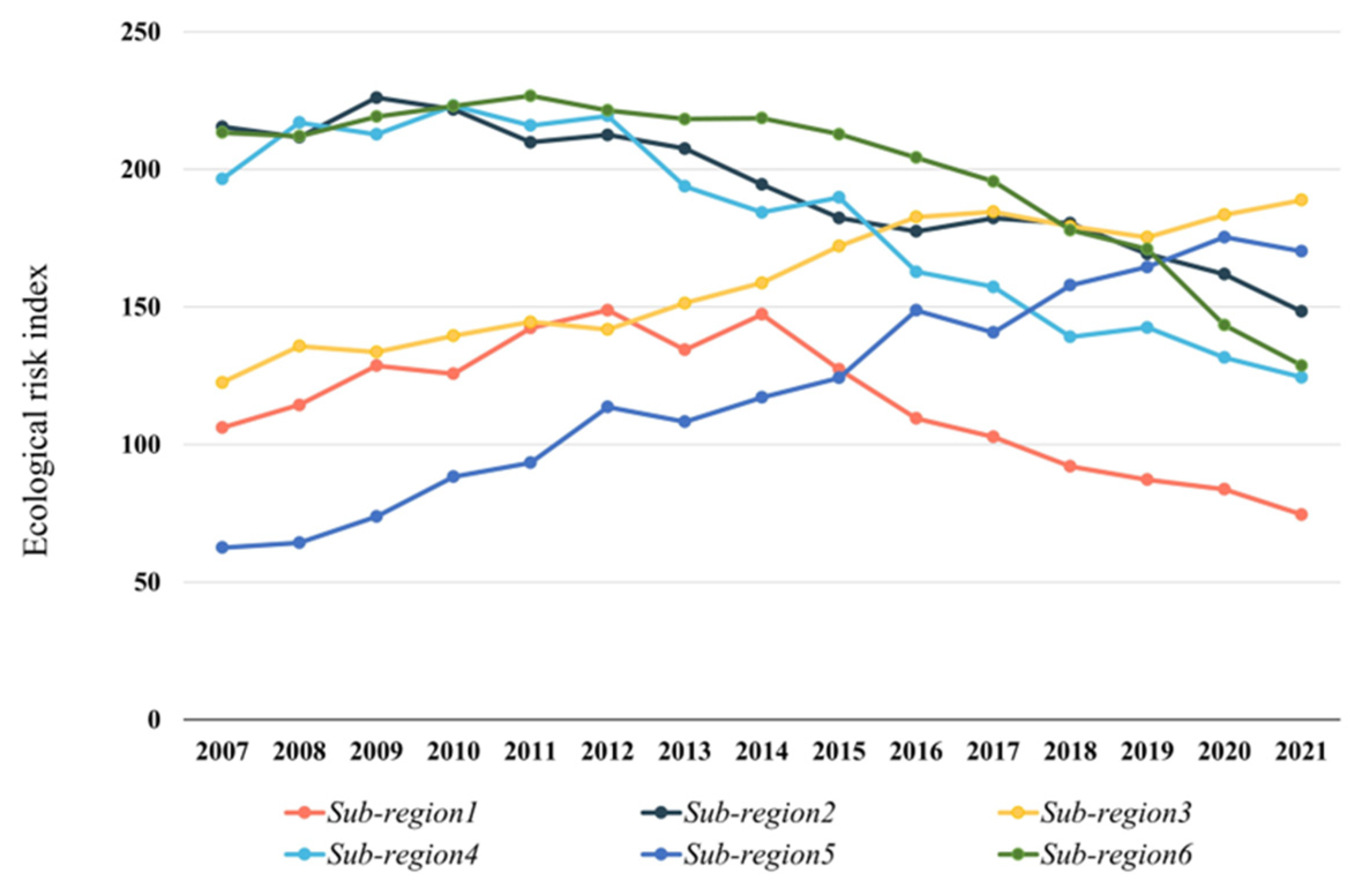
3.1. Descriptive Statistics
3.2. Land Use and Ecological Risk Causality Tests
3.2.1. Unit Root Test
3.2.2. Cointegration Test
3.2.3. Error Correction Model
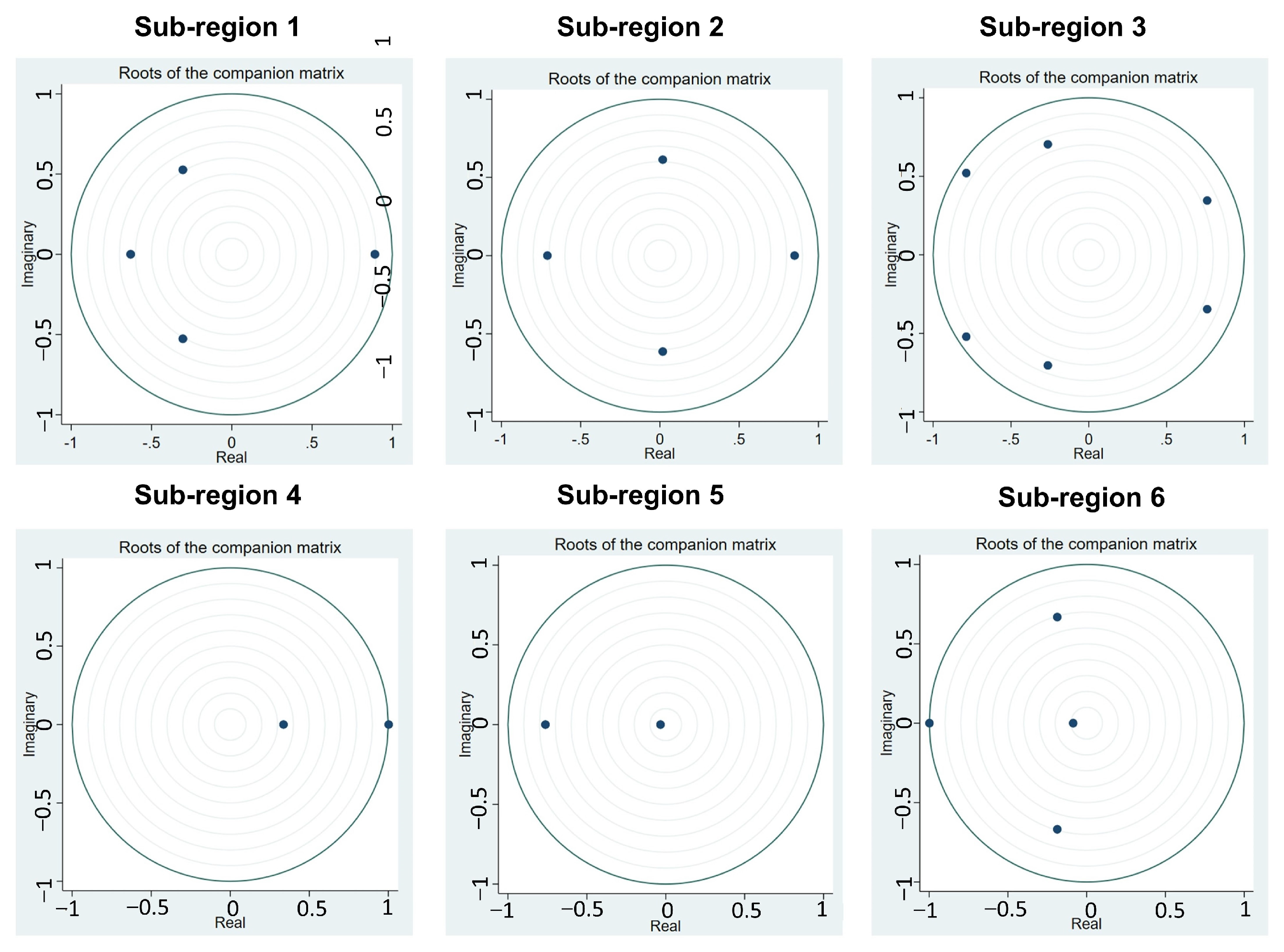
3.2.4. Granger Causality Test
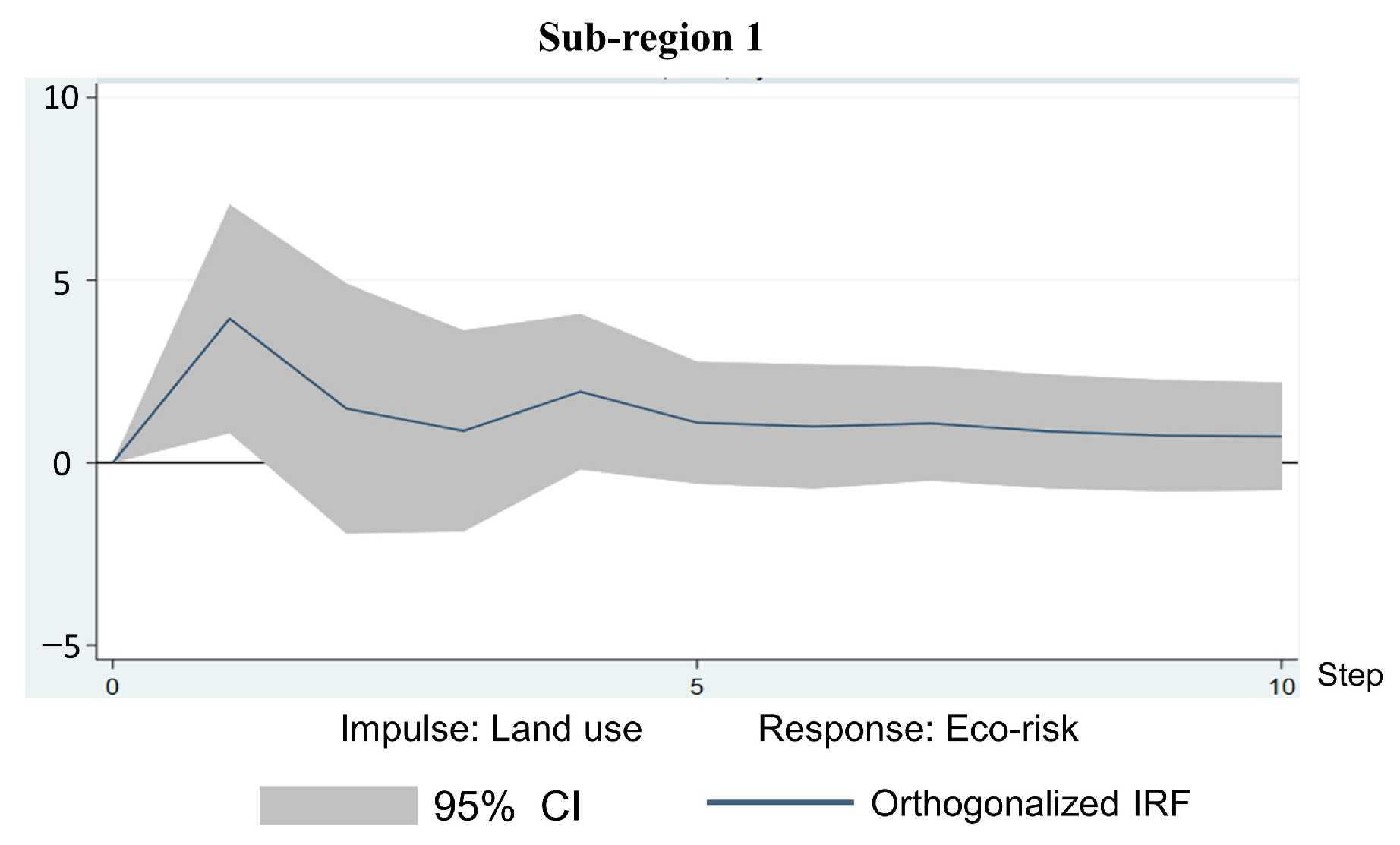
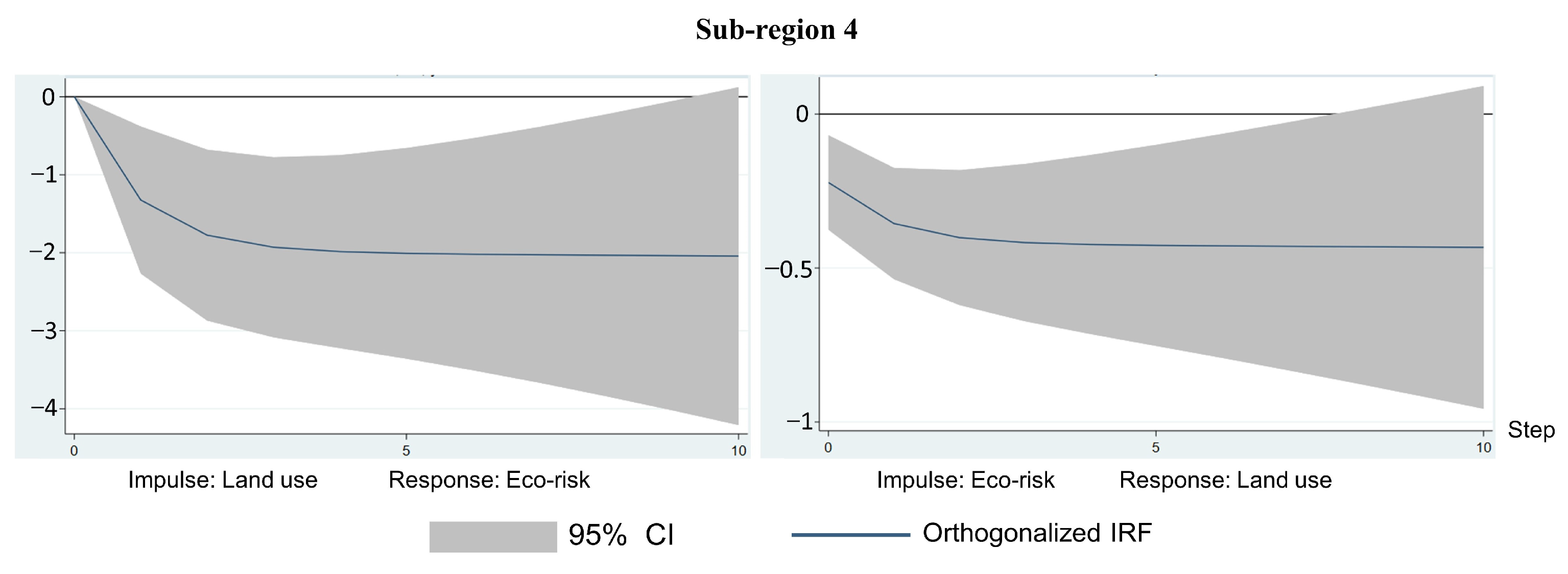
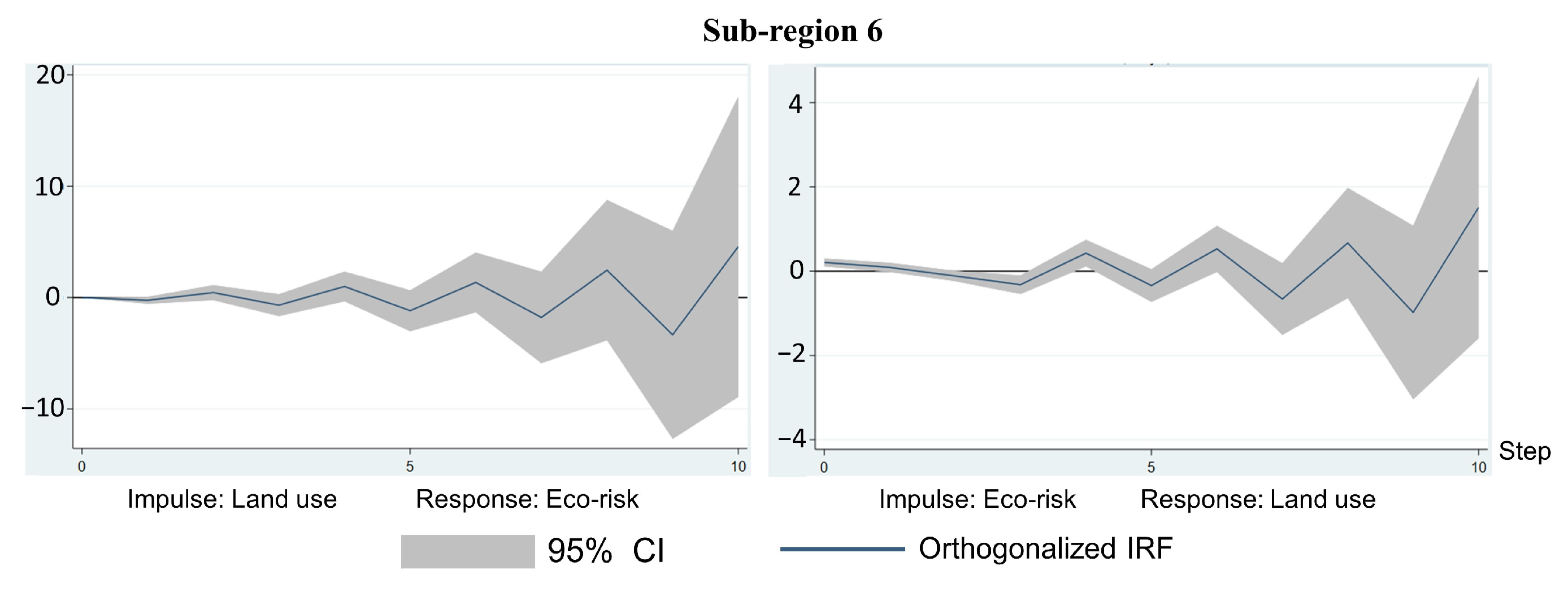
3.2.5. Impulse Response Analysis
4. Discussion
4.1. Land Use and Ecological Risk Cointegration
4.2. Granger Causality Analysis for Different Sub-Regions
4.3. Land Use and Ecological Risk Pulse Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McDowell, N.G.; Allen, C.D.; Anderson-Teixeira, K.; Aukema, B.H.; Bond-Lamberty, B.; Chini, L.; Clark, J.S.; Dietze, M.; Grossiord, C.; Hanbury-Brown, A.; et al. Pervasive Shifts in Forest Dynamics in a Changing World. Science 2020, 368, eaaz9463. [Google Scholar] [CrossRef]
- Jin, X.; Jin, Y.; Mao, X. Ecological Risk Assessment of Cities on the Tibetan Plateau Based on Land Use/Land Cover Changes–Case Study of Delingha City. Ecol. Indic. 2019, 101, 185–191. [Google Scholar] [CrossRef]
- Powers, R.P.; Jetz, W. Global Habitat Loss and Extinction Risk of Terrestrial Vertebrates under Future Land-Use-Change Scenarios. Nat. Clim. Chang. 2019, 9, 323–329. [Google Scholar] [CrossRef]
- Kindu, M.; Schneider, T.; Teketay, D.; Knoke, T. Changes of Ecosystem Service Values in Response to Land Use/Land Cover Dynamics in Munessa–Shashemene Landscape of the Ethiopian Highlands. Sci. Total Environ. 2016, 547, 137–147. [Google Scholar] [CrossRef] [PubMed]
- Liao, N.; Gu, X.; Wang, Y.; Xu, H.; Fan, Z. Analyzing Macro-Level Ecological Change and Micro-Level Farmer Behavior in Manas River Basin, China. Land 2020, 9, 250. [Google Scholar] [CrossRef]
- Hou, D.; O’Connor, D.; Nathanail, P.; Tian, L.; Ma, Y. Integrated Gis and Multivariate Statistical Analysis for Regional Scale Assessment of Heavy Metal Soil Contamination: A Critical Review. Environ. Pollut. 2017, 231, 1188–1200. [Google Scholar] [CrossRef]
- Guo, X.; Fang, C. Integrated Land Use Change Related Carbon Source/Sink Examination in Jiangsu Province. Land 2021, 10, 1310. [Google Scholar] [CrossRef]
- Khaledian, Y.; Kiani, F.; Ebrahimi, S.; Brevik, E.; Aitkenhead-Peterson, J. Assessment and Monitoring of Soil Degradation During Land Use Change Using Multivariate Analysis. Land Degrad. Dev. 2017, 28, 128–141. [Google Scholar] [CrossRef]
- de Baan, L.; Alkemade, R.; Koellner, T. Land Use Impacts on Biodiversity in Lca: A Global Approach. Int. J. Life Cycle Assess. 2013, 18, 1216–1230. [Google Scholar] [CrossRef]
- Peters, M.K.; Hemp, A.; Appelhans, T.; Becker, J.N.; Behler, C.; Classen, A.; Detsch, F.; Ensslin, A.; Ferger, S.W.; Frederiksen, S.B.; et al. Climate–Land-Use Interactions Shape Tropical Mountain Biodiversity and Ecosystem Functions. Nature 2019, 568, 88–92. [Google Scholar] [CrossRef]
- Mahowald, N.M.; Randerson, J.T.; Lindsay, K.; Munoz, E.; Doney, S.C.; Lawrence, P.; Schlunegger, S.; Ward, D.S.; Lawrence, D.; Hoffman, F.M. Interactions between Land Use Change and Carbon Cycle Feedbacks. Glob. Biogeochem. Cycles 2017, 31, 96–113. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Liu, Y.; Hai, X.; Shanguan, Z.; Deng, L. Driving Factors of Ecosystem Services and Their Spatiotemporal Change Assessment Based on Land Use Types in the Loess Plateau. J. Environ. Manag. 2022, 311, 114835. [Google Scholar] [CrossRef] [PubMed]
- Meneses, B.M.; Reis, R.; Vale, M.J.; Saraiva, R. Land Use and Land Cover Changes in Zêzere Watershed (Portugal)--Water Quality Implications. Sci. Total. Environ. 2015, 527, 439–447. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.; House, J.; Bustamante, M.; Sobocká, J.; Harper, R.; Pan, G.-X.; West, P.; Clark, J.; Adhya, T.; Rumpel, C.; et al. Global Change Pressures on Soils from Land Use and Management. Glob. Chang. Biol. 2016, 22, 1008–1028. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, Q.; Tong, X.; Chen, L. Evaluating Land Ecological Security and Examining Its Relationships with Driving Factors Using Gis and Generalized Additive Model. Sci. Total Environ. 2018, 633, 1469–1479. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, D.; Chang, X.; Lin, Z. A New Grading System for Evaluating China’s Cultivated Land Quality. Land Degrad. Dev. 2020, 31, 1482–1501. [Google Scholar] [CrossRef]
- Dormann, C.F.; Schweiger, O.; Augenstein, I.; Bailey, D.; Billeter, R.; De Blust, G.; DeFilippi, R.; Frenzel, M.; Hendrickx, F.; Herzog, F.; et al. Effects of Landscape Structure and Land-Use Intensity on Similarity of Plant and Animal Communities. Glob. Ecol. Biogeogr. 2007, 16, 774–787. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y.; Zhou, Z.; Nanshan, Y.; Meng, J. Dynamic Ecological Risk Assessment and Management of Land Use in the Middle Reaches of the Heihe River Based on Landscape Patterns and Spatial Statistics. Sustainability 2016, 8, 536. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Qian, Q.; Wu, Z.; Zheng, Z.; Huang, Q. The Coupling Relationship between Construction Land Expansion and High-Temperature Area Expansion in China’s Three Major Urban Agglomerations. Int. J. Remote Sens. 2019, 40, 6680–6699. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, Z.; Shen, C.; Li, Y.; Feng, Z.; Zeng, W.; Huang, G. Relationship between the Geographical Environment and the Forest Carbon Sink Capacity in China Based on an Individual-Tree Growth-Rate Model. Ecol. Indic. 2022, 138, 108814. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Yueting, M.; Li, L.; Wang, X.; Lin, Q. Dynamic Simulation of Land Use Change and Assessment of Carbon Storage Based on Climate Change Scenarios at the City Level: A Case Study of Bortala, China. Ecol. Indic. 2022, 134, 108499. [Google Scholar] [CrossRef]
- Hunsaker, C.T.; Graham, R.L.; Suter, G.W.; O’Neill, B.; Jackson, B.L.; Barnthouse, L.W. Regional Ecological Risk Assessment: Theory and Demonstration; Technical Report; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 1989.
- Xu, X.; Xu, L.; Yan, L.; Ma, L.; Lu, Y. Integrated Regional Ecological Risk Assessment of Multi-Ecosystems under Multi-Disasters: A Case Study of China. Environ. Earth Sci. 2015, 74, 747–758. [Google Scholar] [CrossRef]
- Kang, P.; Chen, W.; Hou, Y.; Li, Y. Linking Ecosystem Services and Ecosystem Health to Ecological Risk Assessment: A Case Study of the Beijing-Tianjin-Hebei Urban Agglomeration. Sci. Total Environ. 2018, 636, 1442–1454. [Google Scholar] [CrossRef] [PubMed]
- Pártl, A.; Vačkář, D.; Loučková, B.; Krkoška Lorencová, E. A Spatial Analysis of Integrated Risk: Vulnerability of Ecosystem Services Provisioning to Different Hazards in the Czech Republic. Nat. Hazards 2017, 89, 1185–1204. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Zhang, Y.; Yang, X.; Zhang, K. Risk Assessment of Forest Landscape Degradation Using Bayesian Network Modeling in the Miyun Reservoir Catchment (China) with Emphasis on the Beijing–Tianjin Sandstorm Source Control Program. Land Degrad. Dev. 2018, 29, 3876–3885. [Google Scholar] [CrossRef]
- Shahbaz, M.; Hye, Q.M.A.; Tiwari, A.K.; Leitão, N.C. Economic Growth, Energy Consumption, Financial Development, International Trade and Co2 Emissions in Indonesia. Renew. Sustain. Energy Rev. 2013, 25, 109–121. [Google Scholar] [CrossRef]
- Gries, T.; Redlin, M.; Ugarte, J.E. Human-Induced Climate Change: The Impact of Land-Use Change. Theor. Appl. Climatol. 2019, 135, 1031–1044. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Zhang, Y.; Wang, J. Ecological Response of Land Use Change in a Large Opencast Coal Mine Area of China. Resour. Policy 2023, 82, 103551. [Google Scholar] [CrossRef]
- LIU, J. Macro Survey and Dynamic Research on Remote Sensing of Resources and Environment in China; Press of University of Science and Technology of China: Hefei, China, 1996. [Google Scholar]
- Norton, S.B.; Rodier, D.J.; van der Schalie, W.H.; Wood, W.P.; Slimak, M.W.; Gentile, J.H. A Framework for Ecological Risk Assessment at the Epa. Environ. Toxicol. Chem. 1992, 11, 1663–1672. [Google Scholar] [CrossRef]
- Suter II, G.W. Ecological Risk Assessment; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Xu, X.; Lin, H.; Fu, Z. Probe into the Method of Regional Ecological Risk Assessment—A Case Study of Wetland in the Yellow River Delta in China. J. Environ. Manag. 2004, 70, 253–262. [Google Scholar] [CrossRef]
- Xu, X.; Yan, L.; Xu, L.; Lu, Y.; Ma, L. Ecological Risk Assessment of Natural Disasters in China. Beijing Daxue Xuebao (Ziran Kexue Ban)/Acta Sci. Nat. Univ. Pekin. 2011, 47, 901–908. [Google Scholar]
- Zhang, F.; Yushanjiang, A.; Wang, D. Ecological Risk Assessment Due to Land Use/Cover Changes (Lucc) in Jinghe County, Xinjiang, China from 1990 to 2014 Based on Landscape Patterns and Spatial Statistics. Environ. Earth Sci. 2018, 77, 491. [Google Scholar] [CrossRef]
- Assessment, E.R. Guidelines for Ecological Risk Assessment; Environmental Protection Agency: Washington, DC, USA, 1998. [Google Scholar]
- Guo, K.; Zhang, X.; Liu, J.; Wu, Z.; Chen, M.; Zhang, K.; Chen, Y. Establishment of an Integrated Decision-Making Method for Planning the Ecological Restoration of Terrestrial Ecosystems. Sci. Total Environ. 2020, 741, 139852. [Google Scholar] [CrossRef] [PubMed]
- Iyalomhe, F.O.; Rizzi, J.; Pasini, S.; Torresan, S.; Critto, A.; Marcomini, A. Regional Risk Assessment for Climate Change Impacts on Coastal Aquifers. Sci. Total Environ. 2015, 537, 100–114. [Google Scholar] [CrossRef]
- Clemens, M.; Khurelbaatar, G.; Merz, R.; Siebert, C.; van Afferden, M.; Rödiger, T. Groundwater Protection under Water Scarcity; from Regional Risk Assessment to Local Wastewater Treatment Solutions in Jordan. Sci. Total Environ. 2020, 706, 136066. [Google Scholar] [CrossRef]
- Halicioglu, F. An Econometric Study of Co2 Emissions, Energy Consumption, Income and Foreign Trade in Turkey. Energy Policy 2009, 37, 1156–1164. [Google Scholar] [CrossRef]
- Gil-Alana, L.A. Testing of Fractional Cointegration in Macroeconomic Time Series*. Oxf. Bull. Econ. Stat. 2003, 65, 517–529. [Google Scholar] [CrossRef]
- Inoue, A.; Kilian, L. Joint Bayesian Inference About Impulse Responses in Var Models. J. Econom. 2022, 231, 457–476. [Google Scholar] [CrossRef]


| Type | Unused Land Grade | Forest, Grassland, Water Land Grade | Agricultural Land Grade | Urban Settlement Land Grade |
|---|---|---|---|---|
| Land Use Type | Unused Land or Difficult-to-Use Land | Forest, Grassland, Water Area | Arable Land, Orchard, Artificial Grassland | Urban, Residential Area, Industrial and Mining Land, Transportation Land |
| Grading Index | 1 | 2 | 3 | 4 |
| Sub-Region | Variable | ADF Test | First Difference | Second Difference |
|---|---|---|---|---|
| 1 | Y1 | −1.877 | −4.143 *** | - |
| X1 | −1.056 | −4.798 *** | - | |
| 2 | Y2 | −2.197 | −3.259 + | - |
| X2 | −1.245 | −7.042 *** | - | |
| 3 | Y3 | −1.734 | −3.019 | −4.505 *** |
| X3 | −2.214 | −0.103 | −6.643 *** | |
| 4 | Y4 | −3.662 * | - | - |
| X4 | −3.214 + | - | - | |
| 5 | Y5 | −4.827 *** | −6.607 *** | −8.654 *** |
| X5 | 0.229 | −2.039 | −3.154 + | |
| 6 | Y6 | 0.24 | −7.13 *** | −8.928 *** |
| X6 | −0.035 | −2.909 | −3.276 + |
| Sub-Region | Z-Value | Existence of Long-Term Stable Relationship |
|---|---|---|
| 1 | −3.546 ** | Yes |
| 2 | −4.612 *** | Yes |
| 3 | −2.648 + | Yes |
| 4 | −3.413 ** | Yes |
| 5 | −3.665 ** | Yes |
| 6 | −4.129 *** | Yes |
| Null Hypothesis | Region | Lag Order | Chi-Square Statistics | p-Value | Conclusion |
|---|---|---|---|---|---|
| Land use is not a Granger cause of ecological risk Ecological risk is not a Granger cause of land use | 1 | 2 | 11.122 | 0.004 | Rejected |
| 2 | 1.6832 | 0.431 | Not Rejected | ||
| 2 | 2 | 1.1358 | 0.567 | Not Rejected | |
| 2 | 2.7653 | 0.251 | Not Rejected | ||
| 3 | 3 | 6.1706 | 0.104 | Not Rejected | |
| 3 | 435.15 | 0.000 | Rejected | ||
| 4 | 1 | 10.383 | 0.001 | Rejected | |
| 1 | 14.411 | 0.000 | Rejected | ||
| 5 | 1 | 0.37045 | 0.543 | Not Rejected | |
| 1 | 0.5538 | 0.457 | Not Rejected | ||
| 6 | 3 | 7.5963 | 0.055 | Rejected | |
| 3 | 22.231 | 0.000 | Rejected |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; He, Z.; Liang, X.; Chen, X.; Luo, R.; Qiu, T.; Zhang, K. Examining Relationships between Regional Ecological Risk and Land Use Using the Granger Causality Test Applied to a Mining City, Daye, China. Land 2023, 12, 2060. https://doi.org/10.3390/land12112060
Guo K, He Z, Liang X, Chen X, Luo R, Qiu T, Zhang K. Examining Relationships between Regional Ecological Risk and Land Use Using the Granger Causality Test Applied to a Mining City, Daye, China. Land. 2023; 12(11):2060. https://doi.org/10.3390/land12112060
Chicago/Turabian StyleGuo, Kai, Zhenhao He, Xiaojin Liang, Xuanwei Chen, Renbo Luo, Tianqi Qiu, and Kexin Zhang. 2023. "Examining Relationships between Regional Ecological Risk and Land Use Using the Granger Causality Test Applied to a Mining City, Daye, China" Land 12, no. 11: 2060. https://doi.org/10.3390/land12112060
APA StyleGuo, K., He, Z., Liang, X., Chen, X., Luo, R., Qiu, T., & Zhang, K. (2023). Examining Relationships between Regional Ecological Risk and Land Use Using the Granger Causality Test Applied to a Mining City, Daye, China. Land, 12(11), 2060. https://doi.org/10.3390/land12112060






