Abstract
In the context of green and high-quality development, effectively enhancing industrial carbon emission efficiency is critical for reducing carbon emissions and achieving sustainable economic growth. This study explored this research area using three models: the super-efficient SBM model was used to measure the industrial carbon emission efficiency of 48 cities in the Pearl River Basin from 2009 to 2017; the exploratory spatiotemporal data analysis method was used to reveal the spatiotemporal interaction characteristics of industrial carbon emission efficiency; and the geographical detectors and geographically weighted regression model were employed to explore the influencing factors. The results are as follows: (1) The Pearl River Basin’s industrial carbon emission efficiency steadily increased from 2009 to 2017, with an average annual growth rate of 0.18 percent, but the industrial carbon emission efficiency of some sites remains low; (2) The local spatiotemporal pattern of industrial carbon emission efficiency is solitary and spatially dependent; (3) The spatial variation of industrial carbon emission efficiency is influenced by a number of factors, including the industrialization level, openness to the outside world, the science and technology level, energy consumption intensity, and productivity level, with the productivity level, industrialization level, and openness to the outside world being the most important. Among these factors, the productivity level, science and technology level, openness to the outside world, and industrialization level all have a positive correlation with industrial carbon emission efficiency, but energy consumption intensity has a negative correlation. This study provides an integrated framework using exploratory spatiotemporal analysis and geographically weighted regression to examine carbon emission efficiency among cities. It can serve as a technical support for carbon reduction policies in cities within the Pearl River Basin, as well as a reference for industrial carbon emission studies of other regions of the world.
1. Introduction
Low-carbon development is becoming a critical component in addressing the world’s environmental issues and climate change [1,2,3]. More and more countries have put forward carbon emission (CE) reduction strategies of “carbon peaking” and “carbon neutrality” [4]. As the world’s second-biggest economy and greatest carbon emitter, China faces great challenges in CE reduction [5,6]. In the year 2019, China’s CE accounted for 27% of total global emissions. Therefore, China is facing enormous pressure to decrease CE [7]. Based on this, China’s national 14th Five-Year Plan (2021–2025) formulates targeted CE reduction goals. Total CE and CE per unit of GDP will be reduced by 13.5 percent and 18 percent, respectively, until 2025, while forest coverage will rise to 24.1 percent. Based on such an emission reduction target, the Pearl River Basin (PRB), an area with an extensive development model, will face huge pressure in terms of CE reduction. How to successfully cut CE while ensuring long-term economic growth has become a fundamental concern in the PRB’s development.
As a major source of economic growth, industry also contributes significantly to energy consumption and CE [8,9,10]. According to the National Bureau of Statistics of China and the China Carbon Accounting Database (CEADs), China’s industrial added value accounts for 31.6 percent of value-added GDP, with industrial energy consumption and CE accounting for 66.2 percent and 38.9 percent of the country’s total, respectively. Therefore, the key to China’s “carbon peak” goal is to reduce industrial CE. Since industrial CE mainly comes from energy consumption in industrial production, there are two methods for lowering CE. The first is to reduce CE by controlling industrial energy usage. The second method is to boost industrial carbon emission efficiency (CEE). Industrial carbon emission efficiency (ICEE) can effectively reflect energy utilization and measure regional production capacity, which is important for reducing CE and achieving sustainable economic growth [11]. The first approach is at the expense of industrial development, which will inhibit economic growth. Consequently, the second method is the key to improving ICEE and achieving low-carbon development. However, owing to disparities in resource endowment and energy use across the country, there are spatial differences in ICEE. This means that, to elevate ICEE, it is necessary to accurately measure the regional differences in industrial carbon efficiency. Furthermore, it is necessary to analyze the driving factors of industrial carbon efficiency and put forward corresponding policy suggestions.
The study of ICEE in the Pearl River Basin is of imminent concern. The spatial and temporal analysis of ICEE and the identification of influencing factors are beneficial to the significance of regional carbon emission reduction research.
2. Literature Review
Currently, China is committed to strengthening economic development by conserving energy and reducing emissions in the industrial sector [12,13,14]. Therefore, academics have looked into the link between CE and economic growth. For instance, in China’s metal industry sector, there is a link between economic growth and CE [15,16]; in China, the relationship between CE and economic growth in the transportation industry is being investigated by academics [17], as is ICEE [18]. Simultaneously, CEE has been a key focus of research. The measurement methods, emission reduction potential, temporal and spatial characteristics, and influencing factors of CEE are the main concerns of scholars [12]. As a result, ICEE research is extremely important.
To measure CEE, scholars have taken advantage of DEA methods to explore numerous studies on CEE [19,20,21]. Since CEE is the product of a variety of causes [22,23,24], it contains not only desired outputs but also non-desired outputs [25]. A DEA model that does not consider non-desired outputs will lead to a big deviation in efficiency measurements [26]. To incorporate non-desired outputs into the classic DEA model, Fare postulates the low disposability of pollution factors [27] and constructs a DEA model to assess environmental efficiency. However, the solution of this model is too complicated, and it has some limitations in practical applications. Hailu and Veeman [28] treat the non-desired output variables as inputs, but this treatment is not consistent with the real manufacturing process. Chung et al. [29] put forward a directional distance function that takes into account both intended and non-desired output increases and decreases. The problem of efficiency evaluation considering non-desired outputs has been well solved. However, these solutions cannot eliminate the unproductive parts caused by input–output slack and cannot solve the measurement deviation caused by radial or angle selection. Tone [30] forms a non-radial and non-angular efficiency measurement method by explicitly incorporating the slack variables into the objective function. At the same time, he constructs a Slacks-Based Measure, SBM model (SBM) to avoid the deviation caused by the difference between radial and angular choices. Tone [31] better fits the actual industrial manufacturing process and properly measures the environmental efficiency of industrial manufacture by incorporating undesired outputs into the SBM model. The SBM model makes up for the defects and deficiencies of the conventional DEA model. It also has the ability to resolve the slack phenomenon of input and output in the efficiency measuring model. In addition, it can effectively make up for the traditional DEA model’s inability to further distinguish the DMU from the efficiency of 1. It is a powerful tool for measuring ICEE [32,33].
Due to the different energy consumption levels of different departments, their CEE is also different. Many scholars have also studied the spatial characteristics and trends of CEE in different sectors. For example, Liu [34] discusses the evolution of resources CE and its efficiency in China’s manufacturing industry. He finds that the resources CE and its efficiency in China’s manufacturing industry shows an increasing trend. Zhao et al. [35] study the CEE of transportation departments and find that the total CEE of transportation departments in China is 0.618. The results show that most areas still need to be improved, and the provinces with the highest efficiency level are found along China’s developed coasts. Zhang [36] studies the inter-provincial ICEE in China and finds that there is a spatial aggregation phenomenon among provincial ICEE. In addition, in China’s construction sector, Du et al. [37] investigate the spatial distribution dynamic of provincial CEE and discover a downward tendency from east to west. In addition, even with the same resource endowment and economic development level, the CEE levels in different regions have also been found to differ [38,39].
To further improve CEE, many researchers have looked into the elements that influence CE. Cheng et al. [11] investigate the impact of technological advancement on CE; Isaeva et al. [40] research the impact of tourism and financial development on CE; and Deng et al. [41] analyze the link between economic growth and agricultural CE. The findings reveal that economic growth and the total intensity of agricultural production have a cointegration connection. Furthermore, Economic growth is linked to the CE intensity of five carbon sources: fertilizer, pesticides, agricultural film, agricultural fuel, and agriculture. Agricultural CE is primarily driven by economic development. Xin et al. [42] evaluate the logistics effectiveness of 30 Chinese provinces from 2003 to 2016, and analyze the logistics efficiency of each province and its regional differences, while He et al. [43] examine the impact of renewable energy technology innovation on the total factor carbon performance index from a market viewpoint. However, most of the current research focuses on determining the components that influence CE from an industrial standpoint without considering the spatial effect.
At present, the CEE research focuses on the three following aspects. The first one is the CEE measurement. Previous studies [44,45] have focused on the “single factor” measurement method, which is expressed by the ratio of total CE to a certain factor. However, CEE is the result of a combination of economic development, energy consumption, and other factors. The second is the CEE analysis of different industries. Some scholars have studied the CEE of the manufacturing industry [46], and some scholars have studied the CEE of the transportation industry [47] and agriculture [48]. The third one is the study of CEE in different regions. Sun et al. [49] combine the three-stage DEA model and the super-efficient SBM model to measure the CEE in the east and west regions of China, and make a comparative analysis of the difference of CEE in the east and west regions. Guo et al. [50] use the SBM model to quantify the level of CEE in the Yangtze River Delta region from 1997 to 2014, examine dynamic changes in CEE, and determine the potential for CEE growth. It can be seen that the existing studies mainly combine industrial and socio-economic data to carry out their research. However, these prior studies lack either spatial precision or a precise focus on industry. Either they focus on industrial CEE at the regional level, or they study overall CEE at the level of individual cities. Few studies have examined the CEE of industries at the city scale.
Based on the available research, the present study quantifies ICEE in the PRB using the super-efficiency SBM model and examines the spatial effect of ICEE using the LISA time path and space–time transition. The geographical detectors and a geographically weighted regression model are used to analyze the factors that affect ICEE. The remainder of the article is structured as follows: First, the super-efficient SBM model is used to calculate ICEE within the PRB. Next, the geographical detectors are used to examine how the affecting elements are related to one another. Finally, in order to explain the effects of each ICEE component and to examine the regional heterogeneity of these effects, a spatially weighted regression model is utilized. Based on these analyses, suggestions for improving ICEE and developing a green economy are proposed.
3. Research Area and Methodology
In this study, the ICEE of the PRB is measured using the super-efficient SBM model, which takes into account undesired outputs and provides calculation results that are more consistent with actual industrial production. Exploratory spatiotemporal data analysis is used to analyze the spatial and temporal evolutionary characteristics of ICEE in the PRB. The geographical detectors are then used to explore the main factors affecting the spatial divergences in ICEE. Geographically weighted regression models are used to explore the synergistic relationship between the influencing factors and ICEE.
3.1. Research Area
The PRB is located in southern China (Figure 1), in the tropical and subtropical monsoon climatic zone (102°14′ E 115°53′ E; 21°31′ N 26°49′ N). The PRB consists of the Xijiang, Beijiang, Dongjiang, and the Pearl River Delta rivers. I It flows through Yunnan, Guizhou, Guangxi, Fujian, and Guangdong, and many other areas in the south of China, and has a basin area of more than 440,000 square kilometers, making it one of China’s largest rivers. The upper reaches of the PRB are mostly plateaued with a low level of economic development. The Pearl River Delta’s flat and open lower sections are one of China’s most developed locations. In that region, traditional energy-intensive industries and third-party service industries account for a relatively large proportion of overall industrial activity. Among them, super-large cities represented by Guangzhou and Shenzhen have become important growth poles of regional economic development. At present, as the PRB is in a critical period of economic development, it is under immense strain due to the need to combine economic growth and CE reductions.
Figure 1.
The research area’s location.
3.2. Super-Efficient SBM Model
In this study, the ICEE of 48 places in the PRB was calculated from 2009 to 2017 using the super-efficient SBM model, while the spatial measurement approach was utilized to investigate the spatiotemporal features of regional ICEE and the contributing variables. The classic DEA approach causes “slack” in input components and is unable to appropriately calculate the efficiency value. For this reason, in 2001, Tone proposed an SBM model which includes a non-desired result. The SBM model, like the traditional DEA model, is still unable to provide a detailed categorization of DMUs with an efficiency value of 1. Therefore, Tone created an SBM model based on the classic SBM model, but which employs non-desired outcomes, such as pollution, as the goal function, and then differentiates the differences between efficient DMUs. The specific model is built as follows:
where, n is the number of decision unit DUM; c denotes the cth DMU; f is the fth DMU by current efficiency; z is the input indicator; m denotes the number of input indications; h denotes the hth input indicator; ed and eu are the desired output and non-desired output indices, respectively; r1 and r2 denote the number of desired output and non-desired output indices; l and p denote the lth and the pth desired output and non-desired output indices; ρ is the ICEE value; and λ denotes the weight.
3.3. LISA Time Path
The LISA time route adds a time component to the classic static LISA to present the evolution of the LISA locations in the Moran scatter diagram [51]. The moving path of the LISA coordinates is [(ei,1, eDi,1), (ei,2, eDi,1),…, (ei,t, eDi,t)], where ei,t denotes the standardized value of the number of ICEE in the region i in the t year, and eDi,t is the spatial lag of the region i in the t year [52]. In the Moran scatter plot, the LISA time path can be used to evaluate the degree of stability of the LISA coordinates comprising attribute variables and spatial delays, and to explain the spatial and temporal synergistic changes in ICEE in different places, as well as local spatial differences and their spatial-temporal dynamics. The path length, curvature, and crossover rate are some of the geometric properties [53].
The length of the LISA time path can indicate the dynamic properties of the research area’s local spatial structure, and is expressed as follows:
where, N is the number of cities; T is the annual time interval; Di,t is the LISA coordinate of city unit in year t; m(Di,t, Di,t+1) is the moving distance of city unit i from year t to year t + 1. The larger m is, the stronger the local spatial structure; an m > 1 means that the moving distance of the city unit i is larger than the mean value of the city moving distance.
The LISA time path curvature may be used to indicate the studied area’s local spatial structural volatility, and is expressed as follows:
where, m(Di,1, Di,T) is the city unit i’s traveling distance from the first to the last year. The greater the value of f, the more twisted the LISA time path will be and the more sinuous the local spatial structural volatility; if f > 1, this indicates that the moving curvature of the city unit i is higher than the average value.
The LISA time path intersection rate, which is the convergence of the difference of ICEE values of nearby units, may indicate the degree of diversity of the local spatial structure in the studied region, and is expressed as follows:
where, Qi is the sum of the intersection of the actual LISA time paths in each city, and a larger Qi indicates the existence of a more diverse local spatial structure in the evolution of ICEE in the study area.
3.4. LISA Space–Time Transition
The LISA space–time transition can further reveal the dynamic change process of the regional spatial relationships between neighborhoods, which include four types [54]: type I indicates that the city and its neighborhoods do not change over time; type II indicates that only the city itself changes; type III indicates that only the city’s neighborhoods change; and type IV indicates that both the city itself and its neighborhoods change. Type IV can be further separated into type IV(1) and type IV(2). The former means that the transition direction of the city itself and its neighborhood is the same, while the latter means that they change in opposite directions.
3.5. Spatiotemporal Interaction Visualization
The ESTDA framework has the benefit of introducing graph theory to graphically depict evolving complicated geographical phenomena. The covariance correlation coefficient of the LISA time-shift trajectories in surrounding cities can be calculated and then used to visualize the ICEE interaction network among cities.
3.6. The Geographical Detectors
The Geographical Detectors are a statistical tool for analyzing the geographical variability of geographic phenomena and identifying their underlying causes. The primary premise of the geographic detector is as follows: If research identifies numerous sub-regions, and the sum of the variances is less than the total variance of regions, then the geographic detector is correct. The model accounts for is geographical heterogeneity; if the spatial distribution of the two variables is consistent, a statistical correlation exists between them. The model also includes four sub-detectors: factor detection, risk detection, interaction detection, and ecological detection [55]. This study mainly uses factor detection and interaction detection.
- (1)
- Factor detection. The p-value of each factor is calculated using the factor detector. This is then used to quantitatively analyze the spatial variation of industrial carbon emission efficiency and to detect the extent to which a factor explains the spatial variation of ICEE. The expression for this is as follows:
- (2)
- Interactive detection. The purpose of this sub-detector is to determine the interaction between different independent variables, that is, to measure whether the explanatory power of independent variables H1 and Hm to dependent variable Z increases or decreases during the interaction, or whether the effects of these independent variables on dependent variable Z are independent. The specific method of measurement can be illustrated using driver factors H1 and H2 as examples; here, the explanatory powers p(H1) and p(H2) represent the calculated driver factors of H1 and H2 to the dependent variable Z, respectively. The detector measures the explanatory power p(H1∩H2) of the dependent variable Z when H1 and H2 interact with each other. The magnitudes of the three generated values are then compared to see if the effect of the interaction of the two factors on the dependent variable rises or decreases when compared to the effect of a single component. The basis of the judgment is shown in Table 1.
 Table 1. The basis for judging the two-way interaction mode.
Table 1. The basis for judging the two-way interaction mode.
As the geographical detector requires that the independent variables must be type variables, this study further classified the independent variables, into nine categories by the natural breakpoint method. Table 2 shows the results.

Table 2.
Drivers and classification of ICEE.
3.7. Geographically Weighted Regression
Geographical Weighted Regression (GWR), which takes the geospatial relationship into account, was chosen to analyze the factors influencing ICEE, and the formula is as follows:
where, Zi is the ICEE of the city i; ρ0 is the constant term; (pi, qi) is the spatial location of the city i; ρh is the regression coefficient of the hth influencing factor of the ICEE of the city i; The number of spatial places is denoted by the letter n; mih is the hth influencing factor of the ICEE of the city i; and εi is the stochastic error term of the city i.
3.8. Variable Description and Data Sours
The industrial data, industrial energy consumption data, and socioeconomic data utilized in this study were obtained from the 2010–2018 statistical yearbooks of Guangdong, Yunnan, Guizhou, and Fujian prefecture-level cities. Some relevant data were also obtained from these cities’ social development statistical bulletins and EPS data platforms. The following are descriptions of each input and output variable (Table 3).

Table 3.
Evaluation index system of ICEE in the PRB.
- (1)
- Input variables. Input indicators comprised the labor input factor, capital input factor, and industrial energy input factor. Among these, the average yearly number of individuals employed in industrial firms above the scale replaces the labor input element, whereas the average yearly quantity of net fixed assets of industrial firms over the scale replaces the capital input element. However, because the data on industrial energy consumption of prefecture-level municipalities in the PRB were not fully available and electricity consumption is the major driving factor of ICE energy consumption, industrial electricity consumption was chosen as the energy input factor [56].
- (2)
- Desired output. The desired output indicator uses the industrial value-added of industrial enterprises above the scale.
- (3)
- Non-desired output. For the non-desired output index, the carbon emissions of industrial enterprises above the scale were used. The industrial carbon emissions were estimated using the “Average Carbon Emission Factor of China Regional Power Grids” published by the National Reform Commission. The national power grid boundary is divided into Northeast, North, East, Central, Northwest, and South regions according to the current situation of China’s regional power grid division. According to the research needs of this study, the current year’s ICE is equal to the entire industrial energy consumption of the previous year multiplied by the average carbon emission factor of the southern regional power grid [57].
4. Results
4.1. ICEE Measurement
The super-efficient SBM model with the variable returns to scale (VRS) condition constraint was adopted in this work to estimate the ICEE in the PRB region, and four years, 2009, 2012, 2015, and 2017, were selected for analysis (Table 4).

Table 4.
ICEE in the PRB region from 2009 to 2017.
From 2009 to 2017, the ICEE of the PRB region as a whole showed a trend of dropping, then expanding, and then reducing. However, its efficiency value steadily increased, with an average annual rate of change of 0.18 percent. Chongzuo city had the highest ICEE value in the PRB from 2009 to 2017, followed by Fangchenggang city, Liupanshui city, Beihai city, Guangzhou city, with lowest efficiency value calculated for Shantou city. Eighteen cities had negative annual average change rates. These were Qujing and Fangchenggang, as well as the cities in Wenshan Zhuang and Miao Autonomous Prefecture and Qiandongnan Miao and Dong Autonomous Prefecture. The remainder of the areas had positive yearly average change rates. The initial values of ICEE in Kunming, Guiyang, Liuzhou, and Shenzhen were low, but the growth rate was fast. In 2009, their rankings were 38, 47, 29, and 16, respectively, but these rose to 9, 3, 5, and 1 by 2017, with an average annual growth rate of 16.52 percent, 25.66 percent, 10.91 percent, and 9.55 percent, respectively. These cities therefore belong to the low-level and high-speed growth types. Guiyang City’s average annual growth rate surpassed 20%, which may be attributed to recent changes in Guizhou Province’s resource-based economy and the emergence of the big data sector, causing its CEE to rapidly rise. The initial ICEE values in Yuxi City, Anshun City, and Beihai City were high, with efficiency values of 8, 11, and 6 in 2009, respectively, but the average yearly growth rate was low: 2.03 percent, 2.84 percent, and 0.95 percent. These cities therefore belong to the high-level and low-speed growth types. This could be due to the fact that tourism and agriculture account for a large proportion in the above cities, and these are high energy consumption industries. Relatedly, in most years, several cities, such as Shaoguan, Zhaoqing, Huizhou, Jiangmen, and other regional heavy industrial cities, did not hit the ideal efficiency value, indicating that there is still much space for development.
Spatially, the ICEE in the PRB showed a distribution pattern that can be described as “high in the middle and low in the surroundings” (Figure 2). The ICEE of the cities in the central part of the PRB was high, making this the high-efficiency zone of industrial CE. The ICEE of the cities around the PRB was relatively low, making these areas the low-efficiency zone of industrial CE. The average value of ICEE of most cities was higher than the average value of the PRB as a whole. Among these, the average value of ICEE of 10 cities, including Guangzhou, Shenzhen, Liupanshui, Beihai, Chongzuo, and Fangchenggang, exceeded 0.8, while the average value of ICEE in heavy industrial areas such as Jiangmen, Shantou, and Shaoguan was below 0.4, which is a low level.
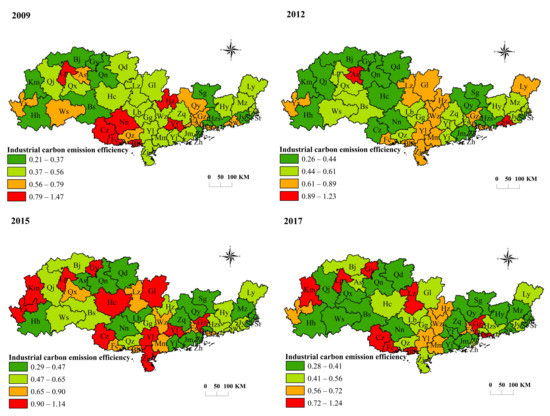
Figure 2.
Spatial distribution pattern of ICEE in the PRB from 2009 to 2017.
4.2. Spatial and Temporal Interactive Dynamic Feature of ICEE
4.2.1. LISA Time Path Geometric Feature Analysis
Throughout the research period, the LISA time path of ICEE in the PRB (Figure 2) shows that 37.5% of the cities had a time path length of more than 1. This indicates that the local pattern of ICEE had a significant pattern of change over time. The length of the time path showed a trend of expansion from the eastern to the central and western sectors. In addition, the relative lengths of Liupanshui, Kunming, Anshun, and some other regions were all greater than 1.25, indicating that their local spatial structures were highly dynamic. In contrast, the eastern regions of Guangzhou, Zhuhai, and Foshan had relatively short time path movement, with lengths less than 0.8, owing to the east’s fast economic development and industrial technology, as well as the high ICEE, which created a relatively stable local spatial structure. From the center to the periphery, the curvature values were all more than 1, and the overall geographical distribution exhibited a decreasing trend, showing that the ICEE of each location in the PRB had a substantial spatial dependency with time. Fangchenggang, Anshun, Zhongshan, and other locations with a larger curvature represent the clear dynamic changes and interaction process between the above regions and their territories. Guiyang, Shenzhen, Dongguan, Guangzhou, and other less curved locations demonstrated a smooth direction of change and spatial dependency. The LISA time path cross rates (Table 5) showed that the time paths of ICEE in the PRB were relatively loose, with an overall crossing rate of 0.0665 in 2009–2017, and a highest crossing rate of 0.1383 in 2009–2012. The local spatiotemporal pattern was relatively homogeneous, and there were fewer multiple local spatial structures in each prefecture-level city.

Table 5.
LISA time path crossing rates.
4.2.2. Analysis of Movement Direction of LISA Time Path
By comparing the local Moran coordinates of each urban unit in 2009 and 2017, the direction of movement of the LISA coordinate points of each urban unit could be calculated (Figure 3). The 0°–90° direction indicates positive synergistic growth of the urban unit and its neighboring units, and the 180°–270° direction indicates the negative synergistic growth direction of the urban unit and its neighboring units [58]. These two moving directions show the spatial dynamic characteristics of the integration of urban units and their domain units [59]. The 90°–180° and 270°–360° directions indicate that the growth of urban units and their neighborhood units proceeded in the opposite direction [60].
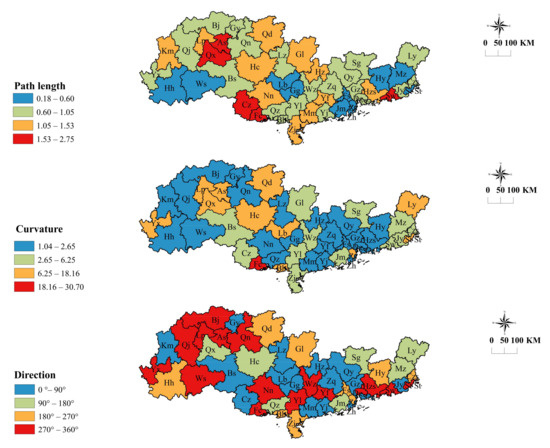
Figure 3.
Spatial distribution of LISA time path geometric features.
On the whole, there were 25 cities with synergistic growth, accounting for 52.08% of the cities in the PRB. This indicates that ICEE had a strong spatial integration and a high positive integration. A total of 16 cities had positive synergistic growth, accounting for 64% of the cities with synergistic growth. In terms of the spatial distribution of each city’s movement direction, the cities with positive synergy were mainly concentrated in Guangzhou, Shenzhen, and other industrially and technologically developed areas, showing characteristics of high synergistic growth. The cities with negative synergy were mainly concentrated in heavy industrial areas such as Jiangmen and Shaoguan, showing low synergistic growth characteristics.
4.2.3. LISA Space–Time Transition Analysis
The space–time transition analysis was used in this research to further define the transfer properties of local spatial correlation types of ICEE in the PRB, and a space–time transition matrix was built (Table 6). The proportions of I-type transition cities in 2009–2012, 2012–2015, and 2015–2017 were 66.6 percent, 70.9 percent, and 87.6 percent, respectively, suggesting that the path dependency of ICEE distribution in the PRB was clear. This spatial relative state of the ICEE of each city became more and more serious after 2009, and it was difficult to change the interaction relationship of ICEE among cities in the short term. The proportions of type II transition cities in Hechi, Kunming, Liupanshui, Guiyang, Zhaoqing, and Hezhou reached 31.3 percent, 29.2 percent, and 12.6 percent, in 2009–2012, 2012–2015, and 2015–2017, respectively, primarily in Hechi, Kunming, Liupanshui, Guiyang, Zhaoqing, and Hezhou. It can be seen that the local spatial correlation structure of ICEE in these regions was fragile. During the research period, the number of cities with changes of type III and type IV was zero, with a tiny fraction of cities having changes of type III and type IV. In order to promote green and high-quality development in underdeveloped areas, the PRB must continue to develop a synergistic mechanism to improve ICEE among regions. Based on the proportion of cities exhibiting these four change types, it is also necessary to achieve innovation in improving efficiency in terms of the intervention of cities themselves and the external forces that exist between regions.

Table 6.
Spatial-temporal transition matrix of ICEE.
4.2.4. Spatiotemporal Network Analysis
This study carved out the spatiotemporal network of ICEE interaction across surrounding cities to further show the spatial aspect underlying the visualization of ICEE (Figure 4 and Figure 5). From the geographical network diagram and the pattern of a topological network of ICEE in the PRB, 102 pairs of negative correlations can be observed, accounting for 49.04%. It can be seen that there was a certain degree of spatiotemporal competition in the evolution of ICEE among neighboring cities. Among the negative associations, 35.29% were weak negative associations, mainly concentrated in the neighboring cities of Guangdong, with a small amount distributed in Guizhou. The pattern of ICEE among neighboring cities was consistent with the evolutionary process of divergence, diffusion, and convergence from the standpoint of development geography theories and laws. Additionally, the imbalance of geographic resource endowment exacerbated the competitive relationship of ICEE among cities, which limited regional development to some extent. The strong negative correlation between Guangzhou and Dongguan, Foshan and Qingyuan, and Nanning and Laibin revealed the uncoordinated characteristics of ICEE development. In each city, there may be some regional attempts at ICE reduction. On the other hand, cities such as Anshun and Bijie, Zhuhai and Jiangmen, Qinzhou and Fangchenggang constituted a strong synergistic area, showing the spatial dynamic of positive synergy; the characteristics of ICEE in these cities were relatively similar, and the geographical concentration of ICEE was revealed.
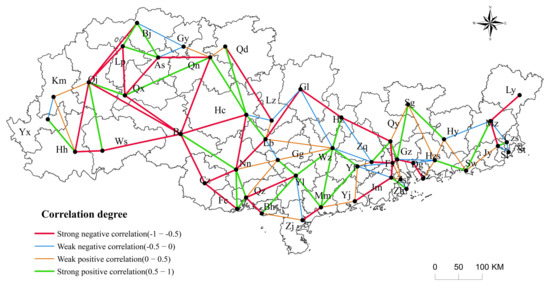
Figure 4.
Geographical network diagram of ICEE.
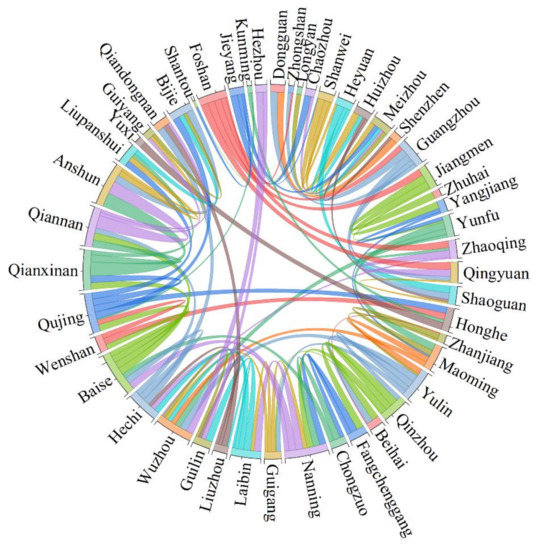
Figure 5.
Topological network diagram of ICEE.
4.3. Examining the Influencing Factors
4.3.1. Identification of Dominant Factors in the Spatial Differentiation of ICEE
The p-values for 2009, 2012, 2015, and 2017 obtained from the geographical detectors were ranked (Table 7), and each factor’s explanatory power passed a significance test at the 1% level.

Table 7.
The results of ICEE spatial differentiation factor detection.
From the whole study period, the productivity level, industrialization level, and degree of openness had a substantial influence on the spatial variation of ICEE, and these were the most important elements influencing ICEE spatial variation. Additionally, their p-values were all greater than 0.3, with productivity level exhibiting the most obvious effect, ranking first in p-values from 2009 to 2017, and reaching 0.41 in 2017. The explanatory powers of science and technology and energy intensity for the spatial divergence of ICEE were average, with p-values ranging from 0.1 to 0.3. The p-value rankings for these factors were 4th or 5th in most years, and their explanatory power for the spatial variation of ICEE is relatively weak. The p-values at all four time points are less than 0.3. On the other hand, the industrialization level was an important potential factor influencing the spatial variation of ICEE in the future, and its p-value increased from 0.18 in 2015 to 0.31 in 2017.
Each influencing factor changed between the different time points. The explanatory powers of the industrialization level and productivity level gradually increased. Specifically, the former increased from 0.18 in 2009 to 0.31 in 2017, and the latter increased from 0.39 in 2009 to 0.41 in 2017. This indicates that the influence of the productivity level and industrialization level on the spatial variation of ICEE was gradually increasing. The order of the explanatory powers of the leading factors also changed greatly. The degree of openness to the outside world dropped from 2nd place in 2009 to 5th place in 2015. However, its p-value ranked 2nd place in most years, which is relatively high. The p-value of science and technology, on the other hand, rose from 5th in 2009 to 4th in 2017. The p-value of energy consumption intensity ranked 3rd in both 2009 and 2017, with no obvious changes.
4.3.2. Identification of the Interaction of Spatial Differentiation of ICEE
Four time periods (2009, 2012, 2015, and 2017) were utilized as study samples to further evaluate the change in the explanatory power of ICEE when different driving factors interacted with each other, and the detection results are shown in Table 8. All drivers were closely related to one another during the study period. The p-values obtained from the interaction of most driving factors increased to different degrees, meaning the combined effect of two factors could improve the explanatory power of ICEE spatial variation. In terms of the type of interaction, all the five drivers were non-linearly enhanced. From the perspective of the time-lapse, the explanatory power of each two-factor interaction was different and showed a fluctuating trend with the time. Specifically, the explanatory power of the interactions of industrialization level and energy consumption intensity, industrialization level and productivity level, openness to the outside world and energy consumption intensity, openness to the outside world and productivity level, and energy consumption and productivity level on the spatial variation of ICEE tended to increase over time. These increased from 0.82, 0.87, 0.55, 0.79, and 0.81 in 2009 to 0.90, 0.91, 0.85, 0.82, and 0.83 in 2017, respectively. In addition, the degree of openness to the outside world and energy consumption intensity were the most significant explanations for the spatial differentiation of CEE. The p-value of this interaction increased from 0.55 in 2009 to 0.85 in 2017. Meanwhile, the explanatory power of the interaction between the industrialization level and science and technology level for ICEE did not change significantly over time and always remained around 0.77. The explanatory power of the interaction of other combinations on ICEE showed a decreasing trend over time. The explanatory power of the interactions between the industrialization level and productivity level and between the science and technology level and productivity level on the spatial variation of ICEE exceeded 0.9 in most years. This shows that the interaction between these two combinations was very important for the spatial variation of ICEE.

Table 8.
The geographical differentiation of ICEE in the PRB yielded interaction detection findings.
4.3.3. Spatial Heterogeneity Analysis of ICEE
The geographical differentiation of the five factors impacting the urban ICEE of the cities was investigated for each one in turn based on the regression findings of the GWR model (Figure 6). The amount of industrialization was shown to be positively connected with ICEE, implying that the higher the level of industrialization, the higher the ICEE. The maximum regression coefficient of the industrialization level was 1.330205, observed for Zhongshan City, and the minimum was 0.435447, in Hezhou City. The maximum value was 3.0548 times the minimum value. In addition, the regression coefficient of the industrialization level decreased from west to east. This indicates that the industrialization level in the western region had a great influence on ICEE. With the improvement in the industrialization level and the upgrading of industrial technology, ICEE was promoted. The industrial development level in the western part of the PRB was lower, and the progress of industrialization was marked by significant energy usage, low treatment, and high emissions at the cost of large resource losses. In the eastern region, capital accumulation and the degree of science and technology were higher, which might be explained by the large number of new knowledge- and information-based industrial enterprises in this region. Ecological-oriented industries are also located there, which reduces the resource consumption and CE, so the effect on the CEE was weakened.
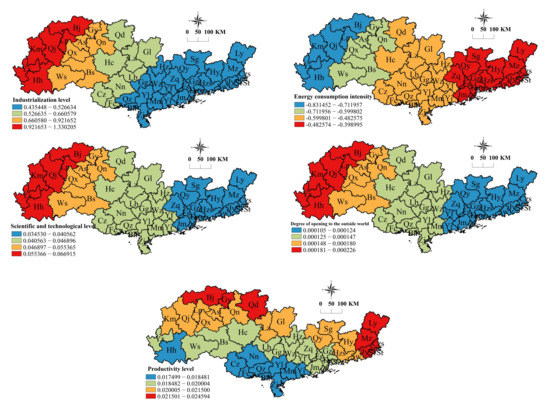
Figure 6.
The spatial distribution of ICEE impact factor regression coefficients.
The relationship between energy consumption intensity and ICEE was always inverse, meaning that the higher the energy consumption intensity, the lower the CEE. In Honghe Hani and Yi Autonomous Prefecture had the greatest regression coefficient of energy consumption intensity at −0.398994, and the smallest was found in Zhongshan, at −0.831451 City. The minimum value was 2.0839 times the maximum value. The regression coefficient of energy consumption intensity increased from west to east as a whole. This indicates that the energy consumption intensity in the eastern region had a great influence on ICEE.
The relationship between ICEE and the degree of science and technology was always positive, implying that the greater the level of research and technology, the higher the ICEE. The biggest scientific and technology level regression coefficient was 0.066915 in Zhongshan City, while the smallest was 0.034529 in Honghe Hani and Yi Autonomous Prefecture, with the maximum value being 1.9379 times the minimum value. The regression coefficient of the science and technology level decreased from west to east, indicating that science and technology in the western region had a great influence on ICEE. The closeness of science and technology level regression coefficients in nearby regions suggested that science and technology level regression coefficients exhibited agglomeration features in space. Science and technology had a greater impact on ICEE in Zhongshan, Zhanjiang, and Zhuhai, whereas it had a lower impact in Honghe Hani and Yi Autonomous Prefecture, Hezhou, and Anshun.
The degree of openness to the outside world exhibited positive regression coefficients for all cities. This demonstrates that the greater the degree of openness to the outside world, the greater the efficiency of industrial CE. The smallest regression coefficient was 0.000105 in Honghe Hani and Yi Autonomous Prefecture, while the greatest was 0.000226 in Zhongshan City, with the maximum value being 2.1524 times the minimum value. The regression coefficients of openness to the outside world exhibited a continuous geographical distribution, suggesting that the regression coefficient of openness to the outside world had agglomeration features in space. The effects of external openness on ICEE were small in Baise, Laibin, and Beihai, and large in Shaoguan, Zhaoqing, and Zhuhai. Science and technology played an important role in improving ICEE. To promote energy conservation and emission reduction, we should increase technology investment, encourage technological innovation and improve the technology level. Moreover, we should vigorously develop energy-saving products, introduce advanced technology, and bring into play the spillover effect of advanced technology to promote energy conservation and emission reduction.
The correlation between the productivity level and ICEE was always positive. The largest regression coefficient was 0.024593 in Honghe Hani and Yi Autonomous Prefecture. The smallest was 0.017498 in Liupanshui City, and the maximum value was 1.4055 times of the minimum value. The regression coefficient of the productivity level decreased from north to south. Theoretically, the growth of the organization, management, and technology of the manufacturing process were linked to an increase in productivity. The enhancement of production technology, as well as a systematic and efficient organization and management system, may promote the efficient allocation of industrial production materials, increase the efficiency of industrial energy use, and therefore promote ICEE. Increased investment in industrial R&D can directly stimulate technological innovation in industrial production, thus improving ICEE. Increased levels of openness to the outside world could encourage foreign-funded enterprises to exert their technology spillover and correlation effects, as well as serving as a model for local industrial ventures.
5. Discussion
The above comprehensive research conclusions provide the following contributions: Firstly, while the PRB’s ICEE has progressively improved, there is still space for improvement, indicating that the PRB still has a long way to go in terms of achieving a low-carbon economy. Secondly, there is a strong dependency on ICEE in the PRB, and it is necessary to strengthen collaboration under the premise of integrated planning. The level of ICEE and the degree of collaboration in the PRB are different. Therefore, each region in the economic zone should formulate appropriate development strategies based on its level of ICEE and pay attention to inter-regional cooperation and coordinated development. Facing the current situation concerning the low cross-rate of ICEE and the low degree of overall synergistic development in the PRB, the PRB should pay attention to diversified and balanced development. Thirdly, there were many factors affecting the spatial variation of ICEE in the PRB, and the degree of influence of these different factors varies.
From the findings of this study, it is clear that the productivity level, industrialization and degree of openness should receive greater attention because they have a great impact on the spatial differentiation of ICEE. At the same time, we should also focus on the combinations of the industrialization level and productivity level, as well as the science and technology level and productivity level, which both had long-term explanatory powers over 0.9. Combining the spatial relationship between the influencing factors and ICEE, we could improve ICEE by reducing energy consumption intensity and improving the productivity, industrialization level and scientific and technological level, to make the PRB a more environmentally friendly and high-quality place to live.
Currently, there are various published studies examining regional CEE. Liu et al. [61] used a spatially lagged time-fixed effects model to conduct an in-depth analysis of the factors influencing CEE in the Yangtze River Economic Zone, and the findings indicated that the efficiency of carbon emissions increased with increasing openness. Some scholars [62,63] studied CEE in the Yangtze River Delta region through spatial econometric models and discovered that there was a clear geographical heterogeneity to CEE. Yang et al. [10] investigated the factors affecting the ICEE in the Chinese provinces using spatial economics and discovered a positive correlation between ICEE and the amount of economic growth, FDI, and technological advancement. The results of our study are consistent with the above research to some extent. However, the majority of earlier research took the form of provincial CE studies. To measure CEE, most of them employed the three-stage DEA models. The majority of earlier research on spatial autocorrelation relied solely on cold–hot spot analyses, excluding any mention of spatiotemporal transitions. Prior research on causal association analysis relied on either geographical weighted regression or geographical detectors, while not combining them both.
In contrast to other research, this study added complexity to the analysis of influential factors and combined spatial autocorrelation analysis with spatial and temporal transition. ICEE at the urban scale in the Pearl River basin was calculated by using the super-efficiency model. Using the LISA spatiotemporal transition, the local variation of ICEE and its stability were investigated. By utilizing geographical detectors, this study additionally investigated the explanatory power of the effect factors on the spatial variation of ICEE. Analysis was performed on the various relationships between the influential factors. The use of geographical weighted regression allowed for a full analysis of the spatial heterogeneity of ICEE. These findings provide a theoretical foundation and technical assistance to aid in the local implementation of green development and in the design of CE reduction initiatives.
Due to the limits of data collection, an analysis of ICEE year by year was not conducted for the study. In a subsequent study, panel data analysis and industry factor decomposition will be used to investigate the CEE. Analyses of the integration of carbon sinks and potential carbon neutrality scenarios will both be conducted. In addition, as a pilot study on the relationship between carbon emission efficiency among cities, this study still needs to carry out a series of follow-up work. In the upstream and downstream of the Pearl River Basin, there are differences in the levels of economic development and urbanization, and the coupling and coordination of urbanization and carbon emissions is a key indicator to support cooperative emission reduction. Future research will also explore the effects of urban agglomeration and the growth of megacities on carbon emission efficiency, carbon peaking, and carbon neutrality.
6. Conclusions
In the research, the SBM model was used to measure ICEE in the PRB. The spatial effect of ICEE was analyzed by using the LISA time path and space–time transition, and its influencing factors were studied by using the geographic detectors and geographically weighted regression model. We now drawn some conclusions:
- (1)
- The PRB’s ICEE showed a consistent upward trend from 2009 to 2017, with an average annual growth rate of 0.18 percent for the entire basin. However, there were still some areas with low ICEE; the PRB’s ICEE had clear spatial differentiation characteristics, with high-value clusters primarily distributed in Guangzhou, Shenzhen, Fangchenggang, Yuxi, and Liupanshui, and low-value clusters primarily distributed in Dongguan and Zhongshan.
- (2)
- By analyzing ICEE in the PRB from 2009 to 2017, this study shows an obvious imbalance. In the temporal path, the crossover rate of ICEE in the PRB was low, and the local spatiotemporal pattern was single. In terms of path length, the local pattern of ICEE in the PRB had a significant pattern of change over time. From the east to the center and western parts of the country, the length of the time path exhibited a pattern of growth, in which the local spatial structure of Liupanshui, Kunming, Anshun and other regions had a strong dynamic. The local spatial structure of ICEE in cities with relatively short time path movement in Guangzhou, Zhuhai, and Foshan in the east is relatively stable. The curvature of ICEE in the PRB was greater than 1, and the total geographical distribution from the center to the periphery displayed a diminishing trend, showing that ICEE in the PRB had a substantial spatial reliance over time. According to the direction of the LISA time path movement, the evolution of the spatial pattern of ICEE in the PRB had strong spatial integration. Of all the cities that exhibited synergistic changes, 16 cities showed positive synergistic growth, accounting for 64%. Additionally, the PRB had high positive integration.
- (3)
- In terms of space–time transition, the path-dependent characteristics of ICEE distribution among prefecture-level cities in the region were more obvious. In addition, the spatial relative state of the ICEE of each city became increasingly serious after 2009. In terms of the spatiotemporal network, there was a certain degree of spatiotemporal competition in the evolution of ICEE among neighboring cities in the PRB. Among them, the industrial CE reduction of Guangzhou and Dongguan, Foshan and Qingyuan, and Nanning and Laibin may have a certain regional closure. On the other hand, the strong negative correlation between cities such as Anshun and Laibin revealed the uncoordinated characteristics of ICEE development. Cities such as Anshun and Bijie, Zhuhai and Jiangmen, Qinzhou and Fangchenggang form a strong synergy zone, demonstrating favorable spatial dynamics. These cities’ ICEE features were generally comparable, and a trend of ICEE regional concentration formed.
- (4)
- The spatial variation of ICEE was influenced by the industrialization level, openness to the outside world, the science and technology level, energy consumption intensity, and productivity level, among which the productivity level, industrialization level, and openness to the outside world were the dominant influencing factors. Different driving factors had different influences on the spatial variation of ICEE. The interplay of the components improved the explanatory power of ICEE’s spatial variation, and the augmentation was mostly non-linear.
- (5)
- The regional heterogeneity of ICEE and its affecting variables were taken into account by the GWR model. The influence of each influencing factor on ICEE showed significant spatial heterogeneity, which showed that the influence of the same factor on ICEE varies in different cities. Among these, the correlation between the industrialization level and ICEE was positive, and the regression coefficient decreased from west to east. The correlation between energy consumption intensity and ICEE was always negative, and the regression coefficient increased from west to east. The correlation between ICEE and the science and technology level was always positive, and the regression coefficient decreased from west to east. The regression coefficients of openness to the outside world were all positive, and the regression coefficients showed contiguous distribution in space. The correlation between productivity level and ICEE was always positive, and the regression coefficients showed a decreasing trend from north to south.
Author Contributions
Conceptualization, J.Y.; methodology, J.Y. and H.J.; validation, J.Y., Y.Q., and H.J.; formal analysis, H.J.; investigation, J.Y.; resources, R.X. and B.Z.; data curation, H.J.; writing—original draft preparation, H.J. and Y.D.; writing—review and editing, J.Y.; visualization, J.Y. and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Philosophy and Social Science Planning Project of Guizhou, China (Grant No. 21GZZD59), and the Scientific Research Project of Guizhou University of Finance and Economics (2021ZXSY05). The authors are grateful to the reviewers for their help and thought-provoking comments.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank the editors and the anonymous reviewers for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tan, S.; Yang, J.; Yan, J.; Lee, C.; Hashim, H.; Chen, B. A holistic low carbon city indicator framework for sustainable devel-opment. Appl. Energy 2017, 185, 1919–1930. [Google Scholar] [CrossRef]
- Ms, A.; Xin, Z.A.; Ys, B. The impact of low-carbon city construction on ecological efficiency: Empirical evidence from qua-si-natural experiments. Resour. Conserv. Recycl. 2020, 157, 10477. [Google Scholar] [CrossRef]
- Shi, Y.; Han, B.; Zafar, M.W.; Wei, Z. Uncovering the driving forces of carbon dioxide emission in Chinese manufacturing industry: An intersectoral analysis. Environ. Sci. Pollut. Res. 2019, 26, 31434–31448. [Google Scholar] [CrossRef]
- Ni, A.; Kra, B.; Rs, C.; Wan, G.A.; Dm, A.; Kai, T.E. Does exports diversification and environmental innovation achievecarbon neutrality target of oecd economies?-sciencedirect. J. Environ. Manag. 2021, 291, 112648. [Google Scholar] [CrossRef]
- Xie, H.; Yu, Y.; Wang, W.; Liu, Y. The substitutability of non-fossil energy,potential carbon emission reduction and energy shadow prices in China. Energy Policy 2017, 107, 63–71. [Google Scholar] [CrossRef]
- Guan, D.; Meng, J.; Reiner, D.M.; Zhang, N.; Shan, Y.; Mi, Z.; Davis, S.J. Structural de-cline in China’s CO2 emission through transitions in industry and energy systems. Nat. Geosci. 2018, 11, 551–555. [Google Scholar] [CrossRef]
- Ning, Z.; Xiao, W. Dynamic total factor carbon emission performance changes in the Chinese transportation indus-try-ScienceDirect. Appl. Energy 2015, 146, 409–420. [Google Scholar] [CrossRef]
- Fatima, T.; Xia, E.; Cao, Z.; Khan, D.; Fan, J.L. Decomposition analysis of energy-related CO2 emission in the industrial sector of China: Evidence from the LMDI approach. Environ. Sci. Pollut. Res. 2019, 26, 21736–21749. [Google Scholar] [CrossRef]
- Liu, N.; Ma, Z.; Kang, J. Changes in carbon intensity in China’s industrial sector: Decomposition and attribution analysis. Energy Policy 2015, 87, 28–38. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, F.; Zhang, F.; Ma, D.; Yang, Q. Spatiotemporal changes in efficiency and influencing factors of China’s in-dustrial carbon emission. Environ. Sci. Pollut. Res. 2021, 28, 36288–36302. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Liu, J.; Zhang, H. Total-factor carbon emission efficiency of China’s provincial industrial sector and its dy-namic evolution. Renew. Sustain. Energy Rev. 2018, 94, 330–339. [Google Scholar] [CrossRef]
- Xie, D. Evaluation and factor analysis of ICEE based on “green-technology efficiency”—The case of Yangtze River basin, China. Land 2021, 10, 1408. [Google Scholar] [CrossRef]
- Lu, Y.; Li, M. ICEE in the Yangtze River Economic Belt and Its Influencing Factors. Int. J. Des. Nat. Ecodynamic 2020, 15, 25–32. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, X.; Pang, Q. Spatial Coupling Analysis on Carbon Emission, Industrial Structure and Ecological Benefits Coor-dination System: Performance of the Yellow River Basin. IOP Conf. Ser. Earth Environ. Sci. 2021, 781, 032058. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. Decoupling economic growth from carbon dioxide emission in China’s metal industrial sectors: A tech-nological and efficiency perspective. Sci. Total Environ. 2019, 691, 1173–1181. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Tam, V.W.Y.; Shuai, C.; Shen, L.; Zhang, Y.; Liao, S. Decoupling China’s economic growth from carbon emission: Empirical studies from 30 Chinese provinces (2001–2015). Sci. Total Environ. 2019, 656, 576–588. [Google Scholar] [CrossRef]
- Wang, L.; Fan, J.; Wang, J.; Zhao, Y.; Guo, R. Spatio-temporal characteristics of the relationship between carbon emission and economic growth in China’s transportation industry. Environ. Sci. Pollut. Res. 2020, 27, 32962–32979. [Google Scholar] [CrossRef]
- Yi, J. Study on Carbon Emission Efficiency of China’s Industrial Industry and Analysis of Its Influencing Factors. Low Carbon Econ. 2017, 8, 20–30. [Google Scholar] [CrossRef][Green Version]
- Chen, J.; Zou, Z. Study on Total Factor Carbon Emission Efficiency in the Yangtze River Economic Zone, China. E3S Web Conf. 2020, 143, 02026. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, N. Research on the Measure of Carbon Emission Efficiency in China Based on DEA Method. J. Quan-Titative Econ. 2019, 36, 35–41. [Google Scholar] [CrossRef]
- Li, L.; Cai, Y.; Liu, L. Research on the Effect of Urbanization on China’s Carbon Emission Efficiency. Sustainability 2019, 12, 163. [Google Scholar] [CrossRef]
- Zhang, R.; Tai, H.; Cheng, K.; Dong, H.; Liu, W.; Hou, J. Carbon Emission Efficiency Network: Evolutionary Game and Sen-sitivity Analysis between Differentiated Efficiency Groups and Local Governments. Sustainability 2022, 14, 2191. [Google Scholar] [CrossRef]
- Guo, X.; Wang, X.; Wu, X.; Chen, X.; Li, Y. Carbon Emission Efficiency and Low-Carbon Optimization in Shanxi Province under “Dual Carbon” Background. Energies 2022, 15, 2369. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, J.; Li, J.; Li, S.; Zhang, D.; Wu, D.; Pan, S.; Chen, W. Spatial correlation among cultivated land intensive use and carbon emission efficiency: A case study in the Yellow River Basin, China. Environ. Sci. Pollut. Res. 2022, 3, 43341–43360. [Google Scholar] [CrossRef]
- Wang, Z.; Du, Y.; University, H.N. Spatial-temporal Differences and Influencing Factors of Carbon Emission Efficiency in Hunan Province Based on SBM-DEA Model. Sci. Geogr. Sin. 2019, 39, 797–806. [Google Scholar] [CrossRef]
- Suo, G.B.; Tian, M.Y.; University, H.G. Research on the Efficiency of Beijing-Tianjin-Hebei City Ecological Civilization Construction Based on SBM-Tobit Model. J. Hebei GEO Univ. 2020, 43, 103–106. [Google Scholar] [CrossRef]
- Fare, R. Multilateral productivity comparisons when some outputs are undesirable: A non-parametric approach. Rev. Econ. Stat. 1989, 71, 90–98. [Google Scholar] [CrossRef]
- Veeman, H.T.S. Non-parametric Productivity Analysis with Undesirable Outputs: An Application to the Canadian Pulp and Paper Industry. Am. J. Agric. Econ. 2001, 83, 605–616. [Google Scholar] [CrossRef]
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and Undesirable Outputs: A Directional Distance Function Approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K. Dealing with Undesirable Outputs in DEA: A Slacks-Based Measure (SBM) Approach; GRIPS Research Report Series; National Graduate Institute for Policy Studies: Tokyo, Japan, 2004. [Google Scholar]
- Lu, C.; Du, Q. Analysis on Transportation Carbon Efficiency and Potential of emission Reduction under Green Development: Evidence from 54 Countries along the Belt and Road. In Proceedings of the 20th COTA International Conference of Transportation Professionals, Xi’an, China, 14–16 August 2020; pp. 5206–5217. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, K.L. Influence of Urbanization and Foreign Direct Investment on Carbon Emission Efficiency: Evidence from Urban Clusters in the Yangtze River Economic Belt. Sustainability 2021, 13, 2722. [Google Scholar] [CrossRef]
- Liu, D. Convergence of energy carbon emission efficiency: Evidence from manufacturing sub-sectors in China. Environ. Sci. Pollut. Res. 2022, 29, 31133–31147. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Zeng, L.; Li, P.; Lu, H.; Hu, H.; Li, C.; Zheng, M.; Li, H.; Yu, Z.; Yuan, D.; et al. China’s transportation sector carbon dioxide emission efficiency and its influencing factors based on the EBM DEA model with undesirable outputs and spatial Durbin model. Energy 2022, 238, 121934. [Google Scholar] [CrossRef]
- Zhang, Y.J. The CO2 emission efficiency, reduction potential and spatial clustering in China’s industry: Evidence from the regional level. Appl. Energy 2020, 174, 213–223. [Google Scholar] [CrossRef]
- Du, Q.; Deng, Y.; Zhou, J.; Wu, J.; Pang, Q. Spatial spillover effect of carbon emission efficiency in the construction industry of China. Pollution 2021, 28, 1–14. [Google Scholar] [CrossRef]
- Ma, D. China’s low carbon economic growth efficiency: An analysis involving carbon sink. Environment 2017, 26, 1147–1158. [Google Scholar] [CrossRef]
- Zhang, S.L.; Hai-Shan, Y.U.; Business, F.O.; University, N. Spatial Econometric Analysis of the Efficiency of Industrial Carbon emission and its Influencing Factors. Sci. Technol. Econ. 2015, 28, 106–110. [Google Scholar] [CrossRef]
- Isaeva, A.; Salahodjaev, R.; Khachaturov, A.; Tosheva, S.; Carayannis, E.G. The Impact of Tourism and Financial Development on Energy Consumption and Carbon Dioxide Emission: Evidence from Post-communist Countries. J. Knowl. Econ. 2022, 13, 773–786. [Google Scholar] [CrossRef]
- Deng, J.L.; Li, T. The impact of socio-economic institutional change on agricultural carbon dioxide emission reduction in China. PLoS ONE 2021, 16, e0251816. [Google Scholar] [CrossRef]
- Xin, Y.; Zheng, K.; Zhou, Y.; Han, Y.; Tadikamalla, P.R.; Fan, Q. Logistics Efficiency under Carbon Constraints Based on a Super SBM Model with Undesirable Output: Empirical Evidence from China’s Logistics Industry. Sustainability 2022, 14, 5142. [Google Scholar] [CrossRef]
- He, A.; Xue, Q.; Zhao, R.; Wang, D. Renewable energy technological innovation, market forces, and carbon emission efficiency. Sci. Total Environ. 2021, 796, 148908. [Google Scholar] [CrossRef]
- Mielnik, O.; Goldemberg, J. The evolution of the“Carbonization Index”in developing countries. Energy Policy 1999, 27, 307–308. [Google Scholar] [CrossRef]
- Sun, J.W. The decrease of CO2 emission intensity is decarboniza- tion at national and global levels. Energy Policy 2005, 33, 957–978. [Google Scholar] [CrossRef]
- Qu, C.; Li, L.; Cheng, Z. Impact of Industrial Agglomeration on Chinese Manufacturing Industry Carbon Emission Efficiency and Its Regional Differences. Soft Sci. 2017, 31, 34–38. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, X.; Sun, L. Research on Measurement and Convergence of Transport Carbon Emission Efficiency in China. En-Vironmental Sci. Technol. 2019, 42, 222–229. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, S.; Hou, M.; Jia, L.; Li, Y.; Deng, Y.; Zhang, X. Spatial-temporal differentiation and its influencing factors of agricultural eco-efficiency in China based on geographic detector. Chin. J. Appl. Ecol. 2021, 32, 4039–4049. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, M. Evaluation of Carbon Emission Efficiency in Coastal Areas of China from the Perspective of Time and Space. Resour. Dev. Mark. 2016, 32, 808–812. [Google Scholar] [CrossRef]
- Guo, B.; Lin, J. Research on Efficiency of Carbon Emissions in Yangtze River Delta Based on the SBM—undesirable Model. J. Ind. Technol. Econ. 2017, 36, 108–115. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, Z.; Cao, F.; Wang, K.; Chen, X. The space-time transition characteristics and its driving mechanism of county-scale inbound tourism in Zhejiang province. Geogr. Res. 2016, 35, 1177–1192. [Google Scholar] [CrossRef]
- Rey, S.J.; Ye, X.; Páez, A.; Buliung, R.N.; Dall’Erba, S. Comparative Spatial Dynamic of Regional Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 63, pp. 441–463. [Google Scholar] [CrossRef]
- Rey, S.J.; Murray, A.T.; Anselin, L. Visualizing regional income distribution dynamic. Lett. Spat. Resour. Sci. 2011, 4, 81–90. [Google Scholar] [CrossRef]
- Rey, S.J. Spatial Empirics for Economic Growth and Convergence. Geogr. Anal. 2010, 33, 195–214. [Google Scholar] [CrossRef]
- Qiu, Y.; Yin, J.; Zhang, T.; Du, Y.; Zhang, B. Spatiotemporal Dynamic Analysis of A-Level Scenic Spots in Guizhou Province, China. ISPRS Int. J. Geo-Inf. 2021, 10, 568. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, S. Analysisof electricity carbon footprint and its ecological stress in China from 2006 to 2015. Acta Sci. Circumstantiae 2018, 38, 4873–4878. [Google Scholar] [CrossRef]
- Lin, X.Q.; Bian, Y.; Wang, D. Spatiotemporal Evolution Characteristics and Influencing Factors of ICEE in Beijing-Tianjin-Hebei Region. Econ. Geogr. 2021, 41, 187–195. [Google Scholar] [CrossRef]
- Guo, Y.G.; Zhang, J.; Lu, S.J.; Wu, R.H. Spatial-temporal change of the inbound tourism economic development in China. Geogr. Sin. 2014, 34, 1299–1304. [Google Scholar] [CrossRef]
- Gao, T.M. Econometric Analysis and Modeling: Application and Examples of EViews; Tsinghua University Press: Beijing, China, 2006. [Google Scholar]
- Yin, J.; Qiu, Y.; Zhang, B. Identification of Poverty Areas by Remote Sensing and Machine Learning: A Case Study in Guizhou, Southwest China. ISPRS Int. J. Geo-Inf. 2021, 10, 11. [Google Scholar] [CrossRef]
- Liu, Q.Z.; Hao, J. Regional Differences and Influencing Factors of Carbon Emission Efficiency in the Yangtze River Economic Belt. Sustainability 2022, 14, 4814. [Google Scholar] [CrossRef]
- Liu, C.X.; Tang, R.E.; Guo, Y.Q.; Sun, Y.H.; Liu, X.Y. Research on the Structure of Carbon Emission Efficiency and Influencing Factors in the Yangtze River Delta Urban Agglomeration. Sustainability 2022, 14, 6114. [Google Scholar] [CrossRef]
- Zhang, R.J.; Tai, H.W.; Cheng, K.T.; Zhu, Y.T.; Hou, J.J. Carbon emission efficiency network formation mechanism and spatial correlation complexity analysis: Taking the Yangtze River Economic Belt as an example. Sci. Total Environ. 2022, 841, 156719. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).