Estimation of Heavy Metal Content in Soil Based on Machine Learning Models
Abstract
:1. Introduction
2. Materials and Methods
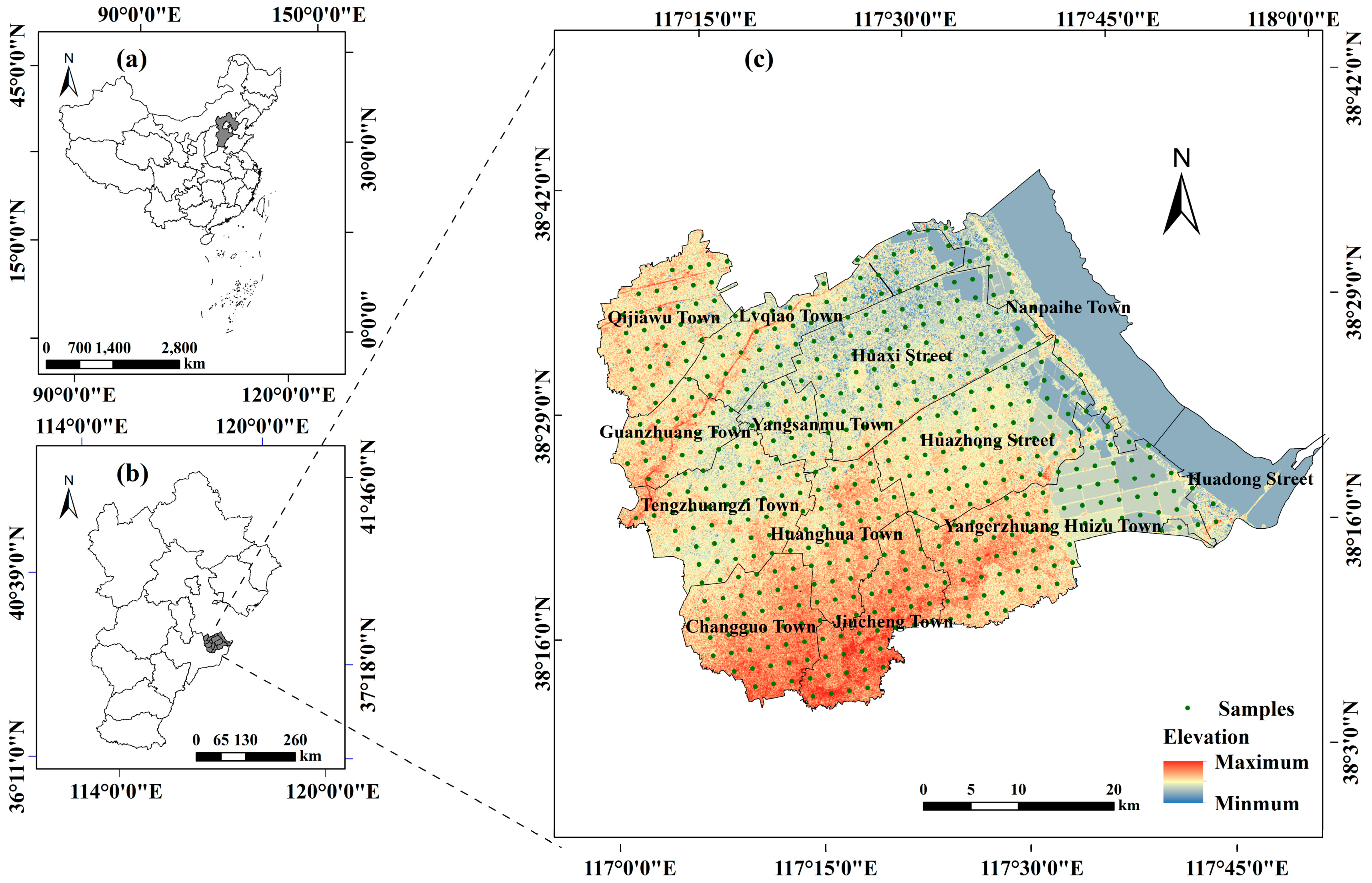
2.1. Study Area
2.2. Methods
2.2.1. LASSO-GA-BPNN Model
2.2.2. SVR Model
2.2.3. RF Model
2.2.4. Inverse Distance Weighting Method
2.2.5. Ordinary Kriging Method
2.2.6. Accuracy Evaluation Index
3. Results and Discussion
3.1. Statistical Characteristics Analysis of Sampled Data
3.2. Model Improvement and Accuracy Comparison
3.2.1. Analysis of LASSO Optimization Results
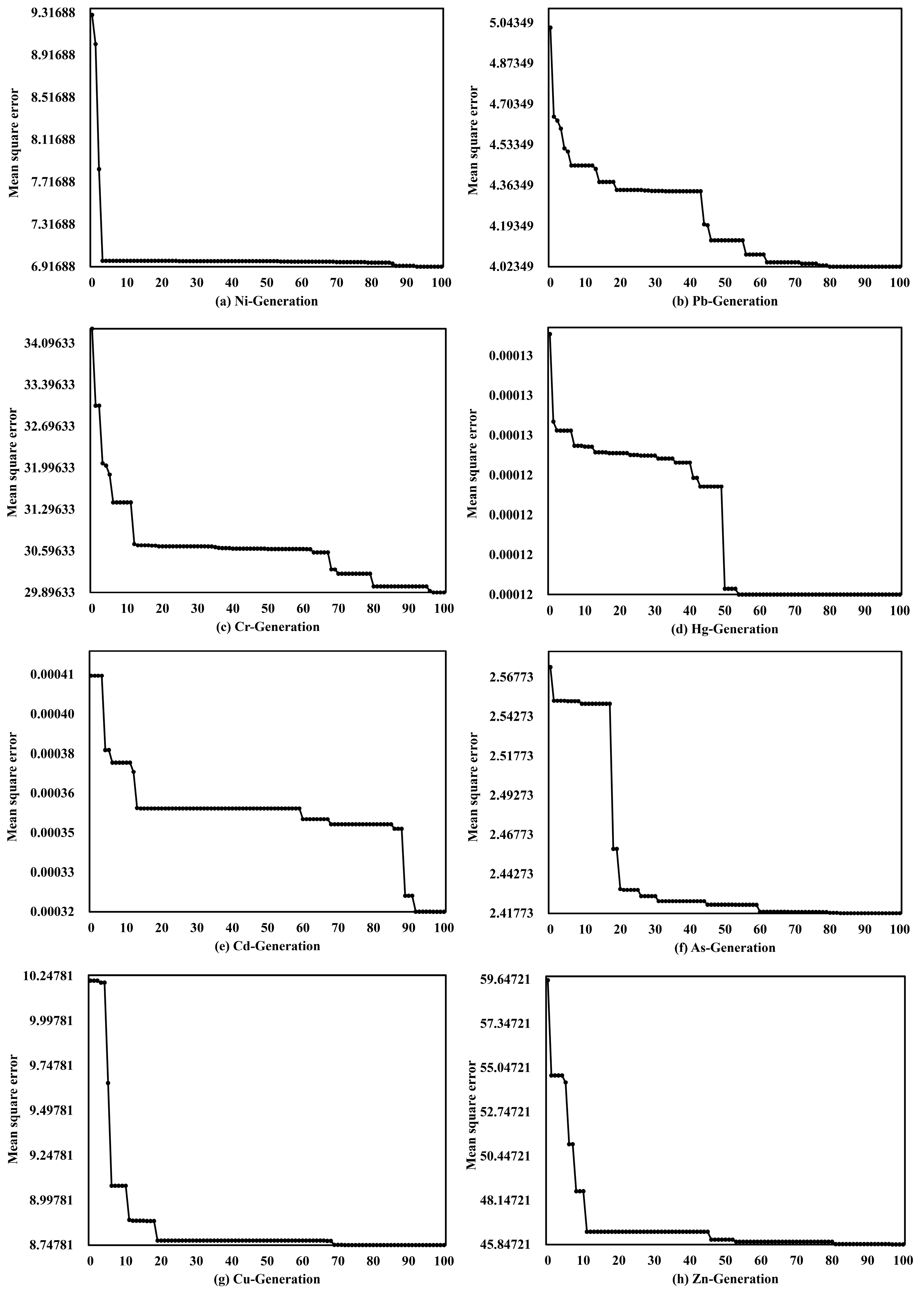
3.2.2. Analysis of GA Optimization Results
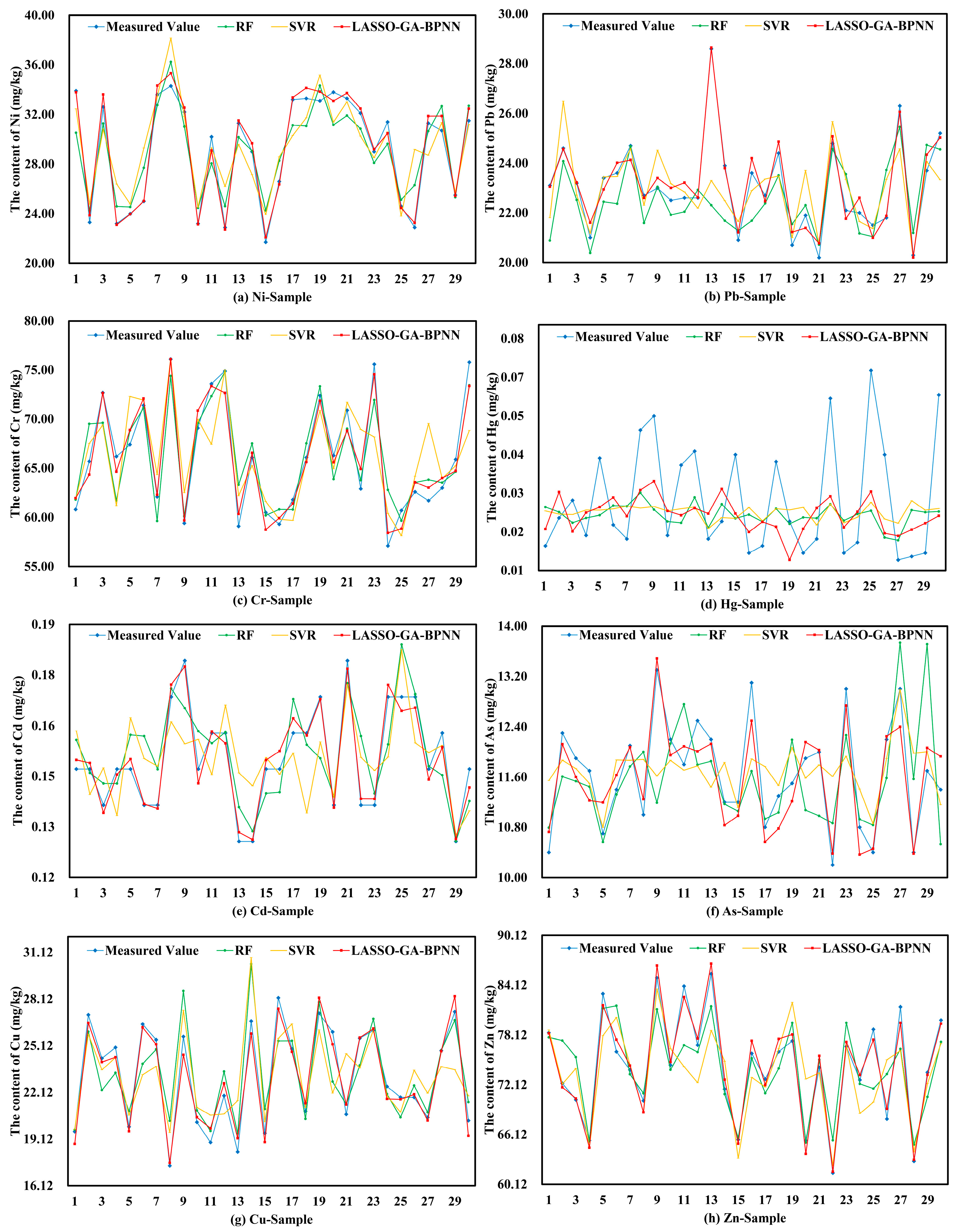
3.2.3. Comparison between LASSO-GA-BPNN and SVR and RF
3.2.4. Comparison between LASSO-GA-BPNN and Spatial Interpolation
3.3. Estimation of Soil Heavy Metal Pollution in Huanghua
3.3.1. Statistical Analysis of Estimated Value
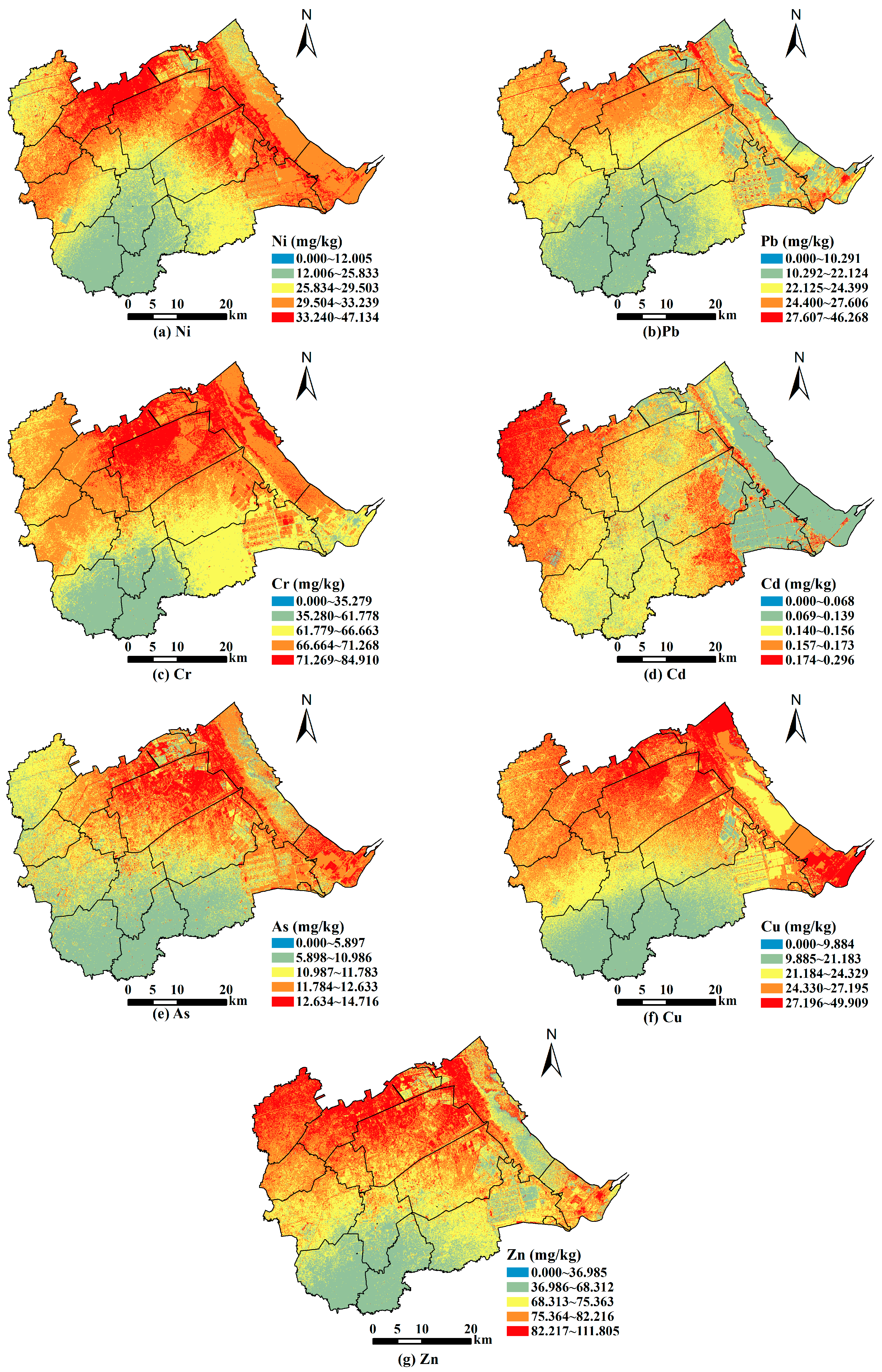
3.3.2. High-Resolution Visualization of the Estimated Value
3.3.3. Comprehensive Pollution Index
4. Conclusions
- (1)
- The simultaneous optimization of BPNN by LASSO and GA can greatly improve the estimation accuracy and generalization ability. On the one hand, LASSO reduces the dimension of high dimensional data and removes redundant variables for each heavy metal, which is more suitable for machine learning estimation models with nonlinear prediction functions. On the other hand, GA solves the defect that the steepest descent method of the LASSO-BPNN model is easy to fall into the local optimal solution.
- (2)
- The LASSO-GA-BPNN model is a more accurate model for the estimate heavy metal content in soil compared to SVR, RF and spatial interpolation. In the comparison of machine learning estimation models, LASSO-GA-BPNN has higher estimation accuracy than the SVR and RF. Similarly, in the comparison of machine learning and spatial interpolation methods, the accuracy of LASSO-GA-BPNN is greater than that of inverse distance weighting and ordinary kriging.
- (3)
- High-resolution visualization of the estimated value can display the local spatial distribution of heavy metals in detail. The overall spatial distribution law of each heavy metal content is very similar, showing the distribution characteristics of low content in the south, high content in the north, and gradually increasing from south to north. However, the local spatial distribution of each heavy metal is different. In addition, the comprehensive pollution level of Huanghua is mainly low pollution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Index | Abbreviation | Name | Wavelength Range (um) | Centre Wavelength (um) |
|---|---|---|---|---|
| Band1 | B1 | Aerosol | 0.43–0.45 | 0.44 |
| Band2 | B2 | Blue | 0.45–0.51 | 0.48 |
| Band3 | B3 | Green | 0.53–059 | 0.56 |
| Band4 | B4 | Red | 0.64–0.67 | 0.655 |
| Band5 | B5 | Near infrared (NIR) | 0.85–0.88 | 0.865 |
| Band6 | B6 | Short wave infrared 1(SWIR1) | 1.57–1.65 | 1.61 |
| Band7 | B7 | Short wave infrared 2(SWIR2) | 2.11–2.29 | 2.2 |
| Index | Name | Formula |
|---|---|---|
| MNDWI | Modified Normalized Difference Water Index | (B3 − B6)/(B3 + B6) |
| DVI | Difference Vegetation Index | B5/B4 |
| CMR | Clay Minerals Ratio | B6/B7 |
| EVI | Enhance Vegetation Index | 2.5 × (B5 − B4)/(B5 + 6 × B4 − 7.5 × B2 + 1) |
| NDVI | Normalized Difference Vegetation Index | (B5 − B4)/(B5 + B4) |
| Greenness | Greenness | −0.294 × B2 − 0.243 × B3 − 0.5424 × B4 + 0.7276 × B5 + 0.0713 × B6 − 0.1608 × B7 |
| Brightness | Brightness | 0.3029 × B2 + 0.2786 × B3 − 0.4733 × B4 + 0.5599 × B5 + 0.508 × B6 − 0.1872 × B7 |
| Wetness | Wetness | 0.1511 × B2 − 0.1973 × B3 − 0.3283 B4 + 0.3407 × B5 − 0.7117 × B6 − 0.4559 × B7 |
References
- Yang, Q.Q.; Li, Z.Y.; Lu, X.N.; Duan, Q.N.; Huang, L.; Bi, J. A review of soil heavy metal pollution from industrial and agricultural regions in China: Pollution and risk assessment. Sci. Total Environ. 2018, 642, 690–700. [Google Scholar] [CrossRef]
- Li, C.X.; Wu, K.N.; Gao, X.Y. Manufacturing industry agglomeration and spatial clustering: Evidence from Hebei Province, China. Environ. Dev. Sustain. 2020, 22, 2941–2965. [Google Scholar] [CrossRef]
- Yu, H.; Yang, J.; Sun, D.; Li, T.; Liu, Y. Spatial Responses of Ecosystem Service Value during the Development of Urban Agglomerations. Land 2022, 11, 165. [Google Scholar] [CrossRef]
- Li, C.; Gao, X.; Wu, J.; Wu, K. Demand prediction and regulation zoning of urban-industrial land: Evidence from Beijing-Tianjin-Hebei Urban Agglomeration, China. Environ. Monit. Assess. 2019, 191, 412. [Google Scholar] [CrossRef]
- Li, C.; Wu, K. An input–output analysis of transportation equipment manufacturing industrial transfer: Evidence from Beijing-Tianjin-Hebei region, China. Growth Change 2022, 53, 91–111. [Google Scholar] [CrossRef]
- Guan, Y.; Shao, C.F.; Ju, M.T. Heavy metal contamination assessment and partition for industrial and mining gathering areas. Int. J. Environ. Res. Public Health 2014, 11, 7286–7303. [Google Scholar] [CrossRef] [Green Version]
- Munyati, C.; Sinthumule, N.I. Comparative suitability of ordinary kriging and Inverse Distance Weighted interpolation for indicating intactness gradients on threatened savannah woodland and forest stands. Environ. Sustain. Indic. 2021, 12, 100151. [Google Scholar] [CrossRef]
- Radocaj, D.; Jug, I.; Vukadinovic, V.; Jurisic, M.; Gasparovic, M. The Effect of soil sampling density and spatial autocorrelation on interpolation accuracy of chemical soil properties in arable cropland. Agronomy 2021, 11, 2430. [Google Scholar] [CrossRef]
- Das, S. Extreme rainfall estimation at ungauged locations: Information that needs to be included in low-lying monsoon climate regions like Bangladesh. J. Hydrol. 2021, 601, 126616. [Google Scholar] [CrossRef]
- Das, S.; Islam, A.M.T. Assessment of mapping of annual average rainfall in a tropical country like Bangladesh: Remotely sensed output vs. kriging estimate. Theor. Appl. Climatol. 2021, 146, 111–123. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.N.; Song, Z.Y.; Yan, J.Y.; Chen, M.Y.; Yin, J.C. Human health risk distribution and safety threshold of cadmium in soil of coal chemical industry area. Minerals 2021, 11, 678. [Google Scholar] [CrossRef]
- Ogunkunle, C.O.; Fatoba, P.O. Contamination and spatial distribution of heavy metals in topsoil surrounding a mega cement factory. Atmos. Pollut. Res. 2014, 5, 270–282. [Google Scholar] [CrossRef] [Green Version]
- Duan, Y.X.; Zhang, Y.M.; Li, S.; Fang, Q.L.; Miao, F.F.; Lin, Q.G. An integrated method of health risk assessment based on spatial interpolation and source apportionment. J. Clean. Prod. 2020, 276, 123218. [Google Scholar] [CrossRef]
- Fu, P.H.; Yang, Y.; Zou, Y.S. Prediction of soil heavy metal distribution using geographically weighted regression kriging. Bull. Environ. Contam. Toxicol. 2022, 108, 344–350. [Google Scholar] [CrossRef]
- He, F.; Yang, J.; Zhang, Y.; Sun, D.; Wang, L.; Xiao, X.; Xia, J. Offshore island connection line: A new perspective of coastal urban development boundary simulation and multi-scenario prediction. GISci. Remote Sens. 2022, 59, 801–821. [Google Scholar] [CrossRef]
- Ghoddusi, H.; Creamer, G.G.; Rafizadeh, N. Machine learning in energy economics and finance: A review. Energy Econ. 2019, 81, 709–727. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, C.; Wang, G.J.; Yan, X.G. Comparison of individual, ensemble and integrated ensemble machine learning methods to predict China’s SME credit risk in supply chain finance. Neural Comput. Appl. 2017, 28, S41–S50. [Google Scholar] [CrossRef]
- Yang, J.; Yang, R.X.; Chen, M.H.; Su, C.H.; Zhi, Y.; Xi, J.C. Effects of rural revitalization on rural tourism. J. Hosp. Tour. Manag. 2021, 47, 35–45. [Google Scholar] [CrossRef]
- Amini, S.; Saber, M.; Rabiei-Dastjerdi, H.; Homayouni, S. Urban land use and land cover change analysis using random forest classification of landsat time series. Remote Sens. 2022, 14, 2654. [Google Scholar] [CrossRef]
- Zhu, X.F.; Xiao, G.F.; Wang, S. Suitability evaluation of potential arable land in the Mediterranean region. J. Environ. Manag. 2022, 313, 115011. [Google Scholar] [CrossRef]
- Yu, H.S.; Yang, J.; Li, T.; Jin, Y.; Sun, D.Q. Morphological and functional polycentric structure assessment of megacity: An integrated approach with spatial distribution and interaction. Sust. Cities Soc. 2022, 80, 103800. [Google Scholar] [CrossRef]
- Huang, Y.T.; Lin, J.J.; Lin, X.M.; Zheng, W.N. Quantitative analysis of Cr in soil based on variable selection coupled with multivariate regression using laser-induced breakdown spectroscopy. J. Anal. At. Spectrom. 2021, 36, 2553–2559. [Google Scholar] [CrossRef]
- Liu, N.; Zhao, G.; Liu, G. Coupling square wave anodic stripping voltammetry with support vector regression to detect the concentration of lead in soil under the interference of copper accurately. Sensors 2020, 20, 6792. [Google Scholar] [CrossRef] [PubMed]
- Fard, R.S.; Matinfar, H.R. Capability of vis-NIR spectroscopy and Landsat 8 spectral data to predict soil heavy metals in polluted agricultural land (Iran). Arab. J. Geosci. 2016, 9, 745. [Google Scholar] [CrossRef]
- Sakizadeh, M.; Mirzaei, R.; Ghorbani, H. Support vector machine and artificial neural network to model soil pollution: A case study in Semnan Province, Iran. Neural Comput. Appl. 2017, 28, 3229–3238. [Google Scholar] [CrossRef]
- Tarasov, D.A.; Buevich, A.G.; Sergeev, A.P.; Shichkin, A.V. High variation topsoil pollution forecasting in the Russian Subarctic: Using artificial neural networks combined with residual kriging. Appl. Geochem. 2018, 88, 188–197. [Google Scholar] [CrossRef]
- Fang, Y.; Xu, L.; Wong, A.; Clausi, D.A. Multi-temporal landsat-8 images for retrieval and broad scale mapping of soil copper concentration using empirical models. Remote Sens. 2022, 14, 2311. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Fathizad, H.; Ardakani, M.A.H.; Sodaiezadeh, H.; Kerry, R.; Heung, B.; Scholten, T. Spatio-temporal analysis of heavy metals in arid soils at the catchment scale using digital soil assessment and a random forest model. Remote Sens. 2021, 13, 1698. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, S.H.; Chen, Y.H.; Shao, S.S.; Wu, J.T.; Fan, M.M.; Chen, F.R.; Gao, C. Machine learning-based source identification and spatial prediction of heavy metals in soil in a rapid urbanization area, eastern China. J. Clean. Prod. 2020, 273, 122858. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, X.; Li, Q.; Shi, Y.; Guo, G.L.; Zhao, L.; Wang, J.; Su, Y.Q.; Zhang, C. Spatial distribution prediction of soil As in a large-scale arsenic slag contaminated site based on an integrated model and multi-source environmental data. Environ. Pollut. 2020, 267, 115631. [Google Scholar] [CrossRef]
- Guan, Q.Y.; Zhao, R.; Wang, F.F.; Pan, N.H.; Yang, L.Q.; Song, N.; Xu, C.Q.; Lin, J.K. Prediction of heavy metals in soils of an arid area based on multi-spectral data. J. Environ. Manag. 2019, 243, 137–143. [Google Scholar] [CrossRef] [PubMed]
- Lamine, S.; Petropoulos, G.P.; Brewer, P.A.; Bachari, N.E.I.; Srivastava, P.K.; Manevski, K.; Kalaitzidis, C.; Macklin, M.G. Heavy metal soil contamination detection using combined geochemistry and field spectroradiometry in the United Kingdom. Sensors 2019, 19, 762. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Yang, Z.; Wang, H.; Du, Y. Study on the prediction of soil heavy metal elements content based on visible near-infrared spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 199, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.H.; Liu, P.J.; Qiao, B.J.; Wu, K.N. The spatial distribution and prediction of soil heavy metals based on measured samples and multi-spectral images in Tai Lake of China. Land 2021, 10, 1227. [Google Scholar] [CrossRef]
- Bian, Z.J.; Sun, L.N.; Tian, K.; Liu, B.L.; Zhang, X.H.; Mao, Z.Q.; Huang, B.A.; Wu, L.H. Estimation of heavy metals in tailings and soils using hyperspectral technology: A case study in a tin-polymetallic mining area. Bull. Environ. Contam. Toxicol. 2021, 107, 1022–1031. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.Y.; Zhao, D.X.; Triantafilis, J. Selecting optimal calibration samples using proximal sensing EM induction and gamma-ray spectrometry data: An application to managing lime and magnesium in sugarcane growing soil. J. Environ. Manag. 2021, 296, 113357. [Google Scholar] [CrossRef]
- Yu, Y.; Ling, Y.; Li, Y.; Lv, Z.; Du, Z.; Guan, B.; Wang, Z.; Wang, X.; Yang, J.; Yu, J. Distribution and influencing factors of metals in surface soil from the Yellow River Delta, China. Land 2022, 11, 523. [Google Scholar] [CrossRef]
- Xia, F.; Zhu, Y.; Hu, B.; Chen, X.; Li, H.; Shi, K.; Xu, L. Pollution characteristics, spatial patterns, and sources of toxic elements in soils from a typical industrial city of Eastern China. Land 2021, 10, 1126. [Google Scholar] [CrossRef]
- Yan, F.P.; Wei, S.G.; Zhang, J.; Hu, B.F. Depth-to-bedrock map of China at a spatial resolution of 100 meters. Sci. Data 2020, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Mcbratney, A.; Santos, M.; Ma, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso: A retrospective. J. R. Stat. Soc. Ser. B 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Liu, B.; Jin, Y.Q.; Xu, D.Z.; Wang, Y.S.; Li, C.Y. A data calibration method for micro air quality detectors based on a LASSO regression and NARX neural network combined model. Sci. Rep. 2021, 11, 21173. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Li, T.Y.; Yang, M.L.; Hu, G.H.; Zhong, W.M. Hybrid strategy integrating variable selection and a neural network for fluid catalytic cracking modeling. Ind. Eng. Chem. Res. 2019, 58, 247–258. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagarion. Read. Cogn. Sci. 1988, 323, 399–421. [Google Scholar] [CrossRef]
- Peng, Y.P.; Zhao, L.; Hu, Y.M.; Wang, G.X.; Wang, L.; Liu, Z.H. Prediction of soil nutrient contents using visible and near-infrared reflectance spectroscopy. Isprs Int. J. Geo-Inf. 2019, 8, 437. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Guo, A.; Li, Y.; Zhang, Y.; Li, X. Simulation of landscape spatial layout evolution in rural-urban fringe areas: A case study of Ganjingzi District. GISci. Remote Sens. 2019, 56, 388–405. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Queen’s University Belfast: Belfast, UK, 2010. [Google Scholar] [CrossRef]
- Li, X.; Luan, F.; Wu, Y. A Comparative assessment of six machine learning models for prediction of bending force in hot strip rolling process. Metals 2020, 10, 685. [Google Scholar] [CrossRef]
- Smola, A.; Lkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Schölkopf, B.; Smola, A.; Müller, K.C. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.X.; Arshad, M.; Wang, J.; Triantafilis, J. Soil exchangeable cations estimation using Vis-NIR spectroscopy in different depths: Effects of multiple calibration models and spiking. Comput. Electron. Agric. 2021, 182, 105990. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wu, P.B.; Yin, A.J.; Yang, X.H.; Zhang, M.; Gao, C. Prediction of soil organic carbon in an intensively managed reclamation zone of eastern China: A comparison of multiple linear regressions and the random forest model. Sci. Total Environ. 2017, 592, 704–713. [Google Scholar] [CrossRef]
- Duroux, R.; Scornet, E. Impact of subsampling and tree depth on random forests. ESAIM-Prob. Stat. 2018, 22, 96–128. [Google Scholar] [CrossRef]
- Peters, J.; De Baets, B.; Verhoest, N.E.C.; Samson, R.; Degroeve, S.; De Becker, P.; Huybrechts, W. Random forests as a tool for ecohydrological distribution modelling. Ecol. Model. 2007, 207, 304–318. [Google Scholar] [CrossRef]
- Metahni, S.; Coudert, L.; Gloaguen, E.; Guemiza, K.; Mercier, G.; Blais, J.F. Comparison of different interpolation methods and sequential Gaussian simulation to estimate volumes of soil contaminated by As, Cr, Cu, PCP and dioxins/furans. Environ. Pollut. 2019, 252, 409–419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Zheng, L. Geostatistics: Modeling Spatial Uncertainty. Comput. Geosci. 2001, 27, 121–123. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Tsakiri, M.; Patias, P. Evaluation of single-date and multi-seasonal spatial and spectral information of Sentinel-2 imagery to assess growing stock volume of a Mediterranean forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 1–14. [Google Scholar] [CrossRef]
- Qiao, P.W.; Yang, S.C.; Lei, M.; Chen, T.B.; Dong, N. Quantitative analysis of the factors influencing spatial distribution of soil heavy metals based on geographical detector. Sci. Total Environ. 2019, 664, 392–413. [Google Scholar] [CrossRef]


| Element | Minimum (mg/kg) | Maximum (mg/kg) | Mean (mg/kg) | Standard Deviation | Variable Coefficient | Background Value (mg/kg) | Exceeding Standard Rate (%) |
|---|---|---|---|---|---|---|---|
| Ni | 18.30 | 47.40 | 29.55 | 4.83 | 0.16 | 34.10 | 17.44 |
| Pb | 15.60 | 37.60 | 23.02 | 2.95 | 0.13 | 21.50 | 64.50 |
| Cr | 43.20 | 118.00 | 67.11 | 9.30 | 0.14 | 68.30 | 40.26 |
| Hg | 0.01 | 0.09 | 0.03 | 0.01 | 0.46 | 0.04 | 11.17 |
| Cd | 0.08 | 0.27 | 0.15 | 0.03 | 0.17 | 0.09 | 99.63 |
| As | 7.20 | 19.60 | 11.69 | 2.10 | 0.18 | 13.60 | 15.77 |
| Cu | 13.60 | 45.90 | 23.47 | 4.86 | 0.21 | 21.80 | 57.14 |
| Zn | 49.40 | 137.30 | 74.11 | 10.82 | 0.15 | 78.40 | 30.43 |
| Element | The Input Layer Information of Neurons in the Input Layer | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni | x | y | Elevation | Slope | Aspect | Band7 | MNDWI | CMR | EVI | Wetness | — | — |
| Pb | x | y | Elevation | Aspect | Band3 | MNDWI | CMR | EVI | Wetness | — | — | — |
| Cr | x | y | Elevation | Aspect | Band3 | Band5 | MNDWI | CMR | EVI | — | — | — |
| Hg | x | y | EVI | — | — | — | — | — | — | — | — | — |
| Cd | x | y | Elevation | Slope | Aspect | Band2 | Band5 | MNDWI | CMR | EVI | NDVI | Greenness |
| As | x | y | Elevation | Aspect | Band2 | MNDWI | CMR | EVI | Wetness | — | — | — |
| Cu | x | y | Elevation | Aspect | Band3 | MNDWI | EVI | — | — | — | — | — |
| Zn | x | y | Elevation | Slope | Aspect | Band1 | Band3 | Band7 | MNDWI | CMR | EVI | Wetness |
| Ni | Pb | Cr | Hg | Cd | As | Cu | Zn | ||
|---|---|---|---|---|---|---|---|---|---|
| Number of neurons in the hidden layer | 5 | 13 | 8 | 9 | 5 | 5 | 8 | 6 | |
| BPNN | RMSE | 3.504 | 2.429 | 7.500 | 0.012 | 0.024 | 1.998 | 3.907 | 10.656 |
| MAE | 2.829 | 1.882 | 5.857 | 0.009 | 0.018 | 1.635 | 2.948 | 8.563 | |
| MAPE | 9.664% | 8.288% | 8.685% | 34.215% | 11.797% | 14.988% | 13.330% | 11.280% | |
| LASSO-BPNN | RMSE | 3.111 | 2.084 | 7.061 | 0.011 | 0.021 | 1.905 | 3.660 | 9.633 |
| MAE | 2.433 | 1.582 | 5.591 | 0.008 | 0.016 | 1.518 | 2.791 | 7.276 | |
| MAPE | 8.361% | 6.883% | 8.318% | 32.479% | 10.823% | 13.842% | 12.762% | 9.506% | |
| LASSO-GA-BPNN | RMSE | 2.630 | 2.006 | 5.468 | 0.011 | 0.018 | 1.555 | 2.958 | 6.771 |
| MAE | 2.082 | 1.589 | 4.399 | 0.008 | 0.014 | 1.242 | 2.302 | 5.318 | |
| MAPE | 7.028% | 6.968% | 6.690% | 31.402% | 8.949% | 11.159% | 10.515% | 7.039% | |
| Model | Index | Ni | Pb | Cr | Hg | Cd | As | Cu | Zn |
|---|---|---|---|---|---|---|---|---|---|
| RF | RMSE | 3.0107 | 2.2912 | 5.6099 | 0.0112 | 0.0199 | 1.7030 | 3.2927 | 7.4969 |
| MAE | 2.4418 | 1.7861 | 4.5704 | 0.0082 | 0.0157 | 1.3941 | 2.4909 | 5.7749 | |
| MAPE | 8.3486% | 7.7330% | 7.0472% | 33.0121% | 10.4033% | 12.7271% | 11.2112% | 7.6586% | |
| SVR | RMSE | 3.2637 | 2.1968 | 6.4591 | 0.0115 | 0.0207 | 1.6806 | 3.4111 | 7.8590 |
| MAE | 2.7125 | 1.7233 | 5.2559 | 0.0085 | 0.0162 | 1.3528 | 2.6123 | 6.2460 | |
| MAPE | 9.4714% | 7.5297% | 8.0791% | 35.2015% | 10.6739% | 12.4429% | 11.9010% | 8.2271% | |
| LASSO-GA-BPNN | RMSE | 2.6300 | 2.0059 | 5.4678 | 0.0107 | 0.0178 | 1.5549 | 2.9577 | 6.7711 |
| MAE | 2.0821 | 1.5886 | 4.3995 | 0.0078 | 0.0137 | 1.2416 | 2.3021 | 5.3180 | |
| MAPE | 7.0284% | 6.9684% | 6.6899% | 31.4023% | 8.9487% | 11.1594% | 10.5146% | 7.0388% |
| Model | Index | Ni | Pb | Cr | Hg | Cd | As | Cu | Zn |
|---|---|---|---|---|---|---|---|---|---|
| Inverse distance weighting | RMSE | 2.8729 | 2.2541 | 6.0623 | 0.0120 | 0.0204 | 1.6044 | 3.3364 | 7.8390 |
| Ordinary kriging | RMSE | 2.9536 | 2.2770 | 6.2126 | 0.0119 | 0.0203 | 1.6114 | 3.5023 | 7.9981 |
| RF | RMSE | 3.0107 | 2.2912 | 5.6099 | 0.0112 | 0.0199 | 1.7030 | 3.2927 | 7.4969 |
| SVR | RMSE | 3.2637 | 2.1968 | 6.4591 | 0.0115 | 0.0207 | 1.6806 | 3.4111 | 7.8590 |
| LASSO-GA-BPNN | RMSE | 2.6300 | 2.0059 | 5.4678 | 0.0107 | 0.0178 | 1.5549 | 2.9577 | 6.7711 |
| Element | Min (mg/kg) | Max (mg/kg) | Mean (mg/kg) | Background Value (mg/kg) | Standard Deviation |
|---|---|---|---|---|---|
| Ni | 3.59 | 47.13 | 29.53 | 34.10 | 3.86 |
| Pb | 10.29 | 46.27 | 23.31 | 21.50 | 2.28 |
| Cr | 52.37 | 84.91 | 66.73 | 68.30 | 4.72 |
| Hg | 0.00 | 0.18 | 0.03 | 0.04 | 0.01 |
| Cd | 0.00 | 0.30 | 0.15 | 0.09 | 0.02 |
| As | 7.94 | 14.72 | 11.60 | 13.60 | 0.88 |
| Cu | 6.17 | 49.91 | 24.11 | 21.80 | 3.27 |
| Zn | 51.18 | 111.80 | 74.73 | 78.40 | 7.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, S.; Hou, M.; Gu, Z.; Jiang, C.; Zhang, W.; Hou, M.; Li, C.; Xi, Z. Estimation of Heavy Metal Content in Soil Based on Machine Learning Models. Land 2022, 11, 1037. https://doi.org/10.3390/land11071037
Shi S, Hou M, Gu Z, Jiang C, Zhang W, Hou M, Li C, Xi Z. Estimation of Heavy Metal Content in Soil Based on Machine Learning Models. Land. 2022; 11(7):1037. https://doi.org/10.3390/land11071037
Chicago/Turabian StyleShi, Shuaiwei, Meiyi Hou, Zifan Gu, Ce Jiang, Weiqiang Zhang, Mengyang Hou, Chenxi Li, and Zenglei Xi. 2022. "Estimation of Heavy Metal Content in Soil Based on Machine Learning Models" Land 11, no. 7: 1037. https://doi.org/10.3390/land11071037
APA StyleShi, S., Hou, M., Gu, Z., Jiang, C., Zhang, W., Hou, M., Li, C., & Xi, Z. (2022). Estimation of Heavy Metal Content in Soil Based on Machine Learning Models. Land, 11(7), 1037. https://doi.org/10.3390/land11071037








