Dasymetric Mapping of Population Using Land Cover Data in JBNERR, Puerto Rico during 1990–2010
Abstract
1. Introduction
2. Materials and Methods
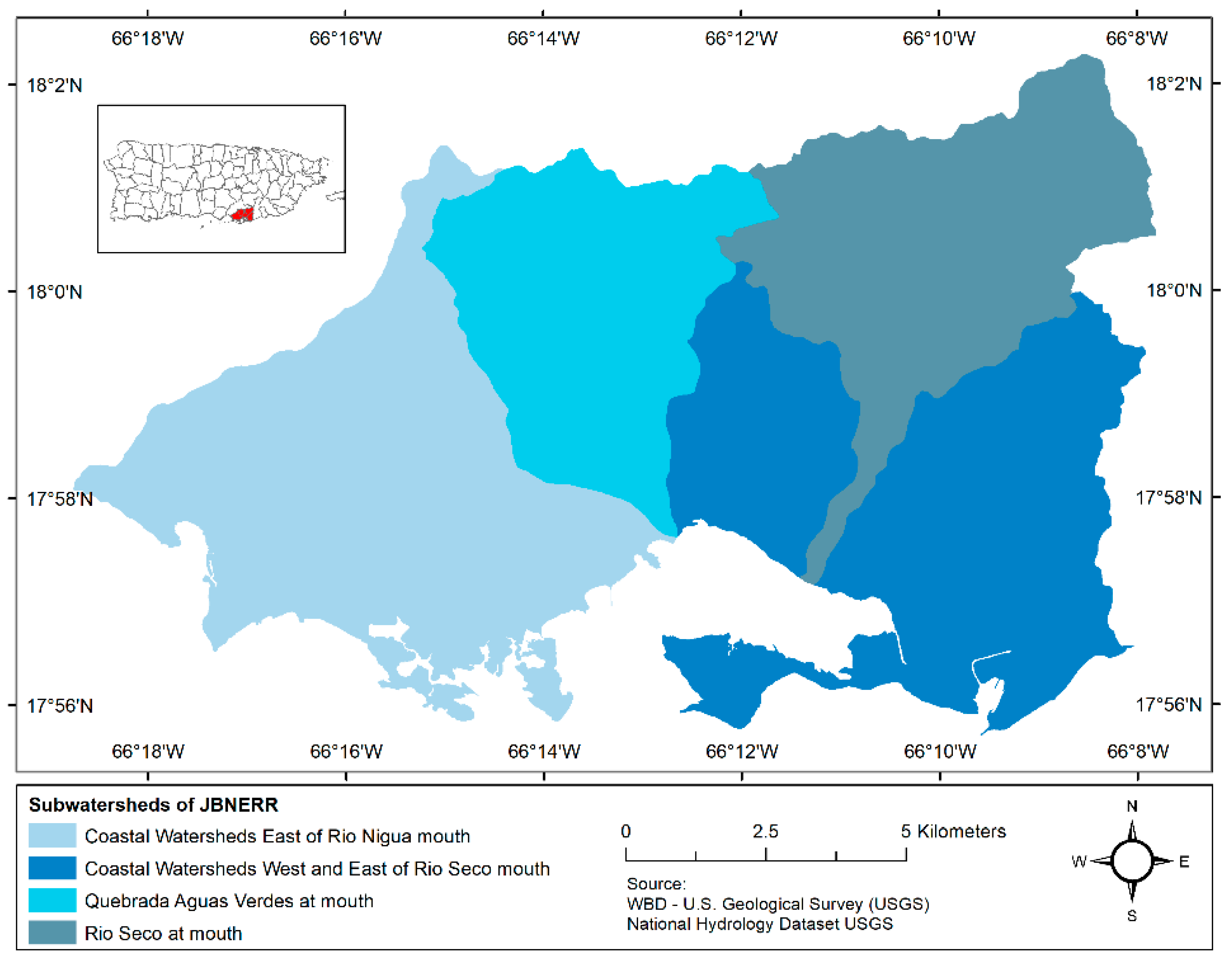
2.1. Study Area
2.2. Methods
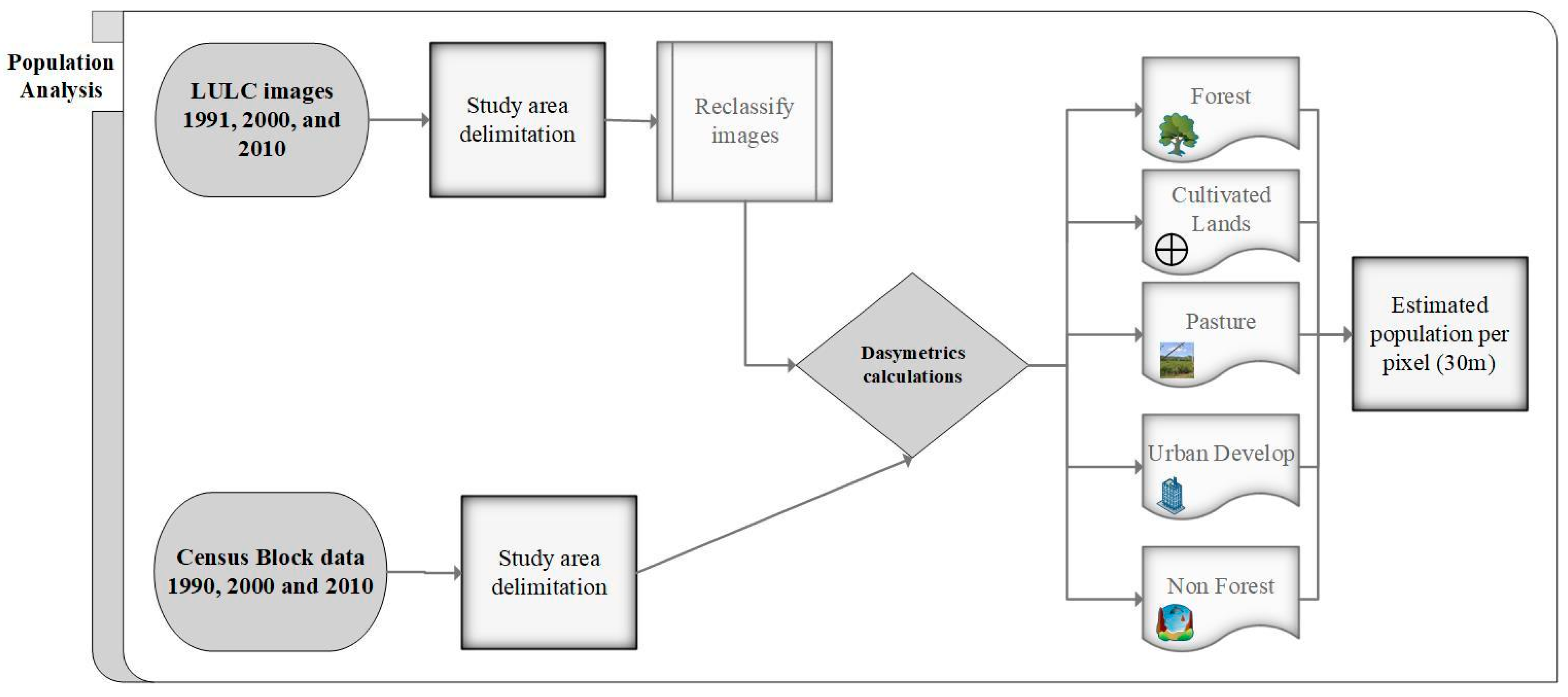
2.2.1. Dasymetric Mapping Statistical Approach
2.2.2. Error Assessment
3. Results
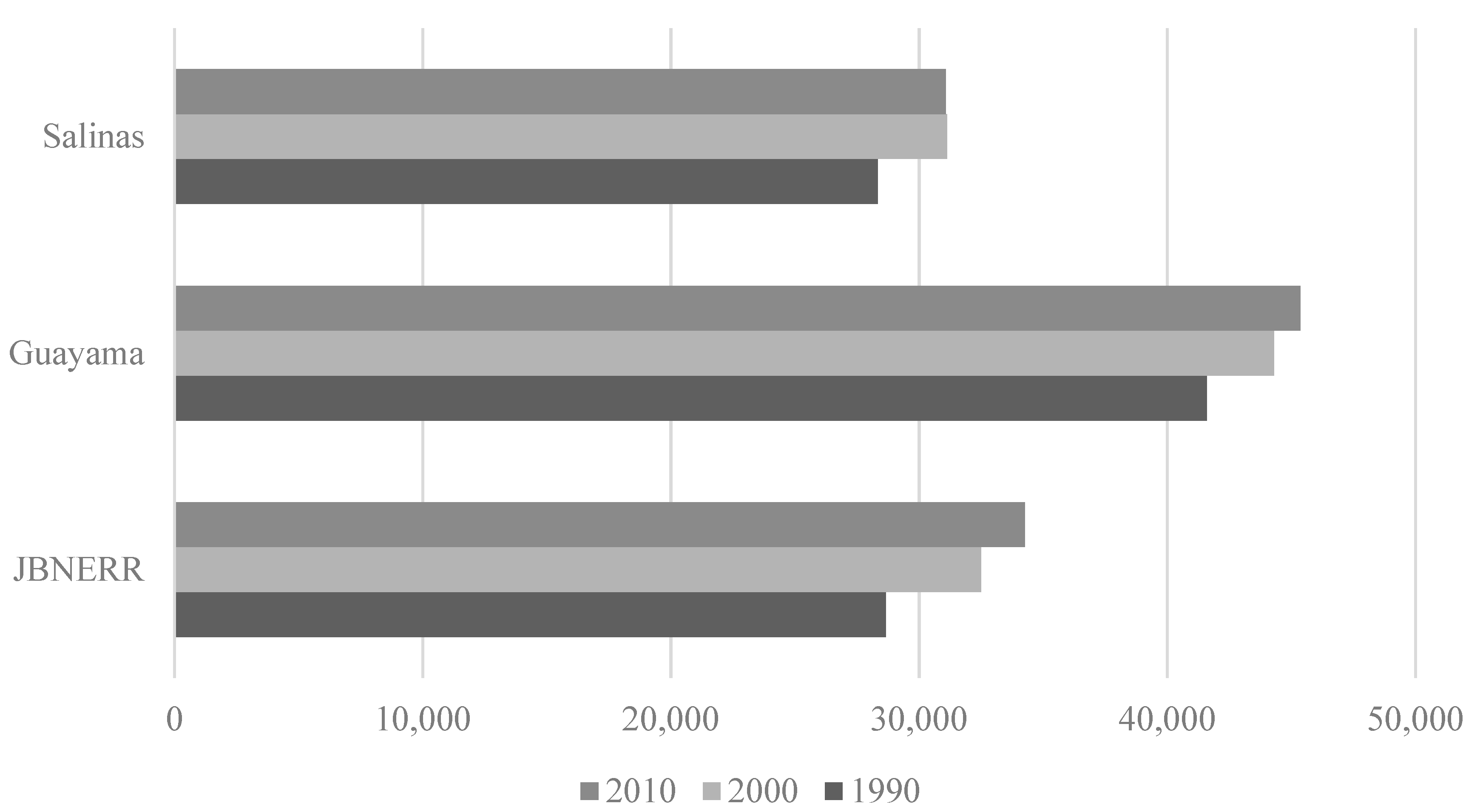
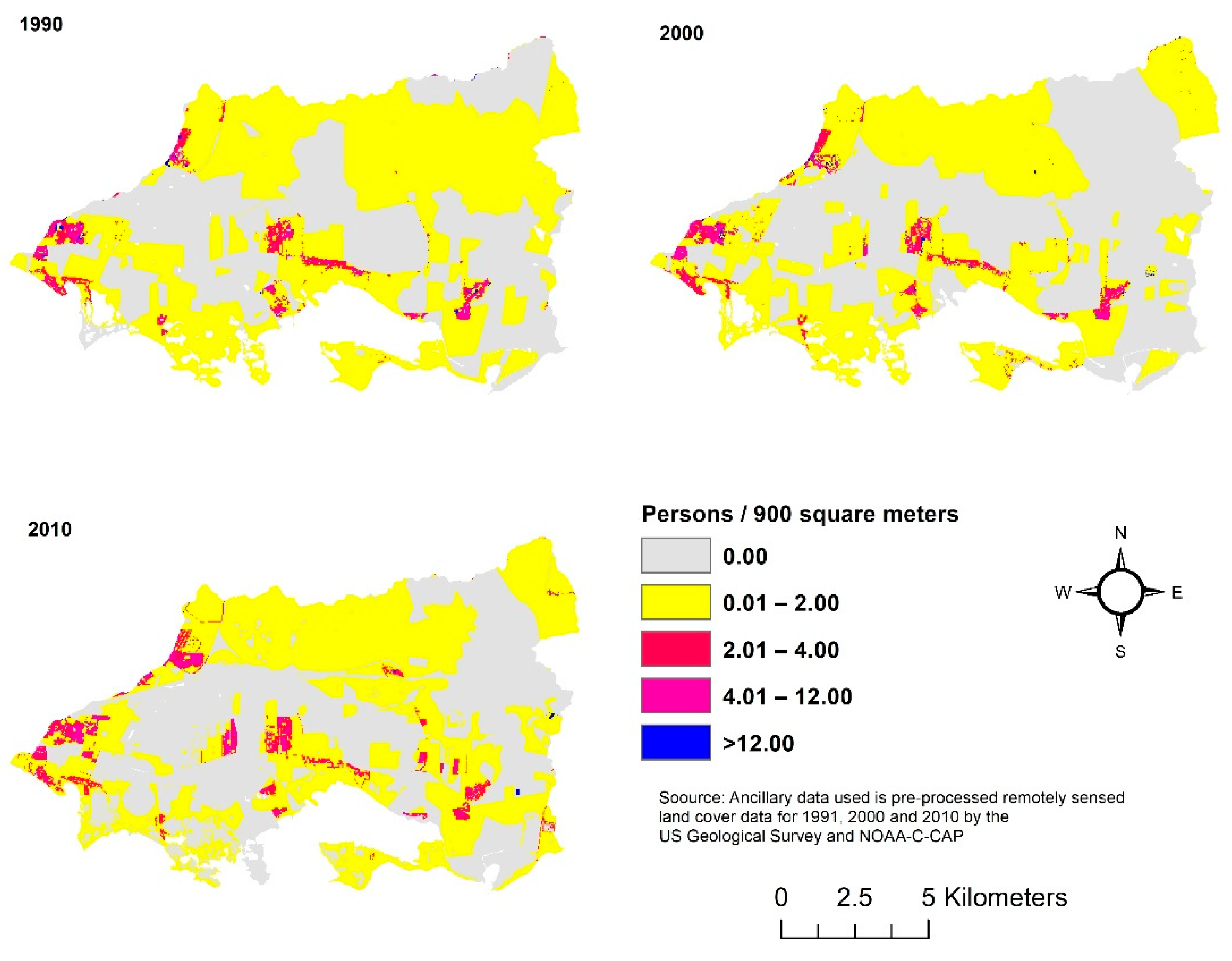
3.1. Population Estimates General Findings
3.2. Intelligent Dasymetric Mapping Error Assessment
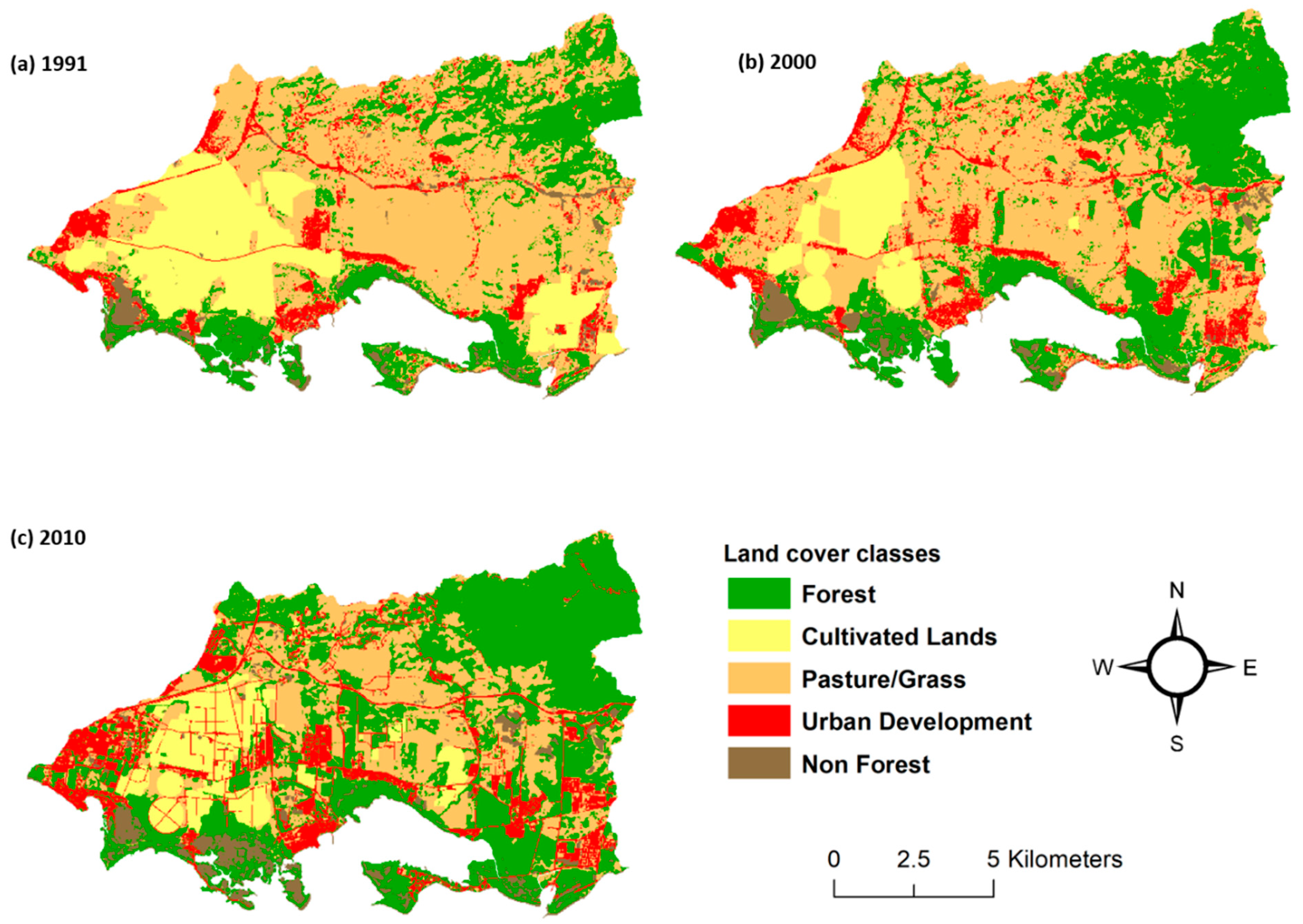
3.3. Dasymetric Population Mapping
4. Discussion
4.1. Uncertainty Sources
4.2. Multiclass Dasymetric Mapping
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| JBNERR | Jobos Bay National Estuarine Research Reserve |
| JBW | Jobos Bay Watershed |
| LULC | land use and land cover |
| IDM | intelligent dasymetric mapping |
References
- Brown, D.G.; Johnson, K.M.; Loveland, T.R.; Theobald, D.M. Rural Land-Use Trends in the Conterminous United States, 1950–2000. Ecol. Appl. 2005, 15, 1851–1863. [Google Scholar] [CrossRef]
- Deng, C. Small-Area Population Estimation: An Integration of Demographic and Geographic Techniques. Ph.D. Thesis, University of Wisconsin-Milwaukee, Milwaukee, WI, USA, 2013. [Google Scholar]
- Smith, S.K.; Nogle, J.; Cody, S. A Regression Approach to Estimate the Average Number of Persons per Household. Demography 2002, 39, 697–712. [Google Scholar] [CrossRef] [PubMed]
- Su, M.D.; Lin, M.C.; Hsieh, H.I.; Tsai, B.W.; Lin, C.H. Multi-Layer Multi-Class Dasymetric Mapping to Estimate Population Distribution. Sci. Total Environ. 2010, 408, 4807–4816. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-Sensed and Ancillary Data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef] [PubMed]
- Fisher, P.F.; Langford, M. Modeling Sensitivity to Accuracy in Classified Imagery: A Study of Areal Interpolation by Dasymetric Mapping. Prof. Geogr. 1996, 48, 299–309. [Google Scholar] [CrossRef]
- Weichselbaum, J.; Papathoma, M. Sharpening Census Information in GIS to Meet Real-World Conditions—The Case for Earth Observation. WIT Trans. Ecol. Environ. 2005, 84, 143–152. [Google Scholar]
- Holloway, S.R.; Schumacher, J.; Redmond, R.L. People and Place: Dasymetric Mapping Using Arc/Info. Cartographic Design Using ArcView and Arc/Info, Missoula Wildl. Spat. Anal. Lab. 1997. Available online: http://pdi.topografia.upm.es/mab/apuntesalumnos/Para%20tema7.PDF (accessed on 26 October 2022).
- Wu, S.S.; Qiu, X.; Wang, L. Population Estimation Methods in GIS and Remote Sensing: A Review. GISci. Remote Sens. 2005, 42, 80–96. [Google Scholar] [CrossRef]
- Wright, J.K. A Method of Mapping Densities of Populatrion with Cape Cod as an Example. Geogr. Rev. 1936, 26, 103–110. [Google Scholar] [CrossRef]
- Langford, M.; Unwin, D.J. Generating and Mapping Population Density Surfaces within a Geographical Information System. Cartogr. J. 1994, 31, 21–26. [Google Scholar] [CrossRef]
- Zoraghein, H.; Leyk, S.; Ruther, M.; Buttenfield, B.P. Exploiting Temporal Information in Parcel Data to Refine Small Area Population Estimates. Comput. Environ. Urban Syst. 2016, 58, 19–28. [Google Scholar] [CrossRef]
- Mennis, J. Generating Surface Models of Population Using Dasymetric Mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar] [CrossRef]
- Zandbergen, P.A.; Ignizio, D.A. Comparison of Dasymetric Mapping Techniques for Small-Area Population Estimates. Cartogr. Geogr. Inf. Sci. 2010, 37, 199–214. [Google Scholar] [CrossRef]
- Mennis, J. Dasymetric Mapping for Estimating Population in Small Areas. Geogr. Compass 2009, 3, 727–745. [Google Scholar] [CrossRef]
- Eicher, C.L.; Brewer, C.A. Dasymetric Mapping and Areal Interpolation: Implementation and Evaluation. Cartogr. Geogr. Inf. Sci. 2001, 28, 125–138. [Google Scholar] [CrossRef]
- Mennis, J.; Hultgren, T. Intelligent Dasymetric Mapping and Its Application to Areal Interpolation. Cartogr. Geogr. Inf. Sci. 2006, 33, 179–194. [Google Scholar] [CrossRef]
- Kennish, M.J. Environmental Threats and Environmental Future of Estuaries. Environ. Conserv. 2002, 29, 78–107. [Google Scholar] [CrossRef]
- Mennis, J. Dasymetric Spatiotemporal Interpolation. Prof. Geogr. 2016, 68, 92–102. [Google Scholar] [CrossRef]
- Rossiter, K. What Are Census Blocks? US Census Bureau. 2011. Available online: https://www.census.gov/newsroom/blogs/random-samplings/2011/07/what-are-census-blocks.html (accessed on 26 October 2022). Geogr. Meas. Am. People, Places, Econ.
- Kennaway, T.; Helmer, E. The Forest Types and Ages Cleared for Land Development in Puerto Rico. GISci. Remote Sens. 2007, 44, 356–382. [Google Scholar] [CrossRef]
- NOAA Office for Coastal Management (NOAA/OCM). C-CAP Land Cover, Puerto Rico, 2010 ID: 48301, InPort. Available online: https://inport.nmfs.noaa.gov/inport/item/48301 (accessed on 17 September 2019).
- Gao, Q.; Yu, M. Discerning Fragmentation Dynamics of Tropical Forest and Wetland during Reforestation, Urban Sprawl, and Policy Shifts. PLoS ONE 2014, 9, 1–11. [Google Scholar] [CrossRef]
- Comarazamy, D.E.; González, J.E.; Luvall, J.C. Quantification and Mitigation of Long-Term Impacts of Urbanization and Climate Change in the Tropical Coastal City of San Juan, Puerto Rico. Int. J. Low-Carbon Technol. 2015, 10, 87–97. [Google Scholar] [CrossRef]
- Bridgman, B.; Maio, M.; Schmitz, J.A. What Ever Happened to the Puerto Rican Sugar Manufacturing Industry? Federal Reserve Bank of Minneapolis: Minneapolis, MN, USA, 2012. [Google Scholar]
- Wang, C.; Yu, M.; Gao, Q. Continued Reforestation and Urban Expansion in the New Century of a Tropical Island in the Caribbean. Remote Sens. 2017, 9, 731. [Google Scholar] [CrossRef]
- Ramos-Scharrón, C.E.; Torres-Pulliza, D.; Hernández-Delgado, E.A. Watershed- and Island Wide-Scale Land Cover Changes in Puerto Rico (1930s–2004) and Their Potential Effects on Coral Reef Ecosystems. Sci. Total Environ. 2015, 506–507, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Mitsova, D.; Esnard, A.M.; Li, Y. Using Enhanced Dasymetric Mapping Techniques to Improve the Spatial Accuracy of Sea Level Rise Vulnerability Assessments. J. Coast. Conserv. 2012, 16, 355–372. [Google Scholar] [CrossRef]
- Zeng, W.; Comber, A. Using Household Counts as Ancillary Information for Areal Interpolation of Population: Comparing Formal and Informal, Online Data Sources. Comput. Environ. Urban Syst. 2020, 80, 101440. [Google Scholar] [CrossRef]
- Fisher, P.F.; Langford, M. Modelling the Errors in Areal Interpolation between Zonal Systems by Monte Carlo Simulation. Environ. Plan. A 1995, 27, 211–224. [Google Scholar] [CrossRef]
- Qiu, F.; Zhang, C.; Zhou, Y. The Development of an Areal Interpolation ArcGIS Extension and a Comparative Study. GISci. Remote Sens. 2012, 49, 644–663. [Google Scholar] [CrossRef]
- Mennis, J. Increasing the Accuracy of Urban Population Analysis with Dasymetric Mapping. Cityscape 2015, 17, 115–126. [Google Scholar]
- Tobler, W.R. Smooth Pycnophylactic Interpolation for Geographical Regions. J. Am. Stat. Assoc. 1979, 74, 519–530. [Google Scholar] [CrossRef]
- Lam, N.S.N. Spatial Interpolation Methods: A Review. Am. Cart. 1983, 10, 129–150. [Google Scholar] [CrossRef]
- Neves, O.M.d.S.; Strauch, J.C.M.; Ajara, C. Dasymetric Methods Applied to Jacarepaguá Watershed. Bol. Ciências Geodésicas 2017, 23, 606–622. [Google Scholar] [CrossRef]
- Titus, J.G.; Anderson, K.E.; Cahoon, D.R.; Gesch, D.B.; Gill, S.K.; Gutierrez, B.T.; Thieler, E.R.; Williams, S.J. The First State of the Coastal Cycle Sensitivity to Carbon Report Sea-Level Rise: Focus on Mid-Atlantic Region; U.S. Climate Change Science Program: Washington, DC, USA, 2009. [Google Scholar]
- Qiu, F.; Sridharan, H.; Chun, Y. Spatial Autoregressive Model for Population Estimation at the Census Block Level Using LIDAR-Derived Building Volume Information. Cartogr. Geogr. Inf. Sci. 2010, 37, 239–257. [Google Scholar] [CrossRef]
- Harvey, J.T. Estimating Census District Populations from Satellite Imagery: Some Approaches and Limitations. Int. J. Remote Sens. 2002, 23, 2071–2095. [Google Scholar] [CrossRef]
- Aquilino, M.; Adamo, M.; Blonda, P.; Barbanente, A.; Tarantino, C. Improvement of a Dasymetric Method for Implementing Sustainable Development Goal 11 Indicators at an Intra-Urban Scale. Remote Sens. 2021, 13, 1–34. [Google Scholar] [CrossRef]
- Aquilino, M.; Tarantino, C.; Adamo, M.; Barbanente, A.; Blonda, P. Earth Observation for the Implementation of Sustainable Development Goal 11 Indicators at Local Scale: Monitoring of the Migrant Population Distribution. Remote Sens. 2020, 12, 1–21. [Google Scholar] [CrossRef]
- Cleckner, H.; Allen, T.R. Dasymetric Mapping and Spatial Modeling of Mosquito Vector Exposure, Chesapeake, Virginia, USA. ISPRS Int. J. Geo-Inf. 2014, 3, 891–913. [Google Scholar] [CrossRef]
- Peña, E.N. Using Census Data, Urban Land-Cover Classification, and Dasymetric Mapping to Measure Urban Growth of the Lower Rio Grande Valley, Texas; University of Southern California: Los Angeles, CA, USA, 2012. [Google Scholar]
- Baynes, J.; Neale, A.; Hultgren, T. Improving Intelligent Dasymetric Mapping Population Density Estimates at 30ĝ€¯m Resolution for the Conterminous United States by Excluding Uninhabited Areas. Earth Syst. Sci. Data 2022, 14, 2833–2849. [Google Scholar] [CrossRef]
- Holt, J.B.; Lo, C.P.; Hodler, T.W. Dasymetric Estimation of Population Density and Areal Interpolation of Census Data. Cartogr. Geogr. Inf. Sci. 2004, 31, 103–121. [Google Scholar] [CrossRef]
- Schroeder, J.P. Hybrid Areal Interpolation of Census Counts from 2000 Blocks to 2010 Geographies. Comput. Environ. Urban Syst. 2017, 62, 53–63. [Google Scholar] [CrossRef]
- Zoraghein, H.; Leyk, S. Enhancing Areal Interpolation Frameworks through Dasymetric Refinement to Create Consistent Population Estimates across Censuses. Int. J. Geogr. Inf. Sci. 2018, 32, 1948–1976. [Google Scholar] [CrossRef]
- Schroeder, J.P. Target-Density Weighting Interpolation and Uncertainty Evaluation for Temporal Analysis of Census Data. Geogr. Anal. 2007, 39, 311–335. [Google Scholar] [CrossRef]
- Schroeder, J.P.; Van Riper, D.C. Because Muncie’s Densities Are Not Manhattan’s: Using Geographical Weighting in the Expectation-Maximization Algorithm for Areal Interpolation. Geogr. Anal. 2013, 45, 216–237. [Google Scholar] [CrossRef] [PubMed]
- Ruther, M.; Leyk, S.; Buttenfield, B.P. Comparing the Effects of an NLCD-Derived Dasymetric Refinement on Estimation Accuracies for Multiple Areal Interpolation Methods. GISci. Remote Sens. 2015, 52, 158–178. [Google Scholar] [CrossRef]
- Whitall, D.R.; Costa, B.M.; Bauer, L.J.; Dieppa, A.; Hile, S.D. A Baseline Assessment of the Ecological Resources of Jobos Bay, Puerto Rico; NOAA Technical Memorandum NOS NCCOS 133 Publisher: Silver Spring, MD, USA, 2011. [Google Scholar]
- Apeti, D.A.; Whitall, D.R.; Pait, A.S.; Dieppa, A.; Zitello, A.G.; Lauenstein, G.G. Characterization of Land-Based Sources of Pollution in Jobos Bay, Puerto Rico: Status of Heavy Metal Concentration in Bed Sediment. Environ. Monit. Assess. 2012, 184, 811–830. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Lu, D. Mapping Population Density Distribution at Multiple Scales in Zhejiang Province Using Landsat Thematic Mapper and Census Data. Int. J. Remote Sens. 2016, 37, 4243–4260. [Google Scholar] [CrossRef]
- Castro-Prieto, J.; Martinuzzi, S.; Radeloff, V.C.; Helmers, D.P.; Quiñones, M.; Gould, W.A. Declining Human Population but Increasing Residential Development around Protected Areas in Puerto Rico. Biol. Conserv. 2017, 209, 473–481. [Google Scholar] [CrossRef]
- Field, R.; Laboy, E.N.; Capellla, J.; Robles, P.O.; González, C.M. Jobos Bay Estuarine Profile: A National Estuarine Research Reserve; Jobos Bay National Estuarine Research Reserve: Salinas, Puerto Rico, 2008. [Google Scholar]
- Junta de Planificación de Puerto Rico. Plan de Mitigación de Peligros Naturales. Municipio de Salinas Versión Final (Natural Hazards Mitigation Plan. Salinas Municipality. Final Versión); Junta de Planificación de Puerto Rico Publisher: Salinas, Puerto Rico, 2019. [Google Scholar]
- Junta de Planificación de Puerto Rico. Plan de Mitigación de Peligros Naturales. Municipio de Guayama. Versión Final (Natural Hazards Mitigation Plan. Guayama Municipality. Final Version); Junta de Planificación de Puerto Rico Guayama: San Juan, Puerto Rico, 2020. [Google Scholar]
- US Census Bureau 2010 Census. TIGER/Line Shapefiles Technical Documentation; US Census Bureau: Washington, DC, USA, 2012. [Google Scholar]

| JBNERR | |||
|---|---|---|---|
| Census | Total * | ∆% | Growth Rate |
| 1990 | 28,667 | ||
| 2000 | 32,489 | 13.33 | 1.33 |
| 2010 | 34,250 | 5.42 | 0.54 |
| Guayama | |||
| Census | Total | ∆% | Growth Rate |
| 1990 | 41,588 | ||
| 2000 | 44,301 | 6.52 | 0.65 |
| 2010 | 45,362 | 2.39 | 0.24 |
| Salinas | |||
| Census | Total | ∆% | Growth Rate |
| 1990 | 28,335 | ||
| 2000 | 31,113 | 9.80 | 0.98 |
| 2010 | 31,078 | (0.11) | (0.01) |
| Census | RMSE | MAE |
|---|---|---|
| 1990 | 2.85 | 0.10 |
| 2000 | 3.01 | 0.11 |
| 2010 | 96.52 | 33.21 |
| 1990 | |||||||
| Land Cover Classes | Frequency | New Pop. | Percentage | Mean Density | Min | Max | Std |
| Density | Density | Density | |||||
| Forest | 231 | 959 | 3.35 | 0.31 | 0.00 | 22.03 | 1.88 |
| Cultivated Lands | 188 | 292 | 1.02 | 0.03 | 0.00 | 2.58 | 0.24 |
| Pasture/Grass | 519 | 1069 | 3.73 | 0.11 | 0.00 | 13.86 | 0.77 |
| Urban development | 616 | 26,321 | 91.82 | 4.43 | 0.00 | 254.76 | 12.33 |
| Non-Forest | 137 | 26 | 0.09 | 0.01 | 0.00 | 0.35 | 0.04 |
| 28,667 | 100 | ||||||
| 2000 | |||||||
| Forest | 409 | 514 | 1.58 | 0.09 | 0.00 | 9.00 | 0.64 |
| Cultivated Lands | 115 | 22 | 0.07 | 0.00 | 0.00 | 0.09 | 0.01 |
| Pasture/Grass | 836 | 2561 | 7.88 | 0.24 | 0.00 | 20.81 | 1.36 |
| Urban development | 927 | 29,167 | 89.78 | 3.73 | 0.00 | 71.21 | 7.07 |
| Non-Forest | 181 | 225 | 0.69 | 0.18 | 0.00 | 15.91 | 1.21 |
| 32,489 | 100 | ||||||
| 2010 | |||||||
| Forest | 803 | 236 | 0.69 | 0.01 | 0.00 | 1.36 | 0.07 |
| Cultivated Lands | 157 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Pasture/Grass | 747 | 853 | 2.49 | 0.05 | 0.00 | 7.94 | 0.48 |
| Urban development | 1305 | 33,161 | 96.65 | 2.09 | 0.00 | 94.00 | 4.79 |
| Non-Forest | 195 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Totals | 34,250 | 100 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cartagena-Colón, M.; Mattei, H.; Wang, C. Dasymetric Mapping of Population Using Land Cover Data in JBNERR, Puerto Rico during 1990–2010. Land 2022, 11, 2301. https://doi.org/10.3390/land11122301
Cartagena-Colón M, Mattei H, Wang C. Dasymetric Mapping of Population Using Land Cover Data in JBNERR, Puerto Rico during 1990–2010. Land. 2022; 11(12):2301. https://doi.org/10.3390/land11122301
Chicago/Turabian StyleCartagena-Colón, Marianne, Hernando Mattei, and Chao Wang. 2022. "Dasymetric Mapping of Population Using Land Cover Data in JBNERR, Puerto Rico during 1990–2010" Land 11, no. 12: 2301. https://doi.org/10.3390/land11122301
APA StyleCartagena-Colón, M., Mattei, H., & Wang, C. (2022). Dasymetric Mapping of Population Using Land Cover Data in JBNERR, Puerto Rico during 1990–2010. Land, 11(12), 2301. https://doi.org/10.3390/land11122301





