A Multi-Objective Optimization of Physical Activity Spaces
Abstract
1. Introduction
2. Literature Review
2.1. Multi-Objective Location Optimization
2.2. MOPSO-Based Location Optimization
3. Data and Methods
3.1. Study Area
3.2. Data
3.3. Methods
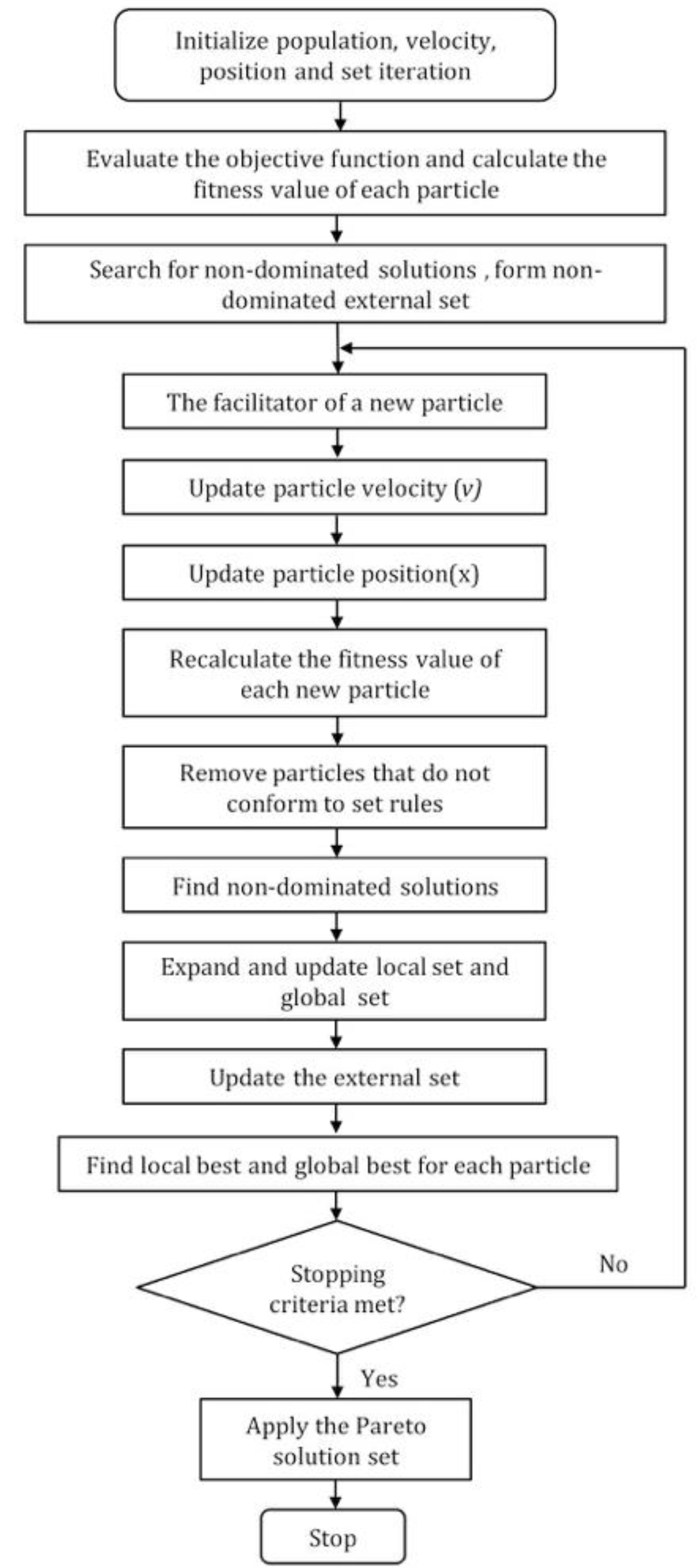
3.3.1. MOPSO
3.3.2. Optimization Objectives
3.3.3. Constraints
3.3.4. Parameter Settings
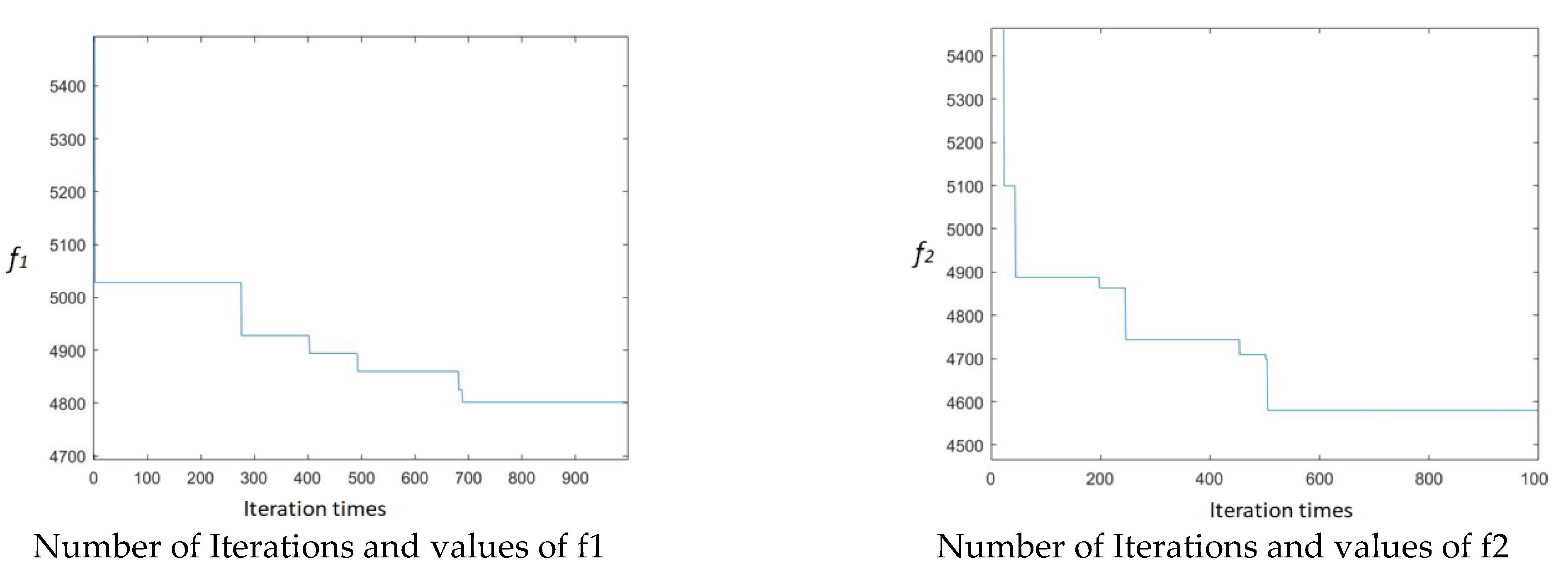
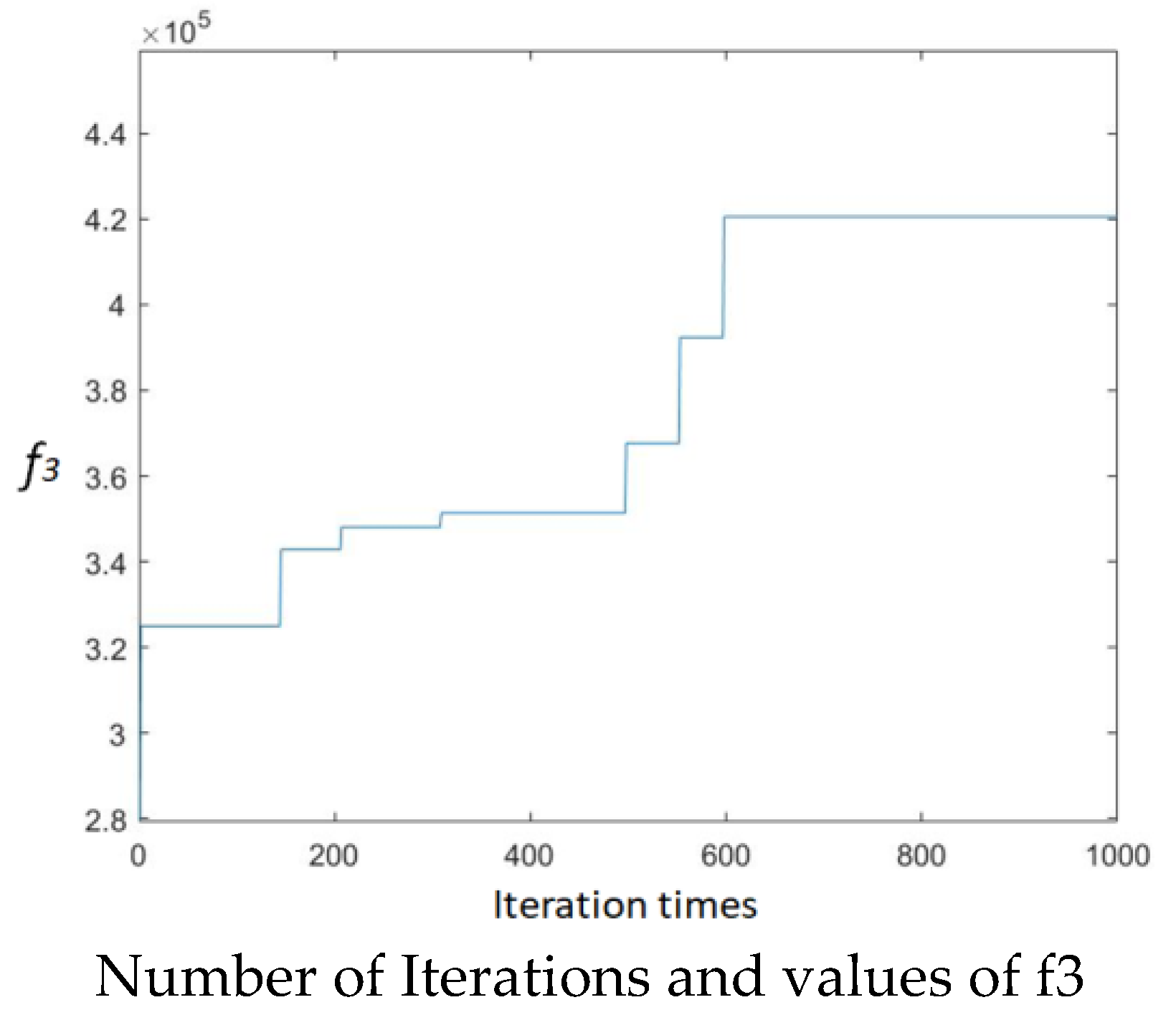
4. Results
5. Discussion
5.1. Spatial Distance between the Planned PAS and the Existing PAS
5.2. Implementation Feasibility
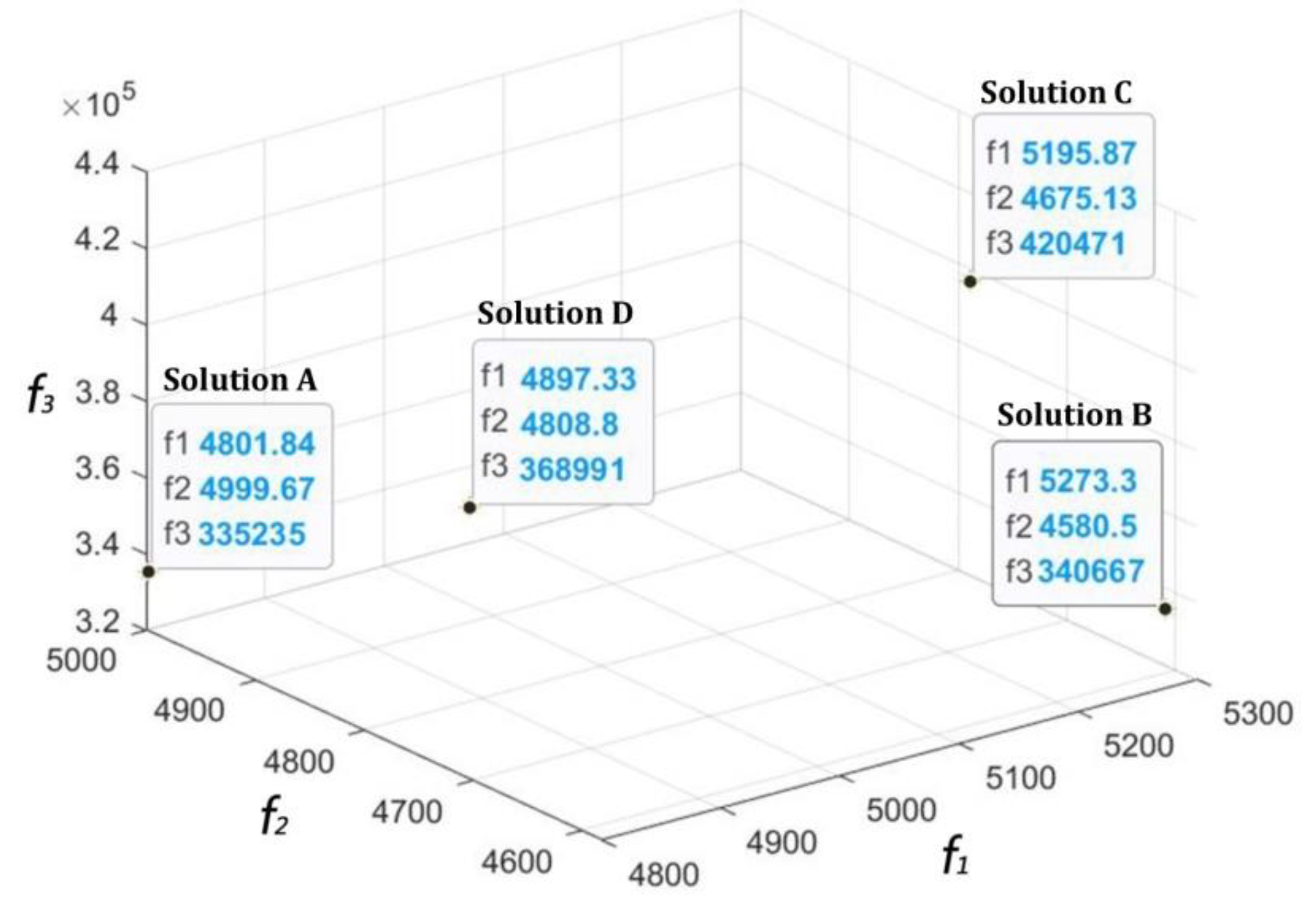
5.3. Optimization Trade-Offs and Optimal Solutions
5.4. Methodology Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elizabeth, A.; Durstine, J.L. Physical activity, exercise, and chronic diseases: A brief review. Sport. Med. Health Sci. 2019, 1, 3–10. [Google Scholar]
- WHO. Noncommunicable-Diseases 2022. Available online: https://www.who.int/zh/news-room/fact-sheets/detail/noncommunicable-diseases (accessed on 1 September 2022).
- Murray, C.J.; Lopez, A.D. Alternative projections of mortality and disability by cause 1990–2020: Global Burden of Disease Study. Lancet 1997, 349, 1498–1504. [Google Scholar] [CrossRef]
- Warburton, D.E.; Nicol, C.W.; Bredin, S.S. Health benefits of physical activity: The evidence. Can. Med. Assoc. J. 2006, 174, 801–809. [Google Scholar] [CrossRef]
- Durstine, J.L.; Gordon, B.; Wang, Z.Z.; Luo, X. Chronic disease and the link to physical activity. J. Sport Health Sci. 2013, 2, 3–11. [Google Scholar] [CrossRef]
- Ades, P.A.; Balady, G.J.; Berra, K. Transforming exercise-based cardiac rehabilitation programs into secondary prevention centers: A national imperative. J. Cardiopulm. Rehabil. 2001, 21, 263–272. [Google Scholar] [CrossRef]
- Hamman, R.F.; Wing, R.R.; Edelstein, S.L.; Lachin, J.M.; Bray, G.A.; Delahanty, L.; Hoskin, M.; Kriska, A.M.; Mayer-Davis, E.J.; Pi-Sunyer, X.; et al. Effect of weight loss with lifestyle intervention on risk of diabetes. Diabetes Care 2006, 29, 2102–2107. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.M.; Shiroma, E.J.; Lobelo, F.; Puska, P.; Blair, S.N.; Katzmarzyk, P.T. Effect of physical inactivity on major non-communicable diseases worldwide: An analysis of burden of disease and life expectancy. Lancet 2012, 380, 219–229. [Google Scholar] [CrossRef]
- Lear, S.A.; Hu, W.H.; Rangarajan, S.; Gasevic, D.; Leong, D.; Iqbal, R.; Casanova, A.; Swaminathan, S.; Anjana, R.M.; Kumar, R.; et al. The effect of physical activity on mortality and cardiovascular disease in 130,000 people from 17 high-income, middle-income, and low-income countries: The PURE study. Lancet 2017, 390, 2643–2654. [Google Scholar] [CrossRef]
- Spence, J.C.; Lee, R.E. Toward a comprehensive model of physical activity. Psychol. Sport Exerc. 2003, 4, 7–24. [Google Scholar] [CrossRef]
- Sallis, J.F.; Bauman, V.; Pratt, M. Environmental and policy interventions to promote physical activity. Am. J. Prev. Med. 1998, 15, 379–397. [Google Scholar]
- McLeroy, K.R.; Bibeau, D.; Steckler, A.; Glanz, K. An ecological perspective on health promotion programs. Health Educ. Q. 1988, 15, 351–377. [Google Scholar] [CrossRef]
- Sallis, J.F.; Cervero, R.B.; Ascher, W.; Henderson, K.A.; Kraft, M.K.; Kerr, J. An ecological approach to creating active living communities. Annu. Rev. Public Health 2006, 27, 297–322. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhou, K.C. Performance assessment of the distribution of community sports facility from the perspective of healthy equity—A case study of the central city of Shanghai. J. Hum. Settl. West China 2019, 34, 1–7. [Google Scholar]
- Guo, J.M.; Zhao, S. Optimization strategy of residents ‘public sports space supply under the concept of healthy city. Contemp. Sport. Technol. 2021, 11, 106–109. [Google Scholar]
- Wei, F.; Wang, X. Measuring spatial accessibility to physical activity spaces in Hangzhou using 2SFCA method. City Plan. Rev. 2019, 43, 112–119. [Google Scholar]
- Kabisch, N.; Haase, D. Green spaces of European cities revisited for 1990–2006. Landsc. Urban Plan. 2013, 110, 113–122. [Google Scholar] [CrossRef]
- Brito, J.N.; Pope, Z.C.; Mitchel, N.R.; Schneider, I.E.; Larson, J.M.; Horton, T.H.; Pereira, M.A. Changes in psychological state measures after green versus suburban walking exercise: A pilot crossover study. Int. J. Environ. Res. Public Health 2019, 16, 2894. [Google Scholar] [CrossRef]
- Wood, L.; Hooper, P.; Foster, S.; Bull, F. Public green spaces and positive mental health -investigating the relationship between access, quantity and types of parks and mental wellbeing. Health Place 2017, 48, 63–71. [Google Scholar] [CrossRef]
- Berman, M.G.; Kross, E.; Krpan, K.M.; Askren, M.K.; Burson, A.; Deldin, P.J.; Kaplan, S.; Sherdell, L.; Gotlib, I.H.; Jonides, J. Interacting with nature improves cognition and affect for individuals with depression. J. Affect. Disord. 2012, 140, 300–305. [Google Scholar] [CrossRef]
- Hanson, S.; Jones, A. Is there evidence that walking groups have health benefits? A systematic review and meta-analysis. Br. J. Sport. Med. 2015, 49, 710–715. [Google Scholar] [CrossRef]
- Pouso, S.; Borja, Á.; Fleming, L.E.; Gómez-Baggethun, E.; White, M.P.; Uyarra, M.C. Contact with blue-green spaces during the COVID-19 pandemic lockdown beneficial for mental health. Sci. Total Environ. 2020, 756, 143984. [Google Scholar] [CrossRef]
- He, J.L.; Zhang, X.F.; Chen, J.F. Sports and city: Integrative development strategy of urban green space and public sports in Germany. Urban Plan. Int. 2017, 32, 44–48. [Google Scholar] [CrossRef]
- Zhao, X.L.; Wang, M.C.; Zhao, W.; Chen, X.C.; Bian, Q. Evolution of British urban parks from the perspective of public health and well-being. Urban Plan. Int. 2021, 36, 47–57. [Google Scholar]
- Zhang, F.Y.; Xiao, Y.; Wu, Y. Spatial layout of public sports venues in urban communities—Based on Yangpu district of Shanghai. J. Shanghai Univ. Sport 2014, 38, 80–83. [Google Scholar]
- Billaudeau, N.; Oppert, J.M.; Simon, C.; Charreire, H.; Casey, R.; Salze, P.; Badariotti, D.; Banos, A.; Weber, C.; Chaix, B. Investigating disparities in spatial accessibility to and characteristics of sport facilities: Direction, strength, and spatial scale of associations with area income. Health Place 2011, 17, 114–121. [Google Scholar] [CrossRef]
- Zhang, H.J.; Yu, K.H. Investigation on condition of sports facility construction in the commercial residential communities in Hangzhou city. Zhejiang Sport Sci. 2007, 2, 45–48. [Google Scholar]
- Ma, Z.H.; Ma, Z.Q.; Dai, J.; Zhang, L. Research on central place theory and spatial distribution of urban sports facilities. J. Beijing Sport Univ. 2004, 27, 445–447. [Google Scholar]
- Shi, Z.G.; Ma, C.; Zhao, Y.P.; Wang, X.L.; Zhang, L.P.; Chu, S.L. Coupling mechanism and optimization path of urban public sports facilities distribution and residents’ leisure sports living space. J. Shandong Sport Univ. 2021, 37, 1–9. [Google Scholar]
- Chen, Y. Optimizing the distribution of community sports service facilities based on GIS. Econ. Geogr. 2010, 30, 1254–1258. [Google Scholar]
- Gu, X.F.; Li, N.; Lu, H.L. Study on locations of urban community sports “fitness circle” facilities based on GIS. Ind. Eng. J. 2014, 17, 87–90. [Google Scholar]
- Cho, C. An equity-efficiency trade-off model for the optimum location of medical care facilities. Socio-Econ. Plan. Sci. 1998, 32, 99–112. [Google Scholar] [CrossRef]
- Hodgson, J.M. A location–allocation model maximizing consumers’ welfare. Reg. Stud. 1981, 15, 493–506. [Google Scholar] [CrossRef]
- Revelle, C.S.; Laporte, G. The plant location problem: New models and research prospects. Oper. Res. 1996, 44, 864–874. [Google Scholar] [CrossRef]
- Zhang, Y.Y. Research on location and distribution of multi-objective emergency resources. China Saf. Sci. J. 2011, 21, 153–158. [Google Scholar]
- Farahani, R.Z.; SteadieSeifi, M.; Asgari, N. Multiple criteria facility location problems: A survey. Appl. Math. Model. 2010, 34, 1689–1709. [Google Scholar] [CrossRef]
- Chen, Z.N.; Yan, X.P. Application of location models in the distribution of common facilities. Econ. Geogr. 2006, 26, 23–26. [Google Scholar]
- Zhang, C.; Zhai, Z.W.; Li, Y.D. Location optimization of emergency medical facilities in downtown Nanjing Based on potentiality. Jiangsu Constr. 2019, 79–83. [Google Scholar]
- Hu, J.C.; Wang, L. Optimizing the distribution of city public sports service facilities based on GIS. J. Harbin Sport Univ. 2013, 31, 10–15. [Google Scholar]
- Çakmak, E.; Önden, İ.; Acar, A.Z.; Eldemir, F. Analyzing the location of city logistics centers in Istanbul by integrating Geographic Information Systems with Binary Particle Swarm Optimization algorithm. Case Stud. Transp. Policy 2021, 9, 59–67. [Google Scholar] [CrossRef]
- ElKady, S.K.; Abdelsalam, H.M. A Simulation-based optimization approach for healthcare facility location allocation decision. In Proceedings of the Science and Information Conference, London, UK, 28–30 July 2015; pp. 500–505. [Google Scholar]
- Larson, R.C.; Stevenson, K.A. On insensitivities in urban redistricting and facility location. Oper. Res. 1972, 20, 595–612. [Google Scholar] [CrossRef]
- Li, X.; Ye, J.A. Optimal spatial search using genetic algorithms and GIS. Acta Geogr. Sin. 2004, 59, 745–753. [Google Scholar]
- Li, L.; Xie, X.L. Research for combination algorithm of Weber multi-point facilities optimization location. Comput. Eng. Appl. 2013, 49, 258–261. [Google Scholar]
- Li, X.L.; Zhou, Q.P.; Tan, C.G.; Tan, Y.L.; Xu, Z.Y. Optimal location of urban sports facilities based on ant colony algorithm. Comput. Mod. 2020, 33–39. [Google Scholar] [CrossRef]
- Chen, W.L.; An, C.R.; Wang, J.C.; Yang, Y.L. A technical method for spatial location optimization based on network Voronoi diagram and multi-objective particle swarm. Geogr. Geo-Inf. Sci. 2014, 30, 1–6. [Google Scholar]
- Mohammadi, R.; Ghomi, S.M.T.F.; Jolai, F. Prepositioning emergency earthquake response supplies: A new multi-objective particle swarm optimization algorithm. Appl. Math. Model. 2016, 40, 5183–5199. [Google Scholar] [CrossRef]
- Liu, J.F.; Zhang, H.Y.; He, K.; Jiang, S.Y. Multi-objective particle swarm optimization algorithm based on objective space division for the unequal-area facility layout problem. Expert Syst. Appl. 2018, 102, 179–192. [Google Scholar] [CrossRef]
- Sevkli, M.; Guner, A.R. A continuous particle swarm optimization algorithm for uncapacitated facility location problem. Lect. Notes Comput. Sci. 2006, 4150, 316–323. [Google Scholar]
- Uno, T.; Kato, K.; Katagiri, H. An application of interactive fuzzy satisficing approach with particle swarm optimization for multiobjective emergency facility location problem with A-distance. In Proceedings of the IEEE Symposium on Computational Intelligence in Multicriteria Decision Making, Honolulu, HI, USA, 1–5 April 2007; pp. 368–373. [Google Scholar]
- Lu, Z. Research on the Application of Multi-Objective Particle Swarm Optimization in the Land of Consolidation Projects Site Location—A Case Study of Qinzhou District in Tianshui City. Master’s Thesis, Gansu Agricultural University, Lanzhou, China, 2017. [Google Scholar]
- Liu, J.D. Intelligent algorithm application in facility location—Taking Guangzhou city as an example. Urban Geotech. Investig. Surv. 2020, 3, 33–39. [Google Scholar]
- Ma, Y.J.; Zhao, X.J.; Qin, L.J.; Liang, P.J.; Zhou, H.J.; Yuan, Y.; Xu, W. Multi-objective location-allocation model of earthquake emergency shelters with multiple constraints: A case study in Wenchang of Hainan. J. Catastrophol. 2018, 33, 218–224. [Google Scholar]
- Tian, J.; Ma, W.Z.; Wang, Y.L.; Wang, K.L. Emergency supplies distributing and vehicle routes programming based on particle swarm optimization. Syst. Eng.-Theory Pract. 2011, 31, 898–906. [Google Scholar]
- Weber, A. On the Location of Industries; University of Chicago Press: Chicago, IL, USA, 1929. [Google Scholar]
- Beasley, J.E.; Chu, P.C. A genetic algorithm for the set covering problem. Theory Methodol. 1996, 94, 392–404. [Google Scholar] [CrossRef]
- Bigman, D.; ReVelle, C. An operational approach to welfare considerations in applied public-facility-location models. Environ. Plan. A 1979, 11, 83–95. [Google Scholar] [CrossRef]
- Murat, A.; Verter, V.; Laporte, G. A multi-dimensional shooting algorithm for the two-facility location–allocation problem with dense demand. Comput. Oper. Res. 2011, 38, 450–463. [Google Scholar] [CrossRef]
- Streifel, C.; Wolch, J.; Dean, M. Malign neglect: Homelessness in an American city. Contemp. Sociol. 1994, 23, 690. [Google Scholar] [CrossRef]
- Zhang, P.G.; Xu, Y.; Hu, S.; Hu, J.J. Sports facility and its layout for residents’ needs. Planners 2017, 33, 132–137. [Google Scholar]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Almiñana, M.; Pastor, J.T. An adaptation of SH heuristic to the location set covering problem. Eur. J. Oper. Res. 1997, 100, 586–593. [Google Scholar] [CrossRef]
- Farhan, B.; Murray, A.T. Siting park-and-ride facilities using a multi-objective spatial optimization model. Comput. Oper. Res. 2008, 35, 445–456. [Google Scholar] [CrossRef]
- Current, J.; Min, H.; Schilling, D. Multiobjective analysis of facility location decisions. Eur. J. Oper. Res. 1990, 49, 295–307. [Google Scholar] [CrossRef]
- Bellettini, G.; Kempf, H. Why not in your backyard? On the location and size of a public facility. Reg. Sci. Urban Econ. 2013, 43, 22–30. [Google Scholar] [CrossRef][Green Version]
- Batta, R.; Lejeune, M.; Prasad, S. Public facility location using dispersion, population, and equity criteria. Eur. J. Oper. Res. 2014, 234, 819–829. [Google Scholar] [CrossRef]
- Drezner, T.; Drezner, Z. The gravity p-median model. Eur. J. Oper. Res. 2007, 179, 1239–1251. [Google Scholar] [CrossRef]
- Liu, M.W.; Li, X. A pareto genetic algorithm for multi-objective site search problem: A case study on hospital location in Shenzhen city. Trop. Geogr. 2010, 30, 650–655. [Google Scholar]
- Wang, Y.Q. Research on location optimization of public sports Facilities based on GIS. Contemp. Sport. Technol. 2019, 9, 182–184. [Google Scholar]
- Li, X.; Ma, X.D.; Xue, X.T.; Khuong, M.H. Spatial supply-demand evaluation and layout optimization for urban green space: A case study of Xuzhou central district. Sci. Geogr. Sin. 2019, 39, 1771–1779. [Google Scholar]
- Zhang, Q.; Guo, X.L.; Peng, C.X.; Sun, H.L.; Qu, D.L. Optimization strategies for urban community sports space based on ten-minute fitness circle: A case study of Yuexiu district in Guangzhou. J. Guangdong Poly. Nor. Univ. 2022, 43, 67–72. [Google Scholar]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; pp. 1051–1056. [Google Scholar]
- Raquel, C.R.; Naval, P.C. An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Washington, DC, USA, 25–29 June 2005; pp. 257–264. [Google Scholar]
- Zhang, G.A.; Zhou, C.; Zhou, H. New multi-objective particle swarm optimization based on extended individual memory. Appl. Res. Comput. 2010, 27, 1665–1668. [Google Scholar]
- Li, H.B.; Li, X.; Liu, X.P.; Ai, B.; Liu, T. Particle-swarm optimization for site selection with contiguity constraints. Natl. Remote Sens. Bull. 2008, 12, 724–733. [Google Scholar]
- Zeng, Z.F.; Du, G.M. Location of public library based on particle swarm optimization. Libr. Inf. Serv. 2010, 54, 119–121. [Google Scholar]
- Du, G.M.; Chen, X.X.; Li, X. Spatial optimal search based on particle swarm optimization. Acta Geogr. Sin. 2006, 61, 1290–1298. [Google Scholar]
- Tao, Z.L.; Cheng, Y.; Dai, W.Q.; Li, X. Spatial optimization of residential care facility locations in 2020 in Beijing: Maximum equity in accessibility. Prog. Geogr. 2015, 34, 1609–1616. [Google Scholar]
- Kennedy, J.; Spears, W.M. Matching algorithms to problems: An experimental test of the particle swarm and some genetic algorithms on the multimodal problem generator. In Proceedings of the IEEE Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 78–83. [Google Scholar]
- Liu, X.W.; Wang, H.; Lei, X.H.; Liao, W.H.; Wang, M.N.; Wang, W.P.; Zhang, P.P. Influence of parameter settings in PSO algorithm on simulation results of Xin’anjiang model. South-North Water Transf. Water Sci. Technol. 2018, 16, 69–74. [Google Scholar]
- Yang, X.C.; Sima, X.; Hong, T. Urban open space system planning method research—A case study of Shenzhen city. Planners 2008, 24, 24–27. [Google Scholar]


| Parameters | Values |
|---|---|
| Number of particles, nPop | 200 |
| Number of external particles, nRep | 4 |
| The grid number, nGird | 7 |
| Maximum iteration, Imax | 1000 |
| Acceleration constants, c1, c2 | 2, 2 |
| Inertia weight, w | According to Formula (3) |
| Value range of X and Y | The range of X and Y dimension |
| Maximum velocity, vXmax and vYmax | 10% of the distance in X and Y dimension |
| Mutation probability, mu | 0.1 |
| Particle flight space dimension, D | 14 |
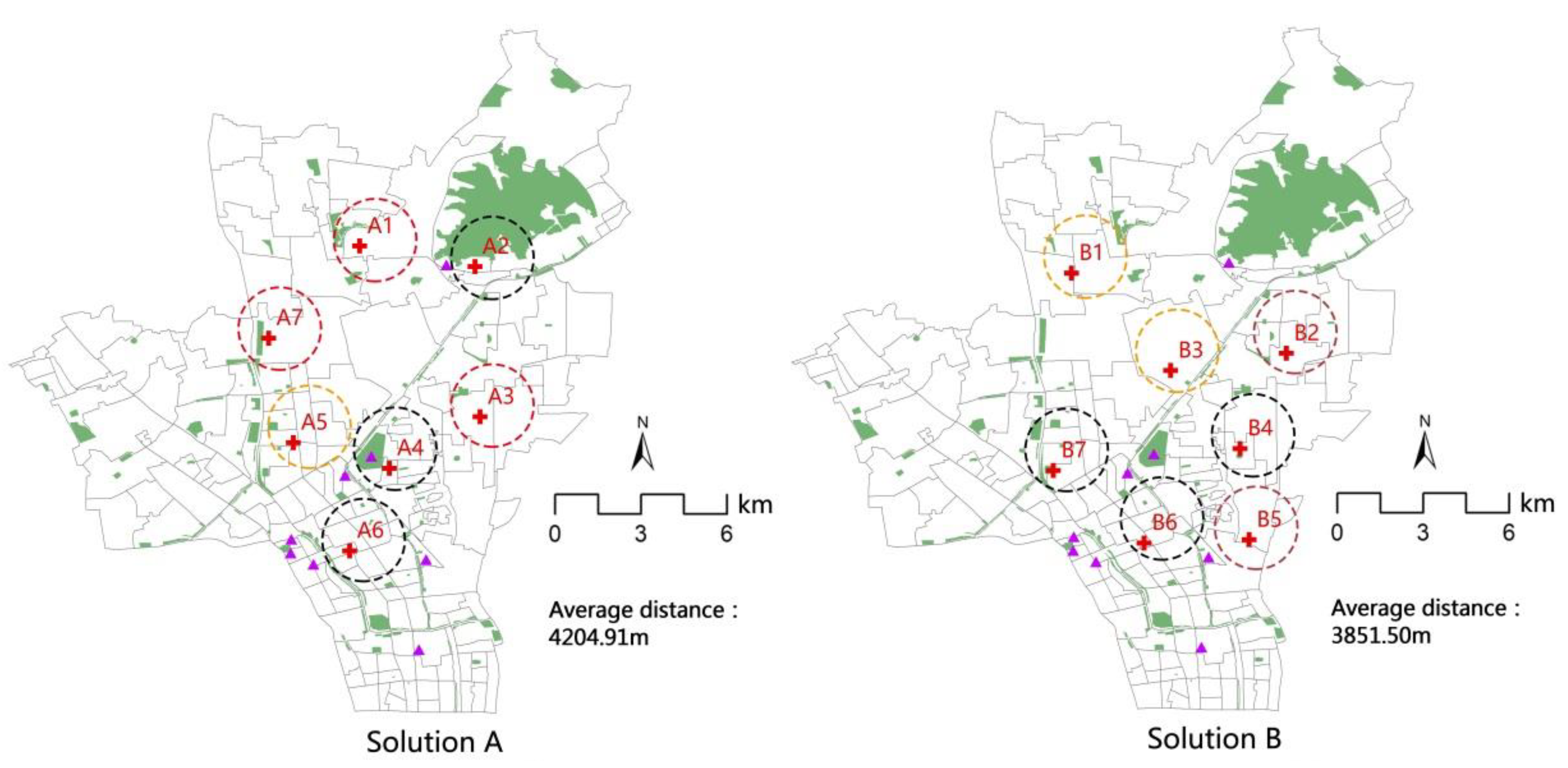
| Solutions | Feasibility | Locations | Land Use Conditions |
|---|---|---|---|
| A | High | A1, A3, A7 are located on abandoned and vacant land | 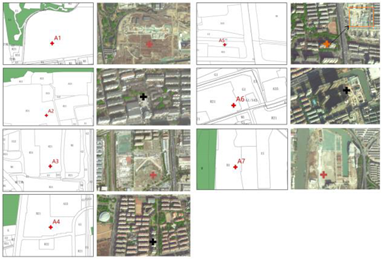 |
| Adjust | A5 can be moved to the northeast industrial land | ||
| Low | A2, A4, A6 lack available land | ||
| B | High | B2, B5 are located in abandoned and vacant land | 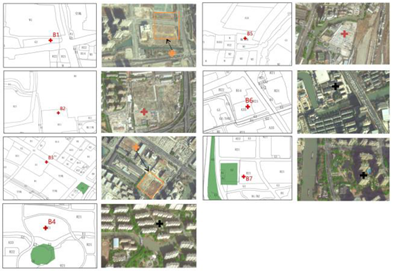 |
| Adjust | B1, B3 are located in UGS and cultural buildings, which can be moved to the vacant land | ||
| Low | B4, B6, B7 lack available land | ||
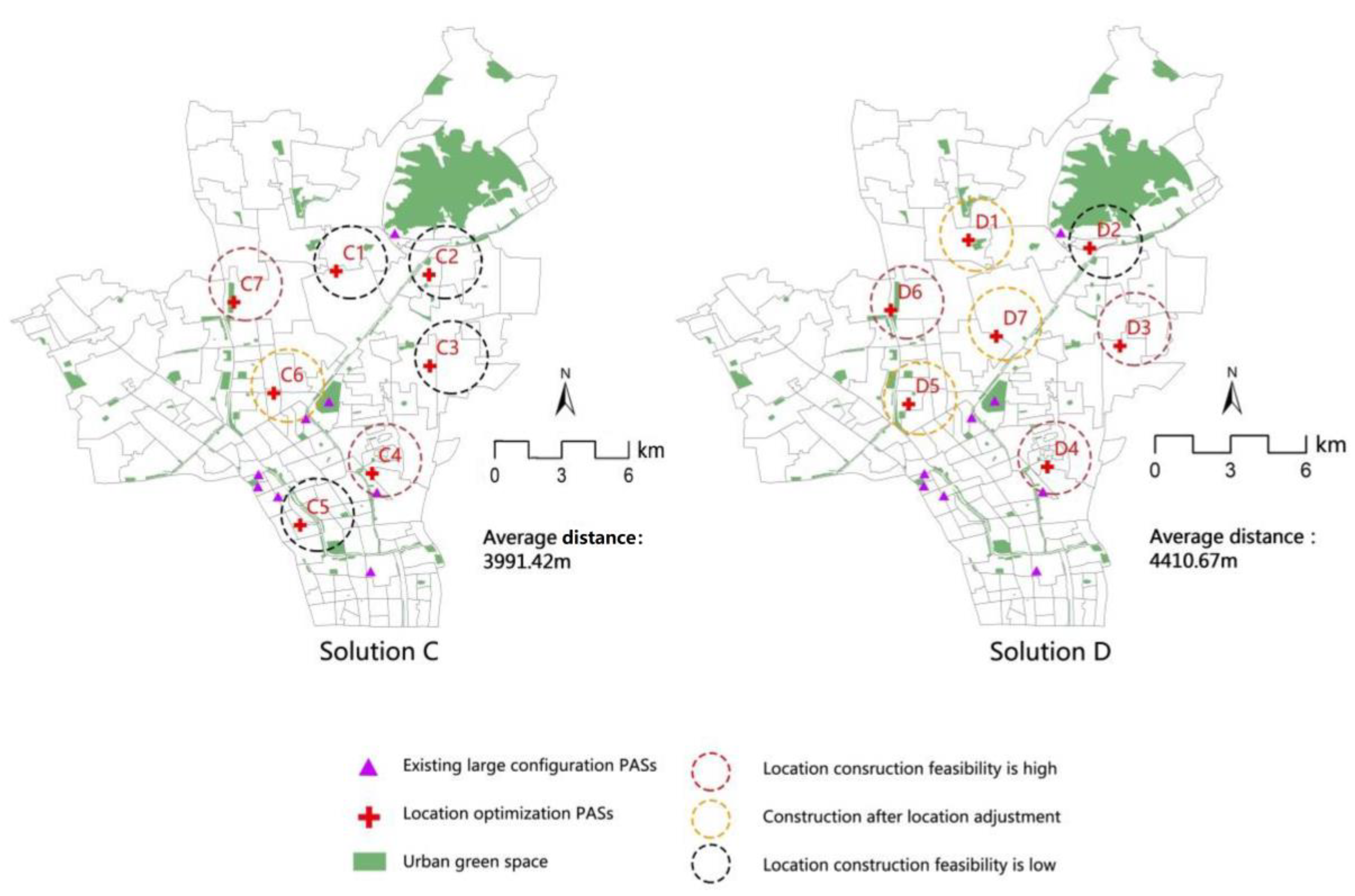
| C | High | C4, C7 are located in vacant land | 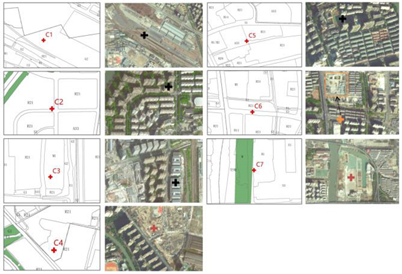 |
| Adjust | C6 is located on the road and can be moved to the industrial land | ||
| Low | C1, C2, C3, C5 are located in nonbuildable areas, such as green buffers | ||
| D | High | D3, D4, D6 are industrial land and abandoned vacant land |  |
| Adjust | D1, D5, D7 can be moved to vacant land | ||
| Low | D2 has no more available land |
| Solutions | Advantages | Disadvantages |
|---|---|---|
| A | PAS has the best connection with UGS; high spatial distribution balance; most locations’ construction feasibility is high | The accessibility and service population are lowest. Three locations are difficult to construct |
| B | The accessibility of PAS is the best. Most locations’ construction feasibility is high | Poor connection between PAS and UGS; the spatial distribution balance is poorest; Three locations are difficult to construct |
| C | Service the most people and the residential accessibility is high | The spatial distribution balance needs to be improved; construction feasibility is lowest and many locations are difficult to construct |
| D | Mean optimal objective; the spatial distribution balance in construction feasibility is highest | A separate objective optimal solution cannot be obtained |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, F.; Xu, W.; Hua, C. A Multi-Objective Optimization of Physical Activity Spaces. Land 2022, 11, 1991. https://doi.org/10.3390/land11111991
Wei F, Xu W, Hua C. A Multi-Objective Optimization of Physical Activity Spaces. Land. 2022; 11(11):1991. https://doi.org/10.3390/land11111991
Chicago/Turabian StyleWei, Fang, Wenwen Xu, and Chen Hua. 2022. "A Multi-Objective Optimization of Physical Activity Spaces" Land 11, no. 11: 1991. https://doi.org/10.3390/land11111991
APA StyleWei, F., Xu, W., & Hua, C. (2022). A Multi-Objective Optimization of Physical Activity Spaces. Land, 11(11), 1991. https://doi.org/10.3390/land11111991






