Next Article in Journal
Applying the FFP Approach to Wider Land Management Functions
Next Article in Special Issue
Model Selection for Ecosystem Respiration Needs to Be Site Specific: Lessons from Grasslands on the Mongolian Plateau
Previous Article in Journal
High Nature Value Farming Systems and Protected Areas: Conservation Opportunities or Land Abandonment? A Study Case in the Madrid Region (Spain)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Land
Volume 10
Issue 7
10.3390/land10070722
land-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

High-Resolution Spatio-Temporal Estimation of Net Ecosystem Exchange in Ice-Wedge Polygon Tundra Using In Situ Sensors and Remote Sensing Data

by
Haruko M. Wainwright
1,*,
Rusen Oktem
1,2,
Baptiste Dafflon
1,
Sigrid Dengel
1,
John B. Curtis
3,
Margaret S. Torn
1,
Jessica Cherry
4 and
Susan S. Hubbard
1
1
Earth and Environmental Sciences Area, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
2
Department of Earth and Planetary Science, University of California, Berkeley, CA 94720, USA
3
Department of Geography, University of Colorado, Boulder, CO 80309, USA
4
Alaska-Pacific River Forecast Center, National Oceanic and Atmospheric Administration, Anchorage, AK 99502, USA
*
Author to whom correspondence should be addressed.
Land 2021, 10(7), 722; https://doi.org/10.3390/land10070722
Submission received: 1 June 2021 / Revised: 29 June 2021 / Accepted: 6 July 2021 / Published: 9 July 2021
(This article belongs to the Special Issue Carbon Cycling in Terrestrial Ecosystems)
Browse Figures
Review Reports Versions Notes

Abstract

:
Land-atmosphere carbon exchange is known to be extremely heterogeneous in arctic ice-wedge polygonal tundra regions. In this study, a Kalman filter-based method was developed to estimate the spatio-temporal dynamics of daytime average net ecosystem exchange (NEEday) at 0.5-m resolution over a 550 m by 700 m study site. We integrated multi-scale, multi-type datasets, including normalized difference vegetation indices (NDVIs) obtained from a novel automated mobile sensor system (or tram system) and a greenness index map obtained from airborne imagery. We took advantage of the significant correlations between NDVI and NEEday identified based on flux chamber measurements. The weighted average of the estimated NEEday within the flux-tower footprint agreed with the flux tower data in term of its seasonal dynamics. We then evaluated the spatial variability of the growing season average NEEday, as a function of polygon geomorphic classes; i.e., the combination of polygon types—which are known to present different degradation stages associated with permafrost thaw—and microtopographic features (i.e., troughs, centers and rims). Our study suggests the importance of considering microtopographic features and their spatial coverage in computing spatially aggregated carbon exchange.

1. Introduction

Climate change has an amplified effect in the Arctic, which has been reported in both observational and modeling studies, e.g., [1,2]. For example, air temperature in the Arctic is expected to increase twice as much as the global average [3]. At the current pace, a significant portion of permafrost—which has sequestered organic carbon over millennia—could be lost in this century [4]. Concern has been mounting over the possibility that increased microbial activity in previously frozen soils could metabolize soil carbon and release greenhouse gases, leading to a positive feedback to climate [5,6]. At the same time, increasing temperature and associated changes in plant species could increase the photosynthetic activity of plants, enhancing the terrestrial CO2 sink [7].
Ice-wedge polygons, which cover much of the high-Arctic regions in the USA, Russia and others, e.g., [8,9], have unique geomorphic characteristics created by frost cracks in the ground and the subsequent growth of wedge-shaped ice within these frost cracks [10,11]. The growth of ice wedges moves soil and creates microtopography, e.g., [12]. Typically, ice-wedge polygons have long narrow depressions (i.e., troughs) along frost cracks and above ice wedges. Low-centered polygons (LCPs) have distinct rims or ridges along the troughs, which create low-elevation areas in the centers (Figure 1a). High-centered polygons (HCPs) have elevated centers surrounded by the troughs and are considered to represent the degraded stage of polygon evolution (Figure 1c), after the ridge of the low-center polygons collapses due to melting of the ice wedges. There are also flat-centered polygons (FCPs) which are at an intermediate stage of degradation between LCPs and HCPs. Recently, Liljedahl et al. [13] reported a wide-spread degradation of ice-wedge polygons across the pan-Arctic region associated with permafrost thaw, with the shifts occurring from LCPs to HCPs. This shift could result in increased water drainage and reduced water inundation [13], which could have a significant impact on vegetation-community dynamics, and on carbon exchange [14].
Extensive studies have sought to characterize the spatio-temporal heterogeneity of carbon fluxes in ice-wedge polygon tundra regions, using (1) chamber-based measurements, e.g., [9,12,15,16,17,18,19,20], (2) flux towers, e.g., [21] and (3) airborne-based measurements, e.g., [22]. These studies have identified the environmental factors that dictate the spatio-temporal variability of carbon exchange, including soil moisture, vegetation and soil types. In particular, the chamber-based studies have found that these factors are variable on the scale of several meters associated with microtopography, e.g., [9,12]. Wainwright et al. [12], for example, observed that soil CO2 effluxes are significantly higher in the centers of HCPs than in the ones of LCPs, which suggests that future polygon degradation could lead to an increase in soil CO2 efflux.
Recent advances in remote sensing—particularly using airborne platforms—have made it possible to capture the spatial variability of the land surface at submeter resolution. This is particularly important for characterizing heterogeneous ice-wedge polygonal ground where ecosystem properties vary laterally over the scales of meters [9,12,23,24]. In addition, unmanned aerial vehicles (UAVs) are increasingly being used to characterize sub-meter topography and vegetation, e.g., [25,26]. Since several studies have established relationships between certain vegetation indices—such as normalized difference vegetation indices (NDVIs)—and carbon exchanges [21,27], high-resolution multispectral optical remote-sensing techniques have been used to facilitate the mapping of carbon exchanges over the ice-wedge polygon tundra. However, airborne campaigns require human control and can be costly, which limits data acquisition to typically one or at most a few times during the growing season.
In parallel, various ground-based sensing technologies have recently been deployed to measure the temporal variability of terrestrial system behavior continuously and autonomously over time. These sensing systems couple various sensors and platforms such as in situ soil and optical sensors, flux towers, geophysics and weather stations, e.g., [24,28]. Such time-lapse sensing and remote data acquisition have been enabled by recent advances in telecommunication technologies and low-cost microcontrollers/computers for automated data acquisition remotely. In particular, flux towers have made a significant contribution to our understanding of temporal (from diurnal to seasonal and annual) changes in land-atmosphere carbon exchanges [29,30]. In addition, robotic technologies have further enabled the development of automated mobile tram systems that can autonomously move and collect terrestrial datasets at high spatial and temporal resolutions. Healey et al. [31], for example, developed such a system with multiple sensors (e.g., normalized difference vegetation index, albedo, radiation), which could move autonomously along a 50-m transect using an above-ground wireline. Such ground-based monitoring systems have a significant advantage in the Arctic region where frequent cloud coverage limits the use of optical satellite images.
In spite of our increasing ability to acquire such diverse datasets using different platforms, significant challenges remain when attempting to capture spatio-temporal ecosystem dynamics continuously over time and space, and to compute the overall or spatially aggregated carbon exchanges. One particular challenge is the integration of different datasets over different spatial scales (i.e., footprints, resolutions, spatial coverages) and sampling frequencies, as well as the integration of direct and indirect information. Chamber measurements are the most direct measurements of carbon fluxes with a footprint of less than one square meter, which can resolve the microtopographic effects. Their spatio-temporal coverage is, however, often limited; typically to several to several tens of locations in the domain and several times in the growing season. The flux towers measure carbon fluxes in a continuous time manner, but their measurements are a spatial aggregate over the tower footprint without resolving microtopography. Although remotely sensed NDVI and other indices can provide information over space and time, they are only proxies for carbon exchanges, and have significant uncertainties. Based on the spatio-temporal coverage of these measurements, it is desirable but challenging to integrate temporally extensive but spatially limited datasets (such as from ground-based sensors) with temporally sparse but spatially extensive datasets (such as from airborne remote sensing platforms). Although there have been several multiscale data-integration approaches available for spatial integration [32,33,34], the integration both in time and space is still at an early stage of development [35,36]. There have recently been several attempts to estimate the spatio-temporal distribution of carbon exchange at the flux-tower or site scale based on remote sensing data and chamber measurements [37] and mechanistic models [38,39,40,41]. However, the new robotics-based ground-based sensor system sensors mentioned above will open opportunities for improving the spatio-temporal estimation.
This study aims to develop a new approach for integrating multiscale multi-type datasets (i.e., airborne images, point measurements and mobile sensors) to quantify the spatiotemporal variability of land-atmosphere carbon exchanges associated with ice-wedge polygon geomorphology. We develop and apply a Kalman filter-based approach to integrate multiscale spatio-temporal datasets. Although the Kalman filter has been extensively applied in various scientific disciplines, including remote sensing and in situ sensor data applications, e.g., [42,43], it has not been used in the context of multiscale and multi-type data integration. The Kalman filter provides a flexible framework that can accommodate multiple datasets with high computational efficiency, as well as integrate the site-specific knowledge and data correlations. In particular, we make use of the recent observations indicating that Arctic tundra properties are highly correlated with one another, due to tightly coupled hydrological, geochemical and ecological processes, e.g., [12,23,44]. Our datasets include airborne LiDAR and multispectral images (which provide submeter information about the variability of topography and vegetation across the site) and a normalized difference vegetation index (NDVI) obtained from a mobile tram system, capable of providing high-temporal information along a 68 m transect during the growing season. Using the Kalman filter, we first estimate NDVI across an ice-wedge-dominated Arctic tundra site over the growing season, and then estimate the daytime net ecosystem exchange (NEEday) through the site-specific relationship between NDVI and chamber-based measurements (collected between 11:00 am–20:00 pm). The estimated NEEday for the area is aggregated over the flux tower footprint, and then compared with the flux-tower NEEday data (averaged between 11:00 am–20:00 pm).
Using the estimated spatio-temporal maps of NEEday, we quantify the difference in NEEday depending on the different polygon types that have been considered as proxies for the different stages of ice-wedge degradation [13,45] as well as microtopographic features (i.e., polygon troughs, rims and centers). We compute the spatially averaged NEEday in each polygon type and feature to investigate the spatial aggregation effects. We demonstrate our approach at the research station developed by the U.S. Department of Energy’s Next Generation Ecosystem Experiment (NGEE)-Arctic project located near Utqiaġvik, Alaska, USA. In the last fifty years, the land-cover changes are known to be minimal in this region compared to other Arctic sites [46], although Liljedahl et al. [13] reported some ice-wedge degradation in this region based on ground observations. This site includes different polygon types [12], which provides us with a unique opportunity to test our approach and to evaluate the impact of polygon geomorphology on spatially aggregated carbon exchanges.

2. Materials and Methods

2.1. NGEE-Arctic Site

The NGEE-Arctic site is located within the Barrow Environmental Observatory near Utqiaġvik (formerly called Barrow), AK, USA. Thaw lakes, drained thaw-lake basins (DTLBs), and ice-wedge polygonal tundra are the main landscape in this region. The NGEE site is located in the interstitial region of DTLBs—as it has been classified by Hinkel et al. [47]—which has been unaffected by the thaw-lake cycle for more than 5000 years [22,47]. Mean annual air temperature in this region is −11.3 °C, and mean annual precipitation is 106 mm [23]. The growing season typically starts from snowmelt in late May or early June, and ends with freezing and snowfall in early-to-mid September.
The site contains different types of ice-wedge polygons (Figure 2). The polygon types were categorized by Wainwright et al. [12] into low-centered polygons (LCPs), flat-centered polygons (FCPs) and high-centered polygons (HCPs). Each polygon type includes distinct microtopographic features—troughs, rims and centers (Figure 1). The vegetation characteristics depend on polygon types and features [9,48]. In well-developed ice-wedge polygons, vascular plants (such as Carex aquatilis) typically fill the wet troughs and centers of LCPs. In contrast, mosses and lichens dominate relatively dry areas, such as the rims of LCPs and the centers of HCPs and FCPs.

2.2. Datasets

2.2.1. Remote Sensing Data

We used the same airborne LiDAR data as Wainwright et al. [12], which were collected using a manned aircraft on 4 October 2005. The LiDAR provided a digital elevation map (DEM) over the entire site at 0.5 m by 0.5 m resolution (Figure 2). We measured the ground surface elevation in September 2011 at 1286 points using a Real-Time Kinematic Global Positioning System (RTK GPS), and found that the root-mean-square error (RMSE) of the Lidar DEM was 6.08 cm compared to the RTK GPS data.
High-resolution Red Green Blue (RGB) images were acquired on 7 August 2013 using a manned aircraft (Figure 2). The image (at 32 cm by 32 cm resolution) was converted to a map of greenness index (gI) using:
gI = G/(R + G + B),
where R, G and B refer to the red, green, and blue chromatic channels, respectively. The gI has been used in Wainwright et al. [12] and Dafflon et al. [26] as an effective index to characterize the vegetation variability based on the RGB image. Before the conversion, we used low-pass filtering with a cubic kernel to remove the centimeter-scale details that are beyond the scope of our work to resolve.

2.2.2. Tram and Flux Datasets

The tram system consisted of a motorized cart that carried several sensors including energy/radiation sensors (Figure 3). The cart was autonomously pulled along a 68 m long traverse, stopping at 0.5 m intervals to collect data at 137 stations. The footprint of each measurement is considered to be on the scale of approximately 0.5 m. Its route spanned different polygon types and features, including HCPs and LCPs. Measurement height above the ground surface varied depending on surface properties between 1 m (snow cover) and 2 m depending on microtopography (further information can be found in [49]). We used the NDVI data measured by an upward- and downward-looking spectral Red/NIR sensor. The NDVI data were collected at irregular time intervals (up to 8 times a day, depending on the time of year/season) from 5 June 2014, and to 21 September 2014. We used the mid-day NDVI data collected daily around noon. Although occasional problems arose with instruments or communications, we were able to successfully collect data over 65 days.
In addition to the measurements obtained by the tram sensors, we manually collected point measurements, including soil moisture (top 20 cm) and chamber CO2 flux data, along the tram transect on eight different occasions during 2014. The soil moisture (dielectric permittivity) and fluxes were recorded at 21 of the 137 tram stations. Soil moisture was estimated using dielectric permittivity measurements from a time domain reflectometer. Small-scale net CO2 fluxes between tundra surface and atmosphere were measured with a transparent closed-dynamic chamber connected to a Los Gatos Research, Inc. (San Jose, CA, USA) portable Greenhouse Gas Analyzer in the same manner as in Wainwright et al. [12] and Vaughn et al. [17]. For each measurement, the chamber was placed on a PVC base (30 cm diameter, installed ~15 cm deep) approximately 24 h prior to measurement. Fluxes were calculated from the slope of the linear section of greenhouse gas concentrations versus time. The chamber flux measurements were done during the day mostly between 11:00 and 20:00 (73% samples are between 11:00 and 15:00).
Tower-based eddy covariance (EC) CO2 fluxes (AmeriFlux ID US-NGB [18]) were measured on a 3.75 m tall tripod in the vicinity of the tram setup, employing a Gill R3-50 sonic anemometer (Gill, Lymington, UK) together with a LI-COR LI-7500A CO2/H2O gas analyzer (LI-COR, Lincoln, NE, USA). We followed the standard calibration and data QA/QC procedures as widely applied across the Ameriflux network (ameriflux.lbl.gov, accessed on 7 July 2021). The tower-based NEE was averaged NEE between 11:00 and 20:00 each day. We assume that NEE in our study is representing the daytime average NEE (NEEday).
To compute the contribution of each location to the flux tower, we used a footprint model developed by Kormann and Meixner [50] in determining the spatial extent of the EC system’s field of view (i.e., footprint). The footprint depends on the measurement height, surface roughness, atmospheric stability, wind direction and friction velocity. Our footprint model is a crosswind-integrated model, which computes the cumulative normalized contribution and how much of the measured flux comes from a particular distance (along with a particular wind direction), and also estimates the relative contribution of NEE from each pixel.

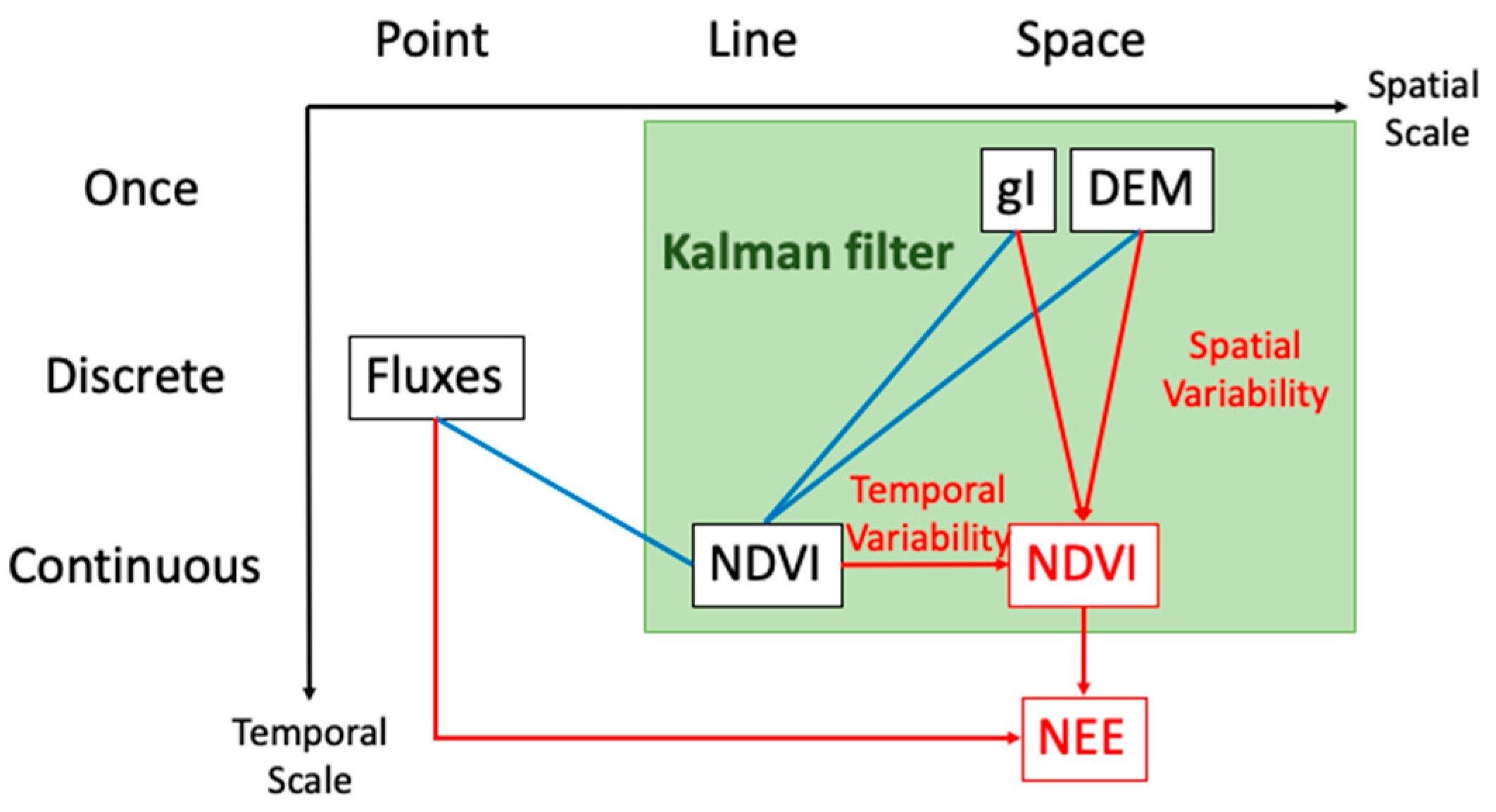
2.3. Integration Strategy

Our goal is to estimate NDVI and NEE over space and time, using (1) the temporally and spatially sparse chamber flux data, (2) the temporally extensive (but spatially limited) tram NDVI data and (3) the spatially extensive (but temporally limited) airborne greenness index (gI) data. Our estimation framework consists of a graphical model connecting multiple datasets at different spatial and temporal scales (Figure 4). Each node represents a variable (i.e., dataset or a target variable), while each connection represents a correlation between two variables [51]. We represent this connection based on the site-specific and general knowledge that a variety of properties are correlated through tightly coupled above/belowground processes described above, including subsurface properties, vegetation, geomorphology and carbon fluxes [12,26]. This estimation framework relies on a two-step approach: (1) the spatio-temporal dynamics of NDVI are first estimated at daily time steps based on the temporally extensive tram NDVI data and spatially extensive gI from the airborne imagery, using the Kalman filter method (described below), and (2) the NEE is then estimated from NDVI based on the correlations that are found between the tram NDVI and chamber measurements.
Previous studies have reported that NDVI is correlated with NEE in terms of seasonal changes without accounting for diurnal variability [21]. NEE has been estimated from NDVI and other satellite-derived metrics in the Arctic ecosystems [52,53]. In this study, we develop a site-specific function to calculate NEEday from NDVI based on the flux chamber measurements. In addition, we assume that NDVI is correlated with gI because (1) they both represent plant vigor or photosynthetic activities [54], and (2) Dafflon et al. [24] documented the correlations between NDVI and gI at our site. The challenge here is that we have only an estimate of gI at one point in time. With respect to seasonal temporal dynamics, we take advantage of the observations by Dafflon et al. [24] showing that spatial correlations were persistent in the ice-wedge tundra over time such that the lower elevations were consistently wetter and greener (represented by higher gI) over the growing season relative to the higher elevation regions. Additionally, it is known that polygon structures did not change significantly between 2013 and 2014. As such, we use the one-time gI map to represent the spatial variability. Since the correlations between the one-time gI and daily NDVI changes over time, we compute the temporally variable correlation parameters between gI and NDVI at the tram locations over the growing season.
The Kalman filter algorithm represents a spatio-temporal process by a linear state-space model [55]. We assume a state vector xt = {xi,t| i = 1, …, n} representing NDVI at all pixels (the number of pixels is n) at Day t. We denote a data vector by zt = {zj,t| j = 1, …, m}, which is a collection of data at Day t, including (1) the NDVI measurements at tram locations (1 ≤ j ≤ mT; the number of the tram measurements is mT), and (2) the gI data at pixels (mT + 1 ≤ j ≤ mT + mVI = m; the number of gI data pixels is mVI). At each time step, the data vector is described as a function of the state vector by the state-observation equation:
zt = H xt + Ku + w(t)
where H is a m-by-n data transfer matrix representing the connection between data and state vectors, K is the matrix defining the intercept term, and u is a unit vector (a vector containing all elements equal to one with the length of m). Physically, the observation equation (Equation (2)) describes all the data as a function of target variables (NDVI in our case), so that—within the estimation framework—this equation transfers the information from the data to the target variables. H and K include the correlation parameters describing the data value as a function of NDVI at each pixel. At the tram pixels, the data are the direct measurements of NDVI:
zj,t = xi,t + wT,
where wT follows an independent identically distributed (i.i.d.) zero-mean normal distribution with a fixed variance, representing a measurement error. For the non-tram locations, we assume that the j-th gI data is linearly correlated with NDVI at the i-th pixel such that:
zj,t = aV(t) xi,t + bV(t) + wV(t),
where aV(t) and bV(t) are the time-varying slope and intercept parameters in the linear correlations, and wV(t) represents the uncertainty in the correlations. We assume that wV(t) follows a zero-mean normal distribution with the variance (σV) of the residual in the linear correlations. In Equation (2), the transfer matrix H is represented by:
Hj,i = 1, if j-th tram station corresponds to i-th pixel (1 ≤ j ≤ mT)
     = aV(t), if j-th gI data corresponds to i-th pixel (mT + 1 ≤ j ≤ m).
The matrix K is an m-by-m matrix where
Kj,j = 0, if j-th tram station corresponds to i-th pixel (1 ≤ j ≤ mT)
     = bV(t), if j-th gI data corresponds to i-th pixel (mT + 1 ≤ j ≤ m).
The parameters aV(t), bV(t), and σV are co-estimated at each time step during the Kalman filter. At each time step, the linear correlation is evaluated between the NDVI and gI, at the tram locations, and then the correlation parameters and the residual variance are calculated.
The temporal evolution of NDVI—the change in NDVI at all the pixels from date t to t + 1—is described as a transition of the state from t to t + 1 in a state-transition equation as:
xt+1 = A xt + B u + v(t)
The matrices A and B determine the magnitude of changes, while the error vector v(t) represents the deviation from the linear model such as natural fluctuation. Although the time evolution of NDVI can be described by a mechanistic model, we use a data-driven, first-order autoregressive (AR1) model in this study, adapted from the spatio-temporal integration approach developed by Chen et al. (2013). In our model, the general form of Equation (7) is changed to:
xi,t+1 = xi,t + vi
This means that the NDVI at the i-th pixel changes from xi,t to xi,t+1 with the magnitude vi (in Equation (7), the matrix A is an identity matrix, and the matrix B is zero). This implementation is the same as Rastetter et al. [56] who implemented the temporal evolution of leaf area index (LAI) using the Kalman filter. Rastetter et al. [56] assumed that the change of LAI in each time step was small and hence the systematic change component could be approximated to be zero, and that the observation equation (equivalent to Equation (2) above) could transfer the information related to the temporal evolution in LAI from the data within the Kalman filter. Similarly, we assume that the daily change in NDVI is relatively small so that vi follows an i.i.d. zero-mean normal distribution with a fixed variance. The variance of vi is determined from taking the variance of the NDVI difference (xi,t+1—xi,t) at all the tram locations. Although the systematic increase and decrease are not included in this formulation, such temporal dynamics are captured based on the tram information represented in Equation (3) with the Kalman filter.
Once the state and observation equations are defined, the standard Kalman filtering algorithm can be used to estimate the spatio-temporal dynamics of xt and its estimation variance (the algorithm is described in Appendix A). The Kalman filter consists of prediction and update at each time step. In the prediction step, the state transition equation (Equation (7)) is used to predict the state vector (i.e., NDVI at all the pixels) at the next time step xt+1 from the previous time step xt. In the update step (or correction step), the estimate of the state vector is improved or corrected by including the tram NDVI and airborne gI data through the observation equation (Equation (2)). In this update step, the information transfers from the data to the target variables (e.g., the estimates of NDVI). The covariance of the state vector is estimated at each step; each diagonal element of the covariance matrix is the estimation variance σxi,t, representing the uncertainty in the estimates.
After NDVI values are estimated over space and time, NEEday at each pixel is estimated based on the NDVI-NEEday relationship. The NEEday at pixel i and time step t (yi,t) is a function of NDVI such that:
yi,t = f(xi,t) + ε t,
We assume an i.i.d. zero-mean normal distribution to represent the error and uncertainty ε t in this relationship. To account for the uncertainty in this relationship, we used the variance propagation formula, in which the variance of yi,t is |f’(xi,t)|2σxi,t + σy, where f’ is the first derivative of the function f, and σxi,t is the estimation variance of NDVI at pixel i and time step t derived from the Kalman filter, and σy is the variance of the residual in the NEEday-NDVI relationship. Once the NEEday map is created, we computed the weighted average of NEEday (Equation (9)) within the EC flux tower footprint to compare with the NEEday from the EC flux tower data. The weights were calculated based on the contribution of each pixel to the tower data in the footprint model.
Our formulation provides a general framework for incorporating multi-type datasets, including time-varying data and stationary data together in the data vector zt. The Kalman filtering approach has been used extensively for remote sensing and environmental science applications as well as for integrating ecosystem or land surface models with eddy-covariance flux tower data [39,56]. Our unique contribution is to seamlessly integrate spatio-temporal disparate datasets sampled over a range of spatial and temporal scales, which addresses the particular challenge of integrating spatially extensive but temporally sparse data with high frequency but spatially sparse data.

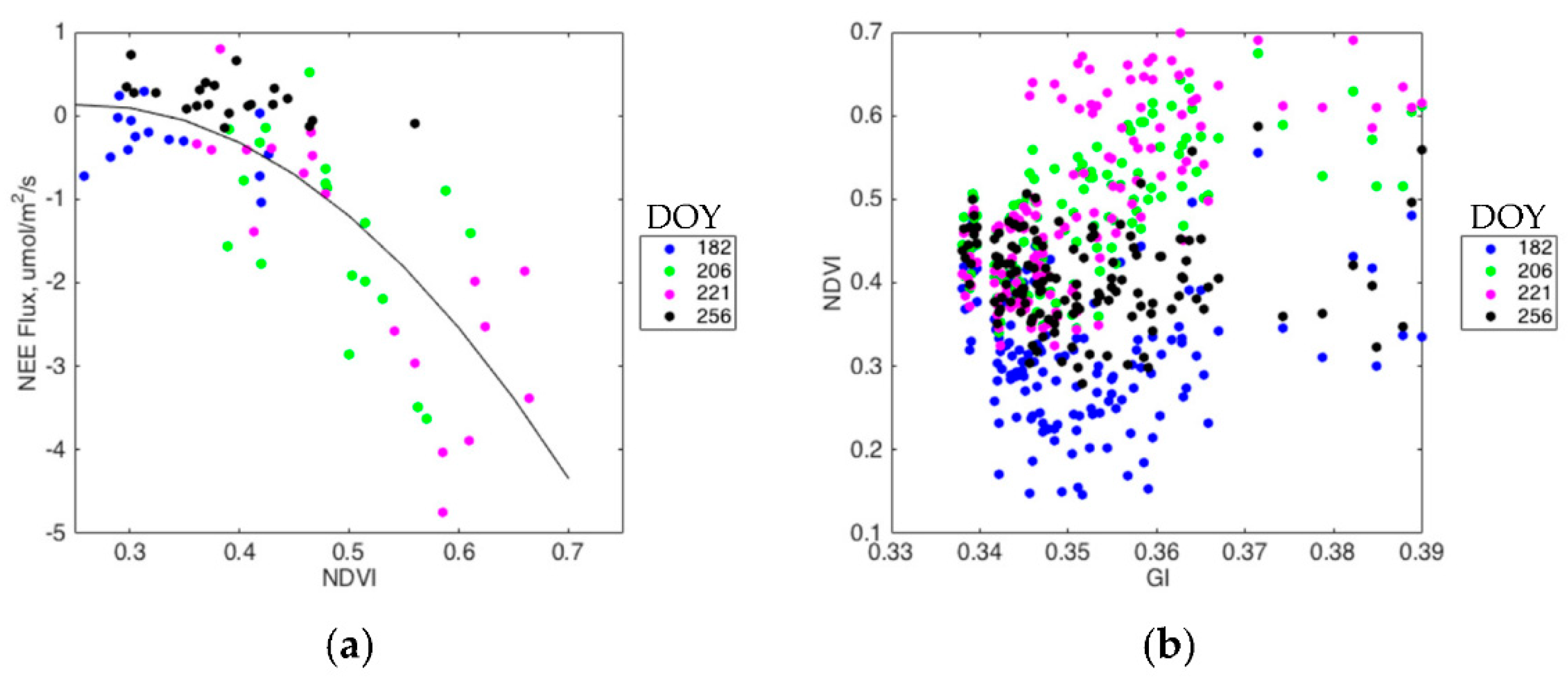
3. Results

The tram data reveals the spatio-temporal variability of NDVI along the 68-m transect (Figure 5a), a variability associated with both the polygon features and types which are associated with distinct plant species as described in Section 2.1. After the snowmelt, NDVI increases more significantly at the polygon troughs and centers of LCPs than the polygon rims and the centers of FCPs. The peak NDVI around the day-of-year (DOY) 221 is higher at the troughs and the centers of LCPs. In parallel, the co-located soil moisture and chamber-measured NEEday show their dependency on microtopographic features (Figure 5c,d). Soil moisture does not change significantly over time during the growing season (Figure 5b). However, the spatial variability of soil moisture (top 20 cm) is significant, with the troughs and the LCP centers fully saturated and the polygon rims dry. In Figure 5d, NEE exhibits small spatial variability in the beginning and end of the growing season (DOY 182 and 256), but the spatial variability becomes larger in the peak season (approximately Day 221) with a significantly higher NEE (i.e., carbon sink) at the troughs and the LCP centers. The highest NEE values (Figure 5d) during the growing season correspond to the highest NDVI timing (i.e., DOY 221 in Figure 5b).
The tram-measured NDVI and chamber-measured NEEday data are significantly correlated with each other over time (Figure 6a). The NDVI–NEEday correlations at different sampling times are temporally consistent along the same trend. Since some nonlinearity is observed in their relationship, we used the Spearman rank correlation that yielded a correlation coefficient of −0.73 (p-value < 0.01). We fitted a quadratic function to represent this trend curve (R2 = 0.57 and p-value of <1 × 10−13). On the other hand, the correlations between the airborne-based gI (one-time acquisition) and the tram-based NDVI (multiple acquisitions) change over time (Figure 6b). The Spearman correlation coefficients are −0.10 (p-value 0.26), 0.63 (p-value < 0.01), 0.65 (p-value < 0.01) and −0.01 (p-value 0.92) on Days 182, 206, 221 and 256, respectively. While the correlations are not significant in the shoulder seasons, they are higher in the middle of the growing season when the NDVI and NEE are most spatially heterogeneous.
Using the Kalman filtering approach and the data-derived correlations, we estimated NDVI and NEEday over the growing season between the complete snowmelt (DOY 185) and the first snow accumulation (DOY 250). Although both NDVI and NEE have a diurnal cycle, we estimated only the daytime values corresponding to the chamber measurements. There were missing days in the tram data, owing to instrument, power or communication failures. We interpolated the tram data for each date over the estimation period.
The temporal evolution of NDVI and NEEday over the site (Figure 7) shows a spatial variability consistent with the tram data (Figure 6). In the early growing season (Figure 7a,d), both NDVI and NEEday are low across the site, and their spatial variability is small. Both NDVI and NEEday increase significantly in July (between DOY 185 and 210), as does their spatial variability. The troughs and LCP centers have higher peak NDVI and NEEday than the HCP centers and rims in the middle of the growing season (DOY 210; Figure 7b,e). Later in the growing season (Figure 7c,f), both NDVI and NEEday decrease significantly at the HCP centers and rims, while they continue to be high at the LCP centers and troughs.
We confirmed the performance of the estimation based on the tram NDVI data at the ten locations (selected randomly) excluded in the estimation (i.e., validation data). Validation results showed the root-mean square error (RMSE) of NDVI to be 0.050. In addition, we compared the distributed NEEday estimates (based on the Kalman filter and our chamber measurements) with the flux tower data by computing the weighted average of NEEday within the tower footprint (Figure 8). The comparison shows that the estimated NEEday closely follows the flux tower data, capturing the seasonal changes and general trend. The correlation statistics between the EC flux tower data and estimated NEEday are R of 0.53 and p-value of <1 × 10−4. Since the EC data has large scatter, we smoothed data with the moving average of the 15-day window to represent the seasonal variability. Different from earlier studies (e.g., Rasteter et al., 2010), the tower data were not included in the estimation, and we did not calibrate any parameters according to the flux tower data. We would note that the flux-tower data often have large deviation and scattering (Fox et al., 2008).
We computed the temporal average of NDVI and NEE over the growing season, and then took the spatial average within the different polygon geomorphic classes (i.e., the combination of the polygon types and features), shown in Table 1. As shown in the table, between the highest (LCP troughs) and lowest values (HCP centers), the average NDVI varies by 37%, while the average NEEday varies by 183%. The polygon troughs have higher NDVI and NEEday than the other features across the different polygon types. Within the LCPs and FCPs, the trough region has the highest average NDVI and NEEday, while the rim area has the lowest. Within the HCPs, the center region has the lowest NDVI and NEEday. The LCP centers have higher average NEE than the HCP centers by 75%. In addition, we computed the spatial coverage of each polygon feature within each polygon type. The HCP region has a large trough area of 50%, while only 14% of the LCP region is covered by the troughs. The high-elevation region in microtopography associated with low NDVI and NEE (i.e., LCP and FCP rims and HCP centers) occupied 50% of the area in each polygon type.
Table 2 shows the spatially averaged values of each polygon type for the average NDVI and NEEday within. Even though there is significant variability depending on the polygon types and features shown in Table 1, none of the average and peak NDVI and NEEday varies significantly as a function of polygon types in Table 2 (within the standard deviation). The average NEEday is slightly higher in the HCPs than others, even though the HCP centers have lower NEEday (Figure 5). This is because HCPs has the highest areal coverage of troughs (Table 1) where both NDVI and NEEday are significantly high.

4. Discussion

In this paper, we have developed an approach to integrate multi-type and multiscale datasets and to estimate the spatio-temporal dynamics of NDVI and NEEday over the site at a resolution that can resolve microtopography associated with ice-wedge polygons. The dynamic maps of NEEday can be compared with the flux-tower data through the weighted average of the NEEday maps over the flux-tower footprint. Our comparison shows a reasonable agreement between the estimates and flux tower data in terms of capturing the seasonal dynamics and trend without any fitting processes. The particular advantage of using the Kalman filter is its ability to account the uncertainty associated with the correlations such that we can determine the estimation variance at each time step. This allows us to use the observations that are only indirectly associated with NEE such as the one-time gI map.
The estimated peak NDVI over the site is 0.3–0.55 within the dry areas and 0.5–0.85 in the wet regions, which is similar to the values found at nearby sites by Engstrom et al. [44] and Beck and Goetz [57]. The peak NEEday ranges from −5.0 to 0.0 umol/m2/s across the site, the range of which is larger than that of the flux tower-measured NEE across different drained lake basins in this region [21]. This can possibly be attributed to the spatial averaging effect that occurs for the flux tower data, which is unable to resolve the spatial variability of fluxes associated with microtopography in ice-wedge polygons. Nor can such microtopographic variability be captured by the low-resolution satellite-based estimations of NDVI and NEEday.
This study also provides improved understanding of spatiotemporal variability in ecosystem functioning and carbon exchanges over ice-wedge polygon tundra, specifically through the correlation between NDVI and NEEday, and their relationship to polygon features. Consistent with previous studies, e.g., [9,12], we find that NDVI and NEEday are significantly affected by ice-wedge polygon geomorphology. This variability is primarily dictated by dry features (i.e., polygon rims, and HCP centers) and wet features (i.e., troughs and HCP/FCP centers), owing to the soil moisture limitations in ecosystem functioning, as shown by previous studies, e.g., [9,12]. However, we also find that troughs have significantly higher plant productivity and CO2 uptake (i.e., high NDVI and NEEday) than other features across different polygon types, and also that the troughs have higher values than LCP centers, even though they both had high soil moisture. This is possibly because low centers tended to have deep ponded water and anoxic conditions that inhibit vegetation growth [13]. In terms of temporal variability, both NDVI and NEEday were low at the dry rims and the center of HCPs throughout the season, while they were more dynamic at the troughs and center of LCPs. Although both NDVI and NEE changed over time, their correlation was consistent along the same curve. In addition, the spatial heterogeneity of NDVI and NEEday was persistent during most of the growing season such that the high NDVI and NEEday regions tended to be the same throughout the season. This is why a single image of gI was able to describe the spatial heterogeneity. This is consistent with the previous findings on the relationship between soil moisture and plant vigor by Dafflon et al. [24], using soil electrical conductivity from electrical resistivity tomography (ERT), and greenness index from pole- and UAS-mounted cameras.
Some of these spatio-temporal characteristics have contributed to the successful data integration. First, the persistent spatial heterogeneity allowed us to use one-time gI data to capture the spatial variability of vegetation vigor, and to use the spatially continuous tram data for quantifying the time-dependent correlations between gI and NDVI over time. In addition, the interlink between the spatial heterogeneity and co-variability among different properties is an important consideration. In general, data requirements and spatial heterogeneity are coupled in spatial statistics or geostatistics such that we need more datasets when the spatial heterogeneity is high [58]. During the early growing season, NDVI and NEEday are relatively spatially homogeneous, even though the data correlation is not significant (i.e., low Spearman correlation coefficients). In the peak season when the spatial heterogeneity is high, the data correlation is high and is able to capture the spatial heterogeneity. This system is suitable for the Kalman filter, which is able to integrate the two models of temporal evolution and data correlations. These two aspects—the data correlation is high to constrain the estimation when the heterogeneity is high—can compensate for one another to reduce estimation uncertainty. In this paper, we focused on the seasonal variability of NEEday.
Having the high-resolution NDVI and NEEday maps enabled us to compute the average and peak values over the growing season, and also the spatial average in each polygon geomorphic class. Our results show that the average NDVI and NEEday vary significantly as a function of the combination of polygon types and features. In particular, the average NEEday varies more than 150% between the highest regions (i.e., LCP troughs) and the lowest regions (i.e., HCP centers). However, the spatial average of NEEday and NDVI (both the average and peak) within each polygon type did not significantly differ, despite the fact that the LCP centers have significantly higher values than the HCP ones, and that the different polygon types were known to have distinct hydrological and ecosystem functioning [12,13,59]. This is because each polygon type includes high and low values associated with the features that are integrated during the spatial aggregation, and because the spatially aggregated effect depends on the spatial coverage of polygon features within each polygon type. This kind of effect is often called the Simpson’s paradox [60], in which a trend or significant effect appears in several groups of data but disappears when these groups are aggregated (or vice versa). Typically, to obtain a representative value for each landscape class or zone, the sample average of point-scale measurements is calculated in each class [12,59]. This approach might, however, may miss a certain feature, or may not represent the spatial coverage of each feature, creating a bias in the spatially averaged estimates. At our site, for example, the HCPs tend to be smaller in terms of polygon size, and to have wider troughs where NDVI and NEEday are both high. This fact highlights the importance of estimating the spatial distribution of NDVI and NEE at high resolution over the landscape.
In addition, our results have some implications regarding to the impact of polygon degradation on carbon exchanges. The HCP centers have significantly lower NEEday than the LCP centers, which suggests that NDVI and NEE could decrease significantly at the centers of polygons when permafrost thaws and the LCPs transition to HCPs. At the same time, our results suggest that we need to consider microtopographic features (e.g., troughs, rims, centers) and their spatial coverage. During the polygon degradation, the size of polygons may not change, but the width of troughs may change when ice wedges melt and the polygon rims collapse [45]. To evaluate such an effect, it would be essential to have high-resolution images and DEM for delineating local-scale polygon features and changes. With our approach, it is possible to monitor the changes in carbon exchange associated with the polygon degradation over space and time, using tram data and infrequent (possibly annual or every a few years) high-resolution areal images.
In this study, we did not include the flux tower data into the integration, and used the tower flux data to validate the estimation results based on the integration of the chamber data, tram data and airborne image. It is possible to expand our framework to integrating the flux tower data so that the flux tower data provide additional constraints in the estimation, although it would increase the computational requirements significantly. Such an approach would enable us to include additional predictors such as temperature or photosynthetically available radiation (PAR) typically measured at the tower, and possibly to represent the diurnal variability. The diurnal variability can be captured by the tram measurements throughout the day, although coordinated chamber measurements are necessary. In addition, evaluating data over multiple years will be useful to provide the information on the relationship of NEE with changing air temperature and longer growing season.

5. Summary

In this study, we first developed the spatio-temporal data integration approach to estimate NDVI and NEE over ice-wedge polygonal tundra during the growing season. The datasets included the spatially extensive but temporally sparse high-resolution airborne RGB image and the temporally extensive but spatially sparse tram data that capture the spatial and temporal variability of NDVI along the 68-m transect. We first applied the Kalman filtering algorithm, which is a numerically efficient spatio-temporal estimation approach, to estimate daily NDVI over the site, and then computed NEEday based on the site-specific NDVI-NEEday relationship. We obtained the daily maps of daytime NDVI and NEEday at 0.5-m resolution over the site (750 m × 750 m). The weighted spatial average of NEEday over the flux tower footprint showed a reasonable agreement with the flux-tower-derived NEEday.
The estimated high-resolution NEEday maps were then used to evaluate the spatial variability of the average NDVI and NEEday during the growing season, depending on the combination of polygon types and features. We found that NDVI and NEEday varied significantly depending on the combination of the polygon types and features over the domain. However, the averaged NDVI and NEEday within each polygon type did not show a significant difference, even though the local effect was significantly different at the centers of different polygon types. This is because high and low NDVI and NEE features co-exist within each polygon type, and that they tend to cancel each out within each polygon type. The averaged NDVI and NEEday were then influenced by the spatial coverage of microtopographic features within each polygon type. In particular, the HCPs and LCPs had similar NDVI and NEEday values on average, even though the LCP centers have significantly higher values than HCPs. This is because the troughs have significantly higher productivity and CO2 uptake than the centers of LCPs, and the HCP areas have a larger spatial coverage of troughs. Our results suggest the importance of considering microtopographic features for carbon exchange, and the need to integrate multi-type multiscale datasets to capture the microtopographic effects on the spatio-temporal dynamics of NDVI and NEE.

Author Contributions

Conceptualization, H.M.W., R.O., B.D., S.D., M.S.T. and S.S.H.; methodology, H.M.W., R.O., B.D. and S.D.; data acquisition, B.D., S.D., J.B.C. and J.C.; validation, H.M.W.; formal analysis, H.M.W., R.O., B.D. and S.D.; writing—original draft preparation, H.M.W., R.O., B.D. and S.D.; writing—review and editing, M.S.T. and S.S.H.; visualization, H.M.W. and J.B.C.; supervision, M.S.T. and S.S.H.; project administration, B.D., M.S.T. and S.S.H.; funding acquisition, B.D., M.S.T. and S.S.H. All authors have read and agreed to the published version of the manuscript.

Funding

The Next-Generation Ecosystem Experiments (NGEE Arctic) project is supported by the Office of Biological and Environmental Research in the DOE Office of Science. This NGEE-Arctic research is supported through contract number DE-AC0205CH11231 to Lawrence Berkeley National Laboratory.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The datasets are available through the project website: https://ngee-arctic.ornl.gov/ (accessed on 7 July 2021). The tram data set is available at Torn et al. (2019; https://doi.org/10.5440/1558782, accessed on 7 July 2021).

Acknowledgments

We wish to thank the Ukpeaġvik Iñupiat Corporation (UIC) and their subsidiary, UIC Science, for supporting this work on Iñupiat ancestral lands. We gratefully acknowledge Stan Wullschleger in Oak Ridge National Laboratory, project PI.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A

The Kalman filter algorithm has been widely described in the literatures (e.g., Hamilton, 1994; Schmidt et al., 2018). We describe the algorithm here for completeness. The Kalman filter consists of a recursive two-step process: (1) a state prediction step and (2) an update step. The goal is to estimate the state vector x t as x ^ t and its error covariance P t at each time step t . The diagonal elements of Pt, σ ^ i , t , is the estimation variance at each pixel, representing the uncertainty in x ^ t .
The prediction step describes the temporal evolution of the state vector xt from the previous step. The state transition equation (Equation (7)) is used to predict the expected value of the state vector as x ^ t | t − 1 based on the estimate at the previous time step x ^ t − 1 :
x ^ t | t − 1 = A x ^ t − 1 + B u
Similarly, the error covariance matrix P t is predicted as P t | t − 1 based on the covariance at the previous step P t − 1 :
P t | t − 1 = AP t − 1   A T + Q
where Q is a diagonal matrix each element of which is the variance of v(t) in Equation (7), representing the uncertainty in the state transition model.
The update step improves (or corrects) the estimate of the state vector by including the data z t . Based on the state-observation equation (Equation (2)), the estimate x ^ t is determined by:
x ^ t = x ^ t | t − 1 + C t [ z t − ( H   x ^ t | t − 1 + K u ) ]
where the Kalman gain C t is determined by:
C t = P t | t − 1   H T [ H   P t | t − 1   H T + R ] − 1 .
where R is a diagonal matrix each element of which is the variance of w(t) in Equation (2). The error covariance is updated as:
P t = ( I − C t   H ) P t | t − 1 ( I − C t   H ) T + K t   R   C t T
where I is an identity matrix each diagonal element of which is one.

References

  1. Hinzman, L.D.; Bettez, N.D.; Bolton, W.R.; Chapin, F.S.; Dyurgerov, M.B.; Fastie, C.L.; Griffith, B.; Hollister, R.D.; Hope, A.; Huntington, H.P.; et al. Evidence and implications of recent climate change in northern Alaska and other arctic regions. Clim. Chang. 2005, 72, 251–298. [Google Scholar] [CrossRef]
  2. Pithan, F.; Mauritsen, T. Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat. Geosci. 2014, 7, 181–184. [Google Scholar] [CrossRef]
  3. Kaufman, D.S.; Schneider, D.P.; McKay, N.P.; Ammann, C.M.; Bradley, R.S.; Briffa, K.; Miller, G.H.; Otto-Bliesner, B.L.; Overpeck, J.T.; Vinther, B.; et al. Recent Warming Reverses Long-Term Arctic Cooling. Science 2009, 325, 1236–1239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Lawrence, D.M.; Slater, A.G. A projection of severe near-surface permafrost degradation during the 21st century. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
  5. Zimov, S.A.; Schuur, E.A.G.; Chapin, F.S., III. Climate Change: Permafrost and the Global Carbon Budget. Science 2006, 312, 1612–1613. [Google Scholar] [CrossRef]
  6. Schuur, E.A.G.; Vogel, J.G.; Crummer, K.G.; Lee, H.; Sickman, J.O.; Osterkamp, T.E. The effect of permafrost thaw on old carbon release and net carbon exchange from tundra. Nat. Cell Biol. 2009, 459, 556–559. [Google Scholar] [CrossRef] [PubMed]
  7. Forkel, M.; Carvalhais, N.; Rödenbeck, C.; Keeling, R. Enhanced seasonal CO2 exchange caused by amplified plant productivity in northern ecosystems. Science 2016, 351, 696–699. [Google Scholar] [CrossRef] [Green Version]
  8. Kutzbach, L.; Wagner, D.; Pfeiffer, E.M. Effect of microrelief and vegetation on methane emission from wet polygonal tundra, Lena Delta, Northern Siberia. Biogeochemistry 2004, 69, 341–362. [Google Scholar] [CrossRef] [Green Version]
  9. Zona, D.; Lipson, D.A.; Zulueta, R.C.; Oberbauer, S.F.; Oechel, W.C. Microtopographic controls on ecosystem functioning in the Arctic Coastal Plain. J. Geophys. Res. Space Phys. 2011, 116, 4. [Google Scholar] [CrossRef] [Green Version]
  10. Leffingwell, E.D.K. Ground-Ice Wedges: The Dominant Form of Ground-Ice on the North Coast of Alaska. J. Geol. 1915, 23, 635–654. [Google Scholar] [CrossRef]
  11. Mackay, J.R. Thermally induced movements in ice-wedge polygons, western arctic coast: A long-term study. Géographie Phys. Quat. 2000, 54, 41–68. [Google Scholar] [CrossRef] [Green Version]
  12. Wainwright, H.M.; Dafflon, B.; Smith, L.J.; Hahn, M.S.; Curtis, J.B.; Wu, Y.; Hubbard, S.S. Identifying mul-tiscale zonation and assessing the relative importance of polygon geomorphology on carbon fluxes in an Arctic tundra ecosystem. J. Geophys. Res. BioGeosci. 2015, 120, 788–808. [Google Scholar] [CrossRef]
  13. Liljedahl, A.; Boike, J.; Daanen, R.P.; Fedorov, A.; Frost, G.; Grosse, G.; Hinzman, L.D.; Iijima, Y.; Jorgenson, J.C.; Matveyeva, N.; et al. Pan-Arctic ice-wedge degradation in warming permafrost and its influence on tundra hydrology. Nat. Geosci. 2016, 9, 312–318. [Google Scholar] [CrossRef]
  14. Billings, W.D.; Peterson, K.M. Vegetational Change and Ice-Wedge Polygons through the Thaw-Lake Cycle in Arctic Alaska. Arct. Alp. Res. 1980, 12, 413. [Google Scholar] [CrossRef]
  15. Kim, Y. Effect of thaw depth on fluxes of CO2 and CH4 in manipulated Arctic coastal tundra of Barrow, Alaska. Sci. Total Environ. 2015, 505, 385–389. [Google Scholar] [CrossRef] [PubMed]
  16. Knoblauch, C.; Spott, O.; Evgrafova, S.; Kutzbach, L.; Pfeiffer, E. Regulation of methane production, oxidation, and emission by vascular plants and bryophytes in ponds of the northeast Siberian polygonal tundra. J. Geophys. Res. BioGeosci. 2015, 120, 2525–2541. [Google Scholar] [CrossRef]
  17. Vaughn, L.J.S.; Conrad, M.E.; Bill, M.; Torn, M.S. Isotopic insights into methane production, oxidation, and emissions in Arctic polygon tundra. Glob. Chang. Biol. 2016, 22, 3487–3502. [Google Scholar] [CrossRef] [Green Version]
  18. Dengel, S.; Torn, M.S. AmeriFlux US-NGB NGEE Arctic Barrow Site. 2020. Available online: https://ameriflux.lbl.gov/sites/siteinfo/US-NGB (accessed on 7 July 2021).
  19. Arora, B.; Wainwright, H.M.; Dwivedi, D.; Vaughn, L.J.S.; Curtis, J.B.; Torn, M.; Dafflon, B.; Hubbard, S.S. Evaluating temporal controls on greenhouse gas (GHG) fluxes in an Arctic tundra environment: An entropy-based approach. Sci. Total. Environ. 2019, 649, 284–299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Eckhardt, T.; Knoblauch, C.; Kutzbach, L.; Holl, D.; Simpson, G.; Abakumov, E.; Pfeiffer, E.-M. Partitioning net ecosystem exchange of CO2 on the pedon scale in the Lena River Delta, Siberia. Biogeosciences 2019, 16, 1543–1562. [Google Scholar] [CrossRef] [Green Version]
  21. Sturtevant, C.S.; Oechel, W. Spatial variation in landscape-level CO2 and CH4 fluxes from arctic coastal tundra: Influence from vegetation, wetness, and the thaw lake cycle. Glob. Chang. Biol. 2013, 19, 2853–2866. [Google Scholar] [CrossRef]
  22. Zulueta, R.C.; Oechel, W.; Loescher, H.W.; Lawrence, W.T.; Paw, K.T. Aircraft-derived regional scale CO2 fluxes from vegetated drained thaw-lake basins and interstitial tundra on the Arctic Coastal Plain of Alaska. Glob. Chang. Biol. 2011, 17, 2781–2802. [Google Scholar] [CrossRef]
  23. Hubbard, S.S.; Gangodagamage, C.; Dafflon, B.; Wainwright, H.; Peterson, J.; Gusmeroli, A.; Tweedie, C. Quantifying and relating land-surface and subsurface variability in permafrost environments using LiDAR and surface geophysical datasets. Hydrogeol. J. 2013, 21, 149–169. [Google Scholar] [CrossRef]
  24. Dafflon, B.; Hubbard, S.; Ulrich, C.; Peterson, J.; Wu, Y.; Wainwright, H.; Kneafsey, T.J. Geophysical estimation of shallow permafrost distribution and properties in an ice-wedge polygon-dominated Arctic tundra region. Geophysics 2016, 81, WA247–WA263. [Google Scholar] [CrossRef]
  25. Andresen, C.G.; Lougheed, V.L. Disappearing Arctic tundra ponds: Fine-scale analysis of surface hydrology in drained thaw lake basins over a 65 year period (1948–2013). J. Geophys. Res. BioGeosci. 2015, 120, 466–479. [Google Scholar] [CrossRef]
  26. Dafflon, B.; Oktem, R.; Peterson, J.; Ulrich, C.; Tran, A.P.; Romanovsky, V.; Hubbard, S.S. Coincident aboveground and belowground autonomous monitoring to quantify covariability in permafrost, soil, and vegetation properties in Arctic tundra. J. Geophys. Res. BioGeosci. 2017, 122, 1321–1342. [Google Scholar] [CrossRef] [Green Version]
  27. McMichael, C.E. Estimating CO2 exchange at two sites in Arctic tundra ecosystems during the growing season using a spectral vegetation index. Int. J. Remote Sens. 1999, 20, 683–698. [Google Scholar] [CrossRef]
  28. Johnson, T.J.; Versteeg, R.; Thomle, J.; Hammond, G.; Chen, X.; Zachara, J.M. Four-dimensional electrical conductivity monitoring of stage-driven river water intrusion: Accounting for water table effects using a transient mesh boundary and conditional inversion constraints. Water Resour. Res. 2015, 51, 6177–6196. [Google Scholar] [CrossRef]
  29. Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Fuentes, J. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
  30. Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef] [Green Version]
  31. Healey, N.C.; Oberbauer, S.F.; Ahrends, H.E.; Dierick, D.; Welker, J.M.; Leffler, A.J.; Tweedie, C.E. A Mobile Instrumented Sensor Platform for Long-Term Terrestrial Ecosystem Analysis: An Example Application in an Arctic Tundra Ecosystem. J. Environ. Inform. 2014, 24, 1–10. [Google Scholar] [CrossRef]
  32. Wainwright, H.M.; Chen, J.; Sassen, D.S.; Hubbard, S.S. Bayesian hierarchical approach and geophysical data sets for estimation of reactive facies over plume scales. Water Resour. Res. 2014, 50, 4564–4584. [Google Scholar] [CrossRef]
  33. Wainwright, H.M.; Seki, A.; Chen, J.; Saito, K. A multiscale Bayesian data integration approach for mapping air dose rates around the Fukushima Daiichi Nuclear Power Plant. J. Environ. Radioact. 2017, 167, 62–69. [Google Scholar] [CrossRef] [Green Version]
  34. Wainwright, H.M.; Liljedahl, A.K.; Dafflon, B.; Ulrich, C.; Peterson, J.E.; Gusmeroli, A.; Hubbard, S.S. Mapping snow depth within a tundra ecosystem using multiscale observations and Bayesian methods. Cryosphere 2017, 11, 857–875. [Google Scholar] [CrossRef] [Green Version]
  35. Wikle, C.K.; Milliff, R.F.; Nychka, D.; Berliner, L.M. Spatiotemporal hierarchical Bayesian modeling: Tropical ocean surface winds. J. Am. Stat. Assoc. 2001, 96, 382–397. [Google Scholar] [CrossRef] [Green Version]
  36. Chen, J.; Hubbard, S.S.; Williams, K.H. Data-driven approach to identify field-scale biogeochemical transitions using geochemical and geophysical data and hidden Markov models: Development and application at a uranium-contaminated aquifer. Water Resour. Res. 2013, 49, 6412–6424. [Google Scholar] [CrossRef]
  37. Fox, A.M.; Huntley, B.; Lloyd, C.R.; Williams, M.; Baxter, R. Net ecosystem exchange over heterogeneous Arctic tundra: Scaling between chamber and eddy covariance measurements. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
  38. Fox, A.; Williams, M.; Richardson, A.D.; REFLEX Team. The Reflex project: Comparing different algorithms and implementations for the inversion of a terrestrial ecosystem model against eddy covariance data. Agric. For. Meteorol. 2009, 149, 1597–1615. [Google Scholar] [CrossRef] [Green Version]
  39. Williams, M.; Richardson, A.D.; Reichstein, M.; Stoy, P.C.; Peylin, P.; Verbeeck, H.; Carvalhais, N.; Jung, M.; Hollinger, D.Y.; Kattge, J.; et al. Improving land surface models with FLUXNET data. Biogeosciences 2009, 6, 1341–1359. [Google Scholar] [CrossRef] [Green Version]
  40. Sachs, T.; Giebels, M.; Boike, J.; Kutzbach, L. Environmental controls on CH4 emission from polygonal tundra on the microsite scale in the Lena river delta, Siberia. Glob. Chang. Biol. 2010, 16, 3096–3110. [Google Scholar] [CrossRef]
  41. Zhang, Y.; Sachs, T.; Li, C.; Boike, J. Upscaling methane fluxes from closed chambers to eddy covariance based on a permafrost biogeochemistry integrated model. Glob. Chang. Biol. 2011, 18, 1428–1440. [Google Scholar] [CrossRef] [Green Version]
  42. Sahoo, A.K.; De Lannoy, G.J.; Reichle, R.; Houser, P. Assimilation and downscaling of satellite observed soil moisture over the Little River Experimental Watershed in Georgia, USA. Adv. Water Resour. 2013, 52, 19–33. [Google Scholar] [CrossRef]
  43. Schmidt, F.; Wainwright, H.M.; Faybishenko, B.; Denham, M.; Eddy-Dilek, C. In Situ Monitoring of Groundwater Contamination Using the Kalman Filter. Environ. Sci. Technol. 2018, 52, 7418–7425. [Google Scholar] [CrossRef] [Green Version]
  44. Engstrom, R.; Hope, A.; Kwon, H.; Stow, D. The Relationship between Soil Moisture and NDVI Near Barrow, Alaska. Phys. Geogr. 2008, 29, 38–53. [Google Scholar] [CrossRef]
  45. Kanevskiy, M.; Shur, Y.; Jorgenson, T.; Brown, D.R.; Moskalenko, N.; Brown, J.; Walker, D.A.; Raynolds, M.K.; Buchhorn, M. Degradation and stabilization of ice wedges: Implications for assessing risk of thermokarst in northern Alaska. Geomorphology 2017, 297, 20–42. [Google Scholar] [CrossRef]
  46. Lin, D.H.; Johnson, D.R.; Andresen, C.; Tweedie, C.E. 2012 High spatial resolution decade-time scale land cover change at multiple locations in the Beringian Arctic (1948–2000s). Environ. Res. Lett. 2012, 7, 025502. [Google Scholar] [CrossRef] [Green Version]
  47. Hinkel, K.M.; Eisner, W.R.; Bockheim, J.G.; Nelson, F.E.; Peterson, K.M.; Dai, X. Institute of Arctic and Alpine Research (INSTAAR) University of Colorado Spatial Extent, Age, and Carbon Stocks in Drained Thaw Lake Basins on the Barrow Peninsula, Alaska. Arct. Antarct. Alp. Res. 2003, 35, 291–300. [Google Scholar] [CrossRef] [Green Version]
  48. Langford, Z.; Kumar, J.; Hoffman, F.M.; Norby, R.J.; Wullschleger, S.D.; Sloan, V.L.; Iversen, C.M. Mapping Arctic Plant Functional Type Distributions in the Barrow Environmental Observatory Using WorldView-2 and LiDAR Datasets. Remote Sens. 2016, 8, 733. [Google Scholar] [CrossRef] [Green Version]
  49. Torn, M.; Dafflon, B.; Dengel, S.; Curtis, B.; Chafe, O.; Moyes, A.; Serbin, S.; Lewin, K.; Breen, A.; Velliquette, T.; et al. NGEE Arctic Tram: Overview of Tram-Mounted Instruments, Co-Located Data, Measurement Position, Elevation and Polygon Characterization, Barrow, Alaska, 2014–2018. 2019. Available online: https://ngee-arctic.ornl.gov/data/pages/NGA177.html (accessed on 8 July 2021). [CrossRef]
  50. Kormann, R.; Meixner, F.X. An Analytical Footprint Model for Non-Neutral Stratification. Bound. Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
  51. Wainwright, M.J.; Jordan, M.I. Graphical Models, Exponential Families, and Variational Inference. Found. Trends Mach. Learn. 2007, 1, 1–305. [Google Scholar] [CrossRef] [Green Version]
  52. La Puma, I.P.; Philippi, T.E.; Oberbauer, S.F. Relating NDVI to ecosystem CO2 exchange patterns in response to season length and soil warming manipulations in arctic Alaska. Remote Sens. Environ. 2007, 109, 225–236. [Google Scholar] [CrossRef]
  53. Loranty, M.M.; Goetz, S.; Rastetter, E.; Rocha, A.V.; Shaver, G.R.; Humphreys, E.; Lafleur, P.M. Scaling an Instantaneous Model of Tundra NEE to the Arctic Landscape. Ecol. Appl. 2011, 14, 76–93. [Google Scholar] [CrossRef]
  54. Toomey, M.; Friedl, M.A.; Frolking, S.; Hufkens, K.; Klosterman, S.; Sonnentag, O.; Baldocchi, D.D.; Bernacchi, C.; Biraud, S.C.; Bohrer, G.; et al. Greenness indices from digital cameras predict the timing and seasonal dynamics of canopyscale photosynthesis. Ecol. Appl. 2015, 25, 99–115. [Google Scholar] [CrossRef] [Green Version]
  55. Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994; Volume 2. [Google Scholar]
  56. Rastetter, E.B.; Williams, M.; Griffin, K.L.; Kwiatkowski, B.L.; Tomasky, G.; Potosnak, M.J.; Stoy, P.C.; Shaver, G.R.; Stieglitz, M.; Hobbie, J.E.; et al. Processing Arctic Eddy-Flux Data Using a Simple Carbon-Exchange Model Embedded in the Ensemble Kalman Filter. Ecol. Appl. 2010, 20, 1285–1301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  57. Beck, P.S.; Goetz, S.J. Corrigendum: Satellite observations of high northern latitude vegetation productivity changes between 1982 and 2008: Ecological variability and regional differences. Environ. Res. Lett. 2012, 7, 029501. [Google Scholar] [CrossRef] [Green Version]
  58. Rubin, Y. Applied Stochastic Hydrogeology; Oxford University Press (OUP): Oxford, UK, 2003. [Google Scholar]
  59. Lara, M.J.; McGuire, A.D.; Euskirchen, E.S.; Tweedie, C.E.; Hinkel, K.M.; Skurikhin, A.N.; Romanovsky, V.E.; Grosse, G.; Bolton, W.R.; Genet, H. Polygonal tundra geomorphological change in response to warming alters future CO2 and CH4 flux on the Barrow Peninsula. Glob. Chang. Biol. 2015, 21, 1634–1651. [Google Scholar] [CrossRef]
  60. Bickel, P.J.; Hammel, E.A.; O’Connell, J.W. Sex Bias in Graduate Admissions: Data from Berkeley. Science 1975, 187, 398–404. [Google Scholar] [CrossRef] [Green Version]
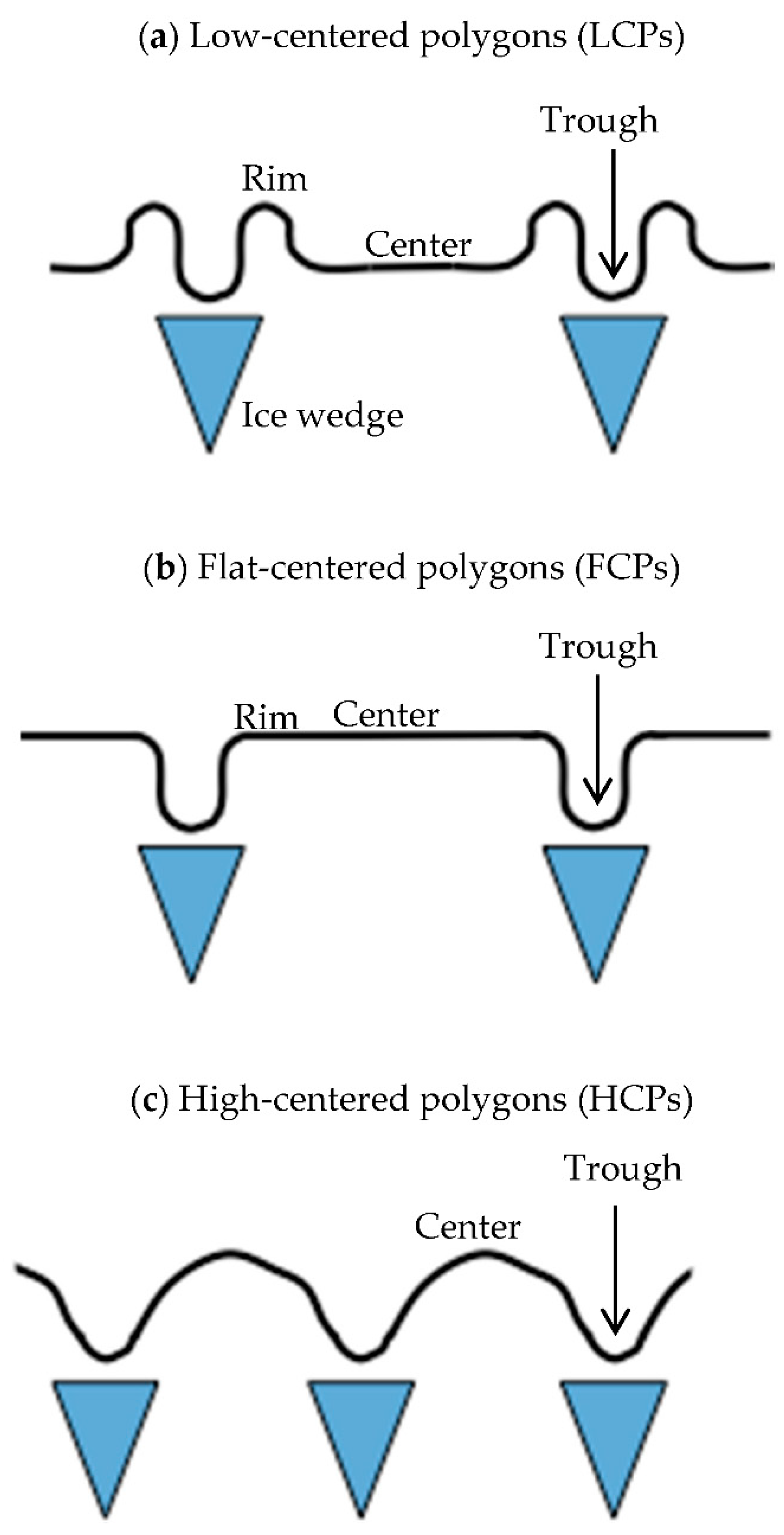
Land 10 00722 g001 550
Figure 1. Schematic diagrams of different polygon types and polygon features (from Wainwright et al., 2015): (a) low-centered, (b) flat-centered and (c) high-centered polygons. In this study, we defined rims only when the polygon edges are higher than the centers.
Figure 1. Schematic diagrams of different polygon types and polygon features (from Wainwright et al., 2015): (a) low-centered, (b) flat-centered and (c) high-centered polygons. In this study, we defined rims only when the polygon edges are higher than the centers.
Land 10 00722 g001
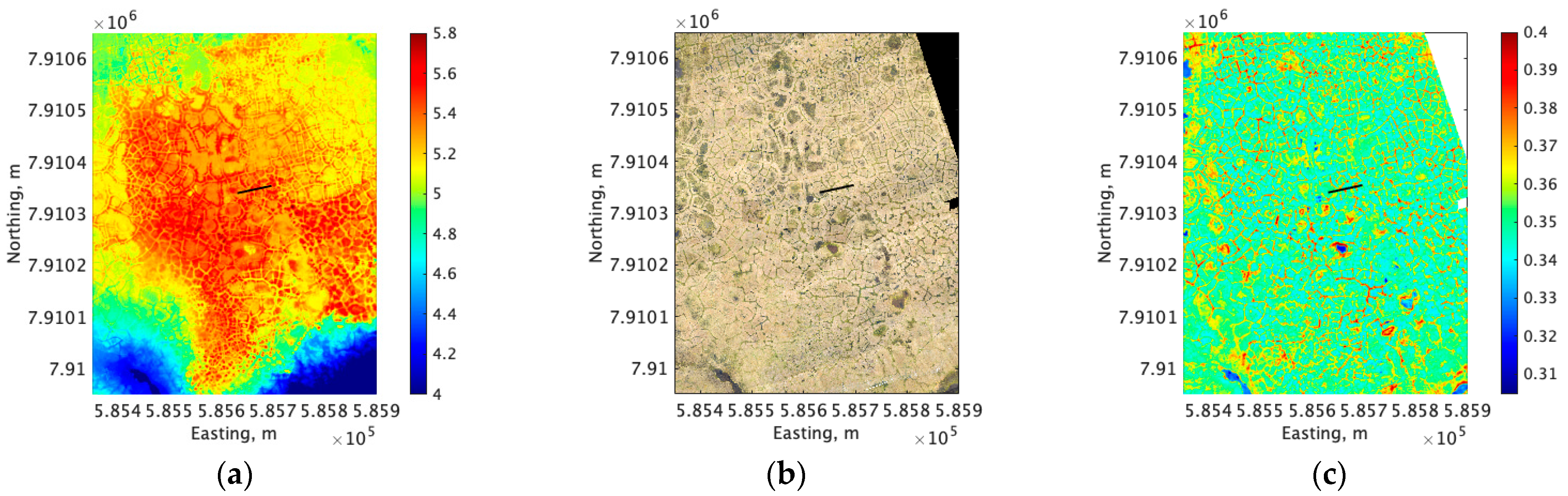
Land 10 00722 g002 550
Figure 2. (a) High-resolution LiDAR digital elevation model (DEM) over the NGEE Arctic site (elevation in meters), (b) orthorectified airborne RGB image, and (c) greenness index (gI) computed from the RGB image. In the plots, the black line is the tram location. In (a), the same DEM was used as Hubbard et al. (2013) and Wainwright et al. (2015).
Figure 2. (a) High-resolution LiDAR digital elevation model (DEM) over the NGEE Arctic site (elevation in meters), (b) orthorectified airborne RGB image, and (c) greenness index (gI) computed from the RGB image. In the plots, the black line is the tram location. In (a), the same DEM was used as Hubbard et al. (2013) and Wainwright et al. (2015).
Land 10 00722 g002
Land 10 00722 g003 550
Figure 3. (a) Tram system installed at the NGEE-Arctic site, and (b) the aerial image of the tram track location with the point-measurement locations. In (a), the tram moves on two rails, carrying a sensor package on its arm. The flux chambers can be seen on the ground.
Figure 3. (a) Tram system installed at the NGEE-Arctic site, and (b) the aerial image of the tram track location with the point-measurement locations. In (a), the tram moves on two rails, carrying a sensor package on its arm. The flux chambers can be seen on the ground.
Land 10 00722 g003
Land 10 00722 g004 550
Figure 4. The structure of the multiscale data integration. The black boxes represent different types of datasets (fluxes, tram NDVI, gI) at different spatial and temporal scales. The red boxes represent the target variables to estimate; i.e., spatially and temporally continuous NDVI and NEE. The blue lines represent the correlations obtained from the datasets. The red lines represent the estimation based on those datasets and correlations.
Figure 4. The structure of the multiscale data integration. The black boxes represent different types of datasets (fluxes, tram NDVI, gI) at different spatial and temporal scales. The red boxes represent the target variables to estimate; i.e., spatially and temporally continuous NDVI and NEE. The blue lines represent the correlations obtained from the datasets. The red lines represent the estimation based on those datasets and correlations.
Land 10 00722 g004
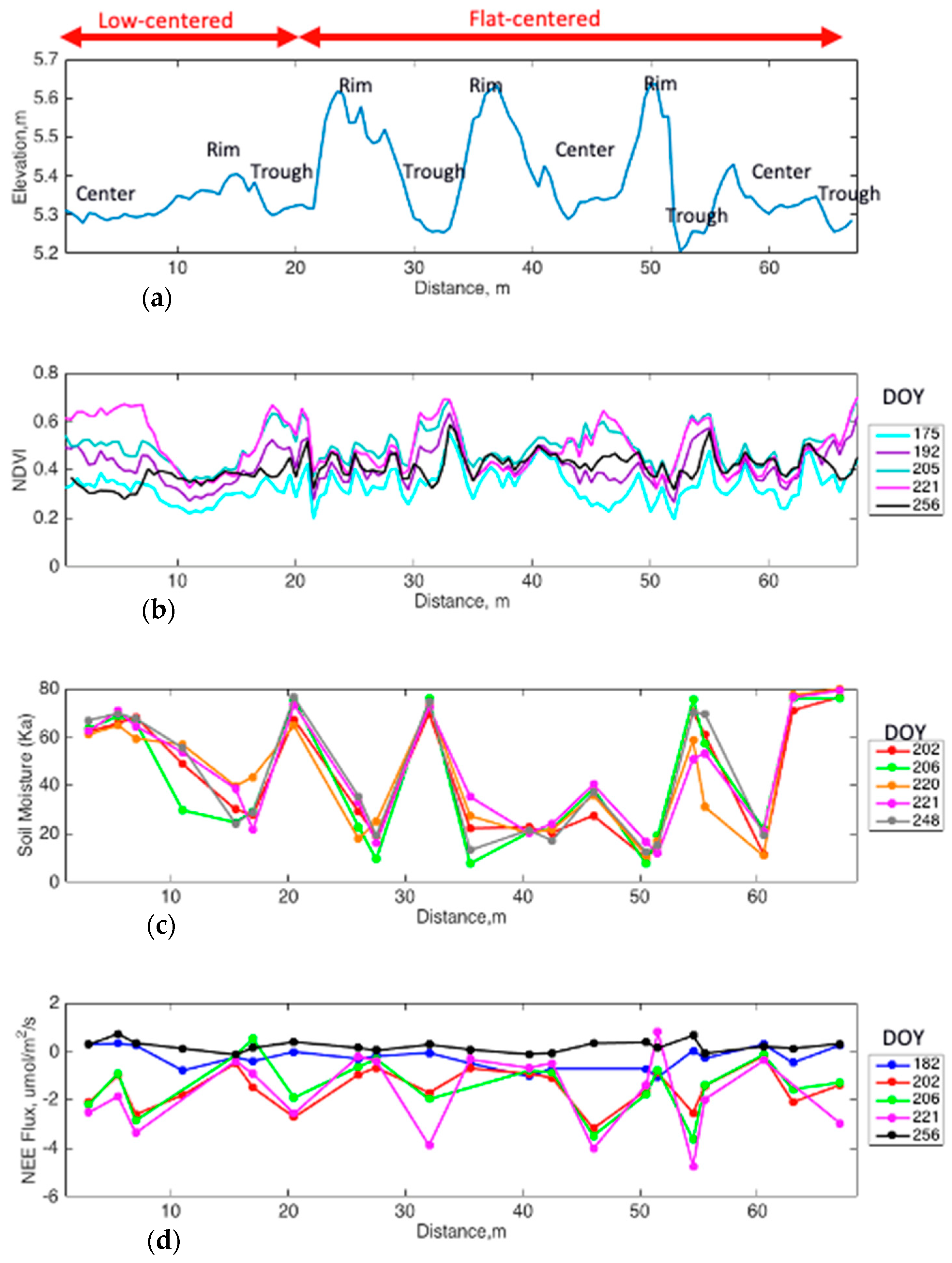
Land 10 00722 g005 550
Figure 5. Spatiotemporal variability of observed properties along the tram transect: (a) LiDAR-based elevation with the polygon type-feature definition, (b) NDVI on the different day of year (DOY), (c) soil moisture (as dielectric permittivity Ka) and (d) NEE. In (b), the NDVI data are shown on selected DOYs. All the measurement dates are shown for soil moisture in (c) and for NEE in (d).
Figure 5. Spatiotemporal variability of observed properties along the tram transect: (a) LiDAR-based elevation with the polygon type-feature definition, (b) NDVI on the different day of year (DOY), (c) soil moisture (as dielectric permittivity Ka) and (d) NEE. In (b), the NDVI data are shown on selected DOYs. All the measurement dates are shown for soil moisture in (c) and for NEE in (d).
Land 10 00722 g005
Land 10 00722 g006 550
Figure 6. Correlations between (a) NDVI and NEEday based the chamber flux measurements on DOY 182, 206, 221 and 256, and (b) NDVI and gI (measured on 7 August 2013). In (b), NDVI was measured on different dates, while gI values are from the one-time data acquisition.
Figure 6. Correlations between (a) NDVI and NEEday based the chamber flux measurements on DOY 182, 206, 221 and 256, and (b) NDVI and gI (measured on 7 August 2013). In (b), NDVI was measured on different dates, while gI values are from the one-time data acquisition.
Land 10 00722 g006
Land 10 00722 g007 550
Figure 7. Changes of NDVI over the site in 2014 on (a) DOY 185, (b) DOY 210 and (c) DOY 240, and the changes of NEEday (in μmol/m2/s) over the site on (d) DOY 185, (e) DOY 210 and (f) DOY 240. In each plot, the black line represents the tram location, and the white triangle is the flux tower location.
Figure 7. Changes of NDVI over the site in 2014 on (a) DOY 185, (b) DOY 210 and (c) DOY 240, and the changes of NEEday (in μmol/m2/s) over the site on (d) DOY 185, (e) DOY 210 and (f) DOY 240. In each plot, the black line represents the tram location, and the white triangle is the flux tower location.
Land 10 00722 g007
Land 10 00722 g008 550
Figure 8. Comparison between the daytime averaged flux tower NEEday (black squares) and the estimated NEEday (weighted-average within the tower footprint) during the growing season. The thick red line represents the mean estimate, while the thin red lines represent the 99-percent confidence interval.
Figure 8. Comparison between the daytime averaged flux tower NEEday (black squares) and the estimated NEEday (weighted-average within the tower footprint) during the growing season. The thick red line represents the mean estimate, while the thin red lines represent the 99-percent confidence interval.
Land 10 00722 g008
Table
Table 1. Spatial average of NEEday and NDVI temporal average (Av.) over the growing season in each polygon type-feature combination. The standard deviation (SD) is also shown. The spatial coverage is the area of each polygon feature within each polygon type (The total area is normalized to 1).
Table 1. Spatial average of NEEday and NDVI temporal average (Av.) over the growing season in each polygon type-feature combination. The standard deviation (SD) is also shown. The spatial coverage is the area of each polygon feature within each polygon type (The total area is normalized to 1).
Av. NDVI(SD)Av. NEEday,
μmol/m2/s		(SD)Spatial Coverage
LCPTrough0.59(0.014)−3.4(0.64)0.14
Center0.52(0.010)−2.1(0.41)0.36
Rim0.44(0.011)−1.4(0.34)0.5
FCPTrough0.58(0.016)−3.2(0.63)0.29
Center0.48(0.016)−1.7(0.37)0.21
Rim0.41(0.016)−1.1(0.27)0.5
HCPTrough0.56(0.013)−2.8(0.56)0.5
Center0.43(0.012)−1.2(0.30)0.5
Table
Table 2. Spatial average of NEE and NDVI temporally averaged (Av.) over the growing season in each polygon type, and the spatial average of peak NEE and NDVI in each polygon type.
Table 2. Spatial average of NEE and NDVI temporally averaged (Av.) over the growing season in each polygon type, and the spatial average of peak NEE and NDVI in each polygon type.
Av. NDVI(SD)Av. NEEday, μmol/m2/s(SD)
LCP0.49(0.011)−2.4(0.42)
FCP0.48(0.016)−2.3(0.43)
HCP0.50(0.012)−2.6(0.45)
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Wainwright, H.M.; Oktem, R.; Dafflon, B.; Dengel, S.; Curtis, J.B.; Torn, M.S.; Cherry, J.; Hubbard, S.S. High-Resolution Spatio-Temporal Estimation of Net Ecosystem Exchange in Ice-Wedge Polygon Tundra Using In Situ Sensors and Remote Sensing Data. Land 2021, 10, 722. https://doi.org/10.3390/land10070722

AMA Style

Wainwright HM, Oktem R, Dafflon B, Dengel S, Curtis JB, Torn MS, Cherry J, Hubbard SS. High-Resolution Spatio-Temporal Estimation of Net Ecosystem Exchange in Ice-Wedge Polygon Tundra Using In Situ Sensors and Remote Sensing Data. Land. 2021; 10(7):722. https://doi.org/10.3390/land10070722

Chicago/Turabian Style

Wainwright, Haruko M., Rusen Oktem, Baptiste Dafflon, Sigrid Dengel, John B. Curtis, Margaret S. Torn, Jessica Cherry, and Susan S. Hubbard. 2021. "High-Resolution Spatio-Temporal Estimation of Net Ecosystem Exchange in Ice-Wedge Polygon Tundra Using In Situ Sensors and Remote Sensing Data" Land 10, no. 7: 722. https://doi.org/10.3390/land10070722

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop