Do ARMA Models Provide Better Gap Filling in Time Series of Soil Temperature and Soil Moisture? The Case of Arable Land in the Kulunda Steppe, Russia
Abstract
1. Introduction
2. Materials and Methods
2.1. The Monitoring Network
2.2. Available Data and Description
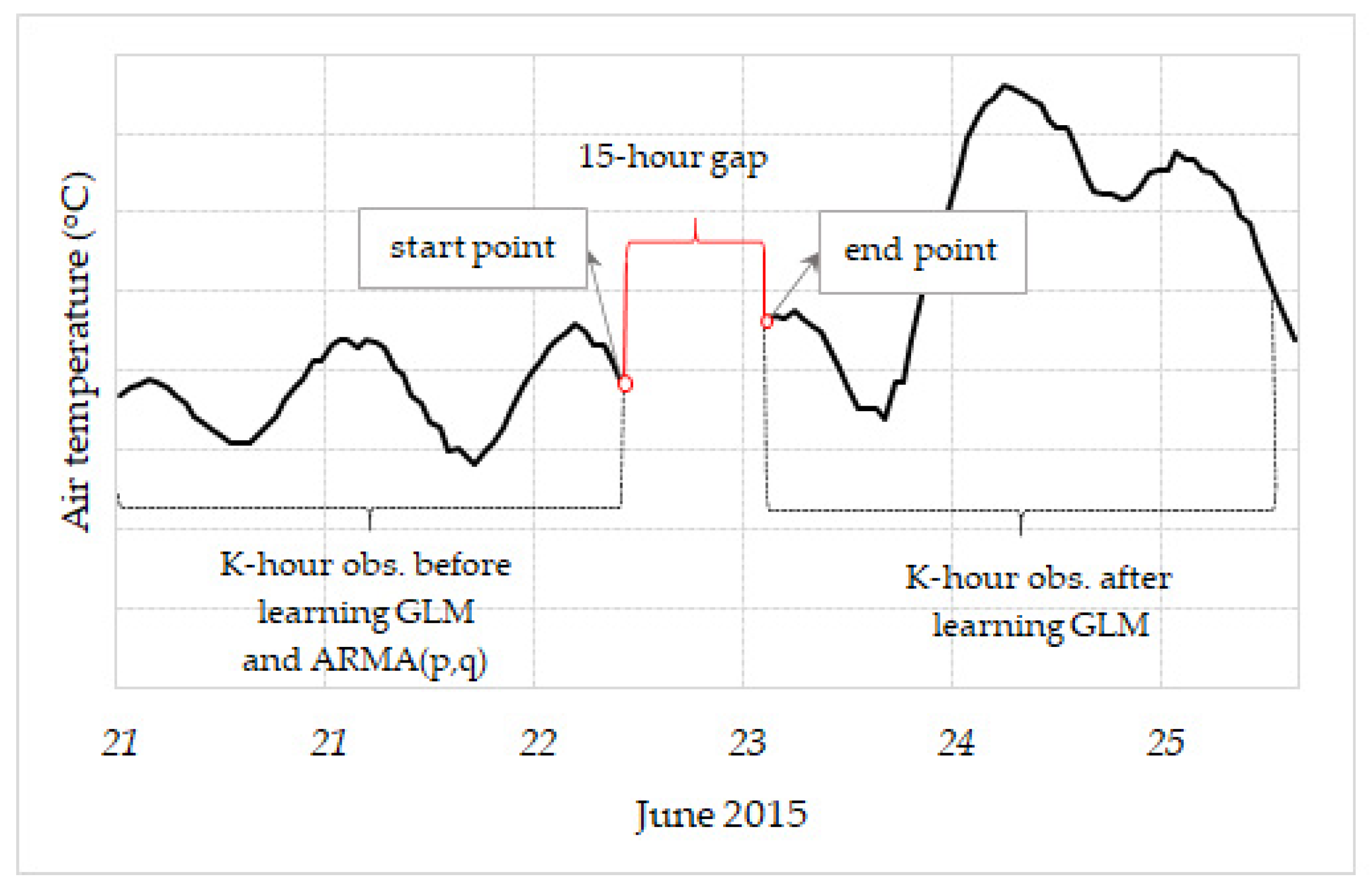
2.3. Methods
3. Results and Discussion
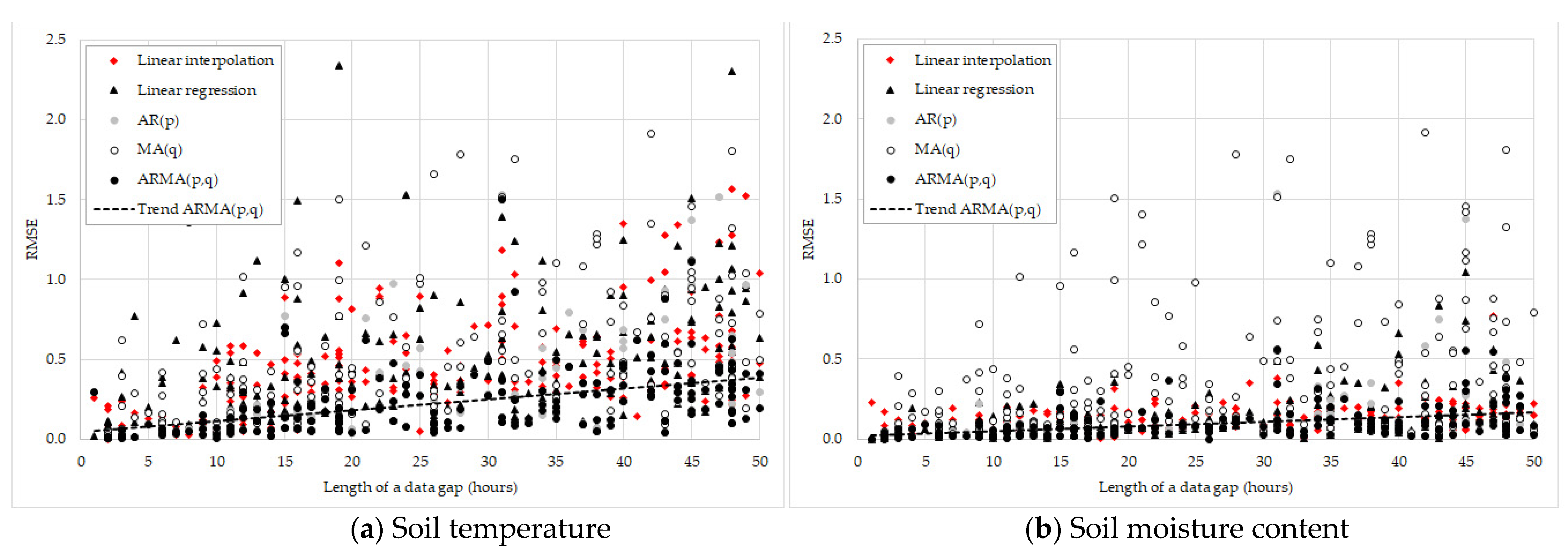
3.1. Mean Error Analysis
3.2. Error Analysis in Gap Size Class
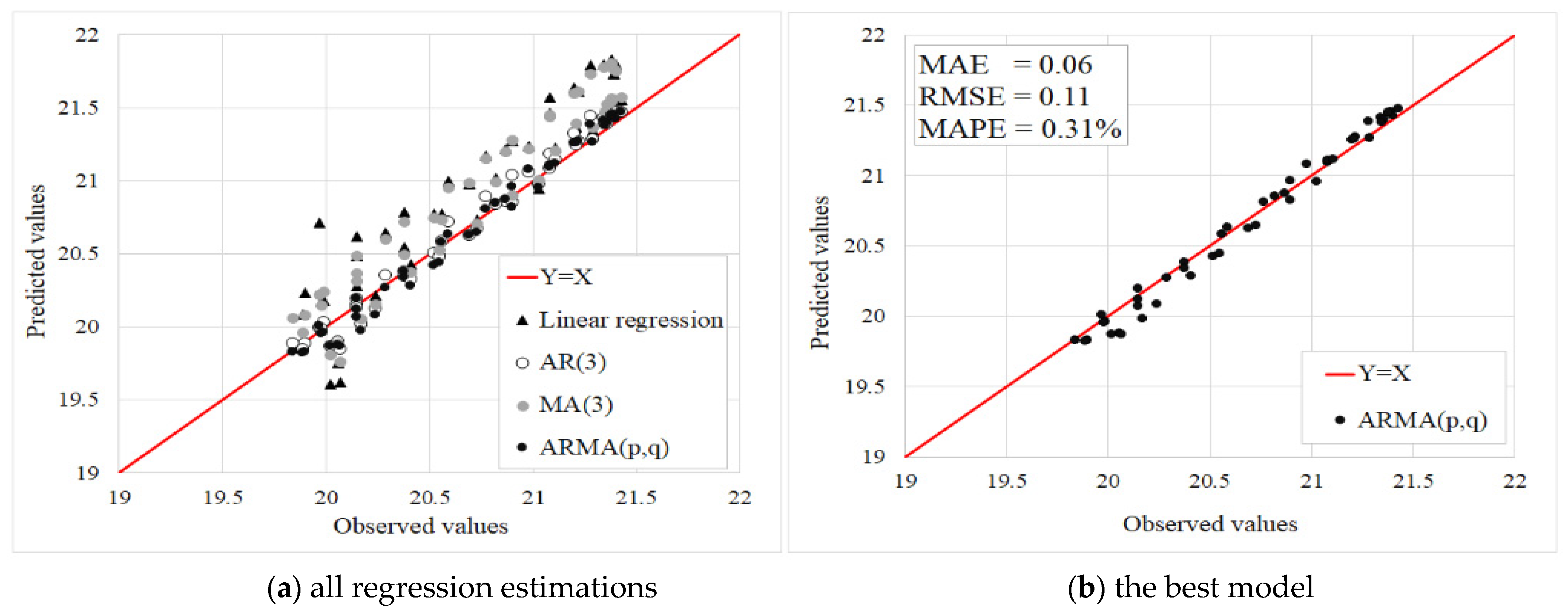
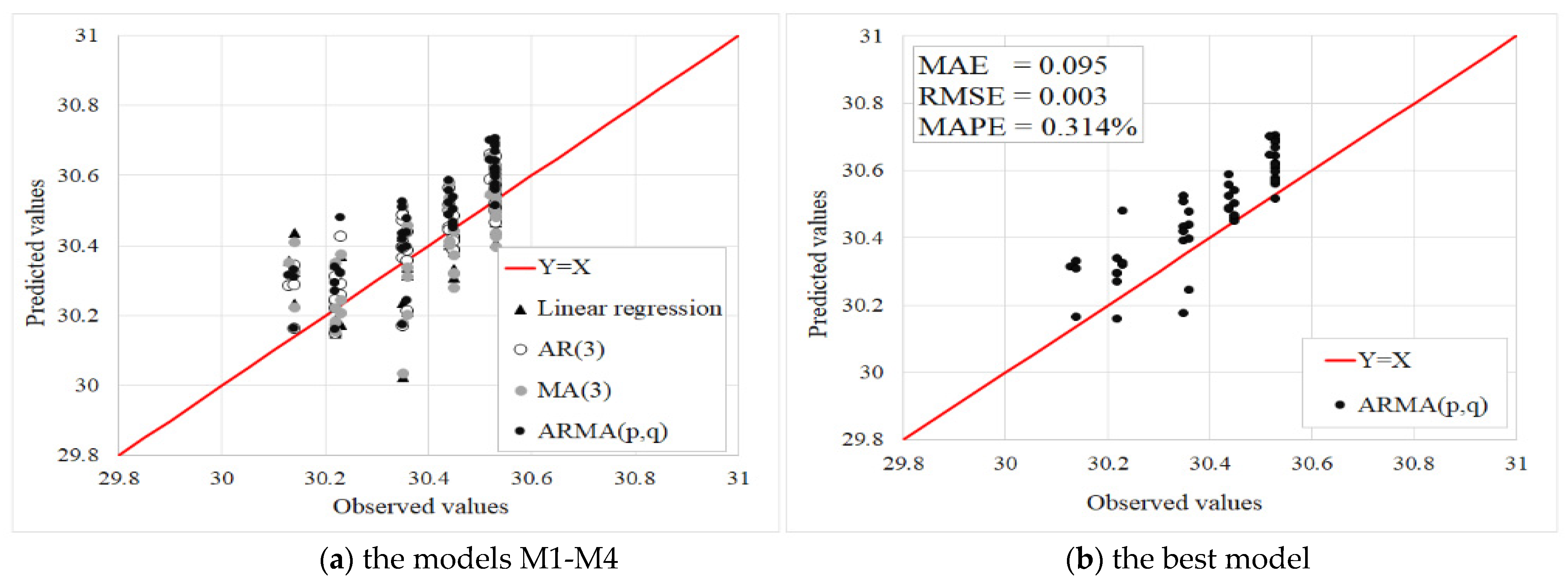
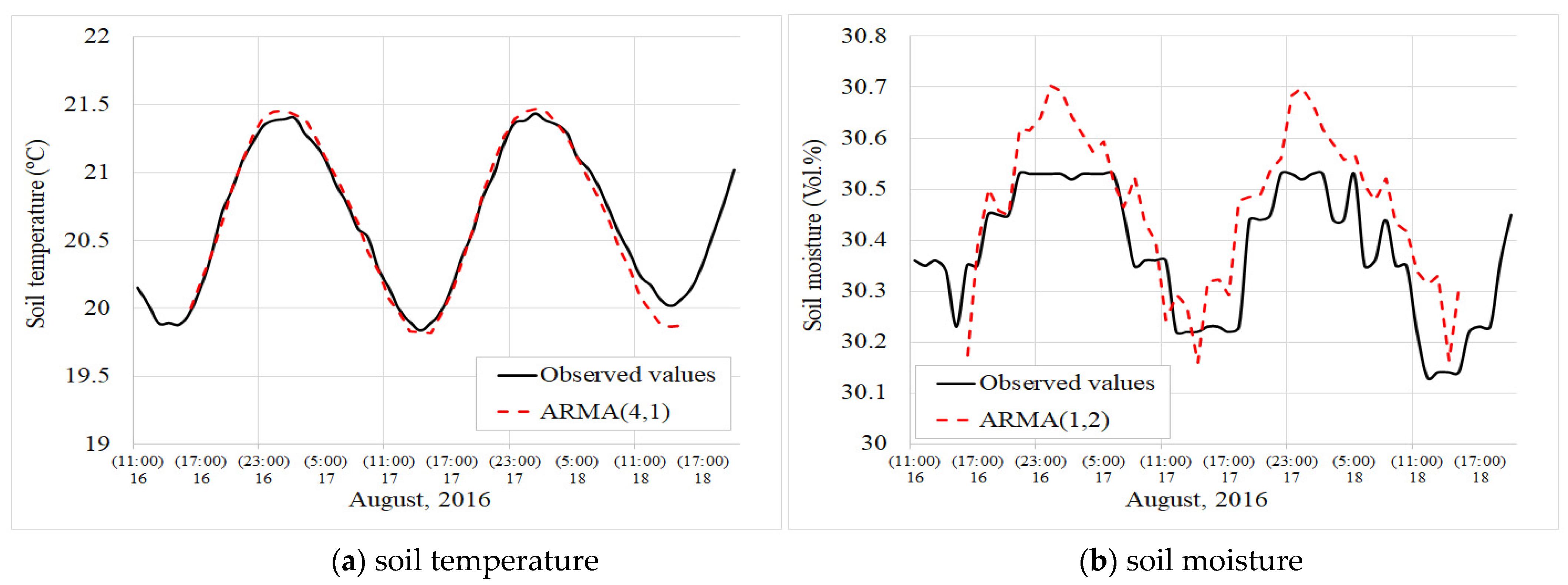
3.3. Examples of Gap Filling and Selection of the Best Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Used Statistic | 2013 1 | 2014 2 | 2015 3 | 2016 3 | 2017 4 | 2018 4 | 2019 4 | |
|---|---|---|---|---|---|---|---|---|
| The weather station | ||||||||
| Air temperature (°C) | Mean (St. dev.) | 13.5 (7.0) | 24.5 (5.5) | 18.0 (7.0) | 17.8 (6.8) | 18.6 (7.0) | 17.1 (7.7) | 16.7 (7.4) |
| Air humidity (%) | Mean (St. dev.) | 60.8 (21.8) | 40.6 (16.8) | 54.4 (19.8) | 56.1 (21.2) | 50.7 (19.8) | 56.6 (20.1) | 49.5 (19.7) |
| Solar radiation (W/m2) | Mean (St. dev.) | 159.4 (226.6) | 286.1 (325.2) | 229.4 (294.1) | 234.1 (297.8) | 264.0 (321.1) | 248.2 (313.6) | 267.3 (321.3) |
| Wind speed (m/s) | Mean (St. dev.) | 2.5 (1.6) | 2.8 (1.8) | 2.8 (1.8) | 2.4 (1.7) | 2.9 (1.8) | 2.8 (1.8) | 1.9 (1.9) |
| Atmospheric pressure (hPa) | Mean (St. dev.) | 996.5 (7.9) | 991.9 (3.4) | 993.6 (7.1) | 994.3 (7.3) | 993.0 (7.1) | 991.2 (6.4) | 994.5 (7.5) |
| Precipitation (mm) | Sum | 37.8 | 4.4 | 243.2 | 325.1 | 151.1 | 219.4 | 87.1 |
| The lysimeter station, measurements at 30 cm | ||||||||
| Soil temperature (°C) | ||||||||
| Arable land (Monolith 1) | Mean (St. dev.) | 15.4 (3.5) | 23.5 (2.1) | 18.3 (3.9) | 18.5 (3.8) | 17.7 (3.9) | 16.9 (5.5) | 16.9 (4.8) |
| Grass land (Monolith 2) | Mean (St. dev.) | 14.6 (3.1) | 20.6 (1.9) | 16.6 (3.4) | 16.5 (3.5) | 15.9 (3.9) | 14.5 (5.0) | 14.3 (4.0) |
| Soil moisture (Vol.-%) | ||||||||
| Arable land (Monolith 1) | Mean (St. dev.) | 21.5 (0.4) | 28.9 (0.3) | 23.6 (3.8) | 29.4 (2.3) | 26.2 (3.4) | 30.7 (2.3) | 29.9 (1.4) |
| Grass land (Monolith 2) | Mean (St. dev.) | 18.7 (0.3) | 18.8 (0.18) | 18.9 (2.3) | 22.8 (4.9) | 22.9 (4.9) | 28.1 (5.7) | 23.7 (4.6) |
Appendix B
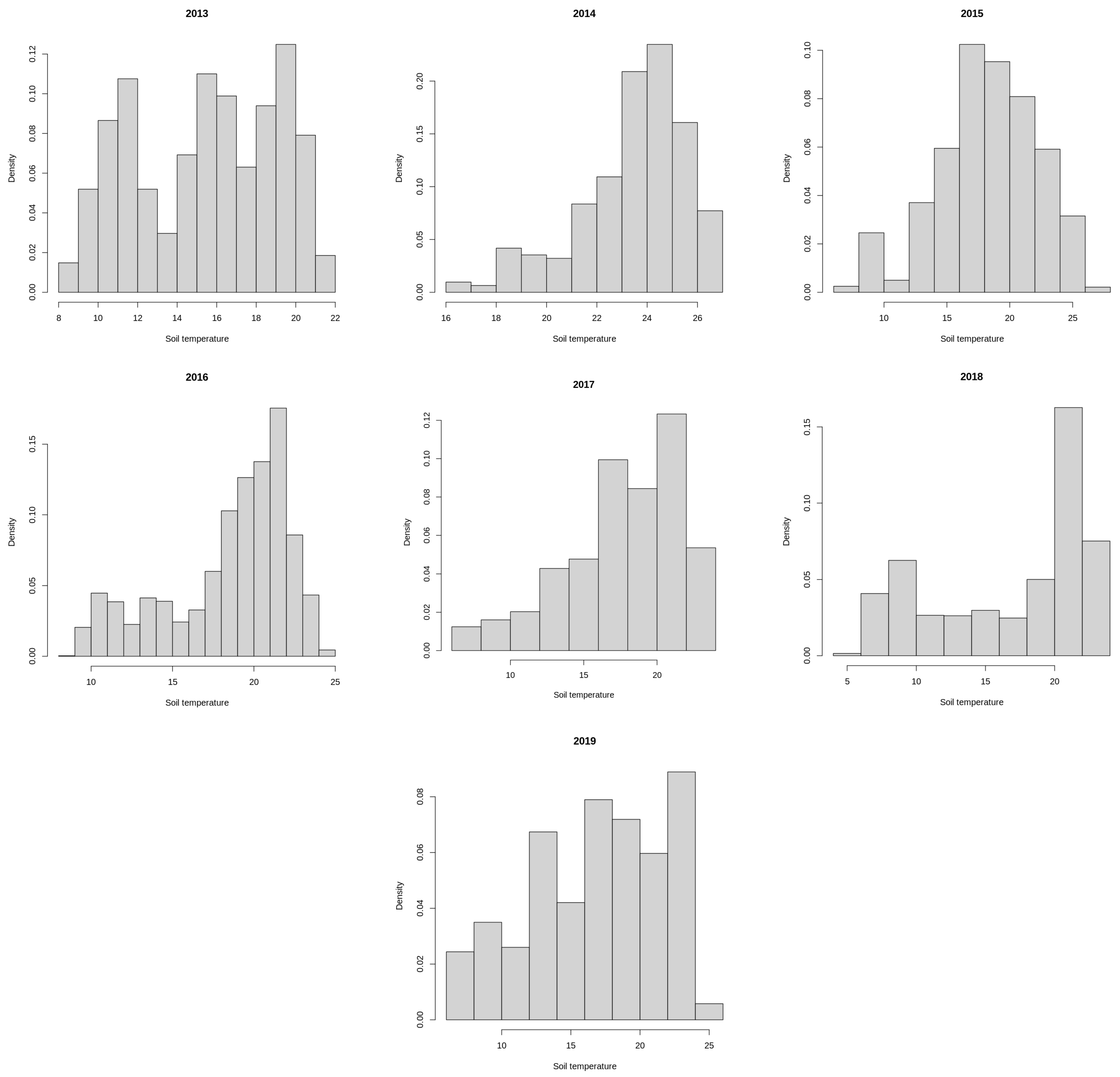
Appendix C
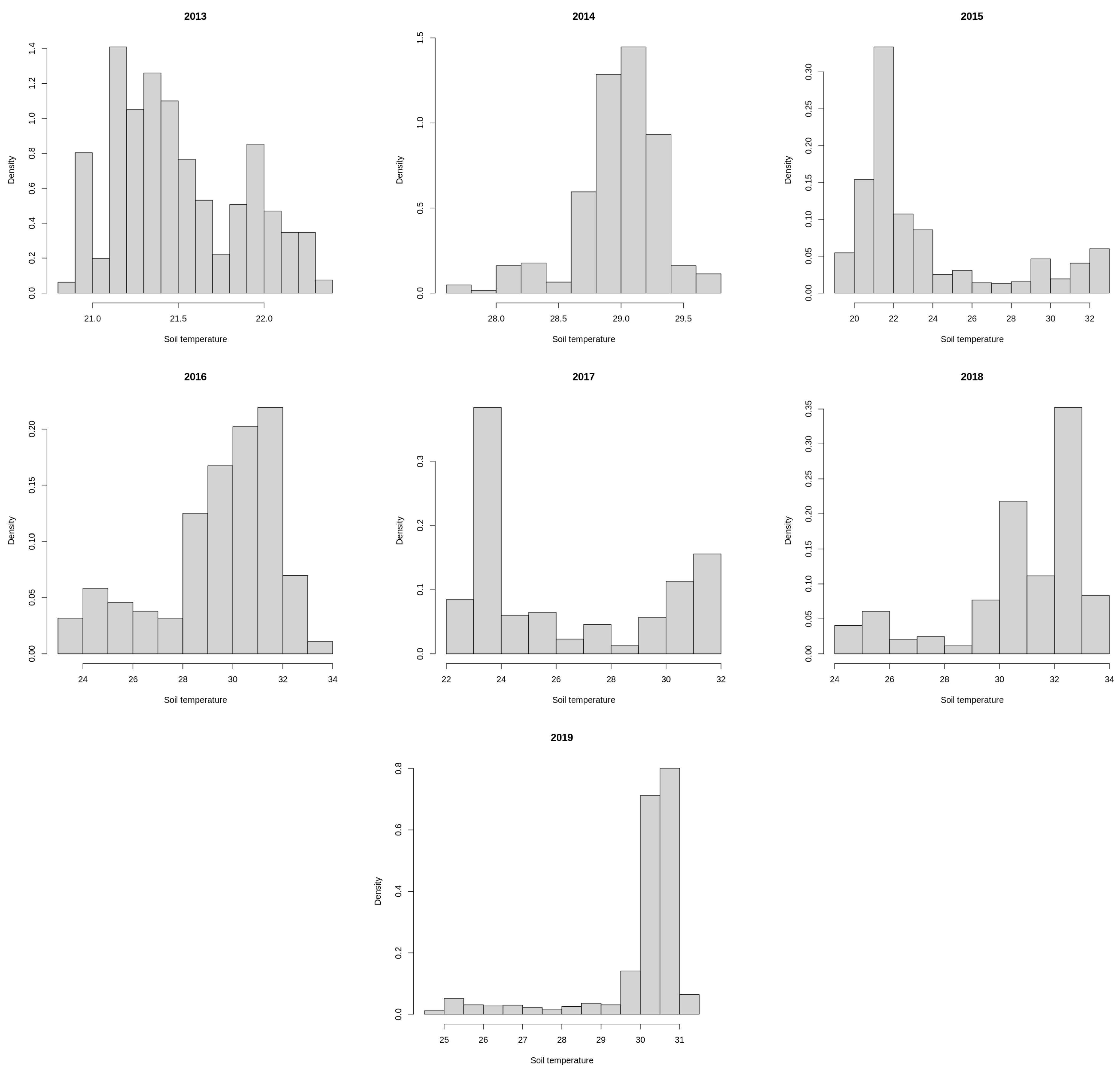
References
- Food and Agriculture Organization of the United Nations (FAO). Drought-Resistant Soils: Optimization of Soil Moisture for Sustainable Plant Production. FAO Land and Water Bulletin 11. Available online: http://www.fao.org/3/a0072e00.htm#Contents (accessed on 2 October 2020).
- Beliaev, V.; Grunwald, L.; Meinel, T.; Schmidt, G.; Bondarovich, A.A.; Scherbinin, V.V.; Ponkina, E.V.; Matsyura, A.V.; Stephan, E.; Illiger, P.; et al. Soil water regime and crop yields in relation to various technologies of cultivation in the Kulunda Steppe (Altai Krai). Vis. Dnipropetr. Univer. Biol. Ecol. 2016, 24, 531–539. [Google Scholar] [CrossRef]
- Belyaev, V.I.; Meinel, T.; Meissner, R.; Grunwald, L.-C.; Volnov, V.V.; Stephan, E.; Sokolova, L.V. Autumn Tillage, Soil Moisture Content, and Crop Yields. In Kulunda: Climate Smart Agriculture; Frühauf, M., Guggenberger, G., Meinel, T., Theesfeld, I., Lentz, S., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 355–366. [Google Scholar] [CrossRef]
- Sadras, V.O.; Villalobos, F.J.; Orgaz, F.; Fereres, E. Effects of Water Stress on Crop Production. In Principles of Agronomy for Sustainable Agriculture; Villalobos, F.J., Fereres, E., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2016; pp. 189–204. [Google Scholar] [CrossRef]
- Cook, F.J.; Orchard, V.A. Relationships between soil respiration and soil moisture. Soil Biol. Biochem. 2008, 40, 1013–1018. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; Allen, R.G., Pereira, L.S., Raes, D., Smith, M., Eds.; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Bondarovich, A.A.; Scherbinin, V.V.; Ponkina, E.V.; Matsyur, A.; Puzanov, A.; Stephan, E.; Balykin, D.; Rupp, H.; Meissner, R. Soil Moisture and Evapotranspiration. In Kulunda: Climate Smart Agriculture; Frühauf, M., Guggenberger, G., Meinel, T., Theesfeld, I., Lentz, S., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 167–181. [Google Scholar] [CrossRef]
- Meissner, R.; Rupp, H.; Bondarovich, A.A.; Rinklebe, J. Soil water management in the Siberian Kulunda—Dry steppe. Mechaniz. Agric. Conser. Res. 2017, 63, 197–201. Available online: https://stumejournals.com/journals/am/2017/5/197 (accessed on 2 October 2020).
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Lisar, S.Y.S.; Motafakkerazad, R.; Mosharraf, M.H.; Rahman, I.M.M. Water Stress in Plants: Causes, Effects and Responses. In Water Stress; Mofizur, R.I., Ed.; Intech Open Limited: London, UK, 2012; pp. 1–16. [Google Scholar] [CrossRef]
- Bavorova, M.; Imamverdiyev, N.; Ponkina, E. Farm-level economics of innovative tillage technologies: The case of no-till in the Altai Krai in Russian Siberia. Envir. Sci. Pollut. Res. 2018, 25, 1016–1032. [Google Scholar] [CrossRef] [PubMed]
- Balykin, D.; Puzanov, A.; Stephan, E.; Meissner, R. Using the Innovative Lysimeter Technology in The German–Russian Research Project “KULUNDA”. In Novel Methods for Monitoring and Managing Land and Water Resources in Siberia; Mueller, L., Sheudshen, A.K., Eulenstein, F., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2016; pp. 387–399. [Google Scholar] [CrossRef]
- Frühauf, M.; Guggenberger, G.; Meinel, T.; Theesfeld, I.; Lentz, S. (Eds.) Kulunda: Climate Smart Agriculture; Springer Nature Switzerland AG: Cham, Switzerland, 2020; Available online: https://www.springer.com/gp/book/9783030159269#otherversion=9783030159276 (accessed on 2 October 2020).
- Nolz, R.; Kammerer, G.; Cepuder, P. Interpretation of lysimeter weighing data affected by wind. Soil Sci. Plant Nutr. 2013, 176, 200–208. [Google Scholar] [CrossRef]
- Peters, A.; Nehls, T.; Schonsky, H.; Wessolek, G. Separating precipitation and evapotranspiration from noise: A new filter routine for high-resolution lysimeter data. Hydrol. Earth Syst. Sci. 2014, 18, 1189–1198. [Google Scholar] [CrossRef]
- Schmidt, A.; Wrzesinsky, T.; Klemm, O. Gap Filling and Quality Assessment of CO2 and Water Vapour Fluxes above an Urban Area with Radial Basis Function Neural Networks. Bound. Layer Meteorol. 2008, 126, 389–413. [Google Scholar] [CrossRef]
- Fleischer, E.; Khashimov, I.; Hölzel, N.; Klemm, O. Carbon exchange fluxes over peatlands in Western Siberia: Possible feedback between land-use change and climate change. Sci. Total Environ. 2016, 545, 424–433. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Merz, C.; Lischeid, G.; Schneider, M. A review on missing hydrological data processing. Environ. Earth Sci. 2018, 77, 47. [Google Scholar] [CrossRef]
- Velikanova, L.I.; Lychenko, N.M. Recovering of data gaps in time series of temperature based on artificial neural networks. Probl. Auto. Contr. 2018, 35, 51–58. [Google Scholar]
- Gold, L.W. Analysis of annual variations in ground temperature at an Ottawa site. Can. J. Earth Sci. 1964, 1, 146–157. [Google Scholar] [CrossRef]
- Lamba, B.S.; Khambete, N.N. Analysis of subsoil temperature at various depths by Fourier technique. Mausam 1991, 42, 269. [Google Scholar]
- Bromba, M.U.A.; Ziegler, H. Application hints for Savitzky-Golay digital smoothing filters. Anal. Chem. 1981, 53, 1583–1586. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agr. For. Meteorol. 2001, 1, 43–69. [Google Scholar] [CrossRef]
- Adeniyi, M.O.; Nymphas, E.F. Estimation of bare soil surface temperature from air temperature and soil depth temperature in a tropical station. Int. J. Nat. Appl. Sci. 2011, 4, 429–437. [Google Scholar]
- Asgharinia, S.; Petroselli, A. A comparison of statistical methods for evaluating missing data of monitoring wells in the Kazeroun Plain, Fars Province, Iran. Groundw. Sustain. Dev. 2020, 10, 100294. [Google Scholar] [CrossRef]
- Astel, A.; Mazerski, J.; Polkowska, Ż.; Namieśnik, J. Application of PCA and time series analysis in studies of precipitation in Tricity (Poland). Adv. Environ. Res. 2004, 8, 337–349. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K. Comparative evaluation of statistical tests for time series analysis: Application to hydrological time series. Hydrol. Sci. J. 2008, 53, 353–366. [Google Scholar] [CrossRef]
- Haselow, L.; Meissner, R.; Rupp, H.; Miegel, K. Evaluation of precipitation measurements methods under field conditions during a summer season: A comparison of the standard rain gauge with a weighable lysimeter and a piezoelectric precipitation sensor. J. Hydrol. 2019, 575, 537–543. [Google Scholar] [CrossRef]
- Abramenkova, I.V.; Kruglov, V.V. Methods of gap recovering in datasets. Soft Syst. 2005, 2, 18–22. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods, 2nd ed.; Springer Nature Switzerland AG: Cham, Switzerland, 2006. [Google Scholar]
- Shapiro-Wilk Normality Test. 2020. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/shapiro.test (accessed on 2 October 2020).
- Augmented Dickey-Fuller Test. 2020. Available online: https://www.rdocumentation.org/packages/aTSA/versions/3.1.2/topics/adf.test (accessed on 2 October 2020).
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 4th ed.; John Wiley: New York, NY, USA, 2008. [Google Scholar]
- Gift, D.; Coulibaly, P. Evaluation of statistical methods for infilling missing values in high-resolution soil moisture data. J. Hydrol. 2011, 400, 95–102. [Google Scholar] [CrossRef]
- Kornelsen, K.; Coulibaly, P. Comparison of Interpolation, Statistical, and Data-Driven Methods for Imputation of Missing Values in a Distributed Soil Moisture Dataset. J. Hydrol. Eng. 2014, 19, 26–43. [Google Scholar] [CrossRef]
| Air Temperature (°C) | Air Humidity (%) | Atmospheric Pressure (hPa) | Solar Radiation (W/m²) | Wind Power (m/sec) | Rainfall (mm) | |
|---|---|---|---|---|---|---|
| Soil temperature (°C) | ||||||
| Arable land (Monolith 1) | 0.51 * | 0.13 * | −0.51 * | −0.04 | −0.19 * | −0.02 |
| Natural steppe vegetation (Monolith 2) | 0.52 * | 0.16 * | −0.50 * | −0.01 | −0.16 * | −0.01 |
| Soil moisture content (Vol.−%) | ||||||
| Arable land (Monolith 1) | 0.01 | −0.04 * | −0.05 * | 0.04 * | 0.002 | −0.007 |
| Natural steppe vegetation (Monolith 2) | −0.11 * | −0.06 * | 0.02 | 0.07 * | 0.08 * | 0.02 |
| Linear Interpolation | Linear Regression | AR (p) | MA (q) | ARMA (p,q) | |
|---|---|---|---|---|---|
| Soil temperature (°C) | |||||
| MBE | 0.03 | 0.04 | 0.03 | −0.06 | −0.02 |
| MAE | 0.39 | 0.43 | 0.27 | 0.45 | 0.19 |
| RMSE | 0.45 | 0.49 | 0.31 | 0.52 | 0.23 |
| MAPE | 2.39% | 2.77% | 1.76% | 2.97% | 1.31% |
| Average optimal window size (hours) | − | 67 | 67 | 68 | 71 |
| Soil moisture content (Vol.%) | |||||
| MBE | 0.01 | −0.003 | 0.04 | −0.01 | 0.01 |
| MAE | 0.10 | 0.12 | 0.11 | 0.35 | 0.08 |
| RMSE | 0.13 | 0.15 | 0.13 | 0.41 | 0.10 |
| MAPE | 0.42% | 0.47% | 0.57% | 2.04% | 0.33% |
| Average optimal window size (hours) | − | 56 | 72 | 59 | 71 |
| Gap-Length Classes | Linear Interpolation | Linear Regression | AR (p) | MA (q) | ARMA (p,q) |
|---|---|---|---|---|---|
| Soil temperature (°C) | |||||
| Short | 0.17 | 0.25 | 0.07 | 0.24 | 0.06 |
| (0.15) | (0.22) | (0.07) | (0.25) | (0.06) | |
| Middle | 0.39 | 0.41 | 0.21 | 0.38 | 0.16 |
| (0.20) | (0.39) | (0.21) | (0.32) | (0.13) | |
| Long | 0.47 | 0.50 | 0.38 | 0.57 | 0.26 |
| (0.28) | (0.33) | (0.30) | (0.40) | (0.19) | |
| Soil moisture content (Vol. %) | |||||
| Short | 0.07 | 0.06 | 0.04 | 0.17 | 0.03 |
| (0.05) | (0.05) | (0.03) | (0.19) | (0.02) | |
| Middle | 0.09 | 0.09 | 0.07 | 0.31 | 0.07 |
| (0.06) | (0.07) | (0.06) | (0.33) | (0.07) | |
| Long | 0.13 | 0.16 | 0.16 | 0.45 | 0.11 |
| (0.08) | (0.15) | (0.21) | (0.42) | (0.10) | |
| N | Linear Interpolation | Linear Regression | AR (p) | MA (q) | ARMA (p,q) | |
|---|---|---|---|---|---|---|
| Soil temperature (°C) | ||||||
| Arable land (Monolith 1) | 93 | 3.16 | 3.41 | 1.95 | 3.29 | 1.62 |
| Grassland (Monolith 2) | 95 | 1.65 | 2.67 | 2.53 | 2.67 | 1.02 |
| Soil moisture content (Vol. %) | ||||||
| Arable land (Monolith 1) | 93 | 0.47 | 0.58 | 0.77 | 3.25 | 0.35 |
| Grassland (Monolith 2) | 95 | 0.37 | 0.44 | 0.34 | 0.90 | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponkina, E.; Illiger, P.; Krotova, O.; Bondarovich, A. Do ARMA Models Provide Better Gap Filling in Time Series of Soil Temperature and Soil Moisture? The Case of Arable Land in the Kulunda Steppe, Russia. Land 2021, 10, 579. https://doi.org/10.3390/land10060579
Ponkina E, Illiger P, Krotova O, Bondarovich A. Do ARMA Models Provide Better Gap Filling in Time Series of Soil Temperature and Soil Moisture? The Case of Arable Land in the Kulunda Steppe, Russia. Land. 2021; 10(6):579. https://doi.org/10.3390/land10060579
Chicago/Turabian StylePonkina, Elena, Patrick Illiger, Olga Krotova, and Andrey Bondarovich. 2021. "Do ARMA Models Provide Better Gap Filling in Time Series of Soil Temperature and Soil Moisture? The Case of Arable Land in the Kulunda Steppe, Russia" Land 10, no. 6: 579. https://doi.org/10.3390/land10060579
APA StylePonkina, E., Illiger, P., Krotova, O., & Bondarovich, A. (2021). Do ARMA Models Provide Better Gap Filling in Time Series of Soil Temperature and Soil Moisture? The Case of Arable Land in the Kulunda Steppe, Russia. Land, 10(6), 579. https://doi.org/10.3390/land10060579






