Commercial Classification and Location Modelling: Integrating Different Perspectives on Commercial Location and Structure
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Case Study
3.2. Data and Variables
3.3. Methodology
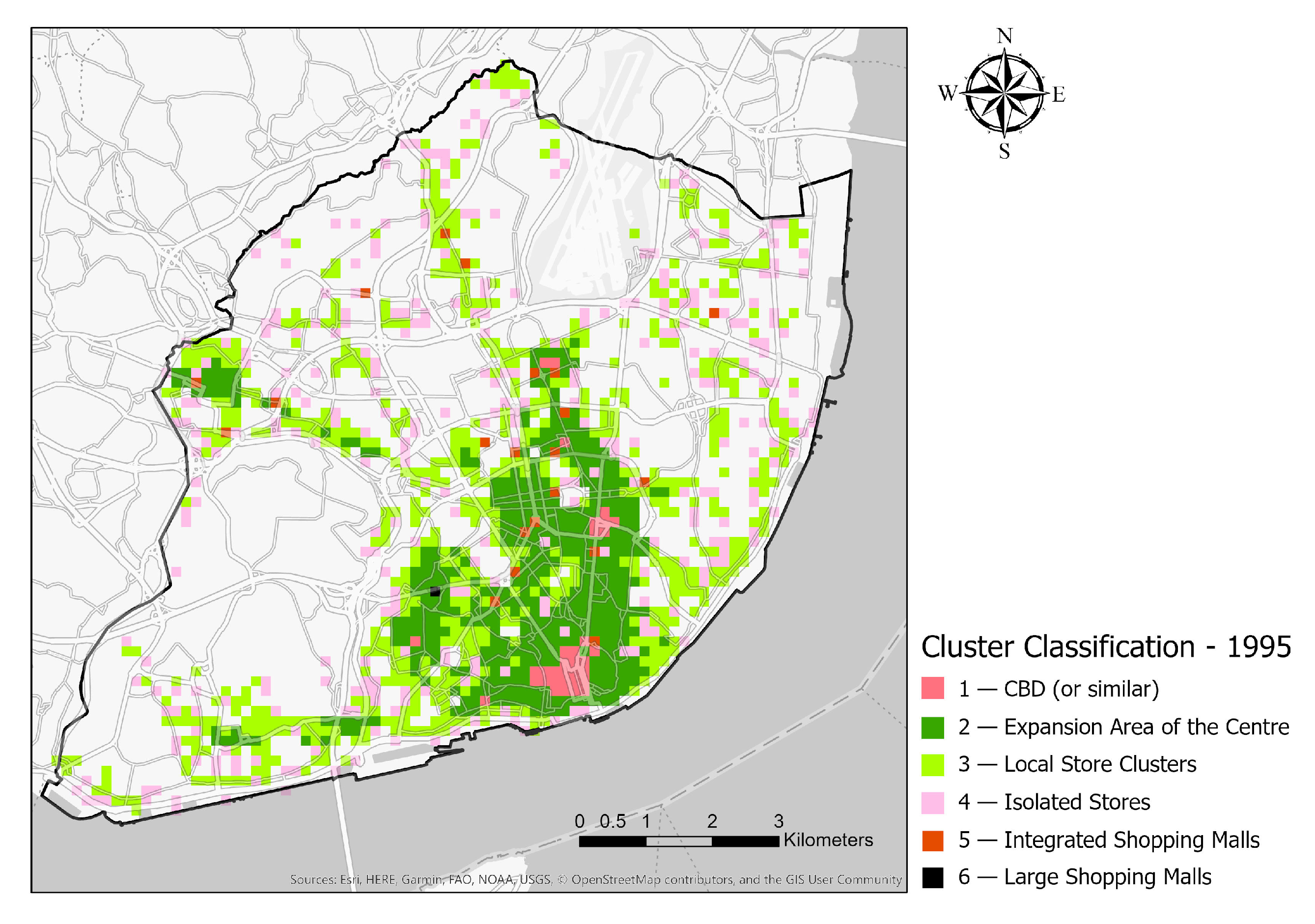
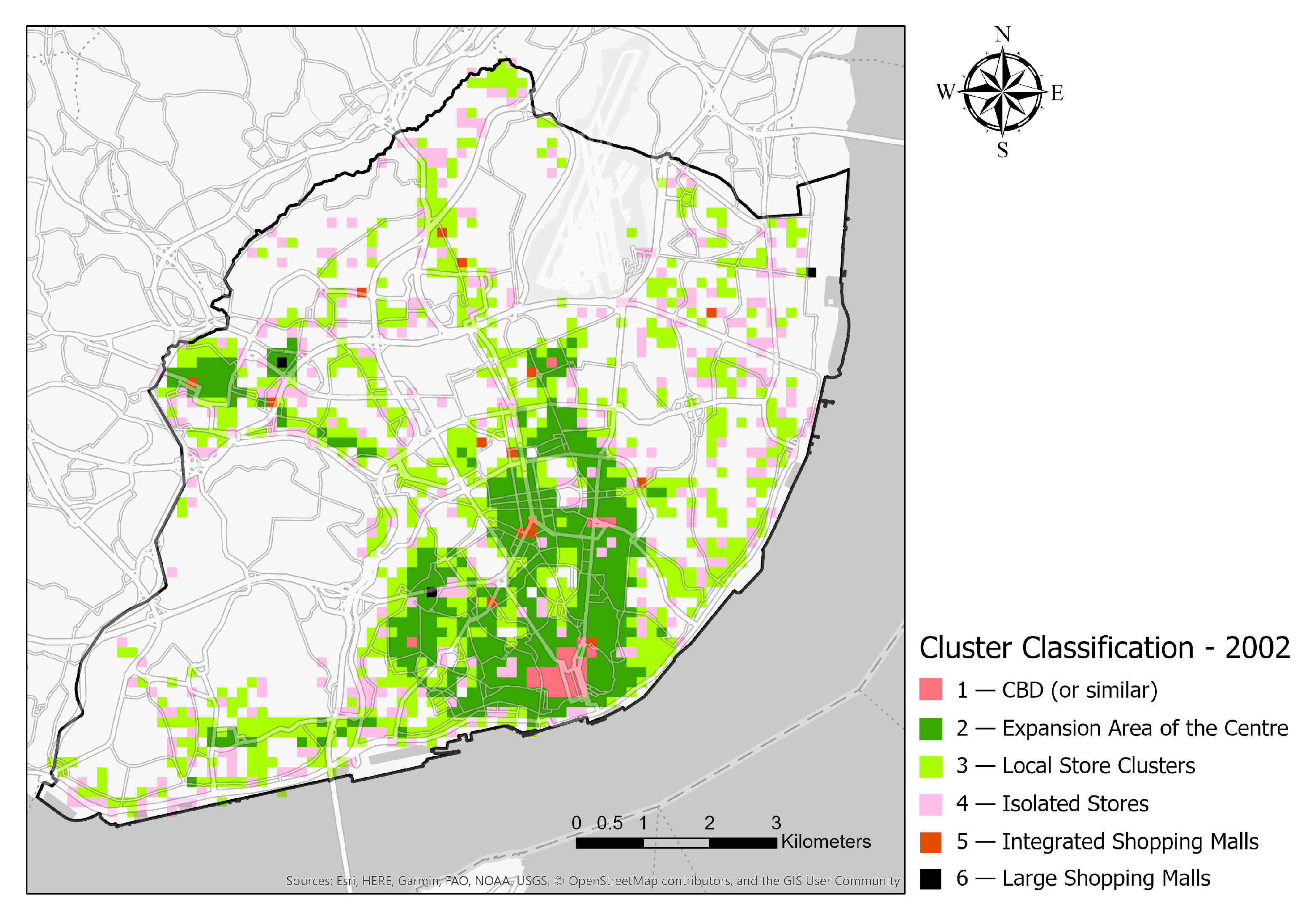
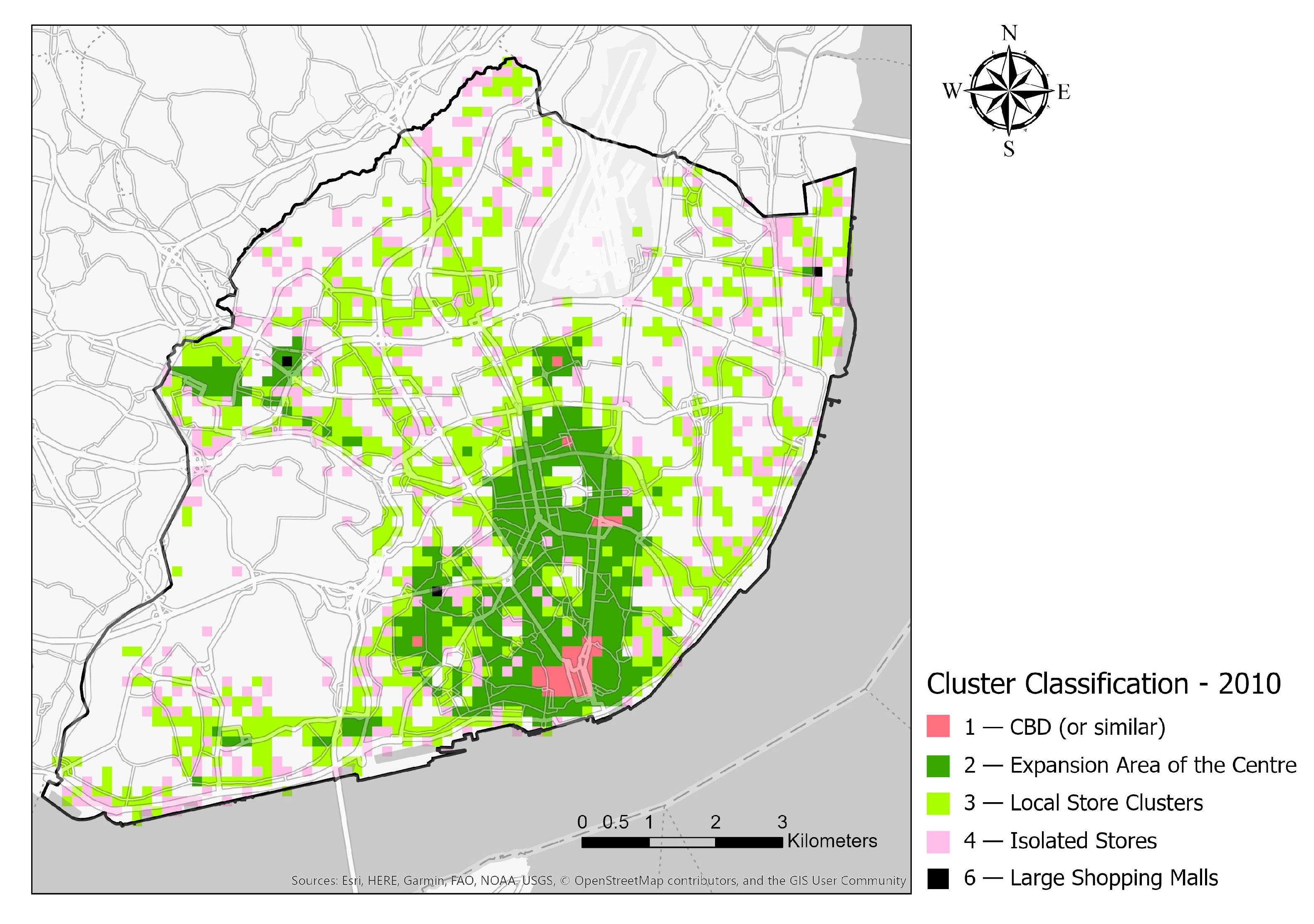
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Cluster | 1—CBD | 2—Expansion Area of the Centre | 3—Local Store Clusters | 4—Isolated Stores | 5—Integrated Shopping Malls | 6—Large Shopping Malls | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | 1995 | 2002 | 2010 | 1995 | 2002 | 2010 | 1995 | 2002 | 2010 | 1995 | 2002 | 2010 | 1995 | 2002 | 1995 | 2002 | 2010 |
| Foodstuffs | 4.62 | 3.79 | 4.00 | 2.56 | 2.43 | 1.91 | 1.35 | 1.27 | 0.94 | 0.35 | 0.26 | 0.21 | 3.43 | 3.07 | 8.00 | 5.67 | 6.67 |
| Personal Use Items | 15.94 | 18.96 | 18.19 | 2.59 | 2.76 | 2.85 | 0.55 | 0.53 | 0.50 | 0.02 | 0.03 | 0.01 | 16.05 | 21.47 | 82.0 | 89.67 | 96.33 |
| Household Items | 5.38 | 5.43 | 3.91 | 1.74 | 1.91 | 1.47 | 0.44 | 0.45 | 0.44 | 0.07 | 0.07 | 0.05 | 5.19 | 5.93 | 30.0 | 26.67 | 16.33 |
| Health and Hygiene | 2.50 | 3.07 | 3.16 | 0.72 | 0.78 | 0.85 | 0.21 | 0.20 | 0.26 | 0.03 | 0.03 | 0.02 | 2.67 | 2.80 | 6.00 | 9.67 | 11.67 |
| Leisure Items | 6.00 | 7.61 | 6.63 | 1.74 | 1.87 | 1.84 | 0.59 | 0.61 | 0.64 | 0.11 | 0.10 | 0.08 | 7.76 | 9.80 | 39.0 | 25.00 | 19.67 |
| Other Items | 7.47 | 8.57 | 9.72 | 2.56 | 2.62 | 2.67 | 0.91 | 0.96 | 0.87 | 0.26 | 0.29 | 0.20 | 6.19 | 7.40 | 29.0 | 25.67 | 25.00 |
| Restaurants | 8.12 | 10.11 | 10.94 | 2.61 | 2.84 | 3.42 | 0.94 | 1.06 | 1.25 | 0.27 | 0.33 | 0.47 | 3.52 | 6.33 | 28.0 | 27.67 | 29.67 |
| Cafes | 3.18 | 3.82 | 4.19 | 1.50 | 1.70 | 2.00 | 0.72 | 0.86 | 1.08 | 0.16 | 0.17 | 0.24 | 3.14 | 4.20 | 11.0 | 13.67 | 13.33 |
| Bars | 1.35 | 1.07 | 1.81 | 0.42 | 0.39 | 0.33 | 0.21 | 0.18 | 0.11 | 0.04 | 0.02 | 0.00 | 0.24 | 0.27 | 0.00 | 0.33 | 0.00 |
References
- Jacobs, J. The Death and Life of Great American Cities; Random House: New York, NY, USA, 1961. [Google Scholar] [CrossRef]
- Jacobs, J. The Economies of Cities; Random House: New York, NY, USA, 1969. [Google Scholar]
- Griffiths, S.; Vaughan, L.; Haklay, M.M.; Emma Jones, C. The Sustainable Suburban High Street: A Review of Themes and Approaches. Geogr. Compass 2008, 2, 1155–1188. [Google Scholar] [CrossRef]
- Sevtsuk, A. Location and Agglomeration: The Distribution of Retail and Food Businesses in Dense Urban Environments. J. Plan. Educ. Res. 2014, 34, 374–393. [Google Scholar] [CrossRef]
- Salgueiro, T.; Erkip, F. Retail Planning and Urban Resilience—An Introduction to the Special Issue. Cities 2014, 36, 107–111. [Google Scholar] [CrossRef]
- Fernandes, J.R.; Cachinho, H.; Ribeiro, C. Comércio Tradicional Em Contexto Urbano: Dinâmicas de Modernização e Políticas Públicas; Universidade do Porto: Porto, Portugal, 2000. [Google Scholar]
- Guimarães, P. O Planeamento Comercial Em Portugal: Os Projectos Especiais de Urbanismo Comercial; Universidade de Lisboa: Lisbon, Portugal, 2015. [Google Scholar]
- Fernandes, J.R.; Chamusca, P. Urban Policies, Planning and Retail Resilience. Cities 2014, 36, 170–177. [Google Scholar] [CrossRef]
- Jacques, T. The State, Small Shops and Hypermarkets: A Public Policy for Retail, France, 1945–1973. Bus. Hist. 2018, 60, 1026–1048. [Google Scholar] [CrossRef]
- Warnaby, G.; Alexander, A.; Medway, D. Town Centre Management in the UK: A Review, Synthesis and Research Agenda. Int. Rev. Retail. Distrib. Consum. Res. 1998, 21, 15–31. [Google Scholar] [CrossRef]
- Cook, I.R. Private Sector Involvement in Urban Governance: The Case of Business Improvement Districts and Town Centre Management Partnerships in England. Geoforum 2009, 40, 930–940. [Google Scholar] [CrossRef]
- Findlay, A.; Sparks, L. Town Centre First, Second, or Not at All? T. Ctry. Plan. 2014, 83, 158–160. [Google Scholar]
- Cao, X. E-Shopping, Spatial Attributes, and Personal Travel. Transp. Res. Rec. J. Transp. Res. Board 2009, 2135, 160–169. [Google Scholar] [CrossRef]
- Oberlo. Global Ecommerce Sales (2019–2024). Available online: https://www.oberlo.com/statistics/global-ecommerce-sales (accessed on 14 February 2021).
- Proudfoot, M.J. City Retail Structure. Econ. Geogr. 1937, 13, 425–428. [Google Scholar] [CrossRef]
- Christaller, W. Central Places in Southern Germany (Translated by Carlisle W. Baskin in 1966); Prentice-Hall: Englewood Cliffs, NJ, USA, 1933. [Google Scholar]
- Guy, C.M. Classifications Centres: Some Methodological Issues. GeoJournal 1998, 45, 255–264. [Google Scholar] [CrossRef]
- Araldi, A.; Fusco, G. Retail Fabric Assessment: Describing Retail Patterns within Urban Space. Cities 2019, 85, 51–62. [Google Scholar] [CrossRef]
- Maoh, H.; Kanaroglou, P. Geographic Clustering of Firms and Urban Form: A Multivariate Analysis. J. Geogr. Syst. 2007, 9, 29–52. [Google Scholar] [CrossRef]
- Elgar, I.; Farooq, B.; Miller, E.J. Modeling Location Decisions of Office Firms: Introducing Anchor Points and Constructing Choice Sets in the Model System. Transp. Res. Rec. 2009, 2133, 56–63. [Google Scholar] [CrossRef]
- Elgar, I.; Farooq, B.; Miller, E.J. Simulations of Firm Location Decisions: Replicating Office Location Choices in the Greater Toronto Area. J. Choice Model. 2015, 17, 39–51. [Google Scholar] [CrossRef]
- Berry, B.J.L. Commercial Structure and Commercial Blight; University of Chicago Press: Chicago, IL, USA, 1963. [Google Scholar]
- Davies, R.L.; Bennison, D.J. Retailing in the City Centre: The Characters of Shopping Streets. Tijdschr. voor Econ. en Soc. Geogr. 1978, 69, 270–285. [Google Scholar] [CrossRef]
- Brown, S. Retail Location: The Post Hierarchical Challenge. Int. Rev. Retail. Distrib. Consum. Res. 1991, 1, 367–381. [Google Scholar] [CrossRef]
- Hotelling, H. Stability in Competition. Econom. J. 1929, 39, 41–57. [Google Scholar] [CrossRef]
- Eaton, B.C.; Lipsey, R.G. The Principle of Minimum Differentiation Reconsidered: Some New Developments in the Theory of Spatial Competition. Rev. Econ. Stud. 1975, 42, 27. [Google Scholar] [CrossRef]
- D’Aspremont, C.; Gabszewicz, J.J.; Thisse, J.-F. On Hotelling’s “Stability in Competition”. Econometrica 1979, 47, 1145–1150. [Google Scholar] [CrossRef]
- McLafferty, S.L.; Ghosh, A. Multipurpose Shopping and the Location of Retail Firms. Geogr. Anal. 1986, 18, 215–226. [Google Scholar] [CrossRef]
- Krugman, P. Increasing Returns and Economic Geography. J. Polit. Econ. 1991, 99, 483. [Google Scholar] [CrossRef]
- Fujita, M.; Krugman, P.; Mori, T. On the Evolution of Hierarchical Urban Systems. Eur. Econ. Rev. 1999, 43, 209–251. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Câmara Municipal de Lisboa. Geodados—Recenseamento Comercial. Available online: https://geodados.cm-lisboa.pt/datasets/6c40669f14c941779b48e2861767ead4_13 (accessed on 11 September 2020).
- Cachinho, H. Consumactor: Da Condição Do Indivíduo Na Cidade Pós-Moderna. Finisterra 2006, 41, 33–56. [Google Scholar] [CrossRef]
- Cachinho, H. Urban Retail Dynamics. From Shopping Spaces to Consumer Places. In Retail Planning for the Resilient City; Salgueiro, T., Cachinho, H., Eds.; CEG: Lisbon, Portugal, 2011; pp. 147–168. [Google Scholar]
- Sequera, J.; Nofre, J. Touristification, Transnational Gentrification and Urban Change in Lisbon: The Neighbourhood of Alfama. Urban Stud. 2019, 57, 3169–3189. [Google Scholar] [CrossRef]
- Reigadinha, T.; Godinho, P.; Dias, J. Portuguese Food Retailers—Exploring Three Classic Theories of Retail Location. J. Retail. Consum. Serv. 2017, 34, 102–116. [Google Scholar] [CrossRef]
- Carpio-Pinedo, J.; Gutiérrez, J. Consumption and Symbolic Capital in the Metropolitan Space: Integrating ‘Old’ Retail Data Sources with Social Big Data. Cities 2020, 106, 102859. [Google Scholar] [CrossRef]
- Ravulaparthy, S.K.; Goulias, K.G. Characterizing the Composition of Economic Activities in Central Locations. Transp. Res. Rec. J. Transp. Res. Board 2014, 2564, 106–117. [Google Scholar] [CrossRef]
- Berry, B.J. Geography of Market Centres and Retail Distribution; Prentice-Hall: London, UK, 1967. [Google Scholar]
- Berry, B.J.L.; Garrison, W.L. A Note on Central Place Theory and the Range of a Good. Econ. Geogr. 1958, 34, 304. [Google Scholar] [CrossRef]
- Berry, B.J.L.; Garrison, W.L. The Functional Bases of the Central Place Hierarchy. Econ. Geogr. 1958, 34, 145. [Google Scholar] [CrossRef]
- Meir, A.; Marcus, M. A Commercial-Blight Perspective on Metropolitan Commercial Structure. Can. Geogr. Le Géographe Can. 1983, 27, 370–375. [Google Scholar] [CrossRef]
- Gaspar, J. A Dinâmica Funcional do Centro de Lisboa; Livros Horizonte: Lisboa, Portugal, 1985. [Google Scholar]
- Thurstain-Goodwin, M.; Unwin, D. Defining and Delineating the Central Areas of Towns for Statistical Monitoring Using Continuous Surface Representations. Trans. GIS 2000, 4, 305–317. [Google Scholar] [CrossRef]
- Batty, M.; Besussi, E.; Maat, K.; Harts, J.J. Representing Multifunctional Cities: Density and Diversity in Space and Time. Built Environ. 2004, 30, 324–337. [Google Scholar] [CrossRef]
- Porta, S.; Strano, E.; Iacoviello, V.; Messora, R.; Latora, V.; Cardillo, A.; Wang, F.; Scellato, S. Street Centrality and Densities of Retail and Services in Bologna, Italy. Environ. Plan. B Plan. Des. 2009, 36, 450–465. [Google Scholar] [CrossRef]
- Piovani, D.; Molinero, C.; Wilson, A. Urban Retail Location: Insights from Percolation Theory and Spatial Interaction Modeling. PLoS ONE 2017, 12, e0185787. [Google Scholar] [CrossRef] [PubMed]
- Zachariadis, V.; Vargas-ruiz, C.; Serras, J.; Ferguson, P.; Ferguson, P. Decoding Retail Location: A Primer for the Age of Big Data and Social Media. In Proceedings of the CUPUM 2015: The 14th International Conference on Computers in Urban Planning and Urban Management, Cambridge, MA, USA, 7–10 July 2015. [Google Scholar] [CrossRef]
- Saraiva, M.; Marques, T.S.; Ribeiro, D.; Ribeiro, P. Multi-Diversity Clusters of Commercial Activities in the City of Porto: How Neighbourhood Concentrations Shape the Municipal Hierarchy. In La Geografía de las Redes Económicas Y la Geografía Económica en Red; Logroño, M.P.A., Marques, T.S., Santos, H., Eds.; Faculdade de Letras da Universidade do Porto, Asociación de Geógrafos Españoles: Porto, Portugal, 2020; pp. 209–217. [Google Scholar] [CrossRef]
- Nelson, P. Information and Consumer Behavior. J. Polit. Econ. 1970, 78, 311–329. [Google Scholar] [CrossRef]
- Zhen, F.; Du, X.; Cao, J.; Mokhtarian, P.L. The Association between Spatial Attributes and E-Shopping in the Shopping Process for Search Goods and Experience Goods: Evidence from Nanjing. J. Transp. Geogr. 2018, 66, 291–299. [Google Scholar] [CrossRef]
- Schmid, B.; Axhausen, K.W. In-Store or Online Shopping of Search and Experience Goods: A Hybrid Choice Approach. J. Choice Model. 2018, 31, 156–180. [Google Scholar] [CrossRef]
- Jensen, P. A Network-Based Prediction of Retail Stores Commercial Categories and Optimal Locations. Phys. Rev. E 2006, 74, 035101. [Google Scholar] [CrossRef]
- Câmara Municipal de Lisboa. Recenseamento Dos Estabelecimentos de Comércio a Retalho e Restauração e Bebidas Da Cidade de Lisboa; CML: Lisboa, Portugal, 2009. [Google Scholar]
- Institututo Nacional de Estatística. Classificação Portuguesa de Atividades Económicas. Available online: http://www.sicae.pt/Legislacao.aspx (accessed on 17 August 2020).
- Direção Geral do Território. Carta Administrativa Oficial de Portugal. Available online: https://www.dgterritorio.gov.pt/cartografia/cartografia-tematica/caop (accessed on 14 February 2021).
- Institututo Nacional de Estatística. Página de Download de Informação Geográfica. Available online: http://mapas.ine.pt/download/index2011.phtml (accessed on 1 August 2020).
- Oliveira, V.; Pinho, P. Lisbon. Cities 2010, 27, 405–419. [Google Scholar] [CrossRef]
- Rubalcaba, L.; Gallego, J.; Gallo, M.T.; Garrido, R. Business Services Location and Market Factors in Major European Cities. Cities 2013, 31, 258–266. [Google Scholar] [CrossRef]
- Cachinho, H. O Comércio a Retalho Na Cidade de Lisboa. Reestruturacão Económica e Dinâmicas Territoriais. Finisterra 1994, 29, 119–144. [Google Scholar] [CrossRef]
- Salgueiro, T.B. Lisboa, Periferia e Centralidades; Celta: Oeiras, Portugal, 2001. [Google Scholar]
- Openshaw, S. The Modifiable Areal Unit Problem; Geo Books: Norwich, UK, 1984. [Google Scholar] [CrossRef]
- ArcGIS. Point Density (Spatial Analyst). Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/point-density.htm (accessed on 14 February 2021).
- Jost, L. Entropy and Diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Simpson, E.H. Measurement of Diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Ai, N.; Zheng, J.; Chen, X.; Kawamura, K. Neighborhood-Specific Traffic Impact Analysis of Restaurant Meal Delivery Trips: Planning Implications and Case Studies in Chicago. J. Urban Plan. Dev. 2021, 147. [Google Scholar] [CrossRef]
- Anselin, L. Under the Hood Issues in the Specification and Interpretation of Spatial Regression Models. Agric. Econ. 2002, 27, 247–267. [Google Scholar] [CrossRef]
- Anselin, L. Cluster Analysis. Available online: https://geodacenter.github.io/workbook/7bk_clusters_1a/lab7b.html#fn1 (accessed on 20 December 2020).
- Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Anselin, L. Exploring Spatial Data with GeoDa: A Workbook; University of Illinois, Urbana-Champaign: Urbana, IL, USA, 2005. [Google Scholar]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Li, X.; Anselin, L.; Koschinsky, J. GeoDa Web—Enhancing Web-Based Mapping with Spatial Analytics. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Mariani, S.; Wardono; Masrukan; Fauzi, F. The Arcview and GeoDa Application in Optimization of Spatial Regression Estimate. J. Theor. Appl. Inf. Technol. 2017, 95, 1286–1299. [Google Scholar]
- Purwaningsih, T.; Cintami, A. Analysis of Factors Affecting the Area of Forest and Land Fires in Indonesia Uses Spatial Regression Geoda and SaTScan. J. Inform. 2019, 12, 58. [Google Scholar] [CrossRef][Green Version]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Cachinho, H. Consumerscapes and the Resilience Assessment of Urban Retail Systems. Cities 2014, 36, 131–144. [Google Scholar] [CrossRef]
- Alho, A.R.; de Abreu Silva, J. Utilizing Urban Form Characteristics in Urban Logistics Analysis: A Case Study in Lisbon, Portugal. J. Transp. Geogr. 2015, 42, 57–71. [Google Scholar] [CrossRef]
- Macário, R. Modeling for Public Policies Inducement of Urban Freight Business Development. In Freight Transport Modelling; Ben-Akiva, M., Meersman, H., Van de Voorde, E., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2013; pp. 405–432. [Google Scholar] [CrossRef]
- Cócola-Gant, A. Tourism and Commercial Gentrification. In Proceedings of the RC21 2015 Conference, Urbino, Italy, 27–29 August 2015. [Google Scholar]
- Larraz, B.; García-Gómez, E. Depopulation of Toledo’s Historical Centre in Spain? Challenge for Local Politics in World Heritage Cities. Cities 2020, 105, 102841. [Google Scholar] [CrossRef]
- Jover, J.; Díaz-Parra, I. Gentrification, Transnational Gentrification and Touristification in Seville, Spain. Urban Stud. 2020, 57, 3044–3059. [Google Scholar] [CrossRef]
- Miller, E.J. Integrated Urban Modeling: Past, Present, and Future. J. Transp. Land Use 2018, 11, 387–399. [Google Scholar] [CrossRef]
| Variable | Description | Mean | |||
|---|---|---|---|---|---|
| 1995 | 2002 | 2010 | |||
| DSS | Density of Commercial Establishments—High Street | number of establishments per block | 8.79 | 8.69 | 7.87 |
| D.S.M. | Density of Commercial Establishments—Shopping Malls | number of establishments per block | 1.10 | 1.62 | 1.43 |
| DVT | Diversity (Variety) | number of categories per block | 3.99 | 3.76 | 3.50 |
| DVC | Diversity (Concentration) | Simpson index | 0.45 | 0.46 | 0.48 |
| CL1 | Clustering (1st order) | average number of establishments in 1st order neighbouring blocks | 8.33 | 8.62 | 7.84 |
| CL2 | Clustering (2nd order) | average number of establishments in 2nd order neighbouring blocks | 7.45 | 7.63 | 6.92 |
| N | 1420 | 1492 | 1721 | ||
| Cluster Variable | 1—CBD | 2—Expansion Area of the Centre | 3—Local Store Clusters | 4—Isolated Stores | 5—Integrated Shopping Malls | 6—Large Shopping Malls |
|---|---|---|---|---|---|---|
| DSS | 53.21 | 15.75 | 5.57 | 1.21 | 11.19 | 6.00 |
| DSM | 1.35 | 0.67 | 0.33 | 0.09 | 37.00 | 227.00 |
| DVT | 8.26 | 6.23 | 3.67 | 1.03 | 7.95 | 8.00 |
| DVS | 0.20 | 0.23 | 0.34 | 0.99 | 0.20 | 0.20 |
| CL1 | 39.59 | 14.86 | 4.97 | 3.00 | 9.90 | 3.75 |
| CL2 | 25.81 | 13.43 | 4.48 | 3.51 | 7.67 | 7.88 |
| N | 34 | 418 | 618 | 328 | 21 | 1 |
| Cluster Variable | 1—CBD | 2—Expansion Area of the Centre | 3—Local Store Clusters | 4—Isolated Stores | 5—Integrated Shopping Malls | 6—Large Shopping Malls |
|---|---|---|---|---|---|---|
| DSS | 59.14 | 16.25 | 5.59 | 1.22 | 7.33 | 0.33 |
| DSM | 3.29 | 1.05 | 0.54 | 0.08 | 53.93 | 223.67 |
| DVT | 7.96 | 6.11 | 3.51 | 0.97 | 3.20 | 0.33 |
| DVS | 0.21 | 0.22 | 0.35 | 0.99 | 0.21 | 0.23 |
| CL1 | 46.27 | 15.84 | 4.99 | 3.51 | 11.74 | 3.83 |
| CL2 | 31.55 | 13.54 | 4.59 | 4.24 | 7.84 | 3.25 |
| N | 28 | 430 | 680 | 336 | 15 | 3 |
| Cluster Variable | 1—CBD | 2—Expansion Area of the Centre | 3—Local Store Clusters | 4—Isolated Stores | 6—Large Shopping Malls |
|---|---|---|---|---|---|
| DSS | 57.16 | 15.22 | 5.32 | 1.20 | 0.67 |
| DSM | 5.38 | 2.14 | 0.77 | 0.09 | 218.00 |
| DVT | 8.00 | 5.76 | 3.38 | 0.94 | 0.67 |
| DVS | 0.22 | 0.23 | 0.36 | 1.00 | 0.25 |
| CL1 | 45.05 | 15.76 | 4.47 | 3.11 | 5.71 |
| CL2 | 30.67 | 13.85 | 4.06 | 3.29 | 3.60 |
| N | 32 | 449 | 824 | 413 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colaço, R.; de Abreu e Silva, J. Commercial Classification and Location Modelling: Integrating Different Perspectives on Commercial Location and Structure. Land 2021, 10, 567. https://doi.org/10.3390/land10060567
Colaço R, de Abreu e Silva J. Commercial Classification and Location Modelling: Integrating Different Perspectives on Commercial Location and Structure. Land. 2021; 10(6):567. https://doi.org/10.3390/land10060567
Chicago/Turabian StyleColaço, Rui, and João de Abreu e Silva. 2021. "Commercial Classification and Location Modelling: Integrating Different Perspectives on Commercial Location and Structure" Land 10, no. 6: 567. https://doi.org/10.3390/land10060567
APA StyleColaço, R., & de Abreu e Silva, J. (2021). Commercial Classification and Location Modelling: Integrating Different Perspectives on Commercial Location and Structure. Land, 10(6), 567. https://doi.org/10.3390/land10060567







